Amalgams of matroids, fibre products
and tropical graph correspondences
Abstract.
We prove that the proper amalgam of matroids and along their common restriction exists if and only if the tropical fibre product of Bergman fans is positive. We introduce tropical correspondences between Bergman fans as tropical subcycles in their product, similar to correspondences in algebraic geometry, and define a “graph correspondence” of the map of lattices. We prove that graph construction is a functor for the “covering” maps of lattices, exploiting a generalization of Bergman fan which we call a “Flag fan”.
1. Introduction
One of the features of matroid theory is that it makes use of numerous inductive constructions such as deletions, contractions and extensions (see, for example, [Oxl11], Chapter 7). In this light, various attempts to “glue” matroids together were studied for a long time. The most basic construction having its roots in graphic matroids is the parallel connection, which sometimes plays even bigger role than the direct sum ([SW23]). Generalizations of parallel connection, called amalgams, were studied in the 1970s and 1980s ([BK88], [PT82]). Among those, the free amalgam stands out as the one satisfying a certain universal property in the category of matroids with morphisms being what is called weak maps. A slightly stronger notion of the free amalgam, the proper amalgam, is naturally called “generalized parallel connection” in some cases.
It turns out, though, that in general amalgamation is complicated — for a given pair of matroids that we try to glue, there may be no free amalgam, or the free amalgam may not be proper, or no amalgams may exist at all. Several criteria guaranteeing the existence of the proper amalgam were established ([Oxl11], Section 11.4), but even the weakest of them is not a necessary condition. Amalgams continue to be investigated — for example, the so-called sticky matroid conjecture was apparently resolved recently ([Bon09], [Shi21]).
Over the last thirty years, tropical geometry, initiated as a combinatorial tool of algebraic geometry inspired by the formalism of toric geometry, has established many connections to matroid theory. From the tropical point of view, a Bergman fan — the tropical variety corresponding to a loopless matroid — can be considered an analog of the smooth tangent cone. Bergman fans are widely used in many of the latest developments ([AHK15], [MRS19], [BEST]).
In particular, in the beginning of the 2010s, a well-behaved intersection theory of the tropical cycles in Bergman fans was developed simultaneously by Allermann, Esterov, Francois, Rau, and Shaw ([Est11], [Sha13], [AR09], [FR12]). This intersection theory possesses many similarities with the intersection theory in algebraic geometry, going as far as the projection formula. This machinery was sufficient to define a tropical subcycle in the product of Bergman fans called the tropical fibre product ([FH13], [Cav+16]), which the authors used to study moduli spaces of curves. They considered the case when the support of the tropical fibre product equals the set-theoretic fibre product of the supports of the factors, finding several sufficient conditions on matroids for this case to occur.
As it turns out, though, the tropical fibre product is worth investigating in wider generality. This becomes evident when considering a simple Example 2.22 (2).
Theorem A (4.1).
The tropical fibre product equals the Bergman fan of the proper amalgam if the proper amalgam exists, and has cones with negative weights otherwise.
Thus, unlike all criteria for the existence of the proper amalgam known to us, Theorem 4.1 is an equivalence. It is also constructive and, moreover, algorithmic in a certain sense, as shown in Section 3.
With tropical counterpart of the proper amalgam in our hands, we seek a categorical justification of its name — the fibre product. As it is justly pointed out in [FH13], the tropical fibre product is not a categorical pullback even in the underlying category of sets. Thus, we aim to extend the notion of morphism of tropical fans to something that does not have to be a map between their supports. This leads naturally to the definition of the tropical correspondences category (Definition 5.4). It formalizes the intuition behind “not exactly graphs” inspired by Example 5.1.
The whole category of tropical correspondences between Bergman fans is too unwieldy. In particular, since we allow the cones of the cycles to have negative weights, we cannot even require correspondences with negative weights to be irreducible. Thus, in Sections 3 and 5 we develop a subcategory of “covering graph correspondences” (Definition 5.6, Lemma 5.8) which is convenient from the combinatorial point of view. These covering graph correspondences between Bergman fans contain strictly more information than weak maps between the groundsets (Remark 5.17).
Theorem B (5.13).
is a functor from the category of covering lattice maps of flats of simple matroids with the usual composition to the category of tropical correspondences between Bergman fans.
The paper is organized as follows. In Section 2, we recall necessary notions from matroid theory and tropical geometry, including the tropical fibre product from [FH13] — Definition 2.21. In Section 3, we introduce the generalization of Bergman fan called a Flag fan and observe its nice behavior with respect to Weil divisors of rational functions generalizing characteristic functions of modular cuts (Lemma 3.7). Section 4 is solely devoted to the proof of Theorem 4.1. In Section 5, we introduce and study tropical correspondences, construct covering graph correspondences, establish their useful combinatorial description (Theorem 5.12), and verify the functoriality (Theorem 5.13). We conclude with an open Question 5.19. Resolving it positively will achieve the best scenario still plausible — that there is a full forgetful functor from the reasonable subcategory of tropical correspondences onto the category of weak maps.
I am grateful to Evgeniya Akhmedova, Alexander Esterov, Tali Kaufman, Anna–Maria Raukh, and Kris Shaw for useful discussions. I want to thank Alexander Zinov for helping me with software calculations which often preceded proofs.
2. Preliminaries
2.1. Matroid theory
In this subsection we recall the necessary notions from the combinatorial matroid theory.
Definition 2.1.
A matroid on the groundset is a collection of subsets called flats with the following properties:
-
•
;
-
•
;
-
•
, where is read “ covers ” and means .
A matroid is called loopless if . It is called simple if, additionally, all flats covering are one-element subsets (in this case all one-element subsets are flats). All matroids in this paper are assumed loopless. A restriction of the matroid on the groundset onto the subset , denoted by , is an image of the map given by . An extension of onto is a matroid on such that . A contraction of is a matroid denoted by on the groundset with flats for .
There is a large number of equivalent definitions of a matroid, usually called cryptomorphisms. Many of them can be found in [Oxl11], Chapter 1. It can be shown that forms a ranked poset with respect to the partial order given by set inclusion. Since intersection of flats is also a flat, there exists an operator of closure , where . Moreover, for each pair of flats and there exists a unique minimal element such that , called join and denoted by . The rank function can be extended from to the whole by defining
A subset is called independent if . The rank of is defined to be . The hyperplanes are flats of rank .
Throughout the paper, we sometimes describe matroids via pictures instead of listing their flats. The points correspond to the elements of the groundset, while lines and planes correspond to flats. Those are instances of matroids representable over drawn in the projectivization of the vector space of representation (more on that in [Oxl11], Chapter 1).
Lemma 2.2.
The difference of ranks can only decrease when adding elements. More precisely, if , then
Proof.
We can add elements of one by one, so take any and let us prove that
The rank function can only increase by 1 when adding an element ([Oxl11], Section 1), and this happens exactly when this element does not belong to the closure of the set, so what we need follows from the implication
which is true, since . ∎
Definition 2.3.
Consider sets and matroids on , on , on such that . A matroid on is called an amalgam of and along if and .
An amalgam is called free if for every amalgam and every independent set in it, is also independent in .
An amalgam is called proper if, for every the following holds:
Both free and proper amalgams are unique, if they exist. This is not always the case, though: sometimes there is no free amalgam, sometimes no amalgams at all (see [Oxl11], Section 11.4). It can be shown that the proper amalgam is always free ([Oxl11], Propositions 11.4.2 and 11.4.3).
Remark 2.4.
The free amalgam is not always proper, though, as shown by the following
Example 2.5.
For as shown on Figure 1 is the only amalgam and hence free, but
Definition 2.6.
A map between groundsets of matroids and is called a strong map if for . A strong map is called an embedding if .
A map between groundsets of matroids and is called a weak map if for any . Equivalently ([Oxl11], Proposition 7.3.11), is independent in for any independent set of . We will sometimes write instead of .
It can be shown that strong maps are also weak maps ([Oxl11], Corollary 7.3.12). Note that the free amalgam has the following universal property in the category of matroids with weak maps. If and are embeddings, then
| (2.1) |
It is not, strictly speaking, a universal property of the pushout, because allowing to be any weak maps may lead to rank of dropping, and then may become “freer” than any amalgam.
Definition 2.7.
A pair of flats is called a modular pair if
The flat is called modular if it forms a modular pair with any .
Definition 2.8.
A subset of flats of on groundset is called a modular cut if it satisfies the following properties:
-
•
;
-
•
;
-
•
if are a modular pair, then .
2.2. Tropical geometry
In this subsection we recall the tropical counterpart of matroid theory involving the techniques needed for our results.
Definition 2.9.
A (reduced or projective) Bergman fan of matroid on groundset is a collection of maximal cones and their faces in for each flag of flats consisting of with defined as
where stands for the image in of the characteristic function of in , i.e., if and otherwise.
A non-reduced or affine Bergman fan, denoted by , is the preimage of the projective Bergman fan in .
An affine Bergman fan is an instance of the main object we work with in this paper.
Definition 2.10 ([AR09], Definition 2.6).
A -dimensional tropical fan in is a collection of cones of dimension , generated by the vectors from the lattice , with integer weights such that the balancing condition holds for each -dimensional face :
where is the smallest subspace of containing cone , and is a normal vector — the generator of the one-dimensional -module chosen such that it “looks inside” . The support of the fan , denoted by , is the set of points in that belong to some cone.
In all our considerations all the cones are going to be simplicial. Moreover, the only generator of cone missing from the generators of is always going to map to when taking quotient by — not some multiple of , which means that this generator can be taken as a representative in all calculations.
The maximal cones of the affine Bergman fan are the following:
and the weights are all equal to 1 (slightly abusing notations, we now mean by ’s actual characteristic vectors in , not their classes in the quotient ). Thus, one can check that the balancing condition for any -dimensional cone containing the all-ones or minus all-ones boils down to the third axiom (the covering axiom) of Definition 2.1; and the balancing condition for a -dimensional cone not containing the all-ones or minus all-ones is trivially satisfied, as any such cone is contained in just two -dimensional cones which cancel each other out in the balancing condition.
It is convenient to consider the refinements of tropical fans ([AR09], Definition 2.8), which are essentially the tropical fans with the same support and the same weight for the interior points of maximal cones. This leads to
Definition 2.11 ([AR09], Definitions 2.12, 2.15).
A tropical cycle is a class of equivalence of tropical fans with respect to equivalence relation “to have a common refinement”. A tropical subcycle of the tropical cycle is a tropical cycle whose support is a subset: .
Apart from the very general Definition 5.4, all the cones in the subcycles will be the faces of the simplicial maximal cones of the fans they lie in.
Considering tropical cycles allows to define new tropical cycles without explicitly listing all the cones, but describing the support and the weights of the interior points of the maximal cones instead. This is useful to us when introducing products and stars.
Definition 2.12.
The product of tropical fans and is a tropical cycle such that , and the weight of is equal to the product of and for interior points of the maximal cones of .
It is known that the tropical cycles and coincide ([FR12], Lemma 2.1), but the fans are different — is a refinement of (see also Lemma 3.10).
Definition 2.13.
Let be a tropical fan and a point (not necessarily in ). The star of in denoted by is a tropical fan with support
and the weight of equal to the weight of for interior points of maximal cones. In particular, the star is empty if and only if does not belong to the support of .
If is a Bergman fan, and is an interior point of the cone of any dimension generated by the flag of flats , then the explicit description of the is known (see, for example, [FR12], Lemma 2.2):
The crucial ingredient of the tropical intersection theory is the possibility to cut out Weil divisors of what is called “rational functions” on tropical fans.
Definition 2.14 ([AR09], Section 3).
A rational function on the tropical fan is a continuous function on the union of its maximal cones which is linear on each of them. A Weil divisor of the rational function on the -dimensional tropical fan is a -dimensional tropical subfan denoted by with the weight on the -dimensional cone of given by
where is any representative of the primitive vector in the ambient space. One shows that this definition does not depend on the choice of representatives.
More elegant, but not as useful in calculations, is the equivalent definition of associated Weil divisor — that it is the -section of the only way to “balance” the graph of in , i.e., to add cones containing direction along the last coordinate corresponding to the value of with some weights, so that the disbalance brought by the non-linearity of on the hyperface junctions of maximal cones is fixed. Thus, the divisor has zero weights if the function is globally linear (mind that the converse is not true, but the counter-examples are not going to occur in this paper).
In the general setting, it is common to take advantage of the opportunity to refine the fan, then take the fine rational function which is not conewise linear before the refinement and consider this to be a rational function on the tropical cycle given by the equivalence class of the fan. In our setting, though, values on the primitive vectors of the generating rays of cones (extended conewise linearly) always suffice for the functions at play; so we do not concern ourselves with the details and refer for them to [AR09]. We may also sometimes abuse the notation and say “value on F” meaning value on the primitive vector of the one-dimensional cone which is itself.
Finally, because of the technical necessity to work with affine fans, all our functions are assumed to be linear on the lineality space , which means that . This guarantees that all the maximal cones of the Weil divisors contain either or as well. Henceforth, when verifying something about the fan, we do it only for positive cones, assuming that negative cones are treated exactly the same.
The most ubiquitous rational function is described in the following
Definition 2.15.
A truncation of the Bergman fan is the Weil divisor of the function which is equal to on and on every other ray. It can be shown (a simple partial case of Lemma 3.1 ahead) that the resulting fan is again a Bergman fan of the truncated matroid, denoted by , whose flats are the same as of except for the hyperplanes.
Cutting out a divisor of is analogous in tropical geometry to taking a general hyperplane section in algebraic geometry, and thus
Definition 2.16.
The degree of the -dimensional affine tropical fan is the weight of the cone in the fan .
It is easy to see that Bergman fans have degree 1. Moreover,
Theorem 2.17 ([Fin13], Theorem 6.5).
Tropical fan of degree 1 with positive weights is a Bergman fan of matroid.
Theorem 2.17 was proven in [Fin13] in more general setting, for tropical varieties, not only for fans, and may be considered an overkill for our needs, where we could use techniques developed in Section 3 instead, but we believe it is a beautiful result, and we are happy to apply it when relevant. Note that without requiring the weights to be positive this is not true, of course, as we are going to see many times.
To define tropical fibre product and to work with tropical intersections effectively, it remains to recall the definition of tropical morphism, the constructions of the pullback and the push-forward.
Definition 2.18 ([AR09], Definition 4.1).
A morphism between tropical fans and is a map from the support of to the support of induced by a -linear map .
In full generality, the maximal cone of maps to some subset of . For instance, the embedding of the refinement into the unrefined fan is a tropical morphism. For tropical morphisms we consider, though, such thing is not going to happen, as generating rays of cones of always map to the generating rays of cones of . This observation also makes the next definitions simpler.
Definition 2.19 ([AR09], Proposition 4.7).
Let be a morphism of tropical fans, and let be a rational function on with its Weil divisor. Then the pullback of is a function defined as , and the pullback of the Weil divisor is the Weil divisor .
One shows that pullback is a linear map from divisors on to divisors on .
Definition 2.20.
Let be a morphism of tropical fans lying in spaces and , respectively. Let be a subcycle. Then, the push-forward is defined as a tropical subcycle of consisting of maximal cones for the cone of if is injective on (and their faces). The weight on the maximal cone should be defined by the formula
where is the index of the sublattice in the lattice (in the notation of Definition 2.10).
Fortunately, again, in our setting the integer lattice map is always surjective, therefore, the index of the sublattice is always . The sum in the definition of the weight is important, though, as there can be several maximal cones of mapping to the same maximal cone of .
Now we are almost ready to recall the main notion for Theorem 4.1 — the tropical fibre product. Its only ingredient not covered so far is the construction of “diagonal” rational functions from Definition 3.3, which arise as the partial case of more general construction from Lemma 3.1. For the clarity of exposition, the definition is postponed to Section 3, so the reader can either look at functions as a black box for now, or comprehend their definition as a separate construction.
Definition 2.21 ([FH13], Definition 3.6).
Let and be matroids on groundsets and , respectively. Let be their common restriction, i.e., a matroid on groundset such that . Let and be projections induced by the embeddings and . Let , like in Definition 3.3, and let . Then, the tropical fibre product is a cycle in defined as
Example 2.22.
We consider three instances of the tropical fibre product to familiarize the reader with the notion:
-
(1)
Assume is a modular flat of one of the matroids, say, . In this case, is not only surjective, but locally surjective, a term defined in [FH13]. It means that for any , the restriction of on some neighborhood of is surjective onto some neighborhood of . This, in its turn, is equivalent to the projection being surjective on . By description of stars of Bergman fans (paragraph after Definition 2.13) we need to show that for any pair of flats of the restriction map
is surjective. We show that for the flat of containing the preimage is, for example, . Indeed, using modularity of ,
and then
so as claimed. In Theorem 3.9 of [FH13] it is shown that when one of the projections is locally surjective, the tropical fibre product is a tropical fan with positive weights. Moreover, its support is equal to the set-theoretic fibre product of and over .

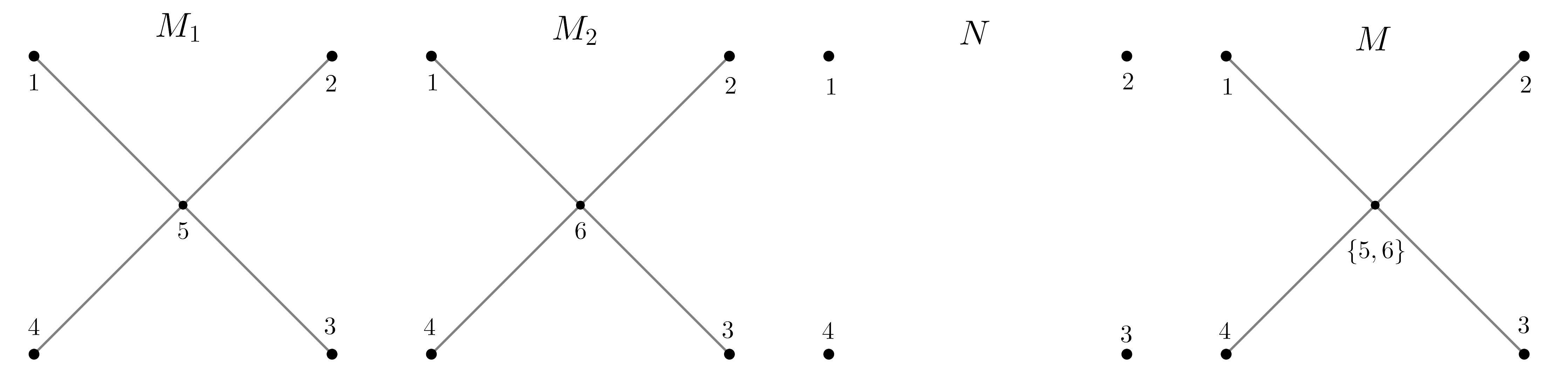
Figure 2. is the tropical fibre product . -
(2)
Consider as shown on Figure 2. In this case one verifies that the tropical fibre product coincides with (the elements and of should be thought of as pairs of respective parallel elements of and — more precisely in Theorem 4.1). Observe that is the proper amalgam of and . Mind that the set-theoretic product is not even a pure-dimensional fan and, therefore, certainly not tropical. It happens because, unlike part (1) of this example, the projections and are not locally surjective on the rays corresponding to flats and respectively. Projective fans illustrating this phenomenon are shown on Figure 3.

Figure 3. Set-theoretic fibre product is in black and gray, is in red. -
(3)
Consider as in Example 2.5. Then, it can be calculated that, after taking two out of three Weil divisors, , where is shown on Figure 4. Then, , but , despite and being a modular pair. Thus, is not defined by the modular cut of (see Lemma 3.1), and the tropical fibre product has two cones with weight , corresponding to the flags and .

Figure 4. Indices discern between elements of and in .
Lemma 2.23.
Restriction commutes with truncation (preserving dimension). More precisely, let be a matroid on groundset with . let and let with . Let be a projection induced by the embedding . Let be a truncation rational function in defined in 2.15, and let be an -dimensional truncation of . Similarly, let be a truncation function in , and let be an -dimensional truncation of . Then, .
Proof.
Since , maximal cones of are generated by characteristic rays of flags of the form . The image of such a cone under is -dimensional if and only if all are different flats of . Any such flag can be restored from the flag of flats in by defining . Thus, there is a bijection between the maximal cones of and maximal cones of with zero intersection with . All the indices of the respective lattices are equal to , as always, as each lattice is generated by the primitive vectors of the generating rays. ∎
Finally, we will need a few more statements providing tying tropical intersections in related objects — the domain and the range of the tropical morphism; or the tropical fan and its star.
Theorem 2.24 (Projection formula, [AR09], Proposition 4.8).
Let be a morphism of tropical fans. Let be a subcycle of , and a rational function on . Then,
If is a rational function on , then the rational function on the star is defined as the linear extension of the restriction of onto the small neighborhood of .
Lemma 2.25.
Taking the star commutes with cutting out Weil divisor. More precisely, if is a tropical fan, a point and a rational function, then
Lemma 2.26 ([FR12], Definition 8.1).
Given morphism of Bergman fans , if is a subcycle obtained from taking Weil divisors of functions , then the support of is contained in .
Remark 2.27.
Let us explain Lemma 2.26 via a more general setting of intersection theory in Bergman fans. In [FR12], Section 4, the intersection of arbitrary subcycles of Bergman fans is defined using diagonal construction from Definition 3.3 below. It is shown there in Theorem 4.5 that the support of is contained in the intersection of the supports of and . Then, in Definition 8.1, a pullback of the arbitrary cycle with respect to the morphism is defined as the intersection in of the cycle — the graph of defined as the push-forward; and the cycle ; this intersection then push-forwarded onto the first factor of . This construction of the pullback coincides with the one we use for those cycles that are cut out by rational functions (see Example 8.2 of [FR12]). Hence, the comment after Definition 8.1 of [FR12] claims that the support of is contained in the preimage of the support of .
3. Flag fans
In this section we introduce the generalization of Bergman fan which we call a Flag fan. This class of tropical fans is stable under taking Weil divisors with respect to certain rational functions which we call (simply, not modular) cut functions.
We begin by recalling the standard setting of modular cuts and tropical modifications. The following lemma is a summary of results established at approximately the same time by Shaw, Francois and Rau in [Sha13] and [FR12].
Lemma 3.1.
Let be a matroid, its Bergman fan, a modular cut. Define rational function
Assume does not contain flats of rank 1. Then , where if and only if
Moreover, the balanced graph of , denoted by , which is the union of the set-theoretic graph and cones containing generator along the last coordinate (see Definition 2.14), is equal to the Bergman fan , where is a one-element extension of on the groundset , and if and only if . Matroid is, in its turn, the contraction of the element of (see Definition 2.1).
In the other direction, if is a subfan of codimension , then there exists a modular cut such that . Function can be defined on the rays of as
More generally, if is a subfan of codimension , then there exists a sequence of functions corresponding to the modular cuts such that . Mind that is a modular cut of , not necessarily of . Functions can be defined on the rays of as
| (3.1) |
In other words,
Remark 3.2.
As shown in [AR09], Proposition 3.7 (b), the order of taking Weil divisors with respect to functions does not matter. We are going to stick to the non-increasing value order, though, as it is easier to track the result. For example, if, say, is not a characteristic function of a modular cut of the initial matroid , but of a modular cut on , then has positive weights, while does not.
The next definition we recall is the partial case of Lemma 3.1 and the main advancement of [FR12] — cutting out the set-theoretic diagonal allowed to define intersection of arbitrary subcycles of Bergman fans.
Definition 3.3 ([FR12], Corollary 4.2).
Given a Bergman fan , the functions cutting the diagonal subcycle are the piecewise linear functions on such that . They are defined by their values on rays by
Let us now relax the requirements for the function by cancelling the modularity condition.
Definition 3.4.
Consider the pair that consists of the ranked poset of subsets of (, also if , then , but not vice versa) and of the edge weight function . Then the Flag fan corresponding to the pair is a tropical fan in such that each cone is generated by the characteristic vectors of the set of pairwise comparable elements of (which we call a flag, as for flats of matroids), and the weight on the maximal cones is given by
As usual, the copies of cones with replaced with are added with the same weights.
Definition 3.5.
A cut on a ranked poset is a subset of flats such that if , then . A cut function on the Flag fan of is a piecewise linear continuation of , a function equal to on the rays for and equal to on the other rays (except, as always, , where the value must be linear extension of ).
Example 3.6.
Here are a few examples of Flag fans to get used to them:
-
(1)
Bergman fan is a Flag fan corresponding to the pair , where
for any . -
(2)
Consider consisting of and sets all covering and all covered by . Note that , but they all have rank in . Let all except for . It is easy to verify that the balancing condition is satisfied, so that we indeed get a tropical fan. Besides being the simplest non-Bergman Flag fan, it is nice to keep in mind because a very similar fan will appear naturally in Example 5.1.
-
(3)
A tropical fibre product from Example 2.22 (3) is a Flag fan. The Hasse diagram of its poset is shown on Figure 5, and all the weights are except for .

Figure 5. The only covering edge with negative weight is in red.
Lemma 3.7.
If is a Flag fan and a cut function on , then is a Flag fan.
Proof.
The idea of proof is straightforward: we take Definition 2.14 and verify the weights on the hyperfaces of maximal cones of . Maximal cone corresponds to the maximal flag of consisting of with , and each of its hyperfaces corresponds to with one missing set. Since is a monotonously non-increasing function, and sets are pairwise comparable, there exists unique such that and . Consider where . Recall that the unique generator of the maximal cone not belonging to the face can be chosen as . Denote by the flag with replaced by . We get
where in is a Flag fan of the segment with induced edge weights. Thus, the weight can be calculated locally — besides weights of covers of , it depends only on the edge weights of and values of on that segment of .
The first thing we notice is that if a hyperface contains both and — that is, the missing level is neither -th nor -st (say, it is -th), then . Indeed, in this case is constant 0 or constant , therefore linear, not just piecewise linear, so its Weil divisor is zero.
Note that the modified pair , where has the same covering relations with the same weights as , except those with different values of , and additional covers between if with those non-zero weights, is also ranked: , and is the Flag fan of this new pair. Indeed, every maximal cone of with non-zero weight has generators with all possible ranks in — from to . ∎
Corollary 3.8 (Algorithmic description).
To construct pair from pair , perform the following steps:
-
(1)
Delete all covers if ;
-
(2)
For all segments such that , add covers with if it is not 0;
-
(3)
Delete those vertices which do not lie in the resulting graph of covers in the same connected component as and (if and are in different connected components, is zero).
Corollary 3.9.
Tropical fibre product from Definition 2.21 is a Flag fan.
Proof.
Functions are pullbacks of cut functions on with respect to the map which preserves inclusion of the sets, therefore, they are also cut functions. Thus, the claim follows from Lemma 3.7 applied multiple times. ∎
Lemma 3.10.
If is a Flag fan corresponding to the pair , and is a Flag fan corresponding to the pair , then is a Flag fan corresponding to the pair , where
Proof.
The cone corresponding to the pair of maximal flags in and is the union of all the cones corresponding to the flags in of the following form:
where , and or . Thus the supports coincide, and the weight of each such maximal cone is equal to the product of the respective weights of the maximal cones in the factors, since each covering edge of both and is used in this flag exactly once. ∎
4. Tropical fibre product
Theorem 4.1.
Let and be matroids on groundsets and , respectively. Let be their common restriction, i.e., a matroid on groundset such that . Let and be projections induced by the inclusions and . Let be the tropical fibre product of and over , as in Definition 2.21. Then:
-
(1)
is a tropical fan of degree 1;
-
(2)
If there exists a proper amalgam of and over , as in Definition 2.3, then induced by is an isomorphism on ;
-
(3)
If all weights of are positive, then the proper amalgam of and over exists.
Proof.
We begin with Claim 1. Let , , . By construction, is a tropical fan of dimension , therefore, to verify that it has degree 1 we need to prove that , where . By the definition of tropical fibre product, we have . Therefore, by commutativity of cutting out Weil divisors ([FR12], Theorem 4.5 (6)), we need .
Observe that , since truncation commutes with restriction by Lemma 2.23. We also know that cut out the diagonal , which is a Bergman fan of a matroid and hence has degree 1, so in . The desired equality then follows from consecutively applying the projection formula 2.24. Indeed, the first time we use it, it yields . Next, , and so forth, until we get , and the claim follows from the fact that is the only -dimensional cone an affine fan can have, and that sums weights over the preimages of the cone.
We proceed to verify Claim 2. We will prove that coincides with the Bergman fan of the matroid on groundset which is obtained from the proper amalgam on groundset by replacing each element of with two parallel copies. It is immediate from the definition of the Bergman fan that and are isomorphic with isomorphism induced by . Denote the copies of in by and .
Observe that — since each flat of restricts to a flat of both and (as and are restrictions of ) and since flags of flats of are also flags of flats in . Therefore, by equation 3.1 from Lemma 3.1, is cut by functions given by
We are going to show that coincides with on all the rays of , a Bergman fan of the matroid that we denote by . Therefore, iterated tropical modifications with respect to functions , which yield , and with respect to functions , which yield , must also coincide.
Consider such that , and denote
Then, , and
with equality attained if is a flat of . Similarly, by Definition 3.3,
Therefore, to show that for all , we need to verify that
| (4.1) |
and that , since both and can only decrease as grows so if . Neither is true for arbitrary in the flat lattice of the initial matroid , but both are true “while it matters”. More precisely, we will show that if one of these equalities fails to hold for -th function, then is not a ray of .
After rearranging equation 4.1 splits into two analogous rank identities:
| (4.2) |
First, observe that the inequality holds in both identities of equation 4.2 by Lemma 2.2 and due to the fact that is the restriction of and , so the ranks of the subsets of are the same in as in or . Moreover, if either one of these inequalities turns out to be strict, or if , then is not a flat of (if it is, then , and equation 4.2 holds trivially).
Take the earliest step which creates the discrepancy between and . Namely, assume that for each and each ray of the equality holds. Now, both sequences of numbers and are monotonously non-increasing as grows, and
which means that . Our tactics is now to show that cannot actually be a flat of , since there must exist a covering flat of in which belongs to the modular cut which yields , and, therefore, does not belong to the support of by Lemma 3.1.
Since is not a flat of , we can define . Now, both and are flats of — the former by assumption, the latter because it is even the flat of which is at the end of the process deleting some of the flats. Take any in such that . Since both and are flats of and respectively, we have . Therefore, for the difference between the initial rank and the final rank is strictly larger than for , so .
Using monotonicity of again, we get (i.e., already was on on the previous step), but, at the same time, since -th step is the first with the discrepancy, which in its turn, by monotonicity of , is not less than . For the sake of clarity these considerations are gathered in Figure 6. So, we have that is a flat under the -st cut and cannot be a flat of by Lemma 3.1. This completes the proof of Claim 2.

We will now verify Claim 3. By Claim 1 and Theorem 2.17 we have that for some matroid , and we want to show that is actually the proper amalgam of and along (with added parallel copies). The reason we cannot simply follow the equivalences constructed for Claim 2 in the opposite direction is that we have no analogues of Corollary 3.6 from [FR12]. More precisely, we do not know what happens to the fan once it ceases to be a Bergman fan for the first time. Theoretically, it can emerge effective again (which actually happens, as our verification of the degree practically means that after enough truncations the fan becomes , with ranks of flats being not the ones prescribed by the definition of proper amalgam.
5. Tropical graph correspondences
In this section we develop first steps in tropical correspondence theory. The motivation is to obtain a category of tropical fans where the tropical fibre product is actually a pullback. While this precise formulation is not achieved (and is likely not possible to achieve, see Remark 5.17), worthwhile statements are established in the process.
5.1. Introducing notions
We begin with the following unsatisfactory observation. Consider the tropical fibre product from Example 2.22 (2) and a fan , where is another amalgam of and with and being parallel elements. Then, neither of the supports of and is contained in the other, and it is not difficult to check (see Figure 7 for projective Bergman fans of and ) that there are no tropical morphisms between them making the diagram commute:

Something can be done, though:
Example 5.1.
Denote the groundset of by , the groundset of by , and consider a Flag fan , where
and all edge weights are 1 except for which is . It is easy to see that is actually a tropical fan and a subfan in .
The push-forward of onto (along ) is an actual graph of tropical morphism (as both map to and cancel each other out, the latter having weight ). The same goes for .
We proceed to build on this example.
Definition 5.2.
Given two simple matroids and their lattices of flats , the lattice morphism is a map such that if , then .
We call a lattice morphism a weak lattice map if for and .
We call a weak lattice map covering if whenever , either or .
Note that covering lattice maps are automatically weak provided that for .
Simple matroids with weak lattice maps form a category , and covering maps form a wide subcategory . The category of simple matroids with weak maps of matroids (Definition 2.6) is denoted by . There is a forgetful functor : it maps simple matroids to themselves, and, given , the map is defined via . The definition is correct since , and all rank-1 flats of are one-element subsets since is simple.
The map is actually a weak map: if , then
In the examples of this section matroids shown are sometimes not simple for the sake of clarity, but what is assumed every time is their simplifications, where each flat of rank is replaced by a single element.
Not only functor is not faithful, it also does not have the right inverse, as shown by the following
Example 5.3.
On Figure 8 there are three different weak lattice maps from the matroid on the left side to the matroid on the right side. The only difference between them is the image of the flat — in the top map it is , in the bottom map it is , and in the central map it is again. Note that the central map is not a covering lattice map ( covers in the left matroid, but not in the right one), while the top and the bottom are compositions of covering lattice maps and, therefore, covering lattice maps themselves. For each of the four top and bottom arrows there is only one lattice map corresponding to the identity map on the groundset. Thus, no matter which lattice map we consider to be the image of the central identity map on the groundset, the map will not be functorial.

Next, we define tropical correspondences between Bergman fans. The whole construction is almost verbatim to the correspondences between, say, smooth projective varieties over , with the (already noted in tropical intersection theory) exception that those are defined on classes of cycles modulo rational equivalence, while groups of tropical cycles are not quotients.
Definition 5.4.
A tropical correspondence between Bergman fans and denoted by is a tropical subcycle in . The identity correspondence is the diagonal . The composition of correspondences and is given by the following formula:
where is a projection, and similarly .
Lemma 5.5.
Bergman fans of simple matroids with tropical correspondences form a category (that we denote with ):
-
•
is a unit: for any , and for any ;
-
•
Composition is associative: for any , we have
Proof.
This is standard: see, for example, Proposition 16.1.1 of [Ful98]. The only non-trivial ingredient needed is the projection formula — Theorem 2.24. Note that Proposition 1.7 of [Ful98], that is used as a justification of one of the equalities in the proof, is actually applied to show that
where denotes the projection . This particular case is obviously true in . ∎
Category has too many morphisms to be useful for us here. In the category of correspondences between smooth projective varieties there is a subcategory of graphs of morphisms of varieties. We want to imitate this subcategory, but our starting point (see Example 5.1 and discussion above it) is that actual graphs of tropical morphisms are not sufficient. Therefore, we establish a larger subcategory which we expect to behave like graphs.
Definition 5.6.
Given matroids and a weak lattice map , we define a graph rank function by the rule:
Similar to Lemma 3.1, a graph rank function is decomposed as a sum of in such a way that value on each does not increase as grows. More precisely,
A graph correspondence is given by
Example 5.7.
Here are a few instances of Definition 5.6:
-
(1)
For the identity lattice map we get from Definition 3.3, and thus .
-
(2)
More generally, if is a strong map between groundsets of matroids and , as in Definition 2.6, and is the dual map, then the set-theoretical graph
is a Bergman fan of matroid on the groundset . Matroid is isomorphic to , with being parallel element to . By Lemma 3.1, since , it is cut by the rank functions, and it is easy to see that they coincide with , where is the lattice map induced by . Thus, equals set-theoretic graph of .
-
(3)
If and are as in Example 5.1, and is given by , then the Flag fan that we constructed in the example equals .
We are going to see that Example 5.7 (3) is not a coincidence.
Lemma 5.8.
The graph correspondence of the covering lattice map is a Flag fan.
Proof.
We need to verify that each is monotonous on flats of and, therefore, on each of the Flag fans on the way (their posets are the subposets of the initial lattice of flats). Then, the claim follows from Lemma 3.7.
Since are monotonously non-increasing as grows, and , we want to show that, if , then . The covering relations can be of two kinds: , where , and , where . As , and exactly one of the subtrahends increases by when replacing with , we want to show that
Since is a covering lattice map, , so both inequalities boil down to the fact that in any matroid with groundset and for any
which is simply Lemma 2.2. ∎
5.2. Graph functor
In this subsection we prove the second main result of the paper — that graph correspondence from Definition 5.6 provides a functor from to (Theorem 5.13). In order to do that, we first describe the edge weights of graph correspondence combinatorially, in terms of , in Theorem 5.12, using that is a Flag fan due to Lemma 5.8. It requires some preparation. Recall the following
Definition 5.9.
A Möbius function on poset is defined for pairs recursively via
One sees that function is designed in such a way that , where is a delta-function, equal to if and otherwise.
We are going to use the following simple property of , which can be found, for example, in [Sta86] (Ch. 3, Exercise 88).
Lemma 5.10.
For a poset with the minimal element (denoted by for convenience)
Proof.
We have
where the penultimate equality follows from . ∎
Remark 5.11.
We are going to use Lemma 5.10 several times, so, to avoid excessive combinatorial abstraction, we define . Lemma 5.10 can be rewritten, then, as whenever has the minimal element. Observe that, if is a meet-semilattice, is the coefficient of in the inclusion-exculsion formula written for the maximal elements of the . Indeed,
Before formulating Theorem 5.12 rigorously, let us give its informal explanation. Basically, it claims that the complete flags of the graph correspondence are of the form
where is a complete flag in , images lie under in (but not necessarily equal to them), and the weights are balanced in such a way that the whole thing is a tropical fan and its push-forward onto is . This way resembles inclusion-exclusion principle (see Remark 5.11).
Theorem 5.12.
Let be a graph correspondence of the covering lattice map . Let be the pair for which is a Flag fan. Then, all the edges of are as follows:
Denote by the subposet of consisting of such that
Then,
Proof.
Denote the Flag fan by , and the corresponding poset and weights pair by . It turns out to be convenient to digress for a moment from considering edges and to focus on the vertices of . Notice that, if we show that only pairs such that can belong to , then the first claim follows. Indeed, the inequality follows from the fact that is the subposet of the initial lattice , and is obtained from the comparison of ranks in . More precisely, observe that since , and their ranks in Definition 5.6 cancel each other out. Thus,
which means that if but , then there can be no edge in between and . But then there can be no edges between and in as well, because any increasing chain must reach from in steps, with the rank in not allowed to jump, so it must grow steadily by 1 on each edge of .
Assume the contrary: there exists with . Take any maximal vertex with this property. Observe that, by definition of , , meaning that the pair has its rank decreased by with each next until minimal such that , and then they continue the descent together. Consider the last step before reaches , namely, maximal that . We will prove that the localization is linear on the star of , so, by Lemma 2.25, does not belong to the next poset and, consequently, to .
We show that , where is any element. Since the characteristic function is linear on the , the claim follows. Note that we are not interested in the whole fan structure of the star, only that the rays are the elements comparable with . Those of them which are below have equal to . For we need to verify the equivalence:
If , then, in particular, . Since is already , the next are going to be for all , so the vertex never disappears and thus belongs to , which contradicts being a maximal element of with . This proves .
If , then
| (5.1) |
which implies since . The strict inequality in equation 5.1 follows from Lemma 2.2 and the fact that . This proves .
It remains to calculate in the case where both vertices belong to . We will perform it by induction on the number of step when the edge appears in (step 2 of Corollary 3.8). This is made possible by the fact that, as we are going to see, all the edge weights on which depends are determined for earlier .
Poset does not always have the top element (which is precisely the reason for the weights to get complicated), but it always has the bottom element . Therefore, in the base of induction consists of a single element . Indeed, if there is another , the edge would appear before, since
We aim to show that .
The edge between vertices and appears when taking the Weil divisor of for such that , and . As we have seen in Corollary 3.8, the weight on the newly-created edge is equal to
which, after expanding according to Definition 2.14, yields
| (5.2) |
Due to the balancing condition written for the hyperface of generated by any chain containing and with missing , the sum in the large brackets is just some . Then, since , the first summand is just . We want to show that for all in the sum, so that the second term is , and that .
Recall that , thus every has the form or . In the former case, , but consists of only, therefore, . Thus, if , we get a contradiction (this vertex should not exist already in ). In the latter case, since , values of on both and are equal to the ranks , respectively, and cannot coincide on them unless they are of the same rank in , in which case could not occur.
To see that , focus on those of the form (in other words, count only the coordinate of any element in the vector ). As we have just seen, if , then cannot cover in , so there is only one such . Now, , because this is the original covering edge from , where all the weights are , so it remains to prove that as well. This is easy, though: coincides with on the whole segment of , and thus all newly-created edges always have weight there. Indeed, for each value of equals if is above certain rank in , so the value of each on the level of missing flats is , thus they never impact the weight of the new edge. It follows that there is only one containing , and its weight is 1, so as claimed. This completes the base of induction.
Let us now find in the case of arbitrary . We begin as previously, fixing such that this edge appears when taking the Weil divisor of , and writing equation 5.2 for its weight. This time, though, we already know that
for that belong to by the induction assumption. We have also seen that (as in the previous paragraph, coincides with on the whole segment ). Thus, the second term of equation 5.2 becomes
The first term still equals , since by exactly the same argument as before — is the only vertex between and containing elements of , and both edges connecting it to and have weight in . Thus, we need
which rearranges to
and this is simply Lemma 5.10. ∎
We can now use Theorem 5.12 to obtain
Theorem 5.13.
In the notation of Definition 5.6, a map between Hom-sets of and given by is a functor: if and are covering lattice maps between simple matroids, then
Proof.
Despite seemingly cumbersome construction of and the fact that in general we have no idea whether the push-forward of the Flag fan is again a Flag fan, or, even if it is, what are its — despite all that, we already possess almost all the necessary tools to verify the claim.
For simplicity, denote . Thus,
and we need to show that
Using the fact that, for the subcycles of Bergman fans which are cut by Weil divisors of rational functions , the intersections via diagonal construction and via ’s coincide ([FR12], Theorem 4.5(6)), we will check the following:
To control edge weights of , where is not necessarily a Bergman fan anymore, we will need an almost verbatim generalization of Theorem 5.12 which we formulate as a standalone lemma.
Lemma 5.14.
In the notation of Theorem 5.13, if is the pair corresponding to the Flag fan , then all the edges of are as follows:
The weight of the edge is given by the formula
Proof.
By Lemma 3.10 the edges of before cutting Weil divisors are of two types. The first type is , where and . The weight of such an edge is , as in . The second type is , where . The weight of such an edge is .
The claim is then verified analogously to Theorem 5.12. First, we show that only vertices with survive in . It follows that for any edge of the pair must cover in . To show this, as before, assume the contrary, and take any maximal surviving vertex with . Consider the step after which the ranks in of all the vertices become equal to the rank of . See that at this step, localized function on the star of is equal to minus the characteristic function of any element of .
Then, we verify that the weights are as claimed using induction on applying . The necessary observations are that
-
•
all the initial covering relations coming from have weights ;
-
•
all the newly-created edges of the type between the vertices present in also have weights , because coincides with on the segment;
-
•
all the initial covering relations coming from inherit their weights from , thus, in induction handling equation 5.2, everything is multiplied by .
∎
According to Lemma 5.14 and Definition 2.20, the weight of the maximal cone generated by the chain of length in the push-forward is given by
| (5.3) |
where we assume summation over only suitable sequences (mind that, unlike , they do not have to be strictly increasing in ). Next, we rearrange
and, likewise,
Substituting into equation 5.3 and rearranging, we get (dropping the subscripts of ’s)
| (5.4) |
The system of sets satisfies the following conditions:
In the initial sum 5.3 we’ve chosen ’s satisfying conditions from the middle column and then ’s and ’s satisfying the rest of conditions. We obtain the same system of sets by first choosing such that
| (5.5) |
and then choosing
| (5.6) |
Thus, the summation in equation 5.4 can be rewritten as
while the desired coefficient of the same maximal cone generated by the chain in is just
where the summation is taken over with same conditions as in 5.5, so we need to show that
By Lemma 5.10, for a poset with bottom element, . Making choices of pairs one by one, we obtain
where the summation goes over pairs that satisfy all the conditions of 5.6 concerning and , and also . Each of those modified subsets has the minimal element , therefore, the whole sum turns into from the end to the beginning. ∎
Remark 5.15.
It is possible to define without itself, using the description from Theorem 5.12, thus avoiding its proof. There are several reasons, though, for which we find our approach preferable. Firstly, the fact that is a Flag tropical fan is now an instance of Lemma 3.7, and we do not need to verify balancing conditions of combinatorially. Secondly, using to construct turns graph correspondence into a rigorous generalization of diagonal and Bergman subfan from [FR12] (Example 5.7 (2)). Thirdly, is defined even if is not a covering lattice map, while it is not a Flag fan and does not admit this kind of description — this may turn out to be valuable to us (see Question 5.19 below). Finally, clearly stores information about in a more compact way. The next statement hints that, maybe, we can even work with instead of when trying to generalize claims like Theorem 5.13.
Lemma 5.16.
If are covering lattice maps, then can be defined as
Proof.
By Definition 5.6 we have
Substituting , we get
Thus, it remains to prove that for any other the sum is not smaller, which is equivalent to
Since is a covering map, applying it does not increase the difference of ranks, therefore,
and after joining both terms with the difference of ranks cannot increase by Lemma 2.2. ∎
Remark 5.17.
As we can see from Theorem 5.13 and Example 5.3, a reasonable subcategory of will not have tropical fibre product as pullback. More precisely, if is a uniform matroid of rank on the groundset , is a uniform matroid of rank on the groundset and is a uniform matroid of rank on the groundset , then the tropical fibre product is , where is a uniform matroid of rank on the groundset . Consider Bergman fan of another amalgam on the groundset with being parallel elements. Then, there are numerous correspondences making and coincide, exactly as in Example 5.3. All of them commute with the projection graph correspondences , though.
Remark 5.18.
Note that in the image of the under the forgetful functor the tropical fibre product does not satisfy the universal property 2.1. We show this by constructing an example of the proper amalgam and another amalgam such that the unique weak map between their groundset can only come from the non-covering lattice map — see Figure 9. One verifies that is the tropical fibre product, but the identity map of the groundsets cannot be obtained from covering lattice map. Indeed, the flat of cannot map to anything other than — if it maps to, say, , then covers in , but the closure of in is the whole groundset, a flat that does not cover . But then covers in and not in .

This insufficiency leads to the following question:
Question 5.19.
Can it be shown that is a functor from the whole to ?
References
- [AHK15] Karim Adiprasito, June Huh and Eric Katz “Hodge Theory for Combinatorial Geometries” In Annals of Mathematics 188, 2015 DOI: 10.4007/annals.2018.188.2.1
- [AR09] Lars Allermann and Johannes Rau “First steps in tropical intersection theory” In Mathematische Zeitschrift 264.3 Springer ScienceBusiness Media LLC, 2009, pp. 633–670 DOI: 10.1007/s00209-009-0483-1
- [BEST] Andrew Berget, Christopher Eur, Hunter Spink and Dennis Tseng “Tautological classes of matroids” In Inventiones mathematicae 233.2, 2023, pp. 951–1039 DOI: 10.1007/s00222-023-01194-5
- [BK88] Achim Bachem and Walter Kern “On sticky matroids” In Discrete Mathematics 69.1, 1988, pp. 11–18 DOI: https://doi.org/10.1016/0012-365X(88)90173-2
- [Bon09] Joseph Bonin “A Note on the Sticky Matroid Conjecture” In Annals of Combinatorics 15, 2009 DOI: 10.1007/s00026-011-0112-7
- [Cav+16] Renzo Cavalieri, Simon Hampe, Hannah Markwig and Dhruv Ranganathan “Moduli spaces of rational weighted stable curves and tropical geometry”, 2016 arXiv:1404.7426 [math.AG]
- [Est11] Alexander Esterov “Tropical varieties with polynomial weights and corner loci of piecewise polynomials”, 2011 arXiv:1012.5800 [math.AG]
- [FH13] Georges Francois and Simon Hampe “Universal Families of Rational Tropical Curves” In Canadian Journal of Mathematics 65.1 Canadian Mathematical Society, 2013, pp. 120–148 DOI: 10.4153/cjm-2011-097-0
- [Fin13] Alex Fink “Tropical cycles and Chow polytopes” In Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry 54.1, 2013, pp. 13–40 DOI: 10.1007/s13366-012-0122-6
- [FR12] Georges François and Johannes Rau “The diagonal of tropical matroid varieties and cycle intersections” In Collectanea Mathematica 64.2 Springer ScienceBusiness Media LLC, 2012, pp. 185–210 DOI: 10.1007/s13348-012-0072-1
- [Ful98] William Fulton “Correspondences” In Intersection Theory New York, NY: Springer New York, 1998, pp. 305–318 DOI: 10.1007/978-1-4612-1700-8˙17
- [MRS19] Lucía López Medrano, Felipe Rincón and Kristin Shaw “Chern–Schwartz–MacPherson cycles of matroids” In Proceedings of the London Mathematical Society 120.1 Wiley, 2019, pp. 1–27 DOI: 10.1112/plms.12278
- [Oxl11] James Oxley “Matroid Theory” Oxford University Press, 2011 DOI: 10.1093/acprof:oso/9780198566946.001.0001
- [PT82] Svatopluk Poljak and Daniel Turzik “A note on sticky matroids” In Discrete Mathematics 42.1, 1982, pp. 119–123 DOI: https://doi.org/10.1016/0012-365X(82)90060-7
- [Sha13] Kristin M. Shaw “A Tropical Intersection Product in Matroidal Fans” In SIAM Journal on Discrete Mathematics 27.1, 2013, pp. 459–491 DOI: 10.1137/110850141
- [Shi21] Jaeho Shin “The Sticky Matroid Conjecture”, 2021 arXiv:2108.04757 [math.CO]
- [Sta86] Richard P. Stanley “Partially Ordered Sets” In Enumerative Combinatorics Boston, MA: Springer US, 1986, pp. 96–201 DOI: 10.1007/978-1-4615-9763-6˙3
- [SW23] Kris Shaw and Annette Werner “On the birational geometry of matroids” In Combinatorial Theory 3.2, 2023 DOI: https://doi.org/10.5070/C63261996