Algebras, Regions, and Observers

In section 2, we learned that one can define operators by smearing a quantum field along the timelike worldline of an observer. Therefore we can consider the algebra generated by such operators (or more precisely by bounded functions of such operators). But what are the algebras that we make this way? In the context of quantum field theory without gravity, this question is answered by the “timelike tube theorem.” This theorem was originally formulated for timelike geodesics in Minkowski space Borch2 ; Araki . It was generalized to free field theories in curved spacetime in Stroh . For a version of the theorem suitable for non-free theories in curved spacetime, see SW ; SW2 .

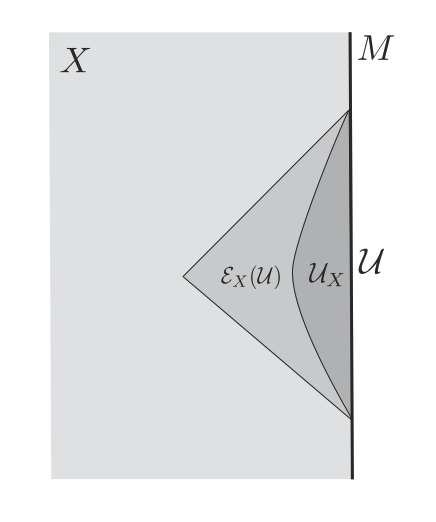
If ${\mathcal{U}}$ is an open set in spacetime, its “timelike envelope” ${\mathcal{E}}({\mathcal{U}})$ consists of all points that can be reached by deforming timelike curves in ${\mathcal{U}}$ through a family of timelike curves, keeping the endpoints fixed (fig. 3). (Thus ${\mathcal{E}}({\mathcal{U}})$ is contained in the intersection $J^{+}({\mathcal{U}})\cap J^{-}({\mathcal{U}})$ of the past and future of ${\mathcal{U}}$, but in general it is smaller. See section 3.3 for an example.) The timelike tube theorem asserts that the algebra of operators⁷⁷7For a more precise explanation of what algebra is intended here, see section 3.2. in ${\mathcal{U}}$ is the same as the algebra of operators in the possibly much larger region ${\mathcal{E}}({\mathcal{U}})$. We will aim to give at least a hint of why this is true, after first explaining an implication, noted in Stroh .

Suppose that we are actually interested in a timelike curve $\gamma$, possibly one of finite extent with endpoints $q,p$ or possibly an infinite or semi-infinite curve. The timelike envelope ${\mathcal{E}}(\gamma)$ consists of all points that can be reached by deforming $\gamma$ through a family of timelike curves, keeping $\gamma$ fixed near its ends. If $\gamma$ has endpoints, they are omitted from ${\mathcal{E}}(\gamma)$ to ensure that ${\mathcal{E}}(\gamma)$ is an open set. We can thicken $\gamma$ (minus its endpoints, if any) to an open set ${\mathcal{U}}$, in such a way that the timelike envelope ${\mathcal{E}}({\mathcal{U}})$ does not depend on ${\mathcal{U}}$ – it is the same as the timelike envelope ${\mathcal{E}}(\gamma)$ of $\gamma$. See fig. 3. The timelike tube theorem says that the algebra ${\mathcal{A}}({\mathcal{U}})$ of operators in region ${\mathcal{U}}$ does not really depend on ${\mathcal{U}}$ but only on $\gamma$. It coincides with ${\mathcal{A}}({\mathcal{E}}(\gamma))$, the algebra of operators in ${\mathcal{E}}(\gamma)$. So we can define an algebra for every (possibly bounded) timelike curve $\gamma$. That in itself is not a surprise, since we arrived at the same conclusion in a more direct way⁸⁸8The timelike tube theorem depends on real analyticity of spacetime, as discussed shortly, and the reasoning in section 2 does not, so the previous analysis was more general. in section 2. But it is nice to see the consistency with what we learned from more elementary arguments.

Strictly speaking, the algebra associated to a curve $\gamma$ in section 2 consists of the quantum fields smeared along $\gamma$, while the timelike tube theorem gives us an algebra ${\mathcal{A}}(\gamma)$ of operators that can be defined in an arbitrarily small neighborhood of $\gamma$. Presumably, these two algebras coincide (assuming that we include all possible local operators in the construction of section 2, including derivatives of operators). A proof might start with an axiomatic characterization of local operators at a point in terms of a limit of the operators in a small ball around that point. Were the two algebras to differ, one might argue that as the notion of an observer characterized by an infinitely thin worldline is an idealization, the physically more relevant algebra would be the one provided by the timelike tube theorem.

The interpretation that we want to give is that the algebra ${\mathcal{A}}(\gamma)$ of operators supported on a curve $\gamma$ is a good stand-in for the algebra ${\mathcal{A}}({\mathcal{E}})$ of the spacetime region ${\mathcal{E}}$ associated to $\gamma$. The algebra ${\mathcal{A}}(\gamma)$ is more operationally meaningful than ${\mathcal{A}}({\mathcal{E}})$, since it is more directly what an observer can measure. And it is also better defined in the presence of gravity than ${\mathcal{A}}({\mathcal{E}})$ would appear to be. Once one takes into account fluctuations in spacetime, it is hard to see how one would directly define ${\mathcal{A}}({\mathcal{E}})$, but as long as an observer is included in the description, the algebra of observables along the observer’s worldline seems to be a meaningful notion, even when the observer’s worldline fluctuates. So ${\mathcal{A}}(\gamma)$ seems like a good substitute for the algebras associated to open sets that one considers in the absence of gravity.

To try to gain some idea of why the timelike tube theorem is true, let us consider the classical limit. Suppose we have a reasonable relativistic wave equation like the Klein-Gordon equation $(\Box+m^{2})\phi=0$, where $\Box$ is the wave operator, or possibly a nonlinear modification of this equation. In fig. 4, we are given a solution in one region of a spacetime $M$, and we want to predict the solution in a larger region. We consider two cases. In fig. 4(a), the solution is given in a “spacelike pancake” ${\mathcal{U}}$, and we want to extend it over the domain of dependence $D({\mathcal{U}})$ of ${\mathcal{U}}$. In fig. 4(b), the solution is given in a “timelike tube” ${\mathcal{U}}$ and we want to extend the solution over the corresponding “timelike envelope” ${\mathcal{E}}({\mathcal{U}})$.

There is a basic asymmetry between the two cases.⁹⁹9 To be precise, this asymmetry holds in any spacetime dimension ${\sf D}>2$. In ${\sf D}=2$, spacetime has one dimension of space and one dimension of time, and there is a perfect symmetry between the two cases of fig. 4. In ${\sf D}>2$, there are more space dimensions than time dimensions, and there is no such symmetry. The counterexample illustrated in fig. 5 fails in ${\sf D}=2$ because in ${\sf D}=2$, the solution with a delta function source along a worldline $\ell$ does not blow up along $\ell$, but instead is discontinuous across $\ell$. Starting with the solution on one side of $\ell$, one can drop the discontinuity and smoothly continue the solution across $\ell$. In ${\sf D}>2$, a solution with such a delta function source blows up along $\ell$ and there is no way to remove the singularity without changing the solution in the original region ${\mathcal{U}}$. The Holmgren uniqueness theorem of classical partial differential equations¹⁰¹⁰10For an accessible exposition of this theorem, see chapter 5 of Smoller . asserts that the extension over the larger region is unique, if it exists, both in fig. 4(a) and in fig. 4(b). But existence is more special and only holds in fig. 4(a).

A simple counterexample (fig. 5) shows that an existence result cannot possibly hold in fig. 4(b). Let $\ell$ be a timelike curve that passes through the region ${\mathcal{E}}({\mathcal{U}})$ but not through ${\mathcal{U}}$. Consider a solution of the equation $(\Box+m^{2})\phi=0$ with a delta function source along $\ell$. If we consider Maxwell’s equations rather than the Klein-Gordon equation, then $\ell$ can be the worldline of a point charge. The field $\phi$ blows up along $\ell$ (in dimension ${\sf D}>2$; see footnote 9). Starting with the solution in the region ${\mathcal{U}}$, there is no way to extend it over ${\mathcal{E}}({\mathcal{U}})$ as a solution, since if one tries to do this, one encounters the blowup along $\ell$. The equation is not obeyed along $\ell$, because of the delta function source.

The existence and uniqueness result in the case of fig. 4(a) is the basis for much of physics. It says that the solution can be predicted from initial data – physics is causal. But by contrast the uniqueness result without a guarantee of existence in fig. 4(b) is not usually useful at the classical level because generically the extension over ${\mathcal{E}}({\mathcal{U}})$ of a solution on ${\mathcal{U}}$ does not exist and it is very hard to predict when it does.

Suppose, however, that we are doing quantum field theory and for simplicity consider a free field $\phi$ with the action

In this case, we can view $\phi$ as an operator-valued solution of the Klein-Gordon equation $(\Box+m^{2})\phi=0$. If we are studying this quantum field theory on $M$, then the field $\phi(x)$ does exist throughout $M$ and therefore existence of the extension from ${\mathcal{U}}$ to ${\mathcal{E}}({\mathcal{U}})$ is not an issue.

But what does uniqueness mean? In some sense, uniqueness means “the field $\phi(x)$ for $x\in{\mathcal{E}}({\mathcal{U}})$ is uniquely determined by $\phi(y)$ for $y\in{\mathcal{U}}$.” As explained by Borchers and Araki in the early 1960’s, the quantum meaning of this statement is really “$\phi(x)$ for $x\in{\mathcal{E}}({\mathcal{U}})$ is contained in the algebra generated by $\phi(y)$ for $y\in{\mathcal{U}}$” or equivalently the operator algebras of the two regions are the same:

This is the timelike tube theorem.

Classically, we could just as well add higher order terms to the action and consider a field that satisfies a nonlinear partial differential equation. Holmgren uniqueness applies equally well to such an equation. Quantum mechanically, although a free quantum field can be viewed as an operator-valued solution of a classical field equation, that is not the case for a non-free quantum field, because of issues involving renormalization. Accordingly, proofs of the timelike tube theorem in non-free theories require additional ingredients, beyond what is needed in free theories. An approach that works for non-free theories in curved spacetime was presented in SW (see SW2 for an informal account).

In this discussion, we have skipped over two important points. First, we have not been precise about what is the algebra that is governed by the timelike tube theorem. See section 3.2. Second, we have omitted to explain a key assumption in the classical Holmgren uniqueness theorem and the quantum timelike tube theorem. These theorems hold in real analytic spacetimes. Real analyticity is not needed for existence and uniqueness in the setting of fig. 4(a), but it is needed for uniqueness in the setting of¹¹¹¹11Actually, it suffices for the spacetime to be, in some coordinate system, real analytic in the time direction Tataru . In free field theory, this is also true for the timelike tube theorem Stroh . fig. 4(b). Is this restriction important for the application of the timelike tube theorem to semiclassical gravity? In semiclassical gravity, one is usually studying the behavior of quantum fields in a background spacetime that in practice is normally real analytic. For instance, in section 4, we consider the static patch in de Sitter space as an example in which it is important to explicitly include an observer in order to define a sensible algebra of observables, and thus in which the timelike tube theorem provides important motivation. This is a typical example in which the starting point is a real analytic spacetime. After picking a semiclassical starting point, one then expands around it. In perturbation theory, the metric certainly fluctuates away from the real analytic starting point, but one expects that in perturbation theory, the gravitational field can be treated like any other quantum field in a real analytic background. Thus it appears that for typical applications of the timelike tube theorem to semiclassical gravity, the restriction of the theorem to real analytic spacetimes is not a problem.

For a region ${\mathcal{U}}$ in spacetime, what precisely is the algebra of operators to which the timelike tube theorem applies? The smallest reasonable candidate is the algebra generated by local operators in ${\mathcal{U}}$ (or more precisely, by bounded functions of smeared local operators). If ${\mathcal{U}}$ is contractible, this is the natural algebra of observables in ${\mathcal{U}}$ in a generic quantum field theory. However, if ${\mathcal{U}}$ is not contractible, then in general, as we discuss shortly, there can be additional operators in ${\mathcal{U}}$, such as Wilson operators defined on noncontractible loops in ${\mathcal{U}}$, that cannot be constructed from local operators in ${\mathcal{U}}$.

The algebra generated by local operators has been called the additive algebra ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$ casini1 ; casini2 . One can then reserve the name ${\mathcal{A}}({\mathcal{U}})$ for the possibly larger algebra of all operators in ${\mathcal{U}}$. The timelike tube theorem is really a theorem about ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$. Thus a more precise statement of the theorem than we have given so far is ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}({\mathcal{U}}))$. This is clear from the proofs, which involve studying algebras of local operators. However, as we will discuss, while the distinction between ${\mathcal{A}}({\mathcal{U}})$ and ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$ exists in quantum field theory in general, there are reasons to believe that this distinction is absent in any theory that emerges at long distances from a full model of quantum gravity.

The motivation for the phrase “additive algebra” is as follows. Let ${\mathcal{B}}$ be a small open ball in ${\mathcal{U}}$. Then as ${\mathcal{B}}$ is contractible, there is no distinction between ${\mathcal{A}}({\mathcal{B}})$ and ${\mathcal{A}}_{\mathrm{add}}({\mathcal{B}})$. Now cover ${\mathcal{U}}$ by open balls ${\mathcal{B}}_{\alpha}$, with $\alpha$ ranging over some set $S$. The additive algebra of ${\mathcal{U}}$ is the same as the algebra generated by the ${\mathcal{A}}({\mathcal{B}}_{\alpha})$, $\alpha\in S$:

In what situation will we have ${\mathcal{A}}({\mathcal{U}})\not={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$, where ${\mathcal{A}}({\mathcal{U}})$ is the algebra of all possible operators in ${\mathcal{U}}$, not necessarily built from local operators? For a typical example, consider a theory with a ${\mathrm{U}}(1)$ gauge field $A$, with curvature $F={\mathrm{d}}A$. Let $\ell$ be a closed loop in ${\mathcal{U}}$, and consider the Wilson operator $W_{\ell}(A)=\exp({\mathrm{i}}\oint_{\ell}A)$. Is this operator contained in ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$? The answer will be “yes” if $\ell$ is the boundary of an oriented two-manifold $D\subset{\mathcal{U}}$, for then $W_{\ell}(A)=\exp({\mathrm{i}}\int_{D}F)$ is a bounded function of a smeared local field in ${\mathcal{U}}$, namely $\int_{D}F$. But even if $\ell$ is not a boundary in ${\mathcal{U}}$, the answer can still be “yes,” for a more subtle reason that was explained in Harlow . Consider a theory that has a charge 1 field $\phi$. Then for an open path $\gamma\subset{\mathcal{U}}$, say with endpoints $q,p$, one can consider the gauge-invariant operator $V_{\gamma}(A)=\overline{\phi}(p)\exp({\mathrm{i}}\int_{\gamma}A)\phi(q).$ In the case that $\gamma$ is a very short path, with $p$ very near $q$, $V_{\gamma}$ can be expanded in terms of local operators at $q$ and so is contained in the additive algebra of any open set containing $\gamma$. If $\ell$ is a closed loop, then $W_{\ell}(A)$ can be “cut” in the sense that if one omits from $\ell$ a number of open intervals of size $\varepsilon$, with the portion retained then being a disjoint union of closed intervals $\gamma_{i}$, $i=1,\cdots,n$, then $W_{\ell}(A)$ appears as the most singular contribution in the operator product $\prod_{i=1}^{n}V_{\gamma_{i}}(A)$ for $\varepsilon\to 0$. Hence, in this situation $W_{\ell}(A)$ is contained in the additive algebra ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$ for any region ${\mathcal{U}}$ containing $\ell$.

However, if the theory has no field of unit charge, and $\ell$ is not a boundary in ${\mathcal{U}}$, then $W_{\ell}(A)$ is contained in ${\mathcal{A}}({\mathcal{U}})$ but not in ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$. This phenomenon is certainly not limited to ${\mathrm{U}}(1)$ gauge theory. In a theory with any gauge group $G$, if some representation $R$ of $G$ is “missing,” in the sense that no local operator of the theory transforms in this representation, then for suitable regions ${\mathcal{U}}$ one will have ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})\not={\mathcal{A}}({\mathcal{U}})$. A Wilson loop in the representation $R$ can be present in ${\mathcal{A}}({\mathcal{U}})$ but not in ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$. A similar role can be played by a $p$-form gauge field $B$ with $p>1$. In a theory that has such a field, one can consider the operator $Q_{S}=\exp({\mathrm{i}}\int_{S}B)$, where $S$ is a $p$-cycle in ${\mathcal{U}}$. If $S$ is not a boundary in ${\mathcal{U}}$ and the theory does not have a string or membrane that couples to $B$ (which would enable one to “cut” the operator $Q_{S}$ in small pieces), then $Q_{S}$ is contained in ${\mathcal{A}}(U)$ but not in ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$. There is also an analog of this for magnetic charges (and their analogs for strings and membranes), with ’t Hooft operators instead of Wilson operators.

We can now easily give an example that shows that it is necessary to specify that the timelike tube theorem applies to ${\mathcal{A}}_{\mathrm{add}}$, not to ${\mathcal{A}}$. Consider ${\mathrm{U}}(1)$ gauge theory without charged fields on a spacetime ${\mathbb{R}}\times S^{1}$ with product metric, where ${\mathbb{R}}$ parametrizes time and $S^{1}$ is parametrized by an angular variable $\phi$. In this spacetime, there is a nontrivial Wilson operator $W_{\ell}=\exp({\mathrm{i}}\oint_{\ell}A)$, where $\ell$ is a closed loop that wraps around the $S^{1}$. Let $p$ and $q$ be two points at the same value of $\phi$ but different values of $t$, and let $\gamma$ be the timelike geodesic that runs from $q$ to $p$ at fixed $t$. If ${\mathcal{U}}$ is a small neighborhood of $\gamma$, there is no nontrivial Wilson operator in ${\mathcal{U}}$, so ${\mathcal{A}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$. But if $p$ is separated in time from $q$ by more than the circumference of the $S^{1}$, then the region ${\mathcal{E}}({\mathcal{U}})$ includes a circle that wraps all the way around the $S^{1}$, so ${\mathcal{A}}({\mathcal{E}}({\mathcal{U}}))\not={\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}({\mathcal{U}}))$. Thus in this example, we have ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}({\mathcal{U}}))$, as guaranteed by the timelike tube theorem, but ${\mathcal{A}}({\mathcal{U}})\not={\mathcal{A}}({\mathcal{E}}({\mathcal{U}}))$.

Let us say that a quantum field theory which may have gauge fields or $p$-form gauge fields for $p>1$ is “complete” if the electrically and magnetically charged particles, strings, and membranes coupling to those gauge fields are a maximal possible set consistent with all principles of low energy physics including Dirac quantization of electric and magnetic charge. Complete theories are precisely the ones with ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}({\mathcal{U}})$ for all ${\mathcal{U}}$, so we might also call them “additive.” It is believed that a quantum field theory that emerges at low energies from a full-fledged (ultraviolet complete) theory of quantum gravity is always complete in this sense. This was originally suggested based on experience with string theory Polchinski . Further arguments were given in BS , and the fullest known argument is based on holographic duality HO .

The claim that a theory that emerges from a full quantum gravity theory will be additive or complete has another interpretation. A theory with “missing” charges (or strings or membranes) has a $p$-form global symmetry in the language of GKSW (where $p$ depends on what is missing). So the statement that a full-fledged theory of quantum gravity is complete can be viewed as an extension to $p$-form global symmetry with $p>1$ of the statement that there are no global symmetries in a full theory of quantum gravity. For discussion of this statement, see for example BS ; EW .

In the spirit of the present article, one can motivate as follows the idea that an ultraviolet-complete theory of quantum gravity should have no missing charges. We assume that a complete gravity theory can be approximated, in an appropriate class of states, by an ordinary quantum field theory weakly coupled to gravity. Suppose that this ordinary quantum field theory is not complete, for example because it has a ${\mathrm{U}}(1)$ gauge field but no state of charge 1. Then if a loop $\ell$ is not a boundary in spacetime, the Wilson operator $W_{\ell}=\exp({\mathrm{i}}\oint_{\ell}A)$ is not measurable by any observer living in the spacetime and described by the theory. After all, given that $\ell$ is not a boundary, $W_{\ell}$ cannot be measured by measuring the curvature $F={\mathrm{d}}A$. To measure $W_{\ell}$ when $\ell$ is not a boundary requires measuring the interference between different histories of a charge 1 particle that differ by the homology class of the worldline of the particle. But the assumption that the theory has no state of charge 1 means that such an experiment is not possible using the resources available in the theory.

What, then, do we mean in claiming that $W_{\ell}$ (or its hermitian part) is an “observable”? In ordinary quantum mechanics, we consider the observer to be external to the system, and we make no particular assumption about what resources the observer can use in probing the system. From that point of view, the observer might be able to introduce a massive charged particle to probe the system and measure $W_{\ell}$. The observer, after all, is described by a more complete theory of the universe that might have the necessary charged particle. An ultraviolet-complete theory of quantum gravity, however, is expected to describe all that there is in the universe that it describes, with no way to add anything from outside. In the context of such a theory, the observer and any apparatus used by the observer must already be described by the theory. So in an ultraviolet complete theory of quantum gravity with a “missing” charge, we would be in the awkward situation that the theory would enable us to define an “observable” $W_{\ell}$ that would be well-defined in an appropriate, long distance limit, but that no one, in principle, could measure.

In addition to the timelike tube theorem, which asserts that ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}({\mathcal{U}}))$, one has causality, which, denoting the domain of dependence of a set ${\mathcal{U}}$ as $D({\mathcal{U}})$, asserts that ${\mathcal{A}}({\mathcal{U}})={\mathcal{A}}(D({\mathcal{U}}))$. If the difference between ${\mathcal{A}}$ and ${\mathcal{A}}_{\mathrm{add}}$ is unimportant, these statements can be combined, relating ${\mathcal{A}}({\mathcal{U}})$ to the algebra of a set that in general is larger than either ${\mathcal{E}}({\mathcal{U}})$ or $D({\mathcal{U}})$. This was noted by Araki Araki in one of the original papers on the timelike tube theorem. However, Araki actually conjectured a further generalization. In the context of quantum fields in Minkowski space, Araki wrote, “ … If $\ell$ is a snake-like line, connecting two mutually timelike points $P_{1}$ and $P_{2}$ but everywhere spacelike, and ${\mathcal{B}}$ is a tube around $\ell$, of a small diameter, then it is rather likely that any solution of the [massless scalar] wave equation vanishing in ${\mathcal{B}}$ might always vanish in the double light cone spanned by $P_{1}$, and $P_{2}$. If such a conjecture turns out to be true, then we immediately have the corresponding theorem for $R({\mathcal{B}})$.” In our terminology, the proposal is that if $\Delta$ is the double cone or causal diamond with vertices $P_{1}$ and $P_{2}$, then ${\mathcal{A}}_{\mathrm{add}}({\mathcal{B}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{B}}\cup\Delta)$. This follows from arguments in Araki’s paper if it is true that any solution of the massless scalar wave equation vanishing in ${\mathcal{B}}$ also vanishes in $\Delta$. This statement does not follow from Holmgren uniqueness in any obvious way and its validity remains unclear sixty years later.

In general, what extension of the timelike tube theorem is conceivable? For any set ${\mathcal{U}}$ in a spacetime $M$, one writes ${\mathcal{U}}^{\prime}$ for the set of points in $M$ that are spacelike separated from ${\mathcal{U}}$. Then ${\mathcal{U}}^{\prime\prime}=({\mathcal{U}}^{\prime})^{\prime}$ is called the causal completion of ${\mathcal{U}}$. For any open set ${\mathcal{U}}$, since ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$ commutes with ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime})$, clearly any statement that ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{V}})$ for some open set ${\mathcal{V}}$ implies that ${\mathcal{A}}_{\mathrm{add}}({\mathcal{V}})$ commutes with ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime})$. If one is hoping to make a general statement that would apply to any quantum field theory, this really forces ${\mathcal{V}}\subset{\mathcal{U}}^{\prime\prime}$, since local operators outside of ${\mathcal{U}}^{\prime\prime}=({\mathcal{U}}^{\prime})^{\prime}$ typically do not commute with ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime})$. So the most optimistic statement that one might hope for would be ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime\prime})$.

For example, if ${\mathcal{U}}$ is a timelike curve in Minkowski space, then ${\mathcal{E}}({\mathcal{U}})={\mathcal{U}}^{\prime\prime}$, and therefore the timelike tube theorem does indeed give ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime\prime})$. In general, ${\mathcal{E}}({\mathcal{U}})\subset{\mathcal{U}}^{\prime\prime}$, but ${\mathcal{U}}^{\prime\prime}$ can be strictly bigger. Indeed, in Araki’s example, ${\mathcal{B}}^{\prime\prime}$ is strictly bigger than ${\mathcal{E}}({\mathcal{B}})$. His conjecture would be a special case of ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime\prime})$, in a situation in which that does not follow directly from the known statement of the timelike tube theorem.

A statement along the lines of ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime\prime})$ would be very attractive, as it would combine ordinary causality with the timelike tube theorem. Extending from a spacelike pancake to its domain of dependence (fig. 4(a)) and from a timelike tube to its timelike envelope (fig. 4(b)) can be regarded as two different cases of extending from ${\mathcal{U}}$ to ${\mathcal{U}}^{\prime\prime}$. However, there are some easy counterexamples to ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime\prime})$.

One type of counterexample¹²¹²12This example is relatively well known but the original reference is not clear. A version of the example of fig. 6 was discussed in Stroh . arises if ${\mathcal{U}}$ is not connected. In Minkowski space in any even dimension ${\sf D}$, let ${\mathcal{O}}$ be a small neighborhood of the origin. Let ${\mathcal{U}}$ be any open set that contains points to the future of ${\mathcal{O}}$ and also points to the past of ${\mathcal{O}}$, but none that can be reached from ${\mathcal{O}}$ by a null geodesic. Then ${\mathcal{O}}\subset{\mathcal{U}}^{\prime\prime}$, so ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime\prime})$ would predict that ${\mathcal{A}}_{\mathrm{add}}({\mathcal{O}})\subset{\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$. In the theory of a massless free scalar field $\phi$, however, this statement is false. By Huygen’s principle along with commutativity at spacelike separation, the commutator function $G(x,y)=[\phi(x),\phi(y)]$ in that theory is supported on the light cone (for ${\sf D}$ even), so it vanishes for $x\in{\mathcal{O}}$, $y\in{\mathcal{U}}$. Thus in this situation, ${\mathcal{A}}_{\mathrm{add}}({\mathcal{O}})$ commutes with ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$, rather than being contained in ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$.

In two dimensions, a small variant of this gives a counterexample with ${\mathcal{U}}$ connected. In fact, the setup is closely related to that suggested by Araki. Consider the spacetime $M={\mathbb{R}}\times S^{1}$, with a product metric, where ${\mathbb{R}}$ parametrizes time and $S^{1}$ parametrizes space. Let the point $P_{2}$ be slightly to the future of $P_{1}$, and let $\ell$ be a spacelike curve that starts at $P_{1}$, spirals once around $S^{1}$ to the right, and ends at $P_{2}$. Let ${\mathcal{B}}$ be an open set that is a slight thickening of $\ell$, and let $\Delta$ be the causal diamond with vertices $P_{1},P_{2}$. Finally, let ${\mathcal{O}}\subset\Delta$ be an open set small enough that any right-moving null geodesic that intersects ${\mathcal{O}}$ does not intersect ${\mathcal{B}}$ (fig 6). Then ${\mathcal{O}}\subset\Delta\subset{\mathcal{B}}^{\prime\prime}$. In two-dimensional quantum field theory, it is possible to have a local field $J$ with the property that $[J(x),J(y)]$ vanishes unless the points $x$ and $y$ are connected by a right-moving null geodesic. For example, $J$ could be a right-moving conserved current (or a chiral component of the stress tensor) in a conformally invariant theory. Let $f$ be a smearing function supported in ${\mathcal{O}}$, and consider the operator $J_{f}=\int{\mathrm{d}}^{2}xf(x)J(x)\in{\mathcal{A}}_{\mathrm{add}}({\mathcal{O}})\subset{\mathcal{A}}_{\mathrm{add}}({\mathcal{B}}^{\prime\prime})$. This operator commutes with ${\mathcal{A}}_{\mathrm{add}}({\mathcal{B}})$, rather than being contained in ${\mathcal{A}}_{\mathrm{add}}({\mathcal{B}})$, as one would expect based on ${\mathcal{A}}_{\mathrm{add}}({\mathcal{B}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{B}}^{\prime\prime})$.

In the context of the present article, we are not primarily interested in applying the timelike tube theorem or a hypothetical generalization to an arbitrary open set. We are primarily interested in observables along the timelike worldline $\gamma$ of an observer. The timelike tube theorem tells us that it does not matter whether we consider a timelike curve $\gamma$ or an open set that is a suitable slight thickening of it, so we will express the following in terms of the algebra associated to a curve. The example just discussed can be slightly modified to give a counterexample in that context. If $P_{2}$ is farther to the future of $P_{1}$ than was assumed so far, then the curve $\gamma$ that wraps around the $S^{1}$ (in general any number of times) en route from $P_{1}$ to $P_{2}$ can be timelike, but almost null. Then the timelike envelope ${\mathcal{E}}(\gamma)$ is a small neighborhood of $\gamma$, but its causal completion ${\mathcal{B}}^{\prime\prime}$, which is the same as $\gamma^{\prime\prime}$ if ${\mathcal{B}}$ is suitably chosen, wraps all the way around the $S^{1}$. The statement ${\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}(\gamma))={\mathcal{A}}_{\mathrm{add}}(\gamma^{\prime\prime})$ is false in general just as before.

In this example, $\gamma^{\prime\prime}$ is the same as the causal diamond¹³¹³13Here $\Delta(\gamma)=J^{+}(\gamma)\cap J^{-}(\gamma)$ is the intersection of the past and future of $\gamma$, or equivalently $J^{-}(P_{2})\cap J^{+}(P_{1})$. $\Delta(\gamma)$ with vertices $P_{1},P_{2}$, so in particular ${\mathcal{E}}(\gamma)\subsetneqq\Delta(\gamma)$. Thus, this example shows that in the statement of the timelike tube theorem, in general ${\mathcal{E}}(\gamma)$ cannot be replaced with¹⁴¹⁴14Similarly, ${\mathcal{E}}(\gamma)\subsetneqq\Delta(\gamma)$ in a simply-connected spacetime $M={\mathbb{R}}\times S^{2}$, with metric ${\mathrm{d}}s^{2}=-{\mathrm{d}}t^{2}+{\mathrm{d}}x^{2}+{\mathrm{d}}y^{2}+\epsilon{\mathrm{d}}z^{2}$, with $x^{2}+y^{2}+z^{2}=1$, $\epsilon\ll 1$. Embedding ${\mathbb{R}}\times S^{1}$ in ${\mathbb{R}}\times S^{2}$ at $z=0$ and choosing $\gamma$ as before, again $\Delta(\gamma)$ is much larger than ${\mathcal{E}}(\gamma)$ if $P_{2}$ is sufficiently far to the future of $P_{1}$. However, as in Araki’s example, it is not clear in this case whether it is always true that ${\mathcal{A}}_{\mathrm{add}}(\gamma)={\mathcal{A}}_{\mathrm{add}}(\Delta(\gamma))$. Free field theory does not provide an immediate counterexample. $\Delta(\gamma)$.

So some simple generalizations of the timelike tube theorem are false in a general quantum field theory, and others, such as Araki’s conjecture, have unclear status. However, the following somewhat fanciful remarks come to mind. Let us go back to the example in which ${\mathcal{U}}$ is not connected and is, for example, the union of a small ball ${\mathcal{B}}_{q}$ around a point $q$ and a small ball ${\mathcal{B}}_{p}$ around a point $p$ to its future. (Similar remarks apply in the other examples.) In this case, for ${\sf D}$ even, massless free field theory provides a counterexample to ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime\prime})$, but the argument was limited to massless free field theory and would not generalize in an obvious way to any other theory. Consider then in a more generic theory an observer¹⁵¹⁵15In this paragraph, unlike the rest of the article, we consider an observer probing the spacetime from outside, not an observer who propagates on a worldline in the spacetime. who has the capability to manipulate the quantum fields in an arbitrary fashion, but only in ${\mathcal{U}}={\mathcal{B}}_{p}\cup{\mathcal{B}}_{q}$. A strategy this observer can follow is to inject into spacetime a probe in the region ${\mathcal{B}}_{q}$, directed on a trajectory $\gamma$ that will carry it to ${\mathcal{B}}_{p}$, and equipped and programmed to make some chosen measurement and record the result. Then the observer retrieves the probe at ${\mathcal{B}}_{p}$ and reads the answer. Does this construction along with the timelike tube theorem prove that ${\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}(\gamma))\subset{\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$? Though we assume no particular limit on the technological capabilities of the observer, we assume that whatever happens in a part of spacetime to which the observer does not have direct access is governed by the theory that is being probed. Thus in particular the probe that the observer injects into spacetime in ${\mathcal{B}}_{q}$ must be something that can be built in this theory. A complex probe cannot be built in free field theory, so there is no tension between existence of this protocol and our earlier observations about free field theory. However, in a sufficiently complex theory – possibly any theory that encompasses the Standard Model, for example – this protocol does indeed hint that ${\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}(\gamma))\subset{\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$. Actually, the observer can choose $\gamma$ at will (assuming that the probe can be equipped with a rocket engine and programmed to travel on a pre-chosen trajectory), and more generally the observer could inject into the system several probes with pre-chosen trajectories $\gamma_{i}$ from ${\mathcal{B}}(q)$ to ${\mathcal{B}}(p)$, each designed and programmed to carry out a particular quantum operation, and then the observer can collect the probes in ${\mathcal{B}}(p)$ and process their (possibly quantum) output at will. All this suggests that in a theory that is sufficiently complex, possibly in the end ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}^{\prime\prime})$ in general.

There is actually a manifestation of the timelike tube theorem that has been much discussed in the literature. This is causal wedge reconstruction, or HKLL reconstruction, in the context of the AdS/CFT correspondence BDHM ; B ; Bal ; HKLL ; HKLL2 ; KLL ; HMPS ; Mor ; H .

In the AdS/CFT correspondence, one considers a conformal field theory on a globally hyperbolic spacetime $M$ of dimension ${\sf D}$. AdS/CFT duality says that an appropriate conformal field theory on $M$ is equivalent to a gravitational theory formulated on a spacetime $X$ that has $M$ for its conformal boundary, and that is globally hyperbolic in the asymptotically AdS sense. In fact, in AdS/CFT duality, one has to consider all possible $X$’s that have a given conformal boundary $M$, but for our purposes here, we can assume that a particular $X$ is important. Causal wedge reconstruction applies in a semiclassical situation in which $X$ can be viewed, in leading order, as a definite spacetime in which quantum fields are propagating.

Let $S$ be a Cauchy hypersurface in $M$, $B$ an open set in $S$, and ${\mathcal{U}}$ the domain of dependence of $B$ in $M$. Then ${\mathcal{U}}$ is its own timelike envelope in $M$, so the timelike tube theorem, applied directly to the region ${\mathcal{U}}$ in the CFT on $M$, says nothing of interest. However, if $M$ is the conformal boundary of $X$ and ${\mathcal{U}}\subset M$, then it makes sense to consider the timelike envelope ${\mathcal{E}}_{X}({\mathcal{U}})$ of ${\mathcal{U}}$ in $X$ (fig. 7). In its simplest form, causal wedge reconstruction then asserts that ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})={\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}_{X}({\mathcal{U}}))$. This can be viewed as a composite of two statements: (1) the basic AdS/CFT duality expressing local operators in $M$ as limits of local operators in $X$, and (2) the timelike tube theorem applied to quantum fields in $X$.

To explain this, we can proceed as follows. First, it is possible to thicken ${\mathcal{U}}$ slightly to an open set ${\mathcal{U}}_{X}\subset X$ such that ${\mathcal{E}}_{X}({\mathcal{U}})={\mathcal{E}}({\mathcal{U}}_{X})$. The timelike tube theorem says that ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}_{X})$ does not depend on the precise choice of ${\mathcal{U}}_{X}$, and always equals ${\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}({\mathcal{U}}_{X}))$. Since this is the case, we can take a limit in which ${\mathcal{U}}_{X}$ becomes arbitrarily “thin.” The basic AdS/CFT relation between local operators on $X$ and local operators on $M$ can be interpreted as a statement

where $\lim_{{\mathcal{U}}_{X}\downarrow{\mathcal{U}}}$ refers to a limit in which the bulk open set ${\mathcal{U}}_{X}$ collapses down to the boundary open set ${\mathcal{U}}$. On the left hand side, ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}_{X})$ is the algebra generated by bulk local operators in the bulk region ${\mathcal{U}}_{X}$, and on the right hand side, ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}})$ is the algebra generated by boundary local operators in the boundary region ${\mathcal{U}}$. Eqn. (10) is a way to express the fact that boundary local operators are the boundary limits of bulk local operators. Since the timelike tube theorem tells us that ${\mathcal{A}}_{\mathrm{add}}({\mathcal{U}}_{X})={\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}({\mathcal{U}}_{X}))={\mathcal{A}}_{\mathrm{add}}({\mathcal{E}}_{X}({\mathcal{U}}))$ regardless of the choice of ${\mathcal{U}}_{X}$, the limit in eqn. (10) is trivial and we learn that

In a globally hyperbolic spacetime that satisfies the null energy condition, ${\mathcal{E}}_{X}({\mathcal{U}})$ is the causal wedge of ${\mathcal{U}}$, and eqn. (11) is the usual statement of causal wedge reconstruction. However, this requires some explanation,¹⁶¹⁶16The following proof is not needed in the rest of the article. Facts used in the proof are explained, for example, in Wald ; GaoWald ; LightRays . On compactness of spaces of causal curves, see for instance sections 2 and 3.3 of LightRays ; on the fact that a causal curve that satisfies a promptness condition is a null geodesic without focal points, see sections 5.1 and 5.2 of that article; on the completeness of a null geodesic in an asymptotically AdS spacetime $X$ whose ends are on the conformal boundary of $X$, see section 7.3; on the fact that a complete null geodesic along which the null energy condition is satisfied as a strict inequality must have focal points, see section 8.2. since the usual definition of the causal wedge is slightly different. The causal wedge of ${\mathcal{U}}$, which we will denote as ${\mathcal{C}}({\mathcal{U}})$, is usually defined to consist of all points $r\in X$ that are contained in a causal curve $\gamma\subset X$ between two points $q,p\in{\mathcal{U}}$, say with $p$ to the future of $q$. (Equivalently, ${\mathcal{C}}({\mathcal{U}})$ is the intersection of the past and future of ${\mathcal{U}}$ in $X$.) Instead, ${\mathcal{E}}_{X}({\mathcal{U}})$ contains all points $r\in X$ that are contained in a causal curve $\gamma\subset X$ between points $q,p\in{\mathcal{U}}$ such that $\gamma$ can be deformed, through a family of causal curves with fixed endpoints, to a causal curve entirely in $M$ (and therefore in ${\mathcal{U}}$). Thus to show that ${\mathcal{E}}_{X}({\mathcal{U}})={\mathcal{C}}({\mathcal{U}})$, we have to show that any causal curve $\gamma\subset X$ that starts and ends at points $q,p\in{\mathcal{U}}$ can be deformed, through a family of causal curves with those fixed endpoints, to a causal curve in $M$. To prove this, let ${\mathcal{R}}_{qp}$ be the space of causal curves in $X$ with initial and final endpoints $q,p$. Pick a causal curve $\zeta_{qp}\subset{\mathcal{U}}$ from $q$ to $p$, and let ${\mathcal{T}}_{\zeta}$ be the space of causal curves in $X$ with initial endpoint $q$ and any final endpoint $s\in\zeta_{qp}$. A causal curve from $q$ to $s$ can be converted to a causal curve from $q$ to $p$ by gluing on the segment $\zeta_{sp}$ of $\zeta_{qp}$. This operation maps ${\mathcal{T}}_{\zeta}$ continuously to ${\mathcal{R}}_{qp}$; on the other hand, ${\mathcal{R}}_{qp}\subset{\mathcal{T}}_{\zeta}$. So a causal curve $\gamma\subset X$ with endpoints $q,p$ can be deformed in ${\mathcal{R}}_{qp}$ to a curve entirely in $M$ if and only if it can be so deformed in ${\mathcal{T}}_{\zeta}$. Hence, to prove that ${\mathcal{E}}_{X}({\mathcal{U}})={\mathcal{C}}({\mathcal{U}})$, it suffices to show that any causal curve $\gamma\subset X$ with endpoints $q,p$ can be deformed in ${\mathcal{T}}_{\zeta}$ to a curve entirely in $M$. This question is topological in nature: is $\gamma$ in the connected component of ${\mathcal{T}}_{\zeta}$ that contains curves that lie entirely in $M$? So the answer is invariant under an infinitesimal perturbation of $X$, and we can make such a perturbation to ensure that the null energy condition is satisfied in $X$ as a strict inequality (not as an equality). We will see later exactly where in $X$ the perturbation should be made. On ${\mathcal{T}}_{\zeta}$, one can define the following continuous function $\varphi$: if $\gamma_{*}\in{\mathcal{T}}_{\gamma}$ has endpoints $q,s\in\zeta_{qp}$, then $\varphi(\gamma_{*})$ is the proper time elapsed from $q$ to $s$ along $\zeta_{qp}$. An important detail is that we allow the case of a causal curve that consists of only one point. Thus in particular ${\mathcal{T}}_{\zeta}$ contains a point $q_{*}$ that corresponds to a causal curve consisting only of the point $q$. The point $q_{*}$ is the absolute minimum of $\varphi$, since $\varphi(q_{*})=0$, and at other points in ${\mathcal{T}}_{\zeta}$, $\varphi>0$. The purpose of including the point $q_{*}$ in the definition of ${\mathcal{T}}_{\zeta}$ is to ensure that ${\mathcal{T}}_{\zeta}$ is compact; this compactness follows from the fact that the initial endpoint of a curve $\gamma_{*}\in{\mathcal{T}}_{\zeta}$ is fixed and its final endpoint $s$ ranges over the compact set $\zeta_{qp}$, along with the fact that in a globally hyperbolic spacetime, the space of causal curves with specified endpoints is compact. Compactness of ${\mathcal{T}}_{\zeta}$ ensures that in every connected component of ${\mathcal{T}}_{\zeta}$, the nonnegative function $\varphi$ has an absolute minimum. Any $\gamma\in{\mathcal{T}}_{\zeta}$ can be deformed in ${\mathcal{T}}_{\zeta}$ to the minimum of $\varphi$ in its connected component. We will conclude the proof by showing that the point $q_{*}$ is the unique local minimum of the function $\varphi$, implying that the local minimum of $\varphi$ to which $\gamma$ can be deformed in ${\mathcal{T}}_{\zeta}$ is actually the absolute minimum $q_{*}$. This in particular implies that $\gamma$ can be deformed in ${\mathcal{T}}_{\zeta}$ to a causal curve entirely in $M$, as we wished to show. To show that $\varphi$ has no other local minimum, we note that any point in ${\mathcal{T}}_{\zeta}$ other than $q_{*}$ is a nontrivial causal curve $\widetilde{\gamma}$ with distinct endpoints in $M$. In general, if the initial point of a causal curve $\widetilde{\gamma}$ is specified (here $q$) and the final point of the curve is constrained by a condition of “promptness” (here $\widetilde{\gamma}$ is supposed to end along $\zeta_{qp}$, and the condition for it to be a local minimum of $\varphi$ means that it arrives on $\zeta_{qp}$ sooner than any nearby causal curve from $q$; this is the promptness condition), then $\widetilde{\gamma}$ must be a null geodesic without focal points. However, in an asymptotically AdS spacetime, any null geodesic between distinct points on the conformal boundary is complete in both directions. As remarked earlier, we can assume that the null energy condition in $X$ is satisfied along $\widetilde{\gamma}$ as a strict inequality. A null geodesic that is complete in both directions and along which the null energy condition is satisfied as a strict inequality always has focal points. So the function $\varphi$ can have no local minimum other than its absolute minimum $q_{*}$, completing the proof.