Adversarial Style Augmentation for Domain Generalization

Yabin Zhang¹, Bin Deng², Ruihuang Li¹, Kui Jia², Lei Zhang¹

Abstract

It is well-known that the performance of well-trained deep neural networks may degrade significantly when they are applied to data with even slightly shifted distributions. Recent studies have shown that introducing certain perturbation on feature statistics (e.g., mean and standard deviation) during training can enhance the cross-domain generalization ability. Existing methods typically conduct such perturbation by utilizing the feature statistics within a mini-batch, limiting their representation capability. Inspired by the domain generalization objective, we introduce a novel Adversarial Style Augmentation (ASA) method, which explores broader style spaces by generating more effective statistics perturbation via adversarial training. Specifically, we first search for the most sensitive direction and intensity for statistics perturbation by maximizing the task loss. By updating the model against the adversarial statistics perturbation during training, we allow the model to explore the worst-case domain and hence improve its generalization performance. To facilitate the application of ASA, we design a simple yet effective module, namely AdvStyle, which instantiates the ASA method in a plug-and-play manner. We justify the efficacy of AdvStyle on tasks of cross-domain classification and instance retrieval. It achieves higher mean accuracy and lower performance fluctuation. Especially, our method significantly outperforms its competitors on the PACS dataset under the single source generalization setting, e.g., boosting the classification accuracy from 61.2% to 67.1% with a ResNet50 backbone. Our code will be available at https://github.com/YBZh/AdvStyle.

1 Introduction

Deep neural networks (DNN) have exhibited impressive performance on many vision tasks, especially when the training and test data follow the same distribution, i.e., the so-called assumption of independent and identical distribution (IID). Unfortunately, the IID assumption may not hold in practical applications. For instance, detection models trained on samples collected in sunny days may be applied to data collected in bad weather (e.g., rainy days). In such cross-domain application scenarios, the DNN models may suffer from significant performance degradation. To solve this issue, domain generalization (DG) has been introduced to improve the generalization performance of DNN models to unseen test domains, and many DG methods have been developed recently (Motiian et al. 2017; Li et al. 2018b; Gong et al. 2019; Zhao et al. 2020; Li et al. 2018a; Du et al. 2020; Volpi et al. 2018b; Yue et al. 2019; Zhou et al. 2020; Geirhos et al. 2019; Nam et al. 2021; Zhou et al. 2021c).

Generally speaking, DG aims to learn a model from the source domain(s) while ensuring that the learned model could perform well to any unseen test domains. The DG problem can be conventionally solved by learning domain invariant features (Motiian et al. 2017; Li et al. 2018b; Gong et al. 2019; Zhao et al. 2020), employing meta-learning strategies (Li et al. 2018a; Du et al. 2020), performing data augmentations (Volpi et al. 2018b; Yue et al. 2019; Zhou et al. 2020; Geirhos et al. 2019; Nam et al. 2021; Zhou et al. 2021c), and so on (Wang et al. 2021a; Zhou et al. 2021a). Recently, performing style augmentation in feature space by conducting feature statistics perturbation has attracted increasing attention due to its simplicity and efficacy (Nuriel, Benaim, and Wolf 2021; Zhou et al. 2021c; Zhang et al. 2022; Li et al. 2022). Specifically, it has been observed in the application of style transfer (Huang and Belongie 2017; Dumoulin, Shlens, and Kudlur 2016) that feature statistics (e.g., mean and standard deviation) characterize the style information, and changing such statistics of image features will result in style-changed but content-preserved output images. Inspired by this observation, researchers have proposed to perform feature statistics perturbation to introduce style-augmented samples (Nuriel, Benaim, and Wolf 2021; Zhou et al. 2021c; Zhang et al. 2022; Li et al. 2022; Chen et al. 2022; Zhong et al. 2022). By expanding the training data with these style-augmented samples, improved generalization performance of DNN models has been observed (Nuriel, Benaim, and Wolf 2021; Zhou et al. 2021c; Zhang et al. 2022; Li et al. 2022).

In such a statistics perturbation-based DG framework, the perturbation strategy is of vital importance. Nuriel et al. (Nuriel, Benaim, and Wolf 2021) and Zhou et al. (Zhou et al. 2021c) respectively introduced the statistics perturbation by randomly swapping or linearly interpolating statistics of two instances within a mini-batch. Li et al. (Li et al. 2022) sampled the feature statistics perturbation from Gaussian distributions, the means and standard deviations of which are estimated from the current mini-batch. Although improved performance has been achieved, existing methods, unfortunately, constrain the representation space of feature statistics perturbation within that of the current mini-batch, limiting the diversity of style augmentations.

To explore a broader style space beyond that spanned by batch statistics, we propose to generate more diverse statistics perturbation. Similar to (Li et al. 2022), we model the feature statistics (i.e., mean and standard deviation) as Gaussian distributions and utilize the vanilla feature statistics as the means of these Gaussians. In (Li et al. 2022), the standard deviations of these Gaussians are estimated from the current mini-batch. In contrast, inspired by the DG objective (see Equ. (6)), we model these standard deviations as learnable parameters and optimize them via adversarial training, resulting in the Adversarial Style Augmentation (ASA) method. Specifically, by maximizing the task loss w.r.t. the learnable standard deviations, we approach the most sensitive perturbation direction and intensity (i.e., the worst-case domain). Meanwhile, by minimizing the task loss w.r.t. the vanilla task model, we update the model against the worst-case domain perturbation. The model is expected to generalize well to tough unseen test domains if it could generalize to the worst-case domain.

The proposed ASA method could be directly implemented by conducting the maximization and minimization steps iteratively (please refer to Fig. 2 for more details). As illustrated in Sec. 4.3, such an iterative optimization strategy could lead to outstanding performance. To facilitate the application of ASA in practice, we take a step further and propose a simple yet effective module, namely AdvStyle, to enable end-to-end training of ASA. Specifically, we input the learnable standard deviations into Gradient Reverse Layers (GRL) (Ganin and Lempitsky 2015; Ganin et al. 2016) before utilizing them to generate statistics perturbations (see Equ. (8) and Fig. 3 for more information). By minimizing the task objective solely, the objective minimization w.r.t. the vanilla model parameters and the maximization w.r.t. the learnable standard deviations are achieved simultaneously, thanks to the gradient reverse function of GRL. The AdvStyle could be easily implemented and it works in a plug-and-play manner.

We apply the proposed method on tasks of cross-domain classification and instance retrieval. On standard DG benchmarks, ASA improves its competitors with higher mean accuracy and lower performance fluctuation. Especially, a significant performance boost is observed on the PACS dataset under the single source generalization setting (e.g., the performance is boosted from 61.2% to 67.1% with a ResNet50 backbone), validating the effectiveness of our proposed ASA method. We summarize our contributions as follows:

•

We propose a novel Adversarial Style Augmentation (ASA) method, which could explore a broader style space by performing feature statistics perturbation with less constraints via adversarial training.
•

To facilitate the application of ASA in practice, we introduce an AdvStyle module so that ASA can be used in a plug-and-play manner.
•

We perform detailed analyses on standard benchmarks of cross-domain classification and instance retrieval. On top of improved mean accuracy, ASA presents lower performance fluctuation, justifying its effectiveness.

Refer to caption — Figure 1: A toy example on the comparison across different style augmentation-based DG methods. In MixStyle (Zhou et al. 2021c), new styles are introduced by linearly interpolating statistics between two styles. pAdaIN (Nuriel, Benaim, and Wolf 2021) is a special case of (Zhou et al. 2021c), where only edge points along the linear connection line are considered via statistics swapping. In (Li et al. 2022), the uncertainty of statistics is modeled via multi-variant Gaussian, whose mean and standard deviation are instantiated with the vanilla statistics points and batch standard deviation, respectively. All these methods limit the representation space of statistics within the space spanned by the mini-batch. In contrast, we approach a broader style space by exploring statistics perturbation along the most sensitive direction and intensity that maximize the task objective.

2 Related Work

Domain generalization. Domain generalization (DG) targets at developing robust DNN models that can perform well on unseen test domains. The representative DG methods learn domain-invariant feature representations (Motiian et al. 2017; Li et al. 2018b; Gong et al. 2019; Zhao et al. 2020), or employ meta-learning (Li et al. 2018a; Du et al. 2020), or perform data augmentation (Volpi et al. 2018b; Yue et al. 2019; Zhou et al. 2020; Geirhos et al. 2019; Wang et al. 2021b; Nam et al. 2021; Zhou et al. 2021c). Our method adopts the data augmentation strategy, more specifically, feature-based augmentation (Nuriel, Benaim, and Wolf 2021; Zhou et al. 2021c; Li et al. 2022; Zhang et al. 2022). It has been empirically observed in the task of style transfer (Huang and Belongie 2017; Dumoulin, Shlens, and Kudlur 2016) that feature statistics can characterize the image styles, and the perturbation on such statistics could yield style-changed but semantic-preserved output. Based on such observation, researchers started to introduce style/distribution augmented training samples by feature statistics perturbation into DG model training (Nuriel, Benaim, and Wolf 2021; Zhou et al. 2021c; Li et al. 2022; Zhang et al. 2022).

To achieve feature statistics perturbation, Nuriel et al. (Nuriel, Benaim, and Wolf 2021) proposed to swap feature statistics between instances within a mini-batch and, similarly, Zhou et al. (Zhou et al. 2021c) linearly interpolated feature statistics between instances. Besides the first and second order statistics used in (Nuriel, Benaim, and Wolf 2021; Zhou et al. 2021c), Zhang et al. (Zhang et al. 2022) implicitly considered high-order statistics for more effective statistics perturbation. Although improved generalization performance has been observed, the augmented statistics highly rely on the observed feature statistics of training instances, limiting the diversity of statistics. To introduce more diverse statistics perturbations, Li et al. (Li et al. 2022) modeled the feature statistics as multi-variate Gaussian distributions and randomly sampled statistics variants from the Gaussians, as illustrated in Fig. 1. This expands the statistics space of instances, which can be described by the standard deviations of Gaussians. However, these Gaussian standard deviations are estimated from the mini-batch statistics, still limiting the statistics diversity.

In this work, we solve the above mentioned problem by acquiring the Gaussian standard deviations with adversarial training. Specifically, instead of estimating Gaussian standard deviations with mini-batch statistics as in (Li et al. 2022), we model the Gaussian standard deviations as learnable parameters, leading to a less constrained statistics space. By maximizing the task objective w.r.t. these standard deviations, we explore the most sensitive direction and intensity for statistics perturbation so that the trained DNN model can perform more robustly on unseen test domains.

Adversarial training. Adversarial training was first introduced in (Goodfellow et al. 2014), where a discriminator is used to distinguish whether a sample comes from the training data or the generative models. Once the discriminator is fully confused by samples from generators, the generative models successfully recover the training data distribution. The adversarial training strategy was later adopted to align feature distributions in domain adaptation (Ganin and Lempitsky 2015; Ganin et al. 2016; Long et al. 2018), generative photo-realistic super-resolution (Ledig et al. 2017; Wang et al. 2018), data augmentation (Zhang et al. 2020; Volpi et al. 2018a; Luo et al. 2020), and so on. Different from most data augmentation methods that introduce augmented samples in the image space (Zhang et al. 2020; Luo et al. 2020), we generate augmented samples in the feature space, which is more computationally efficient. Moreover, different from the existing feature augmentation methods (Volpi et al. 2018a; Chen et al. 2021) that conduct adversarial perturbation on raw features, we adversarially change the feature statistics, resulting in specific perturbations along the style dimension. Furthermore, we propose a simple yet effective module to implement our method in a plug-and-play manner, facilitating its usage.

3 Methods

Denote by ${\bm{x}}\in\mathbb{R}^{B\times C\times HW}$ the features encoded by some stacked neural layers, and we respectively denote by $\mu({\bm{x}})\in\mathbb{R}^{B\times C}$ and $\sigma({\bm{x}})\in\mathbb{R}^{B\times C}$ the mean and standard deviation of features in each channel for an instance, where $B,C,H$ and $W$ represent the batch size, channel dimension, height and width, respectively. Specifically, $\mu({\bm{x}})$ and $\sigma({\bm{x}})$ are computed as:

	$\displaystyle\mu_{b,c}({\bm{x}})$	$\displaystyle=\frac{1}{HW}\sum_{i=1}^{HW}{\bm{x}}_{b,c,i},$		(1)
	$\displaystyle\sigma^{2}_{b,c}({\bm{x}})$	$\displaystyle=\frac{1}{HW}\sum_{i=1}^{HW}\left({\bm{x}}_{b,c,i}-\mu_{b,c}({\bm{x}})\right)^{2}$		(2)

where $\mu_{b,c}({\bm{x}})$ represent the mean in the $c$ -th channel of the $b$ -th instance, and $\sigma^{2}_{b,c}({\bm{x}})$ and ${\bm{x}}_{b,c,i}$ are similarly defined.

It is found in (Huang and Belongie 2017; Dumoulin, Shlens, and Kudlur 2016; Lu et al. 2019) that the feature statistics, e.g., the mean and standard deviation in Equ. (1) and Equ. (2), can characterize the style/distribution of input images, such as lighting conditions and textures. Therefore, performing statistics perturbation could generate style-changed but semantic-preserved augmented samples, providing an effective method for DG tasks (Zhou et al. 2021c; Nuriel, Benaim, and Wolf 2021; Li et al. 2022). Nonetheless, existing methods along this line (Zhou et al. 2021c; Nuriel, Benaim, and Wolf 2021; Li et al. 2022) mostly utilize feature statistics within the mini-batch to compute statistics perturbation, limiting the statistics representation capacity. In the following, we propose to perform statistics perturbation via adversarial training to overcome this limitation.

3.1 Adversarial Style Augmentation

Following (Zhou et al. 2021c; Nuriel, Benaim, and Wolf 2021; Li et al. 2022), we implement our style augmentation module (SAM) based on the framework of AdaIN (Huang and Belongie 2017), which performs style transformation by replacing the feature statistics as:

{\bm{x}}_{t}=\sigma_{t}\left(\frac{{\bm{x}}-\mu({\bm{x}})}{\sigma({\bm{x}})}\right)+\mu_{t},

(3)

where ${\bm{x}}_{t}$ are the features with new styles decided by $\mu_{t}\in\mathbb{R}^{B\times C}$ and $\sigma_{t}\in\mathbb{R}^{B\times C}$ . Existing methods typically introduce $\mu_{t}$ and $\sigma_{t}$ with feature statistics within a mini-batch, e.g., by randomly shuffling or interpolating feature statistics across instances (Zhou et al. 2021c; Nuriel, Benaim, and Wolf 2021) or randomly sampling from a Gaussian distribution estimated from the current mini-batch (Li et al. 2022). Such strategies limit the representation capacity of $\mu_{t}$ and $\sigma_{t}$ within a small statistics space. In this paper, we aim to explore larger style spaces by introducing more diverse $\mu_{t}$ and $\sigma_{t}$ . Specifically, following (Li et al. 2022), we first model the underlying distribution of $\mu_{t}$ and $\sigma_{t}$ as the popular Gaussian with the re-parameterization trick (Kingma and Welling 2013):

	$\displaystyle\mu_{t}$	$\displaystyle=\mu({\bm{x}})+\epsilon_{\mu}\Sigma_{\mu},\quad\epsilon_{\mu}\sim\mathcal{N}(\mathbf{0},\mathbf{1}),$		(4)
	$\displaystyle\sigma_{t}$	$\displaystyle=\sigma({\bm{x}})+\epsilon_{\sigma}\Sigma_{\sigma},\quad\epsilon_{\sigma}\sim\mathcal{N}(\mathbf{0},\mathbf{1}),$		(5)

where $\Sigma_{\mu}\in\mathbb{R}^{C}$ and $\Sigma_{\sigma}\in\mathbb{R}^{C}$ control the direction and intensity of the statistics perturbation, i.e., the representation space of style augmentation. Therefore, the exploration of style space could be achieved by exploring $\Sigma_{\mu}$ and $\Sigma_{\sigma}$ .

Li et al. (Li et al. 2022) constructed $\Sigma_{\mu}$ and $\Sigma_{\sigma}$ as the standard deviations of $\mu({\bm{x}})$ and $\sigma({\bm{x}})$ along the batch dimension. Although effective, this method limits the style augmentation space to that of the current mini-batch. To overcome this limitation, we propose to explore a broader style space by imposing less constraints on $\Sigma_{\mu}$ and $\Sigma_{\sigma}$ .

In (Arjovsky et al. 2019), the DG objective is defined as:

R^{DG}(f)=\min_{f}\max_{e\in\varepsilon_{all}}R^{e}(f),

(6)

where $R^{e}(f)$ refers to the risk of model $f$ within the domain $e$ . Given the training domain(s) $\varepsilon_{tr}$ , DG aims to learn a model $f$ that performs well across a set of unseen but related domains $\varepsilon_{all}\supset\varepsilon_{tr}$ . Assuming that the unknown test domain also belongs to $\varepsilon_{all}$ , the objective of Equ. (6) suggests us to minimize the risk of the worst-case domain among $\varepsilon_{all}$ .

Inspired by the DG objective in Equ. (6), we propose to model $\Sigma_{\mu}$ and $\Sigma_{\sigma}$ as learnable parameters and optimize them via adversarial training, resulting in the following Adversarial Style Augmentation (ASA) method:

\min_{\theta}\max_{\Sigma}\mathcal{L}_{task}({\bm{x}},{\bm{y}},\theta,\Sigma),

(7)

where ${\bm{x}}$ and ${\bm{y}}$ are the input data and their corresponding labels, $\theta$ and $\Sigma$ are the parameters of the vanilla task model and the collection of all $\Sigma_{\mu}$ and $\Sigma_{\sigma}$ , respectively. $\mathcal{L}_{task}(\cdot)$ is the overall objective defined by the considered tasks. For example, $\mathcal{L}_{task}(\cdot)$ is typically instantiated as the cross-entropy loss in category classification. By learning $\Sigma$ with Equ. (7), we simultaneously explore the perturbation direction (e.g., the principal orientation direction of $\Sigma$ ) and intensity (e.g., the Euclidean norm of $\Sigma$ ), which are individually investigated in Sec. 4.3.

Let’s further clarify the relationship between the DG objective in Equ. (6) and our proposed ASA objective in Equ. (7). Since $\Sigma$ controls the representation space of the style perturbation, exploring the worst-case domain of $\varepsilon_{all}$ in Equ. (6) could be achieved by maximizing the task loss with respect to $\Sigma$ in Equ. (7). By iteratively exploring the most sensitive $\Sigma$ (i.e., the worst-case domain) for the current model and optimizing the model against such worst-case perturbation, the model is expect to generalize to the worst-case domain, and therefore to any unseen test domains.

3.2 AdvStyle

One may opt to implement the ASA method in Equ. (7) by optimizing $\theta$ and $\Sigma$ iteratively, as presented in Fig. 2. Here, we propose a simple yet effective module, namely AdvStyle, to instantiate ASA in a plug-and-play manner. Motivated by the seminal adversarial domain adaptation methods (Ganin and Lempitsky 2015; Long et al. 2018), we propose the AdvStyle module as:

{\bm{x}}_{t}=\sigma_{adv}\left(\frac{{\bm{x}}-\mu({\bm{x}})}{\sigma({\bm{x}})}\right)+\mu_{adv},

(8)

where

	$\displaystyle\mu_{adv}$	$\displaystyle=\mu({\bm{x}})+\epsilon_{\mu}GRL(\Sigma_{\mu},\lambda),\quad\epsilon_{\mu}\sim\mathcal{N}(\mathbf{0},\mathbf{1}),$		(9)
	$\displaystyle\sigma_{adv}$	$\displaystyle=\sigma({\bm{x}})+\epsilon_{\sigma}GRL(\Sigma_{\sigma},\lambda),\quad\epsilon_{\sigma}\sim\mathcal{N}(\mathbf{0},\mathbf{1}).$		(10)

where $GRL(\Sigma_{\star},\lambda)$ is the gradient reverse layer (Ganin and Lempitsky 2015), which outputs the vanilla $\Sigma_{\star}$ in the forward pass and multiplies the gradients with $-\lambda$ in the gradient back-propagation. $\lambda$ is a hyper-parameter and validated in Sec. 4.3. The gradient reverse layer is widely adopted to perform adversarial training between feature extractor and domain discriminator in domain adaptation (Ganin and Lempitsky 2015; Long et al. 2018).

To our best knowledge, we are the first to employ gradient reverse layer to perform adversarial training between style statistics (i.e., $\Sigma$ ) and the vanilla model (i.e., $\theta$ ) in DG. Similar to (Zhou et al. 2021c; Nuriel, Benaim, and Wolf 2021; Li et al. 2022), we only activate the AdvStyle module for training and deactivate it in the test stage. As discussed in Sec. 4.3, conducting ASA by simply inserting AdvStyle into the DNN models gives comparable performance to the iterative optimization-based variant (cf. Fig. 2). Therefore, we promote to conduct ASA with AdvStyle.

Method	Art	Cartoon	Photo	Sketch	Mean $\uparrow$	Std. $\downarrow$
ResNet-18	58.6 $\pm$ 2.4	66.4 $\pm$ 0.7	34.0 $\pm$ 1.8	27.5 $\pm$ 4.3	46.6	18.8
+ pAdaIN (Nuriel, Benaim, and Wolf 2021)	61.5 $\pm$ 2.1	71.2 $\pm$ 0.8	41.1 $\pm$ 1.9	33.1 $\pm$ 3.5	51.7	17.7
+ MixStyle (Zhou et al. 2021c)	61.9 $\pm$ 2.2	71.5 $\pm$ 0.8	41.2 $\pm$ 1.8	32.2 $\pm$ 4.1	51.7	18.1
+ DSU (Li et al. 2022)	63.8 $\pm$ 2.0	73.6 $\pm$ 0.5	39.1 $\pm$ 0.8	38.2 $\pm$ 1.2	53.7	17.8
+ EFDMix (Zhang et al. 2022)	63.2 $\pm$ 2.3	73.9 $\pm$ 0.7	42.5 $\pm$ 1.8	38.1 $\pm$ 3.7	54.4	17.0
+ AdvStyle (Ours)	67.8 $\pm$ 0.6	74.5 $\pm$ 0.4	45.5 $\pm$ 1.9	47.2 $\pm$ 1.6	58.7	14.6
ResNet-50	63.5 $\pm$ 1.3	69.2 $\pm$ 1.6	38.0 $\pm$ 0.9	31.4 $\pm$ 1.5	50.5	18.3
+ pAdaIN (Nuriel, Benaim, and Wolf 2021)	67.2 $\pm$ 1.7	74.9 $\pm$ 1.4	43.3 $\pm$ 0.7	36.5 $\pm$ 1.7	55.5	18.5
+ MixStyle (Zhou et al. 2021c)	67.5 $\pm$ 1.5	75.2 $\pm$ 1.3	42.8 $\pm$ 0.8	36.4 $\pm$ 1.2	55.5	18.8
+ DSU (Li et al. 2022)	71.4 $\pm$ 0.2	76.9 $\pm$ 1.3	42.8 $\pm$ 0.3	38.2 $\pm$ 1.1	57.3	19.6
+ EFDMix (Zhang et al. 2022)	75.3 $\pm$ 0.9	77.4 $\pm$ 0.8	48.0 $\pm$ 0.9	44.2 $\pm$ 2.4	61.2	17.6
+ AdvStyle (Ours)	77.3 $\pm$ 0.4	78.8 $\pm$ 0.7	50.3 $\pm$ 1.5	61.8 $\pm$ 1.2	67.1	13.6
VGG16	56.2 $\pm$ 0.5	62.7 $\pm$ 2.2	35.3 $\pm$ 0.7	47.5 $\pm$ 1.7	50.4	11.9
+ pAdaIN (Nuriel, Benaim, and Wolf 2021)	57.1 $\pm$ 1.1	63.7 $\pm$ 1.9	36.7 $\pm$ 0.8	48.7 $\pm$ 1.6	51.6	11.7
+ MixStyle (Zhou et al. 2021c)	57.3 $\pm$ 0.9	64.1 $\pm$ 1.6	37.0 $\pm$ 0.6	48.6 $\pm$ 1.8	51.8	11.7
+ DSU (Li et al. 2022)	58.3 $\pm$ 1.0	65.8 $\pm$ 1.3	38.0 $\pm$ 0.4	49.7 $\pm$ 2.8	53.0	11.9
+ EFDMix (Zhang et al. 2022)	58.9 $\pm$ 1.1	66.2 $\pm$ 0.9	38.6 $\pm$ 0.5	50.6 $\pm$ 2.3	53.6	11.8
+ AdvStyle (Ours)	61.9 $\pm$ 1.0	67.3 $\pm$ 0.6	40.8 $\pm$ 0.6	52.9 $\pm$ 2.5	55.7	11.6
JiGen (Carlucci et al. 2019)	59.7 $\pm$ 1.7	67.8 $\pm$ 0.5	38.7 $\pm$ 1.7	29.0 $\pm$ 3.2	48.8	18.0
+ DSU (Li et al. 2022)	62.6 $\pm$ 1.5	72.8 $\pm$ 0.6	42.0 $\pm$ 1.4	38.3 $\pm$ 2.6	53.9	16.5
+ AdvStyle (Ours)	68.2 $\pm$ 0.9	76.1 $\pm$ 0.5	48.4 $\pm$ 1.5	50.8 $\pm$ 1.3	60.9	13.4
FACT (Xu et al. 2021)	69.7 $\pm$ 1.2	75.2 $\pm$ 0.4	42.7 $\pm$ 1.3	48.9 $\pm$ 2.1	59.1	15.8
+ DSU (Li et al. 2022)	72.7 $\pm$ 1.1	78.3 $\pm$ 0.3	52.9 $\pm$ 1.5	62.1 $\pm$ 1.9	66.5	11.3
+ AdvStyle (Ours)	74.9 $\pm$ 0.7	79.1 $\pm$ 0.4	57.3 $\pm$ 1.4	67.4 $\pm$ 1.2	69.7	9.6

Table 1: Domain generalization results of classification on the PACS dataset under the single source generalization setting, where the listed domain is adopted for training and results are reported on the remaining three domains.

4 Experiments

In this section, we first conduct experiments on tasks of cross-domain classification and instance retrieval to justify the effectiveness of our proposed ASA method, especially the AdvStyle module. Then, ablation studies are provided to analyze the use of our method. Besides, we also justify the effectiveness of our method on the cross-domain segmentation task and generalization performance to images with corruptions in the supplementary material. All experiments are performed under the PyTorch framework on GeForce RTX 2080Ti GPUs.

4.1 Generalization on Classification

Implementation details. We conduct the classification experiments on the benchmark PACS dataset (Li et al. 2017). There are $9,991$ samples from $7$ classes and $4$ domains, i.e., Art, Cartoon, Photo, and Sketch. We closely follow (Zhou et al. 2021b) to prepare the training and test data, set up the optimization strategy, and conduct model selection. Particularly, we perform existing style augmentation-based DG methods (Nuriel, Benaim, and Wolf 2021; Zhou et al. 2021c; Li et al. 2022; Zhang et al. 2022) under the same setting for fair comparison. Experiments are conducted under the single source generalization setting, where we train models on samples of one domain and test them on the remaining three domains. We also validate the effectiveness of our method in the leave-one-domain-out setting, which is detailed in the supplementary material.

The ResNet-18, ResNet-50 (He et al. 2016) and VGG16 (Simonyan and Zisserman 2014) models pre-trained on the ImageNet dataset (Deng et al. 2009) are adopted as the backbones. We also apply our method to existing DG algorithms (Carlucci et al. 2019; Xu et al. 2021) by inserting the plug-and-play module into their backbones. Besides the widely-used mean accuracy across different tasks, we additionally report the standard deviation of classification accuracy across tasks. A smaller standard deviation of accuracy represents smaller performance fluctuation across different tasks, indicating more robust generalization ability.

Results. All results are shown in Tab. 1. Modelling the uncertainty of statistics via multi-variant Gaussian distribution (Li et al. 2022) typically outperforms those methods based on statistics interpolation (Nuriel, Benaim, and Wolf 2021; Zhou et al. 2021c) because the statistics space can be more effectively expanded by nonlinear distribution modelling, as we illustrated in Fig. 1 with the toy example. By introducing statistics perturbation via adversarial training, we further expand the potential style space towards the worst-case domain, leading to notable performance improvement. For example, by using ResNet-50 as backbone, our method boosts its closest competitor, i.e., DSU, from $57.3\%$ to $67.1\%$ on single source domain generalization, resulting in a $144\%$ relative accuracy improvement over the ResNet-50 baseline (i.e., from $6.8\%$ to $16.6\%$ ). Our method also outperforms the recent work (Zhang et al. 2022) that explores broader style spaces by utilizing high-order batch statistics, revealing the advantage of exploring style spaces beyond batch statistics. Additionally, our method achieves the lowest accuracy standard deviation across different tasks with different backbones. This smaller performance fluctuation demonstrates the robust generalization ability of our proposed method.

What’s more, it is also found that our method is complementary to existing DG approaches that adopt self-supervised regularization and data augmentation in the image space. For example, Carlucci et al. (Carlucci et al. 2019) introduced the self-supervised regularization signals by solving a jigsaw puzzle, while Xu et al. (Xu et al. 2021) proposed a Fourier-based image augmentation strategy to enhance the cross-domain generalization ability. As shown in Tab. 1, by coupling with our proposed AdvStyle, these two methods could be significantly boosted, justifying the nice plug-and-play property of our method.

4.2 Generalization on Instance Retrieval

We closely follow (Zhou et al. 2021c; Zhang et al. 2022) to perform the cross-domain instance retrieval task on person re-identification (re-ID) datasets of Market1501 (Zheng et al. 2015) and Duke (Ristani et al. 2016; Zheng, Zheng, and Yang 2017). Specifically, we conduct experiments with the OSNet (Zhou et al. 2019) and report the results of ranking accuracy and mean average precision (mAP). As illustrated in Tab. 2, our AdvStyle boosts the vanilla baseline by a large margin (e.g., the mAP is boosted from 25.0 to 32.0 on the Duke $\to$ MarKet1501 task). Compared to the common augmentation strategies (Zhong et al. ; Ghiasi, Lin, and Le 2018), the style augmentation methods (Zhou et al. 2021c; Li et al. 2022; Zhang et al. 2022) present clear advantages. More importantly, our AdvStyle significantly outperforms other style augmentation competitors (Zhou et al. 2021c; Li et al. 2022; Zhang et al. 2022), validating the effectiveness of expanding the style space via adversarial training.

Method	MarKet1501 $\to$ Duke				Duke $\to$ MarKet1501
	mAP	R1	R5	R10	mAP	R1	R5	R10
OSNet (Zhou et al. 2019)	27.9 $\pm$ 0.1	48.2 $\pm$ 0.5	62.3 $\pm$ 0.1	68.0 $\pm$ 0.1	25.0 $\pm$ 0.1	52.8 $\pm$ 0.8	70.5 $\pm$ 0.2	77.5 $\pm$ 0.4
+ RandomErase (Zhong et al. )	20.5	36.2	52.3	59.3	22.4	49.1	66.1	73.0
+ DropBlock (Ghiasi, Lin, and Le 2018)	23.1	41.5	56.5	62.5	21.7	48.2	65.4	71.3
+ MixStyle (Zhou et al. 2021c)	28.0 $\pm$ 0.3	49.5 $\pm$ 1.1	63.6 $\pm$ 0.8	68.8 $\pm$ 1.1	27.5 $\pm$ 0.2	57.4 $\pm$ 0.4	74.1 $\pm$ 0.5	80.1 $\pm$ 0.1
+ EFDMix (Zhang et al. 2022)	29.9 $\pm$ 0.1	50.8 $\pm$ 0.1	65.0 $\pm$ 0.2	70.3 $\pm$ 0.1	29.3 $\pm$ 0.3	59.5 $\pm$ 0.7	76.5 $\pm$ 0.7	82.5 $\pm$ 0.1
+ DSU (Li et al. 2022)	31.0 $\pm$ 0.2	53.0 $\pm$ 0.3	66.6 $\pm$ 0.2	71.7 $\pm$ 0.3	29.3 $\pm$ 0.2	59.9 $\pm$ 0.2	77.2 $\pm$ 0.5	82.8 $\pm$ 0.4
+ AdvStyle (Ours)	33.2 $\pm$ 0.1	55.7 $\pm$ 0.2	69.1 $\pm$ 0.4	73.5 $\pm$ 0.5	32.0 $\pm$ 0.1	63.2 $\pm$ 0.1	79.7 $\pm$ 0.2	85.0 $\pm$ 0.2

Table 2: Domain generalization results on the cross-domain person re-ID task.

4.3 Ablation and Analyses

Leave-one-domain-out generalization results
Method	Acc. (%)
AdvStyle-based ASA	87.0
Iterative optimization-based ASA	87.0
Single source generalization results
AdvStyle-based ASA	67.1
Iterative optimization-based ASA	68.1

Table 3: Comparisons between the two implementations of the ASA algorithm on PACS dataset. The test domain and training domain are listed in the leave-one-domain-out setting and single source generalization setting, respectively.

Implementations of the ASA method. We compare the two implementations of ASA, i.e., the iterative optimization strategy as shown in Fig. 2 and plugging the AdvStyle modules into DNN models. As illustrated in Tab. 3, the two implementations achieve comparable performance. Though the iterative optimization-based variant presents slightly higher accuracy, we promote the AdvStyle-based variant in practice since it instantiates the ASA in a plug-and-play manner. We adopt the AdvStyle-based variant as the default implementation of ASA in this paper.

Conv-1	Pool-1	Res-1	Res-2	Res-3	Res-4	Acc. (%)
$\checkmark$						56.6
$\checkmark$	$\checkmark$					61.9
$\checkmark$	$\checkmark$	$\checkmark$				64.4
$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$			66.3
$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$		66.4
$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$	67.1
Vanilla ResNet-50 without AdvStyle						50.5

Table 4: Ablation studies on the inserting position of AdvStyle module on the PACS dataset, where all experiments are based on ResNet-50 backbone and follow the single source generalization setting. ‘Conv-1’, ‘Pool-1’, ‘Res-1’, ‘Res-2’, ‘Res-3’, ‘Res-4’ denote whether we apply the AdvStyle after the first convolution layer, the first max pooling layer, the first residual block, the second residual block, the third residual block, the fourth residual block, respectively.

Where to apply AdvStyle. We insert AdvStyle at different positions in the ResNet backbone and present the results in Tab. 4. Consistent performance improvements over the vanilla ResNet are observed no matter where the AdvStyle is inserted. The best performance is achieved when applying the AdvStyle to all the $6$ analyzed positions, which is adopted as the default setting in this paper.

The direction and intensity of statistics perturbation. Compared to its closest competitor-DSU (Li et al. 2022), our AdvStyle introduces different directions (e.g., the principal orientation directions of $\Sigma_{\mu}$ and $\Sigma_{\sigma}$ ) and intensities (e.g., the Euclidean norms of $\Sigma_{\mu}$ and $\Sigma_{\sigma}$ ) for statistics perturbation. To investigate the impact of direction and intensity individually, we introduce the AdvStyle-Direction-Only and AdvStyle-Intensity-Only variants. In the former case, the perturbation direction is learned via our proposed adversarial training strategy, while the perturbation intensity is set with the batch statistics as DSU (Li et al. 2022). In the latter case, in contrast, we set the perturbation direction with the batch statistics as DSU (Li et al. 2022) and learn the perturbation intensity via adversarial training. As illustrated in Tab. 5, AdvStyle-Direction-Only and AdvStyle-Intensity-Only outperform the DSU by 7.6% and 4.3%, respectively, indicating that exploring perturbation direction is more effective than exploring the perturbation intensity. The best result is achieved with AdvStyle by exploring both perturbation direction and intensity simultaneously.

Method	Acc. (%)
DSU (Li et al. 2022)	57.3
AdvStyle-Intensity-Only	61.6
AdvStyle-Direction-Only	64.9
AdvStyle	67.1

Table 5: Domain generalization performance on the PACS dataset. Please refer to the main text for the definitions of AdvStyle-Intensity-Only and AdvStyle-Direction-Only.

Visualization. As illustrated in Fig. 4, a broader style space is successfully achieved by using AdvStyle, which is qualitatively validated by the enlarged overlap regions across domains and quantitatively justified by the reduced $\mathcal{A}$ -distance (Ben-David et al. 2010).

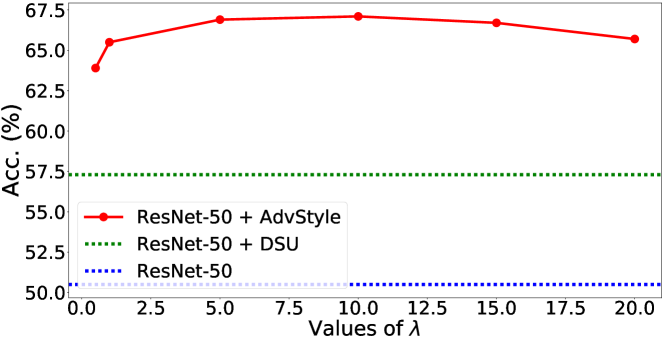
Analyses on the hyper-parameter $\lambda$ . The hyper-parameter $\lambda$ controls the strength of statistics perturbation. As illustrated in Fig. 5, our method performs stable and significantly outperforms baselines within a large range of $\lambda$ (e.g., $0.5\leq\lambda\leq 20$ ). We empirically find that $\lambda=5$ achieves good results across a large range of tasks, which is adopt the default setting in this paper.

5 Conclusions

To expand the potential statistics space for more diverse style augmentations, we proposed a novel style augmentation method, namely Adversarial Style Augmentation (ASA), by performing feature statistics perturbation via adversarial training. To facilitate the application of ASA in practice, we further introduced a novel module, namely AdvStyle, to instantiate ASA in a plug-and-play manner. ASA outperformed existing style augmentation methods on tasks such as classification and instance retrieval. It was also found that expanding style spaces along the direction dimension is more effective than the intensity dimension, which may inspire more studies on the style space exploration.

References

Arjovsky et al. (2019) Arjovsky, M.; Bottou, L.; Gulrajani, I.; and Lopez-Paz, D. 2019. Invariant risk minimization. arXiv preprint arXiv:1907.02893.
Ben-David et al. (2010) Ben-David, S.; Blitzer, J.; Crammer, K.; Kulesza, A.; Pereira, F.; and Vaughan, J. W. 2010. A theory of learning from different domains. Machine learning, 79(1): 151–175.
Carlucci et al. (2019) Carlucci, F. M.; D’Innocente, A.; Bucci, S.; Caputo, B.; and Tommasi, T. 2019. Domain generalization by solving jigsaw puzzles. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2229–2238.
Chen et al. (2022) Chen, C.; Li, Z.; Ouyang, C.; Sinclair, M.; Bai, W.; and Rueckert, D. 2022. MaxStyle: Adversarial Style Composition for Robust Medical Image Segmentation. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2022: 25th International Conference, Singapore, September 18–22, 2022, Proceedings, Part V, 151–161. Springer.
Chen et al. (2021) Chen, T.; Cheng, Y.; Gan, Z.; Wang, J.; Wang, L.; Wang, Z.; and Liu, J. 2021. Adversarial feature augmentation and normalization for visual recognition. arXiv preprint arXiv:2103.12171.
Deng et al. (2009) Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; and Fei-Fei, L. 2009. Imagenet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition, 248–255. Ieee.
Du et al. (2020) Du, Y.; Xu, J.; Xiong, H.; Qiu, Q.; Zhen, X.; Snoek, C. G.; and Shao, L. 2020. Learning to learn with variational information bottleneck for domain generalization. In European Conference on Computer Vision, 200–216. Springer.
Dumoulin, Shlens, and Kudlur (2016) Dumoulin, V.; Shlens, J.; and Kudlur, M. 2016. A learned representation for artistic style. arXiv preprint arXiv:1610.07629.
Ganin and Lempitsky (2015) Ganin, Y.; and Lempitsky, V. 2015. Unsupervised domain adaptation by backpropagation. In International conference on machine learning, 1180–1189. PMLR.
Ganin et al. (2016) Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; and Lempitsky, V. 2016. Domain-adversarial training of neural networks. The journal of machine learning research, 17(1): 2096–2030.
Geirhos et al. (2019) Geirhos, R.; Rubisch, P.; Michaelis, C.; Bethge, M.; Wichmann, F. A.; and Brendel, W. 2019. ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness. ICLR.
Ghiasi, Lin, and Le (2018) Ghiasi, G.; Lin, T.-Y.; and Le, Q. V. 2018. Dropblock: A regularization method for convolutional networks. arXiv preprint arXiv:1810.12890.
Gong et al. (2019) Gong, R.; Li, W.; Chen, Y.; and Gool, L. V. 2019. Dlow: Domain flow for adaptation and generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2477–2486.
Goodfellow et al. (2014) Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; and Bengio, Y. 2014. Generative adversarial nets. Advances in neural information processing systems, 27.
He et al. (2016) He, K.; Zhang, X.; Ren, S.; and Sun, J. 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, 770–778.
Huang and Belongie (2017) Huang, X.; and Belongie, S. 2017. Arbitrary style transfer in real-time with adaptive instance normalization. In Proceedings of the IEEE International Conference on Computer Vision, 1501–1510.
Kingma and Welling (2013) Kingma, D. P.; and Welling, M. 2013. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
Ledig et al. (2017) Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. 2017. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE conference on computer vision and pattern recognition, 4681–4690.
Li et al. (2017) Li, D.; Yang, Y.; Song, Y.-Z.; and Hospedales, T. M. 2017. Deeper, broader and artier domain generalization. In Proceedings of the IEEE international conference on computer vision, 5542–5550.
Li et al. (2018a) Li, D.; Yang, Y.; Song, Y.-Z.; and Hospedales, T. M. 2018a. Learning to generalize: Meta-learning for domain generalization. In Thirty-Second AAAI Conference on Artificial Intelligence.
Li et al. (2018b) Li, H.; Pan, S. J.; Wang, S.; and Kot, A. C. 2018b. Domain generalization with adversarial feature learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 5400–5409.
Li et al. (2022) Li, X.; Dai, Y.; Ge, Y.; Liu, J.; Shan, Y.; and Duan, L.-Y. 2022. Uncertainty Modeling for Out-of-Distribution Generalization. ICLR.
Long et al. (2018) Long, M.; Cao, Z.; Wang, J.; and Jordan, M. I. 2018. Conditional adversarial domain adaptation. Advances in neural information processing systems, 31.
Lu et al. (2019) Lu, M.; Zhao, H.; Yao, A.; Chen, Y.; Xu, F.; and Zhang, L. 2019. A closed-form solution to universal style transfer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 5952–5961.
Luo et al. (2020) Luo, Y.; Liu, P.; Guan, T.; Yu, J.; and Yang, Y. 2020. Adversarial style mining for one-shot unsupervised domain adaptation. Advances in Neural Information Processing Systems, 33: 20612–20623.
Motiian et al. (2017) Motiian, S.; Piccirilli, M.; Adjeroh, D. A.; and Doretto, G. 2017. Unified deep supervised domain adaptation and generalization. In Proceedings of the IEEE international conference on computer vision, 5715–5725.
Nam et al. (2021) Nam, H.; Lee, H.; Park, J.; Yoon, W.; and Yoo, D. 2021. Reducing Domain Gap by Reducing Style Bias. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8690–8699.
Nuriel, Benaim, and Wolf (2021) Nuriel, O.; Benaim, S.; and Wolf, L. 2021. Permuted AdaIN: reducing the bias towards global statistics in image classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 9482–9491.
Ristani et al. (2016) Ristani, E.; Solera, F.; Zou, R.; Cucchiara, R.; and Tomasi, C. 2016. Performance measures and a data set for multi-target, multi-camera tracking. In European conference on computer vision, 17–35. Springer.
Simonyan and Zisserman (2014) Simonyan, K.; and Zisserman, A. 2014. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.
Van der Maaten and Hinton (2008) Van der Maaten, L.; and Hinton, G. 2008. Visualizing data using t-SNE. Journal of machine learning research, 9(11).
Volpi et al. (2018a) Volpi, R.; Morerio, P.; Savarese, S.; and Murino, V. 2018a. Adversarial feature augmentation for unsupervised domain adaptation. In Proceedings of the IEEE conference on computer vision and pattern recognition, 5495–5504.
Volpi et al. (2018b) Volpi, R.; Namkoong, H.; Sener, O.; Duchi, J. C.; Murino, V.; and Savarese, S. 2018b. Generalizing to unseen domains via adversarial data augmentation. Advances in neural information processing systems, 31.
Wang et al. (2021a) Wang, J.; Lan, C.; Liu, C.; Ouyang, Y.; Zeng, W.; and Qin, T. 2021a. Generalizing to Unseen Domains: A Survey on Domain Generalization. IJCAI.
Wang et al. (2018) Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; and Change Loy, C. 2018. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European conference on computer vision (ECCV) workshops, 0–0.
Wang et al. (2021b) Wang, Z.; Luo, Y.; Qiu, R.; Huang, Z.; and Baktashmotlagh, M. 2021b. Learning to diversify for single domain generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 834–843.
Xu et al. (2021) Xu, Q.; Zhang, R.; Zhang, Y.; Wang, Y.; and Tian, Q. 2021. A fourier-based framework for domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 14383–14392.
Yue et al. (2019) Yue, X.; Zhang, Y.; Zhao, S.; Sangiovanni-Vincentelli, A.; Keutzer, K.; and Gong, B. 2019. Domain randomization and pyramid consistency: Simulation-to-real generalization without accessing target domain data. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 2100–2110.
Zhang et al. (2020) Zhang, X.; Wang, Q.; Zhang, J.; and Zhong, Z. 2020. Adversarial autoaugment. ICLR.
Zhang et al. (2022) Zhang, Y.; Li, M.; Li, R.; Jia, K.; and Zhang, L. 2022. Exact feature distribution matching for arbitrary style transfer and domain generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8035–8045.
Zhao et al. (2020) Zhao, S.; Gong, M.; Liu, T.; Fu, H.; and Tao, D. 2020. Domain generalization via entropy regularization. Advances in Neural Information Processing Systems, 33.
Zheng et al. (2015) Zheng, L.; Shen, L.; Tian, L.; Wang, S.; Wang, J.; and Tian, Q. 2015. Scalable person re-identification: A benchmark. In Proceedings of the IEEE international conference on computer vision, 1116–1124.
Zheng, Zheng, and Yang (2017) Zheng, Z.; Zheng, L.; and Yang, Y. 2017. Unlabeled samples generated by gan improve the person re-identification baseline in vitro. In Proceedings of the IEEE international conference on computer vision, 3754–3762.
Zhong et al. (2022) Zhong, Z.; Zhao, Y.; Lee, G. H.; and Sebe, N. 2022. Adversarial style augmentation for domain generalized urban-scene segmentation. arXiv preprint arXiv:2207.04892.
(45) Zhong, Z.; Zheng, L.; Kang, G.; Li, S.; and Yang, Y. ???? Random erasing data augmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, 13001–13008.
Zhou et al. (2021a) Zhou, K.; Liu, Z.; Qiao, Y.; Xiang, T.; and Loy, C. C. 2021a. Domain generalization: A survey. arXiv preprint arXiv:2103.02503.
Zhou et al. (2019) Zhou, K.; Yang, Y.; Cavallaro, A.; and Xiang, T. 2019. Omni-scale feature learning for person re-identification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 3702–3712.
Zhou et al. (2020) Zhou, K.; Yang, Y.; Hospedales, T.; and Xiang, T. 2020. Learning to generate novel domains for domain generalization. In European Conference on Computer Vision, 561–578. Springer.
Zhou et al. (2021b) Zhou, K.; Yang, Y.; Qiao, Y.; and Xiang, T. 2021b. Domain Adaptive Ensemble Learning. IEEE Transactions on Image Processing (TIP).
Zhou et al. (2021c) Zhou, K.; Yang, Y.; Qiao, Y.; and Xiang, T. 2021c. Domain generalization with mixstyle. ICLR.