Adversarial Robustness via Fisher-Rao Regularization

Our work investigates the problem of optimizing the trade-off between accuracy and robustness and advances state-of-the-art methods in very different ways.

• •

  We derive an explicit characterization of the Fisher-Rao Distance (FRD) based on the information-geometric properties of the soft-predictions of the neural classifier. That leads to closed-form expressions of the FRD for the binary and multiclass cases (Theorems 1 and 2, respectively). We further relate them to well-known regularization metrics (presented in Proposition 1).

• •

  We propose a new formulation of adversarial defense, called FIsher-rao REgularizer (Fire). It consists of optimizing a regularized loss, which encourages the predictions of natural and perturbed samples to be close to each other, according to the manifold of the softmax distributions induced by the neural network. Our loss in Eq. (7) consists of two terms: the categorical cross-entropy, which favors natural accuracy, and a Fisher-Rao regularization term, which increases adversarial robustness. Furthermore, we prove for a simple logistic regression and Gaussian model that all Pareto-optimal points in the accuracy-robustness region can be reached by Fire, while state-of-the-art methods fail (cf. Section 4 and Proposition 2).

• •

  Experimentally, on standard benchmarks, we found that FIRE provides an improvement up to roughly 2% of robust accuracy compared to the widely used Kullback-Leibler regularizer [26]. We also observed significant improvements over other state-of-the-art methods. In addition, our method typically requires, on average, less computation time (measured by the training runtime on the same GPU cluster) than state-of-the-art methods.

Adversarial training. Adversarial training (AT) [4] is one of the few defenses that has not been broken so far. Indeed, different variations of this method have been proposed. It is based on an attack-defense scheme where the attacker’s goal is to create perturbated inputs by maximizing a loss to fool the classifier, while the defender’s goal is to classify those attacked inputs rightfully.

Inner attack generation. The inner attacker design is vital to AT since it has to create meaningful attacks. One of the most popular algorithms to generate adversarial examples is Projected Gradient Descent (PGD) [4, 8], which is an iterative attack: the output at each step is the addition of the previous output and the sign of the loss gradient modulated by a fixed step size. The loss maximized in PGD is often the same loss that is minimized for the defense.

Robust defense loss. An essential choice of the defense mechanism is the robust loss used to attack and defend the network. Initially, [4] used the adversarial cross-entropy. However, it was shown that one way to improve adversarial training is through the choice of this loss. TRADES [26] introduces a robustness regularizer based on the Kullback-Leibler divergence. MART [27] uses a robustness regularizer that considers the misclassified inputs and boosted losses.

Additional improvement. Whether it is AT, TRADES or MART, they all have been improved in recent years. Those improvements can either rely on pretraining [28], early stopping [29], curriculum learning [30], adaptative models [31], unlabeled data to improve generalization [32, 33] or additional perturbations on the model weights [34].

It should be noted that the main disadvantage of adversarial training-based methods remains the required computational expenses. Nevertheless, as will be shown in Section 5, Fire can significantly reduce them.

We provide some background on adversarial learning, focusing on adversarial defense’s most popular proposed loss functions. Adversarial examples are slightly modified inputs that can fool a target classifier. Concretely, Szegedy et al. [1] define the adversarial generation problem as:

where $y$ is the true label (supervision) associated to the sample $\boldsymbol{\mathbf{x}}$. This formulation shows that the vulnerable points of a classifier are the ones close to its decision boundaries. Since this problem is difficult to tackle, it is commonly relaxed as follows [35]:

Once adversarial examples are obtained, they can be used to learn a robust classifier as discussed next.

The adversarial problem has been presented in [8] as follows:

where $\varepsilon$ denotes the maximal distortion allowed in the adversarial examples according to the $l_{p}$-norm. Since the exact solution to the above inner max problem is generally intractable, a relaxation is proposed by generating an adversarial example using an iterative algorithm such as PGD.

Statistics on manifolds and information geometry are two different ways in which differential geometry meets statistics. A statistical manifold can be defined as a parameterized family of probability distributions (or density functions) of interest. It is worth to mention that the concept of statistics on manifolds is very different from manifold learning which is a branch of machine learning where the goal is to learn a latent manifold from valued data. In this paper, we are interested in the statistical manifold obtained when fixing the parameters $\boldsymbol{\mathbf{\theta}}$ of a DNN and changing its feature input. We consider the following statistical manifold: $\mathcal{C}\doteq\big{\{}q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}}):\boldsymbol{\mathbf{x}}\in\mathcal{X}\big{\}}$. In particular, the focus is on changes in a neighborhood of a particular sample in an adversarial manner (i.e., considering a worst-case perturbation). Please notice that the statistical manifold is different from the loss landscape. The loss landscape is defined as the changes of the risk function with respect to changes in the model parameters (i.e., $L(\boldsymbol{\mathbf{\theta}})$ vs $\boldsymbol{\mathbf{\theta}}$), while the statistical manifold refers to the changes of the soft-probabilities of the classifier with respect to changes in the input (i.e., $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})$ vs $\boldsymbol{\mathbf{x}}$). In order to understand the effect of a perturbation on the input, we first need to be able to capture the distance over the statistical manifold between different probability distributions, i.e., between two different feature inputs. That is precisely what the FRD computes, as illustrated by the red curve in Fig. 1. It is worth to mention that FRD can be very much different from the euclidean distance since the later does not depend on the shape of the manifold. For a formal mathematical definition of FRD and a short review of basic concepts in information geometry, we refer the reader to Section 6.1.

As discussed in Section 2, the robustness of a classifier is related to the distance between natural examples and the decision boundaries (i.e., points $\boldsymbol{\mathbf{x}}$ such that $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})\approx q_{\boldsymbol{\mathbf{\theta}}}(y^{\prime}|\boldsymbol{\mathbf{x}})$ for $y\neq y^{\prime}$). In fact, if a natural example is far from the decision boundaries, a norm-constrained attack will clearly fail (in this case, the optimization problem (1) will be infeasible). Since the decision boundaries are given by the soft-probabilities $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})$, this can be equivalently studied by analyzing the shape of the statistical manifold $\mathcal{C}$ (which should not be confused with the loss landscape). In fact, if $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})$ is relatively flat (i.e., does not change much) with respect to perturbations of $\boldsymbol{\mathbf{x}}$ around $\boldsymbol{\mathbf{x}}_{0}$, it is clear that adversarial perturbations will not modify the classifier decision at this point. In contrast, if $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})$ changes sharply with perturbations of $\boldsymbol{\mathbf{x}}$ around $\boldsymbol{\mathbf{x}}_{0}$, an adversarial can easily leverage this vulnerability to fool the classifier. This notion of robustness is related to the Lipschitz constant of the network, as discussed in various works (e.g., [36]). To illustrate these ideas clearly, let us consider the logistic regression model $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})=1/[1+\exp(-y\,\boldsymbol{\mathbf{\theta}}^{\intercal}\boldsymbol{\mathbf{x}})]$, where $n=2$ and $\mathcal{Y}=\{-1,1\}$, as a simple example. One way to visualize the statistical manifold $\mathcal{C}$ is to plot $q_{\boldsymbol{\mathbf{\theta}}}(1|\boldsymbol{\mathbf{x}})$ as a function of $\boldsymbol{\mathbf{x}}$ (since $q_{\boldsymbol{\mathbf{\theta}}}(-1|\boldsymbol{\mathbf{x}})=1-q_{\boldsymbol{\mathbf{\theta}}}(1|\boldsymbol{\mathbf{x}})$, this completely characterizes the manifold). This is shown in Fig. 2(a) for the value of $\boldsymbol{\mathbf{\theta}}$ which minimizes the natural missclassification probability $P_{e}$ under a conditional Gaussian model for the input $\boldsymbol{\mathbf{x}}$ (see Section 4 for details). As can be seen, the manifold is quite sharp around a particular region of $\mathcal{X}$. This region corresponds to the neighborhood of the points for which $\boldsymbol{\mathbf{\theta}}^{\intercal}\boldsymbol{\mathbf{x}}\approx 0$ as $\boldsymbol{\mathbf{x}}$ is perturbed in the direction of $\boldsymbol{\mathbf{\theta}}$. Therefore, we can say that this model is clearly non-robust, as its output can be significantly changed by small perturbations on the input. Consider now the same model but with the values of $\boldsymbol{\mathbf{\theta}}$ obtained by minimizing the adversarial missclassification probability $P_{e}^{\prime}$. As can be seen in Fig. 2(b), the statistical manifold is much flatter than in Fig. 2(a), which means that the model is less sensitive to adversarial perturbations on the input. Therefore, it is more robust.

Let us now consider the FRD of the two models around the point $\boldsymbol{\mathbf{x}}=\boldsymbol{\mathbf{0}}$, which gives a point that lies in the decision boundary, by letting $\boldsymbol{\mathbf{\delta}}=\boldsymbol{\mathbf{x}}^{\prime}-\boldsymbol{\mathbf{x}}$ vary in the $\ell_{\infty}$ ball $\mathcal{B}_{\infty,\varepsilon}=\{\boldsymbol{\mathbf{\delta}}:\|\boldsymbol{\mathbf{\delta}}\|_{\infty}\leq\varepsilon\}$, with $\varepsilon=0.1$. Fig. 3(a) displays the FRD for the parameters $\boldsymbol{\mathbf{\theta}}$ which minimize the misclassification error probability $P_{e}$, and Fig. 3(b) shows the FRD for the parameters $\boldsymbol{\mathbf{\theta}}$ which minimize the adversarial misclassification error probability $P_{e}^{\prime}$. Clearly, the abrupt transition of $q_{\boldsymbol{\mathbf{\theta}}}(1|\boldsymbol{\mathbf{x}})$ in Fig.  2(a) corresponds to a sharp increase on the FRD as $\|\boldsymbol{\mathbf{\delta}}\|_{\infty}$ increases. On the contrary, for a flatter manifold as in Fig. 2(b), the FRD increases much more slowly as $\|\boldsymbol{\mathbf{\delta}}\|_{\infty}$ increases. This example shows how FRD reflects the shape of the statistical manifold $\mathcal{C}$.

Our goal in this work is to use the FRD to control the shape of the statistical manifold by regularizing the misclassification risk.

The rest of this section is organized as follows. We begin by introducing the FIRE risk function, which is our main theoretical proposal to improve the robustness of neural networks. We continue with the evaluation of the FRD given by expression (26) for the binary and multiclass classification frameworks and provide some exciting properties and connections with other standard distances and well-known information divergences.

The main proposal of this paper is the Fire risk function, defined as follows:

where $\lambda>0$ controls the trade-off between natural accuracy and robustness to the adversary.

In Fig. 4, we show the shape of the statistical manifold $\mathcal{C}$ as $\lambda$ is varied for the logistic regression model discussed in Section 3.1 (see also Section 4). Notice that when no FRD regularization is used, the manifold in Fig. 4(a) is very similar to the one in Fig. 2(a). As the value of $\lambda$ increases, the weight of the FRD regularization term also increases. As a consequence, the statistical manifold is flattened as expected which is illustrated in Fig. 4(b). However, as shown in Fig. 4(c), setting $\lambda$ to a very high value causes the statistical manifold to become extremely flat. This means that the model is basically independent of the input, and the classification performance will be poor. Notice the similarities between Fig. 2 and Fig. 4.

In what follows, we derive closed-form expressions of the FRD for general classification problems. However, for the sake of clarity, we begin with the binary case.

Let us first consider the binary classification setting, in which $\mathcal{X}\subseteq\mathbb{R}^{n}$ and $\mathcal{Y}=\{-1,1\}$ are input and label spaces, respectively. Consider an arbitrary given model:

Here $h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x}})$ represents an arbitrary parametric representation or latent code of the input $\boldsymbol{\mathbf{x}}$. As a matter of fact, we only need to assume that $h_{\boldsymbol{\mathbf{\theta}}}$ is a smooth function. The FRD for this model can be computed in closed-form, as shown in the following result. The proof is relegated to Section 6.2.

For illustration purposes, Fig. 5(a) shows the behavior of the FRD with respect to changes in the latent code compared with the Euclidean distance. It can be observed that the resulting FRD is rather sensitive to variations in the latent space when $h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x}})\approx 0$ while being close to zero for the region in which $|h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x}})|$ is large and $|h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x^{\prime}}})|\ll|h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x}})|$. This asymmetric behavior is in sharp contrast with the one of the Euclidean distance. However, these quantities are related as shown by the next proposition.

The proof of this proposition is relegated to Section C.1.

Consider the general $M$-classification problem in which $\mathcal{Y}=\{1,\dots,M\}$, and let

be a standard softmax output, where $\boldsymbol{\mathbf{h}}:\mathcal{X}\times\Theta\to\mathbb{R}^{M}$ is a parametric representation function and $z_{y}$ denotes the $y$-th component of the vector $\boldsymbol{\mathbf{z}}$. The FRD for this model can also be obtained in closed-form as summarized below. The proof is given in Section 6.3.

The Fisher-Rao distance (15) has some interesting connections with other distances and information divergences. We are particularly interested in its relation with the KL divergence, which is the adversarial regularization mechanism used in the TRADES method [26]. The next theorem summarizes the mathematical connection between these quantities. The proof of this theorem is relegated to Section C.2.

The above result shows that the KL is a weak approximation of the FRD in the sense that it gives an upper bound and a second-order approximation of the geodesic distance. However, in general, we are interested in distances over arbitrarily distinct softmax distributions, so it is clear that the KL divergence and the FRD can behave very differently. In fact, only the latter measures the actual distance on the statistical manifold $\mathcal{C}\doteq\big{\{}q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}}):\boldsymbol{\mathbf{x}}\in\mathcal{X}\big{\}}$ (for further details, the reader is referred to Section 6.1). In the next section, we show that this has an important consequence on the set of solutions obtained by minimizing the respective empirical risks while varying $\lambda$.

Consider a binary example with a simplified logistic regression model. Therefore, in this section we assume that $\mathcal{Y}=\{-1,1\}$ and the softmax probability

We choose the standard adversary obtained by maximizing the cross-entropy loss, i.e.,

For simplicity¹¹1The analysis can be extended to an arbitrary norm but it is somewhat simplified for the 2-norm case., in this section we assume that the adversary uses the 2-norm (i.e, $\|\cdot\|=\|\cdot\|_{2}$). In such case, $\boldsymbol{\mathbf{x}}^{\prime*}$ can be written as $\boldsymbol{\mathbf{x}}^{\prime*}=\boldsymbol{\mathbf{x}}-\varepsilon\,y\,\boldsymbol{\mathbf{\theta}}/\|\boldsymbol{\mathbf{\theta}}\|_{2}.$

We also assume that the classes are equally likely and that the conditional inputs given the class are Gaussian distributions with the particular form $\boldsymbol{\mathbf{x}}|y\sim\mathcal{N}(y\boldsymbol{\mathbf{\mu}},\boldsymbol{\mathbf{\Sigma}})$. In this case, we can write the natural and adversarial misclassification probabilities as:

where $\Phi$ denotes the cumulative distribution function of the standard normal random variable. The following result provides lower and upper bounds for $P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}})$ in terms of $\varepsilon$ and the eigenvalues of $\boldsymbol{\mathbf{\Sigma}}$. Notice that the bounds get sharper as $\varepsilon$ or the spread of $\boldsymbol{\mathbf{\Sigma}}$ decreases and are tight if $\boldsymbol{\mathbf{\Sigma}}=\sigma^{2}\boldsymbol{\mathbf{I}}$.

The proof of this proposition is relegated to Section 6.4.

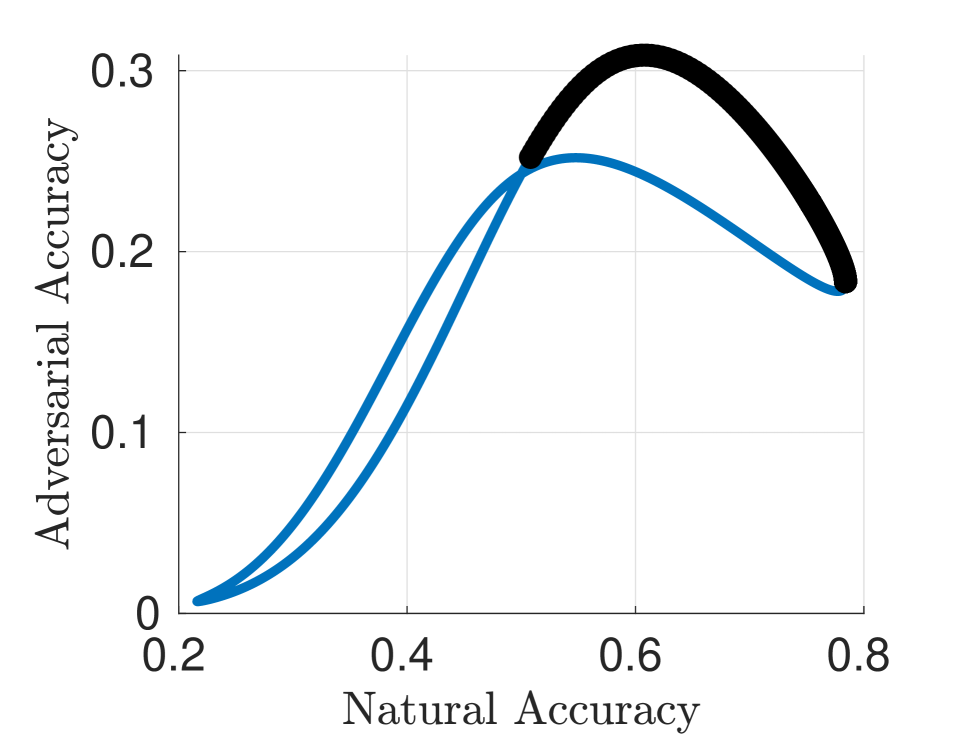
Let us consider the 2-dimensional case, i.e., $n=2$. From expressions (20) and (21), it can be noticed that both $P_{e}(\boldsymbol{\mathbf{\theta}})$ and $P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}})$ are independent of the 2-norm of $\boldsymbol{\mathbf{\theta}}$. Therefore, we can parameterize $\boldsymbol{\mathbf{\theta}}$ as $\boldsymbol{\mathbf{\theta}}=[\cos(\alpha),\sin(\alpha)]^{\intercal}$ with $\alpha\in[0,2\pi)$ without any loss of generality. Thus, $(1-P_{e}(\boldsymbol{\mathbf{\theta}}),1-P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}}))$ for all values of $\alpha$ gives a curve that represents all the possible values of the natural and adversarial accuracies for this setting. Fig. 6(a) shows this curve for a particular choice²²2In this experiment, we obtained the components in $\boldsymbol{\mathbf{\mu}}$ by sampling $\mathcal{N}(0,1/400)$. We also defined a matrix $\boldsymbol{\mathbf{A}}$ with samples of the same distribution and constructed $\boldsymbol{\mathbf{\Sigma}}$ as $\boldsymbol{\mathbf{\Sigma}}=\boldsymbol{\mathbf{A}}\boldsymbol{\mathbf{A}}^{\intercal}$. of $\varepsilon$, $\boldsymbol{\mathbf{\mu}}$, and $\boldsymbol{\mathbf{\Sigma}}$. As can be observed, the solution which maximizes the natural accuracy gives poor adversarial accuracy and viceversa³³3The (normalized) value of $\boldsymbol{\mathbf{\theta}}$ that maximizes $1-P_{e}(\boldsymbol{\mathbf{\theta}})$ is $\theta_{\text{nat}}^{*}=\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\mu}}/\|\boldsymbol{\mathbf{\Sigma}}^{-1}\boldsymbol{\mathbf{\mu}}\|_{2}$ (see, for instance, [38]) and corresponds to $\alpha_{\text{nat}}^{*}\approx 1.814$, giving $1-P_{e}(\boldsymbol{\mathbf{\theta}})\approx 0.784$ and $1-P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}})\approx 0.183$. The value of $\theta$ that maximizes $1-P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}})$ is $\alpha_{\text{adv}}^{*}\approx 2.783$, giving $1-P_{e}(\boldsymbol{\mathbf{\theta}})\approx 0.608$ and $1-P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}})\approx 0.309$.. The set of Pareto-optimal points (i.e., the set of points for which there is no possible improvement in terms of both natural and adversarial accuracy or, equivalently, the set $\{\max_{\boldsymbol{\mathbf{\theta}}}\;\beta(1-P_{e}(\boldsymbol{\mathbf{\theta}}))+(1-\beta)(1-P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}})):0\leq\beta\leq 1\}$) are also shown in Fig. 6(a). In particular, this set contains the Maximum Average Accuracy (MAA) given by

This is a metric of particular importance, which combines with equal weights both natural and adversarial accuracies.

In addition, we present the solution of the (local) Empirical Risk Minimization (ERM)⁴⁴4For experiments, we used $10^{4}$ samples for each different class and a BFGS Quasi-Newton method for optimization. The initial value of $\boldsymbol{\mathbf{\theta}}$ is zero for both TRADES and FIRE. We do not report the result using ACE risk in (4) because in this setting we would obtain the trivial solution $\boldsymbol{\mathbf{\theta}}=\boldsymbol{\mathbf{0}}$, which is a minimizer of $L_{\textrm{ACE}}(\boldsymbol{\mathbf{\theta}})$. for the TRADES risk function as defined in (5) for different values of $\lambda$ in Fig. 6(b). As can be seen, the curve obtained in the $(1-P_{e}(\boldsymbol{\mathbf{\theta}}),1-P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}}))$ space covers a large part of the Pareto-optimal points expect for a segment for which the solution does not behave well. Finally, in Fig. 6(c) we present the result for the proposed Fire risk function in (7) for different values of $\lambda$. In this case, we observed that the curve of solutions in the $(1-P_{e}(\boldsymbol{\mathbf{\theta}}),1-P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}}))$ space covers all the Pareto-optimal points. Moreover, we have observed that, for some $\lambda$, the $\boldsymbol{\mathbf{\theta}}$ which minimizes the Fire risk matches the $\boldsymbol{\mathbf{\theta}}$ which achieves the MAA defined in (24), while TRADES method fails in achieving this particularly relevant point. It should be added that none of the methods cover exactly the set of Pareto-optimal points, which is expected, since all loss functions can be considered surrogates for the quantity $\beta P_{e}(\boldsymbol{\mathbf{\theta}})+(1-\beta)P_{e}^{\prime}(\boldsymbol{\mathbf{\theta}})$, where $0\leq\beta\leq 1$. We performed a similar comparison between FRD and KL using standard datasets. The results are reported in Appendix A

Datasets : We resort to standard benchmarks. First, we use MNIST [39], composed of 60,000 black and white images of size 28$\times$28 - 50,000 for training, and 10,000 for testing - divided into 10 different classes. Then, we test on CIFAR-10, and CIFAR-100 [40], composed of 60,000 color images of size 32$\times$32$\times$3 - 50,000 for training and 10,000 for testing - divided into 10 and 100 classes, respectively. Finally, we also test on CIFAR-10 with additional data thanks to 80 Million Tiny Images [41], an experiment that will be detailed later.

Architectures : In order to provide fair comparisons, we use standard model architectures. For the MNIST simulations, we use the 7-layer CNN as in [26]. For CIFAR-10 and CIFAR-100, we use a WideResNet (WRN) with 34 layers, and a widen factor of 10 (shortened as WRN-34-10) as in [26, 8, 34]. For the simulations with additional data, we use a WRN-28-10 as in [32].

Training procedure: For all standard experiments (without additional data), we use a Stochastic Gradient Descent (SGD) optimizer with a momentum of $0.9$, a weight decay of $5\cdot 10^{-4}$ and Nesterov momentum. We train our models on $100$ epochs with a batch size equal to $256$. The initial learning rate is set to $0.01$ for MNIST and $0.1$ for CIFAR-10 and CIFAR-100. Following [26], the learning rate is divided by $10$ at epochs $75$ and $90$. For our experiments with additional data, we follow the protocol introduced by [32], using a cosine decay [42], and training on $200$ epochs.

Generation of adversarial samples: For all experiments, we use PGD [8] to generate the adversarial examples during training. The loss which is maximized during the PGD algorithm is the Fisher-Rao distance (FRD) for our experiments, and the Kullback-Leibler divergence for the TRADES method. For MNIST, we use 40 steps and 10 steps for the rest. The step size is set to 0.01 for MNIST and 0.007 for the others. The maximal distortion in $l_{\infty}$-norm $\varepsilon$ allowed is $0.031$ for CIFAR-10 and CIFAR-100, and $0.3$ for MNIST. This setting is used in most methods, such as [4, 32].

Additional data: To improve performance, [32] propose the use of additional data when training on CIFAR-10. Specifically, [32] use 500k additional images from 80M-TI ⁶⁶6Images available at https://github.com/yaircarmon/semisup-adv. Those images have been selected such that their $l_{2}$-distance to images from CIFAR-10 are below a threshold.

Hyperparameters: The Rao regularizer used to improve the robustness of neural networks introduces a hyperparameter $\lambda$ to balance natural accuracy and adversarial robustness. We select $\lambda$ = 12 from the CIFAR-10 simulations and use this value for all the other datasets. Further study on the effect of $\lambda$ is provided in Section 5.2.3.

Test metrics: First, we provide the accuracy of the model on clean samples after adversarial training (Natural). Second, we test our models using the recently introduced AutoAttack [9], keeping the same hyperparameters as the ones used in the original paper and code⁷⁷7The AutoAttack code is available on https://github.com/fra31/auto-attack. AutoAttack tests the model under a comprehensive series of attacks and provides a more reliable assessment of robustness than the traditionally used PGD-based evaluation. Given that we care equally about natural and adversarial accuracies, we also compute the average sum of the two, i.e., the Average Accuracy ( Avg. Acc.). This is an empirical version of the Maximum Average Accuracy (MAA) defined in (24). Finally, we report the runtime of each method as the time required to complete the adversarial training. To provide fair comparisons between runtimes, we run the official code of each method on the same $4$ NvidiaV100 GPUs (for further details, see Section 5.2.2).

Consider the family of probability distributions over the classes⁸⁸8Since we are interested in the dependence of $q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}})$ with changes in input $\boldsymbol{\mathbf{x}}$ and, particularly, its robustness to adversarial perturbations, we consider $\boldsymbol{\mathbf{x}}$ as the “parameters” of the model over which the regularity conditions must be imposed. $\mathcal{C}\doteq\big{\{}q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}}):\boldsymbol{\mathbf{x}}\in\mathcal{X}\big{\}}$. Assume that the following regularity conditions hold [44]:

1. (i)

   $\nabla_{\boldsymbol{\mathbf{x}}}\,q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})$ exists for all $\boldsymbol{\mathbf{x}},y$ and $\boldsymbol{\mathbf{\theta}}\in\Theta$;

2. (ii)

   $\sum_{y\in\mathcal{Y}}\nabla_{\boldsymbol{\mathbf{x}}}\,q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})=0$ for all $\boldsymbol{\mathbf{x}}$ and $\boldsymbol{\mathbf{\theta}}\in\Theta$;

3. (iii)

   $\boldsymbol{\mathbf{G}}(\boldsymbol{\mathbf{x}})=\mathbb{E}_{Y\sim q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}})}\big{[}\nabla_{\boldsymbol{\mathbf{x}}}\,\log q_{\boldsymbol{\mathbf{\theta}}}(Y|\boldsymbol{\mathbf{x}})\nabla_{\boldsymbol{\mathbf{x}}}^{\intercal}\,\log q_{\boldsymbol{\mathbf{\theta}}}(Y|\boldsymbol{\mathbf{x}})\big{]}$ is positive definite for any $\boldsymbol{\mathbf{x}}$ and $\boldsymbol{\mathbf{\theta}}\in\Theta$.

Notice that if (i) holds, (ii) also holds immediately for discrete distributions over finite spaces (assuming that $\sum_{y\in\mathcal{Y}}$ and $\nabla_{\boldsymbol{\mathbf{x}}}$ are interchangeable operations) as in our case. When (i)-(iii) are met, the variance of the differential form $\nabla_{\boldsymbol{\mathbf{x}}}^{\intercal}\log q_{\boldsymbol{\mathbf{\theta}}}(Y|\boldsymbol{\mathbf{x}})d\boldsymbol{\mathbf{x}}$ can be interpreted as the square of a differential arc length $ds^{2}$ in the space $\mathcal{C}$, which yields

Thus, $\boldsymbol{\mathbf{G}}$, which is the Fisher Information Matrix (FIM), can be adopted as a metric tensor. We now consider a curve $\boldsymbol{\mathbf{\gamma}}:[0,1]\to\mathcal{X}$ in the input space connecting two arbitrary points $\boldsymbol{\mathbf{x}}$ and $\boldsymbol{\mathbf{x}}^{\prime}$, i.e., such that $\boldsymbol{\mathbf{\gamma}}(0)=\boldsymbol{\mathbf{x}}$ and $\boldsymbol{\mathbf{\gamma}}(1)=\boldsymbol{\mathbf{x}}^{\prime}$. Notice that this curve induces the following curve in the space $\mathcal{C}$: $q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{\gamma}}(t))$ for $t\in[0,1]$. The Fisher-Rao distance between the distributions $q_{\boldsymbol{\mathbf{\theta}}}=q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}})$ and $q_{\boldsymbol{\mathbf{\theta}}}^{\prime}=q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}}^{\prime})$ will be denoted as $d_{R,\mathcal{C}}(q_{\boldsymbol{\mathbf{\theta}}},q_{\boldsymbol{\mathbf{\theta}}}^{\prime})$ and is formally defined by

where the infimum is taken over all piecewise smooth curves. This means that the FRD is the length of the geodesic between points $\boldsymbol{\mathbf{x}}$ and $\boldsymbol{\mathbf{x}}^{\prime}$ using the FIM as the metric tensor. In general, the minimization of the functional in (26) is a problem that can be solved using the well-known Euler-Lagrange differential equations. Several examples for simple families of distributions can be found in [44].

To compute the FRD, we first need to compute the FIM of the family $\mathcal{C}$ with $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})$ given in expression (8). A direct calculation gives:

It is clear from this expression that the FIM of this model is of rank one and therefore singular. This matches the fact that $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})$ has a single degree of freedom given by $h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x}})$. Therefore, the statistical manifold $\mathcal{C}$ has dimension $1$.

To proceed, we consider the following model:

where we have defined $u=h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x}})$. This effectively removes the model ambiguities because $q(y|u)\neq q(y|u^{\prime})$ if and only if $u\neq u^{\prime}$. Note that $q_{\boldsymbol{\mathbf{\theta}}}(y|u)$, for fixed $\boldsymbol{\mathbf{\theta}}$, can be interpreted as a one-dimensional parametric model with parameter $u$. Its FIM is a scalar that can be readily obtained, yielding:

Clearly, the FIM $G(u)$ is non-singular for any $u$ (i.e., $G(u)>0$ for any $u$) as required. Let $\mathcal{D}=\{q_{\boldsymbol{\mathbf{\theta}}}(\cdot|u):u\in\mathcal{U}\}$, where $\mathcal{U}=h_{\boldsymbol{\mathbf{\theta}}}(\mathcal{X})$ and consider two distributions in $\mathcal{D}$: $q_{\boldsymbol{\mathbf{\theta}}}=q_{\boldsymbol{\mathbf{\theta}}}(\cdot|u)$ and $q_{\boldsymbol{\mathbf{\theta}}}^{\prime}=q_{\boldsymbol{\mathbf{\theta}}}(\cdot|u^{\prime})$. Then, the FRD can be evaluated directly as follows [44][Eq. (3.13)]:

Therefore, the FRD between the distributions $q_{\boldsymbol{\mathbf{\theta}}}=q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}})$ and $q_{\boldsymbol{\mathbf{\theta}}}^{\prime}=q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}}^{\prime})$ can be directly obtained by substituting $u=h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x}})$ and $u^{\prime}=h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x}}^{\prime})$ in Equation (6.2), yielding the final result in expression (9).

As in the binary case developed in Section 3.3, the FIM of the family $\mathcal{C}$ with $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})$ given in expression (14) is singular. To shows this, we first notice that $q_{\boldsymbol{\mathbf{\theta}}}(y|\boldsymbol{\mathbf{x}})$ can be written as

where $g_{y}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}})=h_{y}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}})-h_{1}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}})$. Since $g_{1}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}})=0$, this shows that $\mathcal{C}$ has $M-1$ degrees of freedom: $g_{2}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}}),\ldots,g_{M}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}})$. A direct calculation of the FIM gives

Let $\boldsymbol{\mathbf{v}}\in\mathcal{X}$ be an arbitrary vector and define $\beta_{y}\doteq\nabla_{\boldsymbol{\mathbf{x}}}^{\intercal}g_{y}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}})\,\boldsymbol{\mathbf{v}}$ for $y=[2:M]$. Notice that

Therefore, the range of $\boldsymbol{\mathbf{G}}(\boldsymbol{\mathbf{x}})$ is a subset of the span of the set $\{\nabla_{\boldsymbol{\mathbf{x}}}g_{2}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}}),\ldots,\nabla_{\boldsymbol{\mathbf{x}}}g_{M}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}})\}$. Thus, it follows that $\text{rank}(\boldsymbol{\mathbf{G}}(\boldsymbol{\mathbf{x}}))\leq M-1$, which implies that it is singular.

The singularity issue can be overcome by embedding $\mathcal{C}$ into the probability simplex $\mathcal{P}$ defined as follows:

To proceed, we follow [45][Section 2.8] and consider the following parameterization for any distribution $q\in\mathcal{P}$:

We then consider the following statistical manifold:

Notice that the parameter vector $\boldsymbol{\mathbf{z}}$ belongs to the positive portion of a sphere of radius 2 and centered at the origin in $\mathbb{R}^{M}$. As a consequence, the FIM follows by

where $\{\boldsymbol{\mathbf{e}}_{y}\}$ are the canonical basis vectors in $\mathbb{R}^{M}$ and $\boldsymbol{\mathbf{I}}$ is the identity matrix. From expression (37) we can conclude that the Fisher metric is equal to the Euclidean metric. Since the parameter vector lies on a sphere, the FRD between the distributions $q=q(\cdot|\boldsymbol{\mathbf{z}})$ and $q^{\prime}=q(\cdot|\boldsymbol{\mathbf{z}}^{\prime})$ can be written as the radius of the sphere times the angle between the vectors $\boldsymbol{\mathbf{z}}$ and $\boldsymbol{\mathbf{z}}^{\prime}$. This leads to

Finally, we can compute the FRD for distributions in $\mathcal{C}$ using:

Notice that $0\leq d_{R,\mathcal{C}}(q_{\boldsymbol{\mathbf{\theta}}},q_{\boldsymbol{\mathbf{\theta}}}^{\prime})\leq\pi$, $\forall\ \boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{x}}^{\prime}\in\mathcal{X}$, being zero if $q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}})=q_{\boldsymbol{\mathbf{\theta}}}(\cdot|\boldsymbol{\mathbf{x}}^{\prime})$ and $\pi$ when $[q_{\boldsymbol{\mathbf{\theta}}}(1|\boldsymbol{\mathbf{x}}),\dots,q_{\boldsymbol{\mathbf{\theta}}}(M|\boldsymbol{\mathbf{x}})]$ and $[q_{\boldsymbol{\mathbf{\theta}}}(1|\boldsymbol{\mathbf{x}}^{\prime}),\dots,q_{\boldsymbol{\mathbf{\theta}}}(M|\boldsymbol{\mathbf{x}}^{\prime})]$ are orthogonal vectors.

Proof the consistency between Theorem 1 and Theorem 2. This consists in showing the equivalence between the FRD for the binary case, given by Eq. (9), and the multiclass case, given by Eq. (15), for $M=2$. First, notice that the models (8) and (14) coincide if we consider the following correspondence: $h_{\boldsymbol{\mathbf{\theta}}}(\boldsymbol{\mathbf{x}})=h_{2}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}})-h_{1}(\boldsymbol{\mathbf{x}},\boldsymbol{\mathbf{\theta}})$, $y=1\leftrightarrow y=-1$ and $y=2\leftrightarrow y=1$. Then, using standard trigonometric identities, we rewrite the FRD for the multiclass case: