Adversarial network training using higher-order moments in a modified Wasserstein distance

The generative-adversarial network (GAN) is a game-theoretic technique for generating values according to a latent distribution estimated on $n$ example data $x\in\mathbb{R}^{n\times\ell\times u}$.[1] GANs employ a generator, $g:\mathbb{R}^{y}\rightarrow\mathbb{R}^{\ell\times u}$, which maps high-entropy inputs to an immitation datum; these high-entropy inputs $\in\mathbb{R}^{y}$ effectively determine a location in the latent space and are decoded to produces an immitation datum. GANs also employ a discriminator, $d:\mathbb{R}^{\ell\times u}\rightarrow[0,1]$, which is used to evaluate the plausibility that a datum is genuine. Generator and discriminator are trained in an adversarial manner, with the goal of reaching an equilibrium where both implicitly encode the distribution of real data in the latent space. If training is successful, $\hat{X}=g\left(Z\right)$ (where $Z\sim\mathcal{N}(0,1)^{y}$) will produce data resembling a row of $x$; $d\left(\mathbb{R}^{k}\right)$ will correspond to the cumulative density in a unimodal latent space where the latent space density projects the empirical distribution of $x_{i}$.

GANs are typically trained using a cross-entropy loss to optimize the parameters of both $g$ and $d$, which measures the expected bits of surprise that samples from a foreground distribution would produce if they had been drawn from a background distribution. The parameters $\theta_{g}$ are optimized to minimize the surprise of the Bernoulli distribution $1-\Sigma,d(g(Z))$ given the background distribution $0,1$ (i.e., minimizing the surprise from a background that scores $d(\hat{X})=1$). The parameters $\theta_{d}$ are optimized to minimize the surprise of the Bernoulli distribution $1-\Sigma,d(x)$ given the background distribution with $d(x_{i})=1$ and $d\left(\hat{X}\right)=0$.

When two distributions are highly dissimilar from one another, their support may be distinct such that cross-entropy becomes numerically unstable. This causes uninformative loss metrics: two distributions with non-overlapping support are quantified identically to two distributions whose supports are non-overlapping and very far from one another. These factors lead to poor training, particularly given that $g$ will initially produce noise, which will quite likely have poor overlap with real data in the latent space.

For this reason, Wasserstein distance was proposed to replace cross-entropy.[2] Wasserstein distance is the continuous version of the discrete earth-mover distance, which solves an optimal transport problem measuring the minimal movements in Euclidean distance that could be used to transform one probability density to another. Earth-mover distance is well defined, even when the two distributions have disjoint support. This avoids modal collapse while training.

If earth-mover distance is used to measure the distance between distributions $p_{A}$ and $p_{B}$, then the set of candidate solutions $\gamma$ will be functions with domain $\operatorname*{supp}(p_{A})\times\operatorname*{supp}(p_{B})$ and where the marginals equal $p_{A}$ and $p_{B}$. Thus, $\Delta_{EM}(p_{A},p_{B})=\inf_{\gamma\in\Pi(p_{A},p_{B})}\mathbb{E}_{a,b\sim\gamma}\|a-b\|$, where $\Pi(p_{A},p_{B})$ is the set of distributions with marginals $p_{A},p_{B}$.

The discrete formulation can be solved combinatorically via LP; however, the continuous formulation, Wasserstein distance, is computed via the Kantorovich-Rubinstein dual[3], which we show below.

The penalty term, here named $\lambda(p_{A},p_{B},\gamma)$, can be recreated using an adversarial critic function, $f$, which has a unitless codomain:

$\lambda(p_{A},p_{B},\gamma)=\infty$ is achieved when $\gamma\not\in\Pi(p_{A},p_{B})$ because $f$ can be made s.t., w.l.o.g., $|f(a)|\gg 1$ at the value $a$ where $p_{A}(a)\neq\int_{\infty}^{\infty}\gamma(a,b)\partial b$.

Thus,

We can further reorder $\inf_{\gamma}\sup_{f}$ to $\sup_{f}\inf_{\gamma}$: For any function $t$, $h(\beta)=\inf_{a}t(\alpha,\beta)$, and $\delta=\inf_{\alpha}\sup_{\beta}t(\alpha,\beta)=\inf_{\alpha}h(\beta)$, and so $\forall\alpha,h(\beta)\leq t(\alpha,\beta)$. Thus $\inf_{\alpha}\sup_{\beta}t(\alpha,\beta)\geq\inf_{\alpha}\sup_{\beta}h(\alpha)=\inf_{\alpha}\delta=\delta$ (i.e., weak duality). Furthermore, if $t$ is convex in $\alpha$ and concave in $\beta$, then the minimax principle yields $\inf_{\alpha}\sup_{\beta}t(\alpha,\beta)=\sup_{\beta}\inf_{\alpha}t(\alpha,\beta)$ (i.e., strong duality). Because $\Delta_{W}$ is convex in $\gamma$ (here manifest via convexity in $a,b$) and concave in $f$ (manifest via concave uses of $f$ rather then concavity of $f$ itself), we have

$\inf_{\gamma}$ is achieved by concentrating the mass of $\gamma$ where $\|a-b\|+f(b)-f(a)<0$ and setting $\gamma=0$ wherever $\|a-b\|+f(b)-f(a)\geq 0$. Thus $\inf_{\gamma}\mathbb{E}_{a,b\sim\gamma}\left[\|a-b\|+f(b)-f(a)\right]\leq 0$. This constrains that where $\frac{f(a)-f(b)}{\|a-b\|}>1$, the dual penalty term will become $-\infty$, and so we need only consider $f$ s.t. $\frac{f(a)-f(b)}{\|a-b\|}\leq 1$. This is equivalent to constraining $f$ s.t. all secants having a maximum slope $\leq 1$ (i.e., Lipschitz $\|f\|_{L}\leq 1$) yields the weakest penalty, 0:

In WGAN training, our critic functions as $f$, exploiting differences between real and generated sequences. The critic loss function is simply the difference between mean critic values of generated sequences minus mean critic values of real sequences; minimizing this loss will maximize discrimination, with real sequences awarded higher critic scores. With the goal of attaining Lipschitz continuity on $f$, we constrain its parameters $\theta_{f}$, clipping them to small values $\in[-\tau,\tau]$ at the end of each batch step. A small enough $\tau$ will ensure Lipschitz continuity for any finite network. Furthermore, $\|f\|_{L}\leq 1\leftrightarrow\frac{1}{\zeta}\|f\|_{L}\leq\zeta$; therefore, $\tau$ can be chosen rather arbitrarily as long as $\tau\ll 1$, because the cone of functional solutions $\{f:\|f\|_{L}\leq\zeta\leq 1\}$ includes all nonnegative scales of functions for which $\|f\|_{L}\leq 1$. Choice of $\tau$ will influence the optimal choice of learning rate.

When training $g$, the WGAN attempts to fool the critic and thus maximize the loss used by the critic $f$. Thus, $g$’s loss is the negative of $f$’s loss. In practice, $\theta_{g}$ does not influence critic values of real data $f(x_{i})$, and so $g$’s loss needs only be $-\mathbb{E}\left[f(\hat{X})\right]$ to maximize critic scores of generated sequences.

All expectations are taken via Monte Carlo (i.e., by taking the mean of $f$ scores over each batch).

In this manuscript, we propose a modified WGAN, in which we consider other $\lambda^{\prime}$ satisfying

Wasserstein distance employs duality via an adversarial $f$ that concentrates where (w.l.o.g.) $p_{A}(a)\neq\int_{\infty}^{\infty}\gamma(a,b)\partial b$:

This correspond to $f$ exploiting deviations in the first moment of $f$ under distribution $p_{A}$ (w.l.o.g.).

Motivated by the method of moments, we consider the first $m$ moments, $\mu_{1},\mu_{2},\ldots\mu_{m}$. At WGAN convergence, deviations between $p_{A},p_{B}$ and marginals of $\gamma$ should not be exploitable at any $q$ moment:

We continue using a signed deviation for the first moment (i.e., $f(\hat{X})\leq f(x_{i})$), but unsigned deviations for the remaining moments:

Note that $f$ is still used in a convex manner, as its outputs are either unconstrained (in $\lambda_{1}$) or within a bounded polytope $\lambda^{\prime}_{j>1}$; strong duality holds.

The same derivation holds under central moments, which are used in these experiments.

Lipschitz continuity under higher moments of $f$ is achieved by decreasing $\tau$ s.t. $|f|\leq\epsilon\ll\frac{1}{2}$. In this case, both $\mu_{1}$ and the all central moments can be bounded: $\forall j>1,|f^{j}-\mu_{j}|\leq 2\epsilon\ll 1$, and thus $\forall j>1,\frac{{f(a)}^{j}-{f(b)}^{j}}{\|a-b\|}<\frac{f(a)-f(b)}{\|a-b\|}<1$. Thus Lipschitz continuity is ensured by the standard Wasserstein derivation.

Since $f$ concentrates at deviations between distributions, it should approach a Dirac delta before convergence if $g$’s training lags the training of $f$; thus, here we have not investigated using the higher moments informing $\lambda^{\prime}$ when training $f$; $f$ is trained using the same Wasserstein loss using $\lambda$. $\lambda^{\prime}$ is used to train $g$, which corresponds to replacing standard code

with new code

This formulation allows learning from batches in gestalt. When the number of computed moments $m$ equals the batch size $b$, there is sufficient information to recover the entire distribution; furthermore, even relatively few moments can accurately summarize the distribution in practice in a manner reminiscent of the fast multipole method[4, 5].

Considering higher moments at batch size $b$ results in a per-batch runtime $\in\Omega(b^{2})$ or $\in\Omega(m\cdot b)$ if the layer of moments is used to separate the data from critic output. Also, the modified WGAN needs to compute critic scores $f(x_{i})$ when training the generator. This increases computation cost.

Fractional moments can be informative and numerically stable; however, in the general case, they require arithmetic on complex numbers and may negatively influence performance.

Data are produced using 5 replicate trials of 200 epochs. For fairness, each loss function investigated used every random seed $\in 0,1,\ldots 4$.

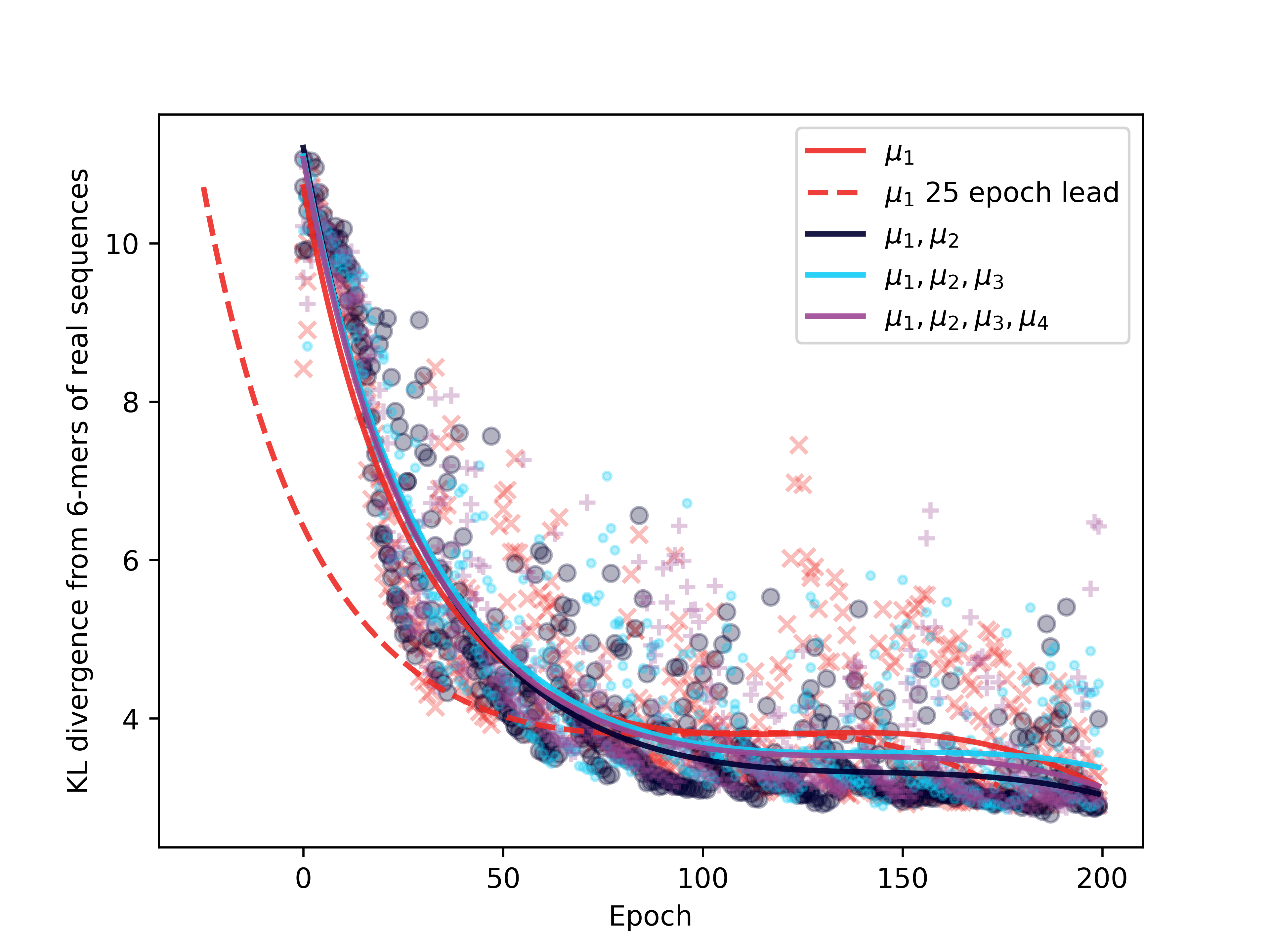
Figure 1 illustrates the relationship between sequence quality produced by $g$ at each epoch and the loss function used.

Figure 2 illustrates the relationship between sequence quality produced by $g$ and the loss function value for each loss function used. Note that for any $m>1$, generator loss uses penalty term $\lambda^{\prime}\geq\lambda$, and so a small $m>1$ loss function necessarily implies a small loss function using a standard WGAN.

O.S. is an employee of A-Alpha Bio and owns stock options in the company.