Adiabatic Pumping of Orbital Magnetization by Spin Precession
Abstract
We propose adiabatic pumping of orbital magnetization driven by coherent spin precession, facilitating the rectification of this precession. The orbital magnetization originates from the adiabatic evolution of valence electrons with a topological bulk contribution expressed as a Chern-Simons form. When the precession cone angle of spin is small, the resulting magnetization is proportional to , contributing to the magnon Zeeman effect. With a large cone angle, the magnetization can reach its natural unit, , in an antiferromagnetic topological insulator with as the elementary charge and as the precession period. This significant magnetization is related to the global properties of the electronic geometric phases in the parameter space spanned by and momentum . When the pumped magnetization is inhomogeneous, induced by spin textures or electronic topological phase domains, a dissipationless charge current is also pumped. At last, we discuss the boundary contributions from the spin-driving edge states, which are intricately linked to the gauge-dependent quantum uncertainty of the Chern-Simons form.
Orbital magnetization has been a focus of recent research in condensed matter physics. It plays a crucial role in the orbital Chern insulator, a topological phase driven by strong correlation where the Chern number is closely related to the orbital magnetization [1, 2, 3, 4, 5]. Electric manipulations of the orbital magnetization and thus topological phase have been reported [6, 7, 8]. An electric field can also induce orbital magnetization in the axion insulator with topological magnetoelectric effect [9, 10, 11, 12, 13] or in transition metals through orbital Hall effect [14, 15, 16, 17], which revives the emerging field of orbitronics [14, 18, 19, 20, 21] that encodes information with the orbital degree of freedom. In addition to the electric means, a spin-based scheme to engineer the orbital magnetization is fundamentally interesting and practically important by bridging the fields of orbitronics and spintronics [22, 23, 24, 25, 26].
This Letter proposes pumping orbital magnetization in magnetic insulators using coherent spin precession. The orbital magnetization of electrons can have intra-atomic and inter-atomic contributions. While the former is partially or completely quenched by the crystal field [20], the latter however can be large and is closely related to the electronic geometric phases [20, 10, 11]. Therefore, we focus on topological systems with prominent geometric phase effects [27, 28, 29, 30, 31, 32, 33, 34]. Such systems exhibit additional advantages. First, abundant 2D van der Waals layers with nontrivial topology and/or magnetism have been suggested by recent theoretical and experimental progresses [27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41], which allows the realization of our proposals by using the 2D atomic legos [42]. Second, the pumping is universal for both ferro- and anti-ferromagnet. Particularly, the pumping in antiferromagnet topological insulators can reach its topological limit, , which could provide a starting point for the study of orbital physics with spin dynamics in topological antiferromagnet [43, 44] that shows potential applications in orbitronics and antiferromagnetic spintronics [23, 24].
In the following, we explore the magnetization pumping in an antiferromagnetic topological insulator. The precession can be driven by a microwave in magnetic resonance or spin torque induced by a current. A large precession cone angle is achievable with easy-plane anisotropy. We focus on the Kane-Mele-Hubbard model with spontaneous magnetic order where the dynamics of valence electrons are capured by a mean-field Hamiltonian. We explore how the magnetization varies as the precession cone angle increases and elaborate the effect of geometric phases. We then discuss the pumping of a dissipationless charge current that arises from the inhomogeneous orbital magnetization in the presence of spin textures or topological phase domains. At last, we address the contributions from boundaries and their relationship with that from the bulk.
Coherent spin precession.— Coherent spin precession is a crucial ingredient in spintronics and magnonics for generating spin and magnon current [45]. Various methods are routinely used to generate the coherent precession, including microwave-induced magnetic resonance or spin-orbit torques induced by current in a neighboring layer, where the spin dynamics are described by the Landau-Lifshitz-Gilbert (LLG) equation [46]
| (1) |
where is the gyromagnetic ratio, represents the spin orientation at the -th site, stands for the effective magnetic field for in the absence of external stimuli, is the external field from microwave or spin-orbit torque, and is the Gilbert damping. A sustained precession can be achieved when external stimuli offset the energy loss due to damping [47].
The precession angle varies in a broad range for different systems. With easy-axis anisotropy, the equilibrium spin orientation is locked to the easy-axis direction and the cone angle of the precession can reach a few degrees around the easy axis [48, 45]. With easy-plane magnetic anisotropy, the spin can coherently rotate in the easy plane with a much larger cone angle, approaching 90 degrees, driven by spin-orbit torques [49, 50, 51, 52].
Model system.— We focus on antiferromagnetic topological insulators where spin magnetization vanishes and the topological electronic structure can enhance the orbital-magnetization pumping. A prototype system is the Kane-Mele Hubbard model [27, 28, 29, 30] where Néel-type antiferromagnetic order forms spontaneously with easy-plane anisotropy. The electronic system is described by the following mean field Hamiltonian [29]
| (2) |
where represents the Kane-Mele model Hamiltonian for the valence electrons
| (3) |
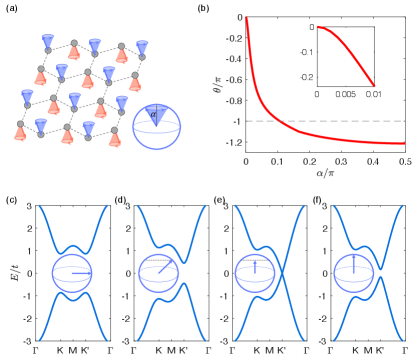
where and are Pauli matrices of sublattice and spin, separately. Here, , , and with and . The lattice constant and inter-site hopping are set to be 1, characterizes the next-nearest-neighbor hopping from the intrinsic spin-orbit coupling that opens a band gap of at the Dirac points . The unit vector represents the spin orientation at site formed spontaneously due to the Hubbard interaction [29] and indicates the exchange field induced by the magnetic order. In the absence of spin precession, the electronic structure and band topology strongly depend on the direction of the Néel vector. When the Néel vector lies in the basal plane, the band structure, as shown in Fig. 1(c), exhibits degenerate valleys at and points. Tilting the Néel vector out of the plane lifts this valley degeneracy, as plotted in Fig. 1(d). As the in-plane spin component vanishes while keeping the out-of-plane component fixed, the band gap closes, as shown in Fig. 1(e). The gap reopens as the out-of-plane spin component increases to the unit as shown in Fig. 1(f). Due to the parity-time () symmetry, each band is doubly degenerate, ensuring vanishing static spin and orbital magnetization. However, nonzero orbital magnetization appears in the presence of spin precession, represented by the periodically varying .
Formalism.— As the precession frequency typically ranges from GHz to THz that is smaller than the typical band gaps of antiferromagnetic topological insulators, the valence electrons are thus pumped adiabatically. The orbital magnetization from adiabatic pumping can be obtained by studying the current density induced by time-varying parameters, e.g., the spin configuration that vary slowly in space and time [53, 54, 55, 56]. By comparing the current density with , the theoretical formulas of orbital magnetization can be extracted [53, 54, 55, 56]. The spatial varying of is assumed for the convenience of derivation. After obtaining the formalism of , one can calculate the magnetization under that is spatially uniform and temporally periodic. As we focus on 2D systems, only has a nonzero -component. The orbital magnetization has two contributions and we focus on the topological part that is more relevant to the physics of interest [53, 55, 56]. This part is expressed as [53]
| (4) |
where is the elementary electron charge, is the spin precession period, and the coefficient is a Chern-Simons form
| (5) |
where is the Levi-Civita symbol with summation over repeated indices, means trace over the occupied bands, with , and . is nonabelian Berry connection and its matrix element where and are electronic states of occupied bands at momentum with band indices . Since the integral is gauge invariant only modulo , the pumped orbital magnetization can differ by an integer multiple of depending on the gauge choice. As shown in the Supplemental Materials [47], this uncertainty manifests in the boundary contributions. Specifically, depending on the crystalline orientation of the edge, the boundary contribution can vary by a quantized current resulting from the Thouless pumping.
The gauge dependence of the integrand makes it difficult to evaluate directly. One efficient way to evaluate is to treat it as a function of an auxiliary parameter [10, 11]. Following the fundamental theorem of calculus,
| (6) |
When the Berry connections can be made smooth and periodic in the Brillouin zone, the equation becomes [10, 11]
| (7) |
and
| (8) |
where the nonabelian Berry curvature . When the starting point is chosen to be zero, one can obtain the accurate value of as Eq. (7) is gauge invariant and path independent.
Besides the pumped orbital magnetization, the topological magnetoelectric coupling constant is also expressed as a Chern-Simons form [9, 10, 11, 12, 13]. This coupling is notably half-quantized, protected by either time-reversal or inversion symmetry, because the coupling represents the response of a pseudovector to a vector or vise versa, where the inversion or time-reversal operation only changes one of their signs. However, these symmetries cannot make the orbital magnetization quantized as the Chern-Simons form in Eq. (5) represents the response of a pseudo-vector to the spin precession characterized by another pseudovector, as defined below.
Precession angle dependence.—By defining the auxiliary parameter as spin precession angle defined in Fig. 1(a), we can obtain the pumped orbital magnetization as a function of spin precession angle. For simplicity, we assume that during the spin precession as these two spin sublattices are locked by strong exchange interaction that is much stronger than the anisotropy. The spin orientations are denoted by a unit vector . Figure 1(b) plots the pumped orbital magnetization as a function of the precession angle following Eq. (7). When , the spin orientation is actually fixed and thus the pumped orbital magnetization vanishes. As increases, the pumped orbital magnetization increases.
When the angle is small, are much smaller than 1. Their influences on the energy band and the eigenstates are perturbative. The Chern-Simons form in Eq. (5) can thus be evaluated by series expansion with respect to [56]. The orbital magnetization reads with a constant
| (9) |
where the second Chern form in the integrand are evaluated at . Therefore, the pumped orbital magnetization is proportional to through . The magnetization depends on the spin precession chirality while is independent of the Néel vector. This dynamically induced magnetization corrects the Landau free energy in the presence of an external field by leading to a dynamical contribution to the magnetic susceptibility. The energy correction also manifests in the field induced energy shift of magnons, i.e., the magnon Zeeman splitting, considering the magnetization induced by a single magnon.
The orbital magnetization induced by pumping processes is intricately linked to a range of magnetoelectric phenomena as suggested by Eq. (9). involves three types of Berry curvature, i.e., , , and . is closely related to the spin-driven ferroelectricity. Specifically, the change of the polarization along -th direction induced by the deviation in spin, , is proportional to . As a result, a spatially varying spin structure leads to a nonzero charge density [57, 58] while temporal precession of spins generates rotating polarization and thus orbital magnetization. Unlike , which is closely related to various Hall effects, is associated with spin dynamics. In specific, characterizes the geometric phase of valence electrons that evolve adiabatically following spin precession. This phase leads to a geometric torque on the spins [59], enabling the control of spin dynamics by engineering valence electrons. The effects of such geometric torque are not yet fully understood.
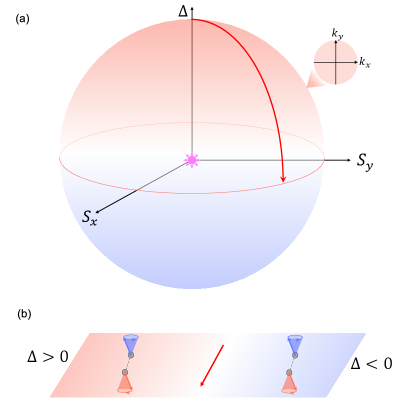
As the spin precession cone angle increases, the orbital magnetization increases rapidly and can reach the order of as reaches . The large pumping has a topological origin. To show this, we consider the low-energy effective model near the K′ point, where massive Dirac dispersion appears described by the effective Hamiltonian where , , and the matrices . The energy bands are doubly degenerate with eigenenergy and . When the spin is along direction, the band gap is determined by , as shown in Fig. 1(f), and a single Dirac cone appears at by reducing as shown in Fig. 1(e). The dispersion is gapped again if there is in-plane spin components as shown in Fig. 1(d). The second Chern form in Eq. (7) resembles the nonabelian gauge field created by a Yang’s monopole in a five-dimensional space around the gap closing point as illustrated in Fig. 2(a). Integrating the second Chern form over a closed surface containing the gap closing point leads to an integer second Chern number with whereas the integration over part of a closed surface, see the red arrow in Fig. 2(a), leads to a fraction of .
Inhomogeneity enabled current pumping.— The pumping of orbital magnetization facilitates the spin texture-enabled generation of an adiabatic charge current. Specifically, when orbital magnetization is spatially inhomogeneous, it generates a dissipationless charge current density, described by . In antiferromagnets, these inhomogeneities are often a result of spatial variations in spin textures. As the magnetic order varies across different regions, the pumped orbital magnetization also varies, thus enabling the controlled generation of a charge current. Such a current can even become quantized as by spatially engineering the electronic band topology. In specific, the electronic band gap is determined by the competition between the spin-orbit coupling and effective exchange field from the magnetic order. By engineering a continuous change of from positive to negative, one can map the parameter space shown in Fig. 2(a) to a domain wall structure in Fig. 2(b). By further introducing a spin precession enclosing a Yang’s monopole inside the parameter space, a quantized magnetization current along the domain wall appears that is experimentally measurable.
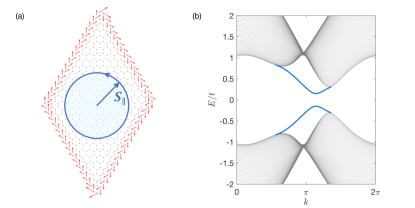
Boundary contribution.— Besides the bulk, the boundary can also have significant contribution to the pumped orbital magnetization. When the Néel vector points out-of-plane, the antiferromagnetic topological insulator can host a quantum spin Hall effect with gapless edge states when . The helical edge states described by the effective Hamiltonian where is the momentum along the boundary, is the velocity, and are the spin Pauli matrices. By tilting the Néel vector, the edge states become gapped by a mass term correction where represents the effective exchange coupling strength. When the spin starts to precess with a frequency of and , a quantized Thouless pumping along the boundary is realized if the adiabatic approximation is valid with . The current along the edge is with being the first Chern number in the parameter space of - [60, 61] as illustrated by red arrows in Fig. LABEL:Fig1(a). This current contributes an out-of-plane orbital magnetization , which is even larger than the bulk contribution.
Nevertheless, the boundary contribution is notably sensitive to the boundary conditions. Firstly, the edge state properties can depend on the crystalline orientation, which remain gapless along certain orientations even in the presence of spin precession while become gapped along others. One example in the Supplemental Materials demonstrates a quantized Thouless pumping along the zigzag boundary, which is absent along the armchair boundary. Secondly, in antiferromagnetic topological insulators, the edge states are not protected by symmetry. Disorders on the boundary can destroy the quantized Thouless pumping.
The sensitivity of boundary contribution suggests that the pumped orbital magnetization can modulated by integer multiples of by engineering the boundary without altering the bulk. This uncertainty of orbital magnetization is a physical manifestation of the gauge dependence of Eq. (5) where can vary by with different gauge choices. Such uncertainty mirrors that of bulk polarization [62, 63], which is also defined by pumping.
Summary.— We have studied the adiabatic pumping of orbital magnetization drive by spin precession in magnetic topological systems. This pumping mechanism enables the rectification of spin precession, resulting in a static orbital magnetization or a dissipationless charge current in the presence of inhomogeneities such as spin textures or electronic topological domains. The orbital magnetization contributes to the dynamical magnetic susceptibility as well as the magnon Zeeman effect when the precession cone angle is small. For large cone angles, the orbital magnetization is related to the global properties of the electronic geometric phases in the parameter spaces spanned by momentum and spin . In addition, a nontrivial quantized boundary contribution may emerge, illustrating the quantum uncertainty associated with the Chern-Simons form in bulk contribution.
The Kane-Mele Hubbard model serves as a prototype model hosting antiferromagnetic topological insulator, which has attracted many attentions [64] and can be realized in moiré systems, like twisted MoTe2 [30]. To experimentally measure the magnetization, the temperature should be lower than the Néel temperature and the electronic band gap. The order of magnitude of the pumped magnetization and adiabatic current can vary widely but can reach the order of with a large precession angle. The pumped magnetic moment per unit cell is proportional to the precession period and the unit-cell size, potentially reaching the order of a Bohr magneton in a moiré supercell about 50 nm2 in area with terahertz frequency precession. The orbital-magnetization pumping is universal in both antiferro- and ferromagnetic systems [47]. We expect similar phenomena in MnBi2Se4 systems with easy-plane anisotropy [34]. Enhancements in this pumping effect are facilitated by strong spin-orbit coupling, narrow energy gap, nontrivial band topology, fast spin dynamics, and large cone angle of precession.
Acknowledgements.
Acknowledgments.— We thank the helpful discussion with Qian Niu, Jiang Xiao, and Ran Cheng. The analytical study is supported by DOE Award No. DE-SC0012509, and the numerical simulation is supported by the Center on Programmable Quantum Materials, an Energy Frontier Research Center funded by DOE BES under award DE-SC0019443. Y.R. acknowledges startup funds provided by the College of Arts and Sciences and the Department of Physics and Astronomy of the University of Delaware.References
- Sharpe et al. [2019] A. L. Sharpe, E. J. Fox, A. W. Barnard, J. Finney, K. Watanabe, T. Taniguchi, M. Kastner, and D. Goldhaber-Gordon, Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene, Science 365, 605 (2019).
- Serlin et al. [2020] M. Serlin, C. Tschirhart, H. Polshyn, Y. Zhang, J. Zhu, K. Watanabe, T. Taniguchi, L. Balents, and A. Young, Intrinsic quantized anomalous Hall effect in a moiré heterostructure, Science 367, 900 (2020).
- Chen et al. [2020] G. Chen, A. L. Sharpe, E. J. Fox, Y.-H. Zhang, S. Wang, L. Jiang, B. Lyu, H. Li, K. Watanabe, T. Taniguchi, et al., Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice, Nature 579, 56 (2020).
- Liu et al. [2019] J. Liu, Z. Ma, J. Gao, and X. Dai, Quantum valley Hall effect, orbital magnetism, and anomalous Hall effect in twisted multilayer graphene systems, Phys. Rev. X 9, 031021 (2019).
- Ren et al. [2021a] Y. Ren, H.-C. Jiang, Z. Qiao, and D. Sheng, Orbital Chern insulator and quantum phase diagram of a kagome electron system with half-filled flat bands, Phys. Rev. Lett. 126, 117602 (2021a).
- Polshyn et al. [2020] H. Polshyn, J. Zhu, M. A. Kumar, Y. Zhang, F. Yang, C. L. Tschirhart, M. Serlin, K. Watanabe, T. Taniguchi, A. H. MacDonald, et al., Electrical switching of magnetic order in an orbital Chern insulator, Nature 588, 66 (2020).
- Zhu et al. [2020] J. Zhu, J.-J. Su, and A. H. MacDonald, Voltage-controlled magnetic reversal in orbital Chern insulators, Phys. Rev. Lett. 125, 227702 (2020).
- Su and Lin [2020] Y. Su and S.-Z. Lin, Current-induced reversal of anomalous Hall conductance in twisted bilayer graphene, Phys. Rev. Lett. 125, 226401 (2020).
- Qi et al. [2008a] X.-L. Qi, T. L. Hughes, and S.-C. Zhang, Topological field theory of time-reversal invariant insulators, Phys. Rev. B 78, 195424 (2008a).
- Xiao et al. [2009] D. Xiao, J. Shi, D. P. Clougherty, and Q. Niu, Polarization and adiabatic pumping in inhomogeneous crystals, Phys. Rev. Lett. 102, 087602 (2009).
- Essin et al. [2009] A. M. Essin, J. E. Moore, and D. Vanderbilt, Magnetoelectric polarizability and axion electrodynamics in crystalline insulators, Phys. Rev. Lett. 102, 146805 (2009).
- Mong et al. [2010] R. S. Mong, A. M. Essin, and J. E. Moore, Antiferromagnetic topological insulators, Phys. Rev. B 81, 245209 (2010).
- He et al. [2022] Q. L. He, T. L. Hughes, N. P. Armitage, Y. Tokura, and K. L. Wang, Topological spintronics and magnetoelectronics, Nat. Mater. 21, 15 (2022).
- Bernevig et al. [2005] B. A. Bernevig, T. L. Hughes, and S.-C. Zhang, Orbitronics: The intrinsic orbital current in -doped silicon, Phys. Rev. Lett. 95, 066601 (2005).
- Kontani et al. [2009] H. Kontani, T. Tanaka, D. Hirashima, K. Yamada, and J. Inoue, Giant orbital Hall effect in transition metals: Origin of large spin and anomalous Hall effects, Phys. Rev. Lett. 102, 016601 (2009).
- Go et al. [2018] D. Go, D. Jo, C. Kim, and H.-W. Lee, Intrinsic spin and orbital Hall effects from orbital texture, Phys. Rev. Lett. 121, 086602 (2018).
- Choi et al. [2023] Y.-G. Choi, D. Jo, K.-H. Ko, D. Go, K.-H. Kim, H. G. Park, C. Kim, B.-C. Min, G.-M. Choi, and H.-W. Lee, Observation of the orbital Hall effect in a light metal Ti, Nature 619, 52 (2023).
- Go et al. [2017] D. Go, J.-P. Hanke, P. M. Buhl, F. Freimuth, G. Bihlmayer, H.-W. Lee, Y. Mokrousov, and S. Blügel, Toward surface orbitronics: giant orbital magnetism from the orbital Rashba effect at the surface of -metals, Sci. Rep. 7, 1 (2017).
- Phong et al. [2019] V. T. Phong, Z. Addison, S. Ahn, H. Min, R. Agarwal, and E. Mele, Optically controlled orbitronics on a triangular lattice, Phys. Rev. Lett. 123, 236403 (2019).
- Go et al. [2021] D. Go, D. Jo, H.-W. Lee, M. Kläui, and Y. Mokrousov, Orbitronics: orbital currents in solids, EPL (Europhysics Letters) 135, 37001 (2021).
- Sala et al. [2023] G. Sala, H. Wang, W. Legrand, and P. Gambardella, Orbital Hanle magnetoresistance in a transition metal, Phys. Rev. Lett. 131, 156703 (2023).
- Žutić et al. [2004] I. Žutić, J. Fabian, and S. D. Sarma, Spintronics: Fundamentals and applications, Rev. Mod. Phys. 76, 323 (2004).
- Baltz et al. [2018] V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono, and Y. Tserkovnyak, Antiferromagnetic spintronics, Rev. Mod. Phys. 90, 015005 (2018).
- Šmejkal et al. [2018] L. Šmejkal, Y. Mokrousov, B. Yan, and A. H. MacDonald, Topological antiferromagnetic spintronics, Nat. Phys. 14, 242 (2018).
- Go et al. [2023] D. Go, K. Ando, A. Pezo, S. Blügel, A. Manchon, and Y. Mokrousov, Orbital pumping by magnetization dynamics in ferromagnets, arXiv:2309.14817 (2023).
- Hayashi and Ando [2023] H. Hayashi and K. Ando, Observation of orbital pumping, arXiv:2304.05266 (2023).
- Hohenadler et al. [2011] M. Hohenadler, T. Lang, and F. Assaad, Correlation effects in quantum spin-Hall insulators: A quantum Monte Carlo study, Phys. Rev. Lett. 106, 100403 (2011).
- Hohenadler et al. [2012] M. Hohenadler, Z. Meng, T. Lang, S. Wessel, A. Muramatsu, and F. Assaad, Quantum phase transitions in the Kane-Mele-Hubbard model, Phys. Rev. B 85, 115132 (2012).
- Hutchinson et al. [2021] J. Hutchinson, P. W. Klein, and K. Le Hur, Analytical approach for the Mott transition in the Kane-Mele-Hubbard model, Phys. Rev. B 104, 075120 (2021).
- Liu et al. [2024] X. Liu, Y. He, C. Wang, X.-W. Zhang, T. Cao, and D. Xiao, Gate-tunable antiferromagnetic Chern insulator in twisted bilayer transition metal dichalcogenides, Phys. Rev. Lett. 132, 146401 (2024).
- Gong et al. [2019] Y. Gong, J. Guo, J. Li, K. Zhu, M. Liao, X. Liu, Q. Zhang, L. Gu, L. Tang, X. Feng, et al., Experimental realization of an intrinsic magnetic topological insulator, Chinese Physics Letters 36, 076801 (2019).
- Otrokov et al. [2019] M. M. Otrokov, I. I. Klimovskikh, H. Bentmann, D. Estyunin, A. Zeugner, Z. S. Aliev, S. Gaß, A. Wolter, A. Koroleva, A. M. Shikin, et al., Prediction and observation of an antiferromagnetic topological insulator, Nature 576, 416 (2019).
- Chang et al. [2023] C.-Z. Chang, C.-X. Liu, and A. H. MacDonald, Colloquium: Quantum anomalous Hall effect, Rev. Mod. Phys. 95, 011002 (2023).
- Chen et al. [2024] X. Chen, A. Ruiz, A. J. Bishop, B. Gunn, R. Basak, T. Zhu, Y. He, M. Vranas, E. Weschke, R. K. Kawakami, et al., Antiferromagnetic order in the layered magnetic topological insulator MnBi2Se4 probed by resonant soft x-ray scattering, Phys. Rev. B 109, 184418 (2024).
- Gong and Zhang [2019] C. Gong and X. Zhang, Two-dimensional magnetic crystals and emergent heterostructure devices, Science 363, eaav4450 (2019).
- Cortie et al. [2020] D. L. Cortie, G. L. Causer, K. C. Rule, H. Fritzsche, W. Kreuzpaintner, and F. Klose, Two-dimensional magnets: forgotten history and recent progress towards spintronic applications, Adv. Funct. Mater. 30, 1901414 (2020).
- Ningrum et al. [2020] V. P. Ningrum, B. Liu, W. Wang, Y. Yin, Y. Cao, C. Zha, H. Xie, X. Jiang, Y. Sun, S. Qin, et al., Recent advances in two-dimensional magnets: Physics and devices towards spintronic applications, Research 2020 (2020).
- Yao et al. [2021] Y. Yao, X. Zhan, M. G. Sendeku, P. Yu, F. T. Dajan, C. Zhu, N. Li, J. Wang, F. Wang, Z. Wang, et al., Recent progress on emergent two-dimensional magnets and heterostructures, Nanotechnology 32, 472001 (2021).
- Olsen et al. [2019] T. Olsen, E. Andersen, T. Okugawa, D. Torelli, T. Deilmann, and K. S. Thygesen, Discovering two-dimensional topological insulators from high-throughput computations, Phys. Rev. Materials 3, 024005 (2019).
- Marrazzo et al. [2019] A. Marrazzo, M. Gibertini, D. Campi, N. Mounet, and N. Marzari, Relative abundance of topological order in exfoliable two-dimensional insulators, Nano Letters 19, 8431 (2019).
- Choudhary et al. [2020] K. Choudhary, K. F. Garrity, J. Jiang, R. Pachter, and F. Tavazza, Computational search for magnetic and non-magnetic 2D topological materials using unified spin–orbit spillage screening, npj Comput. Mater. 6, 1 (2020).
- Geim and Grigorieva [2013] A. K. Geim and I. V. Grigorieva, Van der Waals heterostructures, Nature 499, 419 (2013).
- Bernevig et al. [2022] B. A. Bernevig, C. Felser, and H. Beidenkopf, Progress and prospects in magnetic topological materials, Nature 603, 41 (2022).
- Bonbien et al. [2021] V. Bonbien, F. Zhuo, A. Salimath, O. Ly, A. Abbout, and A. Manchon, Topological aspects of antiferromagnets, Journal of Physics D: Applied Physics 55, 103002 (2021).
- Han et al. [2023] J. Han, R. Cheng, L. Liu, H. Ohno, and S. Fukami, Coherent antiferromagnetic spintronics, Nat. Mater. 22, 684 (2023).
- Ellis et al. [2015] M. O. Ellis, R. F. Evans, T. A. Ostler, J. Barker, U. Atxitia, O. Chubykalo-Fesenko, and R. W. Chantrell, The Landau–Lifshitz equation in atomistic models, Low Temperature Physics 41, 705 (2015).
- [47] See Supplemental Materials for details of spin-torque induced spin precession, geometrical pumping in ferromagnetic case, and boundary-dependent pumping where Refs. [65, 66, 67, 68] are cited.
- Kiselev et al. [2003] S. I. Kiselev, J. Sankey, I. Krivorotov, N. Emley, R. Schoelkopf, R. Buhrman, and D. Ralph, Microwave oscillations of a nanomagnet driven by a spin-polarized current, nature 425, 380 (2003).
- Cheng et al. [2015] R. Cheng, M. W. Daniels, J.-G. Zhu, and D. Xiao, Ultrafast switching of antiferromagnets via spin-transfer torque, Phys. Rev. B 91, 064423 (2015).
- Cheng et al. [2016] R. Cheng, D. Xiao, and A. Brataas, Terahertz antiferromagnetic spin Hall nano-oscillator, Phys. Rev. Lett. 116, 207603 (2016).
- Takeuchi et al. [2021] Y. Takeuchi, Y. Yamane, J.-Y. Yoon, R. Itoh, B. Jinnai, S. Kanai, J. Ieda, S. Fukami, and H. Ohno, Chiral-spin rotation of non-collinear antiferromagnet by spin-orbit torque, Nat. Mater. 20, 1364 (2021).
- Yan et al. [2022] G. Q. Yan, S. Li, H. Lu, M. Huang, Y. Xiao, L. Wernert, J. A. Brock, E. E. Fullerton, H. Chen, H. Wang, et al., Quantum sensing and imaging of spin–orbit-torque-driven spin dynamics in the non-collinear antiferromagnet Mn3Sn, Adv. Mater. 34, 2200327 (2022).
- Trifunovic et al. [2019] L. Trifunovic, S. Ono, and H. Watanabe, Geometric orbital magnetization in adiabatic processes, Phys. Rev. B 100, 054408 (2019).
- Dong and Niu [2018] L. Dong and Q. Niu, Geometrodynamics of electrons in a crystal under position and time-dependent deformation, Phys. Rev. B 98, 115162 (2018).
- Xiao et al. [2021] C. Xiao, Y. Ren, and B. Xiong, Adiabatically induced orbital magnetization, Phys. Rev. B 103, 115432 (2021).
- Ren et al. [2021b] Y. Ren, C. Xiao, D. Saparov, and Q. Niu, Phonon magnetic moment from electronic topological magnetization, Phys. Rev. Lett. 127, 186403 (2021b).
- Brey et al. [1995] L. Brey, H. Fertig, R. Côté, and A. MacDonald, Skyrme crystal in a two-dimensional electron gas, Phys. Rev. Lett. 75, 2562 (1995).
- Freimuth et al. [2013] F. Freimuth, R. Bamler, Y. Mokrousov, and A. Rosch, Phase-space Berry phases in chiral magnets: Dzyaloshinskii-Moriya interaction and the charge of skyrmions, Phys. Rev. B 88, 214409 (2013).
- Michel et al. [2024] S. Michel, A. Fünfhaus, R. Quade, R. Valentí, and M. Potthoff, Bound states and local topological phase diagram of classical impurity spins coupled to a Chern insulator, Phys. Rev. B 109, 155116 (2024).
- Thouless [1983] D. Thouless, Quantization of particle transport, Phys. Rev. B 27, 6083 (1983).
- Qi et al. [2008b] X.-L. Qi, T. L. Hughes, and S.-C. Zhang, Fractional charge and quantized current in the quantum spin Hall state, Nat. Phys. 4, 273 (2008b).
- King-Smith and Vanderbilt [1993] R. King-Smith and D. Vanderbilt, Theory of polarization of crystalline solids, Phys. Rev. B 47, 1651 (1993).
- Vanderbilt and King-Smith [1993] D. Vanderbilt and R. King-Smith, Electric polarization as a bulk quantity and its relation to surface charge, Phys. Rev. B 48, 4442 (1993).
- Rachel [2018] S. Rachel, Interacting topological insulators: a review, Rep. Prog. Phys. 81, 116501 (2018).
- Gurevich and Melkov [2020] A. G. Gurevich and G. A. Melkov, Magnetization oscillations and waves (CRC press, 2020).
- Cheng et al. [2014] R. Cheng, J. Xiao, Q. Niu, and A. Brataas, Spin pumping and spin-transfer torques in antiferromagnets, Phys. Rev. Lett. 113, 057601 (2014).
- Kane and Mele [2005] C. L. Kane and E. J. Mele, Quantum spin Hall effect in graphene, Phys. Rev. Lett. 95, 226801 (2005).
- Ren et al. [2020] Y. Ren, Z. Qiao, and Q. Niu, Engineering corner states from two-dimensional topological insulators, Phys. Rev. Lett. 124, 166804 (2020).