Adaptive lasso and Dantzig selector for spatial point processes intensity estimation

Spatial point processes are stochastic processes which model random locations of points in space, such as random locations of trees in a forest, locations of disease cases, earthquake occurrences and crime events [e.g. 2, 8, 13, 23]. To understand the arrangement of points, the intensity function is the standard summary function [2, 13]. When one seeks to describe the probability of observing a point at location $u\in\mathbb{R}^{d}$ in terms of covariates, the most popular model for the intensity function, $\rho$, is

where, for $p\geq 1$, $\mathbf{z}(u)=\{z_{1}(u),\ldots,z_{p}(u)\}^{\top}$, represent spatial covariates measured at location $u$ and $\bm{\beta}=\{\beta_{1},\ldots,\beta_{p}\}^{\top}$ is a real $p$-dimensional parameter.

The score of the Poisson likelihood, i.e. the likelihood if the underlying process is assumed to be the Poisson process, remains an unbiased estimating equation to estimate $\bm{\beta}$ even if the point pattern does not arise from a Poisson process [25]. Such a method is well-studied in the literature and extended in several ways to gain efficiency [e.g. 18, 19] when the number of covariates is moderate. Standard results cover the consistency and asymptotic normality of the maximum Poisson likelihood under the increasing domain asymptotic (see e.g. [18] and references therein).

When a large number of covariates is available, variable selection is unavoidable. Performing estimation and selection for spatial point processes intensity models has received a lot of attention. Recent developments consider techniques centered around regularization methods [e.g. 10, 14, 24, 27] such as lasso technique. In particular, [10] consider several composite likelihoods penalized by a large class of convex and non-convex penalty functions and obtain asymptotic results under the increasing domain asymptotic framework.

The Dantzig selector is an alternative procedure to regularization techniques. It was initially proposed for linear models by [7] and subsequently extended to more complex models [e.g. 1, 15, 21]. In particular, [15] generalizes this approach to general estimating equations. One of the main advantages of the Dantzig selector is its implementation which, for linear models, results in a linear programming. Since then, the Dantzig selector and lasso procedures have been compared in different contexts [e.g. 3, 22].

In this paper, we compare lasso and Dantzig selector when they are applied to intensity estimation for spatial point processes. We compare these procedures in the complex asymptotic framework where the number of informative covariates, say $s_{n}$ and the number of non-informative covariates, say $p_{n}-s_{n}$, may increase with the mean number of points. Our asymptotic results are developed under a setting which embraces both increasing domain asymptotic and infill asymptotic which are often considered in the literature (see also Section 2). Such a setting is almost never considered in the spatial point processes literature (see again e.g. [18]).

It is well-known that the Poisson likelihood can be approximated as a quasi-Poisson regression model, see e.g. [2]. For the adaptive lasso procedure, our theoretical contributions can also be seen as extension of work such as [16] which provides asymptotic results for estimators from regularized generalized linear models. However, in our spatial framework, the more standard sample size must be substituted by, here, a mean number of points. Furthermore, observations are no more independent, i.e. our results are valid for a large class of spatial dependent point processes. Note also that [16] assumes $s_{n}=s$.

The theoretical contributions of the present paper are two-fold. First, for the adaptive lasso procedure, the question stems from extending the work by [10] which considers only an increasing domain asymptotic, and assumes $s_{n}=s$ and $p_{n}=p$. For the Dantzig selector, our contributions are to extend the standard methodology to spatial point processes, propose an adaptive version and derive theoretical results. This yields different computational and theoretical issues. As revealed by our main result, Theorem 4.1, the adaptive lasso and Dantzig selector procedures share several similarities but also some slight differences. We first prove that both procedures satisfy an oracle property, i.e. methods can correctly select the nonzero coefficients with probability converging to one, and second that the estimators of the nonzero coefficients are asymptotically normal. However, the conditions under which results are valid for the Dantzig selector are slightly more restrictive.

Our conducted simulation study and application to environmental data also demonstrate that both procedures behave similarly.

Let $\mathbf{X}$ be a spatial point process on $\mathbb{R}^{d}$, $d\geq 1$. We view $\mathbf{X}$ as a locally finite random subset of $\mathbb{R}^{d}$. Let $D\subset\mathbb{R}^{d}$ be a compact set of Lebesgue measure $|D|$ which will play the role of the observation domain. A realization of $\mathbf{X}$ in $D$ is thus a set $\mathbf{x}=\{x_{1},\ldots,x_{m}\}$, where $x\in D$ and $m$ is the observed number of points in $D$. Suppose $\mathbf{X}$ has intensity function $\rho$ and second-order product density $\rho^{(2)}$. Campbell theorem states that, for any function $k:\mathbb{R}^{d}\to[0,\infty)$ or $k:\mathbb{R}^{d}\times\mathbb{R}^{d}\to[0,\infty)$

Based on the first two intensity functions, the pair correlation function $g$ is defined by

when both $\rho$ and $\rho^{(2)}$ exist with the convention $0/0=0$. The pair correlation function is a measure of departure of the model from the Poisson point process for which $g=1$. For further background materials on spatial point processes, see for example [2, 23].

For our asymptotic considerations, we assume that a sequence $(\mathbf{X})_{n\geq 1}$ is observed within a sequence of bounded domains $(D_{n})_{n\geq 1}$. We denote by $\rho_{n}$ and $g_{n}$ the intensity and pair correlation of $\mathbf{X}_{n}$. With an abuse of notation, we denote by $\mathbb{E}$ and $\mathrm{Var}$, the expectation and variance under $\mathbf{X}_{n}$. we assume that the intensity $\rho_{n}$ writes $\rho_{n}(u)=\exp\{\bm{\beta}_{0}^{\top}\mathbf{z}(u)\}$, $u\in D_{n}$. We thus let $\bm{\beta}_{0}$ denote the true parameter vector and assume it can be decomposed as $\bm{\beta}_{0}=\{\beta_{01},\ldots,\beta_{0s_{n}},\beta_{0(s_{n}+1)},\ldots,\beta_{0p_{n}}\}^{\top}=(\bm{\beta}^{\top}_{01},\bm{\beta}^{\top}_{02})^{\top}=(\bm{\beta}_{01}^{\top},\mathbf{0}^{\top})^{\top}$. Therefore, $\bm{\beta}_{01}\in\mathbb{R}^{s_{n}}$, $\bm{\beta}_{02}=\mathbf{0}\in\mathbb{R}^{p_{n}-s_{n}}$ and $\bm{\beta}_{0}\in\mathbb{R}^{p_{n}}$, where $s_{n}$ is the number of non-zero coefficients, $p_{n}-s_{n}$ the number of zero coefficients and $p_{n}$ the total number of parameters. We underline that it is unknown to us which coefficients are non-zero and which are zero. Thus, we consider a sparse intensity model where in particular $s_{n}$ and $p_{n}$ may diverge to infinity as $n$ grows.

For any $\bm{\beta}\in\mathbb{R}^{p_{n}}$ or for the spatial covariates $\mathbf{z}(u)$, we use a similar notation, i.e. $\bm{\beta}=(\bm{\beta}_{1}^{\top},\bm{\beta}_{2}^{\top})^{\top}$ and $\mathbf{z}(u)=\{\mathbf{z}_{1}(u)^{\top},\mathbf{z}_{2}(u)^{\top}\}^{\top}$, $u\in D_{n}$. We let $\mu_{n}=\mathbb{E}\{N(D_{n})\}$, that is the expected number of points in $D_{n}$. By Campbell theorem, we have

Note that $\mu_{n}$ is a function of $D_{n},\bm{\beta}_{01},\mathbf{z}_{1}(u),s_{n}$. In this paper, we assume that $\mu_{n}\to\infty$ as $n\to\infty$. That kind of assumption is very general and embraces the well-known frameworks called increasing domain asymptotics and infill asymptotics. For the increasing domain context, $D_{n}\to\mathbb{R}^{d}$ and usually $\bm{\beta}_{01}$ depends on $n$ only through $s_{n}$. For the infill asymptotics, $D_{n}=D$ is assumed to be a bounded domain of $\mathbb{R}^{d}$ and usually $z_{1}(u)=1$, $\bm{\beta}_{01}=\theta_{n}\to\infty$ as $n\to\infty$. In some sense, the parameter $\mu_{n}$ plays the role of the sample size in standard inference.

To reduce notation in the following, unless it is ambiguous, we do not index $\mathbf{X}$, $\rho$, $g$, $\bm{\beta}_{0}$, $\bm{\beta}$, $\mathbf{z}(u)$ with $n$.

Our main result relies upon the following conditions:

1. ($\mathcal{C}$.1)

   The intensity function has the log-linear specification given by (1) where $\bm{\beta}\in\mathbb{R}^{p_{n}}$.

2. ($\mathcal{C}$.2)

   $(\mu_{n})_{n\geq 1}$ is an increasing sequence of real numbers, such that $\mu_{n}\to\infty$ as ${n}\to\infty$.

3. ($\mathcal{C}$.3)

   The covariates $\mathbf{z}$ satisfy

   $$\sup_{n\geq 1}\;\sup_{i=1,\dots,p_{n}}\;\sup_{u\in\mathbb{R}^{d}}|z_{i}(u)|<\infty\qquad\mbox{ and }\qquad\inf_{n\geq 1}\inf_{\bm{\phi}\in\mathbb{R}^{p_{n}},\|\bm{\phi}\|=1}\inf_{u\in D_{n}}\{\bm{\phi}^{\top}\mathbf{z}(u)\}^{2}>0$$

4. ($\mathcal{C}$.4)

   The intensity and pair correlation satisfy

   $$\int_{D_{n}}\int_{D_{n}}\rho(u;\bm{\beta}_{0})\rho(v;\bm{\beta}_{0})|g(u,v)-1|\mathrm{d}u\mathrm{d}v=O(\mu_{n}).$$

5. ($\mathcal{C}$.5)

   The matrix $B_{n,11}(\bm{\beta}_{0})$ satisfies

   $$\liminf_{n}\inf_{\bm{\phi}\in\mathbb{R}^{s_{n}},\|\bm{\phi}\|=1}\bm{\phi}^{\top}\big{\{}(\mu_{n})^{-1}\mathbf{B}_{n,11}(\bm{\beta}_{0})\big{\}}\bm{\phi}>0.$$

6. ($\mathcal{C}$.6)

   For any $\bm{\phi}\in\mathbb{R}^{s_{n}}\setminus\{0\}$, the following convergence holds in distribution as $n\to\infty$:

   $$\sigma_{\bm{\phi}}^{-1}\bm{\phi}^{\top}\mathbf{U}_{n,1}(\bm{\beta}_{0})\stackrel{{\scriptstyle d}}{{\to}}N(0,1)$$

   where $\sigma^{2}_{\bm{\phi}}=\bm{\phi}^{\top}\mathbf{B}_{n,11}(\bm{\beta}_{0})\bm{\phi}$.

7. ($\mathcal{C}$.7)

   The initial estimate $\tilde{\bm{\beta}}$ satisfies $\|\tilde{\bm{\beta}}-{\bm{\beta}_{0}}\|=O_{\mathrm{P}}(\sqrt{p_{n}/{\mu_{n}}})$ and is such that $\|\mathbf{A}_{n,11}(\tilde{\bm{\beta}})^{-1}\|=O_{\mathrm{P}}(\mu_{n}^{-1})$.

8. ($\mathcal{C}$.8)

   As $n\to\infty$, we assume that $s_{n},p_{n}$ and $\mu_{n}$ are such that as $n\to\infty$

   $$\left\{\begin{array}[]{ll}\max\left(\frac{p_{n}^{4}}{\mu_{n}},\frac{s_{n}^{2}p_{n}^{3}}{\mu_{n}}\right)\to 0&\quad\text{ for the AL estimate}\\ \frac{s_{n}^{3}p_{n}^{4}}{\mu_{n}}\to 0&\quad\text{ for the ALDS estimate.}\end{array}\right.$$

9. ($\mathcal{C}$.9)

   Let $a_{n}=\max_{j=1,\ldots,{s_{n}}}\lambda_{n,j}$ and $b_{n}=\min_{j={s_{n}}+1,\ldots,p_{n}}\lambda_{n,j}$. We assume that these sequences are such that, as $n\to\infty$

   $$\left\{\begin{array}[]{lll}a_{n}\sqrt{s_{n}\mu_{n}}\to 0,&b_{n}\sqrt{\frac{\mu_{n}}{p_{n}^{2}}}\to\infty&\quad\text{ for the AL estimate}\\ a_{n}\sqrt{s_{n}^{3}\mu_{n}}\to 0,&b_{n}\sqrt{\frac{\mu_{n}}{p_{n}^{3}}}\to\infty&\quad\text{ for the ALDS estimate.}\end{array}\right.$$

Condition ($\mathcal{C}$.1) specifies the form of intensity models considered in this paper. In particular, note that we do not assume that $\bm{\beta}$ is an element of a bounded domain of $\mathbb{R}^{p_{n}}$. Condition ($\mathcal{C}$.2) specifies our asymptotic framework where we assume to observe in average more and more points in $D_{n}$. As already mentioned, this may cover increasing domain type or infill type asymptotics. To our knowledge, only [11] consider a similar asymptotic framework in order to construct information criteria for spatial point process intensity estimation. The context is however very different here as we consider a large number of covariates and we study methodologies (adaptive lasso or Dantzig) which are able to produce a sparse estimate. Condition ($\mathcal{C}$.3) is quite standard and is not too restrictive. Note that conditions ($\mathcal{C}$.1)-($\mathcal{C}$.3) allow us in Lemma A.2 to prove that in a ‘neighbordhood’ of $\bm{\beta}_{0}$, $\int\rho(u;\bm{\beta})=O(\mu_{n})$, a useful result widely used in our proofs. The last part of Condition ($\mathcal{C}$.3) asserts that at any location the covariates are linearly independent. Condition ($\mathcal{C}$.3) also implies first that $\liminf_{n}\inf_{\bm{\phi},\|\bm{\phi}\|=1}\bm{\phi}^{\top}\big{\{}(\mu_{n})^{-1}\mathbf{A}_{n,11}(\bm{\beta}_{0})\big{\}}\bm{\phi}>0$ and second that $\liminf_{n}\inf_{\bm{\phi},\|\bm{\phi}\|=1}\bm{\phi}^{\top}\big{\{}(\mu_{n})^{-1}\mathbf{A}_{n}(\bm{\beta}_{0})\big{\}}\bm{\phi}>0$. Condition ($\mathcal{C}$.5) is a similar assumption but for the submatrix $\mathbf{B}_{n,11}(\bm{\beta}_{0})$ which corresponds to $\mathrm{Var}\{\mathbf{U}_{n,1}(\bm{\beta}_{0})\}$. Condition ($\mathcal{C}$.4) is also natural. Combined with Condition ($\mathcal{C}$.3), this implies that $\mathrm{\mathbf{missing}}B_{n}(\bm{\beta}_{0})=O(\mu_{n}p_{n})$. When $p_{n}=p$ (and therefore $s_{n}=s$) and in the increasing domain framework, such an assumption can be satisfied by a large class of spatial point processes such as determinantal point processes, log-Gaussian Cox processes and Neyman-Scott point processes [see 10]. When $p_{n}=p$ and in the infill asymptotic framework, these assumptions are also valid for many spatial point processes, as discussed by [11]. Condition ($\mathcal{C}$.6) is required to derive the asymptotic normality of $\hat{\bm{\beta}}_{01}$. Under a specific framework, such a result has already been obtained for a large class of spatial point processes: by [4, 26] under the increasing domain framework and $p_{n}=p$ and [9] when $p_{n}\to\infty$; by [11] in the infill/increasing domain asymptotics frameworks and $p_{n}=p$.

Condition ($\mathcal{C}$.7) is very specific to the ALDS estimate which requires a preliminary estimate of $\bm{\beta}$. That condition is not unrealistic as a simple choice for $\tilde{\bm{\beta}}$ could be the maximum of the composite likelihood function (3), see the remark after Theorem 4.1. Of course, we do not require that $\tilde{\bm{\beta}}$ produces a sparse estimate.

Condition ($\mathcal{C}$.8) reflects the restriction on the number of covariates that can be considered in this study. For the AL estimate, this assumption is very similar to the one required by [16] when $\mu_{n}$ is replaced by $n$ and where the number of non-zero coefficients $s_{n}$ is constant.

Condition ($\mathcal{C}$.9) contains the main ingredients to derive sparsity properties, consistency and asymptotic normality. We first note that if $\lambda_{n,j}=\lambda_{n}$, then $a_{n}=b_{n}=\lambda_{n}$, whereby it is easily deduced that the two conditions on $a_{n}$ and $b_{n}$ cannot be satisfied simultaneously even if $p_{n}=p$. This justifies the introduction of an adaptive version of the Dantzig selector and motivates the use of the adaptive lasso. The condition $a_{n}\sqrt{s_{n}\mu_{n}}\to 0$ for the adaptive lasso is similar to the one imposed by [16] when $\mu_{n}$ is replaced by $n$ and $s_{n}=s$ in their context. However, we require a slightly stronger condition on $b_{n}$ than the one required by [16]. In our setting, their assumption would be written as $b_{n}\sqrt{\mu_{n}/p_{n}}\to\infty$. However, we would have to assume that $\nu_{\max}\big{(}\mathbf{A}_{n}(\bm{\beta}_{0})\big{)}=O(\mu_{n})$. Such a condition is not straightforwardly satisfied in our setting since, for instance, the conditions ($\mathcal{C}$.2)-($\mathcal{C}$.4) only imply that $\nu_{\max}\big{(}\mathbf{A}_{n}(\bm{\beta}_{0})\big{)}=O({p_{n}\mu_{n}})$.

As already mentioned, we do not assume that $\tilde{\bm{\beta}}$ satisfies any sparsity property. We believe this is the main reason why conditions ($\mathcal{C}$.8))-($\mathcal{C}$.9) contain slightly stronger assumptions for the ALDS estimate than for the AL estimate. We now present our main result, whose proof is provided in Appendices B-C.

To derive the consistency of $\hat{\bm{\beta}}_{\mathrm{AL}}$, a careful look at the proof in Appendix B shows that the condition $a_{n}\sqrt{{\mu_{n}s_{n}}/p_{n}}\to 0$ could be sufficient. The convergence rate, i.e. $O_{\mathrm{P}}(\sqrt{p_{n}/\mu_{n}})$, is $\sqrt{p_{n}}$ times the convergence rate of the estimator obtained when $p_{n}$ is constant [see 10, Theorem 1]. It also corresponds to the rate of convergence obtained by [16] for generalized linear models when $p_{n}\to\infty$ and when $\mu_{n}$ corresponds to the standard sample size. It is worth pointing out that a possible diverging number of non-zero coefficients $s_{n}$ does not affect the rate of convergence. It does however impose a more restrictive condition on $a_{n}$. Still on Theorem 4.1 (i), its proof shows that this result remains valid when $\lambda_{n,j}=0$ for $j=1,\dots,p_{n}$. In other words, the maximum composite likelihood estimator is consistent with the same rate of convergence. Hence a simple choice for the initial estimate $\widetilde{\bm{\beta}}$ defining the ALDS estimate is the maximum of the Poisson likelihood given by (3).

Theorem 4.1 (iii) would be the result one would obtain if $p_{n}-s_{n}=0$. Therefore, the efficiency of $\hat{\bm{\beta}}_{\mathrm{AL},1}$ and $\hat{\bm{\beta}}_{\mathrm{ALDS},1}$ is the same as the estimator of $\bm{\beta}_{01}$ obtained by maximizing (3) based on the sub model knowing that $\bm{\beta}_{02}=\mathbf{0}$. In other words, when $n$ is sufficiently large, both estimators are as efficient as the oracle one.

We end this section with the following remark. Despite the asymptotic properties for $\hat{\bm{\beta}}_{\mathrm{AL}}$ and $\hat{\bm{\beta}}_{\mathrm{ALDS}}$ and the conditions under which they are valid, are (almost) identical, the proofs are completely different and rely upon different tools. For $\hat{\bm{\beta}}_{\mathrm{AL}}$, our contribution is to extend the proof by [10] where only the increasing domain framework was considered, i.e. $\mu_{n}=O(|D_{n}|)$ and $D_{n}\to\mathbb{R}^{d}$ as $n\to\infty$ and where $s_{n}=s$ and $p_{n}=p$. The results for $\hat{\bm{\beta}}_{\mathrm{ALDS}}$ are the first ones available for spatial point processes. To handle this estimator, we first have to study existence and optimal solutions for the primal and dual problems.

To lessen notation, we remove the index $n$ in different quantities such as $\mathbf{U}_{n},\lambda_{n,j},\ell_{n}$, and $\mu_{n}$. For the practical point of view, we define $\mu=N(D)$ the number of data points in $D$.

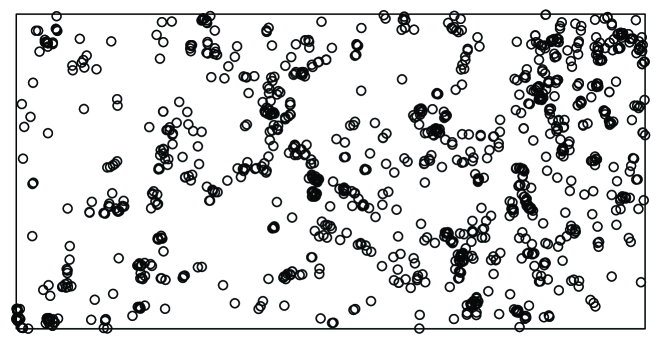
In Sections 6.1-6.2, we compare the AL and ALDS for intensity modeling of a simulated and real data. In particular, the real data example comes from an environmental data where 1146 locations of Acalypha diversifolia trees given by Figure 1 are surveyed in a 50-hectare region ($D=1000m\times 500m$) of the tropical forest of Barro Colorado Island (BCI) in central Panama [e.g. 20]. A main question is how this tree species profits from environmental habitats [12, 26] that could be related to the 15 environmental covariates depicted in Figure 2 and their 79 interactions. With a total of 94 covariates, we perform variable selection using the AL and ALDS to determine which covariates should be included in the model. We center and scale the 94 covariates to sort the important covariates according to the magnitudes of $\hat{\bm{\beta}}$. The subset of such covariates are also considered to construct a realistic setting for the simulation studies.