Adaptive Control for Robotic Manipulation of Deformable Linear Objects with Offline and Online Learning of Unknown Models

The linear deformable objects (DLOs), such as wires, cables, ropes, are highly deformable and exhibit many degrees of freedom (DoFs). The demand on manipulating DLOs is reflected in many applications. For example, sutures are manipulated in suturing to hold tissues together after surgery [1, 2]. In colonoscopy, the shape of the flexible endoscope is controlled to follow the curves of the colon [3]. In 3C manufacturing, USB wires with different colors are sorted to follow the desired color code [4]. Other applications in industry and daily life include inserting a wire [5], threading a needle [6], harnessing a cable [7] or knitting [8].

Different from rigid objects, it is usually difficult to obtain the exact model of deformable objects (and also DLOs), due to the highly deformable nature, in the sense that it is unknown how the motion of robot can affect the change of deformable objects. A review on modeling deformable objects can be found in [9] and [10]. In particular, the model of mass-damper-spring was proposed to describe the deformation of unknown rheological objects in [11]. In [12], the finite-element method was employed to model the soft objects in 3D space. An analytic formulation was proposed in [13, 14] to describe the shape of the DLO and then find its equilibrium configurations, by solving the optimal control problems. In [15, 16], physics engines were utilized to predict the change of the DLO under different sampled control commands then incorporated to sample-based motion planning algorithms. The computation complexity of modeling DLOs in the model-structure-based methods is usually high. Besides, they require the information of the DLO’s structure which is commonly unknown or difficult to describe in reality, and the modeling errors between analysis and reality may affect the manipulation performance.

Data-driven approaches have also been applied to approximate the deformation, without studying the complex dynamics of DLOs beforehand. A model-based reinforcement learning (RL) approach was proposed for robots to control the shape of the DLO in [17], with the current shape as the input and the manipulation policy as the output. In [18], a deep-neural-network-based dynamics model was trained to predict the future shape of the DLO given the current shape and the action. The aforementioned data-driven training methods were done offline before the formal manipulation, which was limited by the generalization ability to the DLO’s shape or motion never seen in the training dataset or the changes of the DLO’s physical properties. Several online data-driven approaches were also proposed to approximate the deformation model. The least squares estimation was used in [19, 20] to estimate the Jacobian matrix (i.e. the matrix relating the change of the DLO to the velocity inputs of the robot) online using only recent data. In [21, 22], the estimated Jacobian matrix was updated online by gradient descent of the approximation errors. In [23], a deep neural network with linear activation function was proposed to directly predict the required control velocity with online training. Compared to the offline methods, the approximation accuracy in the online ones is limited, and the results are only valid in a local sense without exploring the overall configuration of the DLO, and hence the re-approximation is usually required even when the same configuration of the DLO appears again during the manipulation.

This paper considers the problem of robotic manipulation of DLOs with unknown deformation models, where the unknown deformation model is estimated with both the offline and the online learning methods to combine the advantages. In the offline phase, a series of supervised NNs are trained to estimate the Jacobian matrix, by collecting the pairs of the velocity of the robot end effector and the current shape of the DLO. Such estimation model is further updated online during the manipulation with adaption techniques, to compensate the errors due to insufficient training in the offline phase or the changes of the DLO’s properties. The results obtained in the offline phase can be directly migrated to the online phase without any additional formatting. Hence, both complement each other. In addition, an adaptive controller is proposed to manipulate the feature along the DLO into the desired position, by referring to the estimated deformation model. With Lyapunov methods, it is rigorously shown that the convergence of the task errors to zero is guaranteed. Simulation studies are presented to illustrate the performance of the proposed scheme.

Consider an illustration of robotic manipulation of DLOs shown in Fig. 1, where the robot grasps and manipulates the DLO to achieve the desired task, by controlling the motion of its end effector. The end tip and also the overall shape of the DLO can be measured with sensors. In this paper, the manipulation task is simplified as moving the target point on the DLO to the desired position.

Then, the velocity of the target point on the DLO can be related to the velocity of the robot end effector using the Jacobian matrix. Compared to [19, 20, 23, 21, 22], the overall shape of the DLO is considered in the Jacobian matrix as

$$\dot{\bm{y}}=\bm{J}(\bm{\phi})\dot{\bm{r}}$$

(1)

where $\bm{\phi}$ represents the overall shape of the DLO. It can be specifically represented as $\bm{\phi}\stackrel{{\scriptstyle\triangle}}{{=}}[\bm{x}_{1}^{T},\cdots,\bm{x}_{m}^{T}]^{T}$, where $\bm{x}_{i}\in\Re^{l}$ is the position of the $i^{\rm th}$ feature along the DLO and $m$ is the number of features, $\bm{y}\in\Re^{l}$ is the position of the target point on the DLO, $\bm{r}\in\Re^{n}$ is the pose of the robot end effector, $\bm{J}(\bm{\phi})\in\Re^{l\times n}$ is the Jacobian matrix of the DLO with the shape $\bm{\phi}$, which is bounded.

Note that any point along the DLO can be set as the target point, and different points correspond to different Jacobian matrices. Equation (1) can be extended to features as $\dot{\bm{x}_{i}}=\bm{J}^{\bm{x}_{i}}(\bm{\phi})\dot{\bm{r}}$ where $\bm{J}^{\bm{x}_{i}}(\bm{\phi})$ is the Jacobian matrix for the $i^{\rm th}$ feature. For the sake of illustration, the target point in this paper is referred to as $\bm{y}$ and the Jacobian matrix is referred to as $\bm{J}(\bm{\phi})$. Note that the target point in specific manipulation tasks can be defined as one of the features (i.e. $\bm{y}\stackrel{{\scriptstyle\triangle}}{{=}}\bm{x}_{i}$, $\bm{J}(\bm{\phi})\stackrel{{\scriptstyle\triangle}}{{=}}\bm{J}^{\bm{x}_{i}}(\bm{\phi})$).

The Jacobian matrix $\bm{J}(\bm{\phi})$ is dependent on the deformation model of DLOs, which may involve many parameters [24, 25, 26]. Although the parameters can be experimentally calibrated, any modeling bias during the calibration compromises the accuracy of the model. Since the material and dimension vary significantly among different DLOs, and the length of the same DLO also changes when it is manipulated, the model-based calibration methods are not effective for accommodating variations in the material, dimension, and length of the DLO.

When the deformation model is unknown, the Jacobian matrix is also unknown. In this paper, the unknown Jacobian matrix will be estimated in both the offline (before manipulation) and online (during manipulation) manners. The estimated Jacobian matrix, denoted as $\hat{\bm{J}}(\bm{\phi})$, will be employed in the control law to relate the velocity of the robot end effector to the velocity of the target point.

The control input is set as the velocity of the robot end effector as [19, 20, 23, 21, 22]

$$\dot{\bm{r}}=\bm{u}$$

(2)

where $\bm{u}$ denotes the input. The structure of the proposed scheme is shown in Fig. 2. In the phase of offline learning, the dataset can be collected by controlling the robot end effector to follow a set of time-varying paths in an open-loop manner, while recording the variations of features. In the phase of online learning, the robot end effector is controlled to manipulate the target point to the desired position, by keeping updating the previously learnt model.

Prior to the formal manipulation, a data-driven learning method is employed to obtain the initial model of DLOs. As the radial-basis-function neural network (RBFN) is commonly used in adaptive control and machine learning [27], the actual Jacobian matrix is represented with RBFN in this paper as

$${\rm{vec}}(\bm{J}(\bm{\phi}))=\bm{W}\bm{\theta}(\bm{\phi})$$

(3)

where $\bm{W}$ is the matrix of actual weights of the NN (which are unknown), $\bm{\theta}(\bm{\phi})$ represents the vector of activation functions. In addition, $\bm{\theta}(\bm{\phi})=[\theta_{1}(\bm{\phi}),\theta_{2}(\bm{\phi}),\cdots,\theta_{q}(\bm{\phi})]^{T}\in\Re^{q}$. An example of the activation function is the Gaussian radial function, that is

$$\theta_{i}(\bm{\phi})={\rm e}^{\frac{-||\bm{\phi}-\bm{\mu}_{i}||^{2}}{\sigma_{i}^{2}}},\quad i=1,\cdots,q$$

(4)

where $\bm{\phi}=[\bm{x}_{1}^{T},\cdots,\bm{x}_{m}^{T}]^{T}$ is the input vector of the NN.

Equation (3) can be decomposed as

$$\bm{J}_{i}(\bm{\phi})=\bm{W}_{i}\bm{\theta}(\bm{\phi})$$

(5)

where $\bm{J}_{i},(i=1,\cdots,n)$ is the $i^{\rm th}$ column of the Jacobian matrix, and $\bm{W}_{i}$ is the ${((i-1)\times l+1)}^{\rm th}$ to ${(i\times l)}^{\rm th}$ rows of $\bm{W}$. Then (1) can be written as

$$\dot{\bm{y}}=\bm{J}(\bm{\phi})\dot{\bm{r}}=\sum_{i=1}^{n}\bm{J}_{i}(\bm{\phi})\dot{r}_{i}=\sum_{i=1}^{n}\bm{W}_{i}\bm{\theta}(\bm{\phi})\dot{r}_{i}$$

(6)

The estimated Jacobian matrix is represented as

$${\rm{vec}}(\hat{\bm{J}}(\bm{\phi}))=\hat{\bm{W}}\bm{\theta}(\bm{\phi})$$

(7)

where $\hat{\bm{W}}$ is the matrix of estimated weights. The approximation error $\bm{e}_{w}$ is specified as

	$\displaystyle\bm{e}_{w}$	$\displaystyle=\dot{\bm{y}}-\hat{\bm{J}}(\bm{\phi})\dot{\bm{r}}=(\bm{J}(\bm{\phi})-\hat{\bm{J}}(\bm{\phi}))\dot{\bm{r}}$		(8)
		$\displaystyle=\sum_{i=1}^{n}\bm{W}_{i}\bm{\theta}(\bm{\phi})\dot{r}_{i}-\sum_{i=1}^{n}\hat{\bm{W}}_{i}\bm{\theta}(\bm{\phi})\dot{r}_{i}=\sum_{i=1}^{n}\Delta{\bm{W}}_{i}\bm{\theta}(\bm{\phi})\dot{r}_{i}$

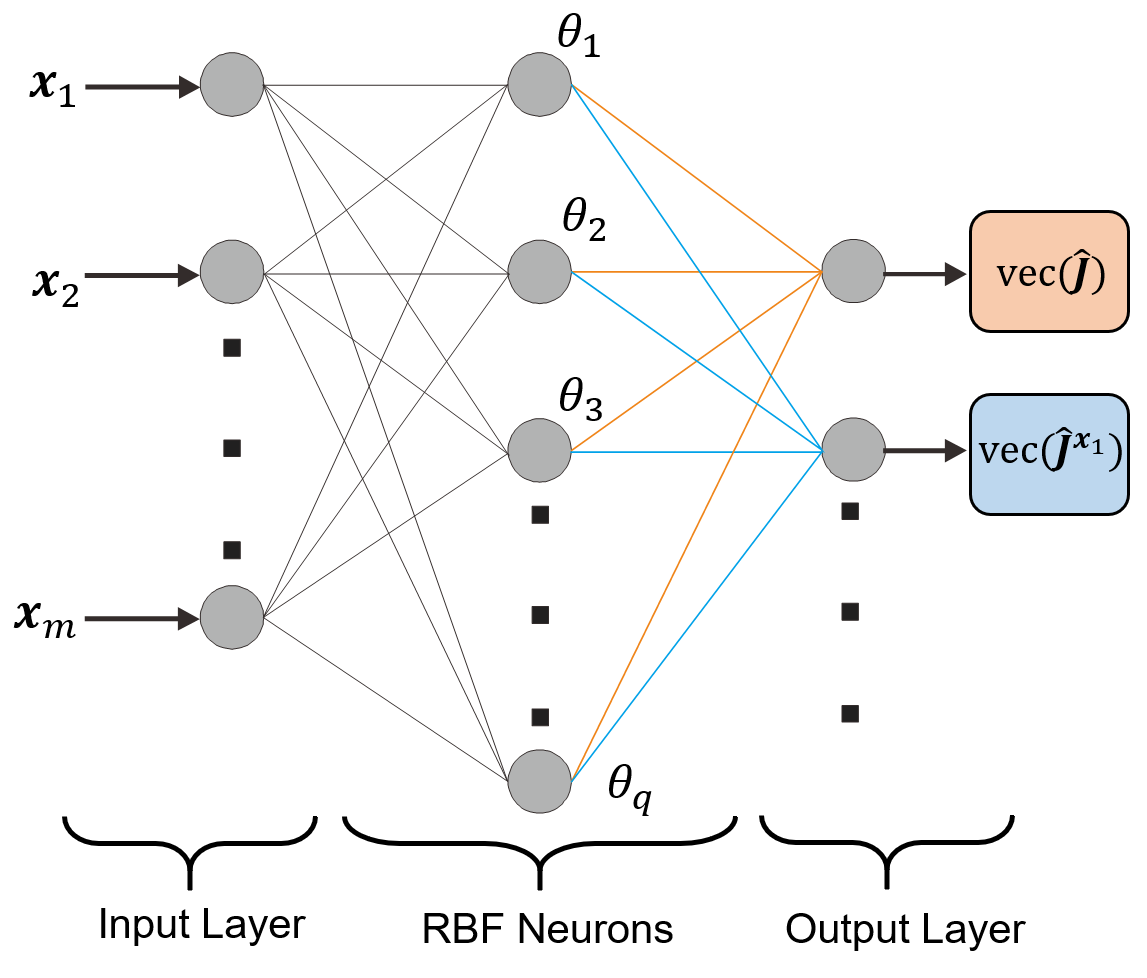
In the offline learning phase, the robot end effector is controlled to move in an open-loop manner to collect the training dataset first, which contains $\bm{x}_{i},\dot{\bm{x}_{i}},\dot{\bm{r}},\dot{\bm{y}},(i=1,\cdots,m)$. As these data can be obtained concurrently, NNs are trained for all the Jacobian matrices of $\bm{J}(\bm{\phi})$ and $\bm{J}^{\bm{x}_{i}}(\bm{\phi}),(i=1,\cdots,m)$ for the sake of efficiency. After all the Jacobian matrices are well estimated by the end of the offline phase, the target point can also be chosen as one of the other features, by replacing the Jacobian matrix with the corresponding one. The structure of the whole NNs is shown in Fig. 3.

Next, the RBF network is trained with the collected data. Considering the noise and the outliers in the data, the smooth $L1$ loss is used for training, which is specified as

$$L(\hat{\bm{J}}(\bm{\phi}))=\sum_{j=1}^{l}{L_{j}}$$

(9)

where

$$L_{j}=\left\{\begin{array}[]{rl}0.5(e_{wj})^{2}/\beta&,|e_{wj}|<\beta\\ |e_{wj}|-0.5\beta&,\rm{otherwise}\end{array}\right.$$

(10)

where $e_{wj}$ is the $j^{\rm th}$ element of $\bm{e}_{w}$.

The k-means clustering on sampled training data is used to calculate the initial value of $\bm{\mu}_{i}$ and $\sigma_{i},(i=1,\cdots,q)$. Then, all parameters including $\bm{\mu}_{i}$, $\sigma_{i}$ and $\hat{\bm{W}}$ are updated by the back propagation of the loss in (9). The Adam optimizer [28] is used for training. Note that the estimated parameters of the NN in the offline phase can be directly migrated to the online phase. In the online phase, the parameters will be further updated to meet the specific manipulation task.

Due to insufficient training data or changes of the parameters of DLOs, the approximation errors may still exist by the end of the offline learning. In this section, an adaptive control scheme is proposed for robotic manipulation of DLOs, by treating the estimated Jacobian matrix as an initial approximation then further updating it during manipulation.

The control input is specified as

$$\bm{u}=\hat{\bm{J}}^{\dagger}(\bm{\phi})(\dot{\bm{y}}_{d}-\bm{K}_{p}\Delta\bm{y})$$

(11)

where $\hat{\bm{J}}^{\dagger}(\bm{\phi})$ is the Moore-Penrose pseudo-inverse of the estimated Jacobian matrix, and it is assumed that $\hat{\bm{J}}(\bm{\phi})$ is full row rank and $\hat{\bm{J}}^{\dagger}(\bm{\phi})$ always exists. In addition, $\Delta\bm{y}=\bm{y}-\bm{y}_{d}$ where $\bm{y}_{d}\in\Re^{l}$ specifies the desired position of the target point, and $\bm{K}_{p}\in\Re^{l\times l}$ is the control gain, which is diagonal and positive definite.

The online updating law of the $j^{\rm th},(j=1,\cdots,l)$ row of $\hat{\bm{W}_{i}}$ is specified as

$$\dot{\hat{\bm{w}}}_{ij}^{T}=\dot{r}_{i}\bm{L}_{i}\bm{\theta}(\bm{\phi})(\Delta y_{j}+\lambda e_{wj})$$

(12)

where $\Delta y_{j}$ is the $j^{\rm th}$ element of the vector $\Delta\bm{y}$, and $\bm{L}_{i}\in\Re^{q\times q}$ is a positive-definite matrix, and $\lambda$ is a positive scalar.

The proposed control scheme by (11) and (12) has several advantages as

1. -

   The well estimated weights of the NN in the offline phase can be directly migrated as the initial values in the online phase.

2. -

   It allows the robot to manipulate the DLO by following the desired path (i.e. $\bm{y}_{d}$) and also update the unknown deformation model concurrently.

3. -

   The update is driven by both the approximation errors (i.e. $\bm{e}_{w}$) and the task errors (i.e. $\Delta\bm{y}$), ensuring the faster convergence of the weights of the NN.

Substituting (11) into (2), the closed-loop equation is obtained as

$$\dot{\bm{r}}=\hat{\bm{J}}^{\dagger}(\bm{\phi})(\dot{\bm{y}}_{d}-\bm{K}_{p}\Delta\bm{y})$$

(13)

Multiplying both sides of (13) with $\hat{\bm{J}}(\bm{\phi})$, we have

$$\hat{\bm{J}}(\bm{\phi})\dot{\bm{r}}=\dot{\bm{y}}_{d}-\bm{K}_{p}\Delta\bm{y}$$

(14)

Note that

$$\hat{\bm{J}}(\bm{\phi})\dot{\bm{r}}=\hat{\bm{J}}(\bm{\phi})\dot{\bm{r}}-{\bm{J}}(\bm{\phi})\dot{\bm{r}}+{\bm{J}}(\bm{\phi})\dot{\bm{r}}=-\sum_{i=1}^{n}\Delta\bm{W}_{i}\bm{\theta}(\bm{\phi})\dot{r}_{i}+\dot{\bm{y}}$$

(15)

Substituting (15) into (14) and using (8) yields

$$\bm{e}_{w}=\Delta\dot{\bm{y}}+\bm{K}_{p}\Delta\bm{y}$$

(16)

That is, the approximation errors are now expressed in terms of the task errors. Hence the convergence of $\bm{e}_{w}$ to zero naturally guarantees the realization of manipulation task.

To prove the convergence, the Lyapunov-like candidate is given as

$$V=\frac{1}{2}\Delta\bm{y}^{T}\Delta\bm{y}+\frac{1}{2}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{l}\hskip 2.84544pt\Delta\bm{w}_{ij}\bm{L}_{i}^{-1}\Delta\bm{w}_{ij}^{T}$$

(17)

Differentiating (17) with respect to time and substituting (16) into it, we have

	$\displaystyle\dot{V}$	$\displaystyle=\Delta\bm{y}^{T}\Delta\dot{\bm{y}}-\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{l}\Delta\bm{w}_{ij}\bm{L}_{i}^{-1}\dot{\hat{\bm{w}}}_{ij}^{T}$		(18)
		$\displaystyle=\Delta\bm{y}^{T}(\bm{e}_{w}-\bm{K}_{p}\Delta\bm{y})-\sum_{i=1}^{n}\sum\limits_{j=1}^{l}\Delta\bm{w}_{ij}\bm{L}_{i}^{-1}\dot{\hat{\bm{w}}}_{ij}^{T}$
		$\displaystyle=-\Delta\bm{y}^{T}\bm{K}_{p}\Delta\bm{y}+\Delta\bm{y}^{T}\bm{e}_{w}-\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{l}\Delta\bm{w}_{ij}\bm{L}_{i}^{-1}\dot{\hat{\bm{w}}}_{ij}^{T}$

Next substituting the update law (12) into (18) and using (8), we have

	$\displaystyle\dot{V}$	$\displaystyle=-\Delta\bm{y}^{T}\bm{K}_{p}\Delta\bm{y}+\Delta\bm{y}^{T}\bm{e}_{w}$		(19)
		$\displaystyle\quad-\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{l}\Delta\bm{w}_{ij}\bm{L}_{i}^{-1}[\dot{r}_{i}\bm{L}_{i}\bm{\theta}(\bm{\phi})(\Delta y_{j}+\lambda e_{wj})]$
		$\displaystyle=-\Delta\bm{y}^{T}\bm{K}_{p}\Delta\bm{y}+\Delta\bm{y}^{T}\bm{e}_{w}-\bm{e}_{w}^{T}\Delta\bm{y}-\lambda\bm{e}_{w}^{T}\bm{e}_{w}$
		$\displaystyle=-\Delta\bm{y}^{T}\bm{K}_{p}\Delta\bm{y}-\lambda\bm{e}_{w}^{T}\bm{e}_{w}\leq 0$

Since $V>0$ and $\dot{V}\leq 0$, $V$ is bounded. The boundedness of $V$ ensures the boundedness of $\Delta\bm{w}_{ij}$ and $\Delta\bm{y}$. From (13), $\dot{\bm{r}}$ is also bounded. The boundedness of $\dot{\bm{r}}$ ensures the boundedness of $\dot{\bm{y}}$ from (1). Hence, $\Delta\bm{y}$ is uniformly continuous. From (19), it can be shown that $\Delta\bm{y}\in L_{2}(0,+\infty)$. Then, it follows [29] that $\Delta\bm{y}\rightarrow\bm{0}$ as $t\rightarrow\infty$. Therefore, the manipulation task is achieved.

Simulations are carried out to study the performance of the proposed method. The simulation environment is built in Unity [30], a 3D game development platform. The simulation of the DLO is based on Obi [31], a unified particle physics for Unity in which realistic deformable objects can be created, such as ropes, cloth, fluids and other softbodies. The ROS [32] and ROS# [33] are used for the communication between the physical simulation in Unity and the control program written in Python scripts. All the simulation and computation are done on a Ubuntu 18.04 desktop (CPU: Intel i7-10700, GPU: Nvidia GeForce RTX 3070, RAM: 16GB).

The simulation scene is shown in Fig. 5. The DLO is modeled with the rod blueprint in Obi Rope package, which is built by chaining oriented particles using stretch/shear and bend/twist constraints. Its length is about 0.5m and radius is about 5mm. The blue points represent the 10 features along the DLO, and the red point represents the target point. Note that one of the features is chosen as the target point for convenience, so the red point is also a feature. The virtual green point in the simulation scene represents the desired position of the target point. The left end of the DLO is grasped and fixed by one robot, and the right end of the DLO is grasped by another robot and the linear velocity of the robot end effector is treated as the control input. This paper considers the positions of features and target point in 3-D world coordinate system, where the parameters are set as $l=3,n=3,m=10$ in following simulations.

This paper considers the robotic manipulation of DLOs with unknown deformation model, where the unknown model has been estimated in both the offline and the online phases. Both phases complement each other. That is, the offline learning can well initiate the estimation for the manipulation task, and the online learning can further reduce the approximation errors during the manipulation. The adaptive control scheme is proposed to achieve the manipulation task in the presence of the unknown deformation model. The convergence of the task errors has been rigorously proved with Lyapunov methods, and simulation results in different scenarios have been presented. Future works will be devoted to the validation of the proposed method on a real robot.