Active Brownian particle under stochastic position and orientation resetting in a harmonic trap

Active particles convert energy into motility and exhibit a wide range of dynamical behaviors [1, 2, 3, 4, 5, 6]. These behaviors are observed across diverse systems, including cytoskeletal filaments in motor protein assays [7, 8, 9, 10], bird flocks [11], fish schools [12], and artificial systems like active colloids and robots. Active particles are inherently out of equilibrium, displaying collective phenomena such as flocking [13, 14, 15], clustering [16, 17, 18], and phase separation [19, 20]. Even at the single-particle level, they exhibit diverse dynamical behaviors, including short-time ballistic motion [21, 22, 23, 24, 25, 26], nonequilibrium steady states in confinement [27, 28, 29, 30], and dynamical transitions in relaxation and first passage properties [31, 32, 33, 34]. Recent studies have demonstrated enhanced control over active agents for decision-making by space dependent rotational diffusion coefficient [35], as well as using external or internal cues, such as magnetic fields [36], chemical gradients [37], and acoustic waves [38, 39], to control their speed and orientation.

Stochastic resetting is a protocol that resets a dynamical system to a specific state, primarily governing the nonequilibrium steady state (NESS) through a continuous influx of probability from resetting. This process can lead to dynamical transitions during the system’s relaxation to the NESS and often results in a non-monotonic mean first passage time [40, 41, 42, 43, 44]. The resetting strategy has broad applications across various systems, including population dynamics and biological processes, particularly in optimizing search problems [45, 46, 47, 48, 49, 50, 51, 52]. The impact of resetting on different diffusive dynamics has also been extensively studied [53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 60]. Resetting has proven to be an optimal navigation strategy for target search, particularly in Brownian motion [40] and under external potentials [65].

The resetting of a free active Brownian agent has been studied recently in [66, 67], with extensions to external confining and absorbing potentials in [68, 69, 70]. Activity introduces new dynamical behavior due to the competition between the internal active timescale and the resetting timescale, first studied in [71]. The first passage properties of active Brownian particle (ABP) and run-and-tumble particle (RTP) under various resetting mechanisms have been explored in [72, 73]. The dynamics of an ABP under position stochastic resetting, orientation stochastic resetting, and combined position and orientation stochastic resetting, focusing on marginal probability distributions, were examined in Kumar et al. [66]. The dynamics under orientation stochastic resetting, using the intermediate scattering function, were studied in [74]. However, the exact dynamics of an ABP under both position and orientation resetting in a harmonic trap, along with an analysis of the steady-state properties, remain unexplored. From the lens of active matter, it is crucial to delve into the intricate interplay between stochastic resetting and activity under the influence of an external force.

In this work, we investigate the exact dynamics of active Brownian particle (ABP) under complete stochastic resetting, involving both position and orientation, in a harmonic trap. We apply the method for exact moment calculations of stiff chains, as described by Hermans et al.[75], to compute the exact moments for the active dynamics case. Using a Fokker-Planck-based approach, we derive the dynamical moment generating equation, which we then use to calculate all dynamical moments. This method has been previously applied to study ABP in a harmonic trap [30], with anisotropic translational noise [76], fluctuating speed [25], and chirality/torque [77], and has also been extended to inertial ABP [26, 78]. Here, we focus on exact moment calculations of ABP under complete stochastic resetting in a harmonic trap using a renewal equation following the Fokker-Planck-based moments calculation. We also characterize the steady-state behavior across various limits and parameter ranges using excess kurtosis.

The remainder of this paper is organized as follows. In Section 2, we introduce the model of an ABP under complete stochastic resetting in a harmonic trap. Using a Fokker-Planck-based approach, we derive the dynamical moment generating equation and apply the final renewal approach to calculate moments under stochastic resetting. This equation is then used to compute the orientation autocorrelation and mean displacement in Section 3. In Section 4, we determine the mean squared displacement and displacement fluctuation. To examine deviations from Gaussian behavior over time, we calculate the fourth-order moment of displacement and the excess kurtosis in Section 5, and characterize the interplay of activity with resetting and trapping in the steady-state phase diagram in Section 6. Finally, we summarize the key results in Section 7.

The standard active Brownian particle in two dimension is described by its position $\mathbf{r}=(x,y)$, and its orientation unit vector ${\bf\hat{u}}=(u_{x},u_{y})$ where $u_{x}=\cos(\theta)$ and $u_{y}=\sin(\theta)$, evolving over time $t$ from their initial values $({\bf r}_{0},{\bf\hat{u}}_{0})$. Stochastic resetting imposed on both ${\bf r}$ and ${\bf\hat{u}}$ intermittently resets to initial values $({\bf r}_{0},{\bf\hat{u}}_{0})$ with rate $r$. The position ${\bf r}$ and orientation ${\bf\hat{u}}$ evolves

	$\displaystyle\dot{\bf r}=v_{0}{\bf\hat{u}}+\sqrt{2D}\bm{\chi}(t)-\mu k{\bf r}\,,$		(1)
	$\displaystyle\dot{\bf\hat{u}}=\sqrt{2D_{r}}\eta(t){\bf\hat{u}}^{\perp}\,,$		(2)
	$\displaystyle({\bf r},{\bf\hat{u}})\rightarrow({\bf r}_{0},{\bf\hat{u}}_{0})\,.$		(3)

Here, $v_{0}$ is the active speed, $D$ is the translation diffusion coefficient, $\mu$ is the mobility, and $k$ is the strength of the harmonic trap. $D_{r}$ is the orientation diffusion coefficient. The noise terms $\bm{\chi}(t)$ and $\eta(t)$ are modeled as Gaussian white noise with zero mean and variances given by $\langle\chi_{i}(t)\chi_{j}(t^{\prime})\rangle=\delta_{ij}\delta(t-t^{\prime})$ and $\langle\eta(t)\eta(t^{\prime})\rangle=\delta(t-t^{\prime})$, respectively. The interplay of the three timescales $D_{r}^{-1}$, $r^{-1}$, and $(\mu k)^{-1}$ would lead to rich behavior for ABP under resetting in a harmonic trap.

We rescale the dynamics using timescale $\tau=D_{r}^{-1}$ and length scale $\ell=\sqrt{D/D_{r}}$. The dynamics (${\bf r}\to{\bf r}/\ell$, ${\bf\hat{u}}\to{\bf\hat{u}}$, $t\to t/\tau$) is now controlled by activity strength defined by Péclet $\mathrm{Pe}=v_{0}\tau/\ell$, resetting rate $r=r\tau$, and trapping strength $\beta=\mu k\ell$. We investigate the dynamics and steady state behavior with varying three dimensionless parameters activity $\mathrm{Pe}$, resetting rate $r$, and trap strength $\beta$.

We consider the initial orientation of ABP along $\langle{\bf\hat{u}}\rangle={\bf\hat{u}}_{0}$ and proceed to calculate mean orientation. To calculate $\langle{\bf\hat{u}}\rangle$, we use $\psi={\bf\hat{u}}$ in the equation (5), leads to $\langle{\bf\hat{u}}\rangle_{s}={\bf\hat{u}}_{0}/(1+s)$. Inverse Laplace transform leads to the average orientation without stochastic resetting $\langle{\bf\hat{u}}(t)\rangle=e^{-t}{\bf\hat{u}}_{0}$. In the presence of stochastic resetting using renewal approach in equation (6) and taking the dot product with the initial orientation, we get the orientation autocorrelation,

$\displaystyle\langle{\bf\hat{u}}(t)\cdot{\bf\hat{u}}(0)\rangle_{r}$

$\displaystyle=$

$\displaystyle\frac{r+e^{-(1+r)t}}{(1+r)}\,.$

(7)

The plot of equation (7) is compared with simulations, as shown in A, figure 5(a). As ($t\to\infty$), the orientation autocorrelation saturates to $r/(1+r)$. In the steady state $\langle{\bf\hat{u}}(t)\cdot{\bf\hat{u}}(0)\rangle_{r}$ varies from $0$ as $r\to 0$ to $1$ as $r\to\infty$.

Now, we proceed to calculate $\langle{\bf r}\rangle_{s}$ we consider the initial position at $\langle{\bf r}\rangle_{0}=0$, using the equation (5) leads to $\langle{\bf r}\rangle_{s}=\mathrm{Pe}\langle{\bf\hat{u}}\rangle_{s}/(s+\beta)$. Substituting $\langle{\bf\hat{u}}\rangle_{s}$ and then inverse Laplace transform gives the mean displacement in the absence of resetting $\langle{\bf r}(t)\rangle$ [30]. The parallel and perpendicular component of the displacement vector to the initial orientation defined as ${\bf\hat{u}}_{0}$ as ${\bf r}_{\parallel}=({\bf r}\cdot{\bf\hat{u}}_{0}){\bf\hat{u}}_{0}$ and ${\bf r}_{\perp}={\bf r}-{\bf r}_{\parallel}$. In the presence of stochastic resetting using renewal approach in equation (6), we get

$\displaystyle\langle{\bf r}_{\parallel}(t)\rangle_{r}=\frac{\mathrm{Pe}{\bf\hat{u}}_{0}(e^{-(\beta+r)t}-e^{-(1+r)t})}{1-\beta}-\frac{r\mathrm{Pe}{\bf\hat{u}}_{0}}{1-\beta}\left[\frac{1-e^{-(1+r)t}}{1+r}-\frac{1-e^{-(\beta+r)t}}{\beta+r}\right]\,.$

(8)

In the absence of harmonic trap ($\beta=0$), equation (8) simplifies to ABP under stochastic resetting [66], see A, figure 5(b). In figure 1(a), we plot equation (8) as solid lines, showing excellent agreement with the simulation results represented by the points. For a small resetting rate ($r$), $\langle{\bf r}_{\parallel}(t)\rangle_{r}$ exhibits non-monotonic behavior: it starts with a small value in the short-time, thermally dominated diffusion regime, reaches a maximum at intermediate times in the activity-dominated regime, and then decays back to smaller values due to trapping, see squares ($\Box$) for $r=0.1$ in figure 1(a). At long times, $\langle{\bf r}_{\parallel}(t)\rangle_{r}$ decays to zero in the absence of stochastic resetting [30], exhibiting the same behavior as for low resetting rates. For intermediate values of the resetting rate ($r$), $\langle{\bf r}_{\parallel}(t)\rangle_{r}$ initially shows a small value in the short-time, thermally dominated diffusion regime, reaches a maximum at intermediate times in the activity-dominated regime, and then does not decay back to smaller values due to the cancellation of trapping effects by stochastic resetting, see circles ($\circ$) for $r=2$ in figure 1(a). For large values of the resetting rate ($r$), $\langle{\bf r}_{\parallel}(t)\rangle_{r}$ initially shows a small value in the short-time, thermally dominated diffusion regime, slightly increases in the activity-dominated regime, and then saturates due to the dominance of stochastic resetting, see triangles ($\triangle$) for $r=20$ in figure 1(a).

At, long times $t\to\infty$, mean parallel displacement $\langle{\bf r}_{\parallel}\rangle^{st}_{r}=\lim_{t\to\infty}\langle{\bf r}_{\parallel}(t)\rangle_{r}$

$\displaystyle\langle{\bf r}_{\parallel}\rangle^{st}_{r}$

$\displaystyle=$

$\displaystyle\frac{r\mathrm{Pe}{\bf\hat{u}}_{0}}{(r+\beta)(1+r)}\,.$

(9)

The mean parallel displacement at steady state show a local maximum at resetting rate $r_{\mathrm{max}}=\sqrt{\beta}$. In figure 1(b), we plot equation (9) (solid lines) as a function of resetting rates ($r$), comparing it with simulation results (points). The maximum mean parallel displacement occurs at resetting rates $r_{\mathrm{max}}=\sqrt{\beta}=1,~{}2,~{}3$ for trap strengths $\beta=1(\mathrm{squares},\Box),~{}4(\mathrm{circles},\circ),~{}9(\mathrm{triangles},\triangle)$, respectively. It is important to compute the second-order moments to further quantify the fluctuating dynamics.

We proceed to compute mean-squared displacement $\langle{\bf r}^{2}\rangle_{s}$ defining observable $\psi={\bf r}^{2}$, utilizing equation (5) with initial position at origin $\langle{\bf r}^{2}\rangle_{0}=0$ leads to the mean-squared displacement in Laplace space $\langle{\bf r}^{2}\rangle_{s}$

$\displaystyle\langle{\bf r}^{2}\rangle_{s}$

$\displaystyle=$

$\displaystyle\frac{1}{s+2\beta}\left[\frac{4}{s}+2\mathrm{Pe}\langle{\bf r}\cdot{\bf\hat{u}}\rangle_{s}\right]~{},$

(10)

where the second term $\langle{\bf r}\cdot{\bf\hat{u}}\rangle_{s}$ calculated assuming $\psi={\bf r}\cdot{\bf\hat{u}}$ in equation (5) as

$\displaystyle\langle{\bf r}\cdot{\bf\hat{u}}\rangle_{s}=\frac{\mathrm{Pe}}{s(s+\beta+1)}~{}.$

(11)

Inverse Laplace transform of equation (10) gives mean-squared displacement $\langle{\bf r}^{2}(t)\rangle$ without stochastic resetting (see B), which previously obtained in Chaudhuri et al. [30]. Finally, using renewal approach in equation (6), we get

	$\displaystyle\langle{\bf r}^{2}(t)\rangle_{r}=e^{-rt}\left[\frac{2}{\beta}\left(1-e^{-2\beta t}\right)+\frac{\mathrm{Pe}^{2}}{\beta(1+\beta)}-\frac{2\mathrm{Pe}^{2}e^{-\beta t}}{1-\beta}\left[\frac{e^{-\beta t}}{2\beta}-\frac{e^{-t}}{1+\beta}\right]\right]$
	$\displaystyle+\frac{(2+2\beta+\mathrm{Pe}^{2})(1-e^{-rt})}{\beta(1+\beta)}+\frac{2r\beta\mathrm{Pe}^{2}[1-e^{-(1+\beta+r)t}]}{(1+\beta+r)(1-\beta^{2})}+\frac{r(\mathrm{Pe}^{2}+2\beta-2)(1-e^{-(2\beta+r)t})}{\beta(2\beta+r)(1-\beta)}\,.$
			(12)

In figure 1(c), we compare the equation (12) represented by solid lines, with simulations depicted by points, showing excellent agreement. The various limiting cases of equation (12) depending on parameters $r$, $\mathrm{Pe}$, and $\beta$ discussed in B.

Moreover, the displacement fluctuations and their limiting cases are discussed in C. The components of the second-order moment, such as those along the initial orientation direction, are also discussed in D.

To calculate the excess kurtosis, we first need to calculate the fourth-order moment of the displacement. In the similar method, we calculated the fourth order moment of displacement under stochastic position and orientation resetting, detailed derivation and final result of $\langle{\bf r}^{4}(t)\rangle_{r}$ in equation (81), see detailed derivation in E. The small time expansion ($t\to 0$), the fourth moment of displacement $\langle{\bf r}^{4}\rangle_{r}$

	$\displaystyle\langle{\bf r}^{4}\rangle_{r}\simeq 32t^{2}+\frac{16}{3}\left(3\mathrm{Pe}^{2}-4r-12\beta\right)t^{3}$
	$\displaystyle+\frac{1}{3}\left[224\beta^{2}+3\mathrm{Pe}^{4}+24r^{2}+144\beta r-96\beta\mathrm{Pe}^{2}-16\mathrm{Pe}^{2}-36r\mathrm{Pe}^{2}\right]t^{4}+\mathcal{O}(t^{5})\,,$		(17)

exhibits small time diffusive behavior $\langle{\bf r}^{4}\rangle_{r}=32t^{2}$, which crosses over to ballistic behavior $\langle{\bf r}^{4}\rangle_{r}\sim t^{3}$ at $t^{*}=6/(3\mathrm{Pe}^{2}-4r-12\beta)$ with $\mathrm{Pe}^{2}>4(r+3\beta)/3$. In figures 2(a), 2(b), and 2(c), we have shown the $\langle{\bf r}^{4}\rangle_{r}$ as a function of time $t$ for resetting rates $r=0.1,~{}2,~{}20$ with $\mathrm{Pe}=10$ and $\beta=4$ in (a), for trap strength $\beta=0.5,~{}4,~{}50$ with $\mathrm{Pe}=10$ and $r=1$ in (b), and for activity $\mathrm{Pe}=1,~{}5,~{}10$ with $\beta=4$ and $r=1$ in (c). The solid lines are the plot of equation (81) which excellently agrees with the simulation results depicted by points. In figures 2(a) and 2(b), we can see the increase of resetting rates $r$ and trapping strengths $\beta$ decreases the $\langle{\bf r}^{4}\rangle_{r}$. On the other hand, the increase of activity parameter $\mathrm{Pe}$ increases the $\langle{\bf r}^{4}\rangle_{r}$. In the long time limit ($t\to\infty$), $\langle{\bf r}^{4}\rangle_{r}$ reaches a steady state due to the effect of the harmonic trap and/or stochastic resetting. The steady state fourth moment of displacement $\langle{\bf r}^{4}\rangle^{st}_{r}$

	$\displaystyle\langle{\bf r}^{4}\rangle^{st}_{r}=\frac{8}{(1+\beta+r)(2\beta+r)(4+2\beta+r)(1+3\beta+r)(4\beta+r)}\times$
	$\displaystyle\left[48\beta^{3}+8(1+r)^{2}(4+r)+\mathrm{Pe}^{4}(8+3r)+8\beta^{2}(20+6\mathrm{Pe}^{2}+11r)\right.$
	$\displaystyle\left.+4\mathrm{Pe}^{2}(8+14r+3r^{2})+2\beta\left[3\mathrm{Pe}^{4}+8\mathrm{Pe}^{2}(7+3r)+24(3+4r+r^{2})\right]\right]\,.$		(18)

In order to quantify the impact of these parameters on position distributions at different times as well as in the steady state, we calculate excess kurtosis which define the deviation from a Gaussian process.

In the absence of activity ($\mathrm{Pe}=0$) and stochastic resetting ($r=0$), Brownian particle in two dimensions in a harmonic trap gives zero kurtosis which signifies the Gaussian process. We calculate the kurtosis in presence of activity and stochastic position and orientation resetting which deviates from zero. Thus, the non-equilibrium nature of the system leading to the deviation from Gaussian nature given by excess kurtosis [30],

$\displaystyle\mathcal{K}_{r}$

$\displaystyle=$

$\displaystyle\frac{\langle{\bf r}^{4}\rangle_{r}}{2\langle{\bf r}^{2}\rangle_{r}^{2}}-1\,.$

(19)

The fourth order moment of displacement $\langle{\bf r}^{4}\rangle_{r}$ and mean-squared displacement $\langle{\bf r}^{2}\rangle_{r}$ have already been calculated as shown in equation (81) and equation (12), respectively. We expand the kurtosis in the small time limit ($t\to 0$),

$\displaystyle\mathcal{K}_{r}$

$\displaystyle\simeq$

$\displaystyle\frac{rt}{3}-\frac{(3\mathrm{Pe}^{4}+16\beta r-4r\mathrm{Pe}^{2})}{96}t^{2}+\mathcal{O}(t^{3})~{}.$

(20)

The next order term $\mathcal{O}(t^{3})$ is shown in equation (86). It has shown the deviation of kurtosis towards positive or negative values in the small time controlled by $r$, $\mathrm{Pe}$, and $\beta$. The positive deviation holds for small activity ($\mathrm{Pe}\to 0$) but it deviates towards negative values with increase of activity. For high activity, the kurtosis deviates towards negative values at $t^{*}=32r/(3\mathrm{Pe}^{4}+16\beta r-4r\mathrm{Pe}^{2})$.

In figures 2(d), 2(e), and 2(f), we have shown the $\mathcal{K}_{r}$ as a function of time $t$ for resetting rates $r=0.1,~{}2,~{}20$ with $\mathrm{Pe}=10$ and $\beta=4$ in (d), for trapping strength $\beta=0.5,~{}4,~{}50$ with $\mathrm{Pe}=10$ and $r=1$ in (e), and for Péclet values $\mathrm{Pe}=1,~{}5,~{}10$ with $\beta=4$ and $r=1$ in (f). The solid lines are the plot of equation (19) which excellently agrees with the simulation results depicted by points. We characterize the activity- and resetting-dominated time regimes using excess kurtosis ($\mathcal{K}_{r}$). At short times, thermal diffusion leads to near-Gaussian behavior ($\mathcal{K}_{r}\sim 0$). Negative $\mathcal{K}_{r}$ indicates a flat, light-tailed with non-zero peak at $\mathrm{Pe}/\beta$ position distribution dominated by activity ($\mathrm{Pe}$), while positive $\mathcal{K}_{r}$ suggests a heavy-tailed with peak at zero position distribution dominated by resetting ($r$). In figure 2(d), we clearly observe activity-dominated behavior ($\mathcal{K}_{r}<0$) at low resetting rates ($r$) and resetting-dominated behavior ($\mathcal{K}_{r}>0$) at high resetting rates ($r$). In figure 2(e), we observe non-monotonic behavior at small trap strength ($\beta$). At short times, $\mathcal{K}_{r}$ shifts to negative values, indicating activity-dominated behavior, crosses zero at intermediate times, and eventually saturates to positive values, reflecting long-term resetting-dominated behavior. The transitions from small to long times are: Gaussian ($\mathcal{K}_{r}=0$) to light-tail ($\mathcal{K}_{r}<0$), back to Gaussian ($\mathcal{K}_{r}=0$), and finally to heavy-tail ($\mathcal{K}_{r}>0$) position distributions. In figure 2(f), we observe activity-dominated behavior ($\mathcal{K}_{r}<0$) at high activity ($\mathrm{Pe}$) and resetting-dominated behavior ($\mathcal{K}_{r}>0$) at low activity ($\mathrm{Pe}$).

To quantify the steady-state properties of position distributions and capture the transitions between activity- and resetting-dominated regions, we calculate the steady-state excess kurtosis and analyze the numerically obtained position distributions.

In the steady state($t\to\infty$), equation (19) results

	$\displaystyle\mathcal{K}^{st}_{r}=\frac{2}{(4+2\beta+r)(1+3\beta+r)(4\beta+r)(2+2\beta+\mathrm{Pe}^{2}+2r)^{2}}\times$
	$\displaystyle\left[12\beta^{4}r-\beta^{3}(6\mathrm{Pe}^{4}-20\mathrm{Pe}^{2}r-2r(26+17r))\right.$
	$\displaystyle\left.+r(1+r)(\mathrm{Pe}^{4}(2+r)+2(1+r)^{2}(4+r)+2\mathrm{Pe}^{2}(2r^{2}+9r+4))\right.$
	$\displaystyle\left.+\beta^{2}(-\mathrm{Pe}^{4}(14+r)+2\mathrm{Pe}^{2}r(32+19r)+2r(17r^{2}+55r+38))\right.$
	$\displaystyle\left.+\beta r(\mathrm{Pe}^{4}(1+3r)+2(1+r^{2})(22+7r)+\mathrm{Pe}^{2}(22r^{2}+80r+52))\right]\,.$		(21)

We now calculate various limiting cases to explore the properties of excess kurtosis. I. Brownian particles in a harmonic trap : In the absence of activity ($\mathrm{Pe}=0$) and stochastic resetting ($r=0$), Brownian particle in two dimensions in a harmonic trap gives $\mathcal{K}_{r}^{st}=0$. It signifies the Gaussian process, and we calculate the steady state kurtosis to quantify the deviation from $\mathcal{K}_{r}^{st}=0$.

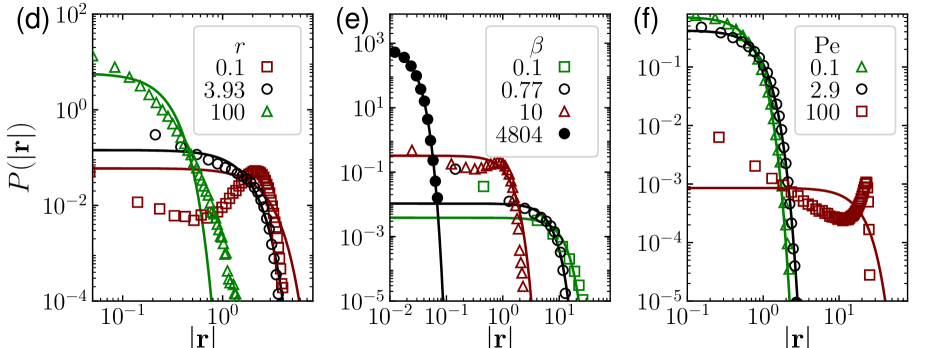
In figures 3(a), 3(b), and 3(c), the steady state kurtosis $\mathcal{K}^{st}_{r}$ from equation (21) is shown as blue solid lines, compared with simulation results represented by blue open points. The black solid points denote the Gaussian behavior at $\mathcal{K}^{st}_{r}=0$. The negative kurtosis $\mathcal{K}^{st}_{r}<0$ indicates persistent active motion, leading to a flat, light-tailed position distribution with a non-zero peak. This is referred to as the activity (A) dominated regime. Positive kurtosis, $\mathcal{K}^{st}_{r}>0$, indicates passive motion, resulting in a narrow, heavy-tailed position distribution peaking at zero. This is referred to as the resetting (R) dominated regime. In figures 3(d), 3(e), and 3(f), we plot the radial distribution from simulations (points) alongside the corresponding Gaussian distribution (solid lines) using the second-order moment.

Figure 3(a) shows a monotonic transition from the activity (A) dominated regime at small resetting rates ($r$) to the resetting (R) dominated regime at larger resetting rates, with a critical resetting rate ($r_{c}$) marking Gaussian behavior. Interestingly, in the resetting dominated regime, the steady-state kurtosis $\mathcal{K}^{st}_{r}$ exhibits a non-monotonic transition, reaching its maximum positive value at intermediate $r$. This is purely due to the interplay between activity ($\mathrm{Pe}$) and resetting ($r$), which occurs even in the absence of a harmonic trap (see G). In figure 3(d), we present the radial distribution for three resetting rates: the activity-dominated regime at $r<r_{c}$, Gaussian behavior at $r=r_{c}$, and the resetting-dominated regime at $r>r_{c}$.

Figure 3(b) shows a non-monotonic transition as a function of trap strength $\beta$. Initially, the resetting (R) dominated regime occurs at weak trap strength, transitioning to the activity (A) dominated regime at stronger trap strengths, with a critical trap strength ($\beta^{I}_{c}$) indicating Gaussian behavior. Subsequently, the activity (A) dominated regime transitions back to the resetting regime at very strong trap strengths, marked by another critical trap strength ($\beta^{II}_{c}$). In figure 3(e), we present the radial distribution for four trap strengths: the resetting-dominated regime at $\beta<\beta_{c}$, Gaussian behavior at $\beta=\beta^{I}_{c}$, the activity-dominated regime at $\beta>\beta_{c}$, Gaussian behavior at $\beta=\beta^{II}_{c}$. In the resetting-dominated regime for $\beta>\beta^{II}_{c}$, the steady-state kurtosis $\mathcal{K}^{st}_{r}$ takes very small positive values, making the heavy-tail visualization nearly impossible.

Figure 3(c) shows a monotonic transition from the resetting (R) dominated regime at small activity ($\mathrm{Pe}$) to the activity (A) dominated regime at larger activity, with a critical resetting rate ($\mathrm{Pe}_{c}$) marking Gaussian behavior. In figure 3(f), we present the radial distribution for three activity ($\mathrm{Pe}$) values: the resetting-dominated regime at $\mathrm{Pe}<\mathrm{Pe}_{c}$, Gaussian behavior at $\mathrm{Pe}=\mathrm{Pe}_{c}$, and the activity-dominated regime at $\mathrm{Pe}>\mathrm{Pe}_{c}$.

In figures 4(a), 4(b), and 4(c), we plot the phase diagram considering $\mathcal{K}^{st}_{r}$ as order parameter to show the activity (A) and resetting (R) dominated regime separating by Gaussian line $\mathcal{K}^{st}_{r}=0$ depicted by black dashed line. Figure 4(a) shows the phase diagram in the $\mathrm{Pe}$-$r$ plane, highlighting two key points: at small resetting rates ($r$), the transition progresses from weak resetting (R) to Gaussian, then to the activity (A) dominated regime. At large resetting rates, increasing activity enhances the resetting (R) dominated regime, resulting in a heavier tail in the distribution. Figure 4(b) shows the phase diagram in the $\mathrm{Pe}$-$\beta$ plane, highlighting a re-entrant transition with increasing trap strength ($\beta$), progressing from resetting (R) to Gaussian, then to activity (A), back to Gaussian, and finally returning to resetting-dominated behavior. The suppression of resetting behavior with increasing trap strength in figure 4(b) is also illustrated in the $r$-$\beta$ plane in figure 4(c).

In this work, we computed the exact analytical moments of a two-dimensional Active Brownian Particle (ABP) subject to complete stochastic resetting (both position and orientation) in a harmonic trap. These analytical results were validated against numerical simulations, demonstrating excellent agreement, and the nonequilibrium steady-state behavior was thoroughly analyzed.

In the steady state, the orientation autocorrelation decays to a non-zero value in the presence of resetting, increasing with the resetting rate and approaching unity as the resetting rate becomes large. The steady state mean displacement exhibits non-monotonic behavior with resetting rate, initially increasing from zero as the resetting rate rises, peaking, and then returning to near-zero at very high resetting rates. We showed that ballistic dynamics emerge in the mean squared displacement (MSD) at intermediate times with increasing activity, though these are suppressed when resetting dominates. Additionally, the MSD reveals that the fluctuation-dissipation relation (FDR) holds in the absence of both activity and resetting, but breaks down, yielding a non-zero excess diffusion coefficient, when either is present.

To distinguish between the activity-dominated (A) and resetting-dominated (R) regimes, we computed the fourth moment of displacement and the corresponding excess kurtosis, providing a complete characterization of the system. In the steady state, excess kurtosis captures the transition between the activity-dominated regime (negative excess kurtosis) and the resetting-dominated regime (positive excess kurtosis), with the Gaussian regime represented by zero excess kurtosis. We anticipate that this rich steady-state behavior can be experimentally validated in active colloids or robotic systems, as shown in [79]. In the future, it will be crucial to explore Active Brownian Particles (ABPs) under two additional stochastic resetting protocols, only position resetting and only orientation resetting in a harmonic trap, to gain valuable insights into optimal resetting strategies in external potentials.

AS acknowledges partial financial support from the John Templeton Foundation, Grant 62213.