Active Bound States Arise From Transiently Nonreciprocal Pair Interactions
Abstract
Static nonreciprocal forces between particles generically drive persistent motion reminiscent of self-propulsion. Here, we demonstrate that reciprocity-breaking fluctuations about a reciprocal mean coupling strength are sufficient to generate this behavior in a minimal two-particle model, with the velocity of the ensuing active bound state being modulated in time according to the nature of these fluctuations. To characterize the ensuing nonequilibrium dynamics, we derive exact results for the time-dependent center of mass mean-squared displacement and average rate of entropy production for two simple examples of discrete- and continuous-state fluctuations. We find that the resulting dimer can exhibit unbiased persistent motion akin to that of an active particle, leading to a significantly enhanced effective diffusivity.
Newton’s third law states that microscopic forces respect action-reaction symmetry, yet many examples of nonreciprocal effective interactions have been identified in living and reactive systems. These range from classical predator-prey Mobilia et al. (2007); Biktashev and Tsyganov (2009) and activator-inhibitor Theveneau et al. (2013) models to interactions mediated by a nonequilibrium medium Hayashi and Sasa (2006); Saha et al. (2019); Soto and Golestanian (2014); Agudo-Canalejo and Golestanian (2019). Nonreciprocity also arises in systems with asymmetric information flows Durve et al. (2018) and memory effects Loos and Klapp (2020); Loos et al. (2019).
The breaking of reciprocal symmetry in many-body systems generates fundamentally nonequilibrium dynamics at the collective scale Ivlev et al. (2015); Saha et al. (2020); You et al. (2020); Fruchart et al. (2021); Zhang and Garcia-Millan (2022). Most strikingly, an imbalance in effective physical forces between particles can drive persistent motion, reminiscent of self-propulsion You et al. (2020). Motile particle clusters Soto and Golestanian (2014); Niu et al. (2018); Saha et al. (2019); Agudo-Canalejo and Golestanian (2019); Lavergne et al. (2019) and self-propelling droplets Meredith et al. (2020) have been experimentally realized in systems with constant nonreciprocal couplings. Furthermore, the thermodynamic implications of reciprocity-breaking were studied in several theoretical models Loos and Klapp (2020); You et al. (2020).
In principle, the introduction of temporal fluctuations in nonreciprocal interactions would provide a mechanism to control the propulsion speed and direction of the ensuing dynamical phase. Such fluctuations may for instance arise generically in physical systems through dynamic properties in the nonequilibrium medium that mediates interactions. Examples include the concentration of so-called doping agents in chemically interacting particle systems Agudo-Canalejo and Golestanian (2019) or of a surfactant in an experimental set-up of self-propelled liquid droplets which allowed for the reversal of the direction of motion Meredith et al. (2020). In a recent study, active motion was shown to emerge from the application of an external random magnetic field on nanoparticle dimers Luis-Hita et al. (2022).
Fluctuating reciprocal interactions in many-body systems lead to nonequilibrium, dissipative structures Alston et al. (2022a) and dynamics Bonazzi et al. (2018). We have previously studied the thermodynamic implications of these interactions in Alston et al. (2022b), where we obtained analytically the non-zero average rate of entropy production in a variety of minimal setups. Though static nonreciprocal couplings have been studied in a similar manner Loos and Klapp (2020); Zhang and Garcia-Millan (2022), a complete thermodynamically-consistent picture for dynamic, nonreciprocal interactions is key to the analysis of important reactive, active and living processes.
In this Letter, we consider a minimal two-particle model of fluctuating nonreciprocal forces. We fix the interactions to be reciprocal on average, yet we let them break the action-reaction principle transiently through temporal fluctuations in the interaction strengths, isolating the impact of reciprocal-symmetry-breaking fluctuations on the collective dynamics and thermodynamic properties of the system. We show that these systems can exhibit collective motion reminiscent of active particles, thus we refer to the resulting 2-particle dimers as active bound states. For particular choices of the fluctuations and in the presence of steric repulsion, the ensuing dynamics can be mapped onto those of Run-and-Tumble Zhang and Pruessner (2022); Garcia-Millan and Pruessner (2021); Solon et al. (2015) and Active Ornstein-Uhlenbeck Martin et al. (2021); Bothe and Pruessner (2021) particles.
Minimal 2-particle model. — We consider a pair of Brownian particles in the overdamped limit with positions and diffusivity . Each particle is confined in a harmonic potential with time-dependent stiffness generated by the other particle. The governing equations then take the form
| (1a) | ||||
| (1b) | ||||
where are uncorrelated zero-mean, unit-variance Gaussian white noises and is a short-range, reciprocal, purely repulsive potential. For the time being, we focus on the case , for which a number of closed form exact results can be derived. We will later show that introducing steric interactions strongly enhances the observed nonequilibrium behavior. Here, we consider binding potential stiffnesses of the form , where is a constant mean stiffness introduced to ensure that the two particles remain in proximity of each other and are governed by zero-mean Markov processes setting the stiffness fluctuations Yuan and Mao (2003); Alston et al. (2022b).
Through a change of variables to the center of mass and interparticle displacement coordinates, we can re-write Eq. (1) as
| (2a) | ||||
| (2b) | ||||
where are again uncorrelated zero-mean unit-variance Gaussian white noise terms (see details in 111Supplemental material). In writing Eq. (2), we have also defined the stiffness asymmetry and the total stiffness fluctuations . Note that is the signature of broken reciprocal symmetry.
We study here both the dynamics and thermodynamics of these two-particle bound states. To quantify their collective dynamics, we derive exact analytical expressions for the time-dependent mean-squared displacement (MSD) of their center of mass, (hereafter, setting by translational symmetry). From Eq. (2a), this MSD can be expressed in terms of the correlator ; as shown in Note (1), the decoupling between the dynamics of and allows us to factorize it and we write
| (3) |
The presence of nonreciprocal and fluctuating interactions drives our two-particle bound states out of equilibrium; to quantify this nonequilibrium behavior, we compute the entropy production rate at the level of Eq. (2). We generically expect three contributions, respectively stemming from (i) the dynamics of the center of mass, (ii) the dynamics of the interparticle displacement and (iii) the stochastic dynamics of the stiffness fluctuations (see Note (1) for a detailed derivation).
Firstly, the center of mass moves following a drift-diffusion process with a time-dependent drift and diffusivity ; this contribution to the entropy production rate thus takes the form Seifert (2012). Secondly, the dynamics of the interparticle displacement can be mapped onto those of a single Brownian particle subject to diffusion in a fluctuating harmonic potential, , a case which we previously studied in Alston et al. (2022b). Finally, a third contribution may come from the two-dimensional Markov process governing the stiffness dynamics, should it not satisfy detailed-balance. Here, we only consider stiffness fluctuations generated by equilibrium processes and this last contribution thus vanishes. The total rate of entropy production can then be written as Cocconi et al. (2020); Alston et al. (2022b)
| (4) |
In what follows, we consider two examples of specific prescriptions for the governing stochastic dynamics of the stiffness fluctuations and show that transiently nonreciprocal pair interactions lead to persistent motion of the center of mass , akin to that of an active particle.
Continuous fluctuations in interaction potentials. — Suppose that the two stiffness fluctuations follow correlated zero-mean Ornstein-Uhlenbeck processes with rate and diffusivity ,
| (5) |
where are zero-mean white noises satisfying
| (6) |
where is the symmetric covariance matrix and quantifies how correlated the stiffness fluctuations are.
The governing equations for the stiffness asymmetry and total stiffness fluctuations then take the form
| (7a) | ||||
| (7b) | ||||
where are now uncorrelated, zero-mean unit-variance Gaussian white noise terms Note (1). In each of the two limits , one of the noise terms disappears. For all , the interparticle displacement behaves as a Brownian particle in a confining potential with a stiffness that itself follows an Ornstein-Uhlenbeck process with mean and variance .
The dynamics for and are independent, which implies that factorises in the second term of Eq. (4). Both contributions to the entropy production rate thus can be written in terms of the variance of the interparticle displacement, assuming that the latter is finite; the first is obtained by the results of Alston et al. (2022b), while the second is deduced from the knowledge of the correlator for :
| (8) |
Again, we note that there is no direct contribution from the switching dynamics as and are governed by equilibrium processes. We show in Note (1) that
| (9) |
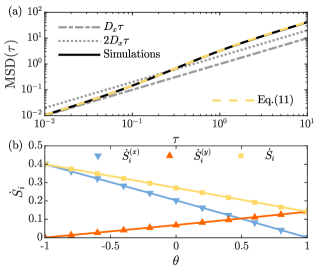
which remains finite only if , in which case Eq. (8) can be computed exactly [see Fig. 1(b)]. Consistently with the second law of thermodynamics, Alston et al. (2022b).
We now consider the limit , which maximises how nonreciprocal the interaction fluctuations can be, generating the most interesting collective dynamics. Here, the total stiffness in a deterministic manner and the dynamics of both and reduce to independent, equilibrium diffusive processes in an external potential. The drift term for the center of mass is the product of these two equilibrium processes Bothe and Pruessner (2021); Bechinger et al. (2016).
The stationary probability distribution for the product can be evaluated formally as where and denote the Boltzmann steady-state probability densities of the corresponding (equilibrium) processes. We can then derive an expression for the stationary distribution for the drift through transformation of probability density functions. It reads
| (10) |
with the modified Bessel function of the second kind.
In the present limit, the MSD for the center of mass is easily calculated as the two-time correlators for and are those of an equilibrium OU process. Using Eq. (3), we obtain
| (11) | ||||
which exhibits the diffusive-ballistic-diffusive scaling characteristic of active particles Bechinger et al. (2016), as shown in Fig. 1(a). Comparing the form of this MSD to that of a general active particle Bechinger et al. (2016); Howse et al. (2007), which we derive in Note (1), we identify an effective self propulsion speed , persistence time and bare diffusivity . At short timescales, , the center of mass follows a diffusive motion with diffusion coefficient . At long times, the dimer exhibits diffusive motion characterized by the long-time effective diffusion coefficient
| (12) |
which is strictly larger than the bare center of mass translational diffusivity when , i.e. in the presence of fluctuations. For sufficiently strong fluctuations, specifically , this effective diffusivity can strikingly exceed that of a single particle. This is in stark contrast with the classical scaling for the diffusivity of identical Langevin processes interacting by equilibrium pair interactions and thus represents a genuinely nonequilibrium feature of the present model. Below, we show numerically that this result holds in the presence of repulsive interactions.
To quantify these nonequilibrium dynamics, we evaluate the rate of entropy production from Eq. (8). For , we note that the variance of the interparticle displacement satisfies , such that the only non-zero contribution to the entropy production rate comes from the center of mass dynamics . Using Eq. (8), we write this as
| (13) |
We discuss the limit in Note (1). In this case, the interactions are always reciprocal, but the fluctuations in the coupling strength alone are sufficient to drive the system out of equilibrium Alston et al. (2022b); Guyon et al. (2004); Zhang and Wang (2017).
Discrete fluctuations in interaction potentials. — We now turn to the case of discrete stiffness fluctuations. We let be correlated symmetric Telegraph processes Gardiner (2009); the symmetric nature of the Markov jump process ensures that , and hence, that pair interactions remain on average reciprocal maintaining the particles in a bound state. The joint probability mass function is generically governed by
| (14) |
in which the position-independent Markov matrix capturing the stochastic dynamics of the stiffnesses reads
| (15) |
with transition rate , correlation parameter and transition rate matrices defined as
| (16) |
The limit leads to bipartite dynamics, where each switching event causes a transition between reciprocal and nonreciprocal interaction. In contrast, corresponds to maximally correlated switching dynamics, such that switching events are always synchronised and the (non)reciprocity of the dynamics is conserved by the fluctuations. While a study of the ensuing dynamics in the general case is of great interest, we consider here the limiting case only, such that . In this limit, the fluctuations of and are uncorrelated.
Similarly to what was done for the continuous case, we further focus on the case where fluctuations are maximally nonreciprocal. Let at initialization, such that and . The synchrony condition imposes that the total stiffness remains zero while the sign of the stiffness asymmetry switches with symmetric Poisson rate , a Telegraph process, leading to nonreciprocal force fluctuations at all times (see details of allowed transitions for the Markov jump process in Note (1)). The dynamics of are exactly those of a diffusive particle in the potential . We note that , while is simply the propagator for an Ornstein-Uhlenbeck process Gardiner (2009). As shown in Note (1), we conclude that the full MSD then takes the form
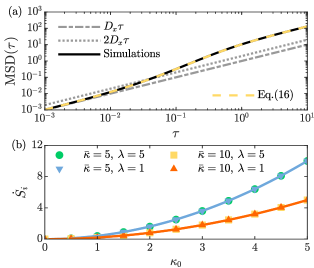
| (17) |
[see Fig. 2(a)] which again can be mapped to the MSD of an active particle with effective self-propulsion speed , persistence time and bare diffusivity Howse et al. (2007); Bechinger et al. (2016); Note (1). Finally, the long-time effective diffusion coefficient reads
| (18) |
which is strictly larger than the bare center of mass translational diffusivity. Remarkably, for sufficiently slow fluctuations, specifically , this effective diffusivity can exceed that of a single particle as we saw for the case of continuous fluctuations [see Fig. 2(a)].
As the dynamics for is at equilibrium, the only non-zero contribution to the entropy production comes from the spontaneous drift of the center of mass. In the present case, the dynamics of and are again entirely decoupled implying that . We can evaluate , Gardiner (2009) and using Eq. (4) write the full entropy production rate as
| (19) |
The independence of Eq. (19) on the switching rate is demonstrated numerically in Fig. 2(b). The case of fluctuating reciprocal couplings, whereby we let at initialization, is discussed in Note (1).
Effect of steric repulsion. — So far, we have ignored the role of steric repulsion; while this allowed us to derive exact analytical results, we now reintroduce a non-vanishing purely repulsive potential in Eq. (1). While the equation governing the center of mass dynamics is unaffected by this change, Eq. (2b) for the interparticle displacement acquires an additional term
| (20) |
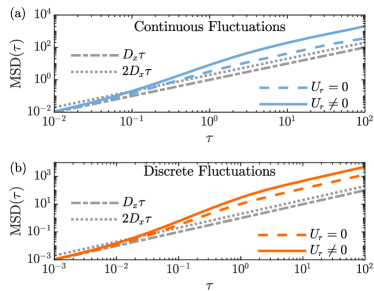
Intuitively, since should penalize particles overlapping, we expect the bound state to be characterized by a finite interparticle displacement, commensurate with the particle diameter. If we further assume that the fluctuations in are small, then is approximately constant and is left to be the sole term responsible for fluctuations in the self-propulsion contribution to the center of mass dynamics in Eq. (2a). Remarkably, when is an OU process, such as in Eq. (7b), the ensuing dynamics of the bound state are then akin to those of an Active Ornstein-Uhlenbeck (AOUP). Similarly, when is governed by a Telegraph process, which is exactly the case which leads to Eq. (17), the dynamics match those of a Run-and-Tumble (RTP) particle.
To study numerically the effect that steric repulsion has on our results, we choose a Weeks-Chandler-Anderson potential for , capped at to give the particles a well-defined diameter Note (1); Brańka and Heyes (1999). For the case of nonreciprocal fluctuations, the MSDs exhibit a longer phase of ballistic motion and an increased long-time diffusion coefficient, as can be seen in Fig. 3. The average rate of entropy production remains qualitatively unchanged by the introduction of steric repulsion showing the characteristic monotonic increase already seen in Fig. 2 Note (1). By keeping the two particles apart, the size of the forces coming from the harmonic potential are on average much larger, driving more persistent motion and hence higher dissipation in the present model.
Discussion and conclusion. — We have demonstrated that reciprocal-symmetry-breaking fluctuations about a reciprocal mean attractive coupling are sufficient to generate two-particle bound states whose center of mass motion can be mapped onto that of a motile active particle, Eq. (2a). For specific choices of the fluctuations and in the presence of steric repulsion, one-dimensional Active Ornstein-Uhlenbeck as well as Run-and-Tumble dynamics are recapitulated. We characterize the dissipative nature of these active bound states by computing the average rate of entropy production, Eq. (4). Remarkably, for sufficiently strong nonreciprocal fluctuations, the long time effective diffusion is observed to exceed that of a single particle, Eqs. (12) and (18), which represents a genuinely nonequilibrium feature of our model.
Fluctuations in the degree of reciprocity of pair interactions arise naturally in a number of physical circumstances, e.g. through mediation by a nonequilibrium medium Durve et al. (2018); Hayashi and Sasa (2006); Saha et al. (2019); Soto and Golestanian (2014); Agudo-Canalejo and Golestanian (2019), in the presence of memory Loos et al. (2019) or from perception within a finite vision cone Loos et al. (2022); Lavergne et al. (2019). In fact, in macroscopic active systems, nonreciprocity is arguably the norm rather than the exception.
A simple model of fluctuating interactions in a two-body system was realized in a recent study on nano-particles subjected to random electric fields Luis-Hita et al. (2022). The resulting pair-interactions were nonreciprocal in nature and lead to persistent motion as predicted in the theory above. Another promising candidate for realizing the dynamics studied here could be size-dependent interactions between droplets exchanging mass through inverse Ostwald ripening dynamics Theveneau et al. (2013). In general, the strength of interactions through a medium depends on the perimeter of a droplet, which is a dynamic quantity due to thermal fluctuations driving constant re-balancing of the Laplace pressure.
Acknowledgements.
LC and HA contributed equally to this work. LC acknowledges support from the Francis Crick Institute, which receives its core funding from Cancer Research UK, the UK Medical Research Council and the Wellcome Trust (FC001317). HA was supported by a Roth PhD scholarship funded by the Department of Mathematics at Imperial College London.References
- Mobilia et al. (2007) M. Mobilia, I. T. Georgiev, and U. C. Täuber, “Phase transitions and spatio-temporal fluctuations in stochastic lattice lotka–volterra models,” Journal of Statistical Physics 128, 447–483 (2007).
- Biktashev and Tsyganov (2009) V. N. Biktashev and M. A. Tsyganov, “Spontaneous traveling waves in oscillatory systems with cross diffusion,” Phys. Rev. E 80, 056111 (2009).
- Theveneau et al. (2013) E. Theveneau, B. Steventon, E. Scarpa, S. Garcia, X. Trepat, A. Streit, and R. Mayor, “Chase-and-run between adjacent cell populations promotes directional collective migration,” Nature Cell Biology 15, 763–772 (2013).
- Hayashi and Sasa (2006) K. Hayashi and S.-i. Sasa, “The law of action and reaction for the effective force in a non-equilibrium colloidal system,” Journal of Physics: Condensed Matter 18, 2825–2836 (2006).
- Saha et al. (2019) S. Saha, S. Ramaswamy, and R. Golestanian, “Pairing, waltzing and scattering of chemotactic active colloids,” New Journal of Physics 21, 063006 (2019).
- Soto and Golestanian (2014) R. Soto and R. Golestanian, “Self-assembly of catalytically active colloidal molecules: Tailoring activity through surface chemistry,” Phys. Rev. Lett. 112, 068301 (2014).
- Agudo-Canalejo and Golestanian (2019) J. Agudo-Canalejo and R. Golestanian, “Active phase separation in mixtures of chemically interacting particles,” Phys. Rev. Lett. 123, 018101 (2019).
- Durve et al. (2018) M. Durve, A. Saha, and A. Sayeed, “Active particle condensation by non-reciprocal and time-delayed interactions,” The European Physical Journal E 41, 49 (2018).
- Loos and Klapp (2020) S. A. M. Loos and S. H. L. Klapp, “Irreversibility, heat and information flows induced by non-reciprocal interactions,” New Journal of Physics 22, 123051 (2020).
- Loos et al. (2019) S. A. M. Loos, S. M. Hermann, and S. H. L. Klapp, “Non-reciprocal hidden degrees of freedom: A unifying perspective on memory, feedback, and activity,” arXiv:1910.08372 (2019).
- Ivlev et al. (2015) A. V. Ivlev, J. Bartnick, M. Heinen, C.-R. Du, V. Nosenko, and H. Löwen, “Statistical mechanics where newton’s third law is broken,” Phys. Rev. X 5, 011035 (2015).
- Saha et al. (2020) S. Saha, J. Agudo-Canalejo, and R. Golestanian, “Scalar active mixtures: The nonreciprocal cahn-hilliard model,” Phys. Rev. X 10, 041009 (2020).
- You et al. (2020) Z. You, A. Baskaran, and M. C. Marchetti, “Nonreciprocity as a generic route to traveling states,” Proceedings of the National Academy of Sciences 117, 19767–19772 (2020).
- Fruchart et al. (2021) M. Fruchart, R. Hanai, P. B. Littlewood, and V. Vitelli, “Non-reciprocal phase transitions,” Nature 592, 363–369 (2021).
- Zhang and Garcia-Millan (2022) Z. Zhang and R. Garcia-Millan, “Entropy production of non-reciprocal interactions,” arXiv:2209.09721 (2022).
- Niu et al. (2018) R. Niu, A. Fischer, T. Palberg, and T. Speck, “Dynamics of binary active clusters driven by ion-exchange particles,” ACS Nano 12, 10932–10938 (2018).
- Lavergne et al. (2019) F. A. Lavergne, H. Wendehenne, T. Bäuerle, and C. Bechinger, “Group formation and cohesion of active particles with visual perception–dependent motility,” Science 364, 70–74 (2019).
- Meredith et al. (2020) C. H. Meredith, P. G. Moerman, J. Groenewold, Y.-J. Chiu, W. K. Kegel, A. van Blaaderen, and L. D. Zarzar, “Predator–prey interactions between droplets driven by non-reciprocal oil exchange,” Nature Chemistry 12, 1136–1142 (2020).
- Luis-Hita et al. (2022) J. Luis-Hita, J. J. Sáenz, and M. I. Marqués, “Active motion induced by random electromagnetic fields,” ACS Photonics 9, 1008–1014 (2022).
- Alston et al. (2022a) H. Alston, A. O. Parry, R. Voituriez, and T. Bertrand, “Intermittent attractive interactions lead to microphase separation in nonmotile active matter,” Phys. Rev. E 106, 034603 (2022a).
- Bonazzi et al. (2018) D. Bonazzi, V. Lo Schiavo, S. Machata, I. Djafer-Cherif, P. Nivoit, V. Manriquez, H. Tanimoto, J. Husson, N. Henry, H. Chaté, R. Voituriez, and G. Duménil, “Intermittent pili-mediated forces fluidize neisseria meningitidis aggregates promoting vascular colonization,” Cell 174, 143–155.e16 (2018).
- Alston et al. (2022b) H. Alston, L. Cocconi, and T. Bertrand, “Non-equilibrium thermodynamics of diffusion in fluctuating potentials,” Journal of Physics A: Mathematical and Theoretical 55, 274004 (2022b).
- Zhang and Pruessner (2022) Z. Zhang and G. Pruessner, “Field theory of free run and tumble particles in d dimensions,” Journal of Physics A: Mathematical and Theoretical 55, 045204 (2022).
- Garcia-Millan and Pruessner (2021) R. Garcia-Millan and G. Pruessner, “Run-and-tumble motion in a harmonic potential: field theory and entropy production,” Journal of Statistical Mechanics: Theory and Experiment 2021, 063203 (2021).
- Solon et al. (2015) A. P. Solon, M. E. Cates, and J. Tailleur, “Active brownian particles and run-and-tumble particles: A comparative study,” The European Physical Journal Special Topics 224, 1231–1262 (2015).
- Martin et al. (2021) D. Martin, J. O’Byrne, M. E. Cates, E. Fodor, C. Nardini, J. Tailleur, and F. van Wijland, “Statistical mechanics of active ornstein-uhlenbeck particles,” Phys. Rev. E 103, 032607 (2021).
- Bothe and Pruessner (2021) M. Bothe and G. Pruessner, “Doi-peliti field theory of free active ornstein-uhlenbeck particles,” Phys. Rev. E 103, 062105 (2021).
- Yuan and Mao (2003) C. Yuan and X. Mao, “Asymptotic stability in distribution of stochastic differential equations with markovian switching,” Stochastic Processes and their Applications 103, 277–291 (2003).
- Note (1) Supplemental material.
- Seifert (2012) U. Seifert, “Stochastic thermodynamics, fluctuation theorems and molecular machines,” Reports on Progress in Physics 75, 126001 (2012).
- Cocconi et al. (2020) L. Cocconi, R. Garcia-Millan, Z. Zhen, B. Buturca, and G. Pruessner, “Entropy Production in Exactly Solvable Systems,” Entropy 22, 1252 (2020).
- Bechinger et al. (2016) C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe, and G. Volpe, “Active particles in complex and crowded environments,” Reviews of Modern Physics 88, 045006 (2016), publisher: American Physical Society.
- Howse et al. (2007) J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh, and R. Golestanian, “Self-motile colloidal particles: From directed propulsion to random walk,” Phys. Rev. Lett. 99, 048102 (2007).
- Guyon et al. (2004) X. Guyon, S. Iovleff, and J.-F. Yao, “Linear diffusion with stationary switching regime,” ESAIM: Probability and Statistics 8, 25–35 (2004).
- Zhang and Wang (2017) Z. Zhang and W. Wang, “The stationary distribution of ornstein–uhlenbeck process with a two-state markov switching,” Communications in Statistics - Simulation and Computation 46, 4783–4794 (2017).
- Gardiner (2009) C. W. Gardiner, Stochastic Methods: A Handbook for the Natural and Social Sciences, 4th ed. (Springer Berlin, Heidelberg, 2009).
- Brańka and Heyes (1999) A. C. Brańka and D. M. Heyes, “Algorithms for brownian dynamics computer simulations: Multivariable case,” Phys. Rev. E 60, 2381–2387 (1999).
- Loos et al. (2022) S. A. M. Loos, S. H. L. Klapp, and T. Martynec, “Long-range order and directional defect propagation in the nonreciprocal xy model with vision cone interactions,” arXiv:2206.10519 (2022).