Accelerating Distributed Stochastic Optimization via Self-Repellent Random Walks

Stochastic optimization algorithms solve optimization problems of the form

with the objective function $f:\mathbb{R}^{d}\to\mathbb{R}$ and $X$ taking values in a finite state space ${\mathcal{N}}$ with distribution ${\bm{\mu}}\triangleq[\mu_{i}]_{i\in{\mathcal{N}}}$. Leveraging partial gradient information per iteration, these algorithms have been recognized for their scalability and efficiency with large datasets (Bottou et al., 2018; Even, 2023). For any given noise sequence $\{X_{n}\}_{n\geq 0}\subset{\mathcal{N}}$, and step size sequence $\{\beta_{n}\}_{n\geq 0}\subset\mathbb{R}_{+}$, most stochastic optimization algorithms can be classified as stochastic approximations (SA) of the form

where, roughly speaking, $H({\bm{\theta}},i)$ contains gradient information $\nabla_{{\bm{\theta}}}F(\theta,i)$, such that ${\bm{\theta}}^{*}$ solves ${\mathbf{h}}({\bm{\theta}})\!\triangleq\!\mathbb{E}_{X\sim{\bm{\mu}}}[H({\bm{\theta}},X)]\!=\!\sum_{i\in{\mathcal{N}}}\mu_{i}H({\bm{\theta}},i)\!=\!{\bm{0}}$. Such SA iterations include the well-known stochastic gradient descent (SGD), stochastic heavy ball (SHB) (Gadat et al., 2018; Li et al., 2022), and some SGD-type algorithms employing additional auxiliary variables (Barakat et al., 2021).¹¹1Further illustrations of stochastic optimization algorithms of the form (2) are deferred to Appendix A. These algorithms typically have the stochastic noise term $X_{n}$ generated by i.i.d. random variables with probability distribution ${\bm{\mu}}$ in each iteration. In this paper, we study a stochastic optimization algorithm where the noise sequence governing access to the gradient information is generated from general stochastic processes in place of i.i.d. random variables.

This is commonly the case in distributed learning, where $\{X_{n}\}$ is a (typically Markovian) random walk, and should asymptotically be able to sample the gradients from the desired probability distribution ${\bm{\mu}}$. This is equivalent to saying that the random walker’s empirical distribution converges to ${\bm{\mu}}$ almost surely (a.s.); that is, ${\mathbf{x}}_{n}\triangleq\frac{1}{n+1}\sum_{k=0}^{n}{\bm{\delta}}_{X_{k}}\xrightarrow[n\to\infty]{a.s.}{\bm{\mu}}$ for any initial $X_{0}\in{\mathcal{N}}$, where ${\bm{\delta}}_{X_{k}}$ is the delta measure whose $X_{k}$’th entry is one, the rest being zero. Such convergence is most commonly achieved by employing the Metropolis Hastings random walk (MHRW) which can be designed to sample from any target measure ${\bm{\mu}}$ and implemented in a scalable manner (Sun et al., 2018). Unsurprisingly, convergence characteristics of the employed Markov chain affect that of the SA sequence (2), and appear in both finite-time and asymptotic analyses. Finite-time bounds typically involve the second largest eigenvalue in modulus (SLEM) of the Markov chain’s transition kernel ${\mathbf{P}}$, which is critically connected to the mixing time of a Markov chain (Levin & Peres, 2017); whereas asymptotic results such as central limit theorems (CLT) involve asymptotic covariance matrices that embed information regarding the entire spectrum of ${\mathbf{P}}$, i.e., all eigenvalues as well as eigenvectors (Brémaud, 2013), which are key to understanding the sampling efficiency of a Markov chain. Thus, the choice of random walker can significantly impact the performance of (2), and simply ensuring that it samples from ${\bm{\mu}}$ asymptotically is not enough to achieve optimal algorithmic performance. In this paper, we take a closer look at the distributed stochastic optimization problem through the lens of a non-linear Markov chain, known as the Self Repellent Random Walk (SRRW), which was shown in Doshi et al. (2023) to achieve asymptotically minimal sampling variance for large values of $\alpha$, a positive scalar controlling the strength of the random walker’s self-repellence behaviour. Our proposed modification of (2) can be implemented within the settings of decentralized learning applications in a scalable manner, while also enjoying significant performance benefit over distributed stochastic optimization algorithms driven by vanilla Markov chains.

Token Algorithms for Decentralized Learning. In decentralized learning, agents like smartphones or IoT devices, each containing a subset of data, collaboratively train models on a graph ${\mathcal{G}}({\mathcal{N}},{\mathcal{E}})$ by sharing information locally without a central server (McMahan et al., 2017). In this setup, $N\!=\!|{\mathcal{N}}|$ agents correspond to nodes $i\!\in\!{\mathcal{N}}$, and an edge $(i,j)\!\in\!{\mathcal{E}}$ indicates direct communication between agents $i$ and $j$. This decentralized approach offers several advantages compared to the traditional centralized learning setting, promoting data privacy and security by eliminating the need for raw data to be aggregated centrally and thus reducing the risk of data breach or misuse (Bottou et al., 2018; Nedic, 2020). Additionally, decentralized approaches are more scalable and can handle vast amounts of heterogeneous data from distributed agents without overwhelming a central server, alleviating concerns about single point of failure (Vogels et al., 2021).

Among decentralized learning approaches, the class of ‘Token’ algorithms can be expressed as stochastic approximation iterations of the type (2), wherein the sequence $\{X_{n}\}$ is realized as the sample path of a token that stochastically traverses the graph ${\mathcal{G}}$, carrying with it the iterate ${\bm{\theta}}_{n}$ for any time $n\geq 0$ and allowing each visited node (agent) to incrementally update ${\bm{\theta}}_{n}$ using locally available gradient information. Token algorithms have gained popularity in recent years (Hu et al., 2022; Triastcyn et al., 2022; Hendrikx, 2023), and are provably more communication efficient (Even, 2023) when compared to consensus-based algorithms - another popular approach for solving distributed optimization problems (Boyd et al., 2006; Morral et al., 2017; Olshevsky, 2022). The construction of token algorithms means that they do not suffer from expensive costs of synchronization and communication that are typical of consensus-based approaches, where all agents (or a subset of agents selected by a coordinator (Boyd et al., 2006; Wang et al., 2019)) on the graph are required to take simultaneous actions, such as communicating on the graph at each iteration. While decentralized Federated learning has indeed helped mitigate the communication overhead by processing multiple SGD iterations prior to each aggregation (Lalitha et al., 2018; Ye et al., 2022; Chellapandi et al., 2023), they still cannot overcome challenges such as synchronization and straggler issues.

Self Repellent Random Walk. As mentioned earlier, sample paths $\{X_{n}\}$ of token algorithms are usually generated using Markov chains with ${\bm{\mu}}\in\text{Int}(\Sigma)$ as their limiting distribution. Here, $\Sigma$ denotes the $N$-dimensional probability simplex, with $\text{Int}(\Sigma)$ representing its interior. A recent work by Doshi et al. (2023) pioneers the use of non-linear Markov chains to, in some sense, improve upon any given time-reversible Markov chain with transition kernel ${\mathbf{P}}$ whose stationary distribution is ${\bm{\mu}}$. They show that the non-linear transition kernel²²2Here, non-linearity in the transition kernel implies that ${\mathbf{K}}[{\mathbf{x}}]$ takes probability distribution ${\mathbf{x}}$ as the argument (Andrieu et al., 2007), as opposed to the kernel being a linear operator ${\mathbf{K}}[{\mathbf{x}}]={\mathbf{P}}$ for a constant stochastic matrix ${\mathbf{P}}$ in a standard (linear) Markovian setting. ${\mathbf{K}}[\cdot]:\text{Int}(\Sigma)\to[0,1]^{N\times N}$, given by

for any ${\mathbf{x}}\in\text{Int}(\Sigma)$, when simulated as a self-interacting random walk (Del Moral & Miclo, 2006; Del Moral & Doucet, 2010), can achieve smaller asymptotic variance than the base Markov chain when sampling over a graph ${\mathcal{G}}$, for all $\alpha\!>\!0$. The argument ${\mathbf{x}}$ for the kernel ${\mathbf{K}}[{\bm{x}}]$ is taken to be the empirical distribution ${\mathbf{x}}_{n}$ at each time step $n\!\geq\!0$. For instance, if node $j$ has been visited more often than other nodes so far, the entry $x_{j}$ becomes larger (than target value $\mu_{j}$), resulting in a smaller transition probability from $i$ to $j$ under ${\mathbf{K}}[{\mathbf{x}}]$ in (3) compared to $P_{ij}$. This ensures that a random walker prioritizes more seldom visited nodes in the process, and is thus ‘self-repellent’. This effect is made more drastic by increasing $\alpha$, and leads to asymptotically near-zero variance at a rate of $O(1/\alpha)$. Moreover, the polynomial function $(x_{i}/\mu_{i})^{-\alpha}$ chosen to encode self-repellent behaviour is shown in Doshi et al. (2023) to be the only one that allows the SRRW to inherit the so-called ‘scale-invariance’ property of the underlying Markov chain – a necessary component for the scalable implementation of a random walker over a large network without requiring knowledge of any graph-related global constants. Conclusively, such attributes render SRRW especially suitable for distributed optimization.³³3Recently, Guo et al. (2020) introduce an optimization scheme, which designs self-repellence into the perturbation of the gradient descent iterates (Jin et al., 2017; 2018; 2021) with the goal of escaping saddle points. This notion of self-repellence is distinct from the SRRW, which is a probability kernel designed specifically for a token to sample from a target distribution ${\bm{\mu}}$ over a set of nodes on an arbitrary graph.

Effect of Stochastic Noise - Finite time and Asymptotic Approaches. Most contemporary token algorithms driven by Markov chains are analyzed using the finite-time bounds approach for obtaining insights into their convergence rates (Sun et al., 2018; Doan et al., 2019; 2020; Triastcyn et al., 2022; Hendrikx, 2023). However, as also explained in Even (2023), in most cases these bounds are overly dependent on mixing time properties of the specific Markov chain employed therein. This makes them largely ineffective in capturing the exact contribution of the underlying random walk in a manner which is qualitative enough to be used for algorithm design; and performance enhancements are typically achieved via application of techniques such as variance reduction (Defazio et al., 2014; Schmidt et al., 2017), momentum/Nesterov’s acceleration (Gadat et al., 2018; Li et al., 2022), adaptive step size (Kingma & Ba, 2015; Reddi et al., 2018), which work by modifying the algorithm iterations themselves, and never consider potential improvements to the stochastic input itself.

Complimentary to finite-time approaches, asymptotic analysis using CLT has proven to be an excellent tool to approach the design of stochastic algorithms (Hu et al., 2022; Devraj & Meyn, 2017; Morral et al., 2017; Chen et al., 2020a; Mou et al., 2020; Devraj & Meyn, 2021). Hu et al. (2022) shows how asymptotic analysis can be used to compare the performance of SGD algorithms for various stochastic inputs using their notion of efficiency ordering, and, as mentioned in Devraj & Meyn (2017), the asymptotic benefits from minimizing the limiting covariance matrix are known to be a good predictor of finite-time algorithmic performance, also observed empirically in Section 4.

From the perspective of both finite-time analysis as well as asymptotic analysis of token algorithms, it is now well established that employing ‘better’ Markov chains can enhance the performance of stochastic optimization algorithm. For instance, Markov chains with smaller SLEMs yield tighter finite-time upper bounds (Sun et al., 2018; Ayache & El Rouayheb, 2021; Even, 2023). Similarly, Markov chains with smaller asymptotic variance for MCMC sampling tasks also provide better performance, resulting in smaller covariance matrix of SGD algorithms (Hu et al., 2022). Therefore, with these breakthrough results via SRRW achieving near-zero sampling variance, it is within reason to ask: Can we achieve near-zero variance in distributed stochastic optimization driven by SRRW-like token algorithms on any general graph?⁴⁴4This near-zero sampling variance implies a significantly smaller variance than even an i.i.d. sampling counterpart, while adhering to graph topological constraints of token algorithms. In this paper, we answer in the affirmative.

Our Contributions.

1. Given any time-reversible ‘base’ Markov chain with transition kernel ${\mathbf{P}}$ and stationary distribution ${\bm{\mu}}$, we generalize first and second order convergence results of ${\mathbf{x}}_{n}$ to target measure ${\bm{\mu}}$ (Theorems 4.1 and 4.2 in Doshi et al., 2023) to a class of weighted empirical measures, through the use of more general step sizes $\gamma_{n}$. This includes showing that the asymptotic sampling covariance terms decrease to zero at rate $O(1/\alpha)$, thus quantifying the effect of self-repellent on ${\mathbf{x}}_{n}$. Our generalization is not for the sake thereof and is shown in Section 3 to be crucial for the design of step sizes $\beta_{n},\gamma_{n}$.

2. Building upon the convergence results for iterates ${\mathbf{x}}_{n}$, we analyze the algorithm (4) driven by the SRRW kernel in (3) with step sizes $\beta_{n}$ and $\gamma_{n}$ separated into three disjoint cases:

1. (i)

   $\beta_{n}=o(\gamma_{n})$, and we say that ${\bm{\theta}}_{n}$ is on the slower timescale compared to ${\mathbf{x}}_{n}$;

2. (ii)

   $\beta_{n}\!=\!\gamma_{n}$, and we say that ${\bm{\theta}}_{n}$ and ${\mathbf{x}}_{n}$ are on the same timescale;

3. (iii)

   $\gamma_{n}=o(\beta_{n})$, and we say that ${\bm{\theta}}_{n}$ is on the faster timescale compared to ${\mathbf{x}}_{n}$.

For any $\alpha\geq 0$ and let $k=1,2$ and $3$ refer to the corresponding cases (i), (ii) and (iii), we show that

featuring distinct asymptotic covariance matrices ${\mathbf{V}}^{(1)}_{{\bm{\theta}}}(\alpha),{\mathbf{V}}^{(2)}_{{\bm{\theta}}}(\alpha)$ and ${\mathbf{V}}^{(3)}_{{\bm{\theta}}}(\alpha)$, respectively. The three matrices coincide when $\alpha=0$,⁶⁶6The $\alpha=0$ case is equivalent to simply running the base Markov chain, since from (3) we have ${\mathbf{K}}[\cdot]={\mathbf{P}}$, thus bypassing the SRRW’s effect and rendering all three cases nearly the same.. Moreover, the derivation of the CLT for cases (i) and (iii), for which (4) corresponds to two-timescale SA with controlled Markov noise, is the first of its kind and thus a key technical contribution in this paper, as expanded upon in Section 3.

3. For case (i), we show that ${\mathbf{V}}^{(1)}_{{\bm{\theta}}}(\alpha)$ decreases to zero (in the sense of Loewner ordering introduced in Section 2.1) as $\alpha$ increases, with rate $O(1/\alpha^{2})$. This is especially surprising, since the asymptotic performance benefit from using the SRRW kernel with $\alpha$ in (3), to drive the noise terms $X_{n}$, is amplified in the context of distributed learning and estimating ${\bm{\theta}}^{*}$; compared to the sampling case, for which the rate is $O(1/\alpha)$ as mentioned earlier. For case (iii), we show that ${\mathbf{V}}_{{\bm{\theta}}}^{(3)}(\alpha)\!=\!{\mathbf{V}}_{{\bm{\theta}}}^{(3)}(0)$ for all $\alpha\!\geq\!0$, implying that using the SRRW in this case provides no asymptotic benefit than the original base Markov chain, and thus performs worse than case (i). In summary, we deduce that ${\mathbf{V}}_{{\bm{\theta}}}^{(1)}(\alpha_{2})\!<_{L}\!{\mathbf{V}}_{{\bm{\theta}}}^{(1)}(\alpha_{1})\!<_{L}\!{\mathbf{V}}_{{\bm{\theta}}}^{(1)}(0)\!=\!{\mathbf{V}}_{{\bm{\theta}}}^{(3)}(0)\!=\!{\mathbf{V}}_{{\bm{\theta}}}^{(3)}(\alpha)$ for all $\alpha_{2}>\alpha_{1}>0$ and $\alpha>0$.⁷⁷7In particular, this is the reason why we advocate for a more general step size $\gamma_{n}=(n+1)^{-a}$ in the SRRW iterates with $a<1$, allowing us to choose $\beta_{n}=(n+1)^{-b}$ with $b\in(a,1]$ to satisfy $\beta_{n}=o(\gamma_{n})$ for case (i).

4. We numerically simulate our SA-SRRW algorithm on various real-world datasets, focusing on a binary classification task, to evaluate its performance across all three cases. By carefully choosing the function $H$ in SA-SRRW, we test the SGD and algorithms driven by SRRW. Our findings consistently highlight the superiority of case (i) over cases (ii) and (iii) for diverse $\alpha$ values, even in their finite time performance. Notably, our tests validate the variance reduction at a rate of $O(1/\alpha^{2})$ for case (i), suggesting it as the best algorithmic choice among the three cases.

In Section 2.1, we first standardize the notations used throughout the paper, and define key mathematical terms and quantities used in our theoretical analyses. Then, in Section 2.2, we consolidate the model assumptions of our SA-SRRW algorithm (4). We then go on to discuss our assumptions, and provide additional interpretations of our use of generalized step-sizes.

In this section, we provide the main results for the SA-SRRW algorithm (4). We first present the a.s. convergence and the CLT result for SRRW with generalized step size, extending the results in Doshi et al. (2023). Building upon this, we present the a.s. convergence and the CLT result for the SA iterate ${\bm{\theta}}_{n}$ under different settings of step sizes. We then shift our focus to the analysis of the different asymptotic covariance matrices emerging out of the CLT result, and capture the effect of $\alpha$ and the step sizes, particularly in cases (i) and (iii), on ${\bm{\theta}}_{n}-{\bm{\theta}}^{*}$ via performance ordering.

Almost Sure convergence and CLT: The following result establishes first and second order convergence of the sequence $\{{\mathbf{x}}_{n}\}_{n\geq 0}$, which represents the weighted empirical measures of the SRRW process $\{X_{n}\}_{n\geq 0}$, based on the update rule in (4b).

Lemma 3.1 shows that the SRRW iterates ${\mathbf{x}}_{n}$ converges to the target distribution ${\bm{\mu}}$ a.s. even under the general step size $\gamma_{n}=(n+1)^{-a}$ for $a\in(0.5,1]$. We also observe that the asymptotic covariance matrix ${\mathbf{V}}_{{\mathbf{x}}}(\alpha)$ decreases at rate $O(1/\alpha)$. Lemma 3.1 aligns with Doshi et al. (2023, Theorem 4.2 and Corollary 4.3) for the special case of $a=1$, and is therefore more general. Critically, it helps us establish our next result regarding the first-order convergence for the optimization iterate sequence $\{{\bm{\theta}}_{n}\}_{n\geq 0}$ following update rule (4c), as well as its second-order convergence result, which follows shortly after. The proofs of Lemma 3.1 and our next result, Theorem 3.2, are deferred to Appendix D. In what follows, $k=1,2$, and $3$ refer to cases (i), (ii), and (iii) in Section 2.2, respectively. All subsequent results are proven under Assumptions A1 to A4, with A3^′ replacing A3 only when the step sizes $\beta_{n},\gamma_{n}$ satisfy case (iii).

In the stochastic optimization context, the above result ensures convergence of iterates ${\bm{\theta}}_{n}$ to a local minimizer ${\bm{\theta}}^{*}$. Loosely speaking, the first-order convergence of ${\mathbf{x}}_{n}$ in Lemma 3.1 as well as that of ${\bm{\theta}}_{n}$ are closely related to the convergence of trajectories $\{{\mathbf{z}}(t)\triangleq({\bm{\theta}}(t),{\mathbf{x}}(t))\}_{t\geq 0}$ of the (coupled) mean-field ODE, written in a matrix-vector form as

where matrix ${\mathbf{H}}({\bm{\theta}})\!\triangleq\![H({\bm{\theta}},1),\!\cdots\!,H({\bm{\theta}},N)]^{T}\!\in\!{\mathbb{R}}^{N\!\times\!D}$ for any ${\bm{\theta}}\in\mathbb{R}^{D}$. Here, ${\bm{\pi}}[{\mathbf{x}}]\in\text{Int}(\Sigma)$ is the stationary distribution of the SRRW kernel ${\mathbf{K}}[{\mathbf{x}}]$ and is shown in Doshi et al. (2023) to be given by $\pi_{i}[{\mathbf{x}}]\propto\sum_{j\in{\mathcal{N}}}\mu_{i}P_{ij}(x_{i}/\mu_{i})^{-\alpha}(x_{j}/\mu_{j})^{-\alpha}$. The Jacobian matrix of (7) when evaluated at equilibria ${\mathbf{z}}^{*}=({\bm{\theta}}^{*},{\bm{\mu}})$ for ${\bm{\theta}}^{*}\in\Theta$ captures the behaviour of solutions of the mean-field in their vicinity, and plays an important role in the asymptotic covariance matrices arising out of our CLT results. We evaluate this Jacobian matrix ${\mathbf{J}}(\alpha)$ as a function of $\alpha\geq 0$ to be given by

The derivation of ${\mathbf{J}}(\alpha)$ is referred to Appendix E.1.⁸⁸8The Jacobian ${\mathbf{J}}(\alpha)$ is $(D\!+\!N)\!\times\!(D\!+\!N)$– dimensional, with ${\mathbf{J}}_{11}\!\in\!{\mathbb{R}}^{D\!\times\!D}$ and ${\mathbf{J}}_{22}(\alpha)\!\in\!{\mathbb{R}}^{N\!\times\!N}$. Following this, all matrices written in a block form, such as matrix ${\mathbf{U}}$ in (9), will inherit the same dimensional structure. Here, ${\mathbf{J}}_{21}$ is a zero matrix since ${\bm{\pi}}[{\mathbf{x}}]-{\mathbf{x}}$ is devoid of ${\bm{\theta}}$. While matrix ${\mathbf{J}}_{22}(\alpha)$ is exactly of the form in Doshi et al. (2023, Lemma 3.4) to characterize the SRRW performance, our analysis includes an additional matrix ${\mathbf{J}}_{12}(\alpha)$, which captures the effect of ${\mathbf{x}}(t)$ on ${\bm{\theta}}(t)$ in the ODE (7), which translates to the influence of our generalized SRRW empirical measure ${\mathbf{x}}_{n}$ on the SA iterates ${\bm{\theta}}_{n}$ in (4).

For notational simplicity, and without loss of generality, all our remaining results are stated while conditioning on the event that $\{{\bm{\theta}}_{n}\!\to\!{\bm{\theta}}^{*}\}$, for some ${\bm{\theta}}^{*}\!\in\!\Theta$. We also adopt the shorthand notation ${\mathbf{H}}$ to represent ${\mathbf{H}}({\bm{\theta}}^{*})$. Our main CLT result is as follows, with its proof deferred to Appendix E.

For $k\in\{1,3\}$, SA-SRRW in (4) is a two-timescale SA with controlled Markov noise. While a few works study the CLT of two-timescale SA with the stochastic input being a martingale-difference (i.i.d.) noise (Konda & Tsitsiklis, 2004; Mokkadem & Pelletier, 2006), a CLT result covering the case of controlled Markov noise (e.g., $k\in\{1,3\}$), a far more general setting than martingale-difference noise, is still an open problem. Thus, we here prove our CLT for $k\in\{1,3\}$ from scratch by a series of careful decompositions of the Markovian noise, ultimately into a martingale-difference term and several non-vanishing noise terms through repeated application of the Poisson equation (Benveniste et al., 2012; Fort, 2015). Although the form of the resulting asymptotic covariance looks similar to that for the martingale-difference case in (Konda & Tsitsiklis, 2004; Mokkadem & Pelletier, 2006) at first glance, they are not equivalent. Specifically, ${\mathbf{V}}^{(k)}_{{\bm{\theta}}}(\alpha)$ captures both the effect of SRRW hyper-parameter $\alpha$, as well as that of the underlying base Markov chain via eigenpairs $(\lambda_{i},{\mathbf{u}}_{i})$ of its transition probability matrix ${\mathbf{P}}$ in matrix ${\mathbf{U}}$, whereas the latter only covers the martingale-difference noise terms as a special case.

When $k=2$, that is, $\beta_{n}=\gamma_{n}$, algorithm (4) can be regarded as a single-timescale SA algorithm. In this case, we utilize the CLT in Fort (2015, Theorem 2.1) to obtain the implicit form of ${\mathbf{V}}^{(2)}(\alpha)$ as shown in Theorem 3.3. However, ${\mathbf{J}}_{12}(\alpha)$ being non-zero for $\alpha>0$ restricts us from obtaining an explicit form for the covariance term corresponding to SA iterate errors ${\bm{\theta}}_{n}-{\bm{\theta}}^{*}$. On the other hand, for $k\in\{1,3\}$, the nature of two-timescale structure causes ${\bm{\theta}}_{n}$ and ${\mathbf{x}}_{n}$ to become asymptotically independent with zero correlation terms inside ${\mathbf{V}}^{(k)}(\alpha)$ in (10), and we can explicitly deduce ${\mathbf{V}}^{(k)}_{{\bm{\theta}}}(\alpha)$. We now take a deeper dive into $\alpha$ and study its effect on ${\mathbf{V}}^{(k)}_{{\bm{\theta}}}(\alpha)$.

Covariance Ordering of SA-SRRW: We refer the reader to Appendix F for proofs of all remaining results. We begin by focusing on case (i) and capturing the impact of $\alpha$ on ${\mathbf{V}}_{{\bm{\theta}}}^{(1)}(\alpha)$.

We show that case (i) is asymptotically better than case (iii) for $\alpha>0$. In view of Proposition 3.4 and Corollary 3.5, the advantages of case (i) become prominent.

In this section, we simulate our SA-SRRW algorithm on the wikiVote graph (Leskovec & Krevl, 2014), comprising $889$ nodes and $2914$ edges. We configure the SRRW’s base Markov chain ${\mathbf{P}}$ as the MHRW with a uniform target distribution ${\bm{\mu}}=\frac{1}{N}{\bm{1}}$. For distributed optimization, we consider the following $L_{2}$ regularized binary classification problem:

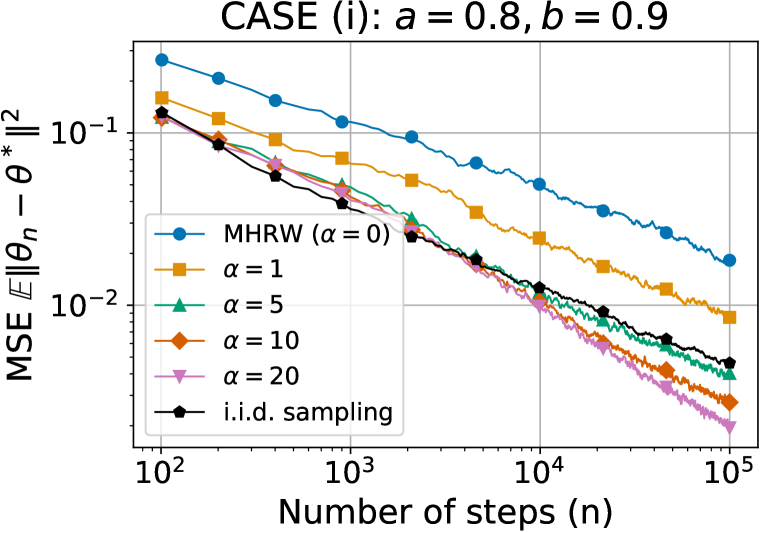
where $\{({\mathbf{s}}_{i},y_{i})\}_{i=1}^{N}$ is the ijcnn1 dataset (with $22$ features, i.e., ${\mathbf{s}}_{i}\in{\mathbb{R}}^{22}$) from LIBSVM (Chang & Lin, 2011), and penalty parameter $\kappa=1$. Each node in the wikiVote graph is assigned one data point, thus $889$ data points in total. We perform SRRW driven SGD (SGD-SRRW) and SRRW driven stochastic heavy ball (SHB-SRRW) algorithms (see (13) in Appendix A for its algorithm). We fix the step size $\beta_{n}\!=\!(n+1)^{-0.9}$ for the SA iterates and adjust $\gamma_{n}\!=\!(n+1)^{\!-a}$ in the SRRW iterates to cover all three cases discussed in this paper: (i) $a\!=\!0.8$; (ii) $a\!=\!0.9$; (iii) $a\!=\!1$. We use mean square error (MSE), i.e., $\mathbb{E}[\|{\bm{\theta}}_{n}\!-\!{\bm{\theta}}^{*}\|^{2}]$, to measure the error on the SA iterates.

Our results are presented in Figures 2 and 3, where each experiment is repeated $100$ times. Figures 2(a) and 2(b), based on wikiVote graph, highlight the consistent performance ordering across different $\alpha$ values for both algorithms over almost all time (not just asymptotically). Notably, curves for $\alpha\geq 5$ outperform that of the i.i.d. sampling (in black) even under the graph constraints. Figure 2(c) on the smaller Dolphins graph (Rossi & Ahmed, 2015) - $62$ nodes and $159$ edges - illustrates that the points of ($\alpha$, MSE) pair arising from SGD-SRRW at time $n=10^{7}$ align with a curve in the form of $g(x)\!=\!\frac{c_{1}}{(x+c_{2})^{2}}\!+\!c_{3}$ to showcase $O(1/\alpha^{2})$ rates. This smaller graph allows for longer simulations to observe the asymptotic behaviour. Additionally, among the three cases examined at identical $\alpha$ values, Figures 3(a) - 3(c) confirm that case (i) performs consistently better than the rest, underscoring its superiority in practice. Further results, including those from non-convex functions and additional datasets, are deferred to Appendix H due to space constraints.

In this paper, we show both theoretically and empirically that the SRRW as a drop-in replacement for Markov chains can provide significant performance improvements when used for token algorithms, where the acceleration comes purely from the careful analysis of the stochastic input of the algorithm, without changing the optimization iteration itself. Our paper is an instance where the asymptotic analysis approach allows the design of better algorithms despite the usage of unconventional noise sequences such as nonlinear Markov chains like the SRRW, for which traditional finite-time analytical approaches fall short, thus advocating their wider adoption.