Accelerated Stochastic ExtraGradient: Mixing Hessian and Gradient Similarity to Reduce Communication in Distributed and Federated Learning
Abstract
Modern realities and trends in learning require more and more generalization ability of models, which leads to an increase in both models and training sample size. It is already difficult to solve such tasks in a single device mode. This is the reason why distributed and federated learning approaches are becoming more popular every day. Distributed computing involves communication between devices, which requires solving two key problems: efficiency and privacy. One of the most well-known approaches to combat communication costs is to exploit the similarity of local data. Both Hessian similarity and homogeneous gradients have been studied in the literature, but separately. In this paper, we combine both of these assumptions in analyzing a new method that incorporates the ideas of using data similarity and clients sampling. Moreover, to address privacy concerns, we apply the technique of additional noise and analyze its impact on the convergence of the proposed method. The theory is confirmed by training on real datasets.
1 Introduction
Empirical risk minimization is a key concept in supervised machine learning (Shalev-Shwartz et al.,, 2010). This paradigm is used to train a wide range of models, such as linear and logistic regression (Tripepi et al.,, 2008), support vector machines (Moguerza and Muñoz,, 2006), tree-based models (Hehn et al.,, 2020), neural networks (Sannakki and Kulkarni,, 2016), and many more. In essence, this is an optimization of the parameters based on the average losses in data. By minimizing the empirical risk, the model aims to generalize well to unseen samples and make accurate predictions. In order to enhance the overall predictive performance and effectively tackle advanced tasks, it is imperative to train on large datasets. By leveraging such ones during the training process, we aim to maximize the generalization capabilities of models and equip them with the robustness and adaptability required to excel in challenging real-world scenarios (Feng et al.,, 2014). The richness and variety of samples in large datasets provides the depth needed to learn complex patterns, relationships, and nuances, enabling them to make accurate and reliable predictions across a wide range of inputs and conditions. As datasets grow in size and complexity, traditional optimization algorithms may struggle to converge in a reasonable amount of time. This increases the interest in developing distributed methods (Verbraeken et al.,, 2020). Formally, the objective function in the minimization problem is a finite sum over nodes, each one containing its own possibly private dataset. In the most general form, we have:
| (1) |
where refers to number of nodes/clients/machines/devices, is the size of the -th local dataset, is the vector representation of a model using features, is the -th data point on the -th node and is the loss function. We consider the most computationally powerful device that can communicate with all others to be a server. Without loss of generality, we assume that is responsible for the server, and the rest for other nodes.
This formulation of the problem entails a number of challenges. In particular, transferring information between devices incurs communication overhead (Sreenivasan et al.,, 2006). This can result in increased resource utilization, which affects the overall efficiency of the training process. There are different ways to deal with communication costs (McMahan et al.,, 2017; Koloskova et al.,, 2020; Alistarh et al.,, 2017; Beznosikov et al.,, 2023). One of the key approaches is the exploiting the similarity of local data and hence the corresponding losses. One way to formally express it is to use Hessian similarity (Tian et al.,, 2022):
| (2) |
where measures the degree of similarity between the corresponding Hessian matrices. The goal is to build methods with communication complexity depends on because it is known that for non-quadratic losses and for quadratic ones (Hendrikx et al.,, 2020). Here is the size of the training set. Hence, the more data on nodes, the more statistically "similar" the losses are and the less communication is needed. The basic method in this case is Mirror Descent with the appropriate Bregman divergence (Shamir et al., 2014a, ; Hendrikx et al.,, 2020):
The computation of requires communication with clients. Our goal is to reduce it. The key idea is that by offloading nodes, we move the most computationally demanding work to the server. Each node performs one computation per iteration (to collect on the server), while server solves the local subproblem and accesses the local oracle much more frequently. While this approach provides improvements in communication complexity over simple distributed version of Gradient Descent, there is room for improvement in various aspects. In particular, the problem of constructing an optimal algorithm has been open for a long time (Shamir et al., 2014b, ; Arjevani and Shamir,, 2015; Yuan and Li,, 2020; Sun et al., 2022a, ). This has recently been solved by the introduction of Accelerated ExtraGradient (Kovalev et al.,, 2022).
Despite the fact that there is an optimal algorithm for communication, there are still open challenges: since each dataset is stored on its own node, it is expensive to compute the full gradient. Moreover, by transmitting it, we lose the ability to keep procedure private (Weeraddana and Fischione,, 2017), since in this case it is possible to recover local data. One of the best known cheap ways to protect privacy is to add noise to communicated information (Abadi et al.,, 2016). To summarize the above, in this paper, we are interested in stochastic modifications of Accelerated ExtraGradient (Kovalev et al.,, 2022), which would be particularly resistant to the imposition of noise on the transmitted packages.
2 Related Works
Since our goal is to investigate stochastic versions of algorithms that exploit data similarity (in particular, to speed up the computation of local gradients and to protect privacy), we give a brief literature review of related areas.
2.1 Distributed Methods under Similarity
In the scalable DANE algorithm was introduced (Shamir et al., 2014b, ). It was a novel Newton-type method that used communication rounds for -strongly convex quadratic losses by taking a step appropriate to the geometry of the problem. This work can be considered as the first that started to apply the Hessian similarity in the distributed setting. A year later was found to be the lower bound for communication rounds under the Hessian similarity (Arjevani and Shamir,, 2015). Since then, extensive work has been done to achieve the outlined optimal complexity. The idea of DANE was developed by adding momentum acceleration to the step, thereby reducing the complexity for quadratic loss to (Yuan and Li,, 2020). Later, Accelerated SONATA achieved for non-quadratic losses by the Catalyst acceleration (Tian et al.,, 2022). Finally, there is Accelerated ExtraGradient, which achieves communication complexity using ideas of the Nesterov’s acceleration, sliding and ExtraGradient (Kovalev et al.,, 2022).
Other ways to introduce the definition of similarity are also found in the literature. In (Khaled et al.,, 2020), the authors study the local technique in the distributed and federated optimization and is taken as measure of gradient similarity. Here is the solution to the problem (1). This kind of data heterogeneity is also examine in (Woodworth et al.,, 2020). The case of gradient similarity of the form is discussed in (Gorbunov et al.,, 2021). Moreover, several papers use gradient similarity in the analysis of distributed saddle point problems (Barazandeh et al.,, 2021; Beznosikov et al.,, 2021; Beznosikov and Gasnikov,, 2022; Beznosikov et al.,, 2022).
2.2 Privacy Preserving
A brief overview of the issue of privacy in modern optimization is given in (Gade and Vaidya,, 2018). In this paper, we are interested in differential privacy. In essence, differential privacy guarantees that results of a data analysis process remain largely unaffected by the addition or removal of any single individual’s data. This is achieved by introducing randomness or noise into the data in a controlled manner, such that the statistical properties of the data remain intact while protecting the privacy of individual samples (Aitsam,, 2022). Differential privacy involves randomized perturbations to the information being sent between nodes and server (Nozari et al.,, 2016). In this case, it is important to design an algorithm that is resistant to transformations.
2.3 Stochastic Optimization
The simplest stochastic methods, e.g. SGD, face a common problem: the approximation of the gradient does not tend to zero when searching for the optimum (Gorbunov et al.,, 2020). The solution to this issue appeared in 2014 with invention of variance reduction technique. There are two main approaches to its implementation: SAGA (Defazio et al.,, 2014) and SVRG (Johnson and Zhang,, 2013). The first one maintains a gradient history and the second introduces a reference point at which the full gradient is computed, and updates it infrequently. The methods listed above do not use acceleration. In recent years, a number of accelerated variance reduction methods have emerged (Nguyen et al.,, 2017; Li et al.,, 2021; Kovalev et al.,, 2020; Allen-Zhu,, 2018).
The idea of stochastic methods with variance reduction carries over to distributed setup as well. In particular, stochasticity helps to break through lower bounds under the Hessian similarity condition. For example, methods that use variance reduction to implement client sampling are constructed. Catalyzed SVRP enjoys complexity in terms of the amount of server-node communication (Khaled and Jin,, 2022). This method combines stochastic proximal point evaluation, client sampling, variance reduction and acceleration via the Catalyst framework (Lin et al.,, 2015). However, it requires strong convexity of each . It is possible to move to weaker assumptions on local functions. There is AccSVRS that achieves communication complexity (Lin et al.,, 2024). In addition, variance reduction turns out to be useful to design methods with compression. There is Three Pillars Algorithm, which achieves for variational inequalities (Beznosikov et al.,, 2024).
The weakness of the accelerated variance reduction methods is that they require a small inversely proportional to step size (Beznosikov et al.,, 2024; Khaled and Jin,, 2022; Lin et al.,, 2024). Thus, one has to “pay” for the convergence to an arbitrary -solution by increasing the iteration complexity of the method. However, there is the already mentioned gain in terms of the number of server-node communications. Meanwhile, accelerated versions of the classic SGD do not have this flaw (Vaswani et al.,, 2020). In some regimes, the accuracy that can be achieved without the use of variance reduction may be sufficient, including for distributed problems under similarity conditions.
3 Our Contribution
New method. We propose a new method based on the deterministic Accelerated ExtraGradient (AEG) (Kovalev et al.,, 2022). Unlike AEG, we add the ability to sample computational nodes. This saves a significant amount of runtime. As mentioned above, sampling was already implemented in Three Pillars Algorithm (Beznosikov et al.,, 2024), Catalyzed SVRP (Khaled and Jin,, 2022) and AccSVRS (Lin et al.,, 2024). However, this was done using SVRG-like approaches. We rely instead on SGD, which does not require decreasing the step size as the number of computational nodes increases.
Privacy via noise. We consider stochasticity not only in the choice of nodes, but also in the additive noise in the transmission of information from client to server. This makes it much harder to steal private data in the case of an attack on the algorithm.
Theoretical analysis. We show that the Hessian similarity implies gradient one with an additional term. Therefore, it is possible to estimate the variance associated with sampling nodes more optimistically. Thus, in some cases ASEG converges quite accurately before getting "stuck" near the solution.
Analysis of subproblem. We consider different approaches to solving a subproblem that occurs on a server. Our analysis allows us to estimate the number of iterations required to ensure convergence of the method.
Experiments. We validate the constructed theory with numerical experiments on several real datasets.
4 Stochastic Version of Accelerated ExtraGradient
Algorithm 1 (ASEG) is the modification of AEG (Kovalev et al.,, 2022). In one iteration, server communicates with clients twice. In the first round, random machines are selected (Line 6). They perform a computation and send the gradient to the server (Line 15). Then the server solves the local subproblem at Line 16 and the solution is used to compute the stochastic (extra)gradient at the second round of communication (Line 17 and Line 26). This is followed by a gradient step with momentum at Line 27.
Let us briefly summarize the main differences with AEG. Line 16 of Algorithm 1 uses a gradient over the local nodes’ batches, rather than all of them, as is done in the baseline method. Moreover, the case where local gradients are noisy is supported. This is needed for privacy purposes. Similarly in Line 27. Note that we consider the most general case where different devices are involved in solving the subproblem and performing the gradient step.
ASEG requires of communication rounds (Line 15 and Line 26), where is the number of nodes involved in the iteration. Unlike our method, AEG does per iteration. AccSVRS does on average. Thus, in experiments, either the difference between the methods is invisible, or AEG loses. ASEG deals with a local gradient , which can have the structure:
where, for example, or . This is the previously mentioned additive noise overlay technique, popular in the federated learning.
5 Theoretical Analysis
Before we delve into analysis, let us introduce some definitions and assumptions to build the convergence theory.
In this paper, complexity is understood in the sense of number of server-node communications. This means that we consider how many times a server exchange vectors with clients. In this case, a single contact is counted as one communication.
We work with functions of a class widely used in the literature.
Definition 1.
We say that the function is -strongly convex on , if
If , we call a convex function.
Definition 2.
We say that the function is -smooth on , if
Definition 3.
We say that is -related to , if
We assume a strongly convex optimization problem (1) with possibly non-convex components.
Assumption 1.
is -strongly convex, is convex and -smooth.
This assumption does not require convexity of local functions. Indeed, -relatedness is a strong enough property to allow them to be non-convex. Within this paper we are interested in the case , since for large datasets in practice (Sun et al., 2022b, ).
Proposition 1.
Proof.
It is obvious that Definition 3 implies smoothness of :
Since is the optimum, . It is known that . We obtain
∎
Thus, from the similarity of the Hessians follows the similarity of the gradients with some correction. Let us introduce a more general assumption on the gradient similarity:
Assumption 2.
Assumption 2 is a generalization of Proposition 1, where the correction term is multiplied by some constant . Formally, it can take any non-negative value, but it is important to analyze only two cases corresponding to different degrees of similarity: and . Indeed, any non-negative values of give asymptotically the same complexity.
A stochastic oracle is available for the function at each node. We impose the standard assumption:
Assumption 3.
the stochastic oracle is unbiased and has bounded variance:
Remark 1.
Hessian similarity of and for is only used to construct Proposition 1 and is not needed anywhere else. The next proofs require only that the server expresses the average nature of the data, while the data on the nodes may be heterogeneous.
We want to obtain a criterion that guarantees convergence of Algorithm 1. The obvious idea is to try to get one for the new algorithm by analogy with how it was done in the non-stochastic case (Kovalev et al.,, 2022):
Lemma 1.
See the proof in Appendix A. We first deal with the case under the gradient similarity condition (), since it removes two additional constraints on the parameters and makes the analysis simpler.
The following theorem is obtained by rewriting the result of Lemma 1 with a finer tuning of the parameters. We take into account and find that .
Theorem 1.
The theorem asserts convergence only to some neighborhood of the solution. To guarantee convergence with arbitrary accuracy, a suitable parameter must be chosen. We propose a corollary of Theorem 1:
Corollary 1.
See the proof in Appendix C. Note that the linear part of the obtained estimate reproduces the convergence of AEG. However, for example, with , an iteration of ASEG costs communications instead of . Thus, our method requires significantly less communication to achieve the value determined by the sublinear term. Moreover, as mentioned earlier, in the Catalyzed SVRP and AccSVRS estimates, an additional multiplier arises due to the use of variance reduction. Comparing to , we notice the superiority of ASEG in terms of chosen approach to measure communication complexity.
Note that if the noise of the gradients sent to the server is weak () and the functions are absolutely similar in the gradient sense (), then ASEG has times less complexity in terms of number of communications.
In the case of a convex objective, it is not possible to implement the method under Assumption 2 with , since the arising correction terms cannot be eliminated. Under Assumption 2 with , we propose a modification of ASEG for convex objective. In this case, we need
to reach an arbitrary -solution. See Appendix D.
The case is more complex and requires more fine-tuned analysis.
See the proof in Appendix B.
Corollary 2.
See the proof in Appendix C. It can be seen from the proof that Assumption 2 with gives worse estimates. Nevertheless, optimal communication complexity can be achieved if we choose large enough , which equalizes two linear terms (at least ). It comes from equality
Thus, even on tasks with a poor ratio of to , if the number of available nodes is large enough, ASEG outperforms AEG, Catalyzed SVRP and AccSVRS.
6 Analysis of the Subprolem
In this section, we are focused on
| (7) |
defined in Line 16 of Algorithm 1. Note that the problem (7) is solved on the server and does not affect the communication complexity. Obviously:
Moreover:
Thus, subproblem is -smooth with and strongly convex.
Despite the fact that the problem (7) does not affect the number of communications, we would still like to spend less server time solving it. The obvious solution is to use stochastic approaches.
6.1 SGD Approach
The basic approach is to use SGD for the strongly convex smooth objective. In this case, the convergence rate of the subproblem by argument norm is given by the following theorem (Stich,, 2019):
Theorem 3.
Using smoothness of the subproblem, we observe:
Let us formulate
Corollary 3.
Our interest is to choose such step that it would be possible to avoid getting stuck in the neighborhood of a subproblem solution. According to (Stich,, 2019), we note the following.
Theorem 4.
In this way, we can achieve optimal convergence rate of SGD. However, we would like to enjoy linear convergence. The idea is to use variance reduction methods.
6.2 SVRG Approach
Another approach to solving the subproblem is to use variance reduction methods, for example, SVRG. Let us take as a starting point and look at the first epoch. It is known from (Gorbunov et al.,, 2019):
where is an epoch size. is the next point after the algorithm finishes current epoch. We can rewrite for -th epoch:
Then we write strong-convexity property:
Using -smoothness of , we obtain
Thus, for a suitable combination of epoch size and step, we expect to obtain linear convergence of the subproblem, which is consistent with the experimental results.
6.3 Loopless Approach
In this section, we filling in some gaps in subproblem analysis. Decision criterion for ASEG is (4). Let us assume that we obtained:
| (8) |
We use this to obtain a lower bound on . The important question is whether it is possible to take fewer steps so that the criterion necessary for the convergence of the whole algorithm is met. In other words, we want to check whether the loopless version of ASEG turns out to be better than the usual one, as in the case of SVRG and KATYUSHA (Kovalev et al.,, 2020).
We are interested in comparing deterministic and random choices of . Let be a random variable describing the number of steps. takes positive discrete values. Let be the number of steps for the subproblem of ASEG, defined deterministically and satisfying (4). Let us assume that
| (9) |
Then from (8) we know that
where is the point obtained through solver steps. Obviously, the reverse is also true. In other words, the condition (9) is the criterion for to solve the initial subproblem. At the same time, we want to minimize to take as few steps as possible.
Proposition 2.
.
Proof.
Let be the probability to choose . Then we have
Since , is a convex function. Using the Jensen’s inequality, we obtain
∎
Thus, in the worst case, if the expectation of is less than the deterministic number of iterations, the criterion cannot be met and there is no probabilistic method of choosing the number of iterations that is better than the deterministic one.
It is worth noting that the same can be said about a pair of SVRG and L-SVRG. It is obvious that SVRG could be reduced to L-SVRG if the number of iterations before updating the gradient is considered as a random variable. Thus, the epoch is from the geometric distribution and one can compare which algorithm gives a more accurate solution after performing the inner loop. For SVRG-rate we have (Gorbunov et al.,, 2020):
| (10) |
where is a step and - some constant. From the Proposition 2 and (10) we obtain:
Thus, in the worst case, loopless versions converges no faster than usual ones.
7 Numerical Experiments
To support theoretical analysis and insights, we solve both logistic regression problem:
and quadratic regression problem:
Here refers to parameters of the model, is the feature description and is the corresponding label. To avoid overfitting, we use -regularization. The penalty parameter is set to , where is a smoothness constant (2). We use SVRG and SARAH as the subtask solvers in Algorithm 1. In all tests, the original datasets are merged into batches . A function is created from part of the acquired ones:
Due to the Hessian similarity, we have the following expression for the smoothness constant
where
Then for the quadratic task we have
For the logistic regression, is estimated by enumerating 100 points in the neighborhood of the solution. In both cases, obtained value is multiplied by . Experiments are performed on three datasets: Mushrooms, W8A, A9A, (Chang and Lin,, 2011).
We investigate how the size of the batches affects the convergence of ASEG on tasks with different parameters. Figure 1 shows the dependence of untuned ASEG convergence on the batch size. In the first experiment the method on nodes solves the problem with and . According to Corollary 2 one should choose to obtain optimal complexity. That is, for any size of the batch, there is non-optimal rate. In the second experiment, the method on nodes solves the problem with , . In this case, ASEG has guaranteed optimal complexity for and converges to rather small values of the criterion.

We compare ASEG to AccSVRS (Figure 2 and Figure 3). 50 nodes are available for Mushrooms and 200 nodes are available for A9A. If the ratio between , , and yields the optimal complexity according to Corollary 2, then due to similarity there is an optimistic estimate on the batching noise provides a significant gain over AccSVRS. Otherwise, it is worth using full batching and obtaining a less appreciable gain.


In ASEG stability experiments (Figure 4, Figure 5, Figure 6, Figure 7) it is tested how white noise in each affects the convergence. It can be seen that increasing the randomness does not worsen the convergence. This can be explained by the fact that the convergence is mainly determined by accuracy of chosen solver.

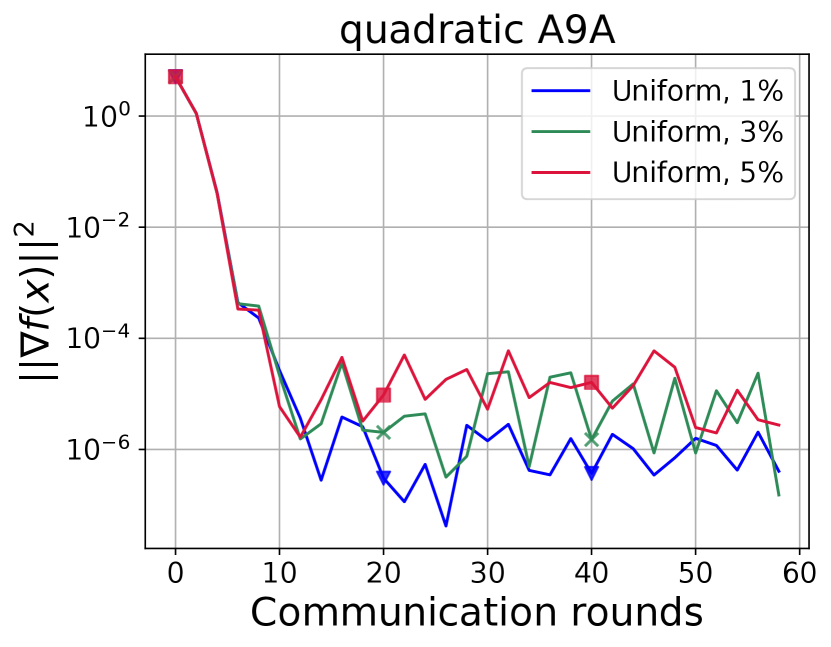










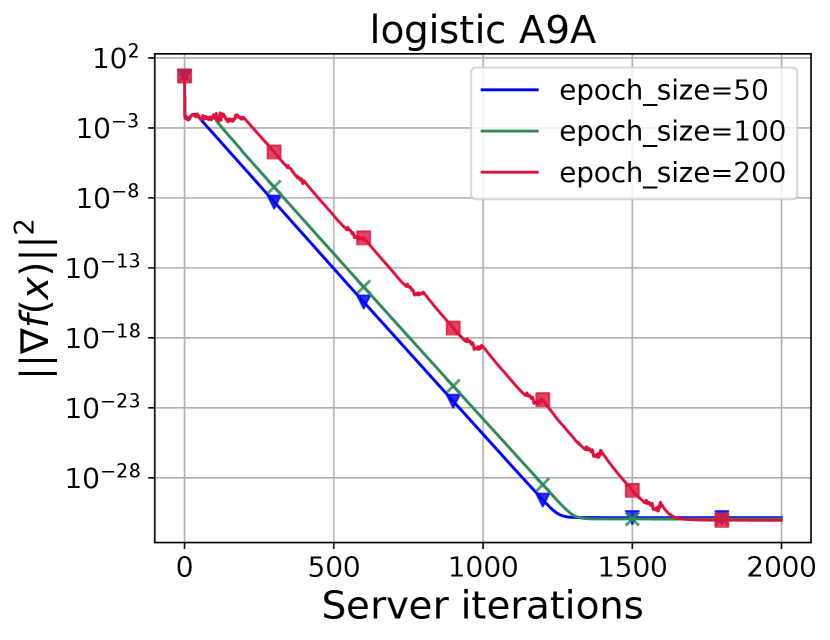
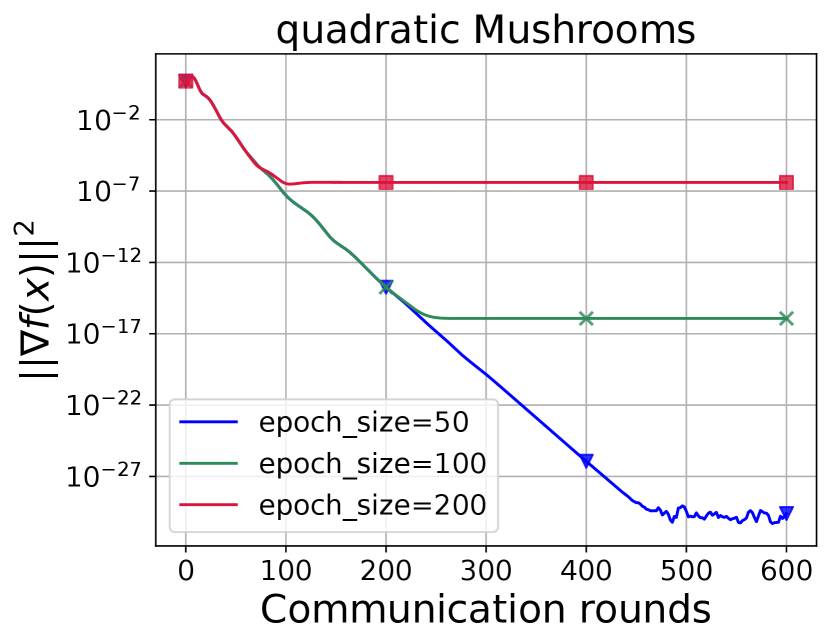
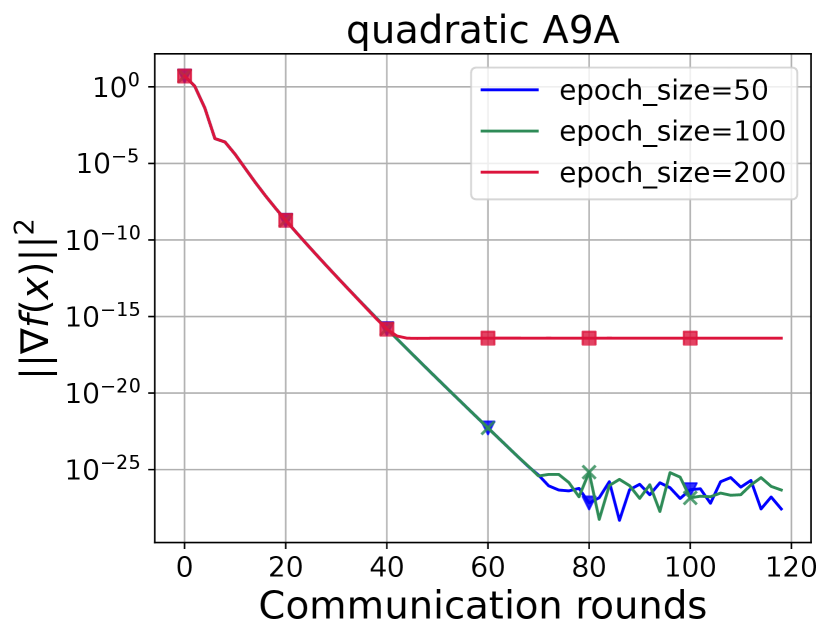
ASEG experiments test how changing the epoch size changes the ASEG and subproblem (Line 16 of Algorithm 1) convergence with SVRG and SARAH solvers (Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15).





















8 Conclusion
Based on the SGD-like approach, we have adapted Accelerated ExtraGradient to solve Federated Learning problems by adding two stochasticities: sampling of computational nodes and application of noise to local gradients. Numerical experiments show that for small values of or a sufficiently large number of available nodes, Algorithm 1 (ASEG) is significantly superior to accelerated variance reduction methods (Figure 3), which is consistent with the theory (Corollary 1). If the problem parameters are not "good" enough, there is a term in the communication complexity of batched ASEG (Corollary 2). Nevertheless, the superiority in the number of communications remains even in this case (Figure 2, Figure 3). Experiments also show the robustness of our method against noise (Figure 4, Figure 5, Figure 6, Figure 7). The server subproblem has also been studied numerically (Figure 10, Figure 11, Figure 14, Figure 15) and theoretically. The analysis shows the inefficiency of randomly choosing the number of solver iterations for the internal subtask (Proposition 2).
Acknowledgements
The work was done in the Laboratory of Federated Learning Problems of the ISP RAS (Supported by Grant App. No. 2 to Agreement No. 075-03-2024-214).
References
- Abadi et al., (2016) Abadi, M., Chu, A., Goodfellow, I., McMahan, H. B., Mironov, I., Talwar, K., and Zhang, L. (2016). Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC conference on computer and communications security, pages 308–318.
- Aitsam, (2022) Aitsam, M. (2022). Differential privacy made easy. In 2022 International Conference on Emerging Trends in Electrical, Control, and Telecommunication Engineering (ETECTE), pages 1–7. IEEE.
- Alistarh et al., (2017) Alistarh, D., Grubic, D., Li, J., Tomioka, R., and Vojnovic, M. (2017). Qsgd: Communication-efficient sgd via gradient quantization and encoding. Advances in neural information processing systems, 30.
- Allen-Zhu, (2018) Allen-Zhu, Z. (2018). Katyusha: The first direct acceleration of stochastic gradient methods. Journal of Machine Learning Research, 18(221):1–51.
- Arjevani and Shamir, (2015) Arjevani, Y. and Shamir, O. (2015). Communication complexity of distributed convex learning and optimization. Advances in neural information processing systems, 28.
- Barazandeh et al., (2021) Barazandeh, B., Huang, T., and Michailidis, G. (2021). A decentralized adaptive momentum method for solving a class of min-max optimization problems. Signal Processing, 189:108245.
- Beznosikov et al., (2022) Beznosikov, A., Dvurechenskii, P., Koloskova, A., Samokhin, V., Stich, S. U., and Gasnikov, A. (2022). Decentralized local stochastic extra-gradient for variational inequalities. Advances in Neural Information Processing Systems, 35:38116–38133.
- Beznosikov and Gasnikov, (2022) Beznosikov, A. and Gasnikov, A. (2022). Compression and data similarity: Combination of two techniques for communication-efficient solving of distributed variational inequalities. In International Conference on Optimization and Applications, pages 151–162. Springer.
- Beznosikov et al., (2023) Beznosikov, A., Horváth, S., Richtárik, P., and Safaryan, M. (2023). On biased compression for distributed learning. Journal of Machine Learning Research, 24(276):1–50.
- Beznosikov et al., (2021) Beznosikov, A., Scutari, G., Rogozin, A., and Gasnikov, A. (2021). Distributed saddle-point problems under data similarity. Advances in Neural Information Processing Systems, 34:8172–8184.
- Beznosikov et al., (2024) Beznosikov, A., Takác, M., and Gasnikov, A. (2024). Similarity, compression and local steps: three pillars of efficient communications for distributed variational inequalities. Advances in Neural Information Processing Systems, 36.
- Chang and Lin, (2011) Chang, C.-C. and Lin, C.-J. (2011). Libsvm: A library for support vector machines. ACM transactions on intelligent systems and technology (TIST), 2(3):1–27.
- Defazio et al., (2014) Defazio, A., Bach, F., and Lacoste-Julien, S. (2014). Saga: A fast incremental gradient method with support for non-strongly convex composite objectives. Advances in neural information processing systems, 27.
- Feng et al., (2014) Feng, J., Xu, H., and Mannor, S. (2014). Distributed robust learning. arXiv preprint arXiv:1409.5937.
- Gade and Vaidya, (2018) Gade, S. and Vaidya, N. (2018). Private optimization on networks. pages 1402–1409.
- Gorbunov et al., (2020) Gorbunov, E., Hanzely, F., and Richtárik, P. (2020). A unified theory of sgd: Variance reduction, sampling, quantization and coordinate descent. In International Conference on Artificial Intelligence and Statistics, pages 680–690. PMLR.
- Gorbunov et al., (2021) Gorbunov, E., Hanzely, F., and Richtárik, P. (2021). Local sgd: Unified theory and new efficient methods. In International Conference on Artificial Intelligence and Statistics, pages 3556–3564. PMLR.
- Gorbunov et al., (2019) Gorbunov, E., Hanzely, F., and Richtárik, P. (2019). A unified theory of sgd: Variance reduction, sampling, quantization and coordinate descent.
- Hehn et al., (2020) Hehn, T. M., Kooij, J. F., and Hamprecht, F. A. (2020). End-to-end learning of decision trees and forests. International Journal of Computer Vision, 128(4):997–1011.
- Hendrikx et al., (2020) Hendrikx, H., Xiao, L., Bubeck, S., Bach, F., and Massoulie, L. (2020). Statistically preconditioned accelerated gradient method for distributed optimization. In International conference on machine learning, pages 4203–4227. PMLR.
- Johnson and Zhang, (2013) Johnson, R. and Zhang, T. (2013). Accelerating stochastic gradient descent using predictive variance reduction. Advances in neural information processing systems, 26.
- Khaled and Jin, (2022) Khaled, A. and Jin, C. (2022). Faster federated optimization under second-order similarity. arXiv preprint arXiv:2209.02257.
- Khaled et al., (2020) Khaled, A., Mishchenko, K., and Richtárik, P. (2020). Tighter theory for local sgd on identical and heterogeneous data. In International Conference on Artificial Intelligence and Statistics, pages 4519–4529. PMLR.
- Koloskova et al., (2020) Koloskova, A., Loizou, N., Boreiri, S., Jaggi, M., and Stich, S. (2020). A unified theory of decentralized sgd with changing topology and local updates. In International Conference on Machine Learning, pages 5381–5393. PMLR.
- Kovalev et al., (2022) Kovalev, D., Beznosikov, A., Borodich, E., Gasnikov, A., and Scutari, G. (2022). Optimal gradient sliding and its application to optimal distributed optimization under similarity. Advances in Neural Information Processing Systems, 35:33494–33507.
- Kovalev et al., (2020) Kovalev, D., Horváth, S., and Richtárik, P. (2020). Don’t jump through hoops and remove those loops: Svrg and katyusha are better without the outer loop. In Algorithmic Learning Theory, pages 451–467. PMLR.
- Li et al., (2021) Li, Z., Bao, H., Zhang, X., and Richtárik, P. (2021). Page: A simple and optimal probabilistic gradient estimator for nonconvex optimization. In International conference on machine learning, pages 6286–6295. PMLR.
- Lin et al., (2024) Lin, D., Han, Y., Ye, H., and Zhang, Z. (2024). Stochastic distributed optimization under average second-order similarity: Algorithms and analysis. Advances in Neural Information Processing Systems, 36.
- Lin et al., (2015) Lin, H., Mairal, J., and Harchaoui, Z. (2015). A universal catalyst for first-order optimization. Advances in neural information processing systems, 28.
- McMahan et al., (2017) McMahan, B., Moore, E., Ramage, D., Hampson, S., and y Arcas, B. A. (2017). Communication-efficient learning of deep networks from decentralized data. In Artificial intelligence and statistics, pages 1273–1282. PMLR.
- Moguerza and Muñoz, (2006) Moguerza, J. M. and Muñoz, A. (2006). Support vector machines with applications.
- Nguyen et al., (2017) Nguyen, L. M., Liu, J., Scheinberg, K., and Takáč, M. (2017). Sarah: A novel method for machine learning problems using stochastic recursive gradient. In International conference on machine learning, pages 2613–2621. PMLR.
- Nozari et al., (2016) Nozari, E., Tallapragada, P., and Cortés, J. (2016). Differentially private distributed convex optimization via functional perturbation. IEEE Transactions on Control of Network Systems, 5(1):395–408.
- Sannakki and Kulkarni, (2016) Sannakki, S. and Kulkarni, A. (2016). A review paper on artificial neural network in cognitive science.
- Shalev-Shwartz et al., (2010) Shalev-Shwartz, S., Shamir, O., Srebro, N., and Sridharan, K. (2010). Learnability, stability and uniform convergence. The Journal of Machine Learning Research, 11:2635–2670.
- (36) Shamir, O., Srebro, N., and Zhang, T. (2014a). Communication-efficient distributed optimization using an approximate newton-type method. In International conference on machine learning, pages 1000–1008. PMLR.
- (37) Shamir, O., Srebro, N., and Zhang, T. (2014b). Communication-efficient distributed optimization using an approximate newton-type method. In International conference on machine learning, pages 1000–1008. PMLR.
- Sreenivasan et al., (2006) Sreenivasan, S., Cohen, R., López, E., Toroczkai, Z., and Stanley, H. E. (2006). Communication bottlenecks in scale-free networks. arXiv preprint cs/0604023.
- Stich, (2019) Stich, S. U. (2019). Unified optimal analysis of the (stochastic) gradient method. arXiv preprint arXiv:1907.04232.
- (40) Sun, Y., Scutari, G., and Daneshmand, A. (2022a). Distributed optimization based on gradient tracking revisited: Enhancing convergence rate via surrogation. SIAM Journal on Optimization, 32(2):354–385.
- (41) Sun, Y., Scutari, G., and Daneshmand, A. (2022b). Distributed optimization based on gradient tracking revisited: Enhancing convergence rate via surrogation. SIAM Journal on Optimization, 32(2):354–385.
- Tian et al., (2022) Tian, Y., Scutari, G., Cao, T., and Gasnikov, A. (2022). Acceleration in distributed optimization under similarity. In International Conference on Artificial Intelligence and Statistics, pages 5721–5756. PMLR.
- Tripepi et al., (2008) Tripepi, G., Jager, K., Dekker, F., and Zoccali, C. (2008). Linear and logistic regression analysis. Kidney international, 73(7):806–810.
- Vaswani et al., (2020) Vaswani, S., Laradji, I., Kunstner, F., Meng, S. Y., Schmidt, M., and Lacoste-Julien, S. (2020). Adaptive gradient methods converge faster with over-parameterization (but you should do a line-search). arXiv preprint arXiv:2006.06835.
- Verbraeken et al., (2020) Verbraeken, J., Wolting, M., Katzy, J., Kloppenburg, J., Verbelen, T., and Rellermeyer, J. S. (2020). A survey on distributed machine learning. Acm computing surveys (csur), 53(2):1–33.
- Weeraddana and Fischione, (2017) Weeraddana, P. and Fischione, C. (2017). On the privacy of optimization. IFAC-PapersOnLine, 50(1):9502–9508.
- Woodworth et al., (2020) Woodworth, B. E., Patel, K. K., and Srebro, N. (2020). Minibatch vs local sgd for heterogeneous distributed learning. Advances in Neural Information Processing Systems, 33:6281–6292.
- Yuan and Li, (2020) Yuan, X.-T. and Li, P. (2020). On convergence of distributed approximate newton methods: Globalization, sharper bounds and beyond. Journal of Machine Learning Research, 21(206):1–51.
In all the appendices, we consider and . Mathematical expectations are implied in the context of the proof.
Appendix A Lemma 1
Here we prove Lemma 1. First, we need the following:
Lemma 2.
Proof.
Using the -strong convexity of , we get
From the properties of the norm we can write
Thus,
The definition of and -Lipschitzness of give
Note that
and the Hessian similarity (Definition 3) implies
Thus,
With , we have
Here we used the fact that:
One can observe that is -strongly convex. Hence,
Now we are ready to construct the expression with the convergence criterion.
This completes the proof of Lemma 2. ∎
Let us move on to proof of Lemma 1:
Proof.
Using Line 27, we write
Here we use the properties of the norm to reveal the inner product. Line 5 of Algorithm 1 gives
Using (11) with and , we get
The last expression
can be neglected due to the condition (4). Consider expectation separately:
Here we added and subtracted under the norm. After rearranging the expressions, we obtain
The choice of defined by (3) gives
Note that
Here we need a technical lemma:
Lemma 4.
Let and . Then:
Proof.
Let us apply the Young’s inequality
Next, we look at the expression, given by the second term:
Let us use the tower property and take the expectation first. Since and are independent, we can enter the expectation into the multipliers of the second summand separately. Then only the first summand will remain, which is estimated based on Assumption 2. Using Assumption 2, we obtain
∎
Appendix B Theorem 2
Proof.
We consider possible values of one by one.
Consider . In this case, we have:
Consider :
Thus, we obtain:
Since , we obtain the required. ∎
Appendix C Corrolary 1, 2
Proof.
Earlier we obtained the recurrence formula:
Let us multiply both sides by weight and rewrite:
Denote and sum up with :
Let us rewrite:
To complete the proof we need to substitute and for Corollary 1 and and for Corollary 2 and look at different .
For Corollary 1 we obtain:
If where , then choose and get:
Otherwise, choose and get:
It remains to remember that method iteration requires communications.
For Corollary 2 we obtain:
If and where , then choose and get:
If and where , then choose and get:
If and where , then choose and get:
If and where , then choose and get:
As in the previous paragraph, the method iteration requires communications. ∎
Appendix D ASEG for the Convex Case
The next algorithm is the adaptation of Algorithm 1 for the convex case. We use time-varying and .
Theorem 6.
Proof.
Let us denote again. Here we apply Lemma 2 with and .
Let us substitute :
Multiply both sides by :
Let us rewrite the last inequality:
Define . Using we obtain:
Next, we apply previous inequality and assume :
∎
Similarly to the case, it is not possible to ensure convergence by a naive choice of . We propose a choice of that will ensure optimal convergence.
Corollary 4.
Proof.
Note that . Thus, using Theorem 6, we obtain:
Divide both sides by :
Let us notice that equalizes the terms of the right part. If , choose . Then we obtain:
Otherwise, choose and obtain:
∎