Ab-initio study of tuning the electronic and magnetic properties of Heusler alloy by Co and Mn compound doping
Abstract
We report the effects of Mn and Co doping on the electronic properties, magnetic exchange interaction, and Curie temperature of intermetallic by Green’s function based Korringa-Kohn-Rostoker method with coherent potential approximation(KKR-CPA). The effect of single and compound doping of Mn and Co at different crystallographic positions on these properties are evaluated by computing the electronic and magnetic structures of . The study revealed the possibility of tuning magnetic exchange interaction() and Curie temperature() upon doping. Moreover, it is noted that doping can stabilize the Jahn-Teller distortion. It is also worth noting that responds in a different way with concentration as well as the site of the dopant. This study helps in understanding and realizing the cause for magnetic properties in , and experimental peers can also use it for further research on doped .
1 Introduction
Energy is the necessary evil of the modern civilization. Reducing the production of greenhouse gas while keeping on with the ever-increasing energy demand is a great challenge to mankind. Renewable energy technologies are one of the most trusted and tested methods to limit greenhouse emissions and global warming. For caloric materials, which is one of the major parts of renewable energy, the efficiency depends on ordering temperature, e.g., Curie temperature() for magnetocaloric (MC) materials. Hence, to achieve the goal of 4/5th of the world’s electricity by 2050 [1] from renewable sources, it is extremely important to be able to tune the of the related materials [2].
Since the theoretical prediction of half-metallic properties in by Groot [3] and experimental observations by [4, 5, 6], Heusler alloys(HA’s) have drawn massive attention from the scientific community [7, 8, 9] ascribed to their wide usage in MC devices [10], magnetic shape memory alloys [11], spintronics [12], and giant magnetoresistance devices [13, 14, 15]. The full HA’s, with generic symbol stabilizes in the structure [16] with a completely ordered phase. The disordered structure has the ground state [17], while the complete disordered system has the [18]. Wyckoff positions of 4a(0, 0, 0), 4b(), and 8c() are occupied by , , and , respectively [11, 19, 20]. The ternary full HA, , exhibits both magnetic and structural phase transition [21]. In this context, Ni-Mn-Ga systems show properties like shape memory effect and magnetic field-induced strain, which is advantageous in actuators and sensors [11, 22]. They also show favorable MC (both conventional and inverse) properties, suitable to replace the century-old Joule-Thomson cooling [23, 24]. Ni-Mn-Ga system exhibits magneto structural phase transition with a huge change in isothermal magnetic entropy( J kg-1 K-1) but a relatively narrow range of working temperature in full-width half maximum() around 290 K for an applied field change of 5 T, typical to the materials with first-order phase transition(FOPT) [25]. However, the thermal hysteresis of FOPT and the Curie temperature is predominant to magnetic refrigeration.
The electronic structure and magnetic properties have been reported for Ni-doped [26] and Co-doped [27] systems, with the dopant at the position only. Off-stoichiometric and , where Q, and R are the dopant elements. For the past few decades, /Al has been under study to understand their martensite phase transition() and Curie temperature() [28, 29]. In , observed that the MC effect is the highest around concentration as magnetic and structural phase change occurs in this region [30]. Partially substituting Ni with Co is generally known to enhance the ferromagnetic coupling and hence the . This increases the possibility that the quaternary system undergoes a martensitic transition together with a meta-magnetic phase transition [31].
Generally, the structural and magnetic properties are highly impacted by the off-stoichiometric combination of the main group element() and transition metals( and ). The effect of replacing , mostly , = Ga, In, etc., is well studied [14, 32, 33]. Substituting the Mn element in the position can stabilize the cubic state of the system [14]. The MnZ atoms interact antiferromagnetically between the surrounding MnZ and normal MnY since the distance between MnY-MnZ is shorter than MnY-MnY and MnZ-MnZ [34]. Here, MnZ has been denoting the Mn atom in the Ga site(), and MnY is the Mn’s normal position(). The doping of the Co element in the position can increase the ferromagnetic interaction between the atoms and the Curie temperature of the material [31]. Additionally, even a small concentration of Co atoms in the position significantly impacts the Curie temperature. Also, the cell volume effect and valence electron concentration per atom ratio() affect inversely, i.e., as the ratio increases, the decreases and vice-versa [35, 36].
From the above discussion, investigation of the effect of doping both the and the sites with elements, resulting to a disordered , is interesting due to site preferences and their compound effect of electronic, magnetic, and thermodynamic properties. We have investigated the effect of Co and Mn in the and site and observed the effect in a restricted cubic phase. The cubic phase has minimum energy in the structure. Increasing the Co concentration above 10% retains the cubic state as the ground state in a structure [37]. At around , the cubic (austenite) phase collapses to the tetragonal (martensitic) phase[27]. We expected Mn doping in the Ga site and Co doping in the Ni site to enhance the material’s magnetic moment and Curie temperature. The concentration varies from a value greater than 10%, i.e., . Additionally, the concentration varies from since the ratio increases up to 8, comparatively for the pure system ( = 7.5). Therefore, the concentration is up to 0.5. This disorder system will be referred to as NiMnGa() hereafter, where is the concentration of Co in the Ni site and Mn in the Ga site, respectively, for brevity. For example, will be denoted as NiMnGa().
Notably, in this work, we have reported systematic studies of the variation of electronic structure, magnetic exchange interactions, and tuning the Curie temperature() of this disordered NiMnGa() system. We have especially looked into patterns of the effect of variation of site occupancy upon a specific substitution for a wide range of concentrations. The results are interpreted from the outcome of electronic structure calculations. This approach enables us to understand the microscopic origin of the macroscopic property(). The study of the substitution of a single element on is, as discussed above, very scattered. The investigation of double doping in is rare and far between. However, they offer exciting phenomena, not only from the perspective of fundamental understanding but also for materials engineering with target properties. For example, the tuning of is technologically relevant as it is one of the crucial factors that act as the working temperature range of many devices, namely, MC, spintronics, etc. [10, 12].
2 Methods
The appropriate method for handling off-stoichiometric compositions is Green’s function-based formalism with coherent potential approximation(CPA), as in the case of [38]. We have performed ab-initio calculations using multiple scattering Green’s function formalism as implemented in spin polarised relativistic Korringa-Kohn-Rostoker(SPRKKR) code [39, 40, 41]. The Perdew-Burke-Ernzerhof within generalized gradient approximation is used as the exchange-correlation functional [42]. First Brillouin zone integrations were performed with 2500 grids of -points, and energy convergence criteria were set as Ry in the calculation in the range. We have implemented full potential spin-polarized scalar relativistic implementation of SPRKKR with angular momentum cut-off as suitable for our system.
The lattice parameter with a minimum energy of NiMnGa() is calculated using the following procedure: (i) Obtain the lattice parameter from the materials project database [43]; (ii) Calculated the self-consistent field of the system, with varying lattice parameter ranging from 94% to 106%, with identical calculation for each lattice parameters. (iii) Fit the lattice parameter vs energy plot obtained in the last step using a 4th order polynomial. The parameter corresponding to the minima of the curve is the optimized lattice parameter. For NiMnGa(), we have taken the optimized lattice parameter of previous calculations that has a minimum change as the starting point and followed the steps above. We have shown the optimization curve of NiMnGa() in Figure (1(a)). Other minimization energy curves are not shown here for brevity. In the present study, doping concentrations are varied by changing the Wyckoff site occupancy of the corresponding element in the input structure. The resultant structure is used for further calculations.
The magnetic exchange energy() was calculated to understand the properties of magnetic interactions. The Heisenberg model is defined as,
| (1) |
where represent atoms in different sublattices, is a different lattice point, is the magnetic orientation of atom at sublattices. The is calculated by the energy difference due to an infinitesimal change of magnetic direction, as formulated by Lichtenstein [44].
Finally, the is estimated using mean field theory, yielding
| (2) |
where is the largest eigenvalue of the determinant, as described in [34]. It must be remembered that mean field calculations generally overestimate the .
3 Results
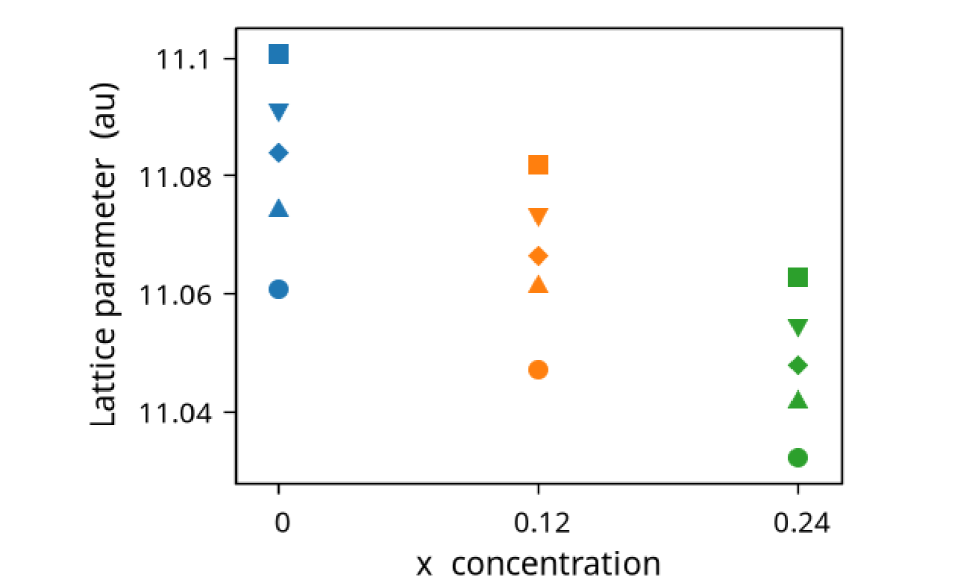
We have calculated the electronic and magnetic properties of NiMnGa() for () and (). The optimized lattice parameter of each sample was calculated using the method described in the sec. (2) and tabulated in Tables (1, 2, 3). Figure (1(d)) shows the variation of lattice parameters with and , which is mostly linear.
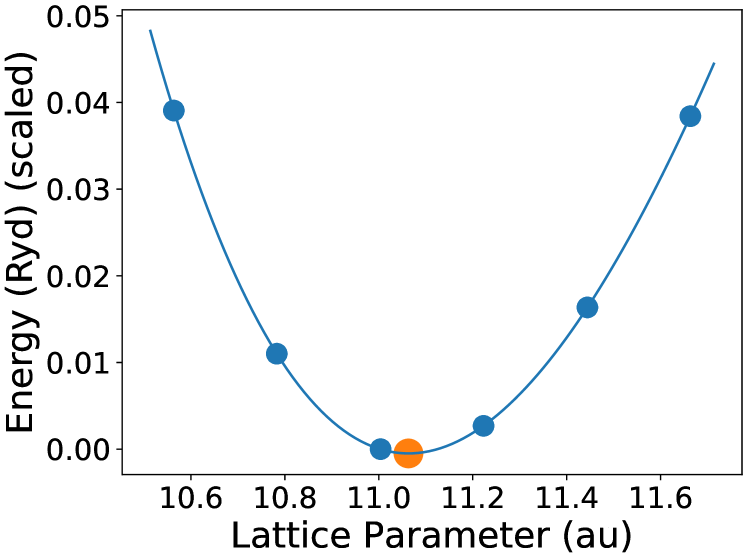
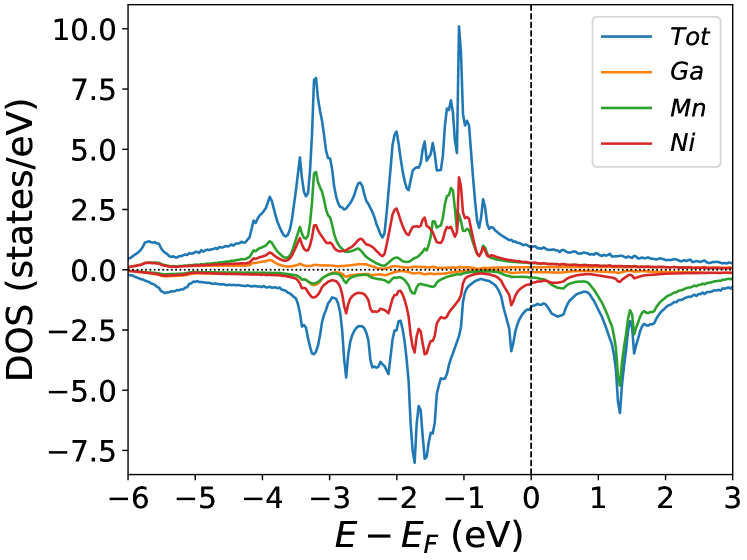
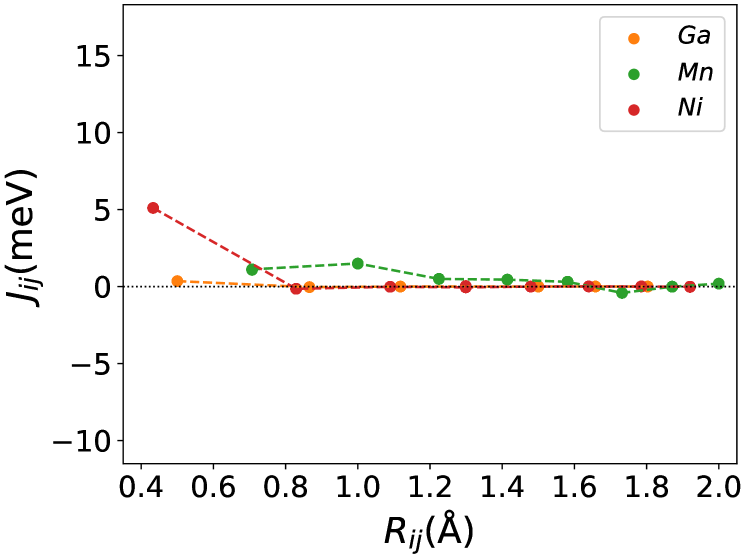
Figures (1(a)-1(c)) shows the calculations of the pure . Figure (1(a)) shows the lattice parameter optimization as described in section (2). Our calculated density of states(DOS) (Figure (1(b))) and magnetic exchange interactions() (Figure (1(c))) with the Mn atom at the center for matches the previous findings [45]. The is highest for Ni-Mn interactions, with the value 5 meV. All the interactions are predominantly ferromagnetic in this case. The complete table of optimized lattice parameters, the total and individual magnetic moment per atom, and Curie temperature of the pure system is tabulated in Table (1).
The change of lattice parameter with in the cubic domain is shown in Figure (1(d)). This trend shows that doping Co at the site decreases the lattice parameter but doping at the site increases the lattice parameter.
3.1 NiMnGa() systems
The NiMnGa() system, doping in Ni site only, though heavily studied within the austenite phase, we have included them for completeness. The doping of Co in the position will decrease the lattice parameter of the material shown in Figure (1(d)) and Table (1). The electronic and magnetic structures of NiMnGa() are shown in Figure (3) as representative of the series. Generally, the and site atoms contribute more to the net magnetic moment of the system. Here the Mn atom loses the moment due to the presence of an effective site(Ni with Co), and the Ni atom holds the magnetic moment up to the other elements present with the Ni atom. While replacing the Ni with Co in the site, the moment of Ni increases up to 14% for , as tabulated in Table (1). The Co atom has a much higher magnetic moment() than Ni(), and the is also much higher than . Increasing the Co concentration causes the magnetic moments of Co and Mn to start decreasing, and the magnetic moment of Ni starts increasing, thereby enhancing the total magnetic moment of the system.
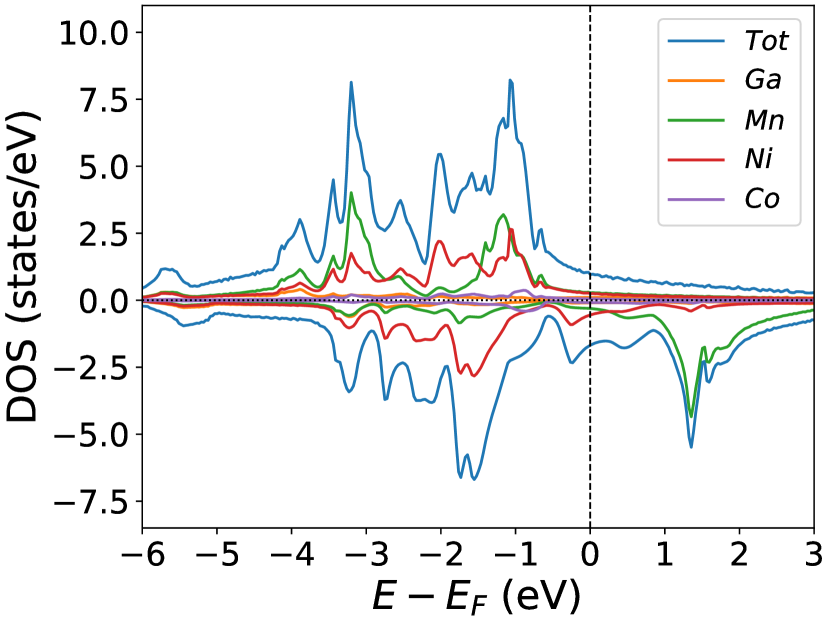
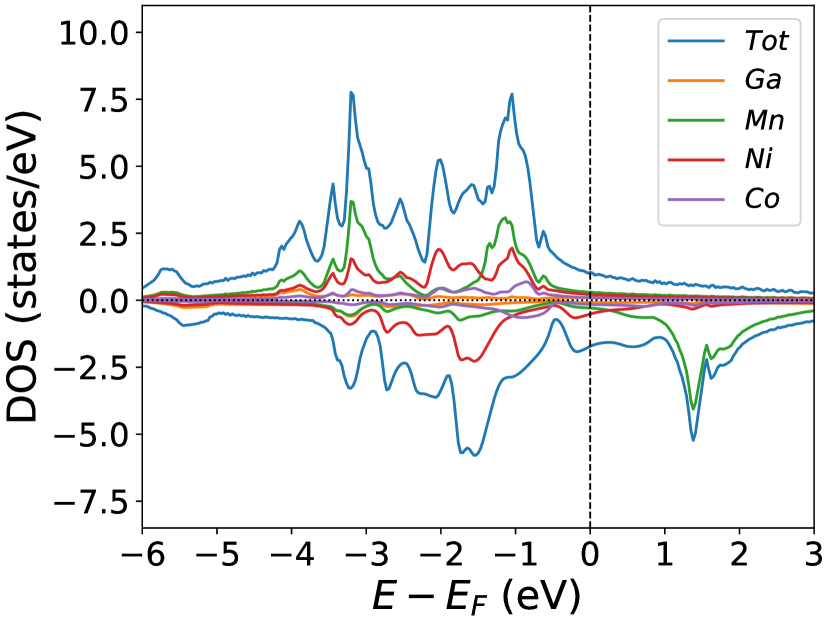
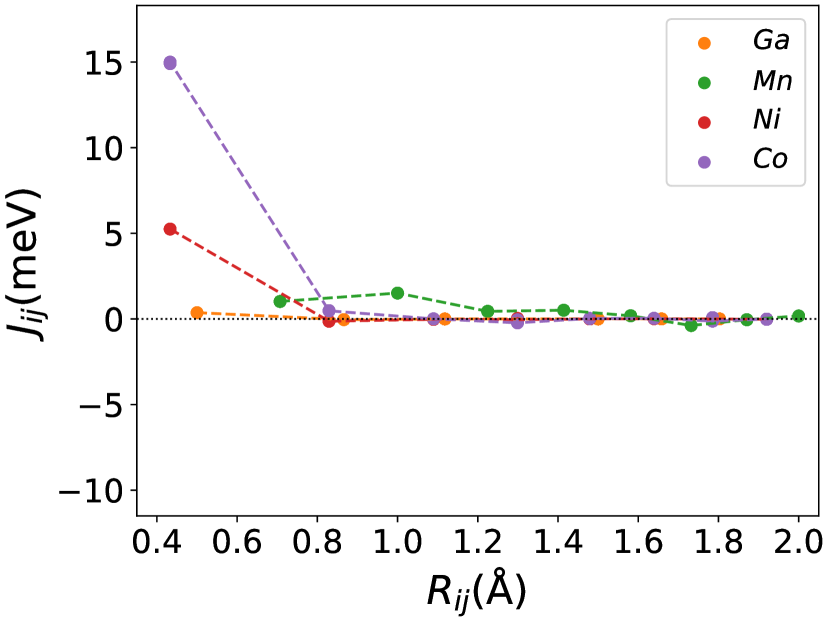
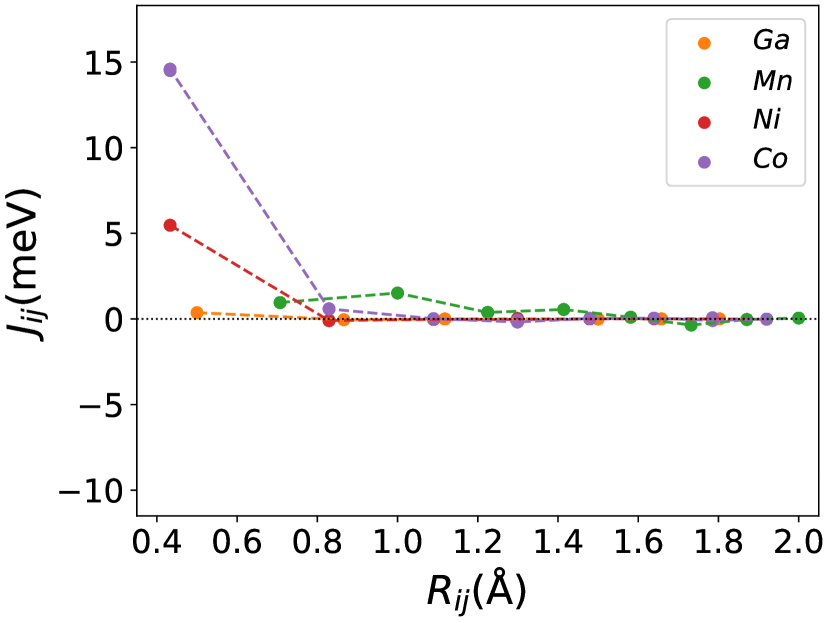
Of course, in the current case, MnZ =0.
The magnetic properties depend substantially on the exchange interactions between all pairs of chemical elements. In Figures (1(c)), (3b.1), (3b.2), the exchange interaction is shown for each atom in the configuration of , and . From these Figures, the interactions between all pairs(Ni-Mn, Co-Mn, Mn-Mn, and Ga-Mn) are ferromagnetic, and especially the Ni-Mn and Co-Mn are more ferromagnetic. The interaction between Ni/Co and Mn atoms in different sublattices is consistently ferromagnetic [46]. In this way, the replacement of Ni with Co in the site enhanced the exchange interaction energy in Co-Mn pair, then the ferromagnetic coupling also increased. These enhanced ferromagnetic coupling caused an increase in the Curie temperature of the material. The pair of exchange coupling of Ni-Mn, Co-Mn, and Mn-Mn are more in the austenite phase than in the martensite phase. This behavior results in the decrease of the martensite temperature with increasing the Co concentration [33].
When increasing the Co concentration at the Ni site(with ) leads to a decrease in the ratio and the lattice parameter(cell volume). This could be causing the to increase, as tabulated in the Table (1).
| Concentrations | Lattice | Magnetic Moment() | ||||||||
| Parameter (au) | Ni | Co | MnY | Ga | MnZ | Total | (K) | |||
| 0 | 0 | 11.061 | 0.29 | - | 3.56 | -0.08 | - | 4.08 | 393 | 7.50 |
| 0.12 | 0 | 11.047 | 0.31 | 1.07 | 3.50 | -0.08 | - | 4.21 | 1138 | 7.44 |
| 0.24 | 0 | 11.032 | 0.33 | 0.95 | 3.45 | -0.09 | - | 4.34 | 1148 | 7.38 |
3.2 NiMnGa() systems
The opposite system of the one discussed in the previous section (§3.1) is NiMnGa() system, where the site is fully ordered, but Ga is replaced by Mn, yielding system. The doping of Mn in the site, will increase the lattice parameter of the material(as shown in Figure (1(d))) and induce the magnetic atom’s moments as tabulated in Table (2). Notably, the moment of Ni increases up to 75% compared to the pure system, as discussed in the earlier section (§3). The MnY magnetic moment increases linearly with the constant magnetic moment of MnZ.
The electronic structure does not change much upon doping(Figure (5a.2)), even though the absence of Co in the Ni site increases the magnetic interactions of Ni-Mn by half(Figure (5b.4)) with respect to in the case of NiMnGa()(Figure (33b.2)). The most dominant interaction is MnY-MnZ interaction, which is antiferromagnetically coupled as shown in Figure (55b.4) for each concentration.
Increasing the doping concentration of Mn in the Ga site(with ), accordingly the ratio starts to increase since Mn has more valence electrons compared to Ga. Additionally, the lattice parameter starts increasing and which leads to an increase in cell volume, while an increase in the Mn in the Ga site. This could be causing the to start decreasing after an initial increase from the pure system. The values of the ratio, lattice parameter, and as tabulated in the Table (2).
| Concentrations | Lattice | Magnetic Moment() | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter (au) | Ni | Co | MnY | Ga | MnZ | Total | (K) | |||
| 0 | 0.15 | 11.074 | 0.35 | - | 3.57 | -0.08 | 3.65 | 4.76 | 741 | 7.65 |
| 0.26 | 11.084 | 0.40 | - | 3.58 | -0.08 | 3.65 | 5.27 | 691 | 7.76 | |
| 0.35 | 11.091 | 0.44 | - | 3.59 | -0.09 | 3.65 | 5.69 | 664 | 7.85 | |
| 0.50 | 11.101 | 0.51 | - | 3.60 | -0.10 | 3.65 | 6.39 | 623 | 8.00 | |
3.3 Complete disorder: NiMnGa() systems
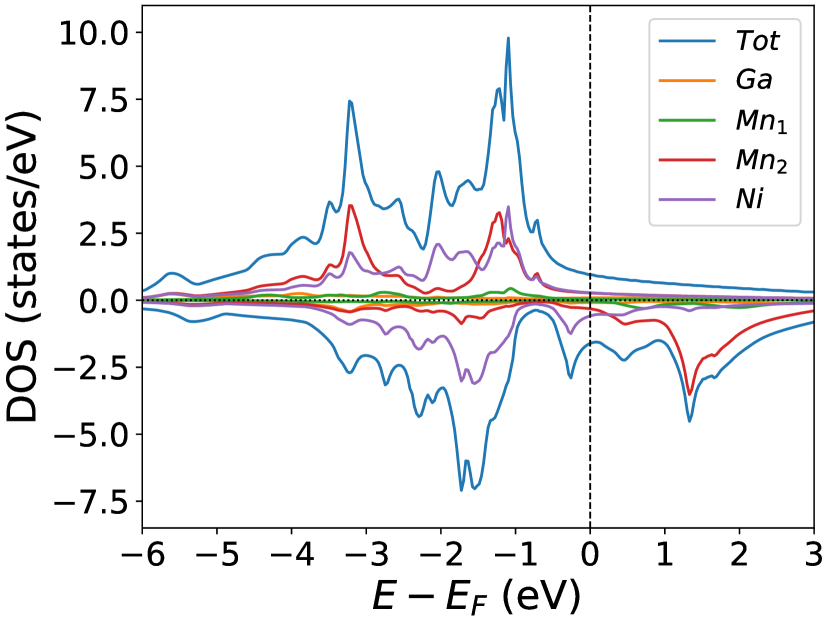
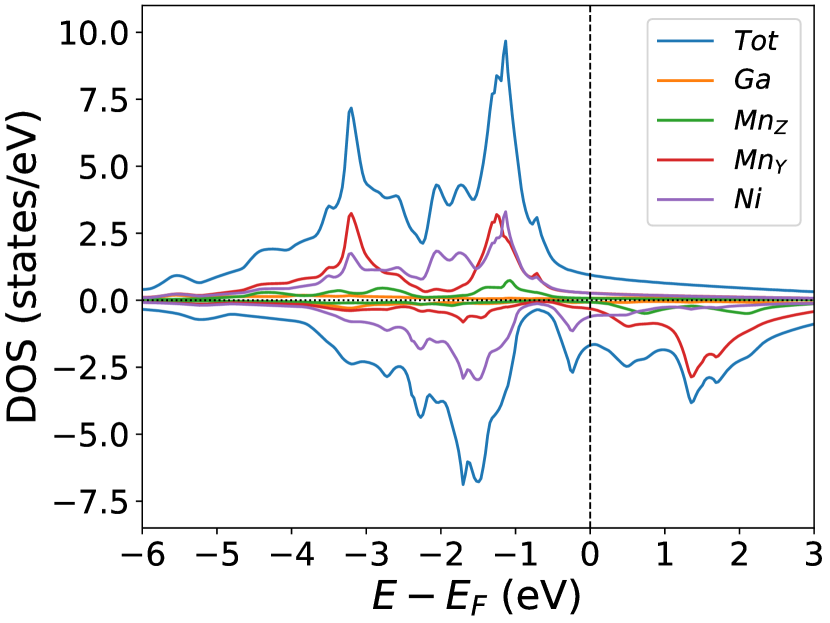
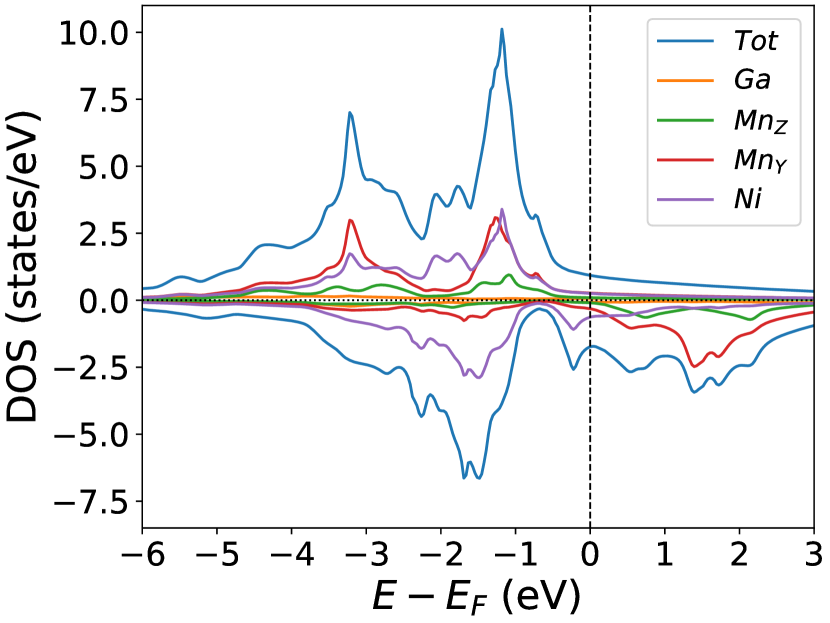
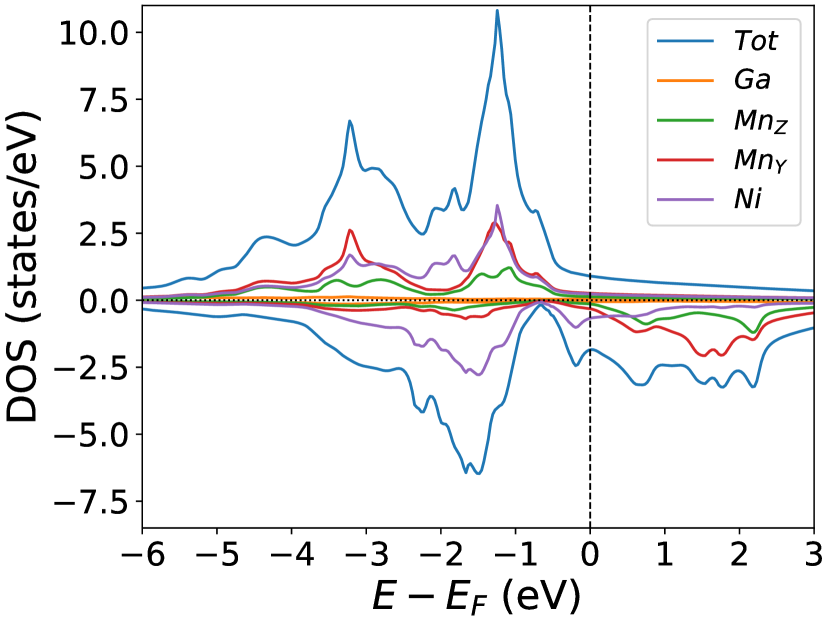
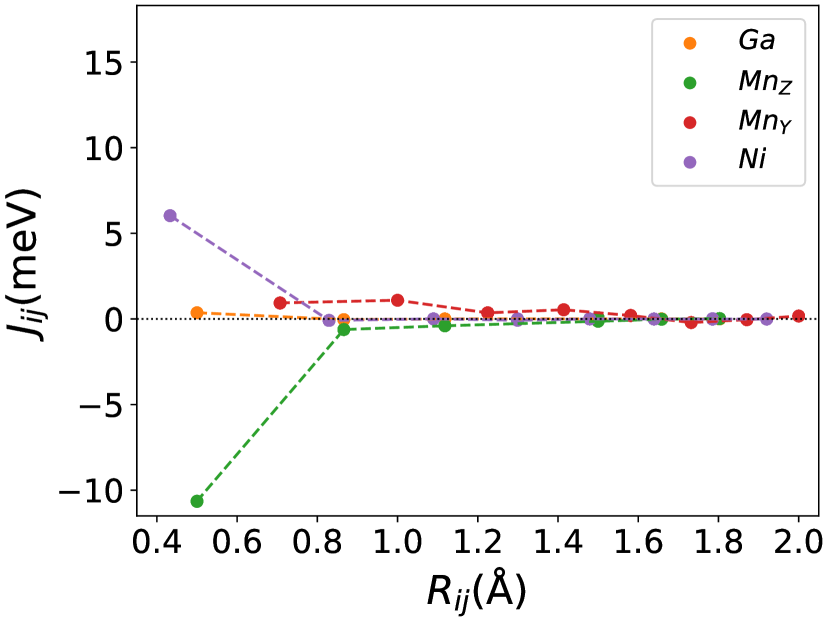
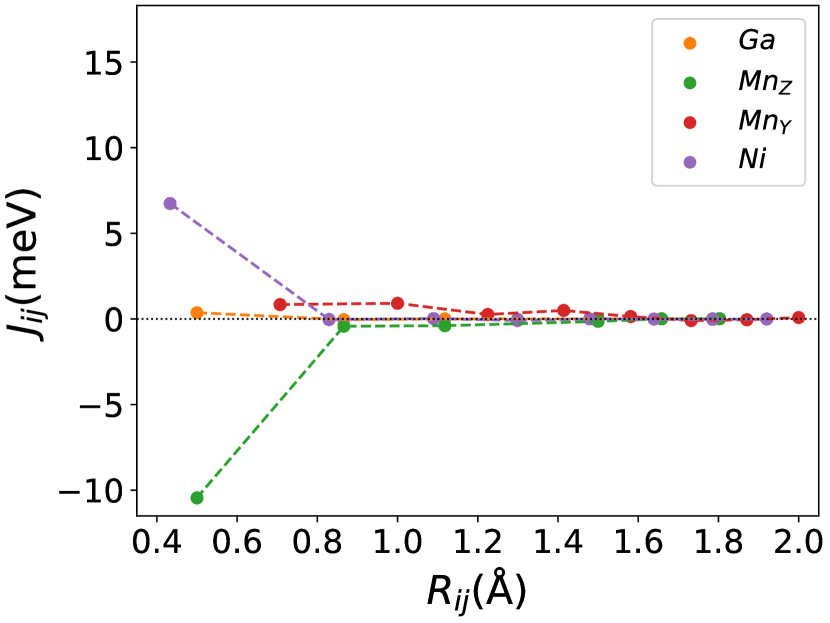
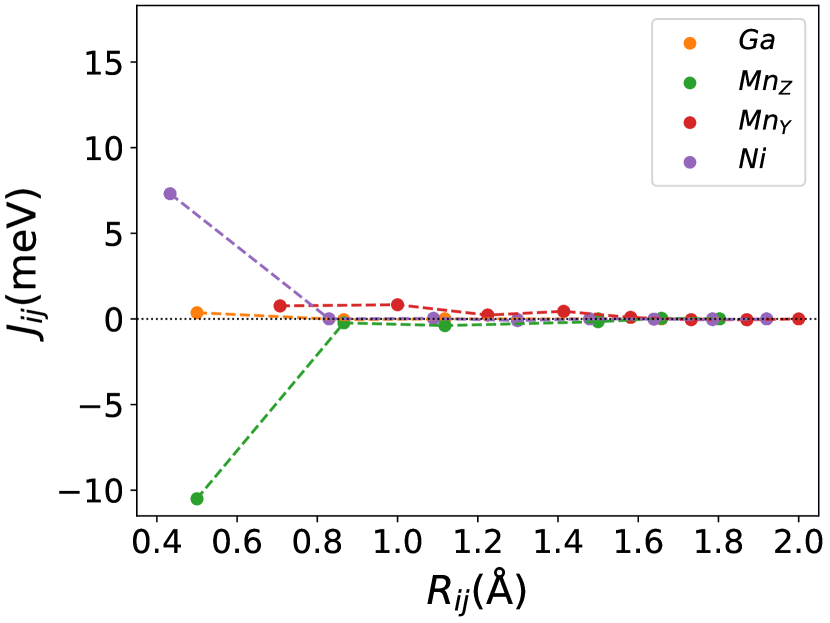
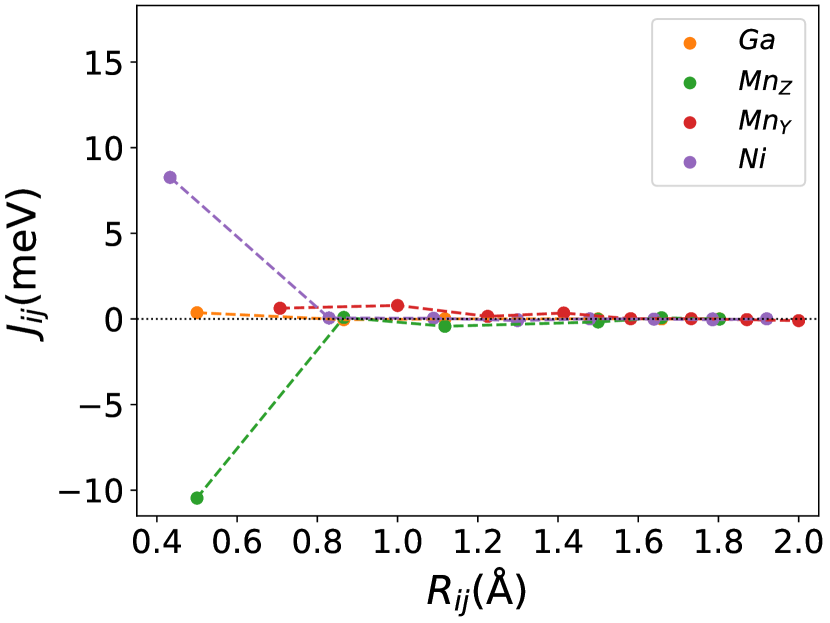
Finally, we study the systems with disorder both at the and sites, i.e., . Figure (6) and Figure (7) represents the electronic and magnetic structures of NiMnGa() for () and ().
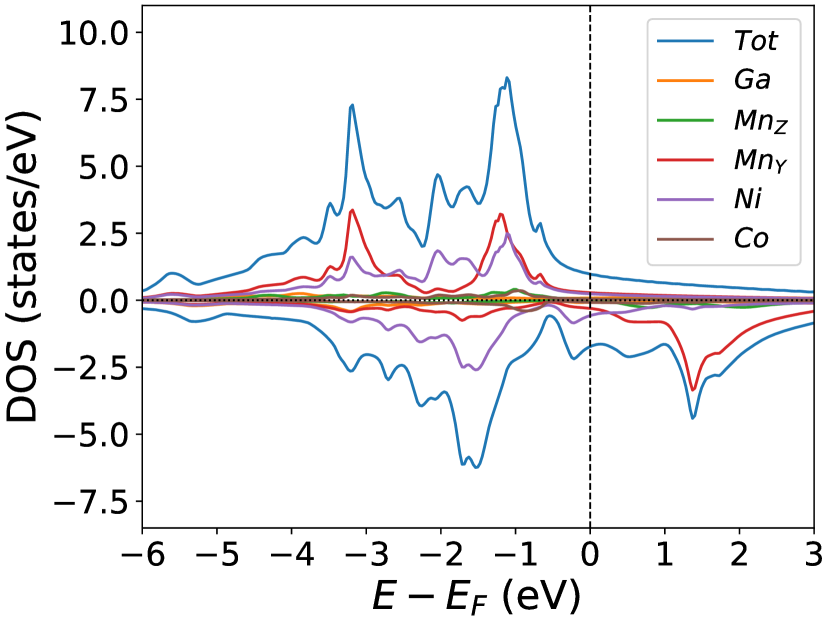
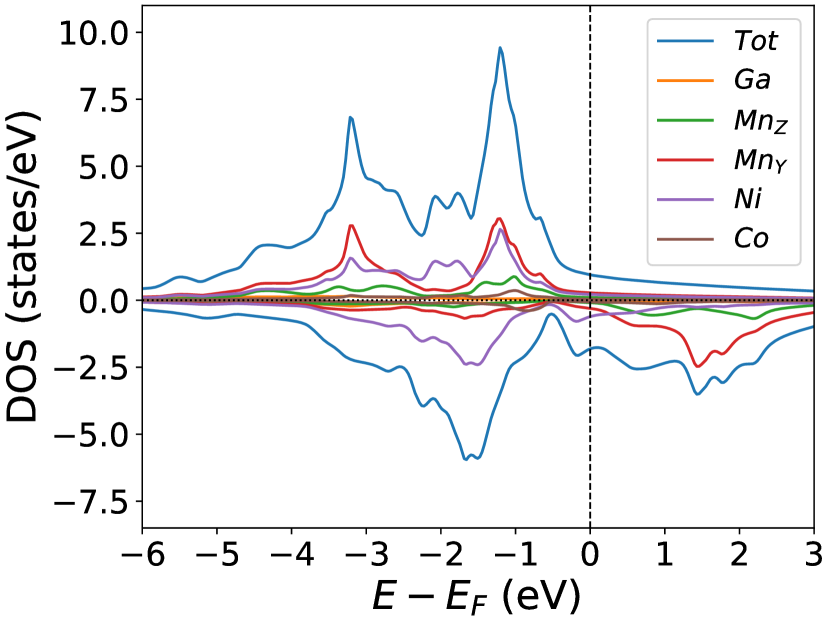
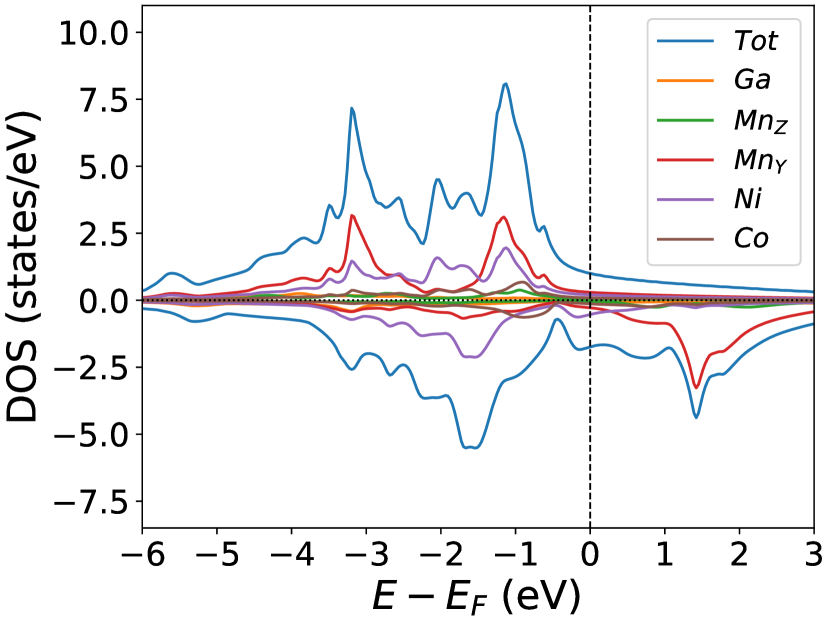
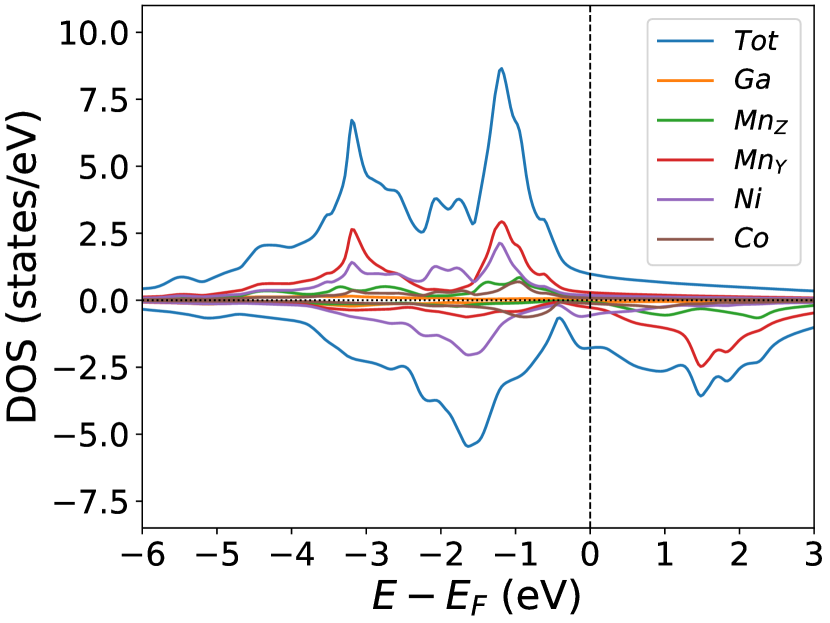
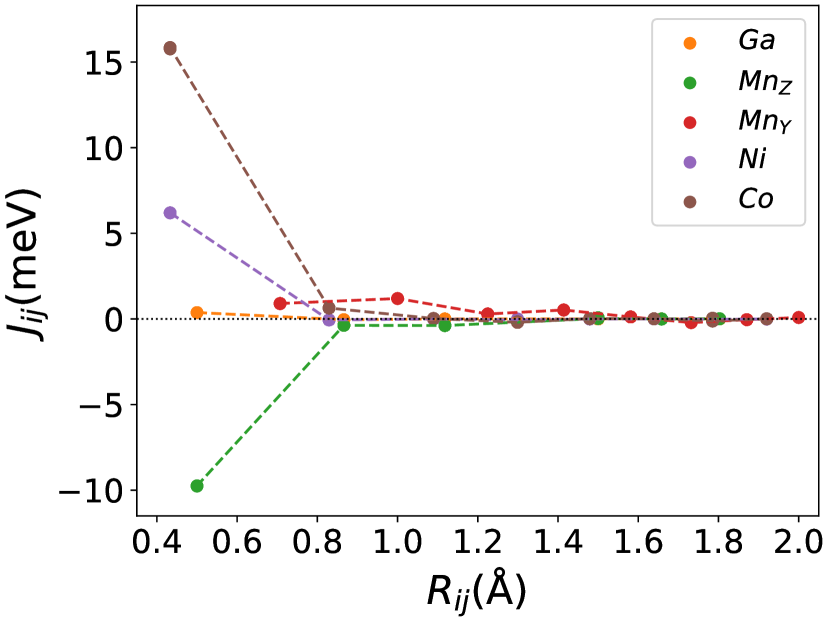
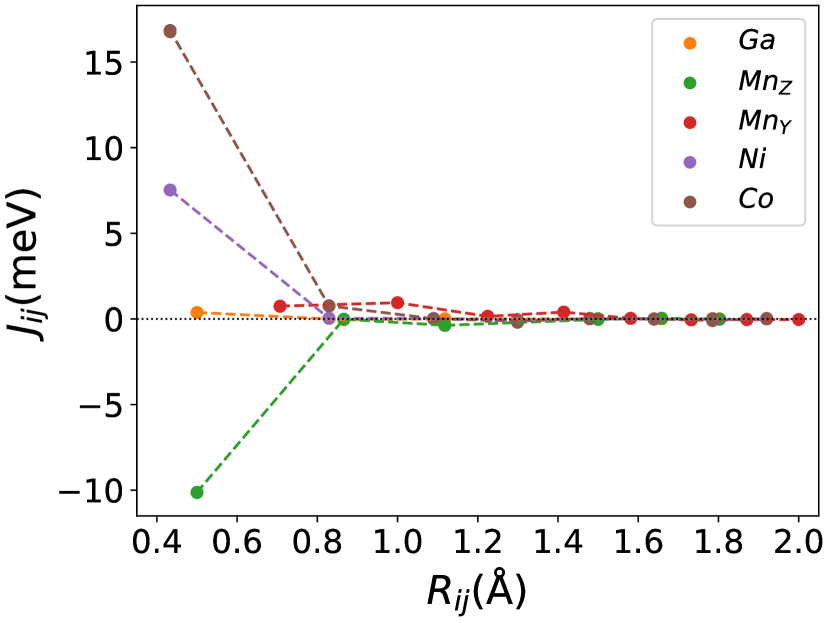
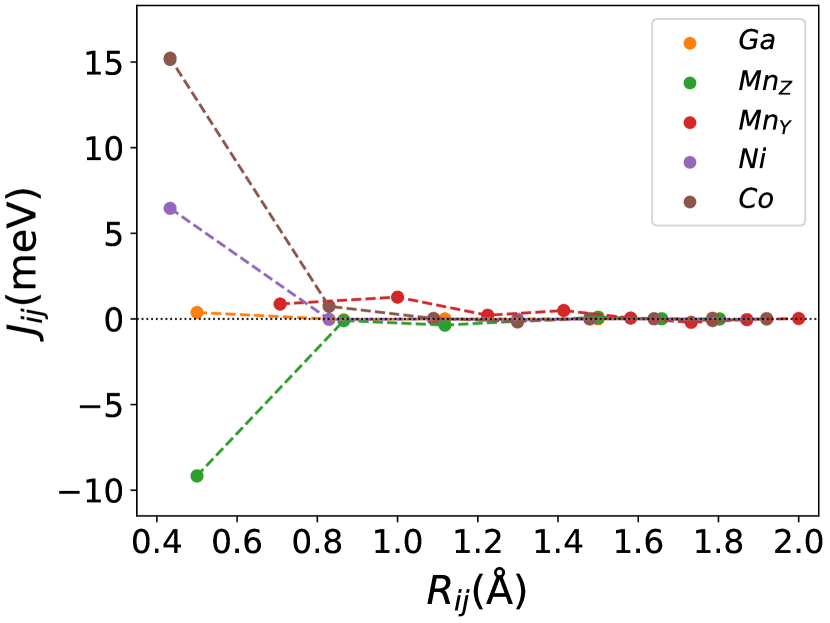
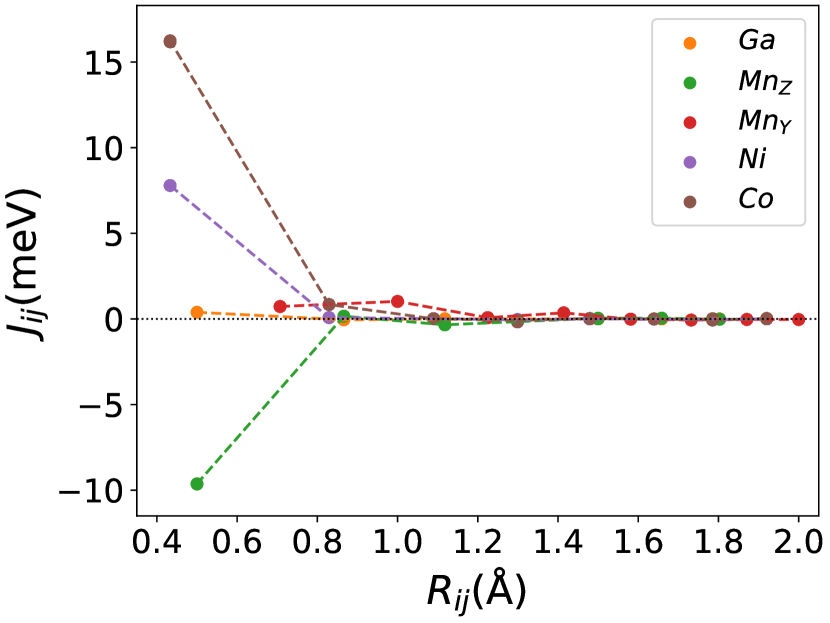
The variation of magnetic moments of NiMnGa() are tabulated in Table (3). This doping trend shows the presence of Co at the Ni site( position) and Mn at the Ga site( position), which causes the total magnetic moment to increase in accordance with the moments of all other magnetic atoms(Ni, Co and MnY). The moment of a non-magnetic Ga atom is small and like a constant.
| Concentrations | Lattice | Magnetic Moment() | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter (au) | Ni | Co | MnY | Ga | MnZ | Total | (K) | |||
| 0.12 | 0.15 | 11.062 | 0.37 | 1.08 | 3.51 | -0.09 | 3.60 | 4.90 | 1375 | 7.59 |
| 0.26 | 11.066 | 0.42 | 1.14 | 3.52 | -0.09 | 3.60 | 5.41 | 1465 | 7.70 | |
| 0.35 | 11.073 | 0.46 | 1.18 | 3.52 | -0.09 | 3.59 | 5.82 | 1538 | 7.79 | |
| 0.50 | 11.082 | 0.52 | 1.26 | 3.54 | -0.10 | 3.59 | 6.52 | 1653 | 7.94 | |
| 0.24 | 0.15 | 11.042 | 0.39 | 1.08 | 3.46 | -0.09 | 3.54 | 5.03 | 1389 | 7.53 |
| 0.26 | 11.048 | 0.44 | 1.13 | 3.47 | -0.09 | 3.54 | 5.54 | 1477 | 7.64 | |
| 0.35 | 11.054 | 0.48 | 1.18 | 3.47 | -0.10 | 3.54 | 5.95 | 1549 | 7.73 | |
| 0.50 | 11.063 | 0.54 | 1.25 | 3.48 | -0.10 | 3.54 | 6.63 | 1662 | 7.88 | |
Replacing Ga with Mn, however, has an enhanced effect on the total magnetic moment. Especially, Mn gives a relatively large magnetic moment compared to others.
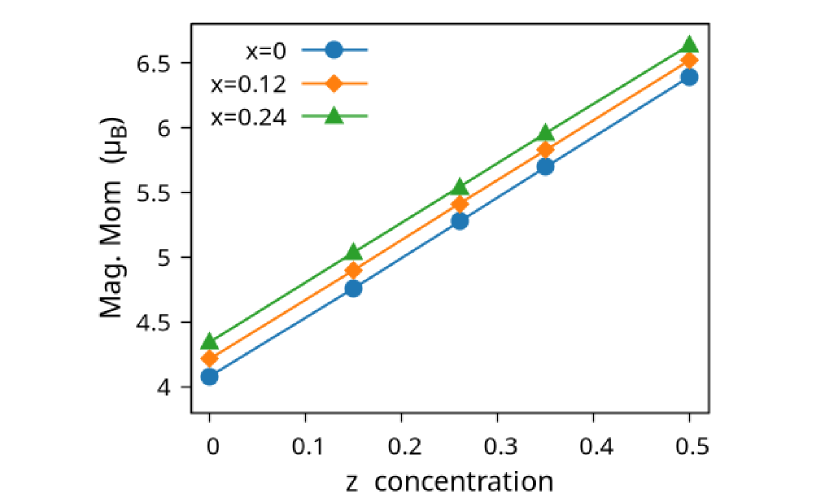
The variation of the magnetic moment of NiMnGa() as a function of doping concentration is shown in Figure (8(a)). The change in magnetic moment of the system is linear within the doping range. This well-behaved nature is good for tuning and applicability of this system.
In Figure (7), we have shown the exchange interactions of NiMnGa(). From the figures, the ferromagnetic interactions are more dominant in the system. The competing antiferromagnetic interaction(MnZ-MnY) is less than the ferromagnetic interaction(Co-MnY). Notably, the Co-MnY has more ferromagnetic interaction with a value above 15 meV. After initial doping of the site, the exchange interaction energies are approximately the same for = 0.12 and 0.24, with corresponding concentrations. This could be the cause of the relatively comparable in NiMnGa().
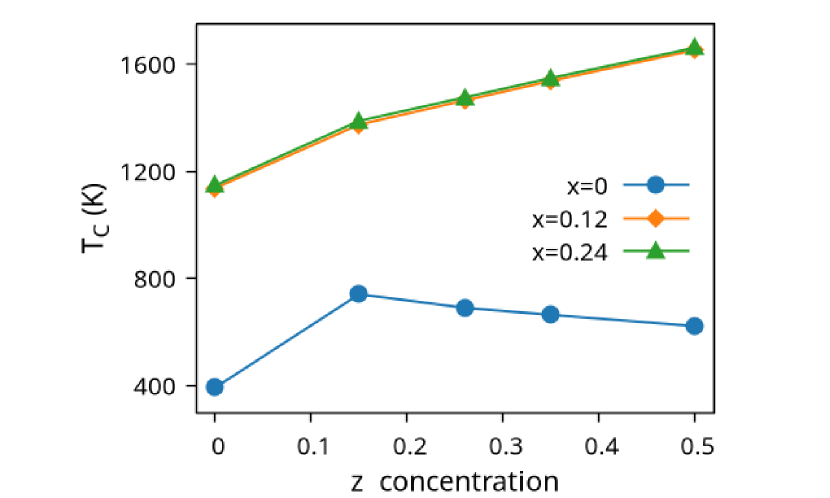
Finally, we have done mean field-based calculations to find the of the systems. Our result shows that doping both and sites increases the . Nevertheless, for NiMnGa(), is highest around , then it starts decreasing. On the other hand, doping a little in the site increases the steadily. Our for NiMnGa() commensurate with [32, 33]. Unfortunately, we are unable to find any literature on the variation of with doping. The variation of is shown in Figure (8(b)) and tabulated in Table (1, 2, 3) for NiMnGa(), NiMnGa() and NiMnGa() respectively.
The ratio and lattice parameter increase even in the presence of Co at the Ni site since Mn is present at the Ga site. Here, the ratio and cell volume increase, however the also increases since the presence of Co at the Ni site. In Table (3), we have reported the lattice parameter(au), Curie temperature(), and ratio values.
4 Discussions
The lattice parameter increases when Mn is doped at the Ga site ascribed to its larger atomic radius i.e., (1.61 Å) (1.36 Å). In contrast, doping of Co at the Ni site decreases its lattice constants even though the atomic radius of Co(1.52 Å) is larger than Ni(1.49 Å). This can be associated with the following reasons: Firstly, the exchange interaction between the Co and Mn is higher than the Ni and Mn, and this can be well understood from Figures ((1(c)), (3b.1-3b.2). Secondly, the - hybridization of Co and Mn is relatively stronger than Ni and Mn [47]. Then the lattice parameter starts to decrease as the Co concentration in the Ni site increases, as shown in Figure (1(d)).
In the pristine() DOS, we observed a pseudogap in the minority channel around 1 eV below the Fermi-level. This pseudogap originated by the hybridization between orbitals of Ni and orbitals of Ga. The gap is terminated by a peak just below the Fermi-level originating from the hybridization of the same orbitals and drives the system to Jahn-Teller instability. In NiMnGa() and NiMnGa() systems, the doping at the Ni site stabilizes the Jahn-Teller instability as the peak smears out and the pseudogap becomes narrower with higher value, as shown in Figure (33a.2) for NiMnGa() and Figure (6) for NiMnGa(). In NiMnGa() systems the pseudogap almost remains the same throughout the doping range as shown in Figure (55a.4).
The magnetic moments of NiMnGa(), NiMnGa(), and NiMnGa() are shown in Table (1), Table (2), and Table (3), respectively. From the tables and Figure (8(a)), which shows the variation of the total magnetic moment as a function of and concentrations, we see the general features: (i) Magnetic moment is increasing linearly with doping. (ii) Magnetic moment increases faster by doping in site than doping in site. This value is due to the overall magnetic moments of site occupants, i.e., Ni and Co have weaker magnetic moment than MnZ. (iii) MnZ has a higher magnetic moment than the MnY site. The antiferromagnetic interaction between the MnY and MnZ atoms is stronger since the inter-atomic distance from MnY to MnZ are smaller compared to Mn of the same sites(MnY to MnY, and MnZ to MnZ). The variation in and affects the atomic moments in various sites and the total magnetic moments. General observations are: (i) Atomistic moments of sites are most susceptible to and concentrations, while and sites moments remain almost unchanged. (ii) Both Ni and Co moment increases with concentration but more with concentrations.
The Curie temperature() has been calculated using mean field approximations(MFA). As expected, MFA overestimates the . For pure , our calculated 392 K is in good agreement with experimental findings 382 K [48](365 K is reported by [32, 33]). For NiMnGa(), the qualitative variation of increases monotonously, with the quantitative value matching the previous findings [27]. for NiMnGa() first increases from 392 K to 741 K for . Higher doping of MnZ decreases the monotonously. For Co-doped systems, both NiMnGa() and NiMnGa() increase monotonously and give approximately the same irrespective of Co concentrations. To get an understanding of the variation of , we have calculated the magnetic pair interaction as shown in Figures ((1(c)), (33b.2), (55b.4), and (7)) for , NiMnGa(), NiMnGa() and NiMnGa() respectively with MnY at the center. When the Co atom is present, i.e., (as in NiMnGa() and NiMnGa() case), Co and MnY is the dominant interaction. The difference is that for NiMnGa(), the maximum interaction is almost constant (33b.2), but for NiMnGa(), the interaction keeps increasing. The same variation is evident from Figure (8(b)) for = 0.15 and 0.24. For NiMnGa(), there is a ferro-antiferro competition between Ni-MnY and MnY-MnZ. This brings the down after the initial increase from pure .
5 Conclusion
We have investigated the electronic and magnetic properties of , with , and . The study of replacing both and is substantially sparse compared to any one of them. We have used DFT and MFA to study the compound effect of dual-doping. Electronic structures, DOS, and magnetic properties including magnetic exchange interactions and moments are calculated using DFT as implemented in the SPRKKR package. The Curie temperature() is calculated using MFA. Our calculation shows the existence of strong Mn-Mn antiferromagnetic interaction between Mn at Ga and Mn at its sub-lattice. Its also noticed that changing concentration at MnZ does not change the magnetic exchange substantially. This is an interesting result, as opposed to the findings in the case of [34].
The ’s are obtained using MFA simulations using the magnetic exchange interaction values obtained from ab-initio calculations. The numerical results for the pure system are close to that reported by experiments.
We point out the calculations are done in cubic() phases only. Though, in the dual-doping case, we have shown the variation of magnetic exchange interaction parameters and magnetic Curie temperatures. These findings will help to design the functional properties like MCE and shape memory alloys by alloying suitably.
6 Acknowledgement
We acknowledge the High Performance Computing Center (HPCC), SRM IST for providing the computational facility to carry out this research work effectively.
References
-
[1]
T. I. R. E. A. (IRENA),
Renewable
energy: A key climate solution.
URL https://www.irena.org/climatechange/Renewable-Energy-Key-climate-solution -
[2]
M. Fitta, W. Sas, T. Korzeniak,
Tunable critical
temperature and magnetocaloric effect in ternary prussian blue analogue, J.
Magn. Magn. Mater 465 (2018) 640–645.
doi:10.1016/j.jmmm.2018.06.053.
URL https://doi.org/10.1016%2Fj.jmmm.2018.06.053 - [3] R. A. de Groot, F. M. Mueller, P. G. van Engen, K. H. J. Buschow, New class of materials: Half-metallic ferromagnets, Phys. Rev. Lett. 50 (25) (1983) 2024–2027. doi:10.1103/physrevlett.50.2024.
- [4] S. Ishida, S. Akazawa, Y. Kubo, J. Ishida, Band theory of Co2MnSn, Co2TiSn and Co2TiAl, J. Phys. F: Met. Phys. 12 (6) (1982) 1111–1122. doi:10.1088/0305-4608/12/6/012.
- [5] S. Fujii, S. Sugimura, Ishida, S. Asano, Hyperfine fields and electronic structures of the heusler alloys Co2MnX (X=Al, Ga, Si, Ge, Sn), J. Phys.: Condens. Matter 2 (43) (1990) 8583–8589. doi:10.1088/0953-8984/2/43/004.
- [6] M. Jourdan, J. Minár, J. Braun, A. Kronenberg, S. Chadov, B. Balke, A. Gloskovskii, M. Kolbe, H. Elmers, G. Schönhense, H. Ebert, C. Felser, M. Kläui, Direct observation of half-metallicity in the heusler compound Co2MnSi, Nat. Commun. 5 (1) (2014) 3974. doi:10.1038/ncomms4974.
-
[7]
K. Elphick, W. Frost, M. Samiepour, T. Kubota, K. Takanashi, H. Sukegawa,
S. Mitani, A. Hirohata,
Heusler alloys for
spintronic devices: review on recent development and future perspectives,
Sci Technol Adv Mat 22 (1) (2021) 235–271, pMID: 33828415.
doi:10.1080/14686996.2020.1812364.
URL https://doi.org/10.1080/14686996.2020.1812364 -
[8]
S. Jiang, K. Yang,
Review
of high-throughput computational design of heusler alloys, Journal of Alloys
and Compounds 867 (2021) 158854.
doi:https://doi.org/10.1016/j.jallcom.2021.158854.
URL https://www.sciencedirect.com/science/article/pii/S0925838821002619 -
[9]
L. Wollmann, A. K. Nayak, S. S. Parkin, C. Felser,
Heusler 4.0:
Tunable materials, Annu. Rev. Mater. Res. 47 (1) (2017) 247–270.
doi:10.1146/annurev-matsci-070616-123928.
URL https://doi.org/10.1146/annurev-matsci-070616-123928 -
[10]
A. Ahmad, S. Mitra, S. K. Srivastava, A. K. Das,
Giant magnetocaloric effect
in Co2FeAl heusler alloy nanoparticles, J. Phys. D: Appl. Phys. 54 (38)
(2021) 385001.
doi:10.1088/1361-6463/ac0aba.
URL https://doi.org/10.1088/1361-6463/ac0aba -
[11]
X. Yang, Y. Wang, M. Du, Y. Xue,
First-principles study of Pt
doping effects on Ni2MnGa and Ni2FeGa ferromagnetic shape memory
alloys, Journal of Applied Physics 126 (8) (2019) 085103.
arXiv:https://doi.org/10.1063/1.5116247, doi:10.1063/1.5116247.
URL https://doi.org/10.1063/1.5116247 -
[12]
L. Bainsla, A. I. Mallick, M. M. Raja, A. A. Coelho, A. K. Nigam, D. D.
Johnson, A. Alam, K. G. Suresh,
Origin of spin
gapless semiconductor behavior in CoFeCrGa: Theory and experiment, Phys.
Rev. B 92 (2015) 045201.
doi:10.1103/PhysRevB.92.045201.
URL https://link.aps.org/doi/10.1103/PhysRevB.92.045201 - [13] A. Kundu, S. Ghosh, R. Banerjee, S. Ghosh, B. Sanyal, New quaternary half-metallic ferromagnets with large curie temperatures, Sci. Rep. 7 (1) (2017) 1803. doi:10.1038/s41598-017-01782-5.
-
[14]
T. Kihara, T. Roy, X. Xu, A. Miyake, M. Tsujikawa, H. Mitamura, M. Tokunaga,
Y. Adachi, T. Eto, T. Kanomata,
Observation
of inverse magnetocaloric effect in magnetic-field-induced austenite phase of
heusler alloys Ni50-xCoxMn31.5Ga18.5(x=9 and 9.7), Phys.
Rev. Materials 5 (2021) 034416.
doi:10.1103/PhysRevMaterials.5.034416.
URL https://link.aps.org/doi/10.1103/PhysRevMaterials.5.034416 - [15] J. Liu, N. Scheerbaum, S. Kauffmann-Weiss, O. Gutfleisch, NiMn-based alloys and composites for magnetically controlled dampers and actuators, Adv Eng Mater 14 (8) (2012) 653–667. doi:10.1002/adem.201200038.
-
[16]
R. Mahat, S. KC, U. Karki, J. Y. Law, V. Franco, I. Galanakis, A. Gupta,
P. LeClair,
Possible
half-metallic behavior of Co2-xCrxFeGe heusler alloys: Theory and
experiment, Phys. Rev. B 104 (2021) 014430.
doi:10.1103/PhysRevB.104.014430.
URL https://link.aps.org/doi/10.1103/PhysRevB.104.014430 -
[17]
Z. Guan, J. Bai, J. Gu, X. Liang, D. Liu, X. Jiang, R. Huang, Y. Zhang,
C. Esling, X. Zhao, L. Zuo,
First-principles
investigation of B2 partial disordered structure, martensitic
transformation, elastic and magnetic properties of all-d-metal Ni-Mn-Ti
heusler alloys, Journal of Materials Science and Technology 68 (2021)
103–111.
doi:https://doi.org/10.1016/j.jmst.2020.08.002.
URL https://www.sciencedirect.com/science/article/pii/S1005030220306940 -
[18]
V. G. de Paula, M. S. Reis,
All-d-metal full heusler
alloys: A novel class of functional materials, Chemistry of Materials
33 (14) (2021) 5483–5495.
arXiv:https://doi.org/10.1021/acs.chemmater.1c01012, doi:10.1021/acs.chemmater.1c01012.
URL https://doi.org/10.1021/acs.chemmater.1c01012 - [19] F. Heusler, Ueber magnetische manganlegierungen, Phys. Ges 12 (219) (1903).
- [20] F. Heusler, W. Starck, E. Haupt, Magnetisch-chemische studien, Phys. Ges 5 (220) (1903).
- [21] E. T. Dilmieva, Y. S. Koshkid’ko, V. V. Koledov, A. P. Kamantsev, A. V. Mashirov, J. Cwik, V. V. Khovaylo, V. G. Shavrov, Formation of a martensitic twins structure in Ni2.16Mn0.84Ga heusler alloy by high magnetic fields under adiabatic and isothermal conditions, Bull. Russ. Acad. Sci.: Phys. 81 (11) (2017) 1283–1288. doi:10.3103/s1062873817110077.
-
[22]
C. Seguí, E. Cesari,
Ordering
mechanism and kinetics in Ni2Mn1-xCuxGa ferromagnetic shape
memory alloys, Journal of Alloys and Compounds 887 (2021) 161302.
doi:https://doi.org/10.1016/j.jallcom.2021.161302.
URL https://www.sciencedirect.com/science/article/pii/S0925838821027110 - [23] A. P. Kamantsev, V. V. Koledov, A. V. Mashirov, E. T. Dilmieva, V. G. Shavrov, J. Cwik, A. S. Los, V. I. Nizhankovskii, K. Rogacki, I. S. Tereshina, Y. S. Koshkid'ko, M. V. Lyange, V. V. Khovaylo, P. Ari-Gur, Magnetocaloric and thermomagnetic properties of Ni2.18Mn0.82Ga heusler alloy in high magnetic fields up to 140 kOe, J Appl Phys 117 (16) (2015) 163903. doi:10.1063/1.4918914.
-
[24]
Franco, V., Blázquez, J.S., Ingale, B., C. A.,
The
magnetocaloric effect and magnetic refrigeration near room temperature:
Materials and models, Annu. Rev. Mater. Res. 42 (1) (2012) 305–342.
doi:10.1146/annurev-matsci-062910-100356.
URL https://doi.org/10.1146/annurev-matsci-062910-100356 - [25] R. Y. Umetsu, X. Xu, R. Kainuma, NiMn-based metamagnetic shape memory alloys, Scr. Mater. 116 (2016) 1–6. doi:10.1016/j.scriptamat.2016.01.006.
- [26] A. Okubo, X. Xu, R. Y. Umetsu, T. Kanomata, K. Ishida, R. Kainuma, Magnetic properties of Co50-xNixMn25Al25 alloys with B2 structure, J Appl Phys 109 (7) (2011) 07B114. doi:10.1063/1.3559536.
-
[27]
T. Kanomata, Y. Kitsunai, K. Sano, Y. Furutani, H. Nishihara, R. Y. Umetsu,
R. Kainuma, Y. Miura, M. Shirai,
Magnetic
properties of quaternary heusler alloys Ni2-xCoxMnGa, Phys. Rev. B
80 (2009) 214402.
doi:10.1103/PhysRevB.80.214402.
URL https://link.aps.org/doi/10.1103/PhysRevB.80.214402 -
[28]
Uijttewaal, M. A., Hickel, T., Neugebauer, J., Gruner, M. E., E. P.,
Understanding
the phase transitions of the Ni2MnGa magnetic shape memory system from
first principles, Phys. Rev. Lett. 102 (2009) 035702.
doi:10.1103/PhysRevLett.102.035702.
URL https://link.aps.org/doi/10.1103/PhysRevLett.102.035702 - [29] S. Singh, B. Dutta, S. W. D’Souza, M. G. Zavareh, P. Devi, A. S. Gibbs, T. Hickel, S. Chadov, C. Felser, D. Pandey, Robust bain distortion in the premartensite phase of a platinum-substituted Ni2MnGa magnetic shape memory alloy, Nat. Commun. 8 (2017) 1006. doi:https://doi.org/10.1038/s41467-017-00883-z.
- [30] V. D. Buchelnikov, V. V. Sokolovskiy, Magnetocaloric effect in Ni-Mn-X (X = Ga, In, Sn, Sb) heusler alloys, The Physics of Metals and Metallography 112 (7) (2011) 633–665. doi:10.1134/s0031918x11070052.
- [31] R. Kainuma, Y. Imano, W. Ito, H. Morito, Y. Sutou, K. Oikawa, A. Fujita, K. Ishida, S. Okamoto, O. Kitakami, T. Kanomata, Metamagnetic shape memory effect in a heusler-type Ni43Co7Mn39Sn11 polycrystalline alloy, Appl. Phys. Lett. 88 (19) (2006) 192513. doi:10.1063/1.2203211.
-
[32]
F. Orlandi, A. Çakır, P. Manuel, D. D. Khalyavin, M. Acet, L. Righi,
Neutron
diffraction and symmetry analysis of the martensitic transformation in
Co-doped Ni2MnGa, Phys. Rev. B 101 (2020) 094105.
doi:10.1103/PhysRevB.101.094105.
URL https://link.aps.org/doi/10.1103/PhysRevB.101.094105 - [33] V. Sokolovskiy, A. Grünebohm, V. Buchelnikov, P. Entel, Ab initio and monte carlo approaches for the magnetocaloric effect in Co and In-doped Ni-Mn-Ga heusler alloys, Entropy 16 (9) (2014) 4992–5019. doi:10.3390/e16094992.
-
[34]
V. V. Sokolovskiy, V. D. Buchelnikov, M. A. Zagrebin, P. Entel, S. Sahoo,
M. Ogura,
First-principles
investigation of chemical and structural disorder in magnetic
Ni2Mn1+xSn1-x heusler alloys, Phys. Rev. B 86 (2012) 134418.
doi:10.1103/PhysRevB.86.134418.
URL https://link.aps.org/doi/10.1103/PhysRevB.86.134418 -
[35]
Z. Ni, X. Guo, Q. Li, Z. Liang, H. Luo, F. Meng,
Effect
of Zn-doping on the phase transition and magnetic properties of heusler
alloys Ni2MnGa1-xZnx (x=0, 0.25, 0.5, 0.75 and 1), Journal of
Magnetism and Magnetic Materials 464 (2018) 65–70.
doi:https://doi.org/10.1016/j.jmmm.2018.05.044.
URL https://www.sciencedirect.com/science/article/pii/S0304885318307790 -
[36]
M. Halder, K. Suresh,
Effect
of Fe substitution at the Ni and Mn sites on the magnetic properties of
Ni50Mn35In15 heusler alloys, Journal of Alloys and
Compounds 647 (2015) 310–314.
doi:https://doi.org/10.1016/j.jallcom.2015.06.121.
URL https://www.sciencedirect.com/science/article/pii/S0925838815302383 - [37] P. Cao, F. Tian, W. Li, L. Vitos, Y. Wang, Ideal superelasticity in Ni-based heusler alloys, Acta Materialia 210 (Mar 2021). doi:10.1016/j.actamat.2021.116816.
- [38] R. Banerjee, A. Mookerjee, Augmented space recursion code and application in simple binary metallic alloy, Int. J. Modern Phys. C 21 (02) (2010) 205–220. doi:10.1142/s0129183110015051.
- [39] H. Ebert, D. Ködderitzsch, J. Minár, Calculating condensed matter properties using the KKR-Green's function method—recent developments and applications, Reports on Progress in Physics 74 (9) (2011) 096501. doi:10.1088/0034-4885/74/9/096501.
- [40] H. Ebert, Fully relativistic band structure calculations for magnetic solids - formalism and application, in: H. Dreyssé (Ed.), Electronic Structure and Physical Properies of Solids, Springer Berlin Heidelberg, Berlin, Heidelberg, 2000, pp. 191–246.
- [41] P. N. Mavropoulos Phivos, The Korringa-Kohn-Rostoker (KKR) Green Function Method I. Electronic Structure of Periodic Systems, in: D. M. J. Grotendorst, S. Blügel (Ed.), Computational Nanoscience: Do It Yourself!, 2006.
-
[42]
J. P. Perdew, K. Burke, M. Ernzerhof,
Generalized Gradient
Approximation Made Simple, Phys. Rev. Lett. 77 (18) (1996) 3865–3868.
doi:10.1103/physrevlett.77.3865.
URL https://doi.org/10.1103%2Fphysrevlett.77.3865 -
[43]
A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia,
D. Gunter, D. Skinner, G. Ceder, K. A. Persson,
Commentary: The materials project:
A materials genome approach to accelerating materials innovation, APL
Materials 1 (1) (2013) 011002.
doi:10.1063/1.4812323.
URL https://doi.org/10.1063%2F1.4812323 -
[44]
A. Liechtenstein, M. Katsnelson, V. Antropov, V. Gubanov,
Local
spin density functional approach to the theory of exchange interactions in
ferromagnetic metals and alloys, J. Magn. Magn. Mater 67 (1) (1987) 65–74.
doi:https://doi.org/10.1016/0304-8853(87)90721-9.
URL https://www.sciencedirect.com/science/article/pii/0304885387907219 - [45] M. B. Sahariah, S. Ghosh, C. S. Singh, S. Gowtham, R. Pandey, First-principles computation of structural, elastic and magnetic properties of Ni2FeGa across the martensitic transformation, J. Phys.: Condens. Matter 25 (2) (2012) 025502. doi:10.1088/0953-8984/25/2/025502.
-
[46]
S. Ghosh, B. Sanyal,
Complex magnetic
interactions in off-stoichiometric NiMnGa alloys, Journal of Physics:
Condensed Matter 22 (34) (2010) 346001.
doi:10.1088/0953-8984/22/34/346001.
URL https://doi.org/10.1088/0953-8984/22/34/346001 - [47] T. Chang-Long, J. Jiu-Xing, T. X. Hua, C. Wei, Effect of Co on magnetic property and phase stability of Ni-Mn-Ga ferromagnetic shape memory alloys: A first-principles study, Chinese Physics B 19 (10) (2010) 107102.
-
[48]
A. U. Saleheen, J.-H. Chen, D. P. Young, I. Dubenko, N. Ali, S. Stadler,
Critical behavior in Ni2MnGa
and Ni2Mn0.85Cu0.15Ga, J Appl Phys 123 (20) (2018) 203904.
doi:10.1063/1.5025196.
URL https://doi.org/10.1063%2F1.5025196