A Unified and Constructive Framework for the Universality of Neural Networks
Abstract
One of the reasons why many neural networks are capable of replicating complicated tasks or functions is their universal property. Though the past few decades have seen tremendous advances in theories of neural networks, a single constructive framework for neural network universality remains unavailable. This paper is the first effort to provide a unified and constructive framework for the universality of a large class of activation functions including most of existing ones. At the heart of the framework is the concept of neural network approximate identity (nAI). The main result is: any nAI activation function is universal. It turns out that most of existing activation functions are nAI, and thus universal in the space of continuous functions on compacta. The framework induces several advantages over the contemporary counterparts. First, it is constructive with elementary means from functional analysis, probability theory, and numerical analysis. Second, it is the first unified attempt that is valid for most of existing activation functions. Third, as a by product, the framework provides the first universality proof for some of the existing activation functions including Mish, SiLU, ELU, GELU, and etc. Fourth, it provides new proofs for most activation functions. Fifth, it discovers new activation functions with guaranteed universality property. Sixth, for a given activation and error tolerance, the framework provides precisely the architecture of the corresponding one-hidden neural network with predetermined number of neurons, and the values of weights/biases. Seventh, the framework allows us to abstractly present the first universal approximation with favorable non-asymptotic rate.
keywords:
Universal approximation , neural networks , activation functions , non-asymptotic analysisMSC:
62M45 , 82C32 , 62-02 , 60-02 , 65-02.[UT-mech]organization=Department of Aerospace Engineering and Engineering Mechanics, The University of Texas at Austin, city=Austin, state=Texas, country=USA
[Oden]organization=Oden Institute for Computational Engineering and Sciences, The University of Texas at Austin, city=Austin, state=Texas, country=USA
Unlike existing universality approaches, our framework is constructive using elementary means from functional analysis, probability theory, non-asymptotic analysis, and numerical analysis.
While existing approaches are either technical or specialized for particular activation functions, our framework is the first unified attempt that is valid for most of the existing activation functions and beyond.
The framework provides the first universality proof for some of the existing activation functions including Mish, SiLU, ELU, GELU, and etc;
The framework provides new proofs for all activation functions
The framework discovers and facilitates the discovery of new activation functions with guaranteed universality property. Indeed, any activation—whose th derivative, with being an integer, is integrable and essentially bounded—is universal. In that case, the activation function and all of its th derivative, are not only a valid activation but also universal.
For a given activation and error tolerance, the framework provides precisely the architecture of the corresponding one-hidden neural network with a predetermined number of neurons, and the values of weights/biases;
The framework is the first that allows for abstractly presenting the universal approximation with the favorable non-asymptotic rate of , where is the number of neurons. This provides not only theoretical insights into the required number of neurons but also guidance on how to choose the number of neurons to achieve a certain accuracy with controllable successful probability. Perhaps more importantly, it shows that neural network may fail, with non-zero probability, to provide the desired testing error in practice when an architecture is selected;
Our framework also provides insights into the developments, and hence providing constructive derivations, of some of the existing approaches.
1 Introduction
Human brain consists of networks of billions of neurons, each of which, roughly speaking, receives information—electrical pulses —from other neurons via dendrites, processes the information using soma, is activated by difference of electrical potential, and passes the output along its axon to other neurons through synapse. Attempt to understand the extraordinary ability of the brain in categorizing, classifying, regressing, processing, etc information has inspired numerous scientists to develop computational models to mimic brain functionalities. Most well-known is perhaps the McCulloch-Pitts model [1], which is also called perceptron by Rosenblatt who extended McCulloch-Pitts model to networks of artificial neurons capable of learning from data [2]. The question is if such a network could mimic some of the brain capability, such as learning to classify. The answer lies in the fact that perceptron networks can represent Boolean logic functions exactly. From a mathematical point of view, perceptron networks with Heaviside activation functions compute step functions, linear combinations of which form the space of simple functions which in turn is dense in the space of measurable functions [3, 4]. That is, linear combination of perceptions can approximate a measurable function to any desired accuracy [5, 6]: the first universal approximation for neural networks. The universal approximation capability partially “explains” why human brains can be trained to virtually learn any tasks.
For training one-hidden layer networks, Widrow-Hoff rule [7] can be used for supervised learning. For many-layer ones, the most popular approach is back-propagation [8] which requires the derivative of activation functions. Heaviside function is, however, not differentiable in the classical sense. A popular smooth approximation is the standard logistic (also called sigmoidal) activation function which is infinitely differentiable. The question is now: are neural networks of sigmoidal function universal? An answer to this question was first presented by Cybenko [9] and Funahashi [10]. The former, though non-constructive (a more constructive proof was then provided in [11] and revisited in [12]), elegantly used the Hahn-Banach theorem to show that sigmoidal neural networks (NNs) with one hidden layer is dense in the space of continuous functions on compacta. The latter used Fourier transform and an integral formulation for integrable function with bounded variation [13] to show the same results for NNs with continuous, bounded, monotone increasing sigmoidal activation function. Recognizing NN output as an approximate back-projection operator, [14] employed inverse Radon transformation to show the universal approximation property in space of squared integrable functions. Making use of the classical Stone-Weierstrass approximation theorem [15] successfully proved NNs with non-decreasing sigmoidal function are dense in space of continuous functions over compacta and dense in space of measurable functions. Using the separability of space of continuous functions over compacta [16] constructed a strictly increasing analytic sigmoidal function that is universal. The work in [17], based on a Kolmogorov theorem, showed that any continuous function on hypercubes can be approximated well with two-hidden layer NNs of sigmoidal functions.
Though sigmoidal functions are natural continuous approximation to Heaviside function, and hence mimicking the activation mechanism of neurons, they are not the only ones having universal approximation property. Indeed, [18] showed, using distributional theory, that NNs with th degree sigmoidal function are dense in space of continuous functions over compacta. Meanwhile, [19] designed a cosine squasher activation function so that the output of one-hidden layer neural network is truncated Fourier series and thus can approximate square integrable functions to any desired accuracy. Following and extending [9], [20] showed that NN is dense in with bounded non-constant activations function and in space of continuous functions over compacta with continuous bounded nonconstant activation functions. Using the Stone-Weierstrass theorem, [6] showed that any network with activations (e.g. exponential, cosine squasher, modified sigma-pi, modified logistic, and step functions) that can transform product of functions into sum of functions is universal in the space of bounded measurable functions over compacta. The work in [21] provided universal approximation for bounded weights (and biases) with piecewise polynomial and superanalytic activation functions (e.g. sine, cosine, logistic functions and piecewise continuous functions are superanalytic at some point with positive radius of convergence).
One hidden-layer NN is in fact dense in space of continuous functions and if the activation function is not polynomial almost everywhere [22, 23]. Using Taylor expansion and Vandermonde determinant, [24] provided an elementary proof of universal approximation for NNs with activation functions. Recently, [25] provides universal approximation theorem for multilayer NNs with ReLU activation functions using partition of unity and Taylor expansion for functions in Sobolev spaces. Universality of multilayer ReLU NNs can also be obtained using approximate identity and rectangular quadrature rule [26]. Restricting in Barron spaces [27, 28], the universality of ReLU NNs is a straightforward application of the law of large numbers [29]. The universality of ReLU NNs can also be achieved by emulating finite element approximations [30, 31].
Unlike others, [32] introduced ellshape function (as derivative of squash-type activation function, for example) as a means to explicitly construct one-hidden layer NNs to approximate continuous function over compacta in multiple dimensions. More detailed analysis was then carried out in [33, 34]. The idea was revisited and extended to establish universal approximation in the uniform norm for tensor product sigmoidal and hyperbolic tangent activations [35, 36, 37, 38, 39]. Similar approach was also taken in [40] using cardinal B-spline and in [41] using the distribution function as sigmoid but for a family of sigmoids with a certain of decaying-tail conditions.
While it is sufficient for most universal approximation results to hold when each weight (and bias) varying over the whole real line , this is not necessary. In fact, universal approximation results for continuous function on compacta can also be obtained using finite set of weights [42, 43, 44]. It is quite striking that one-hidden layer with only one neuron is enough for universality: [45] constructs a smooth, sigmoidal, almost monotone activation function so that one-hidden layer with one neuron can approximate any continuous function over any compact subset in to any desired accuracy.
Universal theorems with convergence rate for sigmoidal and others NNs have also been established. Modifying the proofs in [11, 18], [46] showed that, in one dimension, the error incurred by sigmoidal NNs with hidden units scales as in the uniform norm over compacta. The result was then extended to for bounded continuous function [47]. Similar results were obtained for functions with bounded variations [48] and with bounded -variations [49]. For multiple dimensions, [27] provided universal approximation for sigmoidal NNs in the space of functions with bounded first moment of the magnitude distribution of their Fourier transform with rate in the -norm, independent of dimensions. This result can be generalized to Lipschitz functions (with additional assumptions) [50]. Using explicit NN construction in [32], [35, 36, 37, 38, 39, 33, 34, 41] provided convergence rate of , in the uniform norm for Hölder continuous functions with exponent . Recently, [51] has revisited universal approximation theory with rate in Sobolev norms for smooth activation functions with polynomial decay condition on all derivatives. This improves/extends the previous similar work for sigmoidal functions in [27] and exponentially decaying activation functions in [52]. The setting in [51] is valid for sigmoidal, arctan, hyperbolic tangent, softplus, ReLU, Leaky ReLU, and th power of ReLU, as their central differences satisfy polynomial decaying condition. However, the result is only valid for smooth functions in high-order Barron spaces. For activation functions without decay but essentially bounded and having bounded Fourier transform on some interval (or having bounded variation), the universal approximation results with slower rate in the -norm can be obtained for first order Barron space. These rates can be further improved using stratified sampling [53, 28]. Convergence rates for ReLU NNs in Sobolev spaces has been recently established using finite elements [30, 31].
The main objective of this paper is to provide the first constructive and unified frameworks for a large class of activation functions including most of existing ones. At the heart of this new framework is the introduction of the neural network approximate identity (nAI) concept. The important consequence is: any nAI activation function is universal. The following are the main contributions: i) Unlike existing works, our framework is constructive using elementary means from functional analysis, probability theory, non-asymptotic analysis, and numerical analysis. ii) While existing approaches are either technical or specialized for particular activation functions, our framework is the first unified attempt that is valid for most of the existing activation functions and beyond; iii) The framework provides the first universality proof for some of the existing activation functions including Mish, SiLU, ELU, GELU, and etc; iv) The framework provides new proofs for all activation functions; v) The framework discovers and facilitates the discovery of new activation functions with guaranteed universality property. Indeed, any activation—whose th derivative, with being an integer, is integrable and essentially bounded—is universal. In that case, the activation function and all of its th derivative, are not only a valid activation but also universal. vi) For a given activation and error tolerance, the framework provides precisely the architecture of the corresponding one-hidden neural network with a predetermined number of neurons, and the values of weights/biases; vii) The framework is the first that allows for abstractly presenting the universal approximation with the favorable non-asymptotic rate of , where is the number of neurons. This provides not only theoretical insights into the required number of neurons but also guidance on how to choose the number of neurons to achieve a certain accuracy with controllable successful probability. Perhaps more importantly, it shows that neural network may fail, with non-zero probability, to provide the desired testing error in practice when an architecture is selected; viii) Our framework also provides insights into the developments, and hence providing constructive derivations, of some of the existing approaches.
The paper is organized as follows. Section 2 introduces conventions and notations used in the paper. Elementary facts about convolution and approximate identities that are useful for our purposes are presented in section 3. Section 4 recalls quadrature rules in terms of Riemann sums for continuous functions on compacta and their error analysis using moduli of continuity. This follows by a unified abstract framework for universality in section 6. The key to achieve this is to introduce the concept of neural network approximate identity (nAI), which immediately provides an abstract universality result in Lemma 3. This abstract framework reduces universality proof to nAI proof. Section 7 shows that most of existing activations are nAI. This includes the family of rectified polynomial units (RePU) in which the parametric and leaky ReLUs are a member, a family of generalized sigmoidal functions in which the standard sigmoidal, hyperbolic tangent and softplus are a member, the exponential linear unit (ELU), the Gaussian error linear unit (GELU), the sigmoid linear unit (SiLU), and the Mish. It is the nAI proof of the Mish activation function that guides us to devise a general framework for a large class of nAI functions (including all activations in this paper and beyond) in section 8. Abstract universal approximation result with non-asymptotic rates is presented in section 9. Section 10 concludes the paper.
2 Notations
This section describes notations used in the paper. We reserve lower case roman letters for scalars or scalar-valued function. Boldface lower case roman letters are for vectors with components denoted by subscripts. We denote by the set of real numbers and by the convolution operator. For , where is the ambient dimension, denotes the standard norm in . We conventionally write and for and is the Lebesgue measure in . For , . For simplicity, we use in place of . Note that we also use to denote the uniform norm of continuous function . We define for , as the space of continuous functions on , as the space of continuous functions vanishing at infinity, as the space of bounded functions in , and as the space of functions in with compact support.
3 Convolution and Approximate Identity
The mathematical foundation for our framework is approximate identity, which relies on convolution. Convolution has been used by many authors including [23, 40, 22] to assist in proving universal approximation theorems. Approximate identity generated by ReLU function has been used in [26] for showing ReLU universality in . In this section we collect some important results from convolution and approximate identity that are useful for our developments (see, e.g., [54] for a comprehensive treatment). Let be the translation operator. The following is standard.
Proposition 1.
is uniformly continuous iff .
Let be two measurable functions in , their convolution is defined as
when the integral exists. We are interested in the conditions under which (or ) is integrable for almost every (a.e.) , as our approach requires a discretization of the convolution integral. Below is a relevant case.
Lemma 1.
If then .
We are interested in which is an approximate identity in the following sense.
Definition 1.
A family of functions , where , is called an approximate identity (AI) if: i) The family is bounded in the norm, i.e., for some ; ii) for all ; and iii) as , for any .
An important class of approximate identity is obtained by rescaling functions.
Lemma 2.
If and , then is an AI.
Lemma 3.
For any , , where is an AI. Consequently, for any being a compact subset of , , where is the indicator/characteristic function of .
Proof.
We briefly present the proof here as we will use a similar approach to estimate approximate identity error later. Since it resides in and is uniformly continuous. As a consequence of Proposition 1, for any , there exists such that for . We have
where we have used the second property in Proposition 1. The assertion is now clear as is arbitrarily small and by the third condition of approximate identity. ∎
4 Quadrature rules for continuous functions on bounded domain
Recall that for a bounded function on a compact set, it is Riemann integrable if and only if it is continuous almost everywhere. In that case, Riemann sums converge to Riemann integrals as the corresponding partition size approaches 0. It is well-known (see, e.g. [55, 56], and references therein) that most common numerical quadrature rules—including trapezoidal, some Newton-Cotes formulas, and Gauss-Legendre quadrature formulas—are Riemann sums. In this section, we use the Riemann sum interpretation of quadrature rule to approximate integrals of bounded functions. The goal is to characterize quadrature error in terms of modulus of continuity. We first discuss quadrature error in one dimension and then extend the result to dimensions.
We assume the domain of interest is . Let , a partition of , and the collection of all “quadrature points” such that for . We assume that
be a valid Riemann sum, e.g. trapezoidal rule, and thus converging to as approaches . We define a quadrature rule for as the tensor product of the aforementioned one dimensional quadrature rule, and thus
| (1) |
is a valid Riemann sum for .
Recall the modulus of continuity of a function :
| (2) |
, and is continuous with respect to at (due to the uniform continuity of on ). The following error bound for the tensor product quadrature rule is an extension of the standard one dimensional case [55].
Lemma 4.
Let . Then111The result can be marginally improved using the common refinement for and , but that is not important for our purpose.
where is the norm of the partition .
5 Error Estimation for Approximate Identity with quadrature
We are interested in approximating functions in using neural networks. How to extend the results to is given in A. At the heart of our framework is to first approximate any function in with an approximate identity and then numerically integrate the convolution integral with quadrature (later with Monte Carlo sampling in Section 9). This extends the similar approach in [26] for ReLU activation functions in several directions: 1) we rigorously account for the approximate identity and quadrature errors, 2) our unified framework holds for most activation functions (see Section 7) using the network approximate identity (nAI) concept introduced in Section 6, 4) we identify sufficient conditions under which an activation is nAI (see Section 8), and 5) we provide non-asymptotic rate of convergence (see Section 9). Moreover, this procedure is the key to our unification of neural network universality.
Let and be an approximate identity. From Lemma 3 we know that converges to uniformly as . We, however, are interested in estimating the error for a given . From the proof of Lemma 3, for any , we have
where is the tail mass of .
Next, for any , we approximate
with the Riemann sum defined in (1). The following result is obvious by triangle inequality, continuity of at , the third condition of the definition of , and Lemma 4.
Lemma 5.
Let , be an approximate identity, and be the quadrature rule (1) for with the partition and quadrature point set . Then, for any , and , there holds
| (3) |
In particular, for any , there exist a sufficiently small (and hence large ), and sufficiently small and such that
Remark 1.
Aiming at using only elementary means, we use Riemann sum to approximate the integral, which does not give the best possible convergence rates. To improve the rates, Section 9 resorts to Monte Carlo sampling to not only reduce the number of “quadrature” points but also to obtain a total number of points independent of the ambient dimension .
6 An abstract unified framework for universality
Definition 2 (Network Approximate Identity function).
A univariate function admits a network approximate identity (nAI) if there exist , , , and such that
| (4) |
Thus, up to a scaling, is an approximate identity.
Lemma 6.
If a univariate function is a nAI, then it is universal in .
Proof.
We have explicitly constructed a one-hidden layer neural network with an arbitrary nAI activation in (5) to approximate well any continuous function with compact support in . A few observations are in order: i) if we know the modulus of continuity of and the tail behavior of (from property of ), we can precisely determine the total number of quadrature points , the scaling , and the cut-off radius in terms of (see Lemma 5). That is, the topology of the network is completely determined; ii) The weights and biases of the network are also readily available from the nAI property of , the quadrature points, and ; iii) the coefficients of the output layer is also pre-determined by nAI (i.e. ) and the values of the unknown function at the quadrature points; and iv) any nAI activation function is universal in .
Clearly the Gaussian activation function is an nAI with , , and . The interesting fact is that, as we shall prove in Section 7, most existing activation functions, though not integrable by themselves, are nAI.
Remark 2.
It is important to point out that the universality in Lemma 6 for any nAI activation is in one dimension. In order to extend the universality result to dimensions for an nAI activation function, we shall deploy a special -fold composition of its one-dimensional approximate identity (4). Section 7 provides explicit constructions of such -fold composition for many nAI activation functions, and Section 8 extends the result to abstract nAI function with appropriate conditions.
Remark 3.
Our framework also helps understand some of the existing universal approximation approaches in a more constructive manner. For example, the constructive proof in [11] is not entirely constructive as the key step in equation (4), where the authors introduced the neural network approximation function , is not constructive. Our framework can provide a constructive derivation of this step. Indeed, by applying a summation by part, one can see that resembles a quadrature approximation of the convolution of and the derivative (approximated by forward finite difference) of scaled sigmoidal function. Since the derivative of sigmoidal function, up to a scaling factor, is nAI (see Section 8), the convolution of and a scaled sigmoidal derivative can approximate to any desired accuracy.
Another important example is the pioneered work in [32] that has been extended in many directions in [35, 36, 37, 38, 39, 33, 34, 41, 12]. Though the rest of the approach is constructive, the introduction of the neural network operator is rather mysterious. From our framework point of view, this is no longer the case as the neural network operator is nothing more than a quadrature approximation of the convolution of and ell shape functions constructed from activation functions under consideration. Since these ell shape functions fall under the nAI umbrella, the introduction of neural network operator is now completely justified and easily understood. We would like to point out that our work does not generalize/extend the work in [32]. Instead, we aim at developing a new analytical framework that achieves unified and broad results that are not possible with the contemporary counterparts, while being more constructive and simpler. The ell shape function idea is not sufficient to construct our framework. Indeed, the work in [32] and its extensions [35, 36, 37, 38, 39, 33, 34, 41, 12] have been limited to a few special and standard squash-type activation functions such as sigmoid and arctangent functions. Our work—thanks to other new ingredients such as convolution, numerical quadrature, Monte-Carlo sampling, and finite difference together with the new nAI concept—breaks the barrier. Our framework thus provides not only a new constructive method but also new insights into the work in [32] as its special case.
7 Many existing activation functions are nAI
We now exploit properties of each activation (and its family, if any) under consideration to show that they are nAI for . That is, these activations generate one-dimensional approximate identity, which in turn shows that they are universal by Lemma 6. To show that they are also universal in dimensions222Note that by Proposition 3.3 of [23], with an additional assumption on the denseness of the set of ridge functions in , we can conclude that they are also universal in dimensions. This approach, however, does not provide an explicit construction of the corresponding neural networks. we extend a constructive and explicit approach from [26] that was done for ReLU activation function. We start with the family of rectified polynomial units (RePU)—also parametric and leaky ReLUs—with many properties, then family of sigmoidal functions, then the exponential linear unit (ELU), then the Gaussian error linear unit (GELU), then the sigmoid linear unit (SiLU), and we conclude with the Mish activation with least properties. The proofs for all results in this section, together with figures demonstrating the functions for each activation, can be found in Appendix B and Appendix C.
7.1 Rectified Polynomial Units (RePU) is an nAI
Following [57, 18] we define the rectified polynomial unit (RePU) as
which reduces to the standard rectilinear (ReLU) unit [58] when , the Heaviside unit when , and the rectified cubic unit [59] when .
The goal of this section is to construct an integrable linear combination of RePU activation function for a given . We begin with constructing compact supported ell-shape functions333 ell-shape functions seemed to be first coined in [32]. from RePU in one dimension. Recall the binomial coefficient notation and the central finite differencing operator with stepsize (see Remark 8 for forward and backward finite differences).
Lemma 7 (-function for RePU in one dimension).
Let . For any , define
Then: i) is piecewise polynomial of order at most on each interval for ; ii) is -time differentiable for , continuous for , and discontinuous for . Furthermore, is a subset ; and iii) is even, non-negative, unimodal, and ..
Though there are many approaches to construct -functions in dimensions from -function in one dimension (see, e.g. [32, 35, 36, 37, 38, 39, 40, 41]) that are realizable by neural networks, inspired by [26] we construct -function in dimensions by -fold composition of the one dimensional -function in Lemma 7. By Lemma 5, it follows that the activation under consideration is universal in dimensions. We shall carry out this -fold composition for not only RePU but also the other activation functions. The same procedure for an abstract activation function will be presented in Section 8.
Theorem 1 (-function for RePU in dimensions).
Let , and . Define The following hold:
-
i)
is non-negative with compact support. In particular where , for , and .
-
ii)
is even with respect to each component , and unimodal with .
-
iii)
is piecewise polynomial of order at most in , . Furthermore, is -time differentiable in each , and .
7.2 Sigmoidal and related activation functions are nAI
7.2.1 Sigmoidal, hyperbolic tangent, and softplus activation functions
Recall the sigmoidal and softplus functions [62] are, respectively, given by
It is the relationship between sigmoidal and hyperbolic tangent function, denoted as ,
that allows us to construct their -functions a similar manner. In particular, based on the bell shape geometry of the the derivative of sigmoidal and hyperbolic tangent functions, we apply the central finite differencing with to obtain the corresponding -functions
Since is the derivative of , we apply central difference twice to obtain a -function for : . The following Lemma 8 and Theorem 2 hold for being either or or .
Lemma 8 (-function for sigmoid, hyperbolic tangent, and solfplus in one dimension).
For , there hold: i) for all , = 0, and is even; and ii) is unimodal , and .
Similar to Theorem 1, we construct -function in dimensions by -fold composition of the one dimensional -function in Lemma 8.
Theorem 2 (-function for sigmoid, hyperbolic tangent, and softplus in dimensions).
Let . Define
Then is even with respect to each component , , and unimodal with . Furthermore, and .
7.2.2 Arctangent function
We next discuss arctangent activation function whose shape is similar to sigmoid. Since its derivative has the bell shape geometry, we define the -function for arctangent function by approximating its derivative with central finite differencing, i.e.,
for . Then simple algebra manipulations show that Lemma 8 holds for with . Thus, Theorem 2 also holds for -dimensional arctangent -function
as we have shown for the sigmoidal function.
7.2.3 Generalized sigmoidal functions
We extend the class of sigmoidal function in [63] to generalized sigmoidal (or “squash”) functions.
Definition 3 (Generalized sigmoidal functions).
We say is a generalized sigmoidal function if it satisfies the following conditions:
-
i)
is bounded, i.e., there exists a constant such that for all .
-
ii)
and .
-
iii)
There exist and such that for .
-
iv)
There exist and such that for .
Clearly the standard sigmoidal, hyperbolic tangent, and arctangent activations are members of the class of generalized sigmoidal functions.
Lemma 9 (-function for generalized sigmoids in one dimension).
Let be a generalized sigmoidal function, and be an associated -function defined as
Then the following hold for any : i) There exists a constant such that for , and for ; and ii) For , , converges uniformly to . Furthermore, , and .
Thus any generalized sigmoidal function is an nAI in one dimension. Note that the setting in [63]—in which is non-decreasing, , and —is a special case of our general setting. In this less general setting, it is clear that and thus is sufficient to conclude for any . We will explore this in the next theorem as it is not clear, at the moment of writing this paper, how to show that the -functions for generalized sigmoids, as constructed below, reside in .
Theorem 3 (-function for generalized sigmoids in dimensions).
Suppose that is a non-decreasing generalized sigmoidal function. Let . Define . Then and .
7.3 The Exponential Linear Unit (ELU) is nAI
Following [64, 65] we define the Exponential Linear Unit (ELU) as
for some . The goal of this section is to show that ELU is an nAI. Since the unbounded part of ELU is linear, Section 7.1 suggests us to define, for ,
Lemma 10 (-function for ELU in one dimension).
Let , then Furthermore: for .
Theorem 4 (-function for ELU in dimensions).
Let . Define . Then and thus .
7.4 The Gaussian Error Linear Unit (GELU) is nAI
GELU, introduced in [66], is defined as
where is the cummulative distribution function of standard normal distribution. Since the unbounded part of GELU is essentially linear, Section 7.1 suggests us to define
Lemma 11 (-function for GELU in one dimension).
-
i)
is an even function in both and .
-
ii)
has two symmetric roots with , and ,
Theorem 5 (-function for GELU in dimensions).
Let . Define , then .
7.5 The Sigmoid Linear Unit (SiLU) is an nAI
SiLU, also known as sigmoid shrinkage or swish [66, 67, 68, 69], is defined as By inspection, the second derivative of is bounded and its graph is quite close to bell shape. This suggests us to define
The proofs of the following results are similar to those of Lemma 11 and Theorem 5.
Theorem 6 (-function for SiLU in dimension).
-
i)
is an even function in both and .
-
ii)
has two symmetric roots with , and .
-
iii)
-
iv)
Let . Define , then .
7.6 The Mish unit is an nAI
Mish unit, introduced in [70], is defined as
Due to its similarity with SiLU, we define
Unlike any of the preceding activation functions it is not straightforward to manipulate Mish analytically. This motivates us to devise a new approach to show that Mish is nAI. As shall be shown in Section 8, this approach allows us to unify the nAI property for all activation functions. We begin with the following result on the second derivative of Mish.
Lemma 12.
The second derivative of Mish, , is continuous, bounded, and integrable. That is, for some positive constant and .
Theorem 7.
Let , then the following hold:
-
i)
There exists such that , and
-
ii)
Let . Define , then .
8 A general framework for nAI
Inspired by the nAI proof of the Mish activation function in Section 7.6, we develop a general framework for nAI that requires only two conditions on the th derivative of any activation . The beauty of the general framework is that it provides a single nAI proof that is valid for a large class of functions including all activation functions that we have considered. The trade-off is that less can be said about the corresponding -functions. To begin, suppose that there exists such that
-
C1
Integrability: is integrable, i.e., , and
-
C2
Essential boundedness: there exists such that .
Note that if the two conditions C1 and C2 hold for (e.g. Gaussian activation functions) then the activation is obviously an nAI. Thus we only consider , and the -function for can be defined via the -order central finite difference:
Lemma 13.
For any , there holds:
Proof.
Applying the Taylor theorem gives
The proof is concluded if we can show that
but this is clear by the alternating sum identity
∎
Theorem 8.
Let . Then: i) There exists such that ; ii) There exists such that ; and iii) Let . Define then .
Proof.
The first assertion is straightforward by invoking assumption C2, Lemma 13, and defining For the second assertion, using triangle inequalities and the Fubini theorem yields
and, by defining , the result follows owing to assumption C1. The proof of the last assertion is the same as the proof of Theorem 5. In particular, we have
∎
Remark 5.
Remark 6.
Suppose a function satisfies both conditions C1 and C2. Theorem 8 implies that and all of its th derivative, , are not only a valid activation function but also universal. For example, any differentiable and non-decreasing sigmoidal function satisfies the conditions with , and therefore its derivative and itself are universal.
Remark 7.
In one dimension, if is of bounded variation, i.e. its total variation is finite, then resides in by taking . A simple proof of this fact can be found in [51, Corollary 3]. Thus, is an nAI.
9 Universality with non-asymptotic rates
This section explores Lemma 5 and Lemma 6 to study the convergence of the neural network (5) to the ground truth function as a function of the number of neurons. From (3), we need to estimate the modulus of continuity of (the first and the second terms) and the decaying property of the tail (the third term) of the approximate identity (and hence the tail of the activation ). For the former, we further assume that is Lipschitz so that the first and the second terms can be estimated as and . To balance these two terms, we need to pick the partition such that . From (1) and Lemma 4, we conclude and the total number of quadrature points scales as . It follows from (5) that the total number of neurons is . Conversely, for a given number of neurons , the error from the first two terms scales as , which is quite pessimistic. This is due to the tensor product quadrature rule. The result can be improved using Monte Carlo estimation of integrals at the expense of deterministic estimates. Indeed, let , , be independent and identically distributed (i.i.d.) by the uniform distribution on . A Monte Carlo counterpart of (5) is given as
| (6) |
which, by the law of large numbers, converges almost surely (a.s.) to for every . However, the Monte Carlo mean square error estimate
is not useful for our -norm estimate without further technicalities in exchanging expectation and -norm (see, e.g., [RockafellarWetts98, Theorem 14.60] and [71]).
While most, if not all, literature concerns deterministic and asymptotic rates, we pursue a non-asymptotic direction as it precisely captures the behavior of the Monte Carlo estimate (6) of , and hence of . Within the non-asymptotic setting, we now show that, with high probability, any neural network with the nAI property and neurons converges with rate to any Lipschitz continuous function with compact support in .
Theorem 9.
Let , , be i.i.d. samples from the uniform distribution on . Suppose that is Lipschitz and is continuous. Furthermore, let and for some . There exist three absolute constants , , and :
| (7) |
holds with probability at least .
Proof.
If we define
then , , are independent random variables and . Owing to the continuity of and , we know that there exist two absolute constants and such that . Let , then by Hoeffding inequality [72, 73] we have
| (8) |
for each , where stands for probability. An application of triangle inequality gives
where is meaningful as is continuous. Thus, for a given , there holds
that is,
Consequently, using the tail bound (8) yields
It follows that
| (9) |
with probability at least for any . Clearly, we need to pick either or . The former is more favorable as it makes the error in (9) small with high probability. The latter could lead to large error with high probability. Now, choosing and following the proof of Lemma 5 we arrive at
We now estimate . By Markov inequality we have
where we have used the fact that . Now taking yields
and this concludes the proof. ∎
Remark 9.
The continuity of in Theorem 9 is only sufficient. All we need is the boundedness of . Theorem 9 is thus valid for all activation functions that we have discussed, including those in Section 8. Theorem 9 provides not only theoretical insights into the required number of neurons but also a guide on how to choose the number of neurons to achieve a certain accuracy with controllable successful probability. Perhaps more importantly, it shows that neural networks may fail, with non-zero probability, to provide a desired testing error in practice when an architecture, and hence a number of neurons, is selected.
10 Conclusions
We have presented a constructive framework for neural network universality. At the heart of the framework is the neural network approximate identity (nAI) concept that allows us to unify most of activations under the same umbrella. Indeed, we have shown that most of existing activations are nAI, and thus universal in the space of continuous of functions on compacta. We have shown that for an activation to be nAI, it is sufficient to verify that its th derivative, , is essentially bounded and integrable. The framework induces several advantages over contemporary approaches. First, our approach is constructive with elementary means from functional analysis, probability theory, and numerical analysis. Second, it is the first attempt to unify the universality for most of existing activation functions. Third, as a by product, the framework provides the first universality proof for some of the existing activation functions including the Mish, SiLU, ELU, GELU, etc. Fourth, it provides a new universality proof for most activation functions. Fifth, it discovers new activation functions with guaranteed universality property. Sixth, for each activation, the framework provides precisely the architecture of the one-hidden neural network with predetermined number of of neurons, and the values of weights/biases. Seventh, the framework facilitates us to develop the first abstract universal result with favorable non-asymptotic rates of , where is the number of neurons. Our framework also provides insights into the derivations of some of the existing approaches. Ongoing work is to build upon our framework to study the universal approximation properties of convolutional neural networks and deep neural networks. Part of the future work is also to exploit the unified nature of the framework to study which activation is better, in which sense, for a wide range of classification and regression tasks.
Funding
This work is partially supported by National Science Foundation awards NSF-OAC-2212442, NSF-2108320, NSF-1808576, and NSF-CAREER-1845799; by Department of Energy awards DE-SC0018147 and DE-SC0022211; and by a 2021 UT-Portugal CoLab award, and we are grateful for the support. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. National Science Foundation or the U.S. Department of Energy or the United States Government. We would like to thank Professor Christoph Schwab and Professor Ian Sloan for pointing out a technical mistake in the preprint.
Appendix A Extension to
In this section, we present an approach to extend the results in Sections 5 and 9 to continuous functions. To directly build upon the results in these sections to our extension, without loss of generality, we considers such that . Consider and let be an extension of , and [74]. Next, let us take such that: i) and ii) for any . Define , then it is easy to see that:
-
•
,
-
•
,
-
•
, and
-
•
.
Now, applying Lemma 5 we obtain
for all . Thus, by restricting we arrive at
This, together with Lemma 6, ensures the universality of any nAI activation in . The extension for Lipschitz continuous functions on for Section 9 follows similarly, again using the key extension results in [74].
Appendix B Proofs of results in Section 7
This section presents the detailed proofs of results in Section 7.
Proof of Lemma 7.
We start by defining , where are independent identically distributed uniform random variables on . Following [75, 76, 77], is distributed by the Irwin-Hall distribution with the probability density function
where denotes the largest integer smaller than . Using the definition of RePU, it is easy to see that can be also written in terms of RePU as follows
which in turns implies
| (10) |
In other words, is a dilated version of . Thus, all the properties of holds for . In particular, all the assertions of Lemma 7 hold. Note that the compact support can be alternatively shown using the property of the central finite differencing. Indeed, it is easy to see that for we have
∎
Proof of Theorem 1.
The first three assertions are direct consequences of Lemma 7. For the fourth assertion, since it is sufficient to show and we do so in three steps. Let and define . We first show by induction that for and . The claim is clearly true for . Suppose the claim holds for , then (10) implies
For we have
By the second assertion, we conclude that for any and .
In the second step, we show by induction on for any and any . The result holds for due to the first step. Suppose the claim is true for . For , we have
where we have used (10) and in the last equality, and the first step together with the induction hypothesis in the last inequality.
In the last step, we show by induction on . For , is clear using by the Irwin-Hall probability density function. Suppose the result is true for . For , applying the Fubini theorem gives
where we have used (10) in the second equality, the result of the second step in the second last inequality, and the induction hypothesis in the last inequality. ∎
Proof of Lemma 8.
The proof for is a simple extension of those in [63, 33], and the proof for follows similarly. Note that for sigmoid and hyperbolic tangent. For , due to the global convexity of we have
which is equivalently to for . The fact that is even and = 0 are obvious by inspection. Since the derivative of is negative for and is even, is unimodal. It follows that .
Next integrating by parts gives
| (11) |
Thus all the assertions for holds. ∎
Proof of Theorem 2.
We only need to show as the proof for other assertions is similar to that of Theorem 1, and thus is omitted. For sigmoid and hyperbolic tangent the result is clear as
For softplus function, by inspection, for all and . Lemma 8 gives for . Define and suppose the claim holds for , i.e., . Now apply (11) we have
which ends the proof by induction. ∎
Proof of Lemma 9.
The first assertion is clear by Definition 3. For the second assertion, with a telescope trick similar to [63] we have
To show the convergence is uniform, we consider only as the proof for is similar and for is obvious. We first consider the right tail. For sufficiently large , there exists a constant such that
Similarly, the left tail converges to 0 uniformly as
As a consequence, we have
where we have used the uniform convergence in the third equality.
Using the first assertion we have
∎
Proof of Theorem 3.
The proof is the same as the proof of Theorem 2 for the standard sigmoidal unit, and thus is omitted. ∎
Proof of Lemma 10.
The expression of and direct integration give . Similarly, simple algebra manipulations yield
and thus . The fact that for holds is straightforward by inspecting the extrema of . ∎
Proof of Theorem 4.
From the proof of Lemma 10 we infer that for all : in particular, . Define and suppose the claim holds for , i.e., . We have
which, by induction, concludes the proof. ∎
Proof of Lemma 11.
The first assertion is straightforward. For the second assertion, it is sufficient to consider and . Any root of satisfy the following equation
Since, given , is a positive decreasing function and is an increasing function (starting from ), they can have at most one intersection. Now for sufficiently large , using the the mean value theorem it can be shown that
from which we deduce that that there is only one intersection, and hence only one positive root for . Next, we notice for . For it is easy to see . Thus, for . For , by inspection we have , and hence . In conclusion .
The preceding argument also shows that for , for , and . Using the Taylor formula we have
For the third assertion, it is easy to verify the following indefinite integral (ignoring the integration constant as it will be canceled out)
which, together with simple calculations, yields
From the proof of the second assertion and the Taylor formula we can show
Thus, . ∎
Proof of Theorem 5.
From the proof of Lemma 11 we have and for all where , : in particular, . It is easy to see by induction that
We claim that
and thus . We prove the claim by induction. Clearly it holds for . Suppose it is valid for . Define , we have
where we have used the induction hypothesis in the last inequality, and this ends the proof. ∎
Proof of Lemma 12.
It is easy to see that for
and
for . That is, both the right and the left tails of decay exponentially, and this concludes the proof. ∎
Proof of Theorem 7.
For the first assertion, we note that is continuous and thus the following Taylor theorem with integral remainder for holds
As a result,
where we have used the boundedness of from Lemma 12 in the last inequality.
For the second assertion, we have
whose right hand side is well-defined owing to (see Lemma 12) and the Fubini theorem. In particular,
The proof for follows similarly.
The proof of the last assertion is the same as the proof of Theorem 5 and hence is omitted. ∎
Appendix C Figures
This section provides the plots of the functions for various activations in 1, 2, and 3 dimensions.
Figure 1 (left) plots for RePU unit with in one dimension. The non-negativeness, compact-support, ell shape, smoothness, and unimodal of can be clearly seen. For we plot in Figure 1 (the three right most subfigures) the surfaces of RePU for together with contours to again verify the non-negativeness, compact-support, ell shape, smoothness, and unimodal of . To further confirm these features for , in figure 2 we plot an isosurface for RePU unit with , and isosurfaces for the case in Figure 3. Note the supports of the functions around the origin: the further away from the origin the smaller the isosurface values.



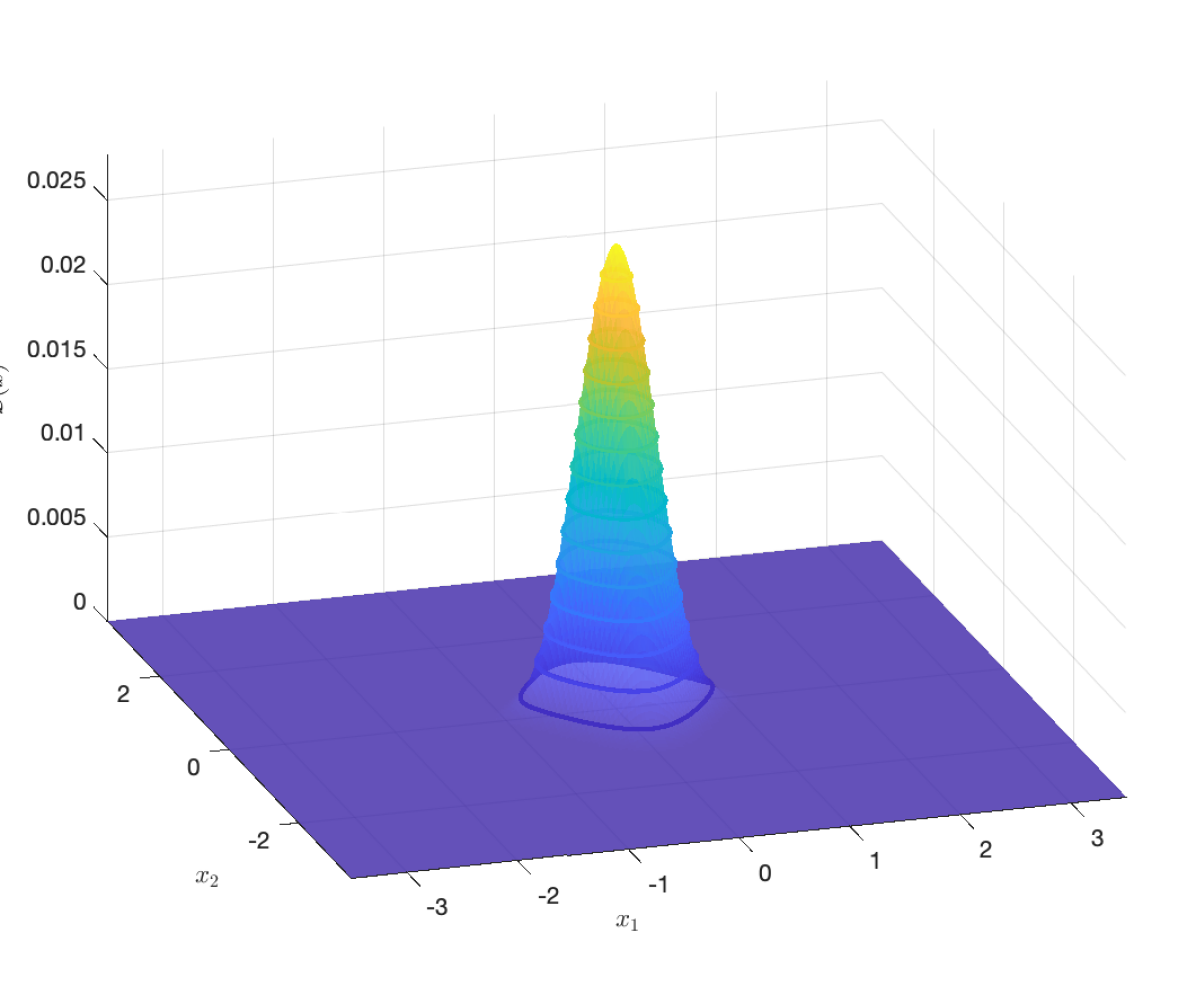








To verify that activation functions in the generalized sigmoidal class behave similarly from our unified framework we plot the functions of the standard sigmoid, softplus, and arctangent activation functions in Figure 4 for . As can be seen, the functions, though have different values, share similar shapes. Note that for we plot the isosurfaces at times the largest value of the corresponding functions.









In figure 5 we present a snapshot of the function of the ELU activation function in one, two, and three dimensions. While it has common features as other functions such as decaying to zero at infinity, it possesses distinct features including asymmetric shape with positive and negative values.



We have shown the nAI proof for dimensions is the same for GELU, SiLU, and Mish. It turns out that they are geometrically very similar and this can be seen in Figure 6. Note that for we plot the isosurfaces at times the largest value of the corresponding functions.









References
-
[1]
W. S. McCulloch, W. Pitts, A logical
calculus of the ideas immanent in nervous activity, Bulletin of Mathematical
Biology 52 (1) (1990) 99–115.
doi:10.1007/BF02459570.
URL https://doi.org/10.1007/BF02459570 -
[2]
F. Rosenblatt,
The
perceptron: A probabilistic model for information storage and organization in
the brain., Psychological Review 65 (6) (1958) 386 – 408.
URL http://ezproxy.lib.utexas.edu/login?url=https://search.ebscohost.com/login.aspx?direct=true&db=pdh&AN=1959-09865-001&site=ehost-live -
[3]
R. Durrett, Probability:
Theory and Examples, Cambridge Series in Statistical and Probabilistic
Mathematics, Cambridge University Press, 2010.
URL https://books.google.com/books?id=evbGTPhuvSoC - [4] H. L. Royden, Real analysis / H.L. Royden, Stanford University, P.M. Fitzpatrick, University of Maryland, College Park., fourth edition [2018 reissue]. Edition, Pearson modern classic, Pearson, New York, NY, 2018 - 2010.
- [5] R. Lippmann, An introduction to computing with neural nets, IEEE ASSP Magazine 4 (2) (1987) 4–22. doi:10.1109/MASSP.1987.1165576.
- [6] N. Cotter, The Stone-Weierstrass theorem and its application to neural networks, IEEE Transactions on Neural Networks 1 (4) (1990) 290–295. doi:10.1109/72.80265.
- [7] B. Widrow, M. E. Hoff, Adaptive switching circuits, 1960 IRE WESCON Convention Record (1960) 96–104Reprinted in Neurocomputing MIT Press, 1988 .
- [8] D. E. Rumelhart, J. L. McClelland, Learning Internal Representations by Error Propagation, 1987, pp. 318–362.
-
[9]
G. Cybenko, Approximation by
superpositions of a sigmoidal function, Mathematics of Control, Signals and
Systems 2 (4) (1989) 303–314.
doi:10.1007/BF02551274.
URL https://doi.org/10.1007/BF02551274 -
[10]
K.-I. Funahashi,
On
the approximate realization of continuous mappings by neural networks,
Neural Networks 2 (3) (1989) 183–192.
doi:https://doi.org/10.1016/0893-6080(89)90003-8.
URL https://www.sciencedirect.com/science/article/pii/0893608089900038 - [11] T. Chen, H. Chen, R.-w. Liu, A constructive proof and an extension of Cybenko’s approximation theorem, in: C. Page, R. LePage (Eds.), Computing Science and Statistics, Springer New York, New York, NY, 1992, pp. 163–168.
- [12] D. Costarelli, Sigmoidal functions approximation and applications, Ph.D. thesis, Department of Mathematics, Roma Tre University (2014).
- [13] Irie, Miyake, Capabilities of three-layered perceptrons, in: IEEE 1988 International Conference on Neural Networks, 1988, pp. 641–648 vol.1. doi:10.1109/ICNN.1988.23901.
- [14] Carroll, Dickinson, Construction of neural nets using the Radon transform, in: International 1989 Joint Conference on Neural Networks, 1989, pp. 607–611 vol.1. doi:10.1109/IJCNN.1989.118639.
-
[15]
K. Hornik, M. Stinchcombe, H. White,
Multilayer
feedforward networks are universal approximators, Neural Networks 2 (5)
(1989) 359–366.
doi:https://doi.org/10.1016/0893-6080(89)90020-8.
URL https://www.sciencedirect.com/science/article/pii/0893608089900208 - [16] V. Maiorov, A. Pinkus, Lower bounds for approximation by MLP neural networks, Neurocomputing 25 (1999) 81–91.
-
[17]
V. Kůrková,
Kolmogorov’s
theorem and multilayer neural networks, Neural Networks 5 (3) (1992)
501–506.
doi:https://doi.org/10.1016/0893-6080(92)90012-8.
URL https://www.sciencedirect.com/science/article/pii/0893608092900128 -
[18]
H. Mhaskar, C. A. Micchelli,
Approximation
by superposition of sigmoidal and radial basis functions, Advances in
Applied Mathematics 13 (3) (1992) 350–373.
doi:https://doi.org/10.1016/0196-8858(92)90016-P.
URL https://www.sciencedirect.com/science/article/pii/019688589290016P - [19] Gallant, White, There exists a neural network that does not make avoidable mistakes, in: IEEE 1988 International Conference on Neural Networks, 1988, pp. 657–664 vol.1. doi:10.1109/ICNN.1988.23903.
-
[20]
K. Hornik,
Approximation
capabilities of multilayer feedforward networks, Neural Networks 4 (2)
(1991) 251–257.
doi:https://doi.org/10.1016/0893-6080(91)90009-T.
URL https://www.sciencedirect.com/science/article/pii/089360809190009T - [21] M. Stinchcombe, H. White, Approximating and learning unknown mappings using multilayer feedforward networks with bounded weights, in: 1990 IJCNN International Joint Conference on Neural Networks, 1990, pp. 7–16 vol.3. doi:10.1109/IJCNN.1990.137817.
-
[22]
M. Leshno, V. Y. Lin, A. Pinkus, S. Schocken,
Multilayer
feedforward networks with a nonpolynomial activation function can approximate
any function, Neural Networks 6 (6) (1993) 861–867.
doi:https://doi.org/10.1016/S0893-6080(05)80131-5.
URL https://www.sciencedirect.com/science/article/pii/S0893608005801315 - [23] A. Pinkus, Approximation theory of the MLP model in neural networks, Acta Numerica 8 (1999) 143–195. doi:10.1017/S0962492900002919.
-
[24]
J.-G. Attali, G. Pagès,
Approximations
of functions by a multilayer perceptron: a new approach, Neural Networks
10 (6) (1997) 1069–1081.
doi:https://doi.org/10.1016/S0893-6080(97)00010-5.
URL https://www.sciencedirect.com/science/article/pii/S0893608097000105 -
[25]
D. Yarotsky,
Error
bounds for approximations with deep ReLU networks, Neural Networks 94
(2017) 103–114.
doi:https://doi.org/10.1016/j.neunet.2017.07.002.
URL https://www.sciencedirect.com/science/article/pii/S0893608017301545 -
[26]
S. Moon, ReLU network with
bounded width is a universal approximator in view of an approximate
identity, Applied Sciences 11 (1) (2021).
doi:10.3390/app11010427.
URL https://www.mdpi.com/2076-3417/11/1/427 - [27] A. Barron, Universal approximation bounds for superpositions of a sigmoidal function, IEEE Transactions on Information Theory 39 (3) (1993) 930–945. doi:10.1109/18.256500.
- [28] J. M. Klusowski, A. R. Barron, Approximation by combinations of ReLU and squared ReLU ridge functions with and controls (2018). arXiv:1607.07819.
- [29] E. Weinan, C. Ma, L. Wu, Barron spaces and the compositional function spaces for neural network models, ArXiv abs/1906.08039 (2019).
- [30] J. He, L. Li, J. Xu, C. Zheng, ReLU deep neural networks and linear finite elements, Journal of Computational Mathematics 38 (3) 502–527.
-
[31]
J. A. A. Opschoor, P. C. Petersen, C. Schwab,
Deep ReLU networks and
high-order finite element methods, Analysis and Applications 18 (05) (2020)
715–770.
arXiv:https://doi.org/10.1142/S0219530519410136, doi:10.1142/S0219530519410136.
URL https://doi.org/10.1142/S0219530519410136 -
[32]
P. Cardaliaguet, G. Euvrard,
Approximation
of a function and its derivative with a neural network, Neural Networks
5 (2) (1992) 207–220.
doi:https://doi.org/10.1016/S0893-6080(05)80020-6.
URL https://www.sciencedirect.com/science/article/pii/S0893608005800206 -
[33]
Z. Chen, F. Cao,
The
approximation operators with sigmoidal functions, Computers & Mathematics
with Applications 58 (4) (2009) 758–765.
doi:https://doi.org/10.1016/j.camwa.2009.05.001.
URL https://www.sciencedirect.com/science/article/pii/S0898122109003071 -
[34]
Z. Chen, F. Cao, J. Hu,
Approximation
by network operators with logistic activation functions, Applied Mathematics
and Computation 256 (2015) 565–571.
doi:https://doi.org/10.1016/j.amc.2015.01.049.
URL https://www.sciencedirect.com/science/article/pii/S009630031500079X - [35] G. Anastassiou, Quantitative Approximations, First edition, Chapman and Hall/CRC, 2001. doi:https://doi.org/10.1201/9781482285796.
- [36] G. Anastassiou, Rate of convergence of some multivariate neural network operators to the unit, Computers & Mathematics With Applications - COMPUT MATH APPL 40 (2000) 1–19. doi:10.1016/S0898-1221(00)00136-X.
-
[37]
G. A. Anastassiou,
Univariate
hyperbolic tangent neural network approximation, Mathematical and Computer
Modelling 53 (5) (2011) 1111–1132.
doi:https://doi.org/10.1016/j.mcm.2010.11.072.
URL https://www.sciencedirect.com/science/article/pii/S0895717710005649 -
[38]
G. A. Anastassiou,
Multivariate
sigmoidal neural network approximation, Neural Networks 24 (4) (2011)
378–386.
doi:https://doi.org/10.1016/j.neunet.2011.01.003.
URL https://www.sciencedirect.com/science/article/pii/S089360801100027X -
[39]
G. A. Anastassiou,
Multivariate
hyperbolic tangent neural network approximation, Computers & Mathematics
with Applications 61 (4) (2011) 809–821.
doi:https://doi.org/10.1016/j.camwa.2010.12.029.
URL https://www.sciencedirect.com/science/article/pii/S089812211000934X -
[40]
D. Costarelli,
Neural
network operators: Constructive interpolation of multivariate functions,
Neural Networks 67 (2015) 28–36.
doi:https://doi.org/10.1016/j.neunet.2015.02.002.
URL https://www.sciencedirect.com/science/article/pii/S0893608015000362 -
[41]
D. Costarelli, R. Spigler,
Approximation by series of
sigmoidal functions with applications to neural networks, Annali di
Matematica Pura ed Applicata (1923 -) 194 (1) (2015) 289–306.
doi:10.1007/s10231-013-0378-y.
URL https://doi.org/10.1007/s10231-013-0378-y -
[42]
C. K. Chui, X. Li,
Approximation
by ridge functions and neural networks with one hidden layer, Journal of
Approximation Theory 70 (2) (1992) 131–141.
doi:https://doi.org/10.1016/0021-9045(92)90081-X.
URL https://www.sciencedirect.com/science/article/pii/002190459290081X -
[43]
Y. Ito,
Representation
of functions by superpositions of a step or sigmoid function and their
applications to neural network theory, Neural Networks 4 (3) (1991)
385–394.
doi:https://doi.org/10.1016/0893-6080(91)90075-G.
URL https://www.sciencedirect.com/science/article/pii/089360809190075G - [44] V. E. Ismailov, Approximation by neural networks with weights varying on a finite set of directions, Journal of Mathematical Analysis and Applications 389 (2012) 72–83.
-
[45]
N. J. Guliyev, V. E. Ismailov, A
single hidden layer feedforward network with only one neuron in the hidden
layer can approximate any univariate function, Neural Comput. 28 (7) (2016)
1289–1304.
doi:10.1162/NECO_a_00849.
URL https://doi.org/10.1162/NECO_a_00849 - [46] C. Debao, Degree of approximation by superpositions of a sigmoidal function, Approximation Theory and its Applications 9 (1993) 17–28.
-
[47]
B. I. Hong, N. Hahm,
Approximation
order to a function in C(R) by superposition of a sigmoidal function,
Applied Mathematics Letters 15 (5) (2002) 591–597.
doi:https://doi.org/10.1016/S0893-9659(02)80011-8.
URL https://www.sciencedirect.com/science/article/pii/S0893965902800118 -
[48]
B. Gao, Y. Xu,
Univariant
approximation by superpositions of a sigmoidal function, Journal of
Mathematical Analysis and Applications 178 (1) (1993) 221–226.
doi:https://doi.org/10.1006/jmaa.1993.1302.
URL https://www.sciencedirect.com/science/article/pii/S0022247X83713028 - [49] G. Lewicki, G. Marino, Approximation by superpositions of a sigmoidal function, Zeitschrift Fur Analysis Und Ihre Anwendungen 22 (2003) 463–470.
-
[50]
G. Lewicki, G. Marino,
Approximation
of functions of finite variation by superpositions of a sigmoidal function,
Applied Mathematics Letters 17 (10) (2004) 1147–1152.
doi:https://doi.org/10.1016/j.aml.2003.11.006.
URL https://www.sciencedirect.com/science/article/pii/S089396590481694X -
[51]
J. W. Siegel, J. Xu,
Approximation
rates for neural networks with general activation functions, Neural Networks
128 (2020) 313–321.
doi:https://doi.org/10.1016/j.neunet.2020.05.019.
URL https://www.sciencedirect.com/science/article/pii/S0893608020301891 - [52] K. Hornik, M. Stinchcombe, H. White, P. Auer, Degree of approximation results for feedforward networks approximating unknown mappings and their derivatives, Neural Computation 6 (6) (1994) 1262–1275. doi:10.1162/neco.1994.6.6.1262.
-
[53]
Y. Makovoz,
Random
approximants and neural networks, Journal of Approximation Theory 85 (1)
(1996) 98–109.
doi:https://doi.org/10.1006/jath.1996.0031.
URL https://www.sciencedirect.com/science/article/pii/S0021904596900313 -
[54]
G. Folland, Real
Analysis: Modern Techniques and Their Applications, A Wiley-Interscience
publication, Wiley, 1999.
URL https://books.google.com/books?id=uPkYAQAAIAAJ -
[55]
C. T. H. Baker, On the nature of
certain quadrature formulas and their errors, SIAM Journal on Numerical
Analysis 5 (4) (1968) 783–804.
URL http://www.jstor.org/stable/2949426 - [56] P. J. Davis, D. P. Rabinowitz, Methods of Numerical Integration, Academic Press, Boston, San Diego, New York, London, 1984.
-
[57]
B. Li, S. Tang, H. Yu,
Better
approximations of high dimensional smooth functions by deep neural networks
with rectified power units, Communications in Computational Physics 27 (2)
(2019) 379–411.
doi:https://doi.org/10.4208/cicp.OA-2019-0168.
URL http://global-sci.org/intro/article_detail/cicp/13451.html - [58] V. Nair, G. E. Hinton, Rectified linear units improve restricted Boltzmann machines, in: Proceedings of the 27th International Conference on International Conference on Machine Learning, ICML’10, Omnipress, Madison, WI, USA, 2010, p. 807–814.
-
[59]
W. E, B. Yu, The deep Ritz
method: A deep learning-based numerical algorithm for solving variational
problems, Communications in Mathematics and Statistics 6 (1) (2018) 1–12.
doi:10.1007/s40304-018-0127-z.
URL https://doi.org/10.1007/s40304-018-0127-z - [60] K. He, X. Zhang, S. Ren, J. Sun, Delving deep into rectifiers: Surpassing human-level performance on imagenet classification (2015). arXiv:1502.01852.
- [61] A. L. Maas, A. Y. Hannun, A. Y. Ng, Rectifier nonlinearities improve neural network acoustic models”, Proc. ICML 30 (1) 2 16489696.
- [62] X. Glorot, A. Bordes, Y. Bengio, Deep sparse rectifier neural networks, in: International Conference on Artificial Intelligence and Statistics.
-
[63]
D. Costarelli, R. Spigler,
Approximation
results for neural network operators activated by sigmoidal functions,
Neural Networks 44 (2013) 101–106.
doi:https://doi.org/10.1016/j.neunet.2013.03.015.
URL https://www.sciencedirect.com/science/article/pii/S0893608013001007 - [64] D.-A. Clevert, T. Unterthiner, S. Hochreiter, Fast and accurate deep network learning by exponential linear units (ELUs) (2016). arXiv:1511.07289.
- [65] G. Klambauer, T. Unterthiner, A. Mayr, S. Hochreiter, Self-normalizing neural networks (2017). arXiv:1706.02515.
- [66] D. Hendrycks, K. Gimpel, Gaussian error linear units (GELUs) (2020). arXiv:1606.08415.
-
[67]
S. Elfwing, E. Uchibe, K. Doya,
Sigmoid-weighted
linear units for neural network function approximation in reinforcement
learning, Neural Networks 107 (2018) 3–11, special issue on deep
reinforcement learning.
doi:https://doi.org/10.1016/j.neunet.2017.12.012.
URL https://www.sciencedirect.com/science/article/pii/S0893608017302976 - [68] P. Ramachandran, B. Zoph, Q. V. Le, Searching for activation functions (2017). arXiv:1710.05941.
- [69] A. M. Atto, D. Pastor, G. Mercier, Smooth sigmoid wavelet shrinkage for non-parametric estimation, in: 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, 2008, pp. 3265–3268. doi:10.1109/ICASSP.2008.4518347.
- [70] D. Misra, Mish: A self regularized non-monotonic activation function (2020). arXiv:1908.08681.
-
[71]
O. A. Hafsa, J.-P. Mandallena,
Interchange of infimum and
integral, Calculus of Variations and Partial Differential Equations 18 (4)
(2003) 433–449.
doi:10.1007/s00526-003-0211-3.
URL https://doi.org/10.1007/s00526-003-0211-3 - [72] M. Mohri, A. Rostamizadeh, A. Talwalkar, Foundations of Machine Learning, 2nd Edition, Adaptive Computation and Machine Learning, MIT Press, Cambridge, MA, 2018.
- [73] S. Shalev-Shwartz, S. Ben-David, Understanding Machine Learning: From Theory to Algorithms, Cambridge University Press, New York, NY, USA, 2014.
-
[74]
V. A. Milman, Extension of functions
preserving the modulus of continuity, Mathematical Notes 61 (2) (1997)
193–200.
doi:10.1007/BF02355728.
URL https://doi.org/10.1007/BF02355728 -
[75]
W. Feller,
An
Introduction to Probability Theory and Its Applications, Vol. 1, Wiley,
1968.
URL http://www.amazon.ca/exec/obidos/redirect?tag=citeulike04-20{&}path=ASIN/0471257087 -
[76]
J. O. Irwin, On the frequency
distribution of the means of samples from a population having any law of
frequency with finite moments, with special reference to Pearson’s type
ii, Biometrika 19 (3/4) (1927) 225–239.
URL http://www.jstor.org/stable/2331960 -
[77]
P. Hall, The distribution of means
for samples of size n drawn from a population in which the variate takes
values between 0 and 1, all such values being equally probable, Biometrika
19 (3/4) (1927) 240–245.
URL http://www.jstor.org/stable/2331961