A tangential and penalty-free finite element method for the surface Stokes problem
Abstract.
Surface Stokes and Navier-Stokes equations are used to model fluid flow on surfaces. They have attracted significant recent attention in the numerical analysis literature because approximation of their solutions poses significant challenges not encountered in the Euclidean context. One challenge comes from the need to simultaneously enforce tangentiality and conformity (continuity) of discrete vector fields used to approximate solutions in the velocity-pressure formulation. Existing methods in the literature all enforce one of these two constraints weakly either by penalization or by use of Lagrange multipliers. Missing so far is a robust and systematic construction of surface Stokes finite element spaces which employ nodal degrees of freedom, including MINI, Taylor-Hood, Scott-Vogelius, and other composite elements which can lead to divergence-conforming or pressure-robust discretizations. In this paper we construct surface MINI spaces whose velocity fields are tangential. They are not -conforming, but do lie in and do not require penalization to achieve optimal convergence rates. We prove stability and optimal-order energy-norm convergence of the method and demonstrate optimal-order convergence of the velocity field in via numerical experiments. The core advance in the paper is the construction of nodal degrees of freedom for the velocity field. This technique also may be used to construct surface counterparts to many other standard Euclidean Stokes spaces, and we accordingly present numerical experiments indicating optimal-order convergence of nonconforming tangential surface Taylor-Hood elements.
Key words and phrases:
surface Stokes equation; finite element method; MINI element2000 Mathematics Subject Classification:
65N12, 65N15, 65N301. Introduction
In this paper, we consider the surface Stokes problem:
| (1.1a) | ||||
| (1.1b) | ||||
Here, is a smooth and connected two-dimensional surface with outward unit normal , is the orthogonal projection onto the tangent space of , and and are the surface gradient and surface divergence operators, respectively. Furthermore, is the tangential deformation operator, and the forcing function is assumed to be tangential to the surface to ensure well-posedness. Further assumptions and notation are given in Section 2; cf. [20] for derivation of the surface Stokes problem and related models and further discussion of their properties. The system of equations (1.1) is subject to the tangential velocity constraint . To address degeneracies related to Killing fields, i.e., non-trivial tangential vector fields in the kernel of , we include a zeroth-order mass term in the momentum equations (1.1a) (cf. Remark 4.1).
We consider surface finite element methods (SFEMs), a natural methodology mimicking the variational formulation and built upon classical Galerkin principles. In this approach the domain is approximated by a polyhedral (or higher-order) surface whose faces constitute the finite element mesh. Similar to the Euclidean setting, SFEMs for the surface Stokes problem based on the standard velocity-pressure formulation must use compatible discrete spaces. Specifically, a discrete inf-sup condition must be satisfied. Given that SFEMs utilize the same framework as their Euclidean counterparts, employing mappings via affine or polynomial diffeomorphisms, one may anticipate that numerous classical inf-sup stable Stokes pairs can be adapted to their surface analogues, readily enabling the construction of stable SFEMs for (1.1).
However, the tangential velocity constraint poses a significant hurdle to constructing stable and convergent SFEMs. As is merely Lipschitz continuous, its outward unit normal is discontinuous at mesh edges and vertices. As a result, the tangential projection of continuous, piecewise smooth functions does not lead to -conforming functions. Moreover, there do not exist canonical, degree-of-freedom-preserving pullbacks for tangential vector fields, in particular, the Piola transform preserves tangentiality and in-plane normal continuity, but not in-plane tangential continuity. Finally, a continuous, tangential, and piecewise smooth vector field on must necessarily vanish on mesh corners except in exceptional cases where all incident triangles are coplanar. Indeed, at a mesh corner there are at least three faces emanating from a common vertex, whose outward unit normal vectors span . Therefore tangentiality of a continuous vector field with respect to each of the three planes implies that it vanishes at the vertex. Thus any piecewise polynomial space simultaneously satisfying both tangentiality and continuity exhibits a locking-type phenomenon with poor approximation properties.
There is a substantial recent literature on numerical approximation of the surface Stokes and related problems such as the surface vector Laplace equation. Most of these circumvent the difficulties described above in one of three ways: by relaxing the pointwise tangential constraint, by relaxing -conformity of the finite element space, or by using a different formulation of the surface Stokes problem. For the former, one can weakly impose the tangential constraint via penalization or Lagrange multipliers [16, 17, 25, 26, 18, 21, 4]. In principle, this allows one to use inf-sup stable Euclidean Stokes pairs to solve the analogous surface problem. However, this methodology requires superfluous degrees of freedom, as the velocity space is approximated by arbitrary vectors in rather than tangential vectors. In addition an unnatural high-order geometric approximation of the unit normal of the true surface is needed to obtain optimal-order approximations. Therefore for problems in which full information of the exact surface is unknown (e.g., free-boundary problem), these penalization schemes lead to SFEMs with sub-optimal convergence properties. However, it was shown recently in [19] that the tangential component of the solution converges optimally for a standard isoparametric geometry approximation in most cases assuming a correct choice of penalty parameters. The only exception is the case where tangential errors are considered along with affine (polyhedral) surface approximations. Alternatively, one may relax -conformity and use finite element trial and test functions that are not continuous on the discrete surface . In this direction, SFEMs utilizing tangentially- and -conforming finite element spaces such as Raviart-Thomas and Brezzi-Douglas-Marini combined with discontinuous Galerkin techniques are proposed and analyzed in [3, 23]; cf. [10] for similar methods for Euclidean Stokes equations. Here, additional consistency, symmetry, and stability terms are added to the method. These terms add some complexity to the implementation, especially for higher-order surface approximations, but are standard in the context of discontinuous Galerkin methods. Optimal-order convergence is observed experimentally for a standard SFEM formulation that does not require higher-order approximations of any geometric information. Discretizations of stream function formulations of the surface Stokes equations have also appeared in the literature [24, 28, 5, 4]. However, as with methods weakly enforcing tangentiality, they require higher-order approximation to the surface normal and in addition require computation of curvature information which can in and of itself be a challenging problem. These methods are also restricted to simply connected surfaces. As a final note, trace SFEMs, in which discretizations of surface PDE are formulated with respect to a background 3D mesh and a corresponding 3D finite element space, are especially important in the context of dynamic surface fluid computations. Trace formulations are well-developed for conforming/tangentially nonconforming methods and stream function formulations, but have not yet appeared for -conforming methods.
In this paper, we design a SFEM for the surface Stokes problem (1.1) using a strongly tangential finite element space that is based on a conforming, inf-sup stable Euclidean pair. The method is based on the standard variational formulation for the Stokes problem and does not require additional consistency terms or extrinsic penalization. As far as we are aware, this is the first SFEM for the surface Stokes problem with these properties. The key issue that we address is the assignment of degrees of freedom (DOFs) of tangential vector fields at Lagrange nodes, in particular, at vertices of the surface triangulation.
To expand on this last point and to describe our proposed approach, consider a vertex/DOF, call , of the triangulation of the discrete geometry approximation , and let denote the set of faces in the triangulation that have as a vertex. We wish to interpret and define the values of tangential vector fields forming our finite element space at this vertex in a way that ensures the resulting discrete spaces have desirable approximation and weak-continuity properties. As the mesh elements in generally lie in different planes, it is immediate that such vector fields are generally multi-valued at .
Let denote the closest point projection onto , and note that, because is smooth, continuous and tangential vector fields are well-defined and single-valued at . Thus, as the Piola transform preserves tangentiality, a natural assignment is to construct finite element functions with the property for some vector field tangent at , where is the Piola transform of the inverse mapping ; see Figure 1. Imposing this condition on Lagrange finite element DOFs likely leads to the sought out approximation and weak-continuity properties, and thus, conceptually may lead to convergent SFEMs for (1.1). However, the implementation of the resulting finite element method requires explicit information about the exact surface and its closest point projection. Therefore this construction is of little practical value.
Instead of this idealized construction, we fix an arbitrary face . Given the value and , we then assign , the Piola transform of with respect to the inverse of the closest point projection onto the plane containing ; see Figure 2. This transform is linear with a relatively simple formula (cf. Definition 2.3), and it only uses geometric information from . Moreover, we show that this construction is only an perturbation from the idealized setting. As a result, the constructed finite element spaces possess sufficient weak continuity properties to ensure that the resulting scheme is convergent for the surface Stokes problem (1.1).
To clearly communicate the main ideas and to keep technicalities at minimum, we focus on a polyhedral approximation to and on the lowest-order MINI pair, which in the Euclidean setting takes the discrete velocity space to be the (vector-valued) linear Lagrange space enriched with cubic bubbles, and the discrete pressure space to be the (scalar) Lagrange space. We expect the main ideas to be applicable to other finite element pairs (e.g, Taylor–Hood, Scott-Vogelius [29, 22, 31, 2]), although the stability must be shown on a case-by-case basis. Below we present numerical experiments demonstrating the viability of our approach for surface approximations paired with a Taylor-Hood finite element space and plan to address generalizations of our approach more fully in future works.
The rest of the paper is organized as follows. In the next section, we introduce the notation and provide some preliminary results. In Section 3, we define the surface finite element spaces based on the classical MINI pair. Here, we show that the spaces have optimal-order approximation properties and are inf-sup stable. We also establish weak continuity properties of the discrete velocity space via an -conforming relative on the true surface. In Section 4, we define the finite element space and prove optimal-order estimates in the energy norm. Finally in Section 5 we provide numerical experiments which support the theoretical results.
2. Notation and Preliminaries
We assume is a smooth, connected, and orientable two-dimensional surface without boundary. The signed distance function of is denoted by , which satisfies in the interior of and in the exterior. We set to be the outward-pointing unit normal (where the gradient is understood as a column vector) and the Weingarten map. The tangential projection operator is , where is the identity matrix, and the outer product of two vectors and satisfies . The smoothness of ensures the existence of sufficiently small such that the closest point projection
is well defined in the tubular region .
For a scalar function we define its extension via . Likewise, for its extension satisfies for . Define the surface gradient , and for a (column) vector field , we let denote the Jacobian matrix of . We then see , i.e., the row of coincides with . The tangential surface gradient (covariant derivative) of is defined by , and the surface divergence operator of is . The deformation of a tangential vector field is defined as the symmetric part of its surface gradient, i.e.,
For a matrix field , the divergence is understood to act row-wise.
Let denote the space of square-integrable functions on and let be the subspace of consisting of -functions with vanishing mean. We let be the Sobolev space of order and exponent on with corresponding norm . We use the notation with , and the convention , . Analogous vector-valued spaces are denoted in boldface (e.g., and ). We let be the subspace of whose members are tangent to , and set
Let be a polyhedral surface approximation of with triangular faces. We assume that is an approximation in the sense that for all . We further assume is sufficiently small to ensure , in particular, the closest point projection is well-defined on . We denote by the set of faces of , and assume this triangulation is shape-regular (i.e., the ratio of the diameters of the inscribed and circumscribed circles of each face is uniformly bounded). For simplicity and to ease the presentation, we further assume that is quasi-uniform, i.e., for all . The image of the mesh elements and the resulting set on the exact surface are given, respectively, by
We use the notation (resp., ) if there exists a constant independent of the mesh parameter such that (resp., ). The statement means and .
Set to be the set of vertices in , and for each , let denote the set of three vertices of . For each , let denote the set of faces having as a vertex. For , we define the patches
so that . The patches and associated with are defined analogously.
The (piecewise constant) outward unit normal of is denoted by , and we shall use the notation , its restriction to . We assume that . The tangential projection with respect to is , and we assume there exists independent of such that on . We let satisfy , where and are surface measures of and , respectively. In particular,
From [11, Proposition 2.5], we have
| (2.1) |
and
| (2.2) |
where are the eigenvalues of , whose corresponding eigenvectors are orthogonal to . We set to be the restriction of to .
Surface differential operators with respect to are denoted and defined analogously to those on . We also set ()
to be the piecewise Sobolev space and norm, respectively. Likewise, is the piecewise Sobolev space with respect to with corresponding norm , and denotes the piecewise deformation operator with respect to .
We end this section by stating a well-known characterization of . For each edge of the mesh, denote by the two triangles in the mesh such that . Let denote the outward in-plane normal to , and note that in general, on . Then a vector field satisfies if and only if [23]
| (2.3) |
where .
2.1. Extensions and lifts
For the rest of the paper, we view the closest point projection as a mapping from the discrete surface approximation to the true surface, i.e., . Restricted to the projection is a bijection, and in particular has a well-defined inverse: . Recall that for a scalar or vector-valued function on , its extension (now to ) is . For a scalar or vector-valued function defined on , we define its lift via . Note that on and likewise, on . For , there holds
| (2.4) |
which follows from a change of variables, the chain rule, and the smoothness assumptions of (cf. [13]).
2.2. Surface Piola transforms
Following [30, 9, 3] we summarize the divergence-conforming Piola transform with respect to a mapping between surfaces. Let and be two sufficiently smooth surfaces, and let be a diffeomorphism with inverse . Let be the surface measure of , and let formally satisfy . Then the Piola transform of a vector field with respect to is given by
Likewise, for its Piola transform with respect to is
Similar to the Euclidean setting, there holds
| (2.5) |
in particular, and are bounded mappings. Moreover, as and are tangent maps, the Piola transform yields tangential vector fields: if is the unit normal of the surface , then on and on .
In the case , , and (so that ), the Piola transform of with is [9, 3]
| (2.6) |
whereas the Piola transform of with respect to the inverse is given by
| (2.7) |
Note that on and on . Moreover, it follows from (2.5) that for all ,
| (2.8a) | ||||
| and | ||||
| (2.8b) | ||||
The following lemma states the equivalence of norms of vector fields and their Piola transforms.
Lemma 2.1.
For , let and be related by (2.7) restricted to . Then if for some , there holds . Moreover,
| (2.9) |
Proof.
The proof for the cases is found in [3, Lemma 4.1]. The case follows from similar arguments and is therefore omitted. ∎
We also need a similar result that relates the norm of the deformation tensors of and its Piola transform . The proof of the following result is given in the appendix.
Lemma 2.2.
For , let and be related via . Then
| (2.10) |
Consequently, by a change of variables,
| (2.11) |
We now apply the above definitions of Piola transforms to mappings between planes (surface triangles), which is critical to our construction of vertex degrees of freedom for vector fields on .
Definition 2.3.
For each vertex in the triangulation, we arbitrarily choose a single (fixed) face . For , we define by
| (2.12) |
where we recall and are the outward unit normals of and , respectively. In particular, is the Piola transform of with respect to the inverse of the closest point projection onto the plane containing (cf. (2.7)).
Remark 2.4.
By properties of the Piola transform, is tangential to , i.e., for all .
We next show that the “ideal” and “practical” interpretations of vectors at vertices discussed in the introduction (cf. Figures 1 and 2) do not differ by too much.
Lemma 2.5.
Fix and let lie in the tangent plane of at . For , let be the Piola transform of to via the inverse of the closest point projection (cf. (2.7)). Then
| (2.13) |
Proof.
3. Finite element spaces and inf-sup stability
By utilizing Lemma 2.5, we can construct tangential finite element spaces on the surface approximation using nodal (Lagrange) basis functions. The essential idea is to enforce continuity at nodal degrees of freedom in a weak sense through the mapping given in Definition 2.3. Although this procedure does not yield a globally continuous finite element space, it preserves in-plane normal continuity and exhibits weak continuity properties. These properties are generally sufficient for achieving convergence in second-order elliptic problems.
In the following discussion, we focus on the construction of the lowest-order MINI Stokes pair for simplicity [1]. However, we expect that Definition 2.3 and Lemma 2.5 provide a general framework for constructing convergent finite element schemes based on classical and conforming finite element pairs such as Taylor-Hood and Scott-Vogelius [2].
3.1. Surface MINI space and approximation properties
Let be the reference triangle with vertices , and for , let be an affine diffeomorphism. The constant Jacobian matrix of is denoted by . Note that the columns of span the tangential space of . For a vector-valued function , its Piola transform with respect to is given by
| (3.1) |
and .
Let be the standard cubic bubble function on , i.e., the product of the three barycentric coordinates of . The local MINI space defined on the reference triangle is given by , where is the space of polynomials of degree with domain , and . We then define the surface finite element spaces on as
where is the restriction of to , is defined in Definition 2.3, and we recall is the set of vertices in .
For , we let denote the linear portion of , i.e., is the unique tangential and piecewise linear vector in satisfying for all . We then have the following identity on each :
| (3.2) |
where we have used the fact for all .
Because the columns of span the tangential space of , we see that functions in the discrete velocity space are tangential, i.e., for all . In addition, due to the normal-preserving properties of the transform , the space is -conforming as the next result shows.
Proposition 3.1.
There holds .
Proof.
Due to the properties of the cubic bubble, it is sufficient to show that the linear component of satisfies the in-plane normal continuity condition (2.3) across all edges in .
Let be a vertex of , and let be two elements that have as a vertex and share a common edge . Denote by the in-plane outward unit normal vector with respect to restricted to .
Using the definitions of the finite element space and the operator , along with the Binet-Cauchy identity, there holds for any ,
where . Therefore,
Because is a linear polynomial on , we conclude that (2.3) is satisfied on all edges. This implies the desired result . ∎
Lemma 3.2.
For each , there exists such that
with .
Proof.
Given , we uniquely define such that each component of is a piecewise linear polynomial and satisfies
| (3.3) |
Let be the elementwise (discontinuous), linear interpolant of with respect to the vertices in , i.e., with for all and . By Lemma 2.5 (with ), (3.3), and the definition of we have for each vertex ,
Consequently, by standard inverse estimates,
Using inverse estimates once again, and applying standard interpolation results yields
Therefore,
and so by (2.9),
∎
Lemma 3.3.
There exists a constant independent of such that
| (3.4) |
Proof.
Fix , and let satisfy [20, 14, 11]
| (3.5) |
where we used (2.4) and (2.2) in the last step. Let be the Scott-Zhang interpolant of the extension onto the space of continuous piecewise linear polynomials with respect to [7, 12], and set . From (2.4), , and approximation properties of the Scott-Zhang interpolant, there holds on each ,
| (3.6) |
3.2. -conforming approximations to discrete functions
While the finite element space is merely -conforming (cf. Proposition 3.1), the following lemma shows that functions in this space are “close” to an -conforming relative.
Lemma 3.4.
Given , denote by its Piola transform via the closest point projection to . Then there exists such that
| (3.8) |
Proof.
On an element , we first write , where is componentwise affine on , and is tangent to (cf. (3.2)). Likewise, is the Piola transform of to . We next let be the unique continuous piecewise linear polynomial with respect to satisfying for each vertex . We then set
Note that , and
Fixing , by norm equivalence (cf. (2.9)) we prove (3.8) by establishing that
| (3.25) |
where . We show (3.25) in three steps.
(i) Employing (2.7), (2.1), and , we have that
Here we interchangeably write and in order to better distinguish dependence on the element . Using and , we then have
| (3.26) |
(ii) We next bound the terms , , and in . Using yields
| (3.27) |
Next we use (2.12) and recall that to compute that for each vertex
| (3.28) |
In the last step we have employed (2.6) and (2.7) to obtain . We then use the fact that and are affine, along with inverse inequalities, to obtain
| (3.29) |
In order to bound , we first proceed similarly as (3.28) to obtain
Using , we thus have similar to above that
| (3.30) |
Recalling that and at vertices , we again use inverse inequalities to obtain
| (3.31) |
(iii) In order to bound , we recall (3.26) and consider first . First note that . Thus using an inverse inequality and , we obtain
Employing inverse inequalities, , and (3.29) also yields
We finally compute using inverse inequalities and (3.30) that
Collecting the above inequalities and employing (3.31) yields
which completes the proof. ∎
3.3. Discrete Korn-type inequalities
From Lemma 3.4, we immediately obtain a discrete Korn-type inequality on the exact surface .
Lemma 3.5.
Given , there holds
| (3.32) |
where .
Proof.
From this result, we obtain a discrete Korn inequality for on .
Lemma 3.6.
There holds
| (3.34) |
4. Finite element method and convergence analysis
For piecewise smooth with and , we define the bilinear forms
The variational formulation for the Stokes problem (1.1) seeks satisfying
| (4.1) | ||||||
Remark 4.1.
In order to ensure the well-posedness of (4.1) and avoid technical complications associated with Killing fields, we include the zeroth-order mass term in the momentum equations, as mentioned earlier in the introduction. A method for incorporating Killing fields into surface finite element methods for the Stokes problem is presented in [3], and the main ideas presented there are applicable to the proposed discretization below.
We define the analogous bilinear forms with respect to the discrete surface :
where the differential operator is understood to act piecewise with respect to . Then the finite element method seeks such that
| (4.2) | ||||||
where is some approximation of that is defined on .
By the inf-sup condition (3.4), the discrete Korn-like inequality (3.34), and standard theory of saddle-point problems, there exists a unique solution (4.2). To derive error estimates, we restrict (4.2) to the discretely divergence–free subspace . Then is uniquely determined by the problem
| (4.3) |
Now set , , and note that
where , and
| (4.4) |
is the matrix arising in the definition of . Therefore (4.3) is equivalent to the statement
| (4.5) |
where the bilinear form given by
encodes geometric error.
Lemma 4.2.
There holds
| (4.6) |
for all tangential .
Proof.
The next lemma states the approximation properties of the discretely divergence–free subspace . The result essentially follows from the inf-sup condition (3.4) and the arguments in [6, Theorem 12.5.17]. For completeness we provide the proof.
Lemma 4.3.
Let satisfy . Then there holds
Proof.
Fix . The inf-sup condition (3.4) implies there exists such that for all , and . Then and . This implies the desired result. ∎
Theorem 4.4.
Proof.
Remark 4.5.
In order to obtain a final energy error bound from (4.10) we must choose so that . A short calculation shows that yields ; a variety of other choices also yield optimal convergence.
Remark 4.6.
Analysis of errors in the velocity is the subject of ongoing work. Numerical experiments presented below indicate that , as expected. However, the conforming approximation error estimate given in Lemma 3.4 seems insufficient to obtain an convergence rate in . In addition, the geometric error estimate in Lemma 2.2 is sufficient to establish optimal convergence in the energy norm, but not an optimal convergence rate. Obtaining geometric error estimates sufficient to achieve optimal convergence is likely possible using techniques introduced in [18] but is significantly more technical than the energy case analyzed here.
5. Numerical Experiments
In this section we briefly comment on the implementation of the finite element method (4.2) and then present numerical experiments demonstrating optimal convergence rates in the energy and norms for both MINI and lowest-order Taylor-Hood elements.
5.1. Implementation notes
The main additional complication in the implementation of the surface MINI method as compared to the Euclidean case arises in choosing two individual degrees of freedom at each vertex and interpreting them on each incident element. In the Euclidean case it is natural to choose individual degrees of freedom to align with the canonical Euclidean basis vectors. Thus natural global basis functions corresponding to a vertex are and , with the usual affine hat function corresponding to . In the surface case there is no such natural choice, so at each vertex one must first fix the master element along with two arbitrary but mutually orthogonal unit vectors and tangent to . The two global degrees of freedom corresponding to are then and .
Once , , and are fixed, the Piola transform formula (2.12) is used to interpret these quantities appropriately on each element . These bookkeeping steps are naturally implemented as a precomputation in which the necessary information is encoded into a DOF handler structure. The precomputation step costs and does not add significantly to the overall computational cost. Once this step is completed the rest of the FEM is implemented in a standard way, but using the DOF handler to correctly compute basis functions on each element.
We now describe more precisely some elements of the precomputation step.
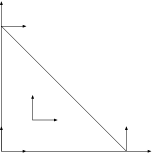
Consider the reference element with associated natural degrees of freedom for the MINI element (cf. Figure 3). Given a vertex , let and be the basis functions corresponding to the vertex degrees of freedom in Figure 3, i.e., and . We translate vertex degrees of freedom from the reference element to physical elements as follows. For each vertex :
-
(1)
Specify a master element .
-
(2)
Choose arbitrary unit orthogonal vectors , lying in the plane containing .
-
(3)
For each triangle , compute , .
-
(4)
For each , let be the local numbering of in .
- (5)
The coefficients serve as a “Rosetta stone” (or DOF handler) to translate the individual reference basis functions elementwise to global basis functions. On the element the global basis functions corresponding to the vertex are concretely given by and , with the standard scalar affine hat function corresponding to . Recall that in the Euclidean case natural global basis functions corresponding to are and . Thus in both the Euclidean and surface cases, the global MINI basis functions may be expressed as the product of a scalar hat function and a vector specifying direction. However, in the surface case the vectors in question are piecewise constant rather than globally constant in order to reflect variation of the tangent plane from element to element. Once these expressions for global basis functions are in hand, the other aspects of the finite element code are essentially standard. Note that sparsity patterns for the resulting system matrices are also similar to the Euclidean case, and the system solve generally has similar expense.
5.2. Numerical results
We take to be the ellipsoid given by . The test solution is ; cf. Figure 4. Note that with on , so is componentwise a rational function and not a polynomial. The pressure is . The incompressibility condition does not hold, so the Stokes system must be solved with nonzero divergence constraint. We employed a MATLAB code built on top of the iFEM library [8].

The left plot in Figure 5 depicts the convergence history for the MINI element on a sequence of uniformly refined meshes. Optimal convergence is clearly observed in both the energy and norms, in particular for the energy norm along with for the error . Recall also that the pressure is approximated by affine functions, which can in theory approximate to order in . Convergence is generally restricted instead to order because the pressure is coupled to the velocity norm in the error analysis, but superconvergence of order may occur on sufficiently structured meshes [15]. We observe an initial superconvergent decrease of order or higher, but the expected asymptotic rate of order is eventually seen; cf. [27] for discussion of similar phenomena in the Euclidean context.


We also approximated using a Taylor-Hood method. The discrete surface was taken to be a quadratic rather than affine approximation to in order to obtain a geometric error commensurate with the expected order of convergence for this element. Vertex degrees of freedom were defined as above, additionally taking into account the fact that the surface normal on a piecewise quadratic surface is, in contrast to the case of an affine surface, not elementwise constant. Quadratic Taylor-Hood vector fields have degrees of freedom at edge midpoints in addition to at vertices, and these were defined in a manner completely analogous to the vertex degrees of freedom. Because the Piola transform preserves normal continuity, this construction guarantees normal continuity at three points on each (closed) edge, thus ensuring -conformity (cf. Proposition 3.1). The right plot in Figure 5 exhibits the expected convergence in the energy norm and convergence for the error in the velocity. This confirms that our methodology has applicability beyond the MINI element; error analysis and extension to other stable Stokes element pairs employing nodal degrees of freedom will be the subject of future work.
Appendix A Proof of Lemma 2.2
Proof.
We divide the proof of Lemma 2.2 into three steps.
Step 1: For a scalar function defined on , we have the identity [12, (2.2.19)]
Consequently, for ,
Here, with an abuse of notation, we have suppressed the superscript for the extension . Thus, we have the identity
| (A.1) |
Since is tangential, there holds , because is constant on . Thus,
| (A.2) |
Step 2: Write with . We then have by (A.2),
where
| (A.3) |
We conclude, by adding and subtracting terms, that
Using , , and (2.2), we have and . Therefore there holds
| (A.4) |
Step 3: In the final step of the proof, we bound the last term in (A.4).
Write . Because is constant on and , there holds . Also by Jacobi’s formula and ,
We then conclude using that
| (A.7) |
| (A.8) |
Acknowledgements
The authors thank Orsan Kilicer for assistance with numerical computations.
References
- [1] D. N. Arnold, F. Brezzi, and M. Fortin, A stable finite element for the Stokes equations, Calcolo, 21 (1984), pp. 337–344 (1985).
- [2] D. Boffi, F. Brezzi, L. F. Demkowicz, R. G. Durán, R. S. Falk, and M. Fortin, Mixed finite elements, compatibility conditions, and applications, vol. 1939 of Lecture Notes in Mathematics, Springer-Verlag, Berlin; Fondazione C.I.M.E., Florence, 2008. Lectures given at the C.I.M.E. Summer School held in Cetraro, June 26–July 1, 2006, Edited by Boffi and Lucia Gastaldi.
- [3] A. Bonito, A. Demlow, and M. Licht, A divergence-conforming finite element method for the surface Stokes equation, SIAM J. Numer. Anal., 58 (2020), pp. 2764–2798.
- [4] P. Brandner, T. Jankuhn, S. Praetorius, A. Reusken, and A. Voigt, Finite element discretization methods for velocity-pressure and stream function formulations of surface Stokes equations, SIAM J. Sci. Comput., 44 (2022), pp. A1807–A1832.
- [5] P. Brandner and A. Reusken, Finite element error analysis of surface Stokes equations in stream function formulation, ESAIM Math. Model. Numer. Anal., 54 (2020), pp. 2069–2097.
- [6] S. C. Brenner and L. R. Scott, The mathematical theory of finite element methods, vol. 15 of Texts in Applied Mathematics, Springer, New York, third ed., 2008.
- [7] F. Camacho and A. Demlow, and pointwise a posteriori error estimates for FEM for elliptic PDEs on surfaces, IMA J. Numer. Anal., 35 (2015), pp. 1199–1227.
- [8] L. Chen, iFEM: An innovative finite element method package in Matlab, tech. rep., University of California-Irvine, 2009.
- [9] B. Cockburn and A. Demlow, Hybridizable discontinuous Galerkin and mixed finite element methods for elliptic problems on surfaces, Math. Comp., 85 (2016), pp. 2609–2638.
- [10] B. Cockburn, G. Kanschat, and D. Schotzau, A locally conservative LDG method for the incompressible Navier-Stokes equations, Math. Comp., 74 (2005), pp. 1067–1095.
- [11] A. Demlow, Higher-order finite element methods and pointwise error estimates for elliptic problems on surfaces, SIAM J. Numer. Anal., 47 (2009), pp. 805–827.
- [12] A. Demlow and G. Dziuk, An adaptive finite element method for the Laplace-Beltrami operator on implicitly defined surfaces, SIAM J. Numer. Anal., 45 (2007), pp. 421–442.
- [13] G. Dziuk, Finite elements for the Beltrami operator on arbitrary surfaces, in Partial differential equations and calculus of variations, vol. 1357 of Lecture Notes in Math., Springer, Berlin, 1988, pp. 142–155.
- [14] G. Dziuk and C. M. Elliott, Finite element methods for surface PDEs, Acta Numer., 22 (2013), pp. 289–396.
- [15] H. Eichel, L. Tobiska, and H. Xie, Supercloseness and superconvergence of stabilized low-order finite element discretizations of the Stokes problem, Math. Comp., 80 (2011), pp. 697–722.
- [16] T.-P. Fries, Higher-order surface FEM for incompressible Navier-Stokes flows on manifolds, Internat. J. Numer. Methods Fluids, 88 (2018), pp. 55–78.
- [17] S. Gross, T. Jankuhn, M. A. Olshanskii, and A. Reusken, A trace finite element method for vector-Laplacians on surfaces, SIAM J. Numer. Anal., 56 (2018), pp. 2406–2429.
- [18] P. Hansbo, M. G. Larson, and K. Larsson, Analysis of finite element methods for vector Laplacians on surfaces, IMA J. Numer. Anal., 40 (2020), pp. 1652–1701.
- [19] H. Hardering and S. Praetorius, Tangential errors of tensor surface finite elements, IMA J. Numer. Anal., 43 (2023), pp. 1543–1585.
- [20] T. Jankuhn, M. A. Olshanskii, and A. Reusken, Incompressible fluid problems on embedded surfaces: modeling and variational formulations, Interfaces Free Bound., 20 (2018), pp. 353–377.
- [21] T. Jankuhn, M. A. Olshanskii, A. Reusken, and A. Zhiliakov, Error analysis of higher order trace finite element methods for the surface Stokes equation, J. Numer. Math., 29 (2021), pp. 245–267.
- [22] V. John, A. Linke, C. Merdon, M. Neilan, and L. G. Rebholz, On the divergence constraint in mixed finite element methods for incompressible flows, SIAM Rev., 59 (2017), pp. 492–544.
- [23] P. L. Lederer, C. Lehrenfeld, and J. Schöberl, Divergence-free tangential finite element methods for incompressible flows on surfaces, Internat. J. Numer. Methods Engrg., 121 (2020), pp. 2503–2533.
- [24] I. Nitschke, A. Voigt, and J. Wensch, A finite element approach to incompressible two-phase flow on manifolds, J. Fluid Mech., 708 (2012), pp. 418–438.
- [25] M. A. Olshanskii, A. Quaini, A. Reusken, and V. Yushutin, A finite element method for the surface Stokes problem, SIAM J. Sci. Comput., 40 (2018), pp. A2492–A2518.
- [26] M. A. Olshanskii and V. Yushutin, A penalty finite element method for a fluid system posed on embedded surface, J. Math. Fluid Mech., 21 (2019), pp. Paper No. 14, 18.
- [27] D. R. Q. Pacheco and O. Steinbach, On the initial higher-order pressure convergence in equal-order finite element discretizations of the Stokes system, Comput. Math. Appl., 109 (2022), pp. 140–145.
- [28] A. Reusken, Stream function formulation of surface Stokes equations, IMA J. Numer. Anal., 40 (2020), pp. 109–139.
- [29] L. R. Scott and M. Vogelius, Norm estimates for a maximal right inverse of the divergence operator in spaces of piecewise polynomials, RAIRO Modél. Math. Anal. Numér., 19 (1985), pp. 111–143.
- [30] P. Steinmann, On boundary potential energies in deformational and configurational mechanics, J. Mech. Phys. Solids, 56 (2008), pp. 772–800.
- [31] C. Taylor and P. Hood, A numerical solution of the Navier-Stokes equations using the finite element technique, Internat. J. Comput. & Fluids, 1 (1973), pp. 73–100.