A Survey on Estimation Schemes in Molecular Communications

The transparent $\mathrm{RX}$ does not impede the diffusion of molecules, nor interact with molecules. We count the number of free molecules that are within the $\mathrm{RX}$ volume as the received signal. The CIR of the transparent $\mathrm{RX}$ is given by [17, eq. (4)]

where $V_{\scriptscriptstyle\mathrm{RX}}$ is the volume of the $\mathrm{RX}$ and $V_{\scriptscriptstyle\mathrm{RX}}=\frac{4}{3}\pi r_{\scriptscriptstyle\mathrm{R}}^{3}$ for the spherical $\mathrm{RX}$. It is noted that $h(t)$ incorporating the flow and degradation of molecules is given by [13, eq. (13)]. It is also noted that (1) is accurate when the $\mathrm{RX}$ is sufficiently far away from the $\mathrm{TX}$, i.e., $d$ is very large relative to $r_{\scriptscriptstyle\mathrm{R}}$. Thus, it is reasonable to assume that the concentration of molecules at every point within the $\mathrm{RX}$ equals the concentration at the central point of the $\mathrm{RX}$. If the $\mathrm{RX}$ is close to the $\mathrm{TX}$, the uniform assumption of concentration does not hold. In this case, $h(t)$ is given by [18, eq. (27)]

where $\mathrm{erf}(\cdot)$ denotes the error function. We note that (1) is more widely applied in existing studies than (II-B1), due to its simplicity, and (1) provides an accurate approximation for (II-B1) if $r_{\scriptscriptstyle\mathrm{R}}<0.15d$ [18].

We now denote $\overline{N}(t)$ as the expected number of molecules observed within the $\mathrm{RX}$ volume at time $t$. If an impulse of $N_{\mathrm{tx}}$ molecules is released from the $\mathrm{TX}$ at time $t_{0}=0$, $\overline{N}(t)$ is given by $\overline{N}(t)=N_{\mathrm{tx}}h(t)$. In Fig. 2, we plot $\overline{N}(t)$ versus time $t$ by adopting (1). From this figure, we observe a peak number of molecules observed within the $\mathrm{RX}$. We denote the time for reaching the peak number of molecules observed as $t_{\mathrm{max}}$. By taking the derivative of (1) with respective to $t$, $t_{\mathrm{max}}$ is calculated as [19, eq. (6)]

By substituting (3) into (1), we obtain the peak CIR, denoted by $h_{\mathrm{max}}$, as

We denote $\overline{N}_{\mathrm{max}}$ as the expected peak number of molecules observed within the RX. Then $\overline{N}_{\mathrm{max}}$ is given by $\overline{N}_{\mathrm{max}}=N_{\mathrm{tx}}h_{\mathrm{max}}$.

In biological systems, many practical $\mathrm{RX}$ surfaces may interact with the molecules of interest, e.g., by providing binding sites for absorption or other reactions [20]. Hence, the transparent $\mathrm{RX}$ model is over-simplified. One practical $\mathrm{RX}$ model is the fully-absorbing $\mathrm{RX}$. In this model, the $\mathrm{RX}$ absorbs molecules as soon as they hit the surface. The fully-absorbing $\mathrm{RX}$ counts the total number of molecules absorbed as the received signal, where the CIR is given by [21, eq. (23)]

Different from the fully-absorbing $\mathrm{RX}$, molecules that reach the $\mathrm{RX}$ may participate in a reversible bimolecular second-order reaction with receptors over the $\mathrm{RX}$ membrane. This type of $\mathrm{RX}$ is named as the reactive $\mathrm{RX}$ whose received signal is the number of activated receptors. The CIR of the reactive $\mathrm{RX}$ is given by [22, eq. (29)] and is omitted here due to its complex format.

Due to the random diffusion (RD) of molecules, the number of molecules observed at the $\mathrm{RX}$ is a random variable (RV) [23]. This randomness influences the performance of estimation. Due to the independent diffusion of molecules, any given molecule released by the $\mathrm{TX}$ is observed by the $\mathrm{RX}$ with a probability of $h(t)$. A binary state model applies and the number of molecules observed at time $t$, denoted by $N_{\mathrm{ob}}(t)$, follows a binomial distribution with $N_{\mathrm{tx}}$ trails and success probability $h(t)$. This is mathematically expressed as

where $\mathcal{B}(N,p)$ represents a binomial distribution. Unfortunately, the binomial distribution is cumbersome to work with in MC systems. Therefore, current studies usually approximate binomial distribution as two distributions for the sake of mathematical tractability, described as follows:

• (a)

  Poisson distribution: When the number of trials $N_{\mathrm{tx}}$ is large and the success probability $h(t)$ is small, $N_{\mathrm{ob}}(t)$ can be approximated as a Poisson RV, given by

  $\displaystyle N_{\mathrm{ob}}(t)\sim\mathcal{P}\left(N_{\mathrm{tx}}h(t)\right),$

  (7)

  where $\mathcal{P}(\varphi)$ represents the Poisson distribution with the mean of $\varphi$. Based on (7), the probability mass function (PMF) of the Poisson RV $N_{\mathrm{ob}}(t)$ is written as

  $\displaystyle\mathrm{Pr}\left(N_{\mathrm{ob}}(t)=\xi\right)=\frac{\left(N_{\mathrm{tx}}h(t)\right)^{\xi}\exp\left(-N_{\mathrm{tx}}h(t)\right)}{\xi!},$

  (8)

  where $\mathrm{Pr}(\cdot)$ stands for the probability.

• (b)

  Gaussian distribution: If the expected number of molecules observed, i.e., $\overline{N}(t)$, is sufficiently large, we can apply the central limit theorem and approximate $N_{\mathrm{ob}}(t)$ as a Gaussian RV, given by

  $\displaystyle N_{\mathrm{ob}}(t)\sim\mathcal{N}\left(N_{\mathrm{tx}}h(t),N_{\mathrm{tx}}h(t)(1-h(t))\right).$

  (9)

  The probability density function (PDF) of $N_{\mathrm{ob}}(t)$ is given by

  $\displaystyle\mathrm{Pr}\left(N_{\mathrm{ob}}(t)=\xi\right)=\frac{\exp\left(-\frac{(\xi-N_{\mathrm{tx}}h(t))^{2}}{2N_{\mathrm{tx}}h(t)(1-h(t))}\right)}{\sqrt{2\pi N_{\mathrm{tx}}h(t)(1-h(t))}}.$

  (10)

In MC systems, the intended $\mathrm{TX}$ may not be the only source of molecules. Other sources, referred to as external sources, may also release the same type of molecules that influence the observation at the $\mathrm{RX}$ and affects the estimation performance. We detail some examples of external sources as follows:

• (a)

  Multiuser interference: Noisy molecules are emitted by $\mathrm{TXs}$ in other MC systems.

• (b)

  Unintended leakage: Molecules can be leaked from membrane-bound containers, e.g., vesicles, within transceivers. A rupture can result in a steady or sudden release of molecules [24].

• (c)

  Output from unrelated biochemical processes: Biocompatibility of the MC system may require the selection of naturally-occurring molecules. Therefore, other processes that produce the same type of molecules are noisy sources for the considered MC system. For example, calcium is commonly used as a messenger molecule within cellular systems [25, Ch. 16]. If calcium is applied as signaling molecules of the MC system in the biological environment, the naturally-occurring calcium would impact the MC system.

• (d)

  Unintended reception of other molecules: Molecules that are highly similar to intended molecules may be recognized by the $\mathrm{RX}$. For example, the receptors at the $\mathrm{RX}$ may bind to other molecules that have a very similar shape and size to intended molecules [25, Ch. 4].

We denote $N_{\mathrm{sig}}(t)$ as the intended observed molecules and $n(t)$ as the observed noise molecules. Since intended molecules and noise molecules are indistinguishable, the total number of molecules observed at the $\mathrm{RX}$ at time $t$ is given by

The analysis of the statistical distribution of $n(t)$ is built upon following assumptions:

• A1)

  We denote $\overline{n}$ as the expected number of noise molecules observed within the $\mathrm{RX}$. We assume that $\overline{n}$ is constant over the entire observation time.

• A2)

  The observation of one noise molecule at the $\mathrm{RX}$ is independent of observations of other noise molecules.

• A3)

  The uniform concentration assumption holds for noise molecules at the $\mathrm{RX}$.

Based on A1)–A3), we model the number of observed noise molecules as a Poisson RV, due to the law of rare events (LRE) [26], i.e., $n(t)\sim\mathcal{P}(\overline{n})$.

ISI exists when the $\mathrm{TX}$ transmits multiple symbols to the $\mathrm{RX}$. Due to the RD of molecules, the molecules from previously sent symbols may arrive at the $\mathrm{RX}$ in the current symbol interval, which influences the estimation in the current symbol interval. ILI exists for the multiple-input multiple-output (MIMO) MC system, where one $\mathrm{TX}-\mathrm{RX}$ channel is influenced by molecules released from other channels.

In RTT protocols, $T$ measures the RTT that is the sum of time required for the transmission from $T$ to $R$ and for the transmission from $R$ to $T$. The first estimation scheme is named as the RTT protocol from peak concentration (RTT-P). In RTT-P, $T$ transmits at time $t_{0}$ and $R$ detects the peak concentration of molecules $A$ from $T$ at time $t_{1}$. According to (3), we can obtain the relationship between $t_{1}-t_{0}$ and $d$. $T$ detects the peak concentration of the feedback signal with type $B$ molecules at time $t_{2}$. Similarly, we can obtain the relation between $t_{2}-t_{1}$ and $d$ based on (3). Accordingly, the distance $d$ is estimated as a function of the RTT $t_{2}-t_{0}$ as

where $\hat{d}$ is the estimated value of $d$.

The second estimation scheme was named as the RTT protocol from threshold concentration (RTT-T). Different from RTT-P, RTT-T defines threshold concentrations $H_{A}$ and $H_{B}$ for $R$ and $T$ to detect the number of molecules observed, respectively. It is assumed that $T$ transmits $N_{\mathrm{tx}}^{A}$ number of molecules $A$ and $R$ transmits $N_{\mathrm{tx}}^{B}$ number of molecules $B$. $R$ records $t_{1}$ when the number of molecules observed reach the threshold concentration $H_{A}$, i.e., $\overline{N}(t_{1}-t_{0})|_{D=D_{A},N_{\mathrm{tx}}=N_{\mathrm{tx}}^{A}}=H_{A}$ by assuming $\overline{N}(t)=N_{\mathrm{ob}}(t)$. Similarly, $T$ records $t_{2}$ when the number of molecules observed reach the threshold concentration $H_{B}$, i.e., $\overline{N}(t_{2}-t_{1})|_{D=D_{B},N_{\mathrm{tx}}=N_{\mathrm{tx}}^{B}}=H_{B}$. If $D_{A}=D_{B}$, $N_{\mathrm{tx}}^{A}=N_{\mathrm{tx}}^{B}$, and $H_{A}=H_{B}$, $d$ is estimated as a function of the RTT $t_{2}-t_{0}$ as

In SA-P, $T$ transmits type $A$ molecules to $R$, and $R$ measures the peak concentration, denoted by $N_{\mathrm{ob,m}}^{A}$. According to (4), we can obtain the relationship between $N_{\mathrm{ob,m}}^{A}$ and $d$ by replacing $\overline{N}_{\mathrm{max}}$ with $N_{\mathrm{ob,m}}^{A}$. Similarly, $R$ transmits type $B$ molecules and $T$ measures the peak concentration, denoted by $N_{\mathrm{ob,m}}^{B}$. By assuming $N_{\mathrm{tx}}^{B}=N_{\mathrm{ob,m}}^{A}$, $\hat{d}$ is obtained as

The estimation performance of SA has been shown in [19].

In this subsection, we summarize the merits and drawbacks of the two-way estimation. One merit of this estimation is that the synchronization between two transceivers is not required. For both RTT and SA protocols, only the time period of two-way transmission, the number of emitted molecules, and peak observed concentration at $T$ are required. Despite this merit, there are several drawbacks. The first drawback is that this estimation is time-consuming since it requires two-way transmission. The second one is that this estimation requires $R$ to immediately send the feedback signal when it detects the type of molecules $A$, which is challenge for a nanomachine. The third drawback is that the instantaneous observation at the $\mathrm{RX}$ is used to approximate its expectation, which affects the estimation performance.

In this subsection, we review the studies that perform the estimation via measuring the peak received signal or the time for reaching the peak received signal.

First, [32] performed the estimation based on the peak number of observed molecules, denoted by $N_{\mathrm{ob,m}}$, at the transparent $\mathrm{RX}$. According to (4), the distance $d$ is estimated as

The estimation performance of this method is affected by the RD of molecules, since the instantaneous observation is used to approximate its expectation.

Second, [11] considered, for the first time, the release of molecules from the $\mathrm{TX}$ as a rectangular pulse, where the CIR at the transparent $\mathrm{RX}$ is denoted by $h_{\mathrm{rec}}(t)$. By taking the derivative of $h_{\mathrm{rec}}(t)$ with respect to $t$, $d$ can be estimated via measuring the time for reaching the peak concentration at the $\mathrm{RX}$ as

where $T_{\mathrm{e}}$ is the emission duration.

As $t_{\mathrm{max}}$ is involved in the estimation of [11], a perfect synchronization between the $\mathrm{TX}$ and the $\mathrm{RX}$ is required. In [35, 36], the authors proposed a low-complexity scheme that does not require the synchronization via adopting two types of molecules. In this scheme, the $\mathrm{TX}$ releases type $A$ molecules at time $t_{0}$ and the $\mathrm{RX}$ records the time of peak concentration of molecules $A$, denoted by $t_{\mathrm{max}}^{A}$. Similarly, the $\mathrm{TX}$ transmits type $B$ molecules at $t_{1}$, and the $\mathrm{RX}$ records the time of peak concentration of molecules $B$, denoted by $t_{\mathrm{max}}^{B}$. According to (3), the relation between $t_{\mathrm{max}}^{A}$ and $d$, and $t_{\mathrm{max}}^{B}$ and $d$ are obtained. Thus, $d$ is estimated as

where $\Delta t_{\scriptscriptstyle\mathrm{RX}}=t_{\mathrm{max}}^{B}-t_{\mathrm{max}}^{A}$ and $\Delta t_{\scriptscriptstyle\mathrm{TX}}=t_{1}-t_{0}$. We note that $\Delta t_{\scriptscriptstyle\mathrm{RX}}$ and $\Delta t_{\scriptscriptstyle\mathrm{TX}}$ are based on the time measurements at the $\mathrm{RX}$ and the $\mathrm{TX}$, respectively. Therefore, synchronization is not required.

In [10, 32, 11, 35, 36], estimation is performed in an unbounded environment. Different from these studies, [34] considered a cylindrical MC environment whose surface is reflecting as shown in Fig. 3. Within the cylindrical environment, a point $\mathrm{TX}$ releases molecules and two ring-shaped $\mathrm{RXs}$ with a certain width $w$ are located on the cylinder perimeter with a radius $r_{\mathrm{v}}$ that is the same as the cylinder’s radius. After the molecules are released, they diffuse randomly with a constant diffusion coefficient $D$ and subject to the Poiseuille flow [43]. As the cylindrical MC environment is a good approximation of the blood vessel environment, it has been widely investigated in existing studies, e.g., [34, 44, 45]. Due to the existence of the Poiseuille flow, advection and diffusion can both transport molecules. In [34], Turan et al. considered a diffusion-domain movement and only focused on the movement in the $x$ axis, i.e., the channel is approximated as a 1D environment. The authors performed the estimation in two scenarios. The first scenario is that the emission time of molecules is known. By measuring the time of peak concentration, the distance can be estimated by a single $\mathrm{RX}$ as

where $D_{\mathrm{e}}$ is the effective diffusion coefficient and $v_{m}$ is the average flow velocity. The second scenario is that the emission time is unknown. Thus, $t_{\mathrm{max}}$ is unknown and (27) contains two unknown parameters, i.e., $d_{1}$ and $t_{\mathrm{max}}$. In this scenario, $d_{1}$ is estimated by using two $\mathrm{RXs}$. Similar to (27), an equation containing $d_{1}$ and $t_{\mathrm{max}}$ can be obtained at the second $\mathrm{RX}$. Thus, $d_{1}$ can be mathematically derived by jointly solving these two equations.

The ML estimation is to find $\hat{\theta}$ that maximizes the joint observation likelihood, which usually achieves high accuracy, but requires high computational complexity and the perfect synchronization between the $\mathrm{TX}$ and the $\mathrm{RX}$. The authors in [19, 37] considered $x_{m}$, i.e., the $m$th data of the data set $\mathbf{x}$, as the number of molecules observed at the transparent $\mathrm{RX}$ at time $t_{m}$ when molecules are released at time $t_{0}$. It is assumed that each observation is independent and follows a Poisson distribution. Thus, $p(\mathbf{x};\theta)$ is given by

Using (28), $d$ is estimated by taking the partial derivative of $p(\mathbf{x};\theta)$ with respect to $d$ and setting it equal to 0. Moreover, [19] derived the CRLB on the variance of $\hat{d}$.

It is noted that [19, 37] only considered the transmission of one symbol from the $\mathrm{TX}$ to the $\mathrm{RX}$. Different from that, [38] considered multiple symbols transmitted from the $\mathrm{TX}$ to the transparent $\mathrm{RX}$, where ISI exists and may impact the estimation performance. Assuming that the $\mathrm{RX}$ makes one observation in each symbol interval, $p(\mathbf{x};\theta)$ is the joint PDF of multiple observations. Based on $p(\mathbf{x};\theta)$, $d$ is estimated.

Previous studies have focused on the distance estimation in a static MC system. Instead of that, [39] considered estimating the initial distance, i.e., the distance between the $\mathrm{TX}$ and the $\mathrm{RX}$ at the initial moment, in a diffusive mobile MC scenario, where both $\mathrm{TX}$ and $\mathrm{RX}$ diffuse with constant diffusion coefficients $D_{\mathrm{TX}}$ and $D_{\mathrm{RX}}$, respectively. A novel two-step scheme was proposed to estimate the initial distance, denoted by $d_{0}$. We denote $d(t)$ as the distance between the $\mathrm{TX}$ and the $\mathrm{RX}$ at time $t$, and the PDF of $d(t)$ is given by [39, eq. (13)], where $d_{0}$ is a parameter of the PDF of $d(t)$. Moreover, [39] proved that the ML estimation based on the joint PDF of multiple values of $d(t)$ can be simplified as performing the estimation based on the PDF of the first value of $d(t)$, i.e., $d(t_{1})$. Therefore, the first step is to estimate the stochastic distance $d(t_{1})$, where the estimation scheme is similar to [19]. The second step is to estimate $d_{0}$ by finding $\hat{d}_{0}$ that maximizes the PDF of $d(t_{1})$.

As the closed-form expression for $\hat{d}$ is difficult to derive in the ML estimation, [38] and [39] used the Newton-Raphson method, which is a method to find successively better approximations to the roots of a real-valued function, in order to calculate $\hat{d}$.

In this section, we review estimation schemes in an environment with non-transparent $\mathrm{RXs}$. Wang et al. in [40] proposed an estimation scheme by applying a fully-absorbing $\mathrm{RX}$. The $\mathrm{RX}$ performs estimation by counting the number of molecules absorbed within a time interval. Specifically, an algorithm was proposed when the $\mathrm{TX}$ and the $\mathrm{RX}$ are unsynchronized. Moreover, the authors considered two optimization methods to improve the performance of estimation. The first method is using molecules with a large diffusion coefficient and the second method is increasing the number of emitted molecules.

Different from [40], the authors in [41] performed the estimation in an environment with multiple fully-absorbing $\mathrm{RXs}$. As one fully-absorbing $\mathrm{RX}$ would impact molecules absorbed by other fully-absorbing $\mathrm{RXs}$, an accurate derivation for the number of molecules absorbed at each $\mathrm{RX}$ is cumbersome. Miao et al. in [41] adopted a curve fitting method to obtain the expression for the number of absorbed molecules. Specifically, [41] used the nonlinear least squares method for curve fitting to obtain the distance, where the Levenberg-Marquardt (LM) method [46] is adopted.

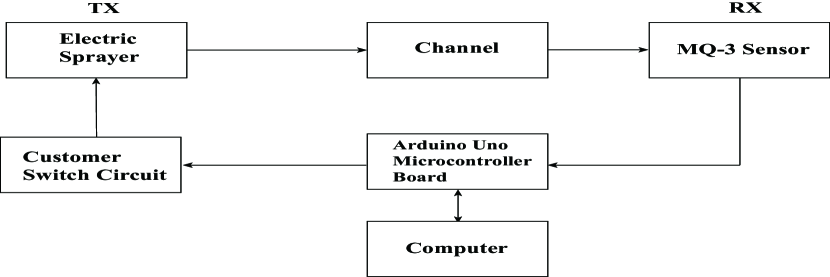
Previous studies focused on the distance estimation in micro-scale ($\mathrm{nm}$ to $\mu\mathrm{m}$) MC systems. With this focus, these studies have considered an ideal channel model where the transmitted molecules do not have an initial velocity, the molecules move according to Brownian motion, and the $\mathrm{TX}$ and the $\mathrm{RX}$ perfectly transmit and receive signals. In nature, MC also exists in the macro-scale ($\mathrm{cm}$ to $\mathrm{m}$) environment. For example, animals like bees, flies and ants use pheromone to send messengers over several meters. Against this background, [42] investigated, for the first time, the distance estimation in the macro-scale environment. Instead of analyzing a theoretical model, [42] established an experimental setup similar to the tabletop platform in [47]. Fig. 4 shows the block diagram of the experimental setup. The $\mathrm{TX}$ is an electric sprayer controlled by a micro-controller via a custom switch circuit to release ethyl alcohol molecules. The $\mathrm{RX}$ receives the molecular signal with an MQ-3 alcohol sensor. The $\mathrm{TX}$ and the $\mathrm{RX}$ are both controlled by an Arduino Uno micro-controller board which is connected to a computer. Five different practical methods were proposed for distance estimation at the $\mathrm{RX}$. The first two methods adopt the supervised machine learning, where multivariate linear regression and neural network regression are used. These methods use the extracted features, e.g., rise time on the rising edge of the measured signal, from the received molecular signals as inputs. The other three methods analyze the collected data, which are less complex but less accurate than machine learning methods. The first data analysis method employs the received power to estimate the distance. The second data analysis method employs the peak time of the received signal. The third method combines the power and peak time of the received signal to estimate the distance.

The ML CIR estimation scheme aims to find the CIR that maximizes the likelihood of observation vector $\mathbf{z}$ [65]. In particular, the ML estimation is given by

We assume that $z[q]$ is a Poisson RV with the mean of $\overline{z}[q]=\overline{c}_{\mathtt{n}}+\sum_{u=1}^{U}\overline{c}_{u}b[q-u+1]=\overline{\mathbf{c}}^{T}\mathbf{b}_{q}$ and $\mathbf{b}_{q}=[b[q],b[q-1],\dots,b[q-U+1],1]^{T}$. Under this assumption, $f_{\mathbf{z}}(\mathbf{z}|\overline{\mathbf{c}},\mathbf{b})$ is given by

We note that [15] solved the ML estimation of the CIR given in (31) by using Algorithm 1, where the following non-linear system of equations is solved³³3A system of nonlinear equations can be solved by using mathematical software packages, e.g., Mathematica. for different $\mathcal{A}_{w}$

where $\mathcal{A}=\{\mathcal{A}_{1},\mathcal{A}_{2},\cdots,\mathcal{A}_{W}\}$ denotes a set which contains all possible $W=2^{U+1}-1$ subsets of the set $\mathcal{F}=\{1,2,\cdots,U,\mathtt{n}\}$, except for the empty set. Here, $\mathcal{A}_{w}$ denotes the $w$-th subset of $\mathcal{A}$, $w=1,2,\cdots,W$. Moreover, let $\overline{\mathbf{c}}^{\mathcal{A}_{w}}$ and $\mathbf{b}_{q}^{\mathcal{A}_{w}}$ denote the reduced-dimension versions of $\overline{\mathbf{c}}$ and $\mathbf{b}_{q}$, respectively, which only contain those elements of $\overline{\mathbf{c}}$ and $\mathbf{b}_{q}$ whose indices are the elements of $\mathcal{A}_{w}$, respectively.

The LSSE CIR estimation scheme aims to choose $\overline{\mathbf{c}}$ that minimizes the sum of the squared errors for the observation vector $\mathbf{z}$. Here, the error vector is defined as $\boldsymbol{\epsilon}=\mathbf{z}-\operatorname*{\mathbb{E}}\left\{\mathbf{z}\right\}=\mathbf{z}-\mathbf{B}\overline{\mathbf{c}}$ where $\mathbf{B}=[\mathbf{b}_{U},\mathbf{b}_{U+1},\dots,\mathbf{b}_{Q}]^{T}$. In particular, the LSSE CIR estimation can be written as

It is noted that [15] also obtained the LSSE estimation of the CIR by solving (34). The solution is given by Algorithm 1 where for a given set $\mathcal{A}_{w}$, $\overline{\mathbf{c}}^{\mathcal{A}_{w}}$ is obtained as

We also note that [61] designed a communication protocol that estimates the CIR based on the least square method, similar to the LSSE CIR estimation in [15].

With the estimation error vector defined as $\mathbf{e}=\overline{\mathbf{c}}-\hat{\overline{\mathbf{c}}}$, the classical CRLB for the deterministic $\overline{\mathbf{c}}$ provides the following lower bound on the sum of the expected square errors [15]

where $\mathrm{tr}\{\cdot\}$ denotes the trace of a matrix. While [15] derived the ML and LSSE estimation schemes of the CIR and the CRLB for a single-input single-output channel, [16] extended these results to a diffusive MIMO system, by incorporating the ILI.