∎
Fax: +65-6779-5452, Tel.: +65-6516-2765,
URL: https://blog.nus.edu.sg/matbwz/
22email: [email protected]
Y. Li 33institutetext: Department of Mathematics, National University of Singapore, Singapore 119076
33email: [email protected]
A structure-preserving parametric finite element method for geometric flows with anisotropic surface energy
Abstract
We propose and analyze structure-preserving parametric finite element methods (SP-PFEM) for evolution of a closed curve under different geometric flows with arbitrary anisotropic surface energy for representing the outward unit normal vector. By introducing a novel surface energy matrix depending on and the Cahn-Hoffman -vector as well as a nonnegative stabilizing function , which is a sum of a symmetric positive definite matrix and an anti-symmetric matrix, we obtain a new geometric partial differential equation and its corresponding variational formulation for the evolution of a closed curve under anisotropic surface diffusion. Based on the new weak formulation, we propose a parametric finite element method for the anisotropic surface diffusion and show that it is area conservation and energy dissipation under a very mild condition on . The SP-PFEM is then extended to simulate evolution of a close curve under other anisotropic geometric flows including anisotropic curvature flow and area-conserved anisotropic curvature flow. Extensive numerical results are reported to demonstrate the efficiency and unconditional energy stability as well as good mesh quality property of the proposed SP-PFEM for simulating anisotropic geometric flows.
Keywords:
geometric flows parametric finite element method anisotropy surface energy structure-preserving area conservation energy-stableMSC:
65M60, 65M12, 35K55, 53C441 Introduction
Anisotropic surface energy along surface/interface is ubiquitous in solids and materials science due to the lattice orientational difference gurtin2002interface ; Cahn94 . It thus generates anisotropic evolution process of interface/surface (or geometric flows with anisotropic surface energy) in material sciences Sutton95 ; Thompson12 ; jiang2012 , imaging sciences niessen1997general ; clarenz2000anisotropic ; dolcetta2002area , and computational geometry wang2015sharp ; Cahn94 ; deckelnick2005computation . In fact, anisotropic geometric flows have significant and broader applications in materials science, solid-state physics and computational geometry, such as grain boundary growth barrett2010finite , foam bubble/film shen2004direct , surface phase formation Ye10a , epitaxial growth Fonseca14 ; gurtin2002interface , heterogeneous catalysis randolph2007controlling , solid-state dewetting Thompson12 ; bao2017parametric ; https://doi.org/10.48550/arxiv.2012.11404 , computational graphics niessen1997general ; clarenz2000anisotropic ; dolcetta2002area .
Assume be a closed curve in two dimensions (2D) associated with a given anisotropic surface energy , where representing the unit outward normal vector, and define the free energy functional of the closed curve associate with anisotropic surface energy as
| (1.1) |
where denotes the arc-length parameter of . By applying the thermodynamic variation, one can obtain the chemical potential (or weighted curvature denoted as ) generated from the energy functional as jiang2019sharp ; taylor1992ii
| (1.2) |
where is a small perturbation of . Different geometric flows associate with the anisotropic surface energy can be easily defined by providing the normal velocity for evolution of . Typical geometric flows widely used in different applications including anisotropic curvature flow, area-conserved anisotropic curvature flow and anisotropic surface diffusion with the corresponding normal velocity given as cahn1991stability ; taylor1992overview ; chen1999uniqueness ; andrews2001volume ; Barrett2020
| (1.3) |
where is chosen such that the area of the region enclosed by is conserved, which is given as
| (1.4) |
We remark here that if for , i.e. isotropic surface energy, then the chemical potential defined in (1.2) collapses to the curvature of , and then the geometric flows defined in (1.3) collapse to curvature flow (or curve-shortening flow), area-conserved curvature flow and surface diffusion, respectively, we refer to the review paper Barrett2020 .
Based on different parametrizations of and mathematical formulations for the geometric flows (1.3), several numerical methods have been proposed for simulating the geometric flows (1.3) with isotropic and anisotropic surface energy corresponding to and , respectively. These numerical methods include the level set method and the phase-field method du2020phase , the marker particle method wong2000periodic ; du2010tangent , the finite element method based on graph formulation deckelnick2005computation ; deckelnick2005fully , the discontinuous Galerkin method xu2009local , the crystalline method carter1995shape ; girao1996crystalline , the evolving surface finite element method (ESFEM) kovacs2019convergent , and the parametric finite element method (PFEM) barrett2007parametric ; barrett2008parametric . Due to that only the normal velocity is given in the anisotropic geometric flows (1.3), different artificial tangential velocities are introduced in different numerical methods, which cause different accuracies and mesh qualities, and thus some methods need to carry out re-mesh frequently during evolution to avoid the collision of mesh points. Among those numerical methods, the PFEM proposed by Barrett, Garcke, and Nürnberg (also called as BGN scheme in the literature) demonstrates several good properties including efficiency and accuracy, unconditional energy stability and asymptotic equal-mesh distribution for isotropic geometric flows. Recently, by introducing a clever approximation of the normal vector, Bao and Zhao proposed a structure-preserving PFEM (SP-PFEM) bao2021structurepreserving ; bao2022volume for surface diffusion. Different techniques have been proposed to extend PFEM or SP-PFEM from isotropic geometric flows to anisotropic geometric flows in the literatures barrett2008numerical ; barrett2008variational ; wang2015sharp ; jiang2016solid ; jiang2019sharp ; li2020energy . Very recently, by introducing a symmetric positive definite surface matrix depending on and the Cahn-Hoffman -vector as well as a stabilizing function bao2021symmetrized ; bao2022symmetrized , we successfully and systematically extended the SP-PFEM method from isotropic surface diffusion to anisotropic surface diffusion under a symmetric (and necessary) condition on as: for . Unfortunately, there are different anisotropic surface energy which is not symmetric, e.g. the -fold anisotropic surface energy wang2015sharp ; bao2017parametric , in different applications. Thus the proposed SP-PFEM in bao2021symmetrized ; bao2022symmetrized cannot be applied to handle anisotropic geometric flows with non-symmetric surface energy .
In fact, it is still open to design a structure-preserving parametric finite element method (SP-PFEM) for anisotropic geometric flows (1.3) with general anisotropy , especially when . The main aim of this paper is to attack this important and challenging problem. The main ingredients in the proposed methods are based on: (i) the introduction of a novel surface energy matrix depending on and the Cahn-Hoffman -vector as well as a stabilizing function , which can be explicitly decoupled into a symmetric positive definite matrix and an anti-symmetric matrix, (ii) a new conservative geometric partial differential equation (PDE), (iii) a new variational formulation, and (iv) a proper approximation of the normal vector. We prove that the proposed SP-PFEM is structure-preserving, i.e. area conservation and energy dissipation, for anisotropic surface diffusion under a very mild condition
| (1.5) |
Finally we extend the proposed SP-PFEM to simulate evolution of a closed curve under other anisotropic geometric flows including anisotropic curvature flow and area-conserved anisotropic curvature flow.
The remainder of this paper is organized as follows: In section 2, by introducing the surface energy matrix , we derive a new conservative PDE and its corresponding variational formulation for anisotropic surface diffusion, and propose the semi-discretization in space and the full-discretization by SP-PFEM. In section 3, we establish the unconditional energy dissipation of the proposed SP-PFEM for anisotropic surface diffusion. In section 4, we extend the proposed SP-PFEM to the anisotropic curvature flow and area-conserved anisotropic curvature flow. Extensive numerical results are reported in section 5 to illustrate the efficiency and accuracy as well as structure-preserving properties of the proposed SP-PFEM. Finally, some concluding remarks are drawn in section 6.
2 The structure-preserving PFEM for anisotropic surface diffusion
In this section, by taking the anisotropic surface diffusion in (1.3), we introduce a surface energy matrix , obtain a conservative geometric PDE and derive its corresponding variational formulation. An SP-PFEM for the variational problem is presented and its structral-preserving property is stated under a very mild condition on the anistropic surface energy .
2.1 The geometric PDE
Let be parameterized by with denoting the time-dependent arc-length parametrization (or ‘Lagrangian coordinate’) of and representing the time. Then the anisotropic surface diffusion of can be described by
| (2.1) |
where represents the unit outward normal vector of . In practice, another popular way (or ‘Eulerian coordinate’) is to adopt being the periodic interval and then parameterize on by , which is given as
| (2.2) |
Then the arc-length parameter is given as satisfying . We assume that the parametrization by is regular during the evolution, i.e., there is a constant such that . The normal velocity can be given by this parametrization as
| (2.3) |
In order to get an explicit formula of from , let be a one-homogeneous extension of from to , e.g.
| (2.4) |
where . Based on this homogeneous extension , we can talk the regularity of by referring to the regularity of , i.e., . Then we introduce the Cahn-Hoffman -vector hoffman1972vector ; wheeler1999cahn as
| (2.5) |
here is the unit tangential vector of , and denoting the clockwise rotation by . Then an explicit formulation of can be expressed as the -vector as jiang2019sharp
| (2.6) |
Thus another equivalent geometric PDE for anisotropic surface diffusion can given as
| (2.7a) | ||||
| (2.7b) | ||||
2.2 The surface energy matrix
Introduce the surface energy matrix as
| (2.8) |
where is the identity matrix, is a nonnegative stabilizing function to be determined later, and and are a symmetric positive matrix and an anti-symmetric matrix, respectively, which are given as
| (2.9) |
Then we get the relationship between the weighted curvature and the newly constructed as
Lemma 1
The weighted curvature defined in (2.6) has the following alternative explicit expression
| (2.10) |
Proof
From (bao2021symmetrized, , Lemma 2.1), we know that
| (2.11) |
Thus it suffices to show . Since , by using the definition of in (2.8), we can simplify as
| (2.12) |
Combining (1) and (2.11), we get the desired equality (2.10).∎
Remark 1
The surface energy matrix given here can not be symmetric unless , which implies . This can only happen when is isotropic. For anisotropic , is essentially different from the symmetric surface energy matrix introduced in bao2021symmetrized ; bao2022symmetrized . Moreover, if we choose to be , then will collapse to the surface energy matrix given in li2020energy . This fact also means different from the stabilizing function in bao2021symmetrized , in this paper we do not need the stabilizing function to be strictly positive.
2.3 A variational formulation and its properties
We then derive the variational formulation for the conservative form (2.13). The functional space with respect to can be given as
| (2.14) |
with the following weighted -inner product
| (2.15) |
Since we assume the parameterization is regular; the weighted -inner product and the space are equivalent to the usual one, which is independent of . The Sobolev space is defined as
| (2.16) |
Moreover, we can extend the above definitions to the functions in and .
Multiplying a test function to (2.13a), integrating over and taking integration by parts, we obtain
| (2.17) |
Similarly, by multiplying a test function to (2.13b), we deduce that
| (2.18) |
Based on the two equations (2.17) and (2.18), the new variational formulation for the conservative form (2.13) can be stated as follows: Suppose the initial curve and the initial weighted curvature , then for any , find the solution satisfying
| (2.19a) | ||||
| (2.19b) | ||||
Denote the area of the region enclosed by as and the free interfacial energy of as , which are given by
| (2.20) |
We can show that the two geometric properties, i.e. area conservation and energy dissipation, still hold for the weak formulation (2.19).
Proposition 2.1 (area conservation and energy dissiption)
Suppose is given by the solution of the variational formulation (2.19), we have
| (2.21) |
The proof is similar to (li2020energy, , Proposition 2.1) and details are omitted for brevity.
2.4 A semi-discretization in space
To obtain the spatial discretization, suppose be an integer, is the mesh size, with , and we know by periodic. The closed curve is approximated by the closed line segments satisfying . And the discretization for test function space with respect to is given by the following space of piecewise linear finite element functions
| (2.22) |
where is the set of polynomials defined on of degree . The mass lumped inner product for two function with respect to is defined as
| (2.23) |
where , and . We note this mass lumped inner product is also valid for and the piecewise constant vector-valued functions with possible jump discontinuities at for .
The discretized unit normal vector , unit tangential vector , and the -vector are such piecewise constant vectors on , which are given as
| (2.24) |
Here we use to represent for short. To make sure are well defined, we need the following assumption on
| (2.25) |
After giving all the continuous objects their discretized versions, we can state the spatial semi-discretization as follows: Let be the approximations of , respectively, with for , find the solution , such that
| (2.26a) | ||||
| (2.26b) | ||||
where
| (2.27) |
and the discretized derivative for a scalar and vector valued functions and , respectively, are given as
| (2.28) |
and assumption (2.25) ensures and are piecewise constant functions with possible jump discontinuities at for , thus the mass lumped inner product terms like in (2.26) are well defined.
Denote the enclosed area and the total energy of the closed line segments as and , respectively, which are given by
| (2.29) |
where . Then following the same statement in the proof of (li2020energy, , Proposition 3.1), we know that the spatial discretization (2.26) still preserves the two geometric properties.
Proposition 2.2 (area conservation and energy dissiption)
Suppose is given by the solution of (2.26), then we have
| (2.30) |
2.5 A structure-preserving PFEM
We then consider the full discretization. Let be the uniform time step, and be the approximation of , where . Suppose , we can similarly give the definitions for the mass lumped inner product as well as the unit normal vector , the unit tangential vector , and the -vector with respect to . By adopting the backward Euler method, the fully-implicit structure-preserving discretization of PFEM for anisotropic surface diffusion (2.7) can then be given as:
Suppose the initial approximation is given by . For any , find the solution , such that
| (2.31a) | ||||
| (2.31b) | ||||
where
| (2.32) |
and
| (2.33) |
The SP-PFEM (2.31) is fully-implicit, and we can apply Newton’s iterative method proposed in bao2021structurepreserving to solve it numerically. If is replaced by , then (2.31) becomes semi-implicit. However, the clever choice is critical in preserving the area conservation, and the semi-implicit PFEM can only preserve the energy dissipation property.
2.6 Main results
Denote the enclosed area and the total energy of the closed line segments as and , respectively, which are given by
| (2.34a) | ||||
| (2.34b) | ||||
Introduce two auxiliary functions as
| (2.35a) | ||||
| (2.35b) | ||||
we define the minimal stabilizing function as (its existence will be given in next section)
| (2.36) |
For the SP-PFEM (2.31), we have
Theorem 2.1 (structure-preserving)
Suppose satisfies
| (2.37) |
and take the stabilizing function for , then the SP-PFEM (2.31) preserves the two geometric properties in the discrete level, i.e.,
| (2.38) |
The area conservation part is a direct result of (bao2021structurepreserving, , Theorem 2.1). And the energy dissipation will be proved in the next section.
3 Energy dissipation of the SP-PFEM (2.31)
In this section, we first show if satisfies (2.37), the minimal stabilizing function defined in (2.36) is well-defined, thus we can always choose a nonnegative stabilizing function for . After that, we will use to give the proof of the unconditional energy stability part of the main theorem 2.1.
3.1 Existence of the minimal stabilizing function defined in (2.36)
From the definition of in (2.36), we observe that if , then intuitively for sufficiently large , we know the . But this approach will fail when , and this can happen if , which suggests us to treat the two cases and separately. To simplify the notations, we introduce a compact set as
| (3.1) |
Then , and .
Proof
First we consider the case . Since satisfies (2.37), we know . Thus there exists a constant , such that
| (3.2) |
here is the Hessian matrix of , and denotes the -norm.
By mean value theorem, we know for all , there exists a constant such that
| (3.3) |
It is easy to see that and . Hence we know
| (3.4) |
And notice that , we can then get the following estimate of :
| (3.5) |
Here we use the fact and .
On the other hand, using the fact , we know that for , it holds
| (3.6) |
For the case , by (2.37), when , we know that
| (3.7) |
Thus for , we know . By continuity of and , there exits an open set such that , and for all and , we have . For a given , we know that . Therefore we can choose a sufficiently large but finite , such that . And by the same argument, there exists an open set , such that and . And we obtain an open cover for as
| (3.8) |
Since is compact, by open cover theorem, there is a finite set of vectors , such that
| (3.9) |
If we take , we have , hence
| (3.10) |
Which means . ∎
Remark 2
The part only requires inequality (3.4), thus condition can be relaxed to is piecewise . And the condition is to ensure the existence of , which suggests we may find a larger such that exists for satisfies . And by the same argument, we can show such exists if and only if .
By the existence of , once the is given, the minimal stabilizing function is then determined, i.e. there is a map from to . Similar to the proof when is symmetric, i.e. in bao2021structurepreserving ; bao2022volume , we can show such map is a sub-linear with respect to when it satisfies (2.37).
Lemma 2 (positive homogeneity and subadditivity)
Let and be three functions satisfying (2.37) with minimal stabilizing functions and , respectively, then we have
(i) if , where is a positive number, then ; and
(ii) if , then .
The proof is similar to (bao2021symmetrized, , Lemma 4.4), and is omitted for brevity.
3.2 Proof of the energy dissipation in (2.38)
To prove the main result, we first need the following lemma:
Lemma 3
Suppose are two non-zero vectors in and to be the corresponding unit normal vectors. Then for any , the following inequality holds
| (3.11) |
Proof
Now we can prove the energy dissipation part in our main result Theorem 2.1.
Proof
The key point of the proof is to establish the following energy estimation
| (3.15) |
Remark 3
The condition in (2.37) is natural, but looks quite complicated and seems not very sharp. However, the proof shows the condition is indeed natural! To see this, inequality (3.11) in Lemma 3 is essential in showing the energy estimate (3.15). And if we take in Lemma 3, then , and the inequality (3.11) becomes
| (3.17) |
which means . Our sufficient energy stable condition (2.37) just replaces with , thus is natural and almost necessary.
4 Extension to other anisotropic geometric flows
In fact, the energy stable condition on in (2.37), the definition of in (2.8), the alternative expression for in (2.10), and the definition of in (2.36) are independent of the anisotropic surface diffusion flow. Thus these definitions and even the proof of energy stability can be directly extended to other anisotropic geometric flows.
4.1 For anisotropic curvature flow
Similar to (2.13), for the anisotropic curvature flow in (1.3), we have a conservative geometric PDE as
| (4.1a) | ||||
| (4.1b) | ||||
Suppose the initial curve and the initial weighted curvature . Based on the conservative form (4.1), the variational formulation for anisotropic curvature flow is as follows: For any , find the solution satisfying
| (4.2a) | ||||
| (4.2b) | ||||
And the SP-PFEM for the anisotropic curvature flow (4.2) is as follows: Suppose the initial approximation is given by , then for any , find the solution , such that
| (4.3a) | ||||
| (4.3b) | ||||
For the SP-PFEM (4.3), we have
Theorem 4.1 (structure-preserving)
Proof
From (bao2021structurepreserving, , Theorem 2.1), we know that
| (4.5) |
Thus by taking in (4.3a), we know that
| (4.6) |
which is the desired decay rate in (4.4).
4.2 For area-conserved anisotropic curvature flow
Similarly, for the area-conserved anisotropic curvature flow in (1.3), the conservative geometric PDE is given as
| (4.7a) | ||||
| (4.7b) | ||||
where is given as (1.4) by replacing and by and , respectively. And the variational formulation can be derived in a similar way.
In order to design a structure-preserving full discretization, we need to properly discretize . Denote with respect to as
| (4.8) |
By adopting this , the SP-PFEM for the area-conserved anisotropic curvature flow in (1.3) is as follows: Suppose the initial approximation is given by ; for any , find the solution , such that
| (4.9a) | ||||
| (4.9b) | ||||
For the above SP-PFEM (4.9), we have
Theorem 4.2 (structure-preserving)
5 Numerical results
In this section, we present numerical experiments to illustrate the high performance of the proposed SP-PFEMs. The implementations and performances of the three SP-PFEMs are very similar. Thus in section 5.1, we only show test results of the SP-PFEM (2.31) for the anisotropic surface diffusion. The morphological evolutions for three anisotropic geometric flows are shown in section 5.2.
To compute the minimal stabilizing function , we first solve the optimization problem (2.36) for uniformly distributed points , and then do linear interpolation for the intermediate points. In Newton’s iteration, the tolerance value is set as .
5.1 Results for the anisotropic surface diffusion
Here we provide convergence tests to show the quadratic convergence rate in space and linear convergence rate in time. To this end, the time step is always chosen as except it is state otherwise. The distance between two closed curves is given by the manifold distance in bao2020energy as
| (5.1) |
where are the interior regions of , respectively, and denotes the area of . Let be the numerical approximation of with mesh size and time step , the numerical error is thus given as
| (5.2) |
To numerically test the energy stability, area conservation and good mesh quality, we introduce the following indicators: the normalized energy , the normalized area loss and the weighted mesh ratio
| (5.3) |
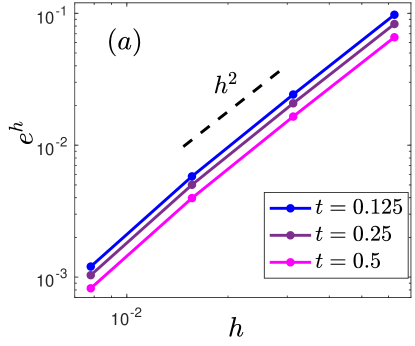
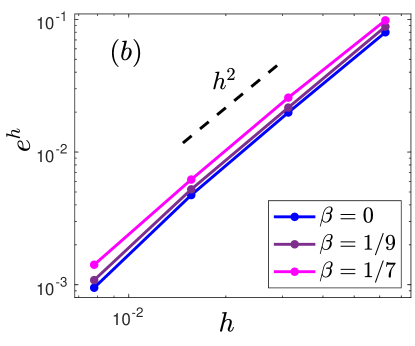
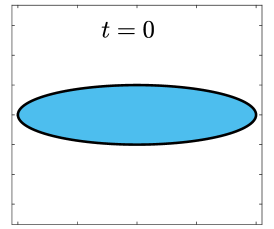
In the following numerical tests, the initial curve is given as an ellipse with length and width . The exact solution is approximated by choosing with and in (2.31). Here are two typical anisotropic surface energies to be taken in our simulations:
-
•
Case I: deckelnick2005computation ;
-
•
Case II: with and jiang2016solid . It is weakly anisotropic when , and otherwise it is strongly anisotropic.
Fig. 1 presents the convergence rates of the proposed SP-PFEM (2.31) at different times and with different anisotropic strengths under a fixed time . It is apparent from this figure that the second-order convergence in space is independent of anisotropies and computation times, which indicates the convergence rate is very robust.
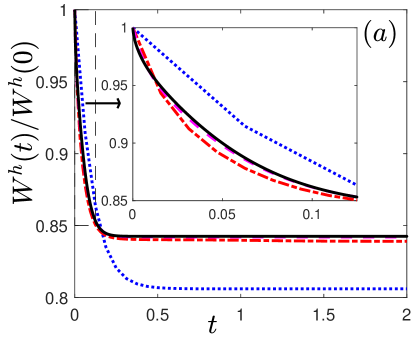
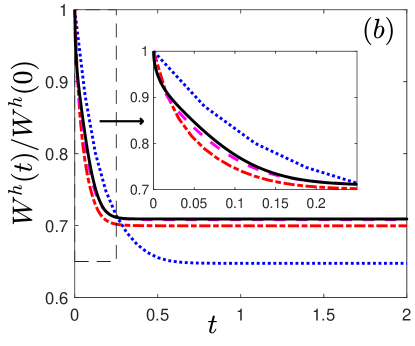
The time evolution of the normalized energy with different , the normalized area loss and the number of Newton iterations with , and the weighted mesh quality with different are summarised in Figs. 2-4, respectively.
(i) The normalized energy is monotonically decreasing when the surface energy satisfies the energy stable condition (2.37) (cf. Fig. 2);
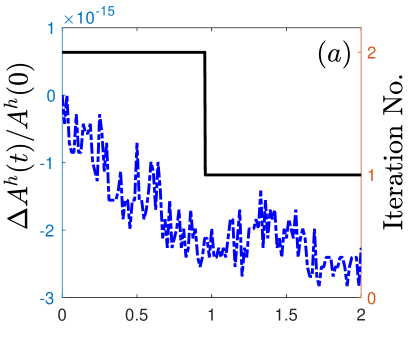
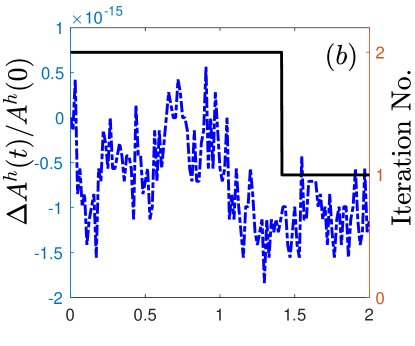
(ii) The normalized area loss is at which is almost at the same order as the round-off error (cf. Fig. 2), which confirms the area conservation in practical simulatoions;
(iii) Interestingly, the numbers of iterations in Newton’s method are initially and finally (cf. Fig. 3). This finding suggests that although the proposed SP-PFEM (2.31) is full-implicit, but it can be solved very efficiently with a few iterations;
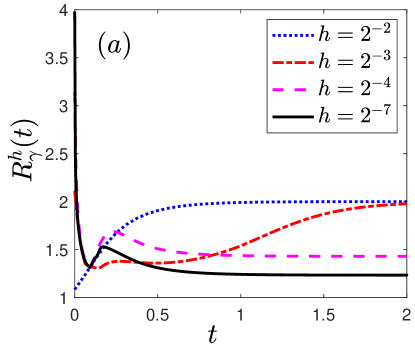
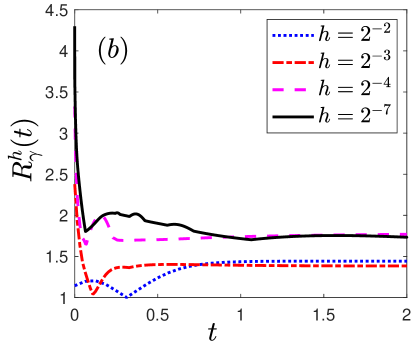
(iv) In Fig. 4 there is a clear trend of convergence of the weighted mesh ratio . Moreover, in contrast to the symmetrized SP-PFEM for symmetric in bao2021symmetrized , keeps small even with the strongly anisotropy .

5.2 Application for morphological evolutions
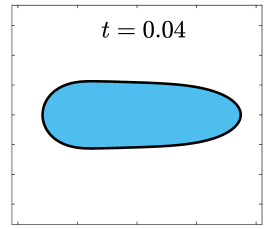
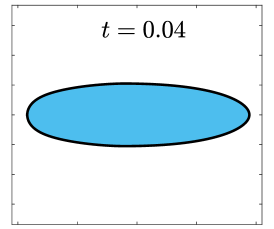
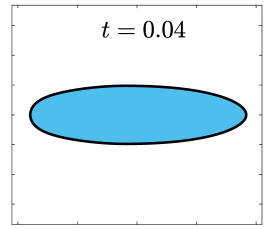
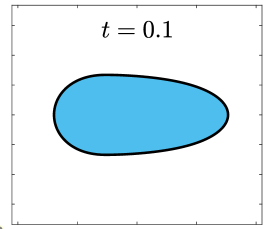
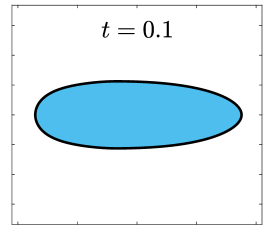
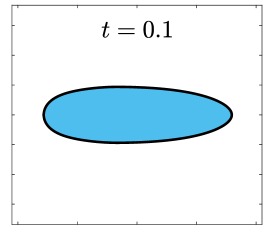
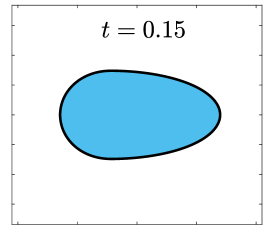
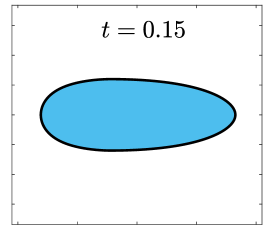
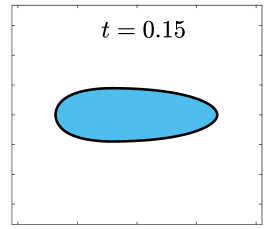
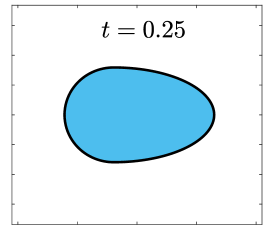
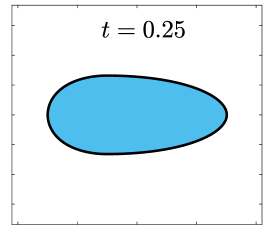
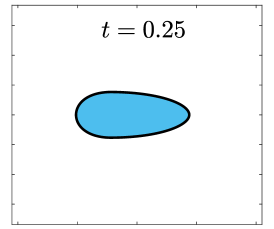
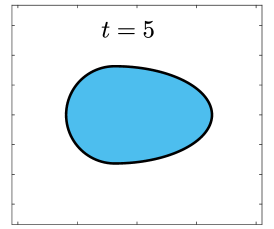
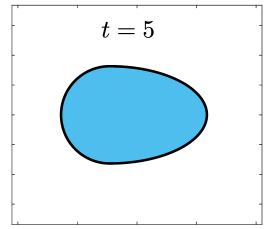
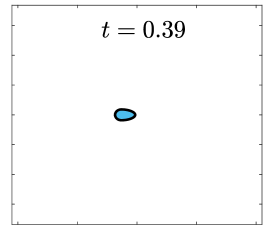
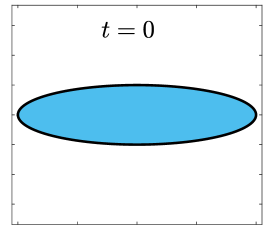
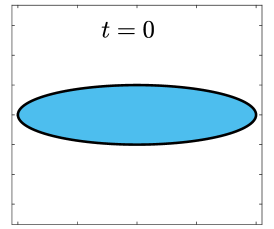
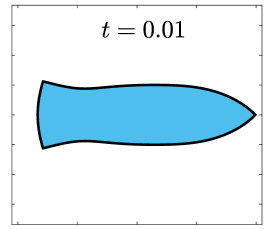
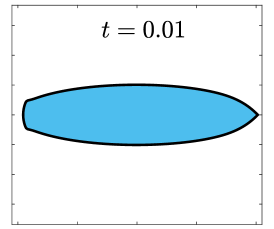
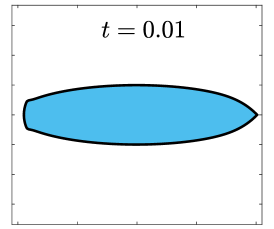
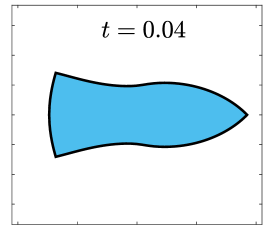
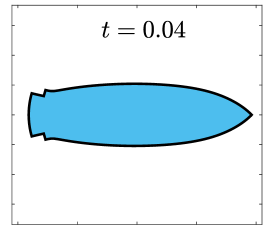
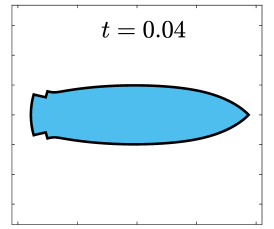
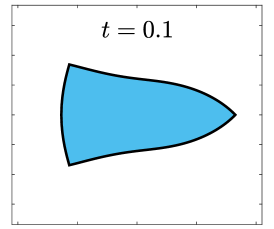
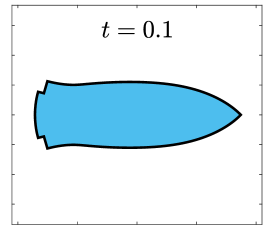
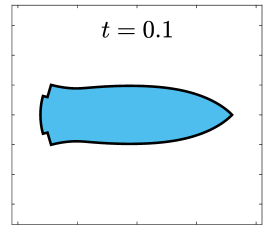
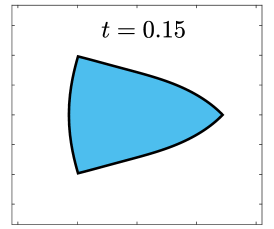
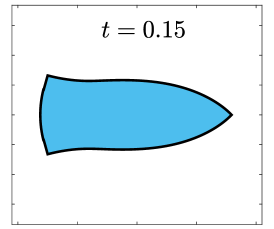
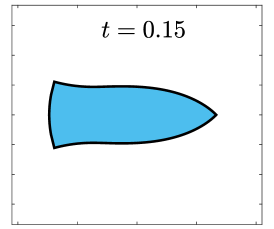
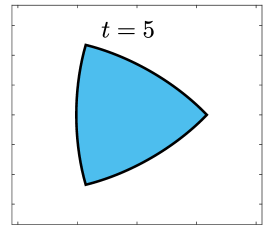
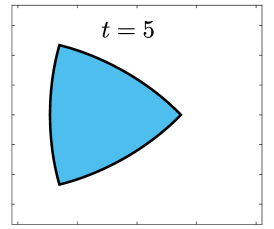
Finally, we apply the proposed SP-PFEMs to simulate the morphological evolutions driven by the three anisotropic geometric flows. Fig 5 plots the morphological evolutions of anisotropic surface diffusion for the four different anisotropic energies: (a) anisotropy in case I; (b)-(d) anisotropies in case II with , respectively. Fig 6 and Fig 7 depict the anisotropic surface diffusion, area-conserved anisotropic curvature flow, and anisotropic curvature flow at different times with anisotropy in case I and in case II with , respectively.
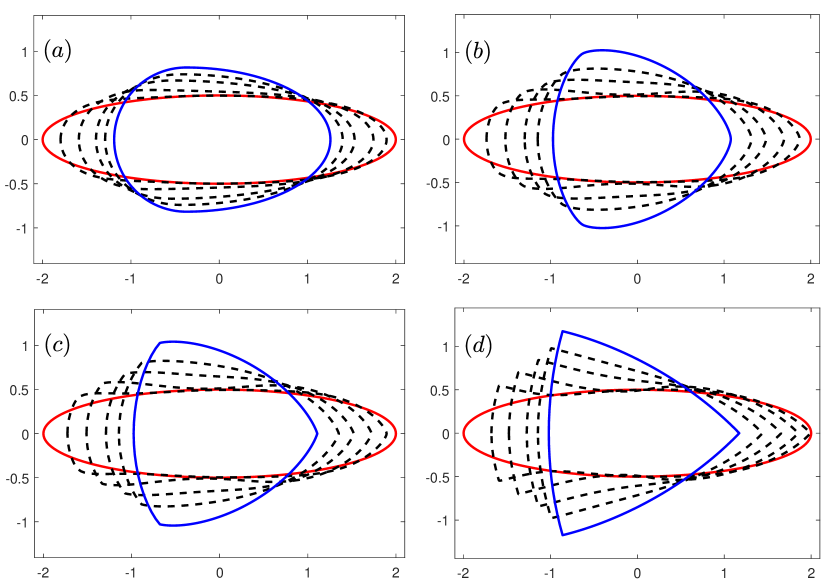
As shown in Fig. 5 (b)-(d), the edges emerge during the evolution and corners become sharper as the strength increases. In contrast, there are no edges or corners in the morphological evolutions with anisotropy in Case I. This suggests that even if it is not a -function, it is more like weak anisotropy! From Fig. 6-7, we can see that the anisotropic surface diffusion and the area-conserved anisotropic curvature flow have the same equilibriums in shapes, while they have different dynamics, i.e., the equilibriums are different in positions, and the anisotropic surface diffusion evolves faster than the area-conserved anisotropic curvature flow.
6 Conclusions
By introducing a novel surface energy matrix depending on the anisotropic surface energy and the Cahn-Hoffman -vector as well as a nonnegative stabilizing function , we proposed conservative geometric partial differential equations for several geometric flows with anisotropic surface energy . We derived their weak formulations and applied PFEM to get their full discretizations. Then we proved these PFEMs are structure-preserving under a very mild condition on with proper choice of the stabilizing function . Though our surface energy matrix is no longer symmetric, our experiments had shown a robust second-order convergence rate in space and linear convergence rate in time and unconditional energy stability. Specifically, the mesh quality of the proposed SP-PFEM, i.e. the weighted mesh ratio is much smaller, is much better than that in the symmetrized SP-PFEM proposed recently for anisotropic surface diffusion with a symmetric surface energy bao2021symmetrized ; bao2022symmetrized . Moreover, our SP-PFEMs work well for the piecewise anisotropy, which is a significant achievement compared with other PFEMs. In the future, we will generalize the surface energy matrix to three dimensions (3D) and propose efficient and accurate SP-PFEM for anisotropic geometric flows in 3D.
References
- (1) B. Andrews, Volume-preserving anisotropic mean curvature flow, Indiana Univ. Math. J., (2001), pp. 783-827.
- (2) W. Bao, H. Garcke, R. Nürnberg, and Q. Zhao, Volume-preserving parametric finite element methods for axisymmetric geometric evolution equations, J. Comput. Phys., 460 (2022), pp. 111180.
- (3) W. Bao, W. Jiang, and Y. Li, A symmetrized parametric finite element method for anisotropic surface diffusion of closed curves, SIAM J. Numer. Anal., to appear (arXiv preprint arXiv:2112.00508), (2021).
- (4) W. Bao, W. Jiang, Y. Wang, and Q. Zhao, A parametric finite element method for solid-state dewetting problems with anisotropic surface energies, J. Comput. Phys., 330 (2017), pp. 380-400.
- (5) W. Bao and Y. Li, A symmetrized parametric finite element method for anisotropic surface diffusion in 3D, arXiv preprint arXiv:2206.01883, (2022).
- (6) W. Bao and Q. Zhao, An energy-stable parametric finite element method for simulating solid-state dewetting problems in three dimensions, J. Comput. Math., to appear (arXiv preprint arXiv:2012.11404), (2020).
- (7) W. Bao and Q. Zhao, A structure-preserving parametric finite element method for surface diffusion, SIAM J. Numer. Anal., 59 (2021), pp. 2775-2799.
- (8) J. W. Barrett, H. Garcke, and R. Nürnberg, A parametric finite element method for fourth order geometric evolution equations, J. Comput. Phys., 222 (2007), pp. 441-467.
- (9) J. W. Barrett, H. Garcke, and R. Nürnberg, Numerical approximation of anisotropic geometric evolution equations in the plane, IMA J. Numer. Anal., 28 (2008), pp. 292-330.
- (10) J. W. Barrett, H. Garcke, and R. Nürnberg, On the parametric finite element approximation of evolving hypersurfaces in R3, J. Comput. Phys., 227 (2008),
- (11) J. W. Barrett, H. Garcke, and R. Nürnberg, A variational formulation of anisotropic geometric evolution equations in higher dimensions, Numer. Math., 109 (2008), pp. 1-44.
- (12) J. W. Barrett, H. Garcke, and R. Nürnberg, A variational formulation of anisotropic geometric evolution equations in higher dimensions, Eur. J. Appl. Math., 21 (2010), pp. 519-556.
- (13) J. W. Barrett, H. Garcke, and R. Nürnberg, Parametric finite element approximations of curvature-driven interface evolutions, in Handb. Numer. Anal, 21 (2020), pp. 275-423.
- (14) J. Cahn, Stability, microstructural evolution, grain growth, and coarsening in a two-dimensional two-phase microstructure, Acta Metall. Mater., 39 (1991), pp. 2189-2199.
- (15) J. W. Cahn and J. E. Taylor Overview no. 113 surface motion by surface diffusion, Acta Metall. Mater., 42 (1994), pp. 1045-1063.
- (16) W. C. Carter, A. Roosen, J. W. Cahn, and J. E. Taylor, Shape evolution by surface diffusion and surface attachment limited kinetics on completely faceted surfaces, Acta Metall. Mater., 43 (1995), pp. 4309-4323.
- (17) Y. Chen, Y. Giga, and S. Goto, Uniqueness and existence of viscosity solutions of generalized mean curvature flow equations, in Fundamental Contributions to the Continuum Theory of Evolving Phase Interfaces in Solids, Springer, 1999, pp. 375-412.
- (18) U. Clarenz, U. Diewald, and M. Rumpf, Anisotropic geometric diffusion in surface processing, IEEE Vis. 2000, 2000.
- (19) K. Deckelnick, G. Dziuk, and C. M. Elliott, Computation of geometric partial differential equations and mean curvature flow, Acta Numer., 14 (2005), pp. 139-232.
- (20) K. Deckelnick, G. Dziuk, and C. M. Elliott, Fully discrete finite element approximation for anisotropic surface diffusion of graphs, SIAM J. Numer. Anal., 43 (2005), pp. 1112-1138.
- (21) I. C. Dolcetta, S. F. Vita, and R. March, Area-preserving curve-shortening flows: from phase separation to image processing, IFB, (2002), pp. 325-343.
- (22) P. Du, M. Khenner, and H. Wong, A tangent-plane marker-particle method for the computation of three-dimensional solid surfaces evolving by surface diffusion on a substrate, J. Comput. Phys., 229 (2010), pp. 813-827.
- (23) Q. Du and X. Feng, The phase field method for geometric moving interfaces and their numerical approximations, in Handb. Numer. Anal, 21 (2020), pp. 425-508.
- (24) I. Fonseca, A. Pratelli and B. Zwicknagl, Shapes of epitaxially grown quantum dots, Arch. Ration. Mech. Anal., 214 (2014), pp. 359-401.
- (25) P. M. Girao and R. V. Kohn, The crystalline algorithm for computing motion by curvature, in Variational Methods for Discontinuous Structures, Springer, 1996, pp. 7-18.
- (26) M. E. Gurtin and M. E. Jabbour, Interface evolution in three dimensions with curvature-dependent energy and surface diffusion: interface-controlled evolution, phase transitions, epitaxial growth of elastic films, Arch. Ration. Mech. Anal., 163 (2002), pp. 171-208.
- (27) D. W. Hoffman and J. W. Cahn, A vector thermodynamics for anisotropic surfaces: I. fundamentals and application to plane surface junctions, Surf. Sci., 31 (1972), pp. 368-388.
- (28) W. Jiang, W. Bao, C. V. Thompson, and D. J. Srolovitz, Phase field approach for simulating solid-state dewetting problems, Acta Mater., 60 (2012), pp. 5578-5592.
- (29) W. Jiang, Y. Wang, Q. Zhao, D. J. Srolovitz, and W. Bao, Solid-state dewetting and island morphologies in strongly anisotropic materials, Scr. Mater., 115 (2016), pp. 123-127.
- (30) W. Jiang and Q. Zhao, Sharp-interface approach for simulating solid-state dewetting in two dimensions: A Cahn-Hoffman -vector formulation, Phys. D, 390 (2019), pp. 69-83.
- (31) B. Kovaács, B. Li, and C. Lubich, A convergent evolving finite element algorithm for mean curvature flow of closed surfaces, Numer. Math., 143 (2019), pp. 797-853.
- (32) Y. Li and W. Bao, An energy-stable parametric finite element method for anisotropic surface diffusion, J. Comput. Phys., 446 (2021), p. 110658.
- (33) W. J. Niessen, B. M. Romeny, L. M. Florack, and M. A. Viergever, A general framework for geometry-driven evolution equations, Int. J. Comput. Vis., 21 (1997), pp. 187-205.
- (34) S. Randolph, J. Fowlkes, A. Melechko, K. Klein, H. Meyer, M. Simpson, and P. Rack, Controlling thin film structure for the dewetting of catalyst nanoparticle arrays for subsequent carbon nanofiber growth, Nanotech., 18 (2007), p. 465354.
- (35) H. Shen, S. Nutt, and D. Hull, Direct observation and measurement of fiber architecture in short fiber-polymer composite foam through micro-CT imaging, Compos. Sci. Technol., 64 (2004), pp. 2113-2120.
- (36) A. P. Sutton and R. W. Balluffi, Interfaces in crystalline materials, Clarendon Press, 1995.
- (37) J. E. Taylor, Mean curvature and weighted mean curvature, Acta Metall. Mater., 40 (1992), pp. 1475-1485
- (38) J. E. Taylor, J. W. Cahn, and C. A. Handwerker, Overview no. 98 i—geometric models of crystal growth, Acta Metall. Mater., 40 (1992), pp. 1443-1474.
- (39) C. V. Thompson, Solid-state dewetting of thin films, Annu. Rev. Mater. Res., 42 (2012), pp. 399-434.
- (40) Y. Wang, W. Jiang, W. Bao, and D. J. Srolovitz, Sharp interface model for solid-state dewetting problems with weakly anisotropic surface energies, Phys. Rev. B, 91 (2015), p. 045303.
- (41) A. Wheeler, Cahn-Hoffman -vector and its relation to diffuse interface models of phase transitions, J. Stat. Phys., 95 (1999), pp. 1245-1280.
- (42) H. Wong, P. Voorhees, M. Miksis, and S. Davis, Periodic mass shedding of a retracting solid film step, Acta Mater., 48 (2000), pp. 1719-1728.
- (43) Y. Xu and C. Shu, Local discontinuous Galerkin method for surface diffusion and Willmore flow of graphs, J. Sci. Comput., 40 (2009), pp. 375-390.
- (44) J. Ye and C. V. Thompson, Mechanisms of complex morphological evolution during solid-state dewetting of single-crystal nickel thin films, Appl. Phys. Lett., 97 (2010), p. 071904.
- (45) Q. Zhao, W. Jiang, and W. Bao, An energy-stable parametric finite element method for simulating solid-state dewetting, IMA J. Num. Anal., 41 (2021), pp. 2026-2055.