A short proof of the existence of a minor-universal countable planar graph
An element of a class of graphs is minor-universal for the class if every other element of the class is its minor. In [2], Diestel and Kühn constructed a minor-universal countable planar graph. Their construction is rather involved. The purpose of this note is to present a significantly simpler construction and proof, based on a suggestion of Georgakopoulos ([3], p.7) to modify the construction of [4]. The idea is as follows:
-
i.
is a copy of embedded in ;
-
ii.
for , is the plane graph obtained from in the following way: in each face of we place a vertex , we connect to each vertex with an edge, and we subdivide each edge exactly times;
-
iii.
we define .

In this note I prove:
Theorem 1.
The graph is minor-universal for countable planar graphs.
By its construction, is countable and planar. It remains to show that it has every other countable planar graph as a minor. This follows directly from the following two lemmata:
Lemma 1.
Every countable planar graph is a minor of a countable, sub-cubic, 2-connected planar graph.
Proof.
Let . It is simple to construct a countable planar graph in that is 2-connected and has finite maximum degree by blowing up each vertex to a locally finite tree and taking the fattening, for details see ([3], Chapter 4). We blow up each vertex of to a finite trivalent tree to get the promised graph . ∎
Lemma 2.
Every countable, sub-cubic, 2-connected planar graph is a minor of .
The rest of this note is devoted to proving Lemma 2.
Proof of Lemma 2
An ear decomposition of a countable graph is a sequence of subgraphs of such that:
-
i.
is a cycle;
-
ii.
for , either or is a simple graph obtained from by connecting two distinct vertices of with a new path (called an ear in this context);
-
iii.
.
We first prove two claims that are used in our proof.
Claim 1.
Every 2-connected countable graph with at least three vertices admits an ear decomposition.
Proof.
We order the edges of . By the infinite version of Menger’s Theorem ([1]), there exists a cycle that contains . Set . Given , we determine as follows. If , then set . Otherwise, let be the edge outside of with the smallest index. It is a well-known exercise that there exists a cycle in that contains both and . Let be the subpath of that meets only at its endpoints and contains . Set . To see that , note that .
∎
Remark 1.
If is a plane graph, then the ear of its ear decomposition lies in a face of .
An -diameter of is a maximal path contained in . An -slice of is a subgraph that is bounded by (but does not contain the edges of) the boundary of a face of and perhaps one of the diameters of that face, and does not contain . An -piece is a subgraph of of the form or for some face of . Recall that, given a separator of a graph and a connected component , the torso of is the induced subgraph of on the vertices .
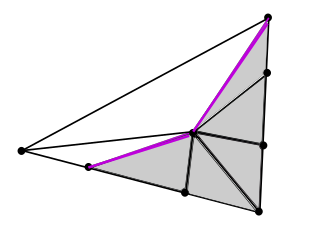
Claim 2.
Every -slice is -connected.
Proof.
Let be an -slice and be a separator of . We say that a connected component is -coarse for if its torso in is the union of a finite set of -pieces. Since is finite, it is entirely contained in some for , so it splits into -coarse components. Therefore must have order at least , since is half the length of an -diameter rounded up, which is the shortest boundary that an -coarse component can have with its complement in . ∎
Recall that an inflated copy (briefly denoted as ) of a graph is a graph together with a map such that for every and with ends , the following are true:
-
i.
is a connected subgraph of ;
-
ii.
is an open path between and ;
-
iii.
the images of the elements of are pairwise disjoint;
-
iv.
.
A graph is a minor of a graph if and only if contains an as a subgraph. We are now ready to prove Lemma 2:
Proof.
Let be a plane graph as in the statement of Lemma 2. We will construct a subgraph of that is an . In particular, we will define as the union of a sequence of , where is an ear decomposition of (Claim 1), such that for every , , and , we have for the corresponding maps that and . This will allow us to define by setting ; the reader is invited to check that this yields an IG. To satisfy these constraints, we also require a consistent way to correspond abstract faces of to slices of . To keep notation simple, we overload our maps to also perform this function.
The following definition is key in our analysis: given a face of , we denote by the set of vertices of that are ends of ears contained in . Note that, since is sub-cubic, each vertex can be the end of at most one ear.
We construct inductively the sequence with the additional useful requirements that for each , is a path, and that for each face of , the slice is -connected and intersects only at one end vertex of each of the paths and in the correct cyclic order.
For the base case, suppose that has length . We consider two disjoint face cycles and of the graph , contained in the same ()-piece, noting that each has length . By Menger’s Theorem and Claim 2, we may also consider disjoint paths inside the piece joining and . We define by mapping the vertices of to these paths in the correct cyclic order, each edge of to an appropriate (open) subpath of , and the two faces and of to the two -slices and bounded by and , respectively. Both and are -connected, and , so is mapped to a -connected slice and is mapped to a -connected slice.
For the inductive step, suppose that we have defined so that each vertex is mapped to a path and each face is mapped to a -connected slice that intersects only at one end vertex of each of the paths and in the correct cyclic order.
Let , of boundary length say , be the unique (Remark 1) face of such that the ear , of length say , lies within , splitting it to two faces and . Let be a face of for some such that is bounded by the slice , has diameter length at least , and all its slices have connectivity at least (e.g. take ) (Claim 2).

By the inductive hypothesis, is -connected. By Menger’s Theorem, there exist disjoint paths in such that begins at the vertex and ends at some . In particular, since is a plane graph, preserves the cyclic order of . We also denote by the diameter of with ends and , where and are the ends of the ear .
For we set . The vertices of the ear we map arbitrarily (but in the correct order) to single vertices of . Each edge of the ear is mapped to the subpath of between the images of its ends. The faces and are mapped to the corresponding slices induced on by . Every other vertex, edge, or face of has the same image under as under .
Firstly, it follows from the construction that is an .
Moreover, for , by the inductive hypothesis, is a path. Also, is a path and, again by the inductive hypothesis, is a single vertex. Therefore, is a path. Trivially, the same holds for vertices in .
Additionally, both and are mapped to slices of connectivity . Since , both of these slices are adequately connected. We have also ensured that they intersect the appropriate vertex images under only at one end vertex each and in the correct cyclic order. These same properties hold, by the inductive hypothesis, for every other face image of . This concludes the induction, and the proof of Lemma 2.
∎
Remark 2.
The above construction is quite manageable, and perhaps can be modified to tackle the problem of minor-universal elements for 2-complexes embeddable in , mentioned in ([3], p.12).
References
- [1] Halin, R. (1974). A note on Menger’s theorem for infinite locally finite graphs. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. 40:111-114.
- [2] Diestel, R. and Kühn, D. (1999). A universal planar graph under the minor relation. Journal of Graph Theory. 32:191-206.
- [3] Georgakopoulos, A. (2022). On graph classes with minor-universal elements. Preprint.
- [4] Georgakopoulos, A. (2006). Infinite highly connected planar graphs of large girth. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. 76(1):235-245.