A Reduced Codebook and Re-Interpolation Approach for Enhancing Quality in Chroma Subsampling
Abstract
Prior to encoding RGB full-color images or Bayer color filter array (CFA) images, chroma subsampling is a necessary and crucial step at the server side. In this paper, we first propose a flow diagram approach to analyze the coordinate-inconsistency (CI) problem and the upsampling process-inconsistency (UPI) problem existing in the traditional and state-of-the-art chroma subsampling methods under the current coding environment. In addition, we explain why the two problems degrade the quality of the reconstructed images. Next, we propose a reduced codebook and re-interpolation (RCRI) approach to solve the two problems for enhancing the quality of the reconstructed images. Based on the testing RGB full-color images and Bayer CFA images, the comprehensive experimental results demonstrated at least 1.4 dB and 2.4 dB quality improvement effects, respectively, of our RCRI approach against the CI and UPI problems for the traditional and state-of-the-art chroma subsampling methods.
Index Terms:
Bayer color filter array (CFA) image, Chroma subsampling, Chroma upsampling, Codebook, Quality enhancement, Re-interpolation, RGB full-color image.I Introduction
As shown at the server side of Fig. 1, in our study, the input image could be a RGB full-color image or a demosaiced RGB full-color image which has been demosaicked from the input Bayer color filter array (CFA) image [2]. To demosaick to a RGB full-color image, several demosaicking methods [18], [9], [41], [15], [29], [38], [25], [26] can be used; here, the demosaicking method in [15] is used. For easy exposition, we take the Bayer CFA pattern in Fig. 3(a) as the representative, but our discussion is also applicable to the other three patterns in Figs. 3(b)-(d). Prior to compression, according to BT.601-5 [13], the RGB full-color image is converted to a YCbCr image using the following RGB-to-YCbCr color transformation:
| (1) |
where for each 22 YCbCr block , , denotes the YCbCr triple-value in zigzag order; denotes the collocated RGB triple-value of the 22 RGB full-color block .
Chroma subsampling has two formats, namely 4:2:0 and 4:2:2. 4:2:0 subsamples the -pair for each 22 CbCr block and 4:2:2 subsamples the -pair for each row of . Throughout this paper, we focus on 4:2:0, although the approach is also is applicable to 4:2:2. 4:2:0 has been used in Bluray discs (BDs) and digital versatile discs (DVDs) for storing movies, sports, TV shows, etc.
After decompressing the encoded subsampled YCbCr image by the decoder, as depicted at the client side of Fig. 1, a chroma upsampling process is performed on the subsampled CbCr image. Further, the upsampled YCbCr image is converted to a reconstructed RGB full-color image using the following YCbCr-to-RGB color conversion:
| (2) |
Suppose the input image is the demosaiced RGB full-color image. By Eq. (2), the upsampled YCbCr image can be directly converted to the reconstructed Bayer CFA image as the output.
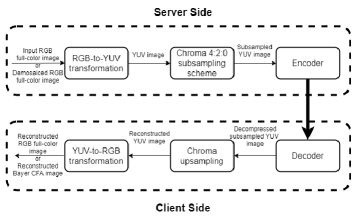
In Subsection I.A, we introduce the related chroma subsampling works for . Then, in Subsection I.B, we introduce the related chroma subsampling works for .
I-A Related Works for
At the server side, suppose the input image is a RGB full-color image. We first introduce the five traditional chroma subsampling methods, namely 4:2:0(A), 4:2:0(L), 4:2:0(R), 4:2:0(DIRECT), and 4:2:0(MPEG-B) [28]. Then, we introduce five state-of-the-art chroma subsampling combinations [43], [33], [4], [22].
Among the five traditional chroma subsampling methods, 4:2:0(DIRECT) subsamples the top-left chroma pair of as the subsampled -pair of . For simplicity, 4:2:0(DIRECT) is abbreviated as 4:2:0(D). 4:2:0(MPEG-B) determines the subsampled -pair by performing the 13-tap filter with mask [2, 0, -4, -3, 5, 19, 26, 19, 5, -3, -4, 0, 2]/64 on the top-left location of . 4:2:0(L) and 4:2:0(R) subsample the -pairs by averaging the chroma components in the left and right columns of , respectively. 4:2:0(A) subsamples the -pair of by averaging the four -pairs of . The subsampled chroma positions of 4:2:0(D) and 4:2:0(MPEG-B) are located at (0, 1); the subsampled chroma positions of 4:2:0(L), 4:2:0(A), and 4:2:0(R) are located at (0, ), (, ), and (1, ), respectively, and the four subsampled chroma positions are marked by the four red bullets in Figs. 2(a)-(d).




According to the new edge-directed interpolation (NEDI) [19] based chroma upsampling process which improved the previous method [1], Zhang et al. [43] proposed an interpolation-dependent image downsampling (IDID) based chroma subsampling method. Their combination is expressed as IDID-NEDI. To improve IDID-NEDI, Wang et al. [33] deployed the palette mode [27] in their JCDU (joint chroma downsampling and upsampling) based chroma subsampling method, and their best combination is expressed as JCDU-BICU, where BICU denotes the bicubic interpolation based chroma upsampling process. The experimental data demonstrated that JCDU-BICU outperforms IDID-NEDI and JCDU-BILI, in which BILI denotes the bilinear interpolation based chroma upsampling process, particularly for screen content images (SCIs) [23].
Following the COPY-based chroma upsampling process and the differentiation technique used in [20], but considering the demosaiced RGB full-color block-distortion as the criterion, Lin et al. [22] proposed a modified 4:2:0(A) chroma subsampling method which selects the best case among the four subsampled -pairs of by considering the ceiling operation-based 4:2:0(A) and the floor operation-based 4:2:0(A). Naturally, Lin et al.’s chroma subsampling method is suitable for the input RGB full-color image. At the client side, they improved the chroma upsampling process [22] by considering the distance between each missing chroma value and its three neighboring known (TN) pixels to achieve good quality performance. Their combination is expressed as “modified 4:2:0(A)-TN”.
Differing from the the chroma subsampling-first luma modification method [5], in [4], based on the subsampled chroma parameter-pair, at the server side, a BILI-based chroma estimation of is deployed in the block-distortion function with two chroma parameters and four luma parameters. Next, using a multiple linear regression technique, a joint chroma subsampling and luma modification (CSLM) method [4] was proposed to determine the subsampled -pair of and the four modified luma values of simultaneously. Their combination is expressed as CSLM-BILI. Experimental data indicated the quality superiority of CSLM-BILI relative to IDID-NEDI [43], JCDU-BICU [33], and modified 4:2:0(A)-TN [22].




I-B Related Works for
For , we mainly introduce the four state-of-the-art chroma subsampling methods [20], [7], [22], [8].
Chen et al. [3] observed that in Eq. (2), the R value is dominated by the Y and V values, and the B value is dominated by the Y and U values, and then the subsampled -pair of equals by considering the Bayer CFA pattern. Although their method benefits the R and B components of the reconstructed Bayer CFA image, it does not benefit the G components at all. To overcome this disadvantage, based on the COPY-based upsampling process to estimate the four chroma-pairs of at the server side, Lin et al. [20] proposed a 22 Bayer CFA block-distortion function to measure the distortion between the original 22 Bayer CFA block and the estimated one. Using a distortion minimization (DM) technique, Lin et al. derived a closed form to determine the subsampled -pair of . Their combination is expressed as DM-COPY.
In the gradient descent-based (GD) method [7], the Bayer CFA block-distortion function used in the DM method [20] is proved to be a convex function. Then, according to the shape similarity of the convex function in the real domain to that in the integer domain, an iterative procedure, in which the closed form derived in DM [20] was used as the initially subsampled -pair of , was proposed to better improve the DM method. In each iteration, the GD method applied the BILI method to estimate the four -pairs of each neighboring chroma block in the eight neighboring chroma blocks, and then the GD method selected the best one with the minimal 22 Bayer CFA block-distortion. Their combination is expressed as GD-BILI [7], and it has better quality than DM-COPY and GD-COPY.
As introduced in the last paragraph of Subsection I.A, Lin et al.’s modified 4:2:0(A) chroma subsampling method [22] only considers the demosaiced RGB full-color block-distortion as the distortion minimization criterion. After performing the modified 4:2:0(A)-TN combination on the demosaiced RGB full-color image, by Eq. (1), the reconstructed Bayer CFA image can be extracted from the reconstructed RGB full-color image. Therefore, ‘modified 4:2:0(A)-TN’ is also applicable for the input Bayer CFA image.
In [8], based on the BILI-based chroma upsampling process at the server side, combining chroma subsampling, luma modification, and the Bayer CFA pattern together, a -BILI combination was proposed. For each 22 YCbCr block , -BILI determined the best solution of the subsampled -pair and the modified luma values for simultaneously. In particular, after analyzing all the sixteen (= ) luma-selection cases, only two luma parameters, namely and , are modified such that the 22 Bayer CFA block-distortion could be minimized. Experimental data demonstrated that the -BILI combination [8] outperforms DM-COPY [20], GD-BILI [7], and modified 4:2:0(A)-TN [22].
I-C Motivation
From the introduction of the related chroma subsampling works for and , we find that under the current coding system in Fig. 1, the traditional and state-of-the-art combinations tend to suffer from the coordinate-inconsistency (CI) problem and/or the chroma upsampling process-inconsistency (UPI) problem because at the client side, the decoder is blind to the chroma subsampling process used at the server side and the future chroma upsampling process prefered by the chroma subsampling method. The two problems will be defined in Section III in detail.
The CI and UPI problems lead to the quality degradation of the reconstructed images, which will be explained in Section III. The two problems prompted us to develop a systematic approach to analyze them, and then to propose an effective approach to solve them for enhancing the quality of the reconstructed images.
I-D Contributions
In this paper, we first analyze the subsampled chroma positions of all considered chroma subsampling methods, and then we partition all these chroma subsampling methods into four classes. Based on the four partitioned chroma subsampling classes and the allowable chroma upsampling processes, we propose a flow diagram approach to analyze the coordinate-inconsistency (CI) problem and the upsampling process-inconsistency (UPI) problem occurring in the traditional and state-of-the-art combinations. We also explain why the two problems lead to the quality degradation of the reconstructed images.
To solve the CI and UPI problems, we propose an effective reduced codebook and re-interpolation (RCRI) approach for enhancing the quality of the reconstructed images. Based on the testing RGB full-color images and Bayer CFA images collected from the IMAX [14] dataset, the Kodak [16] dataset, and the Video [32] dataset, the thorough experimental results justified the significant quality enhancement effects of our RCRI approach against the CI and UPI problems for the traditional and state-of-the-art chroma subsampling methods. For and , the average CPSNR (color peak signal-to-noise ratio) gain and the average PSNR gain of our RCRI approach are at least 1.4 dB and 2.4 dB, respectively.
The rest of this paper is organized as follows. In Section II, based on the subsampled chroma positions, all considered chroma subsampling methods are partitioned into four classes. In Section III, the proposed flow diagram approach is presented to analyze the CI problem and the UPI problem. In Section IV, the proposed RCRI approach is presented to solve the two problems. In Section V, the thorough experimental results are illustrated to justify the significant quality enhancement using our RCRI approach. In Section VI, some concluding remarks are addressed.
II PARTITIONING ALL CONSIDERED CHROMA SUBSAMPLING METHODS INTO FOUR CLASSES
In this section, based on the subsampled chroma positions of all considered chroma subsampling methods, we partition these methods into four classes. It has been known that the subsampled chroma positions of the five traditional chroma subsampling methods are depicted by the four red bullets in Figs. 2(a)-(d) corresponding to the top-left, left, middle, and right black bullets in Fig. 4, respectively. Similar to 4:2:0(D) and 4:2:0(MPEG-B), the subsampled chroma positions of IDID [43] and JCDU [33] are all located at (0, 1), as depicted by the top-left black bullet of Fig. 4.
Based on the subsampled chroma parameter-pair, (, ), which is computationally located at (, ), the DM [20], GD [7], and modified 4:2:0(A) [22] methods apply the same COPY-based chroma upsampling process to estimate the four chroma pairs of each 22 chroma block for building up their own block-distortion functions. Accordingly, the determined values of the subsampled (, )-pairs using the above three methods are all located at (, ), as depicted by the middle black bullet in Fig. 4. Based on the subsampled chroma parameter-pair located at (, ), the CSLM [4] and [8] methods apply the BILI-based chroma upsampling process to estimate the four chroma pairs of each 22 chroma block for building up their own block-distortion functions. Therefore, the subsampled chroma position of the two methods is expressed as (, ).

For all considered chroma subsampling methods, the four subsampled chroma positions (SCPs) are denoted by SCP = {(0, 1), (0, ), (, ), (1, )} corresponding to the four partitioned chroma subsampling classes which are expressed as CS = {, , , }, as depicted in Fig. 4. Accordingly, in our study, instead of considering the original chroma subsampling method used in one combination, we only consider its chroma subsampling class which the chroma subsampling method used belongs to.
III THE ANALYSIS OF THE UPI AND CI PROBLEMS
We first define the UPI problem and explain why it degrades the quality of the reconstructed color images. Next, we propose a flow diagram approach to analyze the CI problem systematically. According to the coordinate displacement analysis, we explain why the CI problem also degrades the quality of the reconstructed color images.
III-A The UPI Problem
Without the loss of generality, we take the CSLM-BILI combination [4] as the example to define the UPI problem.
In CSLM-BILI, as introduced in Subsection I.A, at the server side, a BILI-based chroma estimation of each 22 CbCr block is deployed in the 22 RGB full-color block-distortion function with the parameter-pair, .
At the client side, instead of ‘BILI’, if the decoder adopts the other upsampling process, e.g. ‘COPY’, to upsample the received subsampled chroma image, it causes an upsampling process-inconsistency (UPI) problem because the future chroma upsampling process ‘BILI’ preferred by CSLM-BILI is misused as ‘COPY’ by the decoder.
III-B The CI Problem
Let the set symbol ‘CU’ denote the four chroma upsampling processes, namely COPY, BILI, NEDI, and BICU, used at the client side. Let CSxCU, where the symbol ‘x’ indicates the cross product operator, denote all combinations over the product of CS and CU. For each combination in CSxCU, we propose a flow diagram approach to analyze whether a true CI problem occurs in that combination and to report the coordinate displacement of the true CI problem. Furthermore, we explain why the true CI problem leads to the quality degradation of the reconstructed images.
1) The proposed flow diagram to analyze the true CI problem and to calculate the coordinate displacement: After performing one chroma subsampling CS on the chroma image , it yields a subsampled chroma image , which can be expressed as , , , or . The four possible subsampled chroma images are depicted in Fig. 5(a). For compression, as depicted in Fig. 5(b), each subsampled chroma image is further rearranged to a quarter-sized subsampled chroma image which is stored in an array data structure under an integer coordinate system.
However, at the server side, for compression, moving the subsampled chroma pair of each 22 chroma block from the subsampled chroma position ( SCP) to the new position, namely (0, 1), often causes a coordinate displacement problem. Generally, as depicted by the four arrows between Fig. 5(a) and Fig. 5(b), the corresponding four coordinate displacements equal (0, 0) (= (0, 1) - (0, 1)), (0, ) (= (0, 1) - (0, )), (-, ) (= (0, 1) - (, )), and (-1, ) (= (0, 1) - (1, )) corresponding to , respectively. We conclude that for one chroma subsampling method , at the server side, preparing the quarter-sized subsampled chroma image for compression causes a CI problem due to its nonzero coordinate displacement (NCD) in the set NCD = (0, ), (-, ), (-1, ).
After receiving the compressed quarter-sized subsampled chroma image by the decoder at the client side, each subsampled chroma pixel is moved to , where indicates the upsampled chroma image, for constructing the initially upsampled chroma image , as depicted in Fig. 5(c). Because from Fig. 5(a) to Fig. 5(b), for , it causes a CI problem in the subsampled chroma image , the initially upsampled chroma image in Fig. 5(c) thus inherits the CI problem in Fig. 5(b) and the associated nonzero coordinate displacement in NCD.
Further, all missing chroma pixels in of Fig. 5(c) are reconstructed using the adopted chroma upsampling process in CU. We first consider the chroma upsampling process ‘COPY’. After performing the COPY-based upsampling process on each initially subsampled chroma image in Fig. 5(c), the reconstructed chroma pixels are denoted by black bullets of the upsampled chroma image in Fig. 5(d). For each 22 chroma block in , as depicted in Fig. 5(d), the three missing chroma pixels are reconstructed by copying the top-left subsampled chroma-pair of that block. According to the analysis from Fig. 5(a) to Fig. 5(d), we conclude that for any combination ‘-COPY’, where ‘cs’ is in CS, no true CI problem occurs.
Next, we consider the chroma upsampling process ‘’ {BILI, NEDI, BICU}. After performing the upsampling process ‘’ on each initially subsampled chroma image in Fig. 5(c), the reconstructed chroma pixels are denoted by black cross-marked symbols of the reconstructed chroma image in Fig. 5(d). In Fig. 5(d), each missing chroma pixel in is reconstructed by the upsampling process ‘’ referring to the neighboring chroma pairs of that missing chroma pixel. Consequently, we conclude that for any combination in {, , }x{BILI, NEDI, BICU}, a true CI problem occurs eventually, as depicted in Fig. 5(e). On the other hand, among the sixteen combinations in CSxCU, the true CI problems occur in only nine combinations in {, , }x{BILI, NEDI, BICU}.
From the above analysis of the true CI problems, we find that there are only three distinct coordinate displacements, namely (0, ), (-, ), and (-1, ), corresponding to the three combinations in x{BILI, NEDI, BICU}, the three combinations in x{BILI, NEDI, BICU}, and the three combinations in x{BILI, NEDI, BICU}, respectively. Due to the nonzero coordinate displacement problem, for each 22 upsampled chroma block in Fig. 5(d), the four temporarily upsampled chroma pairs should be replaced by the four correct chroma pairs, as depicted by the four red triangles in Fig. 5(d). The detailed re-interpolation based recovery strategy in our RCRI approach will be presented in Section IV.B.
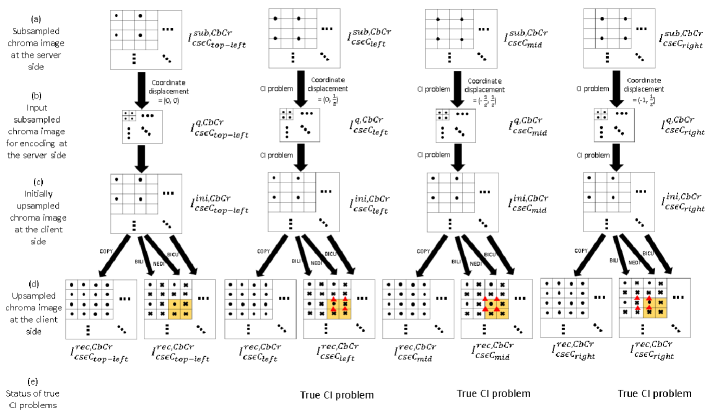
2) Why the true CI problem degrades the quality of the reconstructed image: Because for any combination, at the server side, we do not subsample the luma image at all, the luma image has no CI problem from the chroma subsampling step to the chroma upsampling step at the client side. For any combination in {, , }x{BILI, NEDI, BICU}, we know a true CI problem occurs in the reconstructed chroma image . Consequently, at the client side, the luma pixel and the upsampled chroma pixel lead to a coordinate displacement problem each other. Finally, after converting the upsampled YCbCr image to the reconstructed RGB full-color image (or the reconstructed Bayer CFA image) by Eq. (2), it degrades the quality of the reconstructed image.
IV The Proposed REDUCED CODEBOOK AND RE-INTERPOLATION (RCRI) APPROACH TO SOLVE THE UPI AND CI Problems
To solve the UPI problem, in our RCRI (reduced codebook and re-interpolation) approach, we first build up a reduced codebook in which each codeword occupies four bits. For each codeword, the first two bits represent the chroma subsampling class instead of the chroma subsampling method used at the server side, and the last two bits represent the future chroma upsampling process preferred at the client side. This is why we call it the reduced codebook. Later, a (7, 4)-Hamming code is proposed to increase the robustness against the communication interference. To solve the true CI problem, in our RCRI approach, our coordinate displacement-based re-interpolation strategy will be presented in Subsection IV.B.
IV-A The Reduced Codebook Design in Our RCRI Approach
From Fig. 4, we know there are four chroma subsampling classes, namely , , , and , in CS and there are four chroma upsampling processes, namely COPY, BILI, NEDI, and BICU, in CU. To record the necessary information of each combination in CSxCU, a reduced 4-bit codebook is depicted in Table I. In Table I, for each codeword, the first two bits are used to represent the chroma subsampling class, which corresponds to the chroma subsampling method used at the server side, and the last two bits are used to record the future chroma upsampling process preferred at the client side. For example, the combination ‘JCDU-BICU’ corresponding to ‘-BICU’ is expressed as the 4-bit codeword ‘0011’.
| COPY | BILI | NEDI | BICU | |
|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | |
| 0100 | 0101 | 0110 | 0111 | |
| 1000 | 1001 | 1010 | 1011 | |
| 1100 | 1101 | 1110 | 1111 |
To increase the robustness to tolerate one bit error against the communication interference, we deploy three redundant bits in the 4-bit codeword in Table I to form a (7, 4)-Hamming code [11]. Let each 4-bit codeword in Table I be denoted by ‘’. Using the error correcting code technique, the corresponding (7, 4)-Hamming code is represented as a 7-bit codeword “” in which the redundant 3-bit ‘’ is used for correcting the one bit error. For easy exposition, let = . Based on the three equations with even parity: , , and , the corrupted one bit can be detected and corrected.
For example, suppose the decoder received the 7-bit error correction code, namely = 1100000. From the equality: = , it yields ‘ = 1000’. Based on three even parity equations, it yields , , and . From the resultant 3-bit ‘011’ calculated from the above three even parity equations, we know that the value of is corrupted. Therefore, the value of is corrected from 0 to 1. Equivalently, the corrected 7-bit code should be 1110000, and the corrected 4-bit codeword equals 0001. Taking the first two bits of the corrected 4-bit codeword, namely 00, as a key to query Table I at the client side, the chroma subsampling class used at the server side is reported as . Taking the last two bits of the corrected 4-bit codeword, namely 01, by Table I, the future chroma upsampling process preferred at the client side is reported as BILI. Table II illustrates the error correcting (7, 4)-Hamming codebook used in our RCRI approach. Consequently, for any combination in CSxCU, Table II can be used to solve the UPI problem in a robust way. Table II is kept by the server side and the client side simultaneously.
| COPY | BILI | NEDI | BICU | |
|---|---|---|---|---|
| 0000000 | 1110000 | 1001100 | 0111100 | |
| 0101010 | 1011010 | 1100110 | 0010110 | |
| 1101001 | 0011001 | 0100101 | 1010101 | |
| 1000011 | 0110011 | 0001111 | 1111111 |
IV-B The Re-Interpolation Strategy for Correcting the Deviationly Upsampled Chroma Image
We first consider the three combinations in x{BILI, NEDI, BICU}. As depicted in Fig. 5, we know their common nonzero coordinate displacement vector is (0, ). To solve the true CI problem which occurred in the three combinations, based on the coordinate displacement vector (0, ), for each 22 upsampled chroma block in the temporarily reconstructed chroma image, the four temporarily upsampled chroma pairs, which are denoted by one black bullet and three cross-marked black bullets in Fig. 5(d), are replaced by re-interpolating the four chroma pairs marked by the four red triangles in of Fig. 5(d).
Next, we consider the three combinations in x{BILI, NEDI, BICU}. As depicted in Fig. 5, we know their common nonzero coordinate displacement vector is (-, ). To solve the true CI problem which occurred in the three combinations, based on the coordinate displacement vector (-, ), for each 22 upsampled chroma block in the temporarily reconstructed chroma image of Fig. 5(d), the four temporarily upsampled chroma pairs are replaced by re-interpolating the four chroma pairs marked by the four red triangles in .
By the same argument, for each 22 upsampled chroma block in of Fig. 5(d), the four temporarily upsampled chroma pairs can be recovered by re-interpolating the four chroma pairs marked by the four red triangles in . Consequently, the deviationly upsampled chroma image occurred in the nine combinations (= {, , }x{BILI, NEDI, BICU}) can be recovered using our coordinate displacement-based re-interpolation strategy.
| IDID [43] | JCDU [33] | 4:2:0(L) | 4:2:0(R) | CSLM [4] | ||||||||||||||||
| COPY | BILI | NEDI [43] | BICU | COPY | BILI | NEDI | BICU [33] | COPY | BILI | NEDI | BICU | COPY | BILI | NEDI | BICU | COPY | BILI [4] | NEDI | BICU | |
| CPSNR | 40.0832 | 45.2248 | 45.2343 | 44.5094 | 40.7675 | 45.3701 | 45.0005 | 45.6042 | 41.7039 | 43.6801 | 43.4977 | 43.6427 | 41.6744 | 40.6781 | 40.6171 | 40.5475 | 41.2692 | 42.2481 | 42.1925 | 41.3915 |
| (45.2343) | (45.2343) | (45.2343) | (45.2343) | (45.6042) | (45.6042) | (45.6042) | (45.6042) | (45.1837) | (45.1837) | (45.1837) | (45.1837) | (44.4567) | (44.4567) | (44.4567) | (44.4567) | (46.2224) | (46.2224) | (46.2224) | (46.2224) | |
| Average | 1.4715 | 1.4186 | 2.0526 | 3.5774 | 4.4471 | |||||||||||||||
| CPSNR gain | ||||||||||||||||||||
| SSIMc | 0.9710 | 0.9863 | 0.9865 | 0.9855 | 0.9742 | 0.9864 | 0.9858 | 0.9873 | 0.9779 | 0.9838 | 0.9834 | 0.9840 | 0.9778 | 0.9742 | 0.9741 | 0.9737 | 0.9750 | 0.9792 | 0.9792 | 0.9762 |
| (0.9865) | (0.9865) | (0.9865) | (0.9865) | (0.9873) | (0.9873) | (0.9873) | (0.9873) | (0.9870) | (0.9870) | (0.9870) | (0.9870) | (0.9860) | (0.9860) | (0.9860) | (0.9860) | (0.9896) | (0.9896) | (0.9896) | (0.9896) | |
| Average | 0.0042 | 0.0039 | 0.0047 | 0.0111 | 0.0122 | |||||||||||||||
| SSIMc gain | ||||||||||||||||||||
| FSIMc | 0.9992 | 0.9996 | 0.9997 | 0.9996 | 0.9993 | 0.9997 | 0.9996 | 0.9997 | 0.9995 | 0.9996 | 0.9995 | 0.9996 | 0.9995 | 0.9992 | 0.9992 | 0.9992 | 0.9993 | 0.9995 | 0.9994 | 0.9993 |
| (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | (0.9997) | |
| Average | 0.0002 | 0.0001 | 0.0002 | 0.0004 | 0.0003 | |||||||||||||||
| FSIMc gain | ||||||||||||||||||||
V Experimental Results
Based on the Kodak, IMAX, and Video datasets, and under the newly released versatile video coding (VVC) platform VTM-9.0 [31] for QP = 0, the thorough experimental results are illustrated to justify the quality enhancement effects of our RCRI approach against the CI and UPI problems for the traditional and state-of-the-art chroma subsampling methods.
All the concerned combinations are implemented on a computer with an Intel Core i7-7700 CPU 3.6 GHz and 24 GB RAM. The operating system is the Microsoft Windows 10 64-bit operating system. The program development environment is Visual C++ 2017.
We adopt the quality metrics, namely CPSNR (color peak signal-to-noise ratio), PSNR, SSIM (structure similarity index) [35], and FSIM (feature similarity index) [40], to illustrate the quality enhancement effects of our RCRI approach against the UPI and CI problems existing in the traditional and state-of-the-art combinations. The related quality metrics are defined below.
CPSNR is used to evaluate the average quality of the reconstructed RGB full-color images for one dataset with N images, and it is defined by
| (3) |
with in which P denotes the set of pixel coordinates in one image. Here, N = 24, N = 18, and N = 200 for the Kodak, IMAX, and Video datasets, respectively. and denote the c-color value of the pixel at position p in the th original RGB full-color image and the reconstructed one, respectively. In our experience, for fairness, each image in the Kodak dataset is downsampled to a quarter-sized one such that the average size of the downsampled images is close to the average size of the images in the IMAX dataset. The average CPSNR value equals the mean of the three CPSNR values for the three datasets. Similarly, the average PSNR value is used to evaluate the quality of the reconstructed Bayer CFA images for the three datasets.
For , SSIM [35] is used to measure the joint preservation effects of luminance, contrast, and structure similarity between the original Bayer CFA image and the reconstructed one. For , the SSIMc value is measured by the mean of the three SSIM values for the R, G, and B color planes.
For , FSIM [40] is an image quality metric with high consistency with the subjective evaluation. FSIM first utilizes the primary feature “phase congruency (PC)” and the minor feature “gradient magnitude” to obtain the local quality map, and then FSIM utilizes PC as a weighting function to obtain a quality score. For , the FSIMc value is measured by the mean of the three FSIM values for the R, G, and B color planes.
V-A Quality Enhancement Merit of Our RCRI Approach for
For , this subsection presents the quality enhancement effects of our RCRI approach against the UPI and true CI problems for the traditional and state-of-the-art combinations [43], [33], and [4]. In the five traditional chroma subsampling methods, 4:2:0(L) and 4:2:0(R) are selected to balance our discussion of the experiments. In addition, the quality enhancement effect of our RCRI approach to the state-of-the-art combination [22] is also investigated.
Table III illustrates the CPSNR gains of the reconstructed RGB full-color images using our RCRI approach against the UPI and true CI problems existing in the concerned combinations. For clarifying the quality enhancement effect of our RCRI approach, the CPSNR value of the reconstructed RGB full-color images using our RCRI approach for each combination is tabulated in the parenthesis ‘()’.
After deploying our RCRI approach in IDIDxCU, except for IDID-NEDI [43] without UPI and true CI problems, the CPSNR gains are 5.1511 (= 45.2343 - 40.0832 ) dB, 0.01 (= 45.2343 - 45.2248) dB, and 0.7249 dB w.r.t. IDID-COPY, IDID-BILI, and IDID-BICU, respectively. Suppose the probability of selecting each chroma upsampling process in CU at the client side is the same and equals . For IDID-NEDI, the average CPSNR gain using our RCRI approach equals 1.4715 (= (5.1511 + 0.01 + 0.7249)) dB, achieving a clear quality enhancement effect.
Similarly, after deploying our RCRI approach in JCDUxCU, except for JCDU-BICU [33] without UPI and true CI problems, the CPSNR gains using our RCRI approach are 4.8367 dB, 0.2341 dB, and 0.6037 dB w.r.t. JCDU-COPY, JCDU-BILI, and JCDU-NEDI, respectively; the average CPSNR gain equals 1.4186 (= (4.8367 + 0.2341 + 0.6037)) dB, also achieving a clear quality enhancement effect.
After deploying our RCRI approach in 4:2:0(L)xCU, 4:2:0(R)xCU, and CSLMxCU, the average CPSNR gains equal 2.0526 (= (3.4798 + 1.5036 + 1.6860 + 1.5410)) dB, 3.5774 (= (2.7823 + 3.7786 + 3.8396 + 3.9092)) dB, and 4.4471 (= (4.9532 + 3.9743 + 4.0299 + 4.8309)) dB, respectively, also achieving significant quality enhancement effects.
In addition, our experimental results indicate that for , after deploying our RCRI approach in ‘modified 4:2:0(A)’x(CU {TN}), except for ‘modified 4:2:0(A)’-TN [22], the CPSNR gains for the five combinations are 2.1622 dB, 2.3352 dB, 2.5043 dB, and 2.2331 dB, respectively. Accordingly, the average CPSNR gain of our RCRI approach equals 1.84696 (= (2.1622 + 2.3352 + 2.5043 + 2.2331)) dB, also achieving a clear quality enhancement effect.
V-B Quality Enhancement Merit of Our RCRI Approach for
For , this subsection presents the quality enhancement effects of our RCRI approach against the UPI problems and true CI problems for 4:2:0(L), 4:2:0(R), and the state-of-the-art combinations [20], [7], [8], and [22] under the current coding environment.
From Table IV, we observe that after deploying our RCRI approach in DMxCU, GDxCU, 4:2:0(L)xCU, 4:2:0(R)xCU, and xCU, the average PSNR gains equal 4.8134 (= (5.2940 + 5.6031 + 8.3564)) dB, 5.7962 (= (0.1047 + 7.5368 + 7.2515 + 8.2917)) dB, 2.4466 (= (2.7829 + 2.3125 + 2.7198 + 1.9712)) dB, 4.1248 (= (3.2360 + 4.3958 + 4.4658 + 4.4017)) dB, and 10.1278 (= (9.8250 + 10.0740 + 9.7277 + 10.8843)) dB, respectively, achieving significant quality enhancement effects.
In addition, our experimental results indicate that for , after deploying our RCRI approach in ‘modified 4:2:0(A)’x(CU {TN}), except for ‘modified 4:2:0(A)’-TN [22], the CPSNR gains are 2.0860 dB, 3.1487 dB, 3.5034 dB, and 2.8881 dB, respectively. Accordingly, the average PSNR gain of our RCRI approach equals 2.3252 (= (2.0860 + 3.1487 + 3.5034 + 2.8881)) dB, also achieving a clear quality enhancement effect.
Besides the PSNR improvement, Table IV also demonstrates the SSIM and FSIM improvements of our RCRI approach for .
| DM [20] | GD [7] | 4:2:0(L) | 4:2:0(R) | [8] | ||||||||||||||||
| COPY [20] | BILI | NEDI | BICU | COPY | BILI [7] | NEDI | BICU | COPY | BILI | NEDI | BICU | COPY | BILI | NEDI | BICU | COPY | BILI [8] | NEDI | BICU | |
| PSNR | 46.8980 | 41.6040 | 41.2949 | 41.5416 | 47.4129 | 40.9808 | 41.2661 | 40.2259 | 42.4150 | 42.8854 | 42.4781 | 43.2267 | 41.2777 | 40.1179 | 40.0479 | 40.1120 | 40.9136 | 40.6646 | 41.0109 | 39.8543 |
| [46.8980] | [46.8980] | [46.8980] | [46.8980] | [48.5176] | [48.5176] | [48.5176] | [48.5176] | [45.1979] | [45.1979] | [45.1979] | [45.1979] | [44.5137] | [44.5137] | [44.5137] | [44.5137] | [50.7386] | [50.7386] | [50.7386] | [50.7386] | |
| Average | 4.8134 | 5.7962 | 2.4466 | 4.1248 | 10.1278 | |||||||||||||||
| PSNR gain | ||||||||||||||||||||
| SSIM | 0.9981 | 0.9946 | 0.9943 | 0.9945 | 0.9983 | 0.9936 | 0.9942 | 0.9924 | 0.9955 | 0.9959 | 0.9955 | 0.9961 | 0.9943 | 0.9925 | 0.9924 | 0.9924 | 0.9937 | 0.9931 | 0.9938 | 0.9917 |
| [0.9981] | [0.9981] | [0.9981] | [0.9981] | [0.9987] | [0.9987] | [0.9987] | [0.9987] | [0.9973] | [0.9973] | [0.9973] | [0.9973] | [0.9969] | [0.9969] | [0.9969] | [0.9969] | [0.9991] | [0.9991] | [0.9991] | [0.9991] | |
| Average | 0.0027 | 0.0041 | 0.0016 | 0.0040 | 0.0059 | |||||||||||||||
| SSIM gain | ||||||||||||||||||||
| FSIM | 0.9984 | 0.9975 | 0.9973 | 0.9975 | 0.9986 | 0.9969 | 0.9972 | 0.9965 | 0.9977 | 0.9981 | 0.9979 | 0.9982 | 0.9964 | 0.9967 | 0.9968 | 0.9968 | 0.9971 | 0.9968 | 0.9972 | 0.9964 |
| [0.9984] | [0.9984] | [0.9984] | [0.9984] | [0.9992] | [0.9992] | [0.9992] | [0.9992] | [0.9987] | [0.9987] | [0.9987] | [0.9987] | [0.9983] | [0.9983] | [0.9983] | [0.9983] | [0.9996] | [0.9996] | [0.9996] | [0.9996] | |
| Average | 0.0007 | 0.0019 | 0.0007 | 0.0016 | 0.0027 | |||||||||||||||
| FSIM gain | ||||||||||||||||||||
VI Conclusion
For and , we have presented the proposed RCRI (reduced codebook and re-interpolation) approach to solve the UPI and true CI problems existing in the traditional and state-of-the-art combinations under the current coding environment. Based on the Kodak, IMAX, and Video datasets, the comprehensive experimental results have justified the clear quality enhancement effects after deploying our RCRI approach in the traditional and state-of-the-art combinations [43], [33], [4], [20], [7], [22], [8].
Our future work is to integrate our RCRI approach, the discrete cosine transform (DCT) based subsampling method [44], and the DCT based quantization error-minimization method [45] to achieve better quality of the reconstructed images in JPEG [12]. Moreover, our additional future work is to apply our RCRI approach to enhance the accuracy of the cross-component linear model for chroma component coding [17], [39] and to solve the accuracy degradation problem existing in the luma-guided winner-first voting strategy [6] at the client side for identifying the chroma subsampling method used at the server side for high QP values.
Acknowledgment
The authors appreciate the proofreading help of Ms. C. Harrington to improve the manuscript.
References
- [1] J. Allebach and P. W. Wong, “Edge-directed interpolation,” IEEE International Conference on Image Processing, pp. 707-710, Sep. 1996.
- [2] B. E. Bayer, “Color imaging array,” U.S. Patent 3 971 065, Jul. 1976.
- [3] H. Chen, M. Sun, and E. Steinbach, “Compression of Bayer-pattern video sequences using adjusted chroma subsampling,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 19, no. 12, pp. 1891-1896, Dec. 2009.
- [4] K. L. Chung, J. S. Cheng, and H. B. Yang, “Effective chroma subsampling and luma modification for RGB full-color images using the multiple linear regression technique,” IEEE Access, vol. 8, pp. 118315-118323, Jun. 2020.
- [5] K. L. Chung, T. C. Hsu, and C. C. Huang, “Joint chroma subsampling and distortion-minimization-based luma modification for RGB color images with application,” IEEE Transactions on Image Processing, vol. 26, no. 10, pp. 4626-4638, Oct. 2017.
- [6] K.L. Chung, C.C. Huang, and T.C. Hsu, ”Adaptive Chroma Subsampling-binding and Luma-guided Chroma Reconstruction Method for Screen Content Images," IEEE Trans. Image Processing, vol. 26, no. 12, pp. 6034-6045, Dec. 2017.
- [7] K. L. Chung, Y. L. Lee, and W. C. Chien, “Effective gradient descent-based chroma subsampling method for Bayer CFA images in HEVC,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 29, no. 11, pp. 3281-3290, Nov. 2019.
- [8] K. L. Chung, T. Y. Liu, and J. S. Cheng, “Novel and optimal luma modification-based chroma downsampling for Bayer color filter array images,” IEEE Open Journal of Circuits and Systems, vol.1, pp. 48-59, May 2020.
- [9] L. Condat, “A generic variational approach for demosaicking from an arbitrary color filter array," IEEE 272 International Conference on Image Processing, pp. 1625–1628, Nov. 7–10, 2009.
- [10] C. Dong, C. C. Loy, and X. Tang, “Accelerating the super-resolution convolutional neural network,” in Proc. Eur. Conf. Comput. Vis., Aug. 2016, pp. 1–16.
- [11] R. W. Hamming, Coding and Information Theory, 1986. Prentice-Hall.
- [12] G. Hudson, A. Léger, B. Niss, and I. Sebestyén, “JPEG at 25: Still going strong,” IEEE Multimedia, vol. 24, no. 2, pp. 96–103, Apr./Jun. 2017.
- [13] “ITU-R Recommendation BT-601-5: Studio encoding parameters of digital television for standard 4:3 and wide-screen 16:9 aspect ratios.” International Telecommunications Union, 2011.
- [14] IMAX database. http://www4.comp.polyu.edu.hk/~cslzhang/CDM_Dataset.htm.
- [15] D. Kiku, Y. Monno, M. Tanaka, M. Okutomi, ”Residual interpolation for color image demosaicking," in Proc. IEEE Int. Conf. Image Process. (ICIP), pp. 2304–2308. Sep. 2013.
- [16] Kodak database. http://www.math.purdue.edu/
- [17] J. Li, M. Wang, L. Zhang, K. Zhang, S. Wang, S. Wang, S. Ma, and W. Gao, “Sub-sampled cross-component prediction for chroma component coding,” in Data Compression Conference (DCC), pp. 203-212, Mar. 2020.
- [18] X. Li, B. Gunturk, and L. Zhang, ”Image demosaicing: A systematic survey," Proc. SPIE, vol. 6822, pp. 68221J-1-68221J-15, Jan. 2008.
- [19] X. Li and M. T. Orchard, “New edge-directed interpolation,” IEEE Transactions on Image Processing, vol. 10, no. 10, pp. 1521-1527, Oct. 2001.
- [20] C. H. Lin, K. L. Chung, and C. W. Yu, “Novel chroma subsampling strategy based on mathematical optimization for compressing mosaic videos with arbitrary RGB color filter arrays in H.264/AVC and HEVC,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 26, no. 9, pp. 1722-1733, Sep. 2016.
- [21] T. L. Lin, B. H. Liu, and K. H. Jiang, “An efficient algorithm for luminance optimization in chroma downsampling,” IEEE Transactions on Circuits and Systems for Video Technology, acceptance for publication, 2020.
- [22] T. L. Lin, Y. C. Yu, K. H. Jiang, C. F. Liang, and P. S. Liaw, “Novel chroma sampling methods for CFA video compression in AVC, HEVC and VVC,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 9, pp. 3167-3180, Sep. 2020.
- [23] Y. Lu, S. Li, and H. Shen, “Virtualized screen: A third element for cloud-mobile convergence,” IEEE Multimedia Magazine, vol. 18, no. 2, pp. 4–11, Feb. 2011.
- [24] R. Lukac and K. N. Plataniotis, “Color filter arrays: Design and performance analysis,” IEEE Trans. Consum. Electron., vol. 51, no. 4, pp. 1260–1267, Nov. 2005.
- [25] Y. Monno, D. Kiku, M. Tanaka, and M. Okutomi, “Adaptive residual interpolation for color and multispectral image demosaicking,” Sensors, vol. 17, no. 12, pp. 2787, Dec. 2017.
- [26] Z. Ni, K. K. Ma, H. Zeng, and B. Zhong, “Color image demosaicing using progressive collaborative representation,” IEEE Transactions on Image Processing, vol. 29, pp. 4952-4964, Mar. 2020
- [27] W. Pu, M. Karczewicz, R. Joshi, V. Seregin, F. Zou, J. Sole, Y. C. Sun, T. D. Chuang, P. Lai, S. Liu, S. T. Hsiang, J. Ye, and Y. W. Huang, “Palette mode coding in HEVC screen content coding extension,” IEEE J. Emerging and Selected Topics in Circuits and Systems, vol. 6, no. 4, pp. 420–432, Dec. 2016.
- [28] "Spatial Scalability Filters", document ISO/IEC JTC1/SC29/WG11 ITU-T SG 16 Q.6, Jul. 2005.
- [29] D. S. Tan, W. Y. Chen, K. L. Hua, “DeepDemosaicking: adaptive image demosaicking via multiple deep fully convolutional networks,” IEEE Trans. Image Processing, vol. 27, no. 5, pp. 2408-2419, May. 2018.
- [30] T. Vermeir et al., “Guided chroma reconstruction for screen content coding,” IEEE Trans. Circuits Syst. Video Technol., vol. 26, no. 10, pp. 1884–1892, Oct. 2016.
- [31] Versatile Video Coding (VVC). Available: https://vcgit.hhi.fraunhofer.de/jvet\/VVCSoftware_VTM
- [32] The Video Dataset. ftp://140.118.175.164/CFASS/
- [33] S. Wang, K. Gu, S. Ma, and W. Gao, “Joint chroma downsampling and upsampling for screen content image,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 26, no. 9, pp. 1595-1609, Sep. 2016.
- [34] X. Wang, K. Yu, S. Wu, J. Gu, Y. Liu, C. Dong, Y. Qiao, and C. C. Loy, “ESRGAN: Enhanced super-resolution generative adversarial networks,” in Proc. Eur. Conf. Comput. Vis. Workshops (ECCVW), Sep. 2018, pp. 1–16.
- [35] Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image quality assessment: from error measurement to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600-612, Apr. 2004.
- [36] Z. Wang, D. Liu, J. Yang, W. Han, and T. Huang, “Deep networks for image super-resolution with sparse prior,” in Proc. IEEE Int. Conf. Comput. Vis., Dec. 2015, pp. 370–378.
- [37] J. Yang, J. Wright, T. S. Huang, and Y. Ma, “Image super-resolution via sparse representation,” IEEE Trans. Image Process., vol. 19, no. 11, pp. 2861–2873, Nov. 2010.
- [38] W. Ye and K. K. Ma, “Color image demosaicing using iterative residual interpolation,” IEEE Transactions on Image Processing, vol. 24, no. 12, pp. 5879–5891, Dec. 2015.
- [39] K. Zhang, J. Chen, L. Zhang, X. Li, and M. Karczewicz, “Enhanced cross-component linear model for chroma intra-prediction in video coding,” IEEE Transactions on Image Processing, vol. 27, no. 8, pp. 3983–3997, Aug. 2018.
- [40] L. Zhang, X. Mou, and D. Zhang, “FSIM: A feature similarity index for image quality assessment,” IEEE Transactions on Image Processing, vol. 20, no. 8, pp. 2378-2386, Aug. 2011.
- [41] L. Zhang, X. Wu, A. Buades, X. Li, ”Color demosaicking by local directional interpolation and nonlocal adaptive thresholding," Journal of Electronic imaging, vol. 20, no. 2, pp. 023016, Jun. 2011.
- [42] X. Zhang and X. Wu, “Image interpolation by adaptive 2-D autoregressive modeling and soft-decision estimation,” IEEE Trans. Image Process., vol. 17, no. 6, pp. 887–896, Jun. 2008.
- [43] Y. Zhang, D. Zhao, J. Zhang, R. Xiong, and W. Gao, “Interpolation-dependent image downsampling,” IEEE Transactions on Image Processing, vol. 20, no. 11, pp. 3291-3296, Nov. 2011.
- [44] S. Zhu, C. Cui, R. Xiong, Y. Guo, and B. Zeng, “Efficient chroma subsampling and luma modification for color image compression,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 29, no. 5, pp. 1559-1563, May 2019.
- [45] S. Zhu, M. Li, C. Chen, S. Liu, and B. Zeng, “Cross-space distortion directed color image compression,” IEEE Transactions on Multimedia, vol. 20, no. 3, pp. 525-538, 2018, Mar. 2018.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/bb68a01f-cca9-4711-8413-5518d1295863/x12.png) |
Kuo-Liang Chung (SM01)received his B.S., M.S., and Ph.D. degrees from National Taiwan University, Taipei, Taiwan in 1982, 1984, and 1990, respectively. He has been one Chair Professor of the Department of Computer Science and Information Engineering at National Taiwan University of Science and Technology, Taipei, Taiwan since 2009. He was the recipient of the Distinguished Research Award (2004-2007; 2019-2022) and Distinguished Research Project Award (2009-2012) from the Ministry of Science and Technology of Taiwan. In 2020, he received the K. T. Li Fellow Award from the Institute of Information Computing Machinery, Taiwan. He has been an Editor and Associate Editor of Signals and the Journal of Visual Communication and Image Representation since 2020 and 2011, respectively. His research interests include machine learning, image processing, and video compression. |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/bb68a01f-cca9-4711-8413-5518d1295863/x13.png) |
Chen-Wei Kao received his B.S. degree in Computer Science and Engineering from the National Taiwan Ocean University, Keelung, Taiwan, in 2019. He is currently working towards his M.S. degree in Computer Science and Information Engineering at the National Taiwan University of Science and Technology, Taipei, Taiwan. His research interests include image processing and video compression. |