11email: [email protected] 22institutetext: Department of Physics & Space Science, Royal Military College of Canada, PO Box 17000 Station Forces, Kingston, ON, K7K 0C6, Canada 33institutetext: Department of Physics and Astronomy, University College London, Gower Street, London, WC1E 6BT, UK
A rare phosphorus-rich star in an eclipsing binary from TESS
Abstract
Context. Few exoplanets around hot stars with radiative envelopes have been discovered, although new observations from the TESS mission are improving this. Stars with radiative envelopes have little mixing at their surface, and thus their surface abundances provide a sensitive test case for a variety of processes including potentially star-planet interactions. Atomic diffusion is particularly important in these envelopes, producing chemically peculiar objects such as Am and HgMn stars.
Aims. An exoplanet candidate around the B6 star HD 235349 was identified by TESS. Here we determine the nature of this transiting object and identify possible chemical peculiarities in the star.
Methods. HD 235349 was observed using the long-slit spectrograph at Tartu Observatory, as well as photometrically by the TESS mission. The spectra were modeled to determine stellar parameters and chemical abundances. The photometric light curve was then analyzed in the context of the stellar parameters to determine properties of the transiting object.
Results. We find the transiting object is a low-mass stellar companion, not a planet. However, the primary of this eclipsing binary is a rare type of chemically peculiar star. A strong overabundance of P is found with overabundances of Ne and Nd, and mild overabundances of Ti and Mn, while He is mildly underabundant. There is also clear evidence for vertical stratification of P in the atmosphere of the star. The lack of Hg and weak Mn overabundance suggests that this is not a typical HgMn star. It may be in the class of helium-weak phosphorus-gallium (He-weak PGa) stars, or an intermediate between these two classes.
Conclusions. We show that HD 235349 is a rare type of chemically peculiar star (He-weak PGa) in an eclipsing binary system with a low-mass stellar companion. This appears to be the first He-weak PGa star discovered in an eclipsing binary.
Key Words.:
Stars: individual: HD 235349 – Stars: abundances – Stars: chemically peculiar – Stars: binaries: eclipsing – Planets and satellites: detection – Ephemerides1 Introduction
The Transiting Exoplanet Survey Satellite (TESS) mission (Ricker et al., 2015), recently identified HD 235349 (TOI $1356.01$, TIC , , ) as an Object of Interest based on photometric transits. The TESS lightcurve of HD 235349 contains a periodic transit signature with a depth of per cent and a period of days, reported in the Exoplanet Follow-up Observing Program for TESS (ExoFOP-TESS)111https://exofop.ipac.caltech.edu/tess/ database (and later confirmed by our own inspection of transit times). Based on discrepant previous effective temperature values the star may be among the hottest exoplanet hosts to-date or, alternatively, the large primary of an eclipsing binary. In order to clarify its nature, we carried out a comprehensive analysis of HD 235349 including a detailed chemical composition determination and a radial velocity time series.
HD 235349 is an early-type star with a Gaia Early Data Release 3 (EDR3) parallax distance of pc (Bailer-Jones et al., 2021). It was chosen as one of the first targets in the PIVOT (Planetary InitatiVe at the Observatory of Tartu) project, which is aimed at characterizing stars with exoplanets, protoplanetary disks, or chemical peculiarities. The TESS Object of Interest catalog lists a transit depth of per cent and a classification PC (planetary candidate). The two different primary star temperatures listed by the ExoFOP-TESS database place the transiting companion as either a giant planet (if K) or a low-mass star (if K). These and other available estimates for the primary disagree at high confidence, further motivating a follow-up analysis.
Stars with spectral type earlier than F5 ( ) are of particular interest because, in addition to the more familiar planet-metallicity correlation (Gonzalez, 1997; Fischer & Valenti, 2005), causal links may exist between certain chemically peculiar early-type stars and their planetary systems (Jura, 2015; Kama et al., 2015). More generally, due to the lack of a convective envelope, superficial chemical peculiarities arise in early-type stars for a variety of reasons, such as radiative levitation (Am stars; Catanzaro et al., 2019, and references therein), magnetic flotation with slow rotation (Ap/Bp; Mathys, 2020), gravitational settling with slow rotation and lack of magnetic fields (HgMn; Alecian & Michaud, 1981; Makaganiuk et al., 2011), or “accretion contamination” due to a lack of strong mixing (e.g., Boö; Paunzen, 1998).
We describe our spectroscopic observations in Sect. 2. In Sect. 3, we detail the spectral fitting, abundance analysis, and the radial velocity and photometric lightcurves. We present the resulting stellar composition and parameters in Sect. 4, as well as constraints on the secondary’s properties. The chemical peculiarity of HD 235349 and the nature of its secondary are discussed in Sect. 5.
2 Observations
Spectroscopic observations of HD 235349 were carried out at Tartu Observatory222https://kosmos.ut.ee/en (58∘15’57” N, 26∘27’35” E) in Estonia with the 1.5-meter Cassegrain reflector AZT-12 (see Appendix A for full details) on eleven nights from June, 2020 to April, 2021. A typical session included observations of radial velocity and spectrophotometric standard stars. The long-slit spectrograph ASP-32 at the Cassegrain focus was used with 1800 lines/mm and 1200 lines/mm gratings. The wavelength coverage extended from Å to Å with signal-to-noise ratios (S/N) from to . The full list of observations is given in Table 1.
The data were processed using the iraf333https://iraf.net (Tody, 1986) software built-in packages for CCD pre-processing, spectroscopy, and cross-correlation. Spectrophotometric standards (Vega and 10 Lac) from the CALSPEC database (Bohlin et al., 2020) were used to correct for the complex instrumental profiles of some observed spectra, but absolute flux calibrations were not attempted. After bias removal and flat fielding with a lamp, spectral extraction was performed using the long-slit spectrum processing routines in ctioslit and onedspec packages. Sigma spectra were used to estimate the S/N of science spectra. Thorium-argon arc lamp spectra were recorded before and after each science integration, their dispersion solutions were averaged. Heliocentric correction was carried out with the iraf tasks rvcorrect and dopcor. For abundance analysis, spectra were averaged nightly. The continuum was normalized by fitting a low degree cubic spline using a custom program created in Python programming language. The spectral resolution was measured using Gaussian fits to well-isolated ThAr emission lines close to the central wavelength in each spectral setup. The average Gaussian full width at half maximum was used as the width of instrumental profile of the spectrograph.
| Date | Exp. | S/N | grating | |||
|---|---|---|---|---|---|---|
| (Å) | (Å) | (s) | l/mm | |||
| 2020-06-18 | 4795 | 5666 | 2870 | 1800 | 130 | 1200 |
| 2020-06-18 | 5517 | 6329 | 4210 | 1800 | 150 | 1200 |
| 2020-06-18 | 6228 | 6978 | 4500 | 1800 | 140 | 1200 |
| 2020-09-19 | 3803 | 4750 | 2620 | 2700 | 70 | 1200 |
| 2020-09-19 | 3993 | 4509 | 5030 | 4500 | 130 | 1800 |
| 2020-09-19 | 4344 | 4827 | 5560 | 5400 | 130 | 1800 |
| 2020-09-19 | 4887 | 5320 | 6490 | 5400 | 200 | 1800 |
| 2020-09-19 | 5278 | 5672 | 7200 | 3600 | 150 | 1800 |
| 2020-11-20 | 5915 | 6241 | 8646 | 3600 | 100 | 1800 |
| 2020-11-23 | 5915 | 6240 | 8646 | 4800 | 140 | 1800 |
| 2021-03-22 | 4864 | 5298 | 6910 | 5400 | 140 | 1800 |
| 2021-04-01 | 4889 | 5321 | 6760 | 5400 | 104 | 1800 |
| 2021-04-06 | 4889 | 5321 | 6830 | 5400 | 150 | 1800 |
| 2021-04-10 | 4889 | 5321 | 6780 | 5400 | 140 | 1800 |
| 2021-04-18 | 3704 | 4244 | 4840 | 10800 | 90 | 1800 |
| 2021-04-19 | 4889 | 5321 | 6750 | 5400 | 140 | 1800 |
3 Analysis
3.1 Fundamental parameters based on spectroscopy
3.1.1 Balmer line analysis
Since the fundamental parameters of HD 235349 are not well constrained in the literature, we attempted to derive them from our spectroscopic observations. Balmer lines can provide strong constraints on and . The observations show no sign of emission lines or infilling, and the star is cool enough that the stellar wind should not contribute substantially to the observed lines. Thus we proceeded by directly fitting model spectra to the observations.
To calculate the model spectra we used the zeeman spectrum synthesis code (Landstreet, 1988; Wade et al., 2001), and atlas9 model atmospheres (Kurucz, 1993; Castelli & Kurucz, 2003). Atomic line data are taken from the Vienna Atomic Line Database (VALD, Piskunov et al., 1995; Ryabchikova et al., 1997; Kupka et al., 1999; Ryabchikova et al., 2015).
zeeman has been mostly used for metallic line analysis, particularly of magnetic and chemically peculiar stars. Since it is preferable to use one code for all the spectrum synthesis, we have added the calculation of hydrogen line profiles to the code. The hydrogen Stark broadening profiles use the grid calculated by Lemke (1997), which implements the widely used VCS model of Vidal et al. (1973). Stark broadening profiles are interpolated as necessary, and are implemented for the Lyman through Brackett series, up to of each series. Resonance self broadening is calculated using the theory of Ali & Griem (1965, 1966), and transition data for this calculation were taken from the National Institute of Standards and Technology (NIST) Atomic Spectra Database (Kramida et al., 2020). More advanced calculations exist, and may be implemented in the future, but for the current analysis self broadening is much weaker than Stark broadening. The broadening calculations also include thermal Doppler broadening, van der Waals broadening (with coefficients from VALD, although it is generally negligible), and microturbulence. In our implementation we use the tabulated Stark broadening profiles including thermal broadening of Lemke (1997), which is convolved with a Voigt profile that includes the other broadening terms, and then interpolated onto the wavelength grid used for the model spectrum. The model hydrogen lines here do not include the Zeeman effect, and thus are likely insufficient for strongly magnetic Ap/Bp stars, or polarized spectra, but should be sufficient for HD 235349.
To verify the accuracy of the Balmer line calculations, we tested the spectra against the Kurucz balmer (Kurucz, 1993) and synthe codes (Kurucz 1993, with grids of model spectra from Munari et al. 2005 and Bertone et al. 2008), which have similar physics to zeeman. This produces an excellent agreement over a wide range of temperatures, provided the same model atmospheres are used. Testing against the phoenix code for K-type stars (Allard et al. 2012) provides very good agreement. phoenix models for hotter stars (Husser et al. 2013, up to 12000 K) provide an acceptable agreement, although these models have slightly narrower wings, which in the worst case could lead to a discrepancy in the inferred up to 0.1. Testing against a grid of models from pfant (Coelho et al., 2005) provides a very good agreement, similar to synthe, although this grid only extends to 8000 K. Testing against spectra from the bstar2006 grid of the tlusty code (for cooler B-type stars in the grid, Lanz & Hubeny 2007) provides excellent agreement, except for the line cores of H and H.
In observations of Balmer lines, a very precise continuum normalization is difficult and sometimes not practically possible. To account for possible errors in the continuum placement of the observation, we include a continuum polynomial in the model spectrum for fitting Balmer lines. For this we use a simple quadratic polynomial, in the form . Including this significantly reduced the scatter in best fit and from individual Balmer lines.
In order to determine optimal and values, and probe their probability distributions, we adopted a Markov chain Monte Carlo (MCMC) approach. This is more computationally intensive than simply fitting by minimization, but offers two advantages. First, there tends to be a covariance between and , and MCMC allow us to characterize the correlation in their formal uncertainties. Second, while we include three coefficients for our continuum polynomial, and they will have some influence on the uncertainties of and , we do not care about the values of those coefficients, they are effectively nuisance parameters. An MCMC approach allows us to marginalize over these parameters (in a Bayesian sense), to derive distributions of the parameters of interest. We used the emcee package from Foreman-Mackey et al. (2013), which uses the MCMC affine-invariant ensemble sampler of Goodman & Weare (2010). This package has the advantages of being robustly tested and easy to integrate with existing code. The integration with emcee was implemented as a Python wrapper around the existing Fortran code of zeeman.
For this analysis we used the lower resolution observation from 2020-09-19 with , spanning 3803–4750 Å, since the resolution is sufficient for the Balmer lines and this provides H through H9 in one observation. Consistent results were obtained from the higher resolution observation from the same night spanning 3933–4509 Å, covering the H and H lines. The results for individual lines are presented in Appendix B and Fig. 11. To get the final values shown in Table 5, we take the median of the and distributions for each line, and take the average over the 5 lines as the global best value and the standard deviation as the formal uncertainty. This standard deviation is consistent with the uncertainties on individual lines.
3.1.2 Helium and metal line analysis
In order to derive chemical abundances for a range of elements, as well as and microturbulence (), we fit observations of metallic lines across most of the visible range. A secondary analysis where we derive and from metal lines simultaneously with chemical abundances is discussed in Appendix B. Synthetic spectra were calculated with zeeman, using atlas9 model atmospheres and atomic line data from VALD. The VALD line lists were obtained from an ‘extract stellar’ request with enhanced abundances for peculiar elements. The hyperfine splitting (HFS) calculations in VALD from Pakhomov et al. (2019) were included in the line list. Testing with and without hyperfine splitting components produced consistent results for the best fit abundances, well within our uncertainties.444 The impact of HFS on our final results is small mostly because, at this and resolution, HFS largely has the effect of desaturating strong lines. Lines of elements with a significant nuclear dipole moment (and HFS data in VALD) are relatively weak in this spectrum, so desaturation due to HFS is very small (generally less than 1% of our uncertainties on individual pixels). However, the effect is present in lines of interest to this study (particularly Mn ii and Ga ii), thus it should be included, and may become significant for stars with stronger or sharper lines.
Stellar parameters were derived by directly fitting synthetic spectra to the observations using the minimization code of Folsom et al. (2012). Since He I lines are prominent in the spectrum and in the He abundance is important, we included the Stark broadened profiles of Barnard et al. (1969, 1974, 1975) in the opacity profile calculations for the He I 4471, 4387, 4026, and 4921 Å lines.
For this analysis we used the higher resolution observations (obtained with the 1800 l/mm grating). While the spectral resolution is not particularly high, it is still well below the rotational broadening of the star, so it is sufficient for an abundance analysis. The combination of these observations cover 330 to 500 Å, and generally contain a good number of lines for simultaneously determining stellar parameters, thus we fit each observation independently. Where we had multiple observations covering the same wavelength range we used the highest S/N observation. (The 7292–7943 Å observations were not used, since they contained few detectable lines of interest.) This provides us with 5 spectral windows covering 4014–4500, 4375–4742, 4910–5310, 5281–5663, and 6007–6229 Å. Balmer lines and telluric lines were excluded from these regions. While Balmer lines could be fit simultaneously with the metal lines, they would dominate the resulting (and constraints on and ), thus we prefer to fit them separately so as to obtain an independent constraint from metal lines. Sample best fit spectra are shown in Fig. 1.
When comparing our best fit models to the observations, we noted a number of S II lines with discrepant line strengths. Comparing oscillator strengths for these lines from the VALD and NIST databases, we find significant differences in the theoretical value, with the NIST values rated ‘C’ or better. Using the NIST values produced more consistent results, improving the fit to the observations, thus we adopted the NIST values for S II when available. For similar reasons we adopted the NIST values for the P II 5152.2 and 5191.4 Å lines and Si II 5041.0, 5055.98, and 5056.3 Å lines.
For each of the five identified spectral regions above, we fit for , , and chemical abundances for any elements with detected lines. The 4014–4500 and 4375–4742 regions did not produce reliable values of , thus for these regions we assumed the average value from the other three regions. For the elements Cr, Ga, Pr, and Hg, we do not detect any individual lines, however they are of interest for determining the type of chemical peculiarity in a star, particularly for HgMn stars and helium-weak phosphorus-gallium (He-weak PGa) stars. Thus we used the strongest theoretically predicted line in our observed ranges to place upper limits on the elements. These limits were determined by eye, taking the largest abundance that produced a model reasonably consistent with the observation. The Hg line at 3983.9 Å is particularly interesting for this, as it is usually detected in HgMn stars, and its absence in HD 235349 (illustrated in Fig. 2) suggests this is not a typical HgMn star.
To produce the final results we take the average of the values for each spectral region, and as an uncertainty we use the standard deviation. For elements with abundances from less than three regions, the uncertainty was estimated by eye, accounting for the scatter between different lines, the impact of blending lines, noise in the observation, and potential normalization errors. For elements with abundances from three or more regions we verified that the standard deviation was reasonably consistent with the scatter between lines within one region and the noise in the observations. These uncertainties, from the scatter in independent fits to different spectral regions, should account for errors in the atomic line data and normalization, however they should still be considered somewhat approximate.


3.1.3 Stratification of phosphorus
In the initial abundance analysis, we found a clear wavelength dependence in the P abundance from different spectral windows, while the other abundances and stellar parameters had no significant correlation with wavelength. This could be a hint of vertical stratification in abundance of that element, since the excitation potential of the lower level, and implicitly the depth that the line is formed at, also correlate with wavelength. To investigate this we first looked at chemical abundances derived from individual lines, and then considered a simple parametric model to improve the global fit to all lines.

In order to derive best fit chemical abundances for individual P lines, we first adopt the best fit stellar parameters and abundances for other elements from Table 5. We then look for P lines that are at least marginally detected above the noise and are not in a blend that is dominated by a different element. This produced 29 usable lines between 4045 and 6089 Å. Several lines of varying quality are illustrated in Fig.3. We used the procedure of Khalack et al. (2007) to derive a proxy for the depth that each line is formed at. This takes the point in the atmosphere where the optical depth at the line center () reaches 1. That depth is reported in terms of the optical depth in the continuum at 5000 Å (). Real lines form over a range of depths in the star, with important contributions from above , however this proxy is useful when investigating chemical stratification and looking for correlations between abundance and optical depth. To approximately account for this range of depths, we also calculated the point where . We plot the abundance found for each line against the optical depth for that line in Fig. 4, and find a clear correlation with larger abundances for lower optical depths.
As a second approach we fit a simple parametric model for the vertical distribution of P, by calculating model spectra with this distribution and fitting them to the 29 lines identified above simultaneously. This approach requires an assumption about the functional form of the P distribution, and we considered three options. The first was a linear relation between the P abundance and , the second was a step function with two constant abundances above and below a transition at one depth, and the third was a linear (in ) transition region with constant abundances above and below. All three options reached nearly identical, statistically consistent, values for the best fit models. However the second and third option require more free parameters, and those parameters became increasingly poorly constrained. Thus we conclude that we cannot place a strong constraint on the functional form of the stratified distribution, likely since many of the P lines are very near the noise level in our observations, and adopt the simplest function: a linear relation.
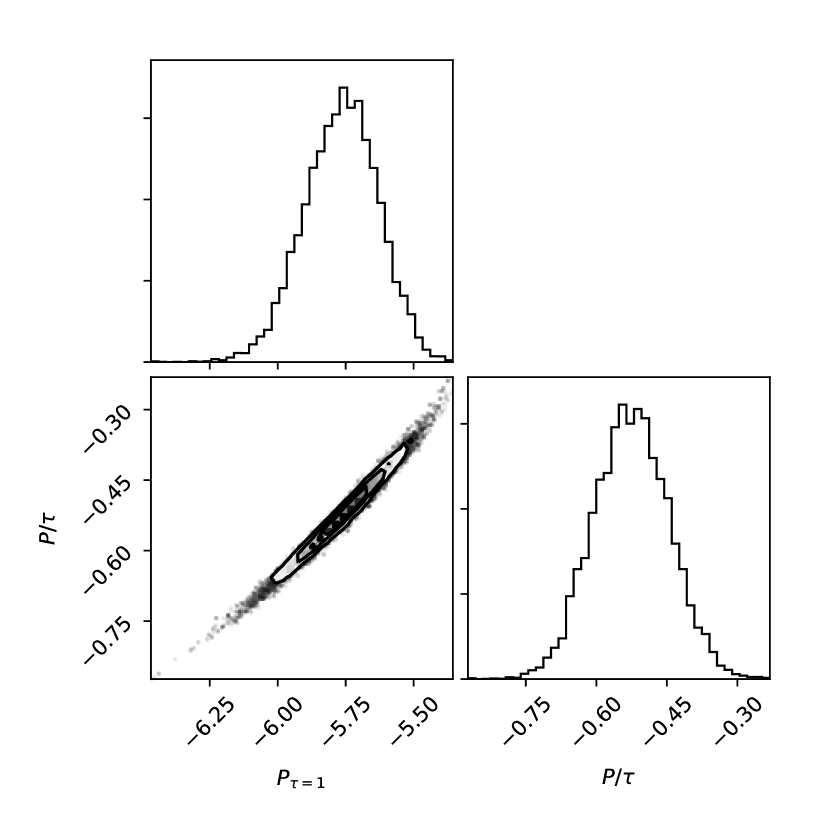
To explore the probability distribution of the parameters, and potentially strong co-variances, we used the same MCMC routine as was used for the Balmer lines in Sect. 3.1.1. The free parameters of the model are the abundance at and the slope of abundance () with . The results of modeling these lines are presented in Sect. 4.2, with the best fit model in Fig. 3, showing clear support for a stratified distribution of P.

3.2 Radial velocity perturbations
Our spectral observations sampled 11 individual nights over a baseline of months. This allowed us to determine the radial velocity amplitude of the primary and constrain the nature of the transiting companion. Radial velocity (RV) measurements were performed on the long-slit spectra using a cross-correlation approach and the iraf task fxcor (Fitzpatrick, 1994). The correlation template was a normalized model spectrum from Munari et al. (2005), specifically the model in their grid closest to our derived parameters. The resulting instantaneous RV values range from to km s-1 and are listed in Table 6. Fitting the RV curve with a pure sine wave and assuming zero eccentricity, we find km s-1.
3.3 Photometric lightcurve
TESS has observed HD 235349 (TOI ) in sectors 15 and 16, where two exoplanet transit-like events were discovered. The depth of those events is ppt. The photometric data from the TESS data portal has strong systematic effects, therefore we measured target and several surrounding comparison stars from cuts of TESS calibrated full-field images using traditional aperture photometry methods. Remaining residuals in the lightcurve were removed by fitting with a low order cubic spline.
The ExoFOP-TESS database reports a period of days for these transits. Phase folding our extraction of the TESS photometry with this period, we find a good agreement in the timing of the eclipses, thus we confirm the period reported in ExoFOP-TESS. Figure 5 shows the phase-folded TESS lightcurve and our radial velocity time-series for HD 235349. The offset of the radial velocity curve from the transit phase curve suggests an eccentric orbit, though we caution that due to possible systematics in our long-slit spectra, stable higher S/N follow-up is necessary to test this.

4 Results
| Parameter | Value | Solar | # |
|---|---|---|---|
| Balmer line averages | |||
| (K) | |||
| metal line averages | |||
| (km s-1) | |||
| (km s-1) | |||
| He | -1.07 | 3 | |
| C | -3.57 | 1 | |
| O | -3.31 | 2 | |
| Ne | -4.07 | 2 | |
| Mg | -4.40 | 4 | |
| Al | -5.55 | 3 | |
| Si | -4.49 | 5 | |
| P | -6.59 | 5 | |
| S | -4.88 | 4 | |
| Ti | -7.05 | 2 | |
| Cr | -6.36 | 1 | |
| Mn | -6.57 | 2 | |
| Fe | -4.50 | 4 | |
| Ni | -5.78 | 2 | |
| Ga | -8.96 | 1 | |
| Pr | -11.28 | 1 | |
| Nd | -10.58 | 1 | |
| Hg | -10.83 | 1 | |
4.1 Stellar parameters

The spectroscopically determined best-fit parameters of HD 235349 are summarized in Table 5. We adopt here the values determined from the hydrogen Balmer lines: K and .
The current mass and age of HD 235349 were determined by comparing its position in an effective temperature () – surface gravity () diagram with stellar evolution models without rotation at solar metallicity (; Ekström et al., 2012), as shown in Fig. 6, and interpolating between models in log mass. From this, we find a stellar mass , radius , and luminosity . We adopt these as our final values. As a consistency check, empirical calibrations of and as polynomial functions of , and [Fe/H] (Torres et al., 2010) give consistent results with the above numbers.
The distance to HD 235349 was recently determined to be pc using the Gaia EDR3 parallax (Bailer-Jones et al., 2021). However, the current value may not be entirely reliable, since the Renormalised Unit Weight Error (RUWE) is 2.842, while ‘good’ solutions should have a RUWE near 1.0 (or ¡ 1.4), and the “Goodness of fit statistic of model wrt along-scan observations” parameter is 38.3435, while good fits to the data should be . The EDR3 parallax ( mas) is also statistically incompatible with the DR2 value ( mas). The newer EDR3 value is likely more reliable (the older value has similar quality warnings), but we consider the possibility that there is a significant systematic error in the value. Relying on the spectroscopic stellar parameters and apparent magnitude, we can compare the Gaia distance with a luminosity-based distance. We use the previously calculated to obtain the stellar bolometric magnitude. Adopting a solar bolometric luminosity W and an absolute bolometric magnitude mag for a luminosity W (Resolution B2 of the XXIXth International Astronomical Union General Assembly in 2015), we obtain
| (1) |
Applying a bolometric correction (Pedersen et al., 2020), we find an absolute magnitude of mag. The apparent magnitude is mag and the reddening (Stassun et al., 2019). Assuming , we find an extinction of .
Using the standard relation
| (2) |
where is in parsecs, we then find that HD 235349 is pc away, consistent within errorbars with the distance from Gaia EDR3 determined by Bailer-Jones et al. (2021).
4.2 Chemical abundances and stratification
The best fit chemical abundances (see Table 5) and plotted relative to solar abundances in Fig. 7 (in units). We find a strong overabundance of P by dex relative to solar, and significant overabundances of Ne by dex, and of Ti by dex. Nd also appears to be strongly overabundant, although this is less certain as it is based on a few marginally detected lines. Mn and Ni are marginally enhanced (by and dex, respectively). C, O, Mg, Al, and Fe are all consistent with solar abundances (within ). He appears to be weakly depleted ( dex), although this abundance is particularly sensitive to . Si also appears to be slightly depleted ( dex). Thus HD 235349 is clearly chemically peculiar, although it does not display the peculiarities typical of an HgMn star, and is only a very mild, marginally He-weak star (although it does have the enhanced P common to the He-weak PGa stars).

The He abundance is particularly temperature sensitive, if our were overestimated by 500 K the He abundance would be within uncertainty of solar (see Appendix B). Alternately, if our was underestimated, that could lead to a larger He underabundance. Ne I lines may show some weak non-local thermodynamic equilibrium (NLTE) effects in B-type stars (Alexeeva et al., 2020) (for Ne II NLTE corrections appear to be negligible). NLTE corrections for Ne I at a near 14 000 K appear to reduce the Ne abundance by a few 0.1 dex (Alexeeva et al., 2020), possibly exceeding our error bar, but unlikely to produce an abundance consistent with solar, or chemically normal B-type stars.
From analyzing individual P lines (Sect. 3.1.3) we find that lines formed mostly at smaller optical depths require significantly larger abundances of P to match the observations than lines formed deeper in the atmosphere. The individual abundances and depths where are plotted in Fig. 4, and we interpret this as evidence for stratification of P in the stellar atmosphere. From simultaneously fitting P lines with synthetic spectra in an MCMC analysis, we find a clear negative slope in abundance with (), and an abundance at that is still enhanced relative to solar ( dex), with an important covariance between these two parameters. This P distribution is better constrained in the range of between -1 and -2, and becomes poorly constrained above -3 or below 0. A set of model P distributions from the final Markov chain are presented in Fig. 4 as overlapping gray lines, thus darker regions correspond to a higher density of models and a higher probability of the parameters. The posterior probability densities of the parameters are shown in Fig. 8. From the combination of the single line analysis and the parametric MCMC model, we find good evidence for stratification of P, with larger abundances higher in the atmosphere. However, since many lines of P are only marginally detected in our observations, higher precision data is needed before more details of the P distribution can be confidently constrained.
4.3 Properties of the transiting secondary
The mass of the secondary star can be constrained in two ways. Firstly, using the observed transit depth (7.5 ppt) and our radius estimate for the primary, we obtain the radius of the secondary, . In this radius estimate we assume the secondary is fully projected on the disk of the primary during photometric minimum, which is supported by the flat bottomed transits, and that the secondary contributes negligibly to the flux in the TESS band, which is supported by the small transit depth (suggesting a small cool object). In that case the ratio is the square root of the transit depth, and the uncertainty on is dominated by the uncertainty on . Using a main sequence mass-radius relation for low-mass stars ( , Eker et al., 2018), we find a secondary mass . Secondly, we can obtain from the radial velocity perturbation amplitude of the primary, given by
| (3) |
where is the orbital period, the orbital eccentricity, here assumed to be zero, is the inclination of the orbit, here assumed to be , and km s-1 (Sect. 3.2). This leads to a mass of . If we instead assumed , would increase by only 0.01 . If we assumed , that would decrease the mass by 0.02 , and would be needed to exceed our formal error bar. We summarize these constraints on in Fig. 9. The results from both constraints are consistent, and point to in the range 0.7 – 0.8 .

| HJD | Phase | ||
|---|---|---|---|
| () | () | ||
| 59112.24255 | 0.5953 | 0.7 | 0.5 |
| 59112.26930 | 0.5964 | 4.9 | 0.5 |
| 59112.32166 | 0.5986 | 7.2 | 2.0 |
| 59112.34425 | 0.5995 | 0.8 | 1.8 |
| 59112.36720 | 0.6005 | 7.2 | 1.9 |
| 59112.41234 | 0.6023 | 3.2 | 1.5 |
| 59112.43522 | 0.6033 | 3.0 | 1.5 |
| 59112.45896 | 0.6043 | 3.0 | 1.5 |
| 59112.50567 | 0.6062 | -0.0 | 1.9 |
| 59112.52948 | 0.6072 | -0.2 | 3.0 |
| 59174.46855 | 0.1576 | -28.5 | 1.9 |
| 59174.49501 | 0.1587 | -24.9 | 2.6 |
| 59177.15675 | 0.2683 | -21.9 | 1.7 |
| 59177.17290 | 0.2690 | -20.6 | 1.6 |
| 59177.19205 | 0.2698 | -20.8 | 1.5 |
| 59177.20641 | 0.2704 | -22.6 | 1.4 |
| 59296.54218 | 0.1842 | -27.0 | 1.9 |
| 59296.56559 | 0.1852 | -23.6 | 1.7 |
| 59296.58920 | 0.1862 | -24.9 | 1.9 |
| 59306.42854 | 0.5913 | -3.1 | 2.7 |
| 59306.45165 | 0.5923 | -3.4 | 2.6 |
| 59306.47458 | 0.5932 | -1.8 | 2.3 |
| 59311.48569 | 0.7996 | -0.1 | 3.4 |
| 59311.50924 | 0.8005 | 0.4 | 4.6 |
| 59311.53243 | 0.8015 | 1.0 | 4.5 |
| 59315.46889 | 0.9636 | -12.1 | 4.9 |
| 59315.49179 | 0.9645 | -10.3 | 4.4 |
| 59315.51495 | 0.9655 | -10.9 | 3.7 |
| 59323.39387 | 0.2899 | -15.4 | 2.1 |
| 59323.41587 | 0.2908 | -15.5 | 2.0 |
| 59323.44422 | 0.2920 | -19.2 | 1.9 |
| 59323.47104 | 0.2931 | -12.2 | 2.3 |
| 59323.50863 | 0.2946 | -12.6 | 2.3 |
| 59323.53542 | 0.2957 | -13.8 | 2.3 |
| 59324.38256 | 0.3306 | -15.5 | 3.7 |
| 59324.40609 | 0.3316 | -14.0 | 3.7 |
| 59324.42935 | 0.3325 | -14.1 | 3.4 |



5 Discussion
5.1 Spectral type and effective temperature
Using a Balmer line analysis, we determined an effective temperature K and for HD 235349. This yields a spectral type B6 III (Pecaut & Mamajek, 2013). These results are consistent with the highest and earliest spectral types from the wide range of past estimates. As noted earlier, the ExoFOP database lists two conflicting effective temperature values for HD 235349. The latest value, from the TESS project, is K. In the databases listed on ViZieR777http://simbad.u-strasbg.fr/simbad/sim-fid, a wider range of estimates can be found, corresponding to a spectral type range from mid-A to mid-B. Spectral type classifications spanning nearly 100 years have typically been B8 or B5 (Cannon, 1927; Hill & Lynas-Gray, 1977).
5.2 Chemical peculiarity
The composition of HD 235349 is clearly peculiar, with a strong overabundance of phosphorus (P, dex), neon (Ne, +0.65 dex), and neodymium (Nd, +1.44 dex). The upper limits for gallium and praseodymium also allow for enhancements of up to 2 dex. Furthermore, Ti, Mn, and Ni may be slightly (a factor of to dex) enhanced, while Si, and S appear underabundant by a similar factor and He appears to be weakly underabundant at 0.25 dex (although the He abundance is sensitive to ).
The star is not an obvious member of the mercury-manganese (HgMn) group of chemically peculiar stars, which extends up to temperatures similar to HD 235349 (up to 14 000 K, e.g. Ghazaryan et al., 2018). Mn is not strongly overabundant in HD 235349, and Hg (particularly the Hg II 3984 Å line) is not detected (see Fig. 2; although the upper limit is only dex enhanced). Thus the star cannot be confidently classified as an HgMn star. We compare chemical abundances for a few elements of interest, for different samples of peculiar stars888 We have divided the sample of helium weak stars from Ghazaryan et al. (2019) into those with good evidence for strong magnetic fields in the literature (‘mag. He-w’) and those lacking evidence for a magnetic field (‘He weak’), since the presence of a strong magnetic field modifies atomic diffusion. , as a function of in Fig. 10. The strongest similarity between HD 235349 and HgMn-type stars is that HgMn stars are typically overabundant in P. Smith & Dworetsky (1993) and Ghazaryan et al. (2018) note a population of hot (¿13 000 K) HgMn stars with mild Mn overabundances (Fig. 10), which is closer to HD 235349.
While the He abundance is only mildly below solar, the P- and potentially Ga-rich pattern is consistent with the rare class of He-weak PGa chemically peculiar stars. These are weakly- or non-magnetic stars which may represent the high temperature end of HgMn stars (Borra et al., 1983). There are a few stars that have been classified as He-weak, despite apparently very modest He underabundances (e.g. Glagolevskij et al., 2007, see Fig. 10). Thus HD 235349 has similarities to the He-weak PGa stars, although given the mild He underabundance (and sensitivity of the He abundance to ) we do not give it this classification with a high level of confidence.
We propose that HD 235349 represents an intermediate case between HgMn and He-weak PGa stars, perhaps with some chemical peculiarities weakened by mixing from the relatively rapid rotation of the star. There is significant evidence to support the idea that He-weak PGa stars represent a continuation of HgMn stars to higher temperatures (e.g. Borra et al., 1983; Rachkovskaya et al., 2006; Hubrig et al., 2014; Monier & Khalack, 2021), with the differences in abundances due to differences in atomic diffusion with increasing temperature and perhaps an increasingly important stellar wind. HD 235349 sits near the border in between these classes of objects (Ghazaryan et al., 2018, 2019), supporting the idea that it is intermediate between these classes.
Theoretical atomic diffusion calculations support this general picture. Early work by Alecian & Michaud (1981) on diffusion suggested that the overabundance of Mn in HgMn stars should fall off with increasing somewhere in the to 18000 K range. HD 235349 falls on the edge of this range, and this trend is generally consistent with other observations of Mn abundances (see Fig. 10). More recent work by Alecian & Stift (2019) consider time dependent diffusion including mass-loss, with a focus on HgMn stars. They consider stratification of P, finding overabundances higher in the atmosphere, and finding that these overabundances can be greatly enhanced by a weak magnetic field.
We find clear evidence for vertical stratification in the abundance of P, with larger abundances higher in the atmosphere. This can be adequately modeled with a linear distribution of P in , although higher S/N observations are needed to provide better constraints on the vertical distribution of P. Stratification of P, as well as some other elements, has been detected in a few HgMn stars (in HD 53929 and HD 63975 by Ndiaye et al. 2018, and in HD 161660 by Catanzaro et al. 2020), and also in HD 213781 which may be a blue horizontal branch star or an evolved HgMn star (Kafando et al., 2016). We find qualitatively consistent results with an apparently gradual increase in P abundance to shallower optical depths. This is also qualitatively consistent with the atomic diffusion models of P by Alecian & Stift (2019).
HD 235349 has a higher than is typical for an HgMn star or a He-weak PGa star. However, we are likely seeing the full equatorial rotation velocity (with close to ), since the system is an eclipsing binary, and with the relatively short period the orbital and rotational axes are likely aligned. The recent survey of HgMn stars by Chojnowski et al. (2020) found an average of 28 km s-1, but also 13 stars with above 60 km s-1. González et al. (2021) report a HgMn star with km s-1 as the highest HgMn star yet discovered. The high of HD 235349 likely enhances mixing in the star through meridional circulation, which may reduce the amount of chemical stratification and the strength of the observed peculiarities of some elements.
We find a low for HD 235349, which implies the star has likely evolved off the main sequence. However, that is not unprecedented among chemically peculiar stars in this temperature range, e.g. the HgMn star HD 63975 ( = 3.27, Ndiaye et al., 2018), the He-weak PGa star HD 23408 ( = 3.3, Mon et al., 1981; Monier & Khalack, 2021), and the He-weak (probably not of the PGa type) HD 5737 ( = 3.2, Leone & Manfre, 1997; Saffe & Levato, 2014). The low may influence atomic diffusion, and contribute to the atypical pattern of chemical abundances observed, although the impact of on atomic diffusion is not well studied.
5.3 Nature of the transiting object
The large radius of HD 235349 rules out a planetary explanation for the transits in the TESS lightcurve, instead strongly favoring a slightly sub-solar mass main sequence star. Recently, it was found from speckle interferometry that HD 235349 has a close fainter ( at 832 nm) companion at the angular distance of 0.263 arcseconds (Howell et al., 2021). It is probable that HD 235349 and this close companion form a true bound stellar system, the distance determined in current work implies the separation between two stars is at least AU (for a distance of pc), but this is too distant to be the transiting object. We rule out contamination of the photometry from a different source blended within a TESS pixel (e.g. an eclipsing binary projected near HD 235349). There is no sign of another bright star within a diameter area, and our optical spectra also contain no indications of another blended bright star. If the % dip in the summed lightcurve were from a different object it would require a faint binary where one component is completely covered, but this would produce a triangular transit whereas the TESS data clearly show a flat bottom. We conclude that the transiting companion must be bound to HD 235349, this assumption leads to a companion mass (Sect. 4.3).
There are very few known eclipsing binaries among HgMn and He-weak stars, although new data from TESS is helping to change this. Binarity is often thought to be important for generating these chemically peculiar stars, by slowing rotation rates through tidal interactions, thereby allowing atomic diffusion to proceed efficiently. Despite this there are only ten known eclipsing binaries among HgMn stars: AR Aur (HD 34364, Nordstrom & Johansen, 1994; Hubrig et al., 2006; Folsom et al., 2010), TYC 455-791-1 (Strassmeier et al., 2017), V772 Cas (HD 10260, Kochukhov et al., 2021a), V680 Mon (HD 267564, Paunzen et al., 2021), HD 72208 (Wraight et al., 2011; Kochukhov et al., 2021c), and TYC 4047-570-1, HD 36892, HD 50984, HD 55776, HD 53004 (Kochukhov et al., 2021c). Possible eclipses have been reported in HD 161701 (Wraight et al., 2011, see also González et al. 2014), and single eclipse-like events in TESS data have been reported for HD 34923 and HD 99803 (Kochukhov et al., 2021b), but more observations are needed to confirm these. The eclipsing binary HD 66051 is of interest (Niemczura et al., 2017) although it appears to contain a magnetic Bp star (Kochukhov et al., 2018), and HD 62658 was also recently discovered to contain an eclipsing magnetic Bp star (Shultz et al., 2019). We are not aware of any eclipsing binaries among the He-weak PGa stars, perhaps due to their rarity and the difficulty in firmly establishing this classification. In this context, the eclipsing binary nature of HD 235349 is an important addition to the known hot chemically peculiar stars.
6 Conclusions
-
1.
Transit-like events visible in the TESS lightcurve are in good agreement with eclipses by a low-mass stellar companion in a binary system, not an exoplanet. The transit depth and radius of the primary star imply a stellar radius for the transiting object, of .
-
2.
Radial velocity variability was detected in the observed spectra, which varies in phase with the transit events, implying a stellar mass for the transiting object. This dynamical mass of is consistent with the mass implied by the inferred radius of the transiting object.
-
3.
Based on fitting observations with model spectra, we classify the primary as a B6 III star, with K and .
-
4.
The primary of the system is a chemically peculiar star, showing a large overabundance of phosphorus, overabundances of neon and titanium, and a weak underabundance of helium. Clear evidence for stratification of phosphorus in the atmosphere of the star was found, with larger abundances at shallower optical depths. The spectral line of Hg II at 3984.0 Å was not detected, suggesting this is not a typical HgMn star. Instead we propose this may be an He-weak PGa star or an intermediate between the He-weak PGa stars and the HgMn stars.
-
5.
This appears to be the first star discovered with He-weak PGa characteristics in an eclipsing binary system.
Acknowledgements.
The authors gratefully acknowledge financial support from the Estonian Ministry of Education and Research through the Estonian Research Council institutional research funding IUT40-1 and from the European Union European Regional Development Fund project KOMEET 2014-2020.4.01.16-0029. This work is based on observations collected with the 1.5-m telescope at Tartu Observatory, Estonia, and includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA’s Science Mission Directorate. This work has also made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna; the VizieR catalogue access tool CDS, Strasbourg, France (DOI : 10.26093/cds/vizier); and the Exoplanet Follow-up Observation Program website, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.References
- Alecian & Michaud (1981) Alecian, G. & Michaud, G. 1981, ApJ, 245, 226
- Alecian & Stift (2019) Alecian, G. & Stift, M. J. 2019, MNRAS, 482, 4519
- Alexeeva et al. (2020) Alexeeva, S., Chen, T., Ryabchikova, T., et al. 2020, ApJ, 896, 59
- Ali & Griem (1965) Ali, A. W. & Griem, H. R. 1965, Physical Review, 140, 1044
- Ali & Griem (1966) Ali, A. W. & Griem, H. R. 1966, Physical Review, 144, 366
- Allard et al. (2012) Allard, F., Homeier, D., & Freytag, B. 2012, Philosophical Transactions of the Royal Society of London Series A, 370, 2765
- Asplund et al. (2009) Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481
- Bailer-Jones et al. (2021) Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147
- Barnard et al. (1969) Barnard, A. J., Cooper, J., & Shamey, L. J. 1969, A&A, 1, 28
- Barnard et al. (1974) Barnard, A. J., Cooper, J., & Smith, E. W. 1974, J. Quant. Spec. Radiat. Transf., 14, 1025
- Barnard et al. (1975) Barnard, A. J., Cooper, J., & Smith, E. W. 1975, J. Quant. Spec. Radiat. Transf., 15, 429
- Bertone et al. (2008) Bertone, E., Buzzoni, A., Chávez, M., & Rodríguez-Merino, L. H. 2008, A&A, 485, 823
- Bohlin et al. (2020) Bohlin, R. C., Hubeny, I., & Rauch, T. 2020, AJ, 160, 21
- Borra et al. (1983) Borra, E. F., Landstreet, J. D., & Thompson, I. 1983, ApJS, 53, 151
- Cannon (1927) Cannon, A. J. 1927, Annals of Harvard College Observatory, 100, 33
- Castelli & Kurucz (2003) Castelli, F. & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, ed. N. Piskunov, W. W. Weiss, & D. F. Gray, Vol. 210, A20
- Catanzaro et al. (2019) Catanzaro, G., Busà, I., Gangi, M., et al. 2019, MNRAS, 484, 2530
- Catanzaro et al. (2020) Catanzaro, G., Giarrusso, M., Munari, M., & Leone, F. 2020, MNRAS, 499, 3720
- Chojnowski et al. (2020) Chojnowski, S. D., Hubrig, S., Hasselquist, S., et al. 2020, MNRAS, 496, 832
- Coelho et al. (2005) Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735
- Eker et al. (2018) Eker, Z., Bakış, V., Bilir, S., et al. 2018, MNRAS, 479, 5491
- Ekström et al. (2012) Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146
- Fischer & Valenti (2005) Fischer, D. A. & Valenti, J. 2005, ApJ, 622, 1102
- Fitzpatrick (1994) Fitzpatrick, M. 1994, in Astronomical Society of the Pacific Conference Series, Vol. 61, Astronomical Data Analysis Software and Systems III, ed. D. R. Crabtree, R. J. Hanisch, & J. Barnes, 79
- Folsom et al. (2012) Folsom, C. P., Bagnulo, S., Wade, G. A., et al. 2012, MNRAS, 422, 2072
- Folsom et al. (2010) Folsom, C. P., Kochukhov, O., Wade, G. A., Silvester, J., & Bagnulo, S. 2010, MNRAS, 407, 2383
- Foreman-Mackey (2016) Foreman-Mackey, D. 2016, The Journal of Open Source Software, 1, 24
- Foreman-Mackey et al. (2013) Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306
- Ghazaryan et al. (2018) Ghazaryan, S., Alecian, G., & Hakobyan, A. A. 2018, MNRAS, 480, 2953
- Ghazaryan et al. (2019) Ghazaryan, S., Alecian, G., & Hakobyan, A. A. 2019, MNRAS, 487, 5922
- Glagolevskij et al. (2007) Glagolevskij, Y. V., Leushin, V. V., & Chountonov, G. A. 2007, Astrophysical Bulletin, 62, 319
- Gonzalez (1997) Gonzalez, G. 1997, MNRAS, 285, 403
- González et al. (2021) González, J. F., Nuñez, N. E., Saffe, C., et al. 2021, MNRAS, 502, 3670
- González et al. (2014) González, J. F., Saffe, C., Castelli, F., et al. 2014, A&A, 561, A63
- Goodman & Weare (2010) Goodman, J. & Weare, J. 2010, Communications in Applied Mathematics and Computational Science, 5, 65
- Hill & Lynas-Gray (1977) Hill, P. W. & Lynas-Gray, A. E. 1977, MNRAS, 180, 691
- Howell et al. (2021) Howell, S., Scott, N., Matson, R., et al. 2021, Frontiers in Astronomy and Space Sciences, 8, 635864
- Hubrig et al. (2014) Hubrig, S., Castelli, F., González, J. F., et al. 2014, MNRAS, 442, 3604
- Hubrig et al. (2006) Hubrig, S., González, J. F., Savanov, I., et al. 2006, MNRAS, 371, 1953
- Husser et al. (2013) Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6
- Jura (2015) Jura, M. 2015, AJ, 150, 166
- Kafando et al. (2016) Kafando, I., LeBlanc, F., & Robert, C. 2016, MNRAS, 459, 871
- Kama et al. (2015) Kama, M., Folsom, C. P., & Pinilla, P. 2015, A&A, 582, L10
- Khalack et al. (2007) Khalack, V. R., Leblanc, F., Bohlender, D., Wade, G. A., & Behr, B. B. 2007, A&A, 466, 667
- Kochukhov et al. (2018) Kochukhov, O., Johnston, C., Alecian, E., Wade, G. A., & BinaMIcS Collaboration. 2018, MNRAS, 478, 1749
- Kochukhov et al. (2021a) Kochukhov, O., Johnston, C., Labadie-Bartz, J., et al. 2021a, MNRAS, 500, 2577
- Kochukhov et al. (2021b) Kochukhov, O., Khalack, V., Kobzar, O., et al. 2021b, MNRAS, 506, 5328
- Kochukhov et al. (2021c) Kochukhov, O., Labadie-Bartz, J., Khalack, V., & Shultz, M. E. 2021c, MNRAS, 506, L40
- Kramida et al. (2020) Kramida, A., Yu. Ralchenko, Reader, J., & and NIST ASD Team. 2020, NIST Atomic Spectra Database (ver. 5.8), [Online]. Available: https://physics.nist.gov/asd [2021, April 20]. National Institute of Standards and Technology, Gaithersburg, MD.
- Kupka et al. (1999) Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119
- Kurucz (1993) Kurucz, R. 1993, smithsonian Astrophys. Obs.
- Landstreet (1988) Landstreet, J. D. 1988, ApJ, 326, 967
- Lanz & Hubeny (2007) Lanz, T. & Hubeny, I. 2007, ApJS, 169, 83
- Lemke (1997) Lemke, M. 1997, A&AS, 122, 285
- Leone & Manfre (1997) Leone, F. & Manfre, M. 1997, A&A, 320, 257
- Makaganiuk et al. (2011) Makaganiuk, V., Kochukhov, O., Piskunov, N., et al. 2011, A&A, 525, A97
- Mathys (2020) Mathys, G. 2020, in Stellar Magnetism: A Workshop in Honour of the Career and Contributions of John D. Landstreet, ed. G. Wade, E. Alecian, D. Bohlender, & A. Sigut, Vol. 11, 35–45
- Mon et al. (1981) Mon, M., Hirata, R., & Sadakane, K. 1981, PASJ, 33, 413
- Monier & Khalack (2021) Monier, R. & Khalack, V. 2021, Research Notes of the American Astronomical Society, 5, 104
- Munari et al. (2005) Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127
- Ndiaye et al. (2018) Ndiaye, M. L., LeBlanc, F., & Khalack, V. 2018, MNRAS, 477, 3390
- Niemczura et al. (2017) Niemczura, E., Hümmerich, S., Castelli, F., et al. 2017, Scientific Reports, 7, 5906
- Nordstrom & Johansen (1994) Nordstrom, B. & Johansen, K. T. 1994, A&A, 282, 787
- Pakhomov et al. (2019) Pakhomov, Y. V., Ryabchikova, T. A., & Piskunov, N. E. 2019, Astronomy Reports, 63, 1010
- Paunzen (1998) Paunzen, E. 1998, Contributions of the Astronomical Observatory Skalnate Pleso, 395
- Paunzen et al. (2021) Paunzen, E., Hümmerich, S., Fedurco, M., et al. 2021, MNRAS, 504, 3749
- Pecaut & Mamajek (2013) Pecaut, M. J. & Mamajek, E. E. 2013, ApJS, 208, 9
- Pedersen et al. (2020) Pedersen, M. G., Escorza, A., Pápics, P. I., & Aerts, C. 2020, MNRAS, 495, 2738
- Piskunov et al. (1995) Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525
- Rachkovskaya et al. (2006) Rachkovskaya, T. M., Lyubimkov, L. S., & Rostopchin, S. I. 2006, Astronomy Reports, 50, 123
- Ricker et al. (2015) Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, Journal of Astronomical Telescopes, Instruments, and Systems, 1, 014003
- Ryabchikova et al. (2015) Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr, 90, 054005
- Ryabchikova et al. (1997) Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, Baltic Astronomy, 6, 244
- Saffe & Levato (2014) Saffe, C. & Levato, H. 2014, A&A, 562, A128
- Shultz et al. (2019) Shultz, M. E., Johnston, C., Labadie-Bartz, J., et al. 2019, MNRAS, 490, 4154
- Smith & Dworetsky (1993) Smith, K. C. & Dworetsky, M. M. 1993, A&A, 274, 335
- Stassun et al. (2019) Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138
- Strassmeier et al. (2017) Strassmeier, K. G., Granzer, T., Mallonn, M., Weber, M., & Weingrill, J. 2017, A&A, 597, A55
- Tody (1986) Tody, D. 1986, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Vol. 627, Instrumentation in astronomy VI, ed. D. L. Crawford, 733
- Torres et al. (2010) Torres, G., Andersen, J., & Giménez, A. 2010, A&A Rev., 18, 67
- Vidal et al. (1973) Vidal, C. R., Cooper, J., & Smith, E. W. 1973, ApJS, 25, 37
- Wade et al. (2001) Wade, G. A., Bagnulo, S., Kochukhov, O., et al. 2001, A&A, 374, 265
- Wraight et al. (2011) Wraight, K. T., White, G. J., Bewsher, D., & Norton, A. J. 2011, MNRAS, 416, 2477
Appendix A Instrument parameters
The key parameters of the AZT-12 telescope at Tartu Observatory, and the long-slit spectrograph mounted there, are given in Table 4.
| Parameter | Specification |
|---|---|
| Telescope Type | Cassegrain reflector |
| Primary Diameter | 1.50 m |
| Secondary Diameter | 0.36 m |
| Focal Ratio | F/16 |
| Cassegrain Focal Length | 24.0 m |
| Cassegrain focus plate scale | 116 |
| Spectrograph type | Long-slit spectrograph |
| at Cassegrain focus | |
| Spectrograph slit width | 2.2 arcsec |
| Spectrograph slit length | arcmin |
| Gratings ( | 300, 600, 1200, 1800, 2400 |
| Spectral resolution |
Appendix B Additional temperature constraints
The primary constraints on and are from the MCMC based fit to five Balmer lines, as described in Sect. 3.1.1. Here we include plots of the posterior distributions (marginalized over the three continuum polynomial coefficients) from the MCMC analysis for each individual line in Fig. 11. We find an important covariance between and for all lines. Covariances between or and the continuum parameters (not shown) are generally weak.





As a secondary analysis we derive and from the fit to metallic lines. Since the star is chemically peculiar, these parameters must be determined simultaneously with chemical abundances, when using metal lines. This was done using the same analysis methodology as described in Sect. 3.1.2 for the metal and He lines, using the same spectral windows and line data, but including and as additional free parameters. The resulting fits to the observations are of a comparable quality to the previous metal line analysis. The best fit values averaged over spectral windows are in Table 9, with uncertainties taken as the standard deviation or estimated as before for elements with abundances from less than three windows. This analysis provides a weaker constraint on and than the Balmer line analysis, but the results are consistent within uncertainties. Similarly, the chemical abundances are consistent within uncertainty, but may have slightly larger systematic errors due to the larger uncertainties in and . The most important difference in abundance is that He becomes more abundant and uncertain (with a larger scatter between windows), putting it within of the solar abundance. Thus the lower from the metal line analysis suggests the star may not be He weak, but it also produces less consistent results from different He lines, suggesting it may be less reliable.
| Parameter | Value | Solar | # |
| (K) | |||
| (km s-1) | |||
| (km s-1) | |||
| He | -1.07 | 3 | |
| C | -3.57 | 1 | |
| O | -3.31 | 2 | |
| Ne | -4.07 | 2 | |
| Mg | -4.40 | 4 | |
| Al | -5.55 | 3 | |
| Si | -4.49 | 5 | |
| P | -6.59 | 5 | |
| S | -4.88 | 4 | |
| Ti | -7.05 | 2 | |
| Cr | -6.36 | 1 | |
| Mn | -6.57 | 2 | |
| Fe | -4.50 | 4 | |
| Ni | -5.78 | 2 | |
| Ga | -8.96 | 1 | |
| Pr | -11.28 | 1 | |
| Nd | -10.58 | 1 | |
| Hg | -10.83 | 1 |