A proposal of adaptive parameter tuning for robust stabilizing control of –level quantum angular momentum systems
Abstract
Stabilizing control synthesis is one of the central subjects in control theory and engineering, and it always has to deal with unavoidable uncertainties in practice. In this study, we propose an adaptive parameter tuning algorithm for robust stabilizing quantum feedback control of -level quantum angular momentum systems with a robust stabilizing controller proposed by [Liang, Amini, and Mason, SIAM J. Control Optim., 59 (2021), pp. 669-692]. The proposed method ensures local convergence to the target state. Besides, numerical experiments indicate its global convergence if the learning parameters are adequately determined.
I Introduction
Stabilizing controller synthesis is one of the central problems in control systems, even if systems are described by quantum mechanics [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]. Unfortunately, stabilizing control is vulnerable to failure due to the existence of uncertainties in practice. There are two conventional approaches to overcome this problem; robust control [12, 13] and adaptive control [14, 15]. Robust control ensures performance of the control system under worst-case scenario against a given set of uncertainties. It has been actively studied for quantum systems[16, 17, 18, 19, 20, 21], as well as classical systems. The most common problem of robust control is that it is difficult to specify the uncertainties in advance, and even if possible, the robust controller tends to yield conservative control performance. On the other hand, adaptive control operates on the system by learning model parameters. Adaptive approaches for quantum system identification and filtering have also been studied [22, 23, 24]. However, these studies do not consider a stochastic continuous measurement signal, which is known as a homodyne measurement signal in physics and one of the commonly used detection models for quantum physics, and no real-time adaptive control framework has been proposed in the previous studies so far.
Recently, Liang et. al. [21] derived certain conditions for robust stabilization of –level quantum angular momentum systems with uncertain parameters and initial state. They revealed that the accurate estimation of the multiplication of the two parameters is essential for their robust stabilization. This fact is important because it ensures robust stabilization by accurate estimation of the multiplication of the parameters only rather than the parameters individually. Motivated by [21], we propose an adaptive parameter tuning algorithm with stabilizing control. To the best of our knowledge, this is the first study on adaptive control for quantum systems with continuous-time measurement feedback. The proposed adaptive law is aimed to minimize the difference between the original and model outputs. The method is simple, but it works well in numerical experiments under certain assumptions, and ensure local convergence.
I-A Contributions
The contributions of this study are summarized as follows:
-
•
An adaptive parameter tuning algorithm for robust quantum stabilizing control is proposed (Equation (6)).
-
•
An asymptotic property of the estimate under steady-state conditions is derived (Proposition 4).
-
•
Local convergence of the proposed method is evaluated under certain assumptions (Theorem 6).
I-B Organization
The rest of this paper is organized as follows. The problem is stated in Section II. In Sec. III, we propose an adaptive parameter tuning algorithm and the analytical results are shown. The proposed method is evaluated numerically and compared with the application of [21] in Sec. IV. We conclude the paper in Sec. V.
I-C Notation
, and are natural, real, and complex numbers, respectively, and . and are real and complex matrices, respectively. implies the Hermitian conjugate of matrix . We use as the identify matrix. For , () indicates that is a positive-(semi)definite matrix. When two positive-semidefinite matrices and satisfy , we denote . The absolute value of a square matrix is defined as and for , the trace norm is defined as . . Denote . indicates the expectation in terms of a random variable or a stochastic process . is Landau’s as .
II Problem Formulation
II-A Measurement-based Feedback Quantum Systems
Let and , and let us consider the following quantum stochastic differential equation [2, 9, 21].
| (1) |
with an initial state , where is a conditional state of the system, is the control input, is the measurement output, ,
, , and , is the coupling constant, and denotes measurement efficiency [25]. is control input and throughout this paper, is assumed bounded. is called the state, which is a quantum counterpart of (conditional) probability law. Equation (1) is called stochastic master equation having different equilibrium points if the control input . We denote each equilibrium point as , , and the target state is described by . Note that consists of an eigenvector of , i.e.,
A stabilization problem of (1) is to ensure that the state converges to a desirable equilibrium point. Therefore, model uncertainty must be considered in practical situations as different uncertainties exist in the model, initial state, and parameters of (1). In this paper, we consider parametric uncertainty and unknown initial condition. Then, the nominal model is described as follows.
| (2) |
with its initial state . The differences from (1) are the initial state and the parameters . Because the accessible state is , the goal of the stabilization problem is to find a feedback controller that ensures as one of the stochastic convergences.
II-B Previous Work
Liang et. al. [21] found certain sufficient conditions when the nominal state stabilization becomes the true state stabilization. One of their main results is that if the ratio of and is close to , then there exists a stabilizing controller. For convenience, we write and , and then the following result holds [21].
Theorem 1 ([21, Propositions 4.16 and 4.18])
Suppose satisfies
| (3) |
where
and , is positive-definite, and . Then, there exists an asymptotically stabilizing control law that ensures
II-C Problem Statement
Before stating our problem, we present a minor modification of Theorem 1.
Corollary 2
Let be a time varying parameter and we assume that there exists that satisfies the following constraint;
| (4) |
where and are the same as defined in Theorem 1, , and . Then, there exists a stabilizing control law.
Proof:
The proof is the same as [21, Propositions 4.16 and 4.18], so we omit it here. ∎
Corollary 2 implies that if we can set the parameter appropriately, the stabilization is achieved even if the initial parameter does not satisfy the condition (3). Therefore, the problem we deal with is how to estimate while stabilizing the state . Adaptive parameter tuning with stabilizing control is a simple and useful solution for the problem, as shown in the next section.
III Proposed Method and Theoretical Results
Owing to the work of Liang et al.[21], there is an acceptable uncertainty of the parameter that ensures the convergence of the state to the target state. Hence, we only focus on the parameter tuning of . The adaptive model is then described as follows (Fig. 1).
| (5) |
where are given and is calculated by our proposed parameter tuning algorithm below.
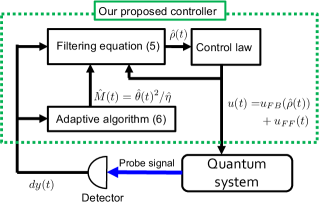
III-A Proposed Adaptive Parameter Tuning Method
For convenience, we use , , and . Then, we propose the following parameter tuning algorithm.
| (6) | ||||
| (7) |
where and . Note that we update as . From the filtering theory [25, 26], can be replaced by , where is a standard Wiener process, and (6) then gives
If the noise is removed, updating by Eq. (6) implies the same as instant gradient method of the cost function with the weight . This is a type of Robbins-Monro algorithm for continuous-time problems [27, 28, 29]. Clearly, if for all , then the parameter tuning law is the continuous-time Robbins-Monro algorithm, which is guaranteed to converge to the true parameter. Unfortunately, the assumption may not hold; therefore, we need to seek the condition when the parameter converges to the region described by (4). Note that the true parameter cannot be an equilibrium point of the system (6). Thus, the noise is unavoidable, so we examine how to choose the parameter and obtain the accurate estimate asymptotically.
Remark 3
Because each unknown parameter is a positive constant, the adaptive parameter must to be positive. However, the solution of (6) is not ensured to be positive, so when becomes negative, we replace it with or a small positive number in practical implementations.
III-B Asymptotic Property of the Estimate
Here, we describe that the choice of the parameters and of (7) is valid from the following proposition. For convenience, we write .
Proposition 4
Suppose that a pair of initial states is in some , , and , and considering (6) with and , the followings hold.
-
1.
For the mean of the ,
-
2.
For the variance of the , ,
Proof:
Denote the integral of by
| (10) |
We only prove the convergence of . Note that and from the assumption. Then, the explicit solution of is
As is a deterministic uncertain parameter and is given, . If , it implies that and therefore, the claim of the theorem trivially holds. The other cases are as follows.
-
1.
If , because and for all , where is arbitrary chosen. From simple calculation and using the above-mentioned properties,
and therefore,
As can be chosen to be arbitrarily large, the first term of the right-hand side of the above equation can be arbitrarily small. As , for and for . Then, the last term of the right-hand side of the equation remains finite and it is less than . Therefore, the claim of the theorem holds for .
-
2.
If , because and for all , where is arbitrary chosen. From simple calculation and using the above-mentioned properties,
and therefore, for
holds. The second term of the right-hand side of the above inequality vanishes as and because can be arbitrarily large, if is large, then as .
∎
From Proposition 4, if and are in the same equilibrium state, the parameter updated by (6) converges to the true value with probability one. Unfortunately, since the true state is not accessible, we cannot confirm whether and are practically in the same equilibrium state. To avoid being trapped in different equilibrium points before learning the parameter accurately, we employ feedforward control in the following subsection.
Remark 5
A key to prove Proposition 4 is that, is a non-increasing function with , while its integral becomes a non-decreasing function with . This is a minor difference from the continuous-time Robbins-Monro algorithms because they require the square integrability of the function (e.g., [28, Theorem 1]). Searching for a preferable function for learning is beyond the scope of this study, and we only use (7) and do not consider other functions. We established some convergence rate problems in [30], which can be referred for details.
III-C Local Convergence Property
In this subsection, we evaluate our tuning algorithm (6) with the following control input.
where is a strictly decreasing, bounded continuous function with , and is a stabilizing feedback control law if satisfies the condition of Corollary 2 (e.g., of (4.22) or (4.23) in [21].) The role of is to eliminate the from the target state before learning the parameter accurately. Then, our proposed method ensures local convergence under certain assumptions. For convenience, we write .
Theorem 6
Let satisfy for a given sufficiently small . Considering and are the solutions of (1) and (5) starting from , , respectively, we choose the feedforward control that satisfies for all and the feedback control that satisfies if satisfies . Let be the solution of the parameter tuning algorithm (6) with and and its initial value satisfy . Suppose that and for all . Besides, assume that the following inequality holds for almost all
| (11) |
and the equality holds iff , where
. Then, for ,
Proof:
See Appendix.
∎
Some readers may think the assumptions of Theorem 6 are too strong to be valid in practice; however, several numerical experiments support that they may hold in many cases, one of which is demonstrated in the following section.
IV NUMERICAL EXPERIMENTS
In this section, we examine the proposed method numerically. The dimension of the quantum system is , and the Euler-Maruyama method is used with time step width. We use the true parameters as and the initial parameters of the adaptive system as , for which the system cannot be stabilized by merely using the feedback control in [21]. The true initial state is randomly generated for each realization and the initial adaptive state is fixed to . The target state is set as . We set the control inputs as follows.
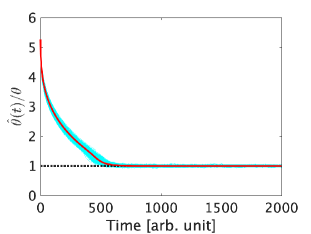
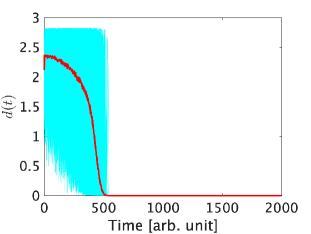
The parameters of (7) are chosen as , and then the simulation is run with 1000 realizations. The results are shown in Figs. 2 and 3. Fig. 2 represents the trajectories of the ratio and Fig. 3 represents the distance [21],
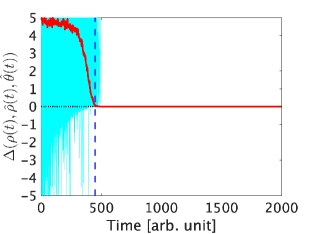
We also evaluate whether the inequality (11) holds in Fig. 4. From the figures, all sample trajectories of and appear to converge to and the target state , respectively. The inequality (11) sometimes does not hold at the beginning of the simulations, but all sample trajectories satisfy it after , shown by the blue dashed line in Fig. 4, until the states converge to the target states. Moreover, even though our proposed method does not ensure satisfying the condition (3) at all times after a certain point, we confirmed that all sample trajectories of the ratio satisfy the condition of Corollary 2, i.e., , after . This result implies that the proposed method ensures that all sample trajectories are in the neighborhood of the true value with a significantly high probability. Although we confirmed that , which does not satisfy the condition of Theorem 6, also works well, but the result is omitted due to the page limitation.
V CONCLUSION AND FUTURE WORK
In this paper, we proposed an adaptive parameter tuning algorithm for robust stabilizing control of quantum angular momentum systems. The asymptotic property of the estimate and local convergence of the states were evaluated analytically, and numerical experiments show that the proposed method works well for systems with large parametric uncertainty.
The relaxation of Theorem 6’s assumptions and the global convergence property are interesting works for future.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the helpful comments and suggestions of the anonymous reviewers.
References
- [1] R. van Handel, J. K. Stockton, and H. Mabuchi, “Feedback control of quantum state reduction,” IEEE Transactions on Automatic Control, vol. 50, no. 6, pp. 768–780, 2005.
- [2] M. Mirrahimi and R. van Handel, “Stabilizing Feedback Controls for quantum systems,” SIAM Journal on Control and Optimization, vol. 46, no. 2, pp. 445–467, 2007.
- [3] K. Tsumura, “Global stabilization of n-dimensional quantum spin systems via continuous feedback,” in Proceedings of 2007 American Control Conference. IEEE, 2007, pp. 2129–2134.
- [4] A. Sarlette, Z. Leghtas, M. Brune, J. M. Raimond, and P. Rouchon, “Stabilization of nonclassical states of one- and two-mode radiation fields by reservoir engineering,” Physical Review A, vol. 86, p. 012114, Jul 2012.
- [5] F. Ticozzi, R. Lucchese, P. Cappellaro, and L. Viola, “Hamiltonian Control of Quantum Dynamical Semigroups: Stabilization and Convergence Speed,” IEEE Transaction on Automatic Control, vol. 57, no. 8, pp. 1931–1944, 2012.
- [6] F. Ticozzi, K. Nishio, and C. Altafini, “Stabilization of Stochastic Quantum Dynamics via Open and Closed Loop Control,” IEEE Transaction on Automatic Control, vol. 58, pp. 74–85, 2013.
- [7] P. Scaramuzza and F. Ticozzi, “Switching quantum dynamics for fast stabilization,” Physical Review A, vol. 91, p. 062314, Jun 2015.
- [8] F. Ticozzi, L. Zuccato, P. D. Johnson, and L. Viola, “Alternating projections methods for discrete-time stabilization of quantum states,” IEEE Transactions on Automatic Control, vol. 63, no. 3, pp. 819–826, 2017.
- [9] W. Liang, N. H. Amini, and P. Mason, “On exponential stabilization of -level quantum angular momentum systems,” SIAM Journal on Control and Optimization, vol. 57, no. 6, pp. 3939–3960, 2019.
- [10] G. Cardona, A. Sarlette, and P. Rouchon, “Exponential stabilization of quantum systems under continuous non-demolition measurements,” Automatica, vol. 112, p. 108719, 2020.
- [11] J. Wen, Y. Shi, J. Jia, and J. Zeng, “Exponential stabilization of two-level quantum systems based on continuous noise-assisted feedback,” Results in Physics, vol. 22, p. 103929, 2021.
- [12] K. Zhou, J. C. Doyle, and K. Glover, Robust and Optimal Control. Prentice Hall Upper Saddle River, NJ, 1996.
- [13] I. R. Petersen, V. A. Ugrinovskii, and A. V. Savkin, Robust Control Design using Methods. Springer Verlag, 2000.
- [14] K. S. Narendra and A. M. Annaswamy, Stable Adaptive Systems. Prentice-Hall, Inc. Upper Saddle River, NJ, USA, 1989.
- [15] M. Krstic, P. V. Kokotovic, and I. Kanellakopoulos, Nonlinear and Adaptive Control Design. John Wiley & Sons, Inc., 1995.
- [16] M. R. James, “Risk-sensitive optimal control of quantum systems,” Physical Review A, vol. 69, no. 3, p. 032108, 2004.
- [17] ——, “A quantum Langevin formulation of risk-sensitive optimal control,” Journal of Optics B: Quantum and Semiclassical Optics, vol. 7, p. S198, 2005.
- [18] D. Dong, C. Chen, B. Qi, I. R. Petersen, and F. Nori, “Robust manipulation of superconducting qubits in the presence of fluctuations,” Scientific Reports, vol. 5, p. 7873, 2015.
- [19] I. G. Vladimirov, I. R. Petersen, and M. R. James, “Risk-sensitive performance criteria and robustness of quantum systems with a relative entropy description of state uncertainty,” in 23rd International Symposium on Mathematical Theory of Networks and Systems, Hong Kong, Jul. 2018, pp. 482–488.
- [20] M. R. James, H. I. Nurdin, and I. R. Petersen, “ Control of Linear Quantum Stochastic Systems,” IEEE Transactions on Automatic Control, vol. 53, no. 8, pp. 1787–1803, 2008.
- [21] W. Liang, N. H. Amini, and P. Mason, “Robust Feedback Stabilization of -Level Quantum Spin Systems,” SIAM Journal on Control and Optimization, vol. 59, no. 1, pp. 669–692, jan 2021.
- [22] S. Bonnabel, M. Mirrahimi, and P. Rouchon, “Observer-based Hamiltonian identification for quantum systems,” Automatica, vol. 45, no. 5, pp. 1144–1155, 2009.
- [23] Z. Leghtas, M. Mirrahimi, and P. Rouchon, “Back and forth nudging for quantum state estimation by continuous weak measurement,” in Proceedings of the 2011 American Control Conference. IEEE, 2011.
- [24] R. S. Gupta and M. J. Biercuk, “Adaptive filtering of projective quantum measurements using discrete stochastic methods,” Physical Review A, vol. 104, p. 012412, 2021.
- [25] L. Bouten, R. van Handel, and M. R. James, “An Introduction to Quantum Filtering,” SIAM Journal on Control and Optimization, vol. 46, no. 6, pp. 2199–2241, 2007.
- [26] A. Bain and D. Crişan, Fundamentals of Stochastic Filtering, ser. Stochastic Modelling and Applied Probability. Springer Verlag, 2009, vol. 60.
- [27] H. Robbins and S. Monro, “A Stochastic Approximation Method,” The Annals of Mathematical Statistics, vol. 22, no. 3, pp. 400–407, 1951.
- [28] H.-F. Chen, “Continuous-time stochastic approximation: convergence and asymptotic efficiency,” Stochastics and Stochastic Reports, vol. 51, no. 3-4, pp. 217–239, 1994.
- [29] H. Kushner, “Stochastic approximation: a survey,” Wiley Interdisciplinary Reviews: Computational Statistics, vol. 2, no. 1, pp. 87–96, 2010.
- [30] S. Enami and K. Ohki, “Convergence analysis of adaptive tuning parameter for robust stabilizing control of -level quantum systems,” in Proceedings of 60th Annual Conference of the Society of Instrument and Control Engineers of Japan, 2021.
- [31] X. Mao, “Stochastic versions of the LaSalle theorem,” Journal of Differential Equations, vol. 153, no. 1, pp. 175–195, 1999.
- [32] H. J. Kushner, Stochastic Stability and Control, Academic Press, 1967.
Proof of Theorem 6
To prove Theorem 6, we evaluate , where , and . Our proof mainly follows the argument of the proof of Theorem 2.1 in [31].
First, we evaluate and .
Lemma 7
If holds for some small , then
where is a nonnegative number and iff .
Proof:
If holds for some small , there exists that satisfies and . This implies that if holds for a small , then
holds. Since , the -th diagonal element of needs to be nonpositive and the other diagonal elements are nonnegative, and . The -th diagonal element of becomes , so is nonnegative and iff .
∎
Therefore, . Similar argument gives and from the assumptions. Note that in (5) can be replaced by . Let be the infinitesimal generator [32]. Using the classical Ito calculus, the infinitesimal generators of and are as follows.
Since , , , , and ,
| (12) |
where .
Next, we calculate the infinitesimal generator of and . From simple calculation,
From the definition of ,
Since the expectation of the right-hand side of the above inequality is at most for small , , where the Dynkin’s formula [32] is used. Let and . Note that iff . Then,
| (13) |
Note that
Together with the assumption (11), for all and using Dynkin’s formula [32],
holds. Note that the integrand of the last term of the left-hand side of the first inequality converges to zero faster than the other terms. The other terms of the left-hand side are positive and need to be finite. Hence, a.s. Since or fluctuates randomly if or , implies that and converge to the origin. From the assumption that and stay in the neighborhood of , the convergence of and implies converges to . Furthermore, since is not integrable and, although we skip the proof, is continuous in , a.s. Therefore, a.s.