A Practical, Progressively-Expressive GNN

The 1-dimensional Weisfeiler-Leman ($1$-WL) test, also known as color refinement [49] algorithm, is a widely celebrated approach to (approximately) test GI. Although extremely fast and effective for most graphs ($1$-WL can provide canonical forms for all but $n^{-1/7}$ fraction of $n$-vertex graphs [5]), it fails to distinguish members of many important graph families, such as regular graphs. The more powerful $k$-WL algorithm first appeared in [57], and extends coloring of vertices (or 1-tuples) to that of $k$-tuples. $k$-WL is progressively expressive with increasing $k$, and can distinguish any finite set of graphs given a sufficiently large $k$. $k$-WL has many interesting connections to logic, games, and linear equations [11, 28]. Another variant of $k$-WL is called $k$-FWL (Folklore WL), such that $(k+1)$-WL is equally expressive as $k$-FWL [11, 26]. Our work focuses on $k$-WL.

$k$-WL iteratively recolors all $n^{k}$ $k$-tuples defined on a graph $G$ with $n$ nodes. At iteration 0, each $k$-tuple $\overrightarrow{\boldsymbol{v}}=(v_{1},...,v_{k})\in V(G)^{k}$ is initialized with a color as its atomic type $\bm{at_{k}}(G,\overrightarrow{\boldsymbol{v}})$. Assume $G$ has $d$ colors, then $\bm{at_{k}}(G,\overrightarrow{\boldsymbol{v}})\in\{0,1\}^{2\binom{k}{2}+kd}$ is an ordered vector encoding. The first $\binom{k}{2}$ entries indicate whether $v_{i}=v_{j}$, $\forall i,j,1{\leq}i{<}j{\leq}k$, which is the node repetition information. The second $\binom{k}{2}$ entries indicate whether $(v_{i},v_{j})\in E(G)$. The last $kd$ entries one-hot encode the initial color of $v_{i}$, $\forall i,1\leq i\leq k$. Importantly, $\bm{at_{k}}(G,\overrightarrow{\boldsymbol{v}})=\bm{at_{k}}(G^{\prime},\overrightarrow{\boldsymbol{v^{\prime}}})$ if and only if $v_{i}\mapsto v^{\prime}_{i}$ is an isomorphism from $G[\overrightarrow{\boldsymbol{v}}]$ to $G^{\prime}[\overrightarrow{\boldsymbol{v^{\prime}}}]$. Let $\bm{wl}_{k}^{(t)}(G,\overrightarrow{\boldsymbol{v}})$ denote the color of $k$-tuple $\overrightarrow{\boldsymbol{v}}$ on graph $G$ at $t$-th iteration of $k$-WL, where colors are initialized with $\bm{wl}_{k}^{(0)}(G,\overrightarrow{\boldsymbol{v}})=\bm{at_{k}}(G,\overrightarrow{\boldsymbol{v}})$.

At the $t$-th iteration, $k$-WL updates the color of each $\overrightarrow{\boldsymbol{v}}\in V(G)^{k}$ according to

$\displaystyle\scriptstyle\bm{wl}_{k}^{(t+1)}(G,\overrightarrow{\boldsymbol{v}})=\text{HASH}\Big{(}\bm{wl}_{k}^{(t)}(G,\overrightarrow{\boldsymbol{v}}),\Big{\{}\mskip-10.0mu\Big{\{}\bm{wl}_{k}^{(t)}(G,\overrightarrow{\boldsymbol{v}}[x/1])\Big{|}x\in V(G)\Big{\}}\mskip-10.0mu\Big{\}},\ldots,\Big{\{}\mskip-10.0mu\Big{\{}\bm{wl}_{k}^{(t)}(G,\overrightarrow{\boldsymbol{v}}[x/k])\Big{|}x\in V(G)\Big{\}}\mskip-10.0mu\Big{\}}\Big{)}$

(1)

Let $\bm{gwl}_{k}^{(t)}(G)$ denote the encoding of $G$ at $t$-th iteration of $k$-WL. Then,

$\displaystyle\bm{gwl}_{k}^{(t)}(G)=\text{HASH}\bigg{(}\bigg{\{}\mskip-10.0mu\bigg{\{}\bm{wl}_{k}^{(t)}(G,\overrightarrow{\boldsymbol{v}})\Big{|}\overrightarrow{\boldsymbol{v}}\in V(G)^{k}\bigg{\}}\mskip-10.0mu\bigg{\}}\bigg{)}$

(2)

Two $k$-tuples $\overrightarrow{\boldsymbol{v}}$ and $\overrightarrow{\boldsymbol{u}}$ are connected by an edge if $|\{i\in[k]|v_{i}=u_{i}\}|={k-1}$, or informally if they share $(k$$-$$1)$ entries. Then, $k$-WL defines a super-graph $S_{k\text{-wl}}(G)$ with its nodes being all $k$-tuples in $G$, and edges defined as above. Eq. (1) defines the rule of color refinement on $S_{k\text{-wl}}(G)$. Intuitively, $k$-WL is akin to (but more powerful as it orders subgroups of neighbors) running 1-WL algorithm on the supergraph $S_{k\text{-wl}}(G)$. As $t\rightarrow\infty$, the color $\bm{wl}_{k}^{(t+1)}(G,\overrightarrow{\boldsymbol{v}})$ converges to a stable value, denoted as $\bm{wl}_{k}^{(\infty)}(G,\overrightarrow{\boldsymbol{v}})$ and the corresponding stable graph color denoted as $\bm{gwl}_{k}^{(\infty)}(G)$. For two non-isomorphic graphs $G,G^{\prime}$, $k$-WL can successfully distinguish them if $\bm{gwl}_{k}^{(\infty)}(G)\not=$ $\bm{gwl}_{k}^{(\infty)}(G^{\prime})$. The expressivity of $\bm{wl}_{k}^{(t)}$ can be exactly characterized by first-order logic with counting quantifiers. Let $\mathbf{C}_{k}^{t}$ denote all first-order formulas with at most $k$ variables and $t$-depth counting quantifiers, then $\bm{wl}^{(t)}_{k}(G,\overrightarrow{\boldsymbol{v}})=\bm{wl}^{(t)}_{k}(G^{\prime},\overrightarrow{\boldsymbol{v^{\prime}}})$ $\Longleftrightarrow$ $\forall\phi\in\mathbf{C}^{t}_{k},\phi(G,\overrightarrow{\boldsymbol{v}})=\phi(G^{\prime},\overrightarrow{\boldsymbol{v^{\prime}}})$. Additionally, there is a $t$-step bijective pebble game that are equivalent to $t$-iteration $k$-WL in expressivity. See Appendix.A.2 for the pebble game characterization of $k$-WL.

Despite its power, $k$-WL uses all $n^{k}$ tuples and has $O(kn^{k})$ complexity at each iteration.

Our first proposed adaptation to $k$-WL is to remove ordering in each $k$-tuple, i.e. changing $k$-tuples to $k$-multisets. This greatly reduces the number of supernodes to consider by $O(k!)$ times.

Let $\tilde{\boldsymbol{v}}=\{\mskip-5.0mu\{v_{1},...,v_{k}\}\mskip-5.0mu\}$ be the corresponding multiset of tuple $\overrightarrow{\boldsymbol{v}}=(v_{1},...,v_{k})$. We introduce a canonical order function on $G$, $o_{G}:V(G)\rightarrow[n]$, and a corresponding indexing function $o^{-1}_{G}(\tilde{\boldsymbol{v}},i)$, which returns the $i$-th element of $v_{1},...,v_{k}$ sorted according to $o_{G}$. Let $\bm{mwl}_{k}^{(t)}(G,\tilde{\boldsymbol{v}})$ denote the color of the $k$-multiset $\tilde{\boldsymbol{v}}$ at $t$-th iteration of $k$-MultisetWL, formally defined next.

At $t=0$, we initialize the color of $\tilde{\boldsymbol{v}}$ as $\bm{mwl}_{k}^{(0)}(G,\tilde{\boldsymbol{v}})=\text{HASH}\big{(}\{\mskip-5.0mu\{\bm{at}_{k}(G,p(\tilde{\boldsymbol{v}}))|p\in\text{perm[k]}\}\mskip-5.0mu\}\big{)}$ where perm[k]¹¹1This function should also consider repeated elements; we omit this for clarity of presentation. denotes the set of all permutation mappings of $k$ elements. It can be shown that $\bm{mwl}_{k}^{(0)}(G,\tilde{\boldsymbol{v}})=\bm{mwl}_{k}^{(0)}(G^{\prime},\tilde{\boldsymbol{v}}^{\prime})$ if and only if $G[\tilde{\boldsymbol{v}}]$ and $G^{\prime}[\tilde{\boldsymbol{v}}^{\prime}]$ are isomorphic.

At $t$-th iteration, $k$-MultisetWL updates the color of every $k$-multiset by

	$\displaystyle\bm{mwl}_{k}^{(t+1)}(G,\tilde{\boldsymbol{v}})=\text{HASH}\bigg{(}\bm{mwl}_{k}^{(t)}(G,\tilde{\boldsymbol{v}}),\bigg{\{}\mskip-10.0mu\bigg{\{}$	$\displaystyle\{\mskip-5.0mu\{\bm{mwl}_{k}^{(t)}(G,\tilde{\boldsymbol{v}}[x/o^{-1}_{G}(\tilde{\boldsymbol{v}},1)])\big{|}x\in V(G)\}\mskip-5.0mu\},$		(3)
	$\displaystyle...,$	$\displaystyle\{\mskip-5.0mu\{\bm{mwl}_{k}^{(t)}(G,\tilde{\boldsymbol{v}}[x/o^{-1}_{G}(\tilde{\boldsymbol{v}},k)])\big{|}x\in V(G)\}\mskip-5.0mu\}\bigg{\}}\mskip-10.0mu\bigg{\}}\bigg{)}$

Where $\tilde{\boldsymbol{v}}[x/o^{-1}_{G}(\tilde{\boldsymbol{v}},i)])$ denotes replacing the $i$-th (ordered by $o_{G}$) element of the multiset with $x\in V(G)$. Let $S_{k\text{-mwl}}(G)$ denote the super-graph defined by $k$-MultisetWL. Similar to Eq. (2), the graph level encoding is $\bm{gmwl}_{k}^{(t)}(G)=\text{HASH}(\{\mskip-5.0mu\{\bm{mwl}_{k}^{(t)}\big{(}G,\tilde{\boldsymbol{v}}\big{)}\big{|}\forall\tilde{\boldsymbol{v}}\in V(S_{k\text{-mwl}}(G))\}\mskip-5.0mu\}\big{)}$.

Interestingly, although $k$-MultisetWL has significantly fewer number of node groups than $k$-WL, we show it is no less powerful than $k$-$1$-WL in terms of distinguishing graphs, while being upper bounded by $k$-WL in distingushing both node groups and graphs.

Theorem 2 is proved by using a variant of a series of CFI [11] graphs which cannot be distinguished by $k$-WL. This theorem shows that $k$-MultisetWL is indeed very powerful and finding counter examples of $k$-WL distinguishable graphs that cannot be distinguished by $k$-MultisetWL is very hard. Hence we conjecture that $k$-MultisetWL may have the same expressivity as $k$-WL in distinguishing undirected graphs, with an attempt of proving it in Appendix.A.4.10. Additionally, the theorem also implies that $k$-MultisetWL is strictly more powerful than ($k-1$)-MultisetWL.

We next give a pebble game characterization of $k$-MultisetWL, which is named doubly bijective $k$-pebble game presented in Appendix.A.3. The game is used in the proof of Theorem 2.

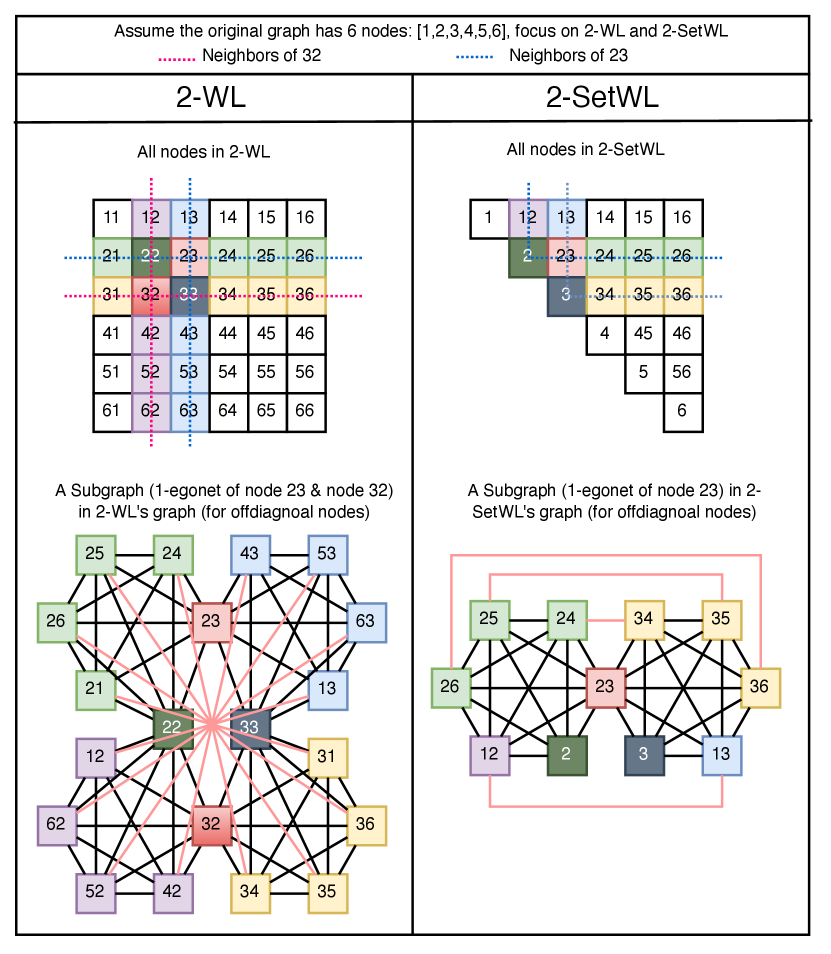
Next, we propose further removing repetition inside any $k$-multiset, i.e. transforming $k$-multisets to $k(\leq)$-sets. We assume elements of $k$-multiset $\tilde{\boldsymbol{v}}$ and $k(\leq)$-set $\hat{\boldsymbol{v}}$ in $G$ are sorted based on the ordering function $o_{G}$, and omit $o_{G}$ for clarity. Let $s(\cdot)$ transform a multiset to set by removing repeats, and let $r(\cdot)$ return a tuple with the number of repeats for each distinct element in a multiset. Specifically, let $\hat{\boldsymbol{v}}=s(\tilde{\boldsymbol{v}})$ and $\hat{\boldsymbol{n}}=r(\tilde{\boldsymbol{v}})$, then $m:=|\hat{\boldsymbol{v}}|=|\hat{\boldsymbol{n}}|\in[k]$ denotes the number of distinct elements in $k$-multiset $\tilde{\boldsymbol{v}}$, and $\forall i\in[m]$, $\hat{\boldsymbol{v}}_{i}$ is the $i$-th distinct element with $\hat{\boldsymbol{n}}_{i}$ repetitions. Clearly there is an injective mapping between $\tilde{\boldsymbol{v}}$ and $(\hat{\boldsymbol{v}},\hat{\boldsymbol{n}})$; let $f$ be the inverse mapping such that $\tilde{\boldsymbol{v}}=f(s(\tilde{\boldsymbol{v}}),r(\tilde{\boldsymbol{v}}))$. Equivalently, each $m$-set $\hat{\boldsymbol{v}}$ can be mapped with a multiset of $k$-multisets: $\hat{\boldsymbol{v}}\leftrightarrow\{\mskip-5.0mu\{\tilde{\boldsymbol{v}}=f(\hat{\boldsymbol{v}},\hat{\boldsymbol{n}})\ |\ \sum_{i=1}^{m}\hat{\boldsymbol{n}}_{i}=k,\forall i\ \hat{\boldsymbol{n}}_{i}\geq 1\}\mskip-5.0mu\}$. Based on this relationship, we extend the connection among $k$-multisets to $k(\leq)$-sets: given $m_{1},m_{2}\in[k]$, a $m_{1}$-set $\hat{\boldsymbol{v}}$ is connected to a $m_{2}$-set $\hat{\boldsymbol{u}}$ if and only if $\exists\hat{\boldsymbol{n}}_{v},\hat{\boldsymbol{n}}_{u}$, $f(\hat{\boldsymbol{v}},\hat{\boldsymbol{n}}_{v})$ is connected with $f(\hat{\boldsymbol{u}},\hat{\boldsymbol{n}}_{u})$ in $k$-MultisetWL. Let $S_{k\text{-swl}}(G)$ denote the defined super-graph on $G$ by $k(\leq)$-SetWL. It can be shown that this is equivalent to either (1) $(|m_{1}-m_{2}|=1)\land(|\hat{\boldsymbol{v}}\cap\hat{\boldsymbol{u}}|=\min(m_{1},m_{2}))$ or (2) $(m_{1}=m_{2})\land(|\hat{\boldsymbol{v}}\cap\hat{\boldsymbol{u}}|=m_{1}-1)$ is true. Notice that $S_{k\text{-swl}}(G)$ contains a sequence of $k$$-$$1$ bipartite graphs with each reflecting the connections among the ($m$$-$$1$)-sets and the $m$-sets. It also contains $k$$-$$1$ subgraphs, i.e. the connections among the $m$-sets for $m=2,...,k$. Later on we will show that these $k$$-$$1$ subgraphs can be ignored without affecting $k(\leq)$-SetWL.

Let $\bm{swl}_{k}^{(t)}(G,\hat{\boldsymbol{v}})$ denote the color of $m$-set $\hat{\boldsymbol{v}}$ at $t$-th iteration of $k(\leq)$-SetWL. Now we formally define $k(\leq)$-SetWL. At $t=0$, we initialize the color of a $m$-set $\hat{\boldsymbol{v}}$ ($m\in[k]$) as:

$\displaystyle\bm{swl}_{k}^{(0)}(G,\hat{\boldsymbol{v}})=\text{HASH}\big{(}\{\mskip-5.0mu\{\bm{mwl}_{k}^{(0)}(G,f(\hat{\boldsymbol{v}},\hat{\boldsymbol{n}}))\ \big{|}\ \hat{\boldsymbol{n}}_{1}+...+\hat{\boldsymbol{n}}_{m}=k,\forall i\ \hat{\boldsymbol{n}}_{i}\geq 1\}\mskip-5.0mu\}\big{)}$

(4)

Clearly $\bm{swl}_{k}^{(0)}(G,\hat{\boldsymbol{v}})=\bm{swl}_{k}^{(0)}(G^{\prime},\hat{\boldsymbol{v}}^{\prime})$ if and only if $G[\hat{\boldsymbol{v}}]$ and $G^{\prime}[\hat{\boldsymbol{v}}^{\prime}]$ are isomorphic. At $t$-th iteration, $k(\leq)$-SetWL updates the color of every $m$-set $\hat{\boldsymbol{v}}$ by

	$\displaystyle\bm{swl}_{k}^{(t+1)}(G,\hat{\boldsymbol{v}})=\text{HASH}\bigg{(}\bm{swl}_{k}^{(t)}(G,\hat{\boldsymbol{v}}),\{\mskip-5.0mu\{\bm{swl}_{k}^{(t)}(G,\hat{\boldsymbol{v}}\cup\{x\})\ |\ x\in V(G)\setminus\hat{\boldsymbol{v}}\}\mskip-5.0mu\},\{\mskip-5.0mu\{\bm{swl}_{k}^{(t)}(G,\hat{\boldsymbol{v}}\setminus{x})\ |\ x\in\hat{\boldsymbol{v}}\}\mskip-5.0mu\},$
	$\displaystyle\bigg{\{}\mskip-10.0mu\bigg{\{}\{\mskip-5.0mu\{\bm{swl}_{k}^{(t)}(G,\hat{\boldsymbol{v}}[x/o^{-1}_{G}(\hat{\boldsymbol{v}},1)])\ |\ x\in V(G)\setminus\hat{\boldsymbol{v}}\}\mskip-5.0mu\},...,\{\mskip-5.0mu\{\bm{swl}_{k}^{(t)}(G,\hat{\boldsymbol{v}}[x/o^{-1}_{G}(\hat{\boldsymbol{v}},m)])\ |\ x\in V(G)\setminus\hat{\boldsymbol{v}}\}\mskip-5.0mu\}\bigg{\}}\mskip-10.0mu\bigg{\}}\bigg{)}$		(5)

Notice that when $m=1$ and $m=k$, the third and second part of the hashing input is an empty multiset, respectively. Similar to Eq. (2), we formulate the graph level encoding as $\bm{gswl}_{k}^{(t)}(G)=\text{HASH}(\{\mskip-5.0mu\{\bm{swl}_{k}^{(t)}\big{(}G,\hat{\boldsymbol{v}}\big{)}\ \big{|}\ \forall\hat{\boldsymbol{v}}\in V(S_{k\text{-swl}}(G))\}\mskip-5.0mu\}\big{)}$.

To characterize the relationship of their expressivity, we first extend $k$-MultisetWL on sets by defining the color of a $m$-set $\hat{\boldsymbol{v}}$ on $k$-MultisetWL as $\bm{mwl}_{k}^{(t)}(G,\hat{\boldsymbol{v}}):=\{\mskip-5.0mu\{\bm{mwl}_{k}^{(t)}(G,f(\hat{\boldsymbol{v}},\hat{\boldsymbol{n}}))\ \big{|}\ \sum_{i=1}^{m}\hat{\boldsymbol{v}}_{i}=k,\forall i\ \hat{\boldsymbol{n}}_{i}\geq 1\}\mskip-5.0mu\}$. We prove that $k$-MultisetWL is at least as expressive as $k(\leq)$-SetWL in terms of separating node sets and graphs.

We also conjecture that $k$-MultisetWL and $k(\leq)$-SetWL could be equally expressive, and leave it to future work. As a single $m$-set corresponds to $\binom{k-1}{m-1}$ $k$-multisets, moving from $k$-MultisetWL to $k(\leq)$-SetWL further reduces the computational cost greatly.

Notice that for two arbitrary graphs $G$ and $G^{\prime}$ with equal number of nodes, the number of $k(\leq)$-sets and the connections among all $k(\leq)$-sets in $k(\leq)$-SetWL are exactly the same, regardless of whether they are dense or sparse. We next propose to account for the sparsity of a graph $G$ to further reduce the complexity of $k(\leq)$-SetWL. As the graph structure is encoded inside every $m$-set, when the graph becomes sparser, there would be more sparse $m$-sets with a potentially large number of disconnected components. Based on the hypothesis that the induced subgraph over a set (of nodes) with fewer disconnected components naturally contains more structural information, we propose to restrict the $k(\leq)$-sets to be $(k,c)(\leq)$-sets: all sets with at most $k$ nodes and at most $c$ connected components in its induced subgraph. Let $S_{k,c\text{-swl}}(G)$ denote the super-graph defined by $(k,c)(\leq)$-SetWL, then $S_{k,c\text{-swl}}(G)=S_{k\text{-swl}}(G)[\{\hat{\boldsymbol{v}}|\text{\#components}(G[\hat{\boldsymbol{v}}])\leq c\}]$, which is the induced subgraph on the super-graph defined by $k(\leq)$-SetWL. Fortunately, $S_{k,c\text{-swl}}(G)$ can be efficiently and recursively constructed based on $S_{(k-1,c)\text{-swl}}(G)$, and we include the construction algorithm in the Appendix A.5. $(k,c)(\leq)$-SetWL can be defined similarly to $k(\leq)$-SetWL (Eq. (4) and Eq. (5)), however while removing all colors of sets that do not exist on $S_{k,c\text{-swl}}(G)$.

$(k,c)(\leq)$-SetWL is progressively expressive with increasing $k$ and $c$, and when $c=k$, $(k,c)(\leq)$-SetWL becomes the same as $k(\leq)$-SetWL, as all $k(\leq)$-sets are then considered. Let $\bm{swl}_{k,c}^{(t)}(G,\hat{\boldsymbol{v}})$ denote the color of a $(k,c)(\leq)$-set $\hat{\boldsymbol{v}}$ on $t$-th iteration of $(k,c)(\leq)$-SetWL, then $\bm{gswl}_{k,c}^{(t)}(G)=\text{HASH}(\{\mskip-5.0mu\{\bm{swl}_{k,c}^{(t)}\big{(}G,\hat{\boldsymbol{v}}\big{)}\big{|}\forall\hat{\boldsymbol{v}}\in S_{k,c\text{-swl}}(G)\big{)}\}\mskip-5.0mu\}$.

All color refinement algorithms described above run on a super-graph; thus, their complexity at each iteration is linear to the number of supernodes and number of edges of the super-graph. Instead of using big$\mathcal{O}$ notation that ignores constant factors, we compare the exact number of supernodes and edges. Let $G$ be the input graph with $n$ nodes and average degree $d$. For $k$-WL, there are $n^{k}$ supernodes and each has $n*k$ number of neighbors, hence $S_{k\text{-wl}}(G)$ has $n^{k}$ supernodes and $kn^{k+1}/2$ edges. For $m\in[k]$, there are $\binom{n}{m}$ $m$-sets and each connects to $m$ number of $(m-1)$-sets. So $S_{k\text{-swl}}$ has $\sum_{i=1}^{k}\binom{n}{i}\leq\binom{n}{k}\frac{n-k+1}{n-2k+1}$ supernodes and $\sum_{i=2}^{k}i\binom{n}{i}=n\sum_{i=1}^{k-1}\binom{n-1}{i}\leq n\binom{n-1}{k-1}\frac{n-k+1}{n-2k+2}$ edges (derivation in Appendix). Here we ignore edges within $m$-sets for any $m\in[k]$ as they can be reconstructed from the bipartite connections among $(m-1)$-sets and $m$-sets, described in detail in Sec. 4.1. Consider e.g., $n=30,k=5$; we get $\frac{|V(S_{k\text{-wl}}(G))|}{|V(S_{k\text{-swl}}(G))|}=139$, $\frac{|E(S_{k\text{-wl}}(G))|}{|E(S_{k\text{-swl}}(G))|}=2182$. Directly analyzing the savings by restricting number of components is not possible without assuming a graph family. In Sec. 5.3 we measured the scalability for $(k,c)(\leq)$-SetGNN with different number of components directly on sparse graphs, where $(k,c)(\leq)$-SetWL shares similar scalability.

$k$-FWL is a stronger GI algorithm and it has the same expressivity as $k$+$1$-WL [26], in this section we also demonstrate how to extend the set to $k$-FWL to get $k(\leq)$-SetFWL. Let $\bm{fwl}_{k}^{(t)}(G,\overrightarrow{\boldsymbol{v}})$ denote the color of $k$-tuple $\overrightarrow{\boldsymbol{v}}$ at $t$-th iteration of $k$-FWL. Then $k$-FWL is initialized the same as the $k$-WL, i.e. $\bm{fwl}_{k}^{(0)}(G,\overrightarrow{\boldsymbol{v}})$ = $\bm{wl}_{k}^{(0)}(G,\overrightarrow{\boldsymbol{v}})$. At $t$-th iteration, $k$-FWL updates colors with

$\displaystyle\scriptstyle\bm{fwl}_{k}^{(t+1)}(G,\overrightarrow{\boldsymbol{v}})=\text{HASH}\Big{(}\bm{fwl}_{k}^{(t)}(G,\overrightarrow{\boldsymbol{v}}),\Big{\{}\mskip-10.0mu\Big{\{}\big{(}\bm{fwl}_{k}^{(t)}(G,\overrightarrow{\boldsymbol{v}}[x/1]),...,\bm{fwl}_{k}^{(t)}(G,\overrightarrow{\boldsymbol{v}}[x/k])\big{)}\Big{|}x\in V(G)\Big{\}}\mskip-10.0mu\Big{\}}\Big{)}$

(6)

Let $\bm{sfwl}_{k}^{(t)}(G,\hat{\boldsymbol{v}})$ denote the color of $m$-set $\hat{\boldsymbol{v}}$ at $t$-th iteration of $k(\leq)$-SetFWL. Then at $t$-th iteration it updates with

$\displaystyle\scriptstyle\bm{sfwl}_{k}^{(t+1)}(G,\hat{\boldsymbol{v}})=\text{HASH}\Big{(}\bm{sfwl}_{k}^{(t)}(G,\hat{\boldsymbol{v}}),\Big{\{}\mskip-10.0mu\Big{\{}\big{\{}\mskip-10.0mu\big{\{}\bm{sfwl}_{k}^{(t)}(G,\hat{\boldsymbol{v}}[x/1]),...,\bm{sfwl}_{k}^{(t)}(G,\hat{\boldsymbol{v}}[x/m])\big{\}}\mskip-10.0mu\big{\}}\Big{|}x\in V(G)\Big{\}}\mskip-10.0mu\Big{\}}\Big{)}$

(7)

The $k(\leq)$-SetFWL should have better expressivity than $k(\leq)$-SetWL. We show in the next section that $k(\leq)$-SetWL can be further improved with less computation through an intermediate step while this is nontrivial for $k(\leq)$-SetFWL. We leave it to future work of studying $k(\leq)$-SetFWL.

$(k,c)(\leq)$-SetWL defines a super-graph $S_{k,c\text{-swl}}$, which aligns with Eq. (5). We first rewrite Eq. (5) to reflect its connection to $S_{k,c\text{-swl}}$. For a supernode $\hat{\boldsymbol{v}}$ in $S_{k,c\text{-swl}}$, let $\mathcal{N}^{G}_{\text{left}}(\hat{\boldsymbol{v}})=\{\hat{\boldsymbol{u}}\ |\ \hat{\boldsymbol{u}}\in S_{k,c\text{-swl}},\hat{\boldsymbol{u}}\leftrightarrow\hat{\boldsymbol{v}}\text{ and }|\hat{\boldsymbol{u}}|=|\hat{\boldsymbol{v}}|-1\}$, and $\mathcal{N}^{G}_{\text{right}}(\hat{\boldsymbol{v}})=\{\hat{\boldsymbol{u}}\ |\ \hat{\boldsymbol{u}}\in S_{k,c\text{-swl}},\hat{\boldsymbol{u}}\leftrightarrow\hat{\boldsymbol{v}}\text{ and }|\hat{\boldsymbol{u}}|=|\hat{\boldsymbol{v}}|+1\}$. Then we can rewrite Eq. (5) for $(k,c)(\leq)$-SetWL as

$\displaystyle\bm{swl}_{k,c}^{(t+1)}(G,\hat{\boldsymbol{v}})=\bigg{(}\bm{swl}_{k,c}^{(t)}(G,\hat{\boldsymbol{v}}),\bm{swl}_{k,c}^{(t+\frac{1}{2})}(G,\hat{\boldsymbol{v}}),\{\mskip-5.0mu\{\bm{swl}_{k,c}^{(t)}(G,\hat{\boldsymbol{u}})\ |\ \hat{\boldsymbol{u}}\in\mathcal{N}^{G}_{\text{left}}(\hat{\boldsymbol{v}})\}\mskip-5.0mu\},\{\mskip-5.0mu\{\bm{swl}_{k,c}^{(t+\frac{1}{2})}(G,\hat{\boldsymbol{u}})\ |\ \hat{\boldsymbol{u}}\in\mathcal{N}^{G}_{\text{left}}(\hat{\boldsymbol{v}})\}\mskip-5.0mu\}\bigg{)}$

(8)

where $\bm{swl}_{k,c}^{(t+\frac{1}{2})}(G,\hat{\boldsymbol{v}}):=\{\mskip-5.0mu\{\bm{swl}_{k,c}^{(t)}(G,\hat{\boldsymbol{u}})\ |\ \hat{\boldsymbol{u}}\in\mathcal{N}^{G}_{\text{right}}(\hat{\boldsymbol{v}})\}\mskip-5.0mu\}$. Notice that we omit HASH and apply it implicitly. Eq. (8) essentially splits the computation of Eq. (5) into two steps and avoids repeated computation via caching the explicit $t$$+$$\frac{1}{2}$ step. It also implies that the connection among $m$-sets for any $m\in[k]$ can be reconstructed from the bipartite graph among $m$-sets and $(m-1)$-sets.

Next we formulate $(k,c)(\leq)$-SetGNN formally. Let $h^{(t)}(\hat{\boldsymbol{v}})\in\mathbb{R}^{d_{t}}$ denote the vector representation of supernode $\hat{\boldsymbol{v}}$ on the $t$-th iteration of $(k,c)(\leq)$-SetGNN. For any input graph $G$, it initializes representations of supernodes by

$\displaystyle h^{(0)}(\hat{\boldsymbol{v}})=\text{BaseGNN}(G[\hat{\boldsymbol{v}}])$

(9)

where the BaseGNN can be any GNN model. Theoretically the BaseGNN should be chosen to encode non-isomorphic induced subgraphs distinctly, mimicking HASH. Based on empirical tests of several GNNs on all (11,117) possible $8$-node non-isomorphic graphs [6], and given GIN [61] is simple and fast with nearly $100\%$ separation rate, we use GIN as our BaseGNN in experiments.

$(k,c)(\leq)$-SetGNN iteratively updates representations of all supernodes by

	$\displaystyle\scriptstyle h^{(t+\frac{1}{2})}(\hat{\boldsymbol{v}})$	$\displaystyle=\sum_{\hat{\boldsymbol{u}}\in\mathcal{N}^{G}_{\text{right}}(\hat{\boldsymbol{v}})}\text{MLP}^{(t+\frac{1}{2})}(h^{(t)}(\hat{\boldsymbol{u}}))$		(10)
	$\displaystyle h^{(t+1)}(\hat{\boldsymbol{v}})$	$\displaystyle=\text{MLP}^{(t)}\Big{(}h^{(t)}(\hat{\boldsymbol{v}}),h^{(t+\frac{1}{2})}(\hat{\boldsymbol{v}}),\sum_{\hat{\boldsymbol{u}}\in\mathcal{N}^{G}_{\text{left}}(\hat{\boldsymbol{v}})}\text{MLP}^{(t)}_{A}(h^{(t)}(\hat{\boldsymbol{u}})),\sum_{\hat{\boldsymbol{u}}\in\mathcal{N}^{G}_{\text{left}}(\hat{\boldsymbol{v}})}\text{MLP}^{(t)}_{B}(h^{(t+\frac{1}{2})}(\hat{\boldsymbol{u}}))\Big{)}$		(11)

Then after $T$ iterations, we compute the graph level encoding as

$\displaystyle h^{(T)}(G)=\text{POOL}(\{\mskip-5.0mu\{h^{(T)}(\hat{\boldsymbol{v}})\ |\ \hat{\boldsymbol{v}}\in V(S_{k,c\text{-swl}})\}\mskip-5.0mu\})$

(12)

where POOL can be chosen as summation. We visualize the steps in Figure 1. Under mild conditions, $(k,c)(\leq)$-SetGNN has the same expressivity as $(k,c)(\leq)$-SetWL.