A Novel Passivity-Based Trajectory Tracking Control For Conservative Mechanical Systems
Abstract
Most passivity based trajectory tracking algorithms for mechanical systems can only stabilise reference trajectories that have constant energy. This paper overcomes this limitation by deriving a single variable Hamiltonian model for the reference trajectory and solving along the constrained trajectory to obtain a reference potential. This potential is then used as the model to shape the energy of the true system such that its free solutions include the desired reference trajectory. The proposed trajectory tracking algorithm interconnects the reference and true systems through a virtual spring damper along with an outer-loop energy pump/damper that stabilises the desired energy level of the interconnected system, ensuring asymptotic tracking of the desired trajectory. The resulting algorithm is a fully energy based trajectory tracking control for non-stationary trajectories of conservative mechanical systems.
Keywords Trajectory Tracking, Passivity Based Control, Port Hamiltonian Systems
1 Introduction
The industry standard trajectory tracking control algorithms for mechanical systems depend on the well known Euler-Lagrange formulation of the dynamics in terms of generalised coordinates (for example [SHV06])
| (1) |
for a bounded generalised inertia matrix , Coriolis matrix , potential , and exogenous generalised input . The goal is to find an input such that the systems trajectory converges asymptotically to a known reference trajectory . The standard approach (computed torque with passive damping injection) exploits the Euclidean structure of the generalised coordinates explicitly in creating an error . A trajectory and state dependent feed-forward torque is computed to bring the error dynamics into a time-varying linear structure
| (2) |
where is the residue torque. From here the algebraic passivity properties of and are exploited to show a control (from to ) stabilizes the error coordinates and hence .
Although this approach has been an effective tool in nonlinear control design for many years, it is subject to funamental limitations:
-
1.
The error is a Euclidean difference that has no physical interpretation in terms of the structure of the mechanical system and is only defined locally (in a coordinate patch) for a general system with a manifold state-space.
-
2.
The feed-forward computed torque has no clear physical interpretation. Computing this requires real-time measurements of as well as and a good model of the system.
As a consequence, systems for which the state space is inherently non-Euclidean, such as mobile robots moving in , or systems where the model is uncertain, such as manipulators moving objects that are not well characterised, are difficult to address using the classical tracking framework. Furthermore, due to the complex nonlinear dependence of the feed-forward control on the system state many of the tricks used for velocity free passivity based control, or passivity based robust disturbance rejection [SSF07] cannot be exploited.
In this paper, I propose a ‘true’ passivity based tracking control for conservative mechanical systems. The key innovation is to use the reference trajectory as a parametrization for a single coordinate Hamiltonian system with kinetic and potential energy inherited from the full system. The desired reference trajectory behaviour corresponds to constant velocity motion of the single parameter reference system and the exogenous input that generates this trajectory is uniquely defined. Due to the fact that the system has a single coordinate the input associated to the reference trajectory can be integrated to generate a reference potential. Interpreting the reference input as shaping the potential of the reference system, the constant velocity solution becomes a ‘free’ solution of the single coordinate Hamiltonian reference system.
The second contribution of the paper is to show how to use the reference potential to shape the true system potential energy in such a way that the reference trajectory is a free solution of the (shaped) full Hamiltonian system. The proposed control then interconnects the shaped reference and shaped true system using non-linear spring dampers in order that the response of both systems is synchronised. This step is the primary control that forces the true system to converge towards the desired reference behaviour. The final stage of the control introduces an energy pump that stabilises the energy level in both true and reference system to the desired reference energy level ensuring that the response of the interconnected systems converges asymptotically to the desired reference trajectory.
The resulting control is inherently energy based and does not involve linearisation of the dynamics. The response should be highly robust to model errors and external disturbances and particularly well suited to trajectory tracking in the presence of unknown but energy bounded disturbances. The philosophy of the design draws strongly from the inspiration of Full et al. [FK99] and Westervelt et al. [WGK03] in stabilising an embedded behaviour in a larger mechanical system to obtain emergent behaviour in the zero dynamics. A limitation of the approach is that the desired trajectory is only tracked up to an arbitrary time-offset ; that is, .
2 Literature Review
Trajectory tracking control for dynamical mechanical systems is a classical problem robotics [SL91, SHV06]. The industry standard method for trajectory tracking is that of computed torque control, first developed in the seventies [Mar73, Pau82]. The summary of this approach covered in the introduction of the paper was based on classical robotics texts [Cra89, SL91, SHV06]. Set point regulation has received considerably more attention. In 1981 Takegaki et al. [TA81] demonstrated that a PD control with gravity compensation can regulate a robotic manipulator to any fixed point in its workspace, and this work was generalised to adaptive passivity based set point regulation during the eighties [MG86, LS89] with the global stability analysis for PD, PID, and PI2D controls provided in the nineties [Kel95, OLNS98, Lef00]. Although approximate trajectory tracking can be accomplished with joint based PD [Kod87, KMA88] most theoretical developments of these techniques have been aimed at regulation of set-point or constant energy trajectories [Lef00].
A seminal contribution to tracking trajectory control is the work by Fujimoto et al. [FSS03] in 2003. In this work the authors state; “The key idea to realize [the objective of tracking control] is to embed the desired trajectory into the Hamiltonian function of the original system.” They provide a characterisation of a generalised canonical transform that transforms a port Hamiltonian system into one written in terms of the error coordinates
| (3) |
(compare to (2)) which can be stabilised using passive damping injection. The approach is conceptually rigorous but formally requires the solution of a Partial Differential Equation (PDE) to find the canonical transformation that defines the global error coordinates. This requirement is reminiscent of the IDA-PCA algorithms [OLNS98] developed around the same time and the complexity of the design process has limited their adoption in the wider community.
A separate research thread I draw from in this paper is summarised in the philosophy stated in Westervelt et al. [WGK03] “to encode the dynamic task via a lower dimensional target, itself represented by a set of differential equations” [NFK00] motivated by the study of how biological systems move [FK99]. This work has been important in development of advanced trajectory tracking algorithms for gait control for humanoid robots [WGK03] in particular, and in general for control of robotic motion. I also draw from the pioneering work by Spong [Spo95] on energy pumping for stabilisation of constant energy set-points for under-actuated mechanical systems.
3 Problem formulation
Let denote (local) generalized coordinates for a fully actuated mechanical system with generalized inertia matrix and potential function . Lagrange’s equations yield dynamics (3) for a Coriolis matrix . The passivity of the system is expressed algebraically by the relationship that
is skew symmetric along trajectories of the system. The Hamiltonian for this system is
| (4) |
and passivity of the system ensures that
| (5) |
where is notation for the power bracket between a generalised input and a velocity, and can be read as a simple inner product in local coordinates.
The trajectory tracking problem is associated with a pre-specified reference trajectory . In this paper, I will consider only non-stationary reference trajectories that are bounded, twice differentiable with bounded differentials. The non-stationary assumption,
| (6) |
is the only unusual assumption. Indeed, stationary trajectories are exactly those trajectories that can be easily tackled using classical passivity based techniques [OLNS98]. This assumption emphasises the fundamental differences between the present and previous energy based approaches to tracking. Although I believe that it may be possible to relax this condition in future work, the assumption considerably simplifies the present work. In fact, I will assume slightly more than (6), that the velocity is bounded away from zero. That is, that there exists a uniform bound such that for all time.
The nominal goal of the trajectory tracking problem is to find a control signal for (3) depending on the known reference trajectory and its derivatives along with state measurements such that for any initial condition the solution of the closed-loop system (3) converges to the reference, asymptotically. The proposed algorithm achieves asymptotically for some time-offset . Although this is not explicitly a solution to the classical trajectory tracking problem it is clearly applicable to a wide range of applied problems and the difference again emphasises the difference in approach.
4 Reference trajectory
In this section, I consider the dynamics of the reference trajectory. The approach taken is to reparametrize the reference trajectory as a one parameter mechanical system constrained to follow a reference path. The key advantage of this reformulation is to derive a potential function that encodes the information necessary to generate the exogeneous generalised force input associated with the reference trajectory. The goal of the section is to formulate a closed Hamiltonian system for which the reference trajectory is a free solution.
The starting position is to consider the reference as a solution of the mechanical system (3). In particular, there must be a reference input associated with the actual generalised forces required to track the reference trajectory. More correctly, we consider a reference trajectory to be a quadruple of variable trajectories defined on a time interval that satisfy the system relationship
| (7) |
for . Note that the reference trajectory information, including the reference input can be computed in advance.
Let be a path parameter for the reference trajectory. That is we consider the map , . Consider the mechanical system obtained by taking to be a generalised coordinate for a new one-dimensional mechanical system that characterises the motion of the reference along its predefined trajectory. That is, as varies in one dimension, the reference variable moves along the constrained path . Define the partial differentials of with respect to by
For a solution one has and
The kinetic energy of the constrained reference system is
| (8) |
which defines while the potential is a simple reparameterization .
The Lagrangian for this system is given by . Consider the Euler-Lagrange equations where is a scalar exogenous input added as a driving term. It is easily verified that
| (9) |
The dynamics (9), for a general input , models the motion of a mechanical single variable system along the parametrization provided by . The reference trajectory itself is recovered by the particular solution and will correspond to a particular choice of scalar reference input . Since the defining equations are time-invariant, then any solution , , will also be a solution (9) associated with the offset reference trajectory for . It follows that the scalar reference input can be computed as function of path parameter independent of time. Substituting the relationships , , characteristic of the trajectory , into (9) yields
| (10) |
Define a reference potential
The potential encodes information on the scalar reference input associated with the reference trajectory for the scalar system (9). The input (10) should be thought of as a potential shaping input where the term cancels the effect of the potential inherited from the full system, while the term is associated with a new shaped potential that compensates the energy balance for variation in the kinetic energy along the reference trajectory. That is, the reference potential shapes the potential of the reference system to supply the power required to track the reference trajectory.
Lemma 4.1.
For any let be the reference trajectory offset by time and fix . Then
| (11) |
Proof.
Recalling (5) then by construction
Note that
where the last line follows since for the solution considered. Differentiating this relationship one has
∎
Set where is a coupling input from the reference system to the true system and will be defined in §5. The Euler-Lagrange equations for (9) become
| (12) |
The dynamics (12) are associated with the port Hamiltonian system with Hamiltonian
| (13) |
One has
where is the power port for the scalar reference system.
It is easily verified that the unforced or zero dynamics of (12) (with ) include the solution , as expected. This solution is associated with a constant (shaped) energy level
| (14) |
since along the reference trajectory. This energy level is, however, not a minimum energy level for the system, with trajectories in phase portrait (Fig. 1) that lie inside the lines all corresponding to lower energy levels. The minimum energy trajectories for the reference system will correspond to the stationary points . These stationary points occur at points where and their stability will depend on the sign of (see Fig. 1). The variation in is a function of the reference trajectory, both in the change in magnitude of as well as the distribution of inertia in . Thus, reference trajectories with high accelerations and complex inertia matrices will lead to complex zero dynamics in the reference system, while tracking simply trajectories with near constant velocities and homogeneous inertia will lead to simple zero dynamics. Interestingly, the unforced system also includes solutions associated with negative time evolution of the reference system, and a zero energy solution in particular.
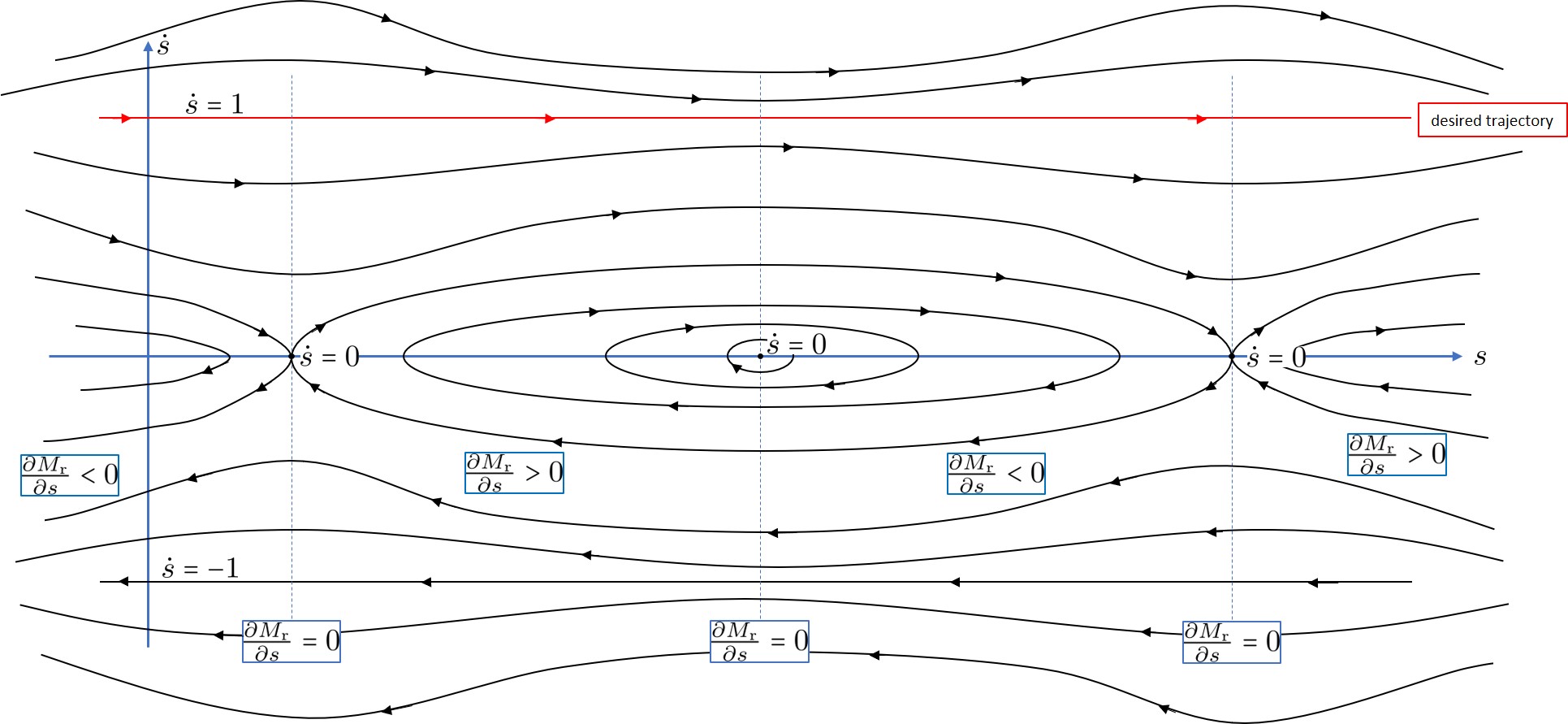
5 Shaping, Interconnection and Synchronisation
In this section I present the first part of the proposed tracking control design. The idea is to shape the potential of the true system with the reference potential and then couple the true and reference systems together using passive interconnections. The resulting control synchronises the state of the true system (3) with the state of the reference system (12). The final closed-loop system will require an additional energy pumping control discussed in §6 to stabilise the desired energy level set.
The principle control used for synchronization between the true and reference systems is a spring potential introduced between and . Let be a positive definite smooth cost function with if and only if . Note that there is no need to compute the linear error in order to find such a spring potential function although the potential used in the classical tracking algorithms is an example of such a potential.
The generalised inertia provides a Riemannian metric on the tangent bundle . Using this metric one can measure the speed of a trajectory by computing . In a similar manner one can measure the desired speed of the reference trajectory at a point by computing . Note that the reference speed is associated with the desired reference trajectory and does not depend on the velocity of the path parameter . Since only non-stationary reference trajectories were considered, the reference speed . The ratio of these two speeds as a function of time
| (15) |
can be interpreted as a measure of the speed at which the true system is moving relative to a desired reference speed associated with a point on the reference trajectory specified by the path parameter . If and then , that is the true trajectory is moving at the same speed as the desired trajectory.
The integral of (15),
| (16) |
can be interpreted as a (relative) path parameter for the true system, analogous to the path parameter introduced for the reference trajectory . If and then . The new path parameter will be used as a storage variable in a copy of the reference potential that can be used to shape the potential for the true system.
Define , the dual (generalised) torque to a velocity , to be the unique element that solves
| (17) |
for all . Note that in the case where the velocity is zero. Recalling the reference input associated with the reference trajectory (7), define the constraint force
| (18) |
By construction and thus does no work on the system. In the asymptotic case, where then and . It follows that in this case is the component of the reference input orthogonal to the dual torque . That is, the component of the reference input that acts orthogonal to the velocity of the system as a constraint force and steers the system to follow the desired trajectory. The power required to accelerate and decelerate the system along the trajectory is not provided by the constraint force and must be separately modelled. The active force in direction will be coupled to the potential (22).
A key requirement of the proposed control, separate from the synchronisation of and , is to synchronise the two path parameters and . To this end define a second potential
Note that since both and are scalars, then this potential can be defined globally as a simple quadratic error. The introduction of this potential will bound growth of with respect to growth of , and vice-versa, ensuring that the two path parameters remain close during the system transient.
Theorem 5.1.
Remark 5.2.
Note that both and are asymptotically of order for . Since is full rank positive definite it follows that (20) is well defined even for vanishing . For , I choose even though the limit may not be zero. The resulting definition may be discontinuous at . Since the reference trajectory is chosen this discontinuity will not be present in the asymptotic solution of the system. The transient response analysis of the system depends only on existence of the solutions but some care must be taken in the application of Barbalat’s lemma.
Proof.
Consider the combined energy of the system
| (23) |
where (4) is the Hamiltonian for the true system, (13) is the Hamiltonian for the reference system, the two terms and are shaping potentials for the true and reference system, and and are the potentials associated with the spring forces introduced to synchronise the states.
Recall that the time derivative along trajectories of the Hamiltonians are
Substituting from (20) one has
Similarly, computing and substituting from (21) one has
Finally, differentiating and substituting for the relevant expressions one obtains
It follows from LaSalles principle that . Furthermore, since the feedback interconnections are smooth and bounded except at points , and these are isolated points in the trajectory, it follows that the derivatives of are uniformly bounded except on a countable collection of times. It follows that is piecewise uniformly continuous and applying a generalisation of Barbalat’s lemma [WXX11] it follows that except on a set of measure zero. Since is continuous, then converges to a constant. ∎
The proposed synchronisation control is a closed passive interconnection of Hamiltonian systems and resulting combined system is itself a passive Hamiltonian system. Theorem 5.1 demonstrates that the combined solution will converge asymptotically to a trajectory that lies in the set of forward invariant trajectories characterised by and . As shown in the next section, the free trajectories and certainly lie in this forward invariant set. However, without additional control, the damping term will continue to extract energy from the system, even if it is in small increments due to small disturbances, until the limiting trajectory has zero kinetic energy and lies at a local minimum of the combined potential . (Note that for then by construction.) Such solutions also lie in (a separate component of) the forward invariant set of the combined system trajectories. In particular, synchronisation of the trajectories by itself is not sufficient to ensure the desired trajectory tracking and in the next section I propose an additional external energy pumping control to stabilise the energy level the combined system.
6 Energy Regulation
This section presents two results; firstly an explicit demonstration that the reference trajectory is a forward invariant trajectory for the combined Hamiltonian system considered in Theorem 5.1. Secondly, I characterise the energy level of the reference trajectory for the combined system and propose a simple energy pump outer loop control that stabilises this energy level in the system and consequently stabilises the desired trajectory.
Lemma 6.1.
Let be a real constant and consider . Consider the trajectory
| (24) | ||||
| (25) |
with additionally
| (26) |
Then for all and is a forward invariant solution of the combined system in Theorem 5.1 with and .
Proof.
Recalling (15) and using (24) and (25) one has that for all
since . From (26) it follows that for all and both and hold along the trajectory. From (24) it follows that and hence
Recalling (21) it follows that and it was shown that is a solution of the dynamics (12) in §5. Using this in (20) one has
Recalling (18) and solving for one has
where since and . The constant is given by
where the final relationship follows from Lemma 4.1. Evaluating and substituting for and one obtains
where the final line follows since along trajectories . It follows from (7) that is solution of (3). This completes the proof. ∎
Remark 6.2.
A key property of the proposed design is that the trajectory tracking can only be achieved up to an unknown constant time offset (24). This comes from the fundamental approach where the desired trajectory is embedded as zero dynamics in a larger system and then stabilised. The philosophy of this approach draws strongly from the inspiration of Full et al. [FK99] and Westervelt et al. [WGK03] in stabilising zero dynamics of a larger system to obtain the desired behaviour as an emergent behaviour rather than forcing the desired response directly. The consequence is that it is not the trajectory that is stabilised, rather it is a set of dynamics that generate the trajectory that is stabilised, and since these dynamics are time-invariant the best that can be achieved is stabilisation up to a time-offset.
Although the trajectory is a free trajectory of the interconnected system, it is not the only such solution. Understanding the full phase portrait of the interconnected system is far more complicated than those for the reference trajectory shown in Fig. 1 and beyond the scope of this paper (or the author). However, the desired reference trajectory is closely associated with the shape of the phase portrait for the solution in the reference system, and a similar phase portrait for that is ‘embedded’ in the dynamics of the true system. Consider the energy level (23) of the interconnected system along the free trajectory . Both and potentials are zero, and (14) is also zero. Finally, is also zero along this trajectory by the same argument used to derive (14). Thus, the desired trajectory is characterised by the zero energy level set of interconnected system. Furthermore, it is straightforward to see that the energy of the true and reference systems separately are also zero. From the phase portrait of the reference system (Fig. 1) the only two zero energy solutions are characterised . Recalling (15) it is clear that and since converges to a constant, the solution cannot lie in the limit set of the closed-loop system. Thus, trajectories (Lemma 6.1), for some offset , are the only forward invariant trajectories of the interconnected system that lie in the limit set of the closed-loop system with energy .
This suggests a very simple outer level control whose goal is to stabilize the energy level of the interconnected system, while also stabilizing the internal energy of the true and reference systems to zero. This approach is highly reminiscent of the energy pumping controls proposed in the late nineties [Spo95]. Since we have control in both the true system and the reference system then it is possible to inject energy in both systems at the same time and minimize the need for energy exchange during asymptotic tracking of the trajectory, as well as ensuring that the separate systems independently stabilise to zero energy level sets.
Choose a constant gain , then the proposed “energy pump” inputs are
| (27) | |||
| (28) |
where is applied to the true system and to the reference system. The action of will inject energy
into the true system, acting to decrease the energy level when is positive and increase energy levels when it is negative. Similarly, will stabilise the energy levels in the reference system to zero. Both controls will become inactive along the desired trajectory and will only contribute infinitesimally to stabilise the energy level of the interconnected system.
7 Graphical Representation
The full control can be graphically described in the bond graph shown in Figure 2. In this bond graph, the only external energy to the system is supplied (and removed) through the energy pump shown in the centre top of the figure and the stabilising dissipation term in the bottom right. The remainder of the graph describes the interconnection of the true and reference systems. The upper interconnection branch is the direct coupling of to through a spring potential . The lower left modulated transformer (MTF) and the potential is the coupling of the reference potential to the true system. The spring-damper coupling of and is shown in the bottom right of the diagram.
8 Conclusion
The proposed control architecture is fully non-linear and based on energy principles. Due to its foundation, the approach is expected to provide highly robust control with strong passivity properties with respect to external disturbances. There is considerable potential to consider implementations on non-standard state spaces such as for mobile robotic vehicles as well as extensions based on the principles of passive systems [SSF07]. Although the approach is derived for conservative mechanical systems it should be able to be applied to more liberal systems (with dissipative elements) as long as suitable conditions on the existence of are provided.
Acknowledgments
This research was supported by the Australian Research Council through the “Australian Centre of Excellence for Robotic Vision” CE140100016.
References
- [Cra89] J.J. Craig. Introduction to Robotics mechanics and control. Addison-Wesley publishing company inc., second edition, 1989.
- [FK99] R. Full and D. Koditschek. Templates and anchors: Neuromechanical hypotheses of legged locomotion on land. Journal of Experimental Biology, 202:3325–3332, 1999.
- [FSS03] Kenji Fujimoto, Kazunori Sakurama, and Toshiharu Sugie. Trajectory tracking control of port-controlled Hamiltonian systems via generalized canonical transformations. Automatica, 39:2059–2069, 2003.
- [Kel95] Rafael Kelly. A tuning procedure for stable pid control of robot manipulators. Robotica, 13(2):141–148, 1995.
- [KMA88] S. Kawamura, F. Miyazaki, and S. Arimoto. Is a local linear PD feedback control law effective for trajectory tracking of robot motion? In Proceedings of the International Conference on Robotics and Automation (ICRA), pages 1335–1340, 1988.
- [Kod87] D.E. Koditschek. Quadratic lyapunov functions for mechanical systems. Technical Report 8703, Centre for Systems Science, Yale University, Department of Electrical Engineering, 1987.
- [Lef00] Adriaan Arie Johannes Lefeber. Tracking Control of Nonlinear Mechanical Systems. phdthesis, 2000. Universiteit Twente.
- [LS89] Weiping Li and Jean-Jacques Slotine. An indirect adaptive robot controller. Systems & Control Letters, 12:259–266, 1989.
- [Mar73] B. Markewitz. Analysis of a computed torque drive methods and comparison with conventional position servo for a computed controlled manipulator. Technical Report 33-601, Jet Propulsion Lab, California Institute of Technology, 1973.
- [MG86] R.H. Middleton and G.C. Goodwin. Adaptive computed torque control for rigid link manipulators. In Proceedings of the 25th Conference on Decision and Control, pages 68–73, 1986.
- [NFK00] J. Nakanishi, T. Fukuda, and D. Koditschek. A brachiating robot controller. IEEE Transactions Robotic Automation, 16:109–203, 2000.
- [OLNS98] R. Ortega, A. Loria, P. J. Nicklasson, and H. Sira-Rmirez. Passivity-based control of Euler–Lagrange systems. London, Springer, 1998.
- [Pau82] R. P. Paul. Robot Manipulators: Mathematics, Programming, and Control. MIT Press Cambridge, MA, USA, 1982.
- [SHV06] M. W. Spong, S. Hutchinson, and M. Vidyasagar. Robot Modeling and control. Wiley, 2006.
- [SL91] J. Slotine and W. Li. Applied nonlinear control. Prentice Hall, 1991.
- [Spo95] M.W. Spong. The swing up control problem for the acrobot. IEEE Control Systems Magazine, 15(1):49–55, 1995.
- [SSF07] Cristian Secchi, Stefano Stramigioli, and Cesare Fantuzzi. Control of interactive robotic interfaces: A port-Hamiltonian approach, volume 29 of Springer Tracts in Advanced Robotics. Springer, Berlin, 2007.
- [TA81] Morikazu Takegaki and Suguru Arimoto. A new feedback method for dynamic control of manipulators. Journal of Dynamic Systems, Measurement, and Control, 103(2):119–125, 1981.
- [WGK03] E. R. Westervelt, J. W. Grizzle, and D. E. Koditschek. Hybrid zero dynamics of planar biped walkers. IEEE Transactions on Automatic Control, 48(1):42–56, 2003.
- [WXX11] Zhaojing Wu, Yuanqing Xia, and Xuejun Xie. Stochastic barbalat’s lemma and its applications. IEEE Transactions on Automatic Control, 57(6):1537–1543, 2011.