A note on the non-planar corrections for the Page curve in the PSSY model via the IOP matrix model correspondence

The PSSY model Penington:2019kki consists of a black hole in JT gravity with an end-of-the-world (EOW) brane behind the horizon with tension $\mu\geq 0$. Its Euclidean action is

	$\displaystyle S=$	$\displaystyle\;S_{\text{JT}}+\mu\int_{\text{Brane}}ds,$		(1)
	$\displaystyle S_{\text{JT}}=$	$\displaystyle\;-\frac{S_{0}}{4\pi}\left(\int_{\mathcal{M}}\sqrt{g}R+2\int_{\partial M}\sqrt{h}K\right)-\left(\frac{1}{2}\int_{\mathcal{M}}\sqrt{g}\phi(R+2)+\int_{\partial\mathcal{M}}\sqrt{h}\phi K\right).$		(2)

We impose the standard asymptotic boundary condition

$\displaystyle ds^{2}|_{\partial\mathcal{M}}=\frac{d\tau^{2}}{z_{\epsilon}^{2}},\;\;\;\phi|_{\partial\mathcal{M}}=\frac{1}{z_{\epsilon}},$

(3)

where $\tau$ is the boundary Euclidean time, and $z_{\epsilon}$ is the near-boundary cutoff.

Suppose that there are $k$ orthogonal states $|i\rangle_{\mathbb{R}}$ of the “radiation” system $\mathbb{R}$, which are entangled with $k$ interior of the EOW brane microstates $|\psi_{i}\rangle_{\mathbb{B}}$ of the black hole $\mathbb{B}$. A pure state $|\Psi\rangle$ representing this entanglement is given by

$\displaystyle|\Psi\rangle=\frac{1}{\sqrt{k}}\sum\limits_{i=1}^{k}\,\ket{\psi_{i}}_{\mathbb{B}}\ket{i}_{\mathbb{R}},$

(4)

where the radiation system $\mathbb{R}$ can be interpreted as the early radiation of an evaporating black hole. The reduced density matrix $\rho_{\mathbb{R}}$ and its resolvent $R(\lambda)$ are defined by

	$\displaystyle\rho_{\mathbb{R}}$	$\displaystyle:=\Tr_{\mathbb{B}}\ket{\Psi}\bra{\Psi}=\frac{1}{k}\,\sum\limits_{i,j=1}^{k}\,\ket{j}\bra{i}_{\mathbb{R}}\,\braket{\psi_{i}}{\psi_{j}}_{\mathbb{B}},$		(5)
	$\displaystyle R(\lambda)$	$\displaystyle:=\sum\limits_{i=1}^{k}R_{ii}(\lambda)\,,\;\;\;R_{ij}(\lambda):=\left(\frac{1}{\lambda\mathds{1}-\rho_{\mathbb{R}}}\right)_{ij}\,=\,\frac{1}{\lambda}\,\delta_{ij}+\sum\limits_{n=1}^{\infty}\,\frac{1}{\lambda^{n+1}}\,(\rho_{\mathbb{R}}^{n})_{ij}\,.$		(6)

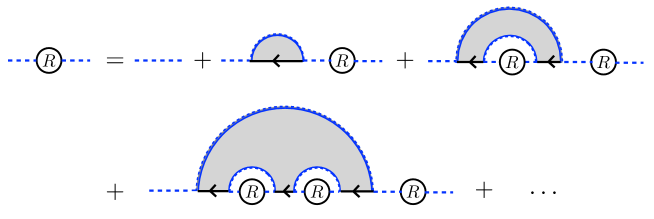
When $e^{\mathbb{S}}$, which is the dimensions of $\bf{B}$, and $k$, which is the dimension of $\bf{R}$, are large, only planar diagrams are dominant in the Schwinger-Dyson equation of $R_{ij}(\lambda)$, as Fig. 1, thus we obtain

$\displaystyle R_{ij}(\lambda)=\,\frac{1}{\lambda}\,\delta_{ij}+\frac{1}{\lambda}\sum\limits_{n=1}^{\infty}\,\frac{Z_{n}^{\text{Disk}}}{(kZ_{1}^{\text{Disk}})^{n}}\,R(\lambda)^{n-1}R_{ij}(\lambda),$

(7)

where $\delta_{ij}/\lambda$ is like “bare propagator” and $Z_{n}^{\text{Disk}}$ is the bulk partition function on a disk topology with $n$ asymptotic boundaries represented by the black solid arrows and $n$ blue curved lines for the EOW branes. In a microcanonical ensemble with fixed energy $E$, the ratio of the bulk partition functions is simplified as

$\displaystyle\frac{Z_{n}^{\text{Disk}}}{(Z_{1}^{\text{Disk}})^{n}}=e^{-(n-1)\mathbb{S}},\;\;\;e^{\mathbb{S}}:=e^{S_{0}}\rho_{\text{Disk}}(E)\Delta E,\;\;\;\rho_{\text{Disk}}(E):=\frac{\sinh(2\pi\sqrt{2E})}{2\pi^{2}},$

(8)

where $E$ dependence appears through $\mathbb{S}$, and $\Delta E$ is the width of the microcanonical energy window. Performing the infinite sum in eq. (7), we obtain

$\displaystyle R(\lambda)^{2}+\left(\,\frac{e^{\textbf{S}}-k}{\lambda}-ke^{\textbf{S}}\,\right)\,R(\lambda)+\dfrac{k^{2}e^{\textbf{S}}}{\lambda}\,=0,$

(9)

and a solution of $R(\lambda)$ with the asymptotic behavior $R(\lambda)\to k/\lambda$ at $\lambda\to+\infty$ is

	$\displaystyle R(\lambda)$	$\displaystyle=\frac{ke^{\textbf{S}}}{2\lambda}\left(\left(e^{-\textbf{S}}-k^{-1}\right)+\lambda-\sqrt{(\lambda-\lambda_{+})(\lambda-\lambda_{-})}\right){\qquad\left(\mbox{for}\,\,\,\lambda>\lambda_{+}\right)},$		(10)
		$\displaystyle\qquad\qquad\mbox{where}\quad\lambda_{\pm}:=\left(k^{-\frac{1}{2}}\pm e^{-\textbf{S}/2}\right)^{2}.$		(11)

$R(\lambda)$ for $\lambda<\lambda_{+}$ can be obtained by the analytic continuation. From the definition of $R(\lambda)$ in (6), using

$\displaystyle\frac{1}{\lambda+i\epsilon}=\mbox{P}\left(\frac{1}{\lambda}\right)-i\pi\delta(\lambda),$

(12)

the spectral density $D(\lambda)$ of $\rho_{\mathbb{R}}$ is given by

	$\displaystyle D(\lambda)$	$\displaystyle=-\frac{1}{\pi}\imaginary R(\lambda+i\epsilon)$
		$\displaystyle=\frac{ke^{\textbf{S}}}{2\pi\lambda}\sqrt{(\lambda-\lambda_{-})(\lambda_{+}-\lambda)}\theta(\lambda-\lambda_{-})\theta(\lambda_{+}-\lambda)+\left(k-e^{\mathbf{S}}\right)\delta(\lambda)\theta(k-e^{\mathbf{S}})\,,$		(13)

where $\theta(\lambda)$ is the Heaviside step function¹¹1From (11), we have $\displaystyle R(\lambda)=\frac{ke^{\textbf{S}}}{2\lambda}\left(\left(e^{-\textbf{S}}-k^{-1}\right)+\lambda+\sqrt{(\lambda_{+}-\lambda)(\lambda_{-}-\lambda)}\right){\qquad\mbox{for}\quad\left(\lambda_{+}\geq\lambda_{-}\geq\lambda\geq 0\right)}.$ (14) The relative sign in front of square root changes between $\lambda>\lambda_{+}$ and $0\leq\lambda<\lambda_{-}$ because we change both of the argument $\theta_{+}$ and $\theta_{-}$ by $\pi$ in $\lambda-\lambda_{+}:=r_{+}e^{i\theta_{+}}$ and $\lambda-\lambda_{-}:=r_{-}e^{i\theta_{-}}$. See, for instance, Lu:2014jua . Thus, $\lambda=0$ pole in $R(\lambda)$ gives a Dirac delta function proportional to $\displaystyle\frac{{ke^{\textbf{S}}}}{2}\left(e^{-\textbf{S}}-k^{-1}+\sqrt{\lambda_{+}\lambda_{-}}\right)=\left(k-e^{\textbf{S}}\right)\theta(k-e^{\textbf{S}}).$ (15) .

One can check that the normalization of $D(\lambda)$ is

$\displaystyle\int D(\lambda)d\lambda=k,\quad\int D(\lambda)\lambda\,d\lambda=1.$

(16)

The first normalization means that the size of $\rho_{\mathbb{R}}$ is $k$, and the second normalization means that $\Tr_{\mathbb{R}}\rho_{\mathbb{R}}=1$. $D(\lambda)$ is simplified as

$\displaystyle D(\lambda)=\frac{k^{2}}{2\pi\lambda}\sqrt{\lambda\left(\frac{4}{k}-\lambda\right)}\theta(\lambda)\theta\left(\frac{4}{k}-\lambda\right)\,,\quad\mbox{when}\quad k=e^{\textbf{S}}\,.$

(17)

Using (11) and (13), the entanglement entropy $S_{\mathbb{R}}$ of the auxiliary system $\mathbb{R}$ can be calculated as

	$\displaystyle S_{\mathbb{R}}=$	$\displaystyle\;-\int d\lambda D(\lambda)\lambda\log\lambda$
	$\displaystyle=$	$\displaystyle\;-\frac{ke^{\textbf{S}}}{2\pi}\int_{\lambda_{-}}^{\lambda_{+}}d\lambda\sqrt{(\lambda-\lambda_{-})(\lambda_{+}-\lambda)}\log\lambda.$		(18)

This integral can be computed exactly, and the result is

$\displaystyle S_{\mathbb{R}}=\log m-\frac{m}{2n},\;\;\;m:=\min\{k,e^{\textbf{S}}\},\;\;\;n:=\max\{k,e^{\textbf{S}}\},$

(19)

which perfectly matches the Page’s result for $n\geq m\gg 1$ Page:1993df . If $k=e^{\textbf{S}}$, the entanglement entropy is

$\displaystyle S_{\mathbb{R}}=\log k-\frac{1}{2}\,,\quad\mbox{if}\quad k=e^{\textbf{S}}.$

(20)

The IOP matrix model Iizuka:2008eb is a matrix model given by the following Hamiltonian

$\displaystyle H_{IOP}=mA_{ij}^{\dagger}A_{ji}+Ma_{i}^{\dagger}a_{i}+H_{int},\;\;\;H_{int}=ha_{i}^{\dagger}a_{l}A_{ij}^{\dagger}A_{jl},$

(21)

where the sum of subscripts is taken from $1$ to $N$. Here, $a_{i}$ is the annihilation operator for a harmonic oscillator in the fundamental of $U(N)$, and $A_{ij}$ is the annihilation operator for an oscillator in the adjoint. This matrix model was introduced as a toy model of the gauge dual of an AdS black hole, where the adjoint fields can be interpreted as background $N$ D0-branes for the black hole, and the fundamental fields can be interpreted as strings stretched from a probe D0-brane.

To solve the spectrum density analytically in the large $N$ limit with fixed ’t Hooft coupling $\lambda_{\text{'t Hooft}}:=hN$, we also take the large $M$ limit $M\gg m$ and $M\gg T$ so that $a_{i}^{\dagger}a_{i}\sim 0$ in the thermal ensemble at finite temperature $T$. We consider the following time-ordered Green’s functions at finite temperature

	$\displaystyle e^{iMt}\Big{\langle}\mbox{T}\,a_{i}(t)\,a_{j}^{\dagger}(0)\Big{\rangle}_{T}$	$\displaystyle=:G(t)\delta_{ij},$		(22)
	$\displaystyle\Big{\langle}\mbox{T}A_{ij}(t)A_{kl}^{\dagger}(0)\Big{\rangle}_{T}$	$\displaystyle=:L(t)\delta_{il}\delta_{jk}.$		(23)

With the Fourier transformation $\tilde{f}(\omega)=\int dt\,e^{i\omega t}f(t)$, free thermal propagators in frequency space are given by

	$\displaystyle\tilde{G}_{0}(\omega)$	$\displaystyle=\frac{i}{\omega+i\epsilon},$		(24)
	$\displaystyle\tilde{L}_{0}(\omega)$	$\displaystyle=\frac{i}{1-y}\left(\frac{1}{\omega-m+i\epsilon}-\frac{y}{\omega-m-i\epsilon}\right),\;\;\;y:=e^{-m/T},$		(25)

where $\tilde{G}_{0}(\omega)$ does not depend on $T$ in the large $M$ limit, and $\tilde{L}(\omega)$ in the large $N$ limit becomes the free propagator $\tilde{L}_{0}(\omega)$ since the backreaction from the fundamental is suppressed by $1/N$.

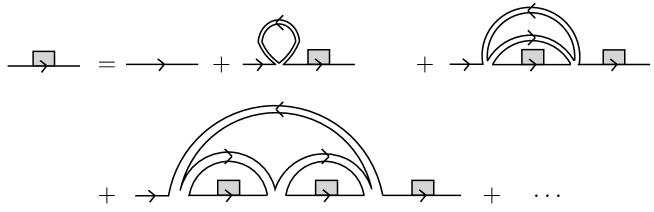
In the limit where $N$ and $M$ are large, the Schwinger-Dyson equation of $\tilde{G}(\omega)$ is shown in Fig. 2, which has the same graphical structure as the Schwinger-Dyson equation of $R(\lambda)$ in the PSSY model. See Figure 2 of Iizuka:2008eb and Figure (2.25) of Penington:2019kki as well. The Schwinger-Dyson equation of $\tilde{G}(\omega)$ is given by

$\displaystyle\tilde{G}(\omega)=\tilde{G}_{0}(\omega)+y\tilde{G}_{0}(\omega)\tilde{G}(\omega)\sum_{n=0}^{\infty}\left(\frac{-i\lambda_{\text{'t Hooft}}}{1-y}\right)^{n+1}\tilde{G}(\omega)^{n}.$

(26)

Performing the infinite sum, we obtain

$\displaystyle\tilde{G}(\omega)^{2}-i(1-y)\left(\frac{1}{\omega}+\frac{1}{\lambda_{\text{'t Hooft}}}\right)\tilde{G}(\omega)-\frac{1-y}{\omega\lambda_{\text{'t Hooft}}}=0,$

(27)

and its solution is

	$\displaystyle\tilde{G}(\omega)$	$\displaystyle=\frac{i}{2\omega}\frac{1-y}{\lambda_{\text{'t Hooft}}}\left(\frac{\lambda_{\text{'t Hooft}}}{1-y}(1-y)+\omega-\sqrt{\left(\omega-\omega_{+}\right)\left(\omega-\omega_{-}\right)}\right)\,\,\,(\mbox{for}\,\,\,\omega>\omega_{+})\,,$		(28)
		$\displaystyle\qquad\qquad\mbox{where}\quad\omega_{\pm}:=\frac{\lambda_{\text{'t Hooft}}}{1-y}\left(1\pm\sqrt{y}\right)^{2}\geq 0\,,$		(29)

where $0\leq y\leq 1$ and we take the branch such that $\tilde{G}(\omega)$ at $\omega\to+\infty$ becomes the free propagator given by (24). $\tilde{G}(\omega)$ for $\omega<\omega_{+}$ can be obtained by the analytic continuation. Again using (12) and (28), the spectral density $F(\omega)$ of the two-point function of fundamental fields is obtained as²²2From (28), we have $\displaystyle\tilde{G}(\omega)$ $\displaystyle=\frac{i}{2\omega}\frac{1-y}{\lambda_{\text{'t Hooft}}}\left(\frac{\lambda_{\text{'t Hooft}}}{1-y}(1-y)+\omega+\sqrt{\left(\omega_{+}-\omega\right)\left(\omega_{-}-\omega\right)}\right),\,\,\,(\mbox{for}\,\,\,\omega_{+}\geq\omega_{-}\geq\omega>0)\,.$ (30) Again, the relative sign in front of the square root changes between $\omega>\omega_{+}$ and $0\leq\omega<\omega_{-}$. Thus, $\omega\to 0$ pole gives a Dirac delta function proportional to $\displaystyle\frac{1}{2}\frac{1-y}{\lambda_{\text{'t Hooft}}}\left(\frac{\lambda_{\text{'t Hooft}}}{1-y}(1-y)+\sqrt{\omega_{+}\omega_{-}}\right)=(1-y)\theta(1-y).$ (31)

	$\displaystyle F(\omega)$	$\displaystyle=\frac{1}{\pi}\real\tilde{G}(\omega+i\epsilon)$		(32)
		$\displaystyle=\frac{1}{2\pi\omega}\frac{1-y}{\lambda_{\text{'t Hooft}}}\sqrt{(\omega-\omega_{-})(\omega_{+}-\omega)}\theta(\omega-\omega_{-})\theta(\omega_{+}-\omega)$
		$\displaystyle\qquad+(1-y)\theta(1-y)\delta(\omega)\,.$		(33)

Note that our convention of the propagators includes a factor $i$ in the numerator as seen in eq. (24). $F(\omega)$ is normalized as

$\displaystyle\int F(\omega)d\omega=1,\;\;\;\int F(\omega)\omega d\omega=\frac{y\lambda_{\text{'t Hooft}}}{1-y}.$

(34)

As seen in Fig. 1 and 2, in the planar limit, the Schwinger-Dyson equations in the PSSY model and the IOP matrix model have the same graphical structure. From now on, we elaborate on the correspondence of each diagram.

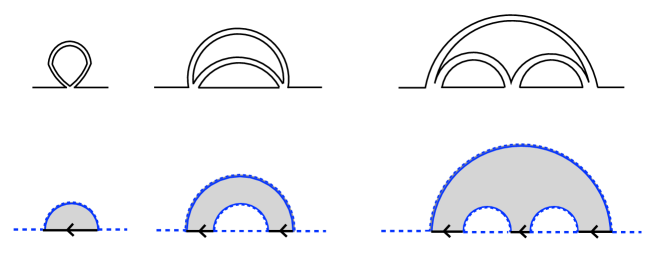
From diagrams in the IOP matrix model, one can uniquely construct the corresponding diagrams in the PSSY model and vice versa. The Feynman diagram correspondence can be obtained by the following prescription. See Fig. 3.

1. 1.

   Extend vertices in the IOP matrix model horizontally and draw straight lines with horizontal arrows from right to left. These arrows represent the asymptotic boundaries with the time direction from the ket to the bra in the PSSY model.

2. 2.

   Rewrite the adjoint correlators in the IOP matrix model as blue solid curves in the PSSY model. These blue solid curves correspond to EOW branes in the PSSY model.

3. 3.

   Fill in regions above the right-to-left horizontal arrows corresponding to asymptotic boundaries with a gray shadow. These shaded regions correspond to bulk geometries in the PSSY model.

Figure 4 shows examples of corresponding planar diagrams, where we omit arrows in the IOP matrix model for easier comparison. Due to the correspondence between these diagrams, there is also the correspondence between the solutions of the Schwinger-Dyson equations in the planar limit. The correspondence between parameters in both models is examined in the next subsection.

Due to the correspondence, there is one-to-one Feynman diagram correspondence between the IOP matrix model Feynman diagrams and the PSSY model Feynman diagrams. Thus, the correspondence goes beyond the planar limit. For example, Figure 5 shows examples of corresponding non-planar diagrams. From the perspective of the PSSY model, the left figure includes two bulk geometries with a crossing, and the right figure includes a twisted bulk geometry that is anchored to the asymptotic boundaries.

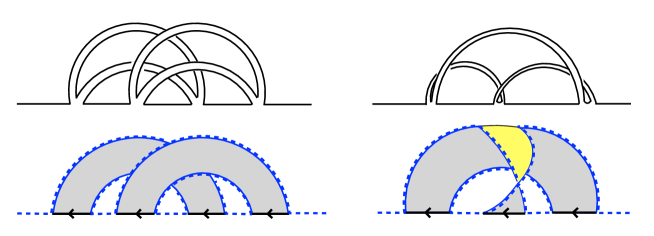
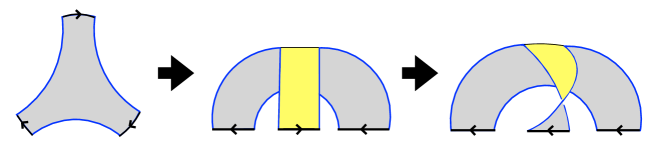
Let us look into a little more on the twisted bulk geometry in Figure 5. We can construct this twisted bulk geometry from a bulk geometry for $Z_{3}^{\text{Disk}}$ as follows. First, prepare the bulk geometry for $Z_{3}^{\text{Disk}}$ shown at left in Figure 6. Next, fold the top part downward so that the yellow reverse side is visible as shown in the middle figure. Finally, twist the folded part so that the middle arrow is facing left as shown in the right figure.

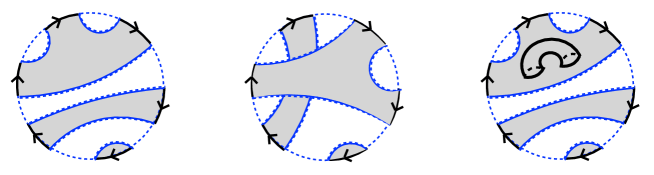
Following our prescription in reverse, we can also construct the corresponding diagrams in the IOP matrix model from the ones in the PSSY model. However, note that not all bulk geometries in the PSSY model correspond to diagrams in the IOP matrix model. To see this point, for instance, let us consider three examples of bulk geometries that contribute to $\Tr(\rho^{6}_{\mathbb{R}})$ as shown in Figure 7. In the IOP matrix model, there are diagrams corresponding to the planar one and the non-planar one with a crossing such as the left and middle geometries in Figure 7, respectively. However, there is no diagram in the IOP matrix model for the non-planar geometry with an extra handle such as the right geometry where non-planar effects are due to the extra handle in bulk, not crossings.

These clearly show that the correspondence works as long as we neglect the extra-handle-in-bulk diagrams. Thus in this paper, using the PSSY and the IOP model correspondence, in Subsection 3.3, we calculate the exact non-planar effects associated with a crossing as the middle figure in Fig. 7.

Given the one-to-one Feynman diagram correspondence, it is straightforward to read off the parameter correspondence between them. One can observe that the spectral densities $D(\lambda)$ in (13) and $F(\omega)$ (33) have the same structures. In fact, after rescaling, the spectral density of the IOP matrix model at infinite temperature limit agrees with the spectral density $D(\lambda)$ (17) of the PSSY model when $k=e^{\mathbb{S}}$.

The reason why we need to take an infinite temperature in the IOP matrix model is as follows. In the propagator $\tilde{L}_{0}(\omega)$ (25) of the IOP matrix model, there is a difference of a factor $y$ between the two terms. See eq. (3.1) of Iizuka:2008eb as well. However, there is no such difference in the PSSY model side. To eliminate this difference, we need to take the following infinite temperature limit

$\displaystyle y=e^{-m/T}\to 1\quad\text{and}\quad\lambda_{\text{'t Hooft}}\to 0\,\quad\text{with}\;\,\lambda_{y}:=\frac{\lambda_{\text{'t Hooft}}}{1-y}=\mbox{fixed}.$

(35)

In this infinite temperature limit, the spectral density $F(\omega)$ (33) becomes

$\displaystyle F(\omega)=$

$\displaystyle\;\frac{1}{2\pi\omega\lambda_{y}}\sqrt{\omega(4\lambda_{y}-\omega)}\theta(\omega)\theta(4\lambda_{y}-\omega).$

(36)

Since there is a correspondence between the Feynman diagrams in the IOP matrix model and the PSSY model, this $F(\omega)$ should correspond to $D(\lambda)$ up to some normalization.

Let us compare $D(\lambda)$ in the PSSY model given by (13) and $F(\omega)$ in the IOP matrix model given by (33). Then it is clear that under the $y\to 1$ limit, one needs $k=e^{\mathbb{S}}$ limit for the correspondence to work³³3We will later see in the discussion section that in order to go beyond $k=e^{\mathbb{S}}$ limit, one needs to consider a rectangular model. As long as we are considering a square matrix in the IOP model, one has to take $k=e^{\mathbb{S}}$ limit for the correspondence to the PSSY model to work. Note that even in the rectangular model, one always needs $y\to 1$ limit in the IOP model for the correspondence to the PSSY model for $k\neq e^{\mathbb{S}}$.. Thus we focus on this limit. Furthermore, in order to take into account the normalization difference between $F(\omega)$ in the IOP matrix model (34) and $D(\lambda)$ in the PSSY model (16), we divide $D(\lambda)$ in (17) by $k$ as

$\displaystyle\frac{1}{k}D(\lambda)=\frac{k}{2\pi\lambda}\sqrt{\lambda\left(\frac{4}{k}-\lambda\right)}\theta(\lambda)\theta\left(\frac{4}{k}-\lambda\right)\,,\quad\mbox{when}\quad k=e^{\textbf{S}}\,.$

(37)

Let’s compare (36) and (37). One might naively think that $\omega$ in the IOP matrix model corresponds to $\lambda$ in the PSSY model. However, this cannot be true since their dimensions do not match. To make $\omega$ dimensionless and also to match the parameter range in $\theta$-functions, we define

$\displaystyle\tilde{\omega}:=\frac{\omega}{\lambda_{y}k}\quad\mbox{such that}\quad 0\leq\omega\leq 4\lambda_{y}\,\Leftrightarrow\,0\leq\tilde{\omega}\leq\frac{4}{k}.$

(38)

Then, we can define

$\displaystyle\tilde{F}(\tilde{\omega}):=\lambda_{y}kF(\omega)\quad\mbox{such that}\quad\int d\tilde{\omega}\tilde{F}(\tilde{\omega})=\int d\omega F(\omega)=1.$

(39)

Thus, we obtain

$\displaystyle\tilde{F}(\tilde{\omega})=\frac{k}{2\pi\tilde{\omega}}\sqrt{\tilde{\omega}\left(\frac{4}{k}-\tilde{\omega}\right)}\theta\left(\tilde{\omega}\right)\theta\left(\frac{4}{k}-\tilde{\omega}\right).$

(40)

It is then clear that there is a parameter correspondence between the two models as follows

		$\displaystyle\tilde{\omega}\,(\mbox{IOP})\,\leftrightarrow\,\lambda\,(\mbox{PSSY})\,,\quad\tilde{F}(\tilde{\omega})\,(\mbox{IOP})\,\leftrightarrow\,\frac{1}{k}D(\lambda)\,(\mbox{PSSY})\,,$		(41)
		$\displaystyle\qquad\qquad\qquad N\,(\mbox{IOP})\,\leftrightarrow\,k=e^{\mathbb{S}}\,(\mbox{PSSY})\,$		(42)

at $y\to 1$ limit. Note that, for the planar limit, we consider the large $N$ limit in the IOP matrix model and the large $k$, $e^{\mathbb{S}}$ limit in the PSSY model, and they correspond as (42).

Let us investigate the correspondence in more detail. In the PSSY model, the spectral density $D(\lambda)$ is computed from the resolvent $R(\lambda)$

	$\displaystyle R(\lambda)=\Tr\frac{1}{\lambda\mathds{1}-\rho_{\mathbb{R}}}=\sum_{l=1}^{k}\bra{l}_{\mathbb{R}}\frac{1}{\lambda\mathds{1}-\rho_{\mathbb{R}}}\ket{l}_{\mathbb{R}},$		(43)
	$\displaystyle\mbox{where}\quad\rho_{\mathbb{R}}=\frac{1}{k}\,\sum\limits_{i,j=1}^{k}\,\ket{j}\bra{i}_{\mathbb{R}}\,\braket{\psi_{i}}{\psi_{j}}_{\mathbb{B}}.$		(44)

In the IOP matrix model, the two-point function $\tilde{G}(\omega)$ in the large $M$ limit can be expressed as

	$\displaystyle N\tilde{G}(\omega)=\sum_{l=1}^{N}\Big{\langle}a_{l}\frac{i}{\omega\mathds{1}-H_{int}}a^{\dagger}_{l}\Big{\rangle}_{T}$
	$\displaystyle\implies\quad-i\lambda_{y}N^{2}\tilde{G}(\omega)=\sum_{l=1}^{N}\Big{\langle}a_{l}\frac{1}{\frac{\omega}{\lambda_{y}N}\mathds{1}-\frac{1-y}{N^{2}}a_{j}^{\dagger}a_{i}A^{\dagger}_{jk}A_{ki}}a^{\dagger}_{l}\Big{\rangle}_{T}.$		(45)

Since we take $M$ to be large so that the number of fundamental fields is always one in the evaluation of $\tilde{G}(\omega)$, we can treat $a_{l}^{\dagger}\ket{v}$ as an $N$-dimensional one-particle excited state basis, where $\ket{v}$ is the ground state for the fundamental field. Comparing eqs.  (44) and (45), we obtain the following additional relationships⁴⁴4To be precise, since the trace of a matrix is invariant under the transformation of a basis, there is the ambiguity of a unitary matrix $U$ in the correspondence (47) as $\displaystyle\qquad\frac{H_{int}}{\lambda_{y}N}\,\,\,\,(\mbox{IOP})\,$ $\displaystyle\leftrightarrow\,\,\,\,U\rho_{\mathbb{R}}U^{\dagger}\,\,\,\,(\mbox{PSSY})\,.$ (46)

	$\displaystyle\qquad\frac{H_{int}}{\lambda_{y}N}=\frac{1-y}{N^{2}}a_{j}^{\dagger}a_{i}A^{\dagger}_{jk}A_{ki}\,(\mbox{IOP})\,$	$\displaystyle\leftrightarrow\,\,\,\,\rho_{\mathbb{R}}\,\,\,\,(\mbox{PSSY})\,,$		(47)
	$\displaystyle-i\lambda_{y}N^{2}\tilde{G}(\omega)\,\,\,(\mbox{IOP})\,$	$\displaystyle\leftrightarrow\,\,R(\lambda)\,(\mbox{PSSY})\,.$		(48)

in addition to the parameter correspondence given by (41) and (42). In (47), naively one might wonder if this term vanishes in the $y\to 1$ limit. However, the adjoint propagator is also proportional to $1/(1-y)$ as seen in (25), thus this is a well-defined limit even in $y\to 1$.

Furthermore, $\ket{l}_{\mathbb{R}}$, which forms an orthonormal basis for the radiation Hilbert space, corresponds to the one-fundamental excited state $a_{l}^{\dagger}\ket{v}$ that is again orthogonal. Given these correspondences, one can also see the relationship

	$\displaystyle\text{Random ensemble average of }\braket{\psi_{i}}{\psi_{j}}_{\mathbb{B}}\,(\mbox{PSSY})$
	$\displaystyle\leftrightarrow\,\,\text{ Expectation value of }\frac{1-y}{N}A^{\dagger}_{jl}A_{li}\,\,\,(\mbox{IOP}).$		(49)

In the PSSY model, the Gaussian random property of $\braket{\psi_{i}}{\psi_{j}}_{\mathbb{B}}$ is crucial for connected wormhole contributions. From the viewpoint of the IOP matrix model, this Gaussian randomness comes from the fact that the adjoint fields $A^{\dagger}$ behave like Gaussian free fields. In random matrix theory, the spectral density $D(\lambda)$ (13) up to the normalization is known as the Marchenko-Pastur distribution Pastur:1967zca , see, for instance, Muck:2024fpb . The reason why the Marchenko-Pastur distribution appears is that $\braket{\psi_{i}}{\psi_{j}}_{\mathbb{B}}$ in the PSSY model can be interpreted as a Gram matrix Balasubramanian:2022gmo ; Balasubramanian:2022lnw ; Climent:2024trz and $H_{int}$ in the IOP matrix model is proportional to $A^{\dagger}A$.

Non-planar $1/N^{2}$ correction of the two-point function $\tilde{G}(\omega)$ in the IOP matrix model was computed by Iizuka:2008eb . By using the PSSY model and the IOP matrix model correspondence, it is straightforward to obtain the non-planar $1/k^{2}$ correction of the reduced density matrix and its von Neumann entropy in the PSSY model. Especially, the spectral density $D(\lambda)$ (17) in the PSSY model and the rescaled one $\tilde{F}(\tilde{\omega})$ (40) in the IOP matrix model corresponds in the planar limit. Then the non-planar $1/N^{2}$ correction of the von Neumann entropy in the IOP matrix model would be a part of the non-planar $1/k^{2}$ correction of the entanglement entropy in the PSSY model.

The non-planar $1/N^{2}$ correction of $\tilde{G}(\omega)$ is calculated in Iizuka:2008eb , and it is

	$\displaystyle\tilde{G}(\omega)$	$\displaystyle=\tilde{G}^{(0)}(\omega)+{1\over N^{2}}\tilde{G}^{(1)}(\omega)+{\cal{O}}\left({1\over N^{4}}\right)\,,$		(50)
	$\displaystyle\tilde{G}^{(0)}(\omega)$	$\displaystyle=\frac{i}{2\lambda_{y}}\left(1-\sqrt{1-\frac{4\lambda_{y}}{\omega}}\right)\,,$		(51)
	$\displaystyle x_{0}$	$\displaystyle:=-i\lambda_{y}\tilde{G}^{(0)}(\omega)=\frac{1}{2}\left(1-\sqrt{1-\frac{4\lambda_{y}}{\omega}}\right)\,,$		(52)
	$\displaystyle\tilde{G}^{(1)}(\omega)$	$\displaystyle=\frac{ix_{0}^{3}(1-x_{0})^{4}}{(1-2x_{0})^{4}(\omega(1-x_{0})^{2}-\lambda_{y})}=\frac{i\lambda_{y}^{3}}{(\omega-4\lambda_{y})^{5/2}\omega^{3/2}}\,.$		(53)

By using this result, we obtain the non-planar $1/N^{2}$ correction of the spectral density

	$\displaystyle F(\omega)$	$\displaystyle=F^{(0)}(\omega)+{1\over N^{2}}F^{(1)}(\omega)+{\cal{O}}\left({1\over N^{4}}\right),$		(54)
	$\displaystyle F^{(0)}(\omega)$	$\displaystyle=\frac{1}{\pi}\real\tilde{G}^{(0)}(\omega)=\frac{\sqrt{\omega(4\lambda_{y}-\omega)}}{2\pi\lambda_{y}\omega}\theta(\omega)\theta\left(4\lambda_{y}-\omega\right),$		(55)
	$\displaystyle F^{(1)}(\omega)$	$\displaystyle=\frac{1}{\pi}\real\tilde{G}^{(1)}(\omega)=\frac{\lambda_{y}^{3}}{\pi\omega^{3/2}(4\lambda_{y}-\omega)^{5/2}}\theta(\omega)\theta\left(4\lambda_{y}-\omega\right).$		(56)

Since $\tilde{G}^{(1)}(\omega)$ (53) is a rational function of $x_{0}$ and $\omega$, $F^{(1)}(\omega)$ has branch points at $\omega=0,4\lambda_{y}$ that are the same branch points of $F^{(0)}(\omega)$. This property comes from the fact that the perturbation equation determining $\tilde{G}^{(1)}(\omega)$ is written in terms of $\tilde{G}^{(0)}(\omega)$. Note that even though the branch points of $F^{(0)}(\omega)$ and $F^{(1)}(\omega)$ are the same, $F^{(1)}(\omega)$ is singular than $F^{(0)}(\omega)$.

Given the correspondence we discussed in the previous subsection, we can read off the $1/k^{2}$ corrections in the PSSY model from (38), (39), (41), (42), and (56) as

	$\displaystyle\frac{1}{k}D^{(0)}(\lambda)$	$\displaystyle=\frac{k}{2\pi\lambda}\sqrt{\lambda\left(\frac{4}{k}-\lambda\right)}\theta(\lambda)\theta\left(\frac{4}{k}-\lambda\right)\,,$		(57)
	$\displaystyle\frac{1}{k}D^{(1)}(\lambda)$	$\displaystyle=\frac{1}{\pi k^{3}}\frac{1}{\lambda^{3/2}(\frac{4}{k}-\lambda)^{5/2}}\theta(\lambda)\theta\left(\frac{4}{k}-\lambda\right)\,,$		(58)

when $k=e^{\textbf{S}}$. Here $D^{(0)}(\lambda)$ and $D^{(1)}(\lambda)$ are the same order since

$\displaystyle\frac{1}{k}D^{(0)}(\lambda)=\order{k}\,,\quad\frac{1}{k}D^{(1)}(\lambda)=\order{k}\,\quad\mbox{for $\lambda\sim\frac{1}{k}$}.$

(59)

With this, one can calculate the entanglement entropy for the radiation $S_{\mathbb{R}}$ as

	$\displaystyle S_{\mathbb{R}}$	$\displaystyle:=-\int D(\lambda)\lambda\log\lambda$
		$\displaystyle=-\int\left(D^{(0)}(\lambda)+\frac{1}{k^{2}}D^{(1)}(\lambda)+\order{1\over k^{4}}\right)\lambda\log\lambda.$		(60)

The leading term can be evaluated as

$\displaystyle-\int D^{(0)}(\lambda)\lambda\log\lambda=-\frac{k^{2}}{2\pi}\int_{0}^{4/k}\sqrt{\lambda\left({4\over k}-\lambda\right)}\log\lambda\,d\lambda=\log k-\frac{1}{2},$

(61)

which agrees with eq. (20). The subleading term is

	$\displaystyle-\frac{1}{k^{2}}\int D^{(1)}(\lambda)\lambda\log\lambda\,d\lambda$	$\displaystyle=-\frac{1}{\pi k^{4}}\int_{0}^{4/k}\frac{\lambda}{\lambda^{3/2}\left(\frac{4}{k}-\lambda\right)^{5/2}}\log\lambda\,d\lambda=\frac{C}{k^{2}},$		(62)
	$\displaystyle\mbox{where}\quad C$	$\displaystyle:=-\frac{1}{\pi}\int_{0}^{4}\frac{x^{2}}{\left(x(4-x)\right)^{5/2}}\log\left(\frac{x}{k}\right)dx,$		(63)

where we change the integration variable $\lambda=x/k$.

$C$ does not converge due to more singular nature of $D^{(1)}(\lambda)$ than $D^{(0)}(\lambda)$. To regularize this integral, we introduce a small cutoff $\epsilon$ so that $C$ is regularized as

	$\displaystyle C_{\epsilon}$	$\displaystyle:=-\frac{1}{\pi}\int_{0}^{4-\epsilon}\frac{x^{2}}{\left(x(4-x)\right)^{5/2}}\log\left(\frac{x}{k}\right)dx$		(64)
		$\displaystyle=\frac{\log\frac{k}{4}}{3\pi\epsilon^{3/2}}+\frac{\log\frac{k}{4}+2}{8\pi\sqrt{\epsilon}}+\frac{1}{12}+\order{\epsilon^{1/2}}.$		(65)

The first and second terms are divergent but they are regulator dependent. On the other hand, $1/12$ is a regulator-independent one. Thus, we focus on this $1/12$ by subtracting the UV divergent terms⁵⁵5One might be able to justify this argument along the line of “renormalized entanglement entropy” of Liu:2012eea ..

Therefore, after subtracting the regulator-dependent divergent terms at $\epsilon\to 0$, we obtain a finite result

$\displaystyle S_{\mathbb{R}}=\log k-\frac{1}{2}+\frac{1}{12k^{2}}+{\cal{O}}\left({1\over k^{4}}\right)\,,\quad\mbox{when}\quad k=e^{\mathbb{S}}.$

(66)

Since the leading term (61) in $S_{\mathbb{R}}$ agrees with $S_{\mathbb{R}}$ (20) in the planar limit, we expect that the sub-leading term in $S_{\mathbb{R}}$ (66) corresponds to a part of non-planar $1/k^{2}$ corrections of $S_{\mathbb{R}}$ in the PSSY model. As shown in Fig. 7, non-planar corrections of $S_{\mathbb{R}}$ in the PSSY model come from non-planar diagrams with extra-handle-in-bulk and crossings. We expect that the sub-leading term in $S_{\mathbb{R}}$ (66) corresponds to the non-planar correction of $S_{\mathbb{R}}$ from crossings, not extra-handle-in-bulk.