A nonlinear semigroup approach to Hamilton-Jacobi equations–revisited

Inspired by Aubry-Mather theory and weak KAM theory for classical Hamiltonian systems, an action minimizing method for contact Hamiltonian systems was developed in a series of papers [16, 17, 18, 19, 20]. Let $H:T^{*}M\times\mathbb{R}\to\mathbb{R}$ be a contact Hamiltonian. It turns out that the dependence of $H$ on the contact variable $u$ plays a crucial role in exploiting the dynamics generated by $H$. By using previous dynamical approaches, some progress on viscosity solutions of Hamilton-Jacobi (HJ) equations have been achieved [16, 18, 20]. In particular, the structure of the set of solutions can be sketched if $H$ is uniformly Lipschitz in $u$ based on the works mentioned before. Shortly after [18] occurred, [12] generalized the results to ergodic problems by using PDE approachs. More recently, for a class of HJ equations with non-monotone dependence on $u$, the first breakthrough was achieved by Jin-Yan-Zhao [11] under the Tonelli conditions. In that work, they provided a description of the solution set of the stationary equation (formulated as (E₀) below) and revealed a bifurcation phenomenon with respect to the value $c$ in the right hand side, which opened a way to exploit further properties of viscosity solutions beyond well-posedness for HJ equations with non-monotone dependence on $u$. The main results in this paper are motivated by [11].

Let us consider the stationary equation:

$${H}(x,Du)+\lambda(x)u=c,\quad x\in M.$$

(E0)

Throughout this paper, we assume $M$ is a closed, connected and smooth Riemannian manifold. $D$ denotes the spacial gradient with respect to $x\in M$. Denote by $TM$ and $T^{*}M$ the tangent bundle and cotangent bundle of $M$ respectively. Let $H:T^{*}M\rightarrow\mathbb{R}$ satisfy

• (C):

  $H(x,p)$ is continuous;

• (CON):

  $H(x,p)$ is convex in $p$, for any $x\in M$;

• (CER):

  $H(x,p)$ is coercive in $p$, i.e. $\lim_{\|p\|_{x}\rightarrow+\infty}H(x,p)=+\infty$, where $\|\cdot\|_{x}$ denotes the norms induced by $g$ on both $TM$ and $T^{*}M$.

Correspondingly, one has the Lagrangian associated to $H$:

$$L(x,\dot{x}):=\sup_{p\in T^{*}_{x}M}\{\langle\dot{x},p\rangle_{x}-H(x,p)\},$$

where $\langle\cdot,\cdot\rangle_{x}$ represents the canonical pairing between $T_{x}M$ and $T^{*}_{x}M$. The Lagrangian $L(x,\dot{x})$ satisfies the following properties:

• (LSC):

  $L(x,\dot{x})$ is lower semicontinous in $\dot{x}$, and continuous on the interior of its domain $\textrm{dom}(L):=\{(x,\dot{x})\in TM:\ L(x,\dot{x})<+\infty\}$;

• (CON):

  $L(x,\dot{x})$ is convex in $\dot{x}$, for any $x\in M$.

We also assume $\lambda(x)$ is continuous and satisfies

• ($\pm$):

  there exist $x_{1},x_{2}\in M$ such that $\lambda(x_{1})>0$ and $\lambda(x_{2})<0$.

Throughout this paper, we define

$$\lambda_{0}:=\|\lambda(x)\|_{\infty}>0,$$

(1.1)

where $\|\cdot\|_{\infty}$ stands for the supremum norm of the functions on their domains. From an economical point of view, the assumption ($\pm$) may be corresponding to a model with fluctuating interest rates. To be more precise, the rates depend on the space variable and admit values above and below zero at some places. From a theoretical point of view, it is a toy model of the HJ equations with non-monotone dependence on $u$. Based on this model, we revealed some different phenomena from the cases with monotone dependence on $u$ can be revealed.

In [14], the well-posedness of the Lax-Oleinik semigroup was verified for contact HJ equations under very mild conditions. By virtue of that, we generalize the results in [11] to the cases from the Tonelli conditions to the assumptions (C), (CON) and (CER) above. Henceforth, for simplicity of notation, we omit the word “viscosity”, if it is not necessary to be mentioned.

The definition of $c_{0}$ is inspired by [5]. In light of that, $c_{0}$ is called the critical value. Now we consider the most general case

$$H(x,u(x),Du(x))=c,\quad x\in M,$$

where the Hamiltonian $H(x,u,p)$ is continuous, superlinear in $p$ and uniformly Lipschitz in $u$. It was pointed out in [12] that there is a constant $c\in\mathbb{R}$ such that the above equation has viscosity solutions. Here we give some examples on the set $\mathfrak{C}$ of all such $c$’s, which reveals the essential difference between the monotone cases and the non-monotone cases:

• •

  for classical Tonelli Hamiltonian $H(x,p)$, the set $\mathfrak{C}=\{c_{0}\}$. The number $c_{0}$ is called the effective Hamiltonian or the Mañé critical value;

• •

  for the discounted Hamilton-Jacobi equation, i.e., the Hamiltonian is of the form $\lambda u+H(x,p)$ with $\lambda>0$, the set $\mathfrak{C}=\mathbb{R}$, see for example [6];

• •

  for the model (E₀) considered here, the set $\mathfrak{C}=[c_{0},+\infty)$. Here we note that the non-emptiness of $\mathfrak{C}$ is proved under (CER) instead of $H(x,p)$ is superlinear in $p$. In view of the existence result in [12], it means Proposition 1.2 is a non-trivial generalization of [11];

• •

  for the Hamiltonian periodically depending on $u$, i.e., $H(x,u+1,p)\equiv H(x,u,p)$, the set $\mathfrak{C}$ is a bounded closed interval, see [15].

Different from the Tonelli case considered in [11], some new ingredients are needed for a priori estimates of subsolutions under the assumptions (C), (CON) and (CER). Those estimates will be provided in Section 3. The remaining parts of the proof of Proposition 1.2 are similar to the one in [11]. We postpone it to Appendix A.3 for consistency.

Motivated by Proposition 1.2, we are devoted to exploiting more detailed information of this model. First of all, we obtain

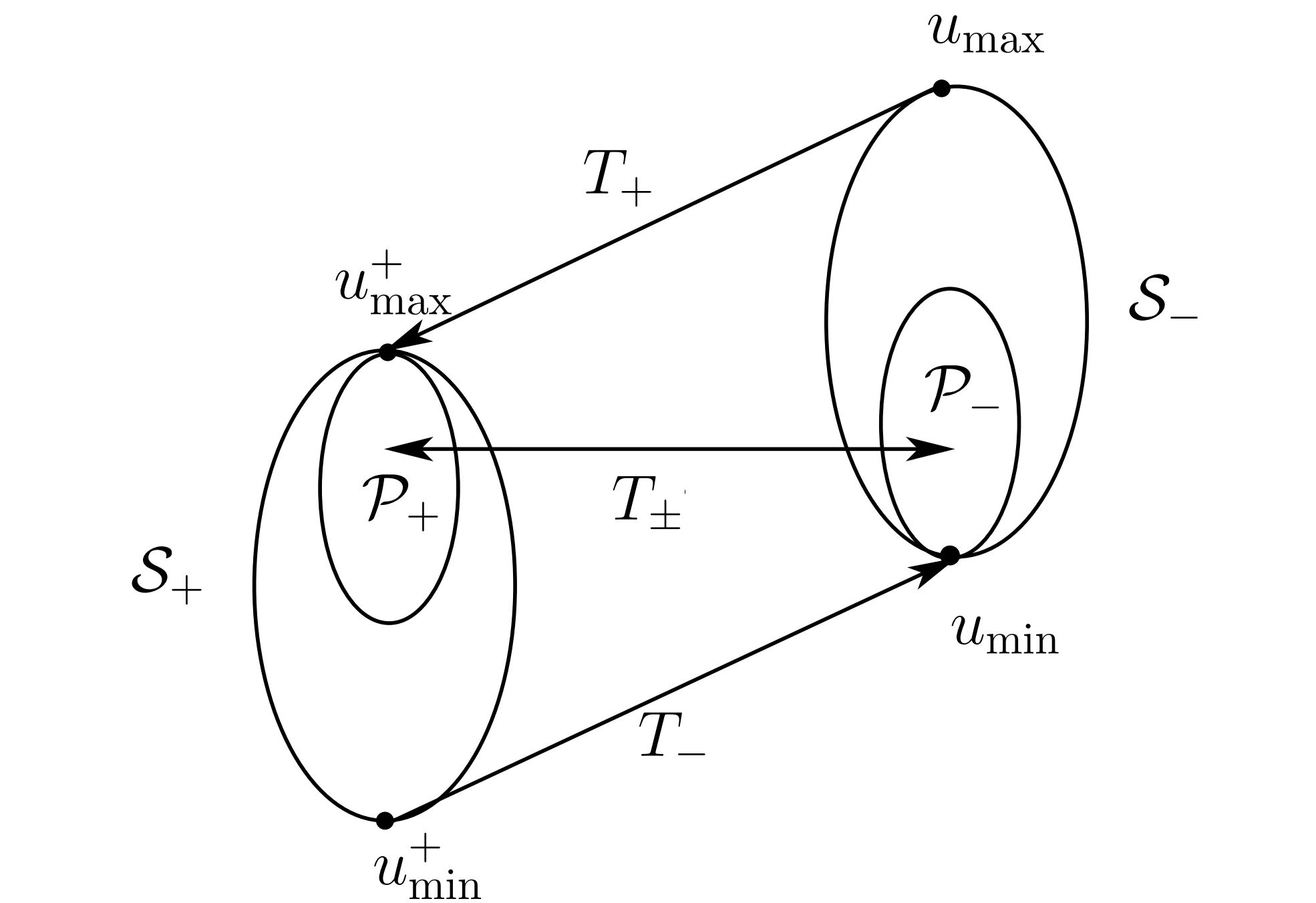
Let $\mathcal{S}_{-}$ (resp. $\mathcal{S}_{+}$) be the set of all backward (resp. forward) weak KAM solutions. Given $u_{\pm}\in\mathcal{S}_{\pm}$, if

$$u_{-}=\lim_{t\to\infty}T_{t}^{-}u_{+},\quad u_{+}=\lim_{t\to\infty}T_{t}^{+}u_{-},$$

then $u_{-}$ (resp. $u_{+}$) is called a conjugated backward (resp. forward) weak KAM solution. See Figure 1 for a rough description of structure of the solution set of (E₀) in general cases, where $\mathbb{T}_{\pm}:=\lim_{t\to\infty}T_{t}^{\pm}$, and $\mathcal{P}_{-}$ (resp. $\mathcal{P}_{+}$) denotes the set of all conjugated backward (resp. forward) weak KAM solutions. For further statement on conjugated weak KAM solutions, one can refer to [10, Theorem 6.5 and Theorem 7.1].

By Proposition 1.2(2), (E₀) has at least two solutions if $c>c_{0}$. Then a natural question is to figure out what happens if $c=c_{0}$. In [11], Jin, Yan and Zhao considered the following example:

It was shown that $c_{0}=0$ and there are uncountably many solutions of (1.2) in the critical case. A rough picture of certain solutions is given by Figure 2. See [11, Theorem 3.5] for more details.

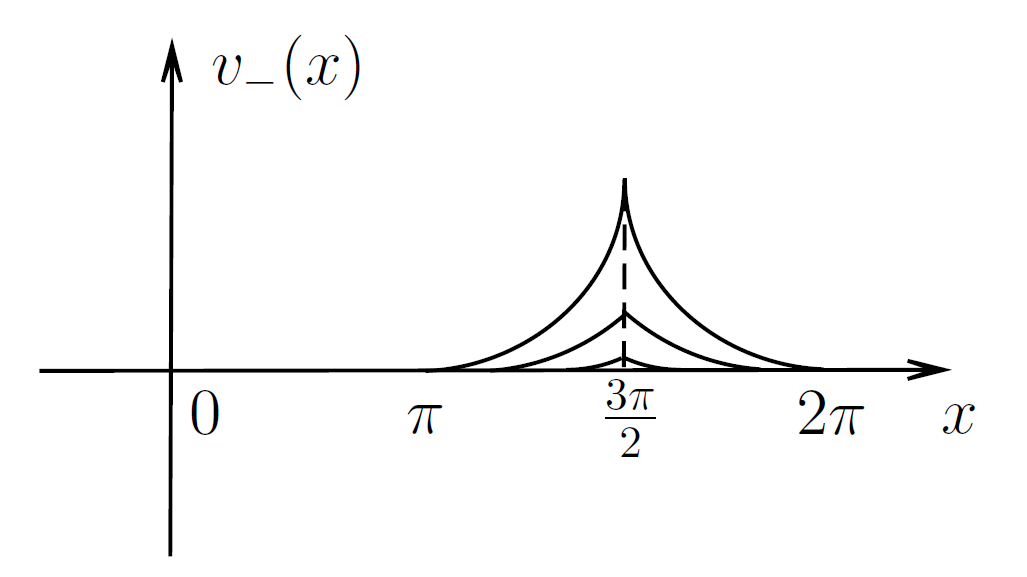
As a complement, we consider

We will prove that the critical value is also $c_{0}=0$, but (1.3) admits a unique solution in the critical case. A rough picture of the solution is given by Figure 3. See Remark 4.2 below for certain generalization of Example 1.5. Those two examples above show various possibilities about the solution set of (E₀) in the critical case.

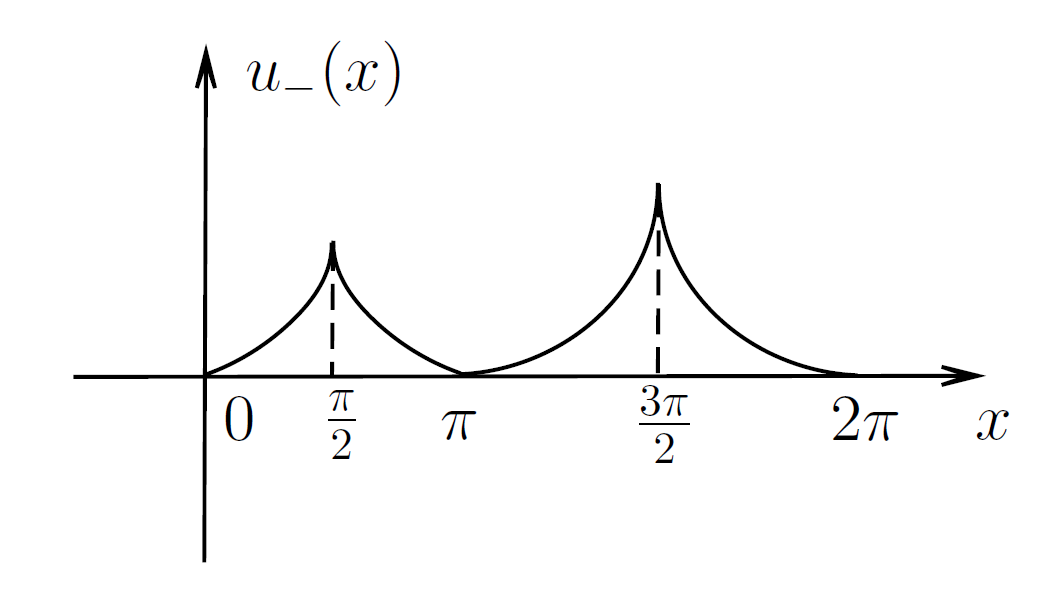
In the second part, we consider the evolutionary equation:

$$\left\{\begin{aligned} &\partial_{t}u(x,t)+H(x,Du(x,t))+\lambda(x)u(x,t)=c,\quad(x,t)\in M\times(0,+\infty).\\ &u(x,0)=\varphi(x),\quad x\in M,\\ \end{aligned}\right.$$

(CP)

where $\varphi\in C(M)$. It is well known that the viscosity solution of (CP) is unique (see [10, Corollary 3.2] for instance). By [14, Theorem 1], this solution can be represented by $u(x,t):=T_{t}^{-}\varphi(x)$, where $T^{-}_{t}:C(M)\rightarrow C(M)$ is defined implicitly by

$$T^{-}_{t}\varphi(x)=\inf_{\gamma(t)=x}\left\{\varphi(\gamma(0))+\int_{0}^{t}\bigl{[}L(\gamma(\tau),\dot{\gamma}(\tau))-\lambda(\gamma(\tau))T^{-}_{\tau}\varphi(\gamma(\tau))+c\bigl{]}{d}\tau\right\},$$

(T-)

where the infimum is taken among absolutely continuous curves $\gamma:[0,t]\rightarrow M$ with $\gamma(t)=x$.

In order to obtain equi-Lipschitz continuity of $\{T_{t}^{-}\varphi\}_{t\geq\delta}$ for a given $\delta>0$, we have to strengthen the assumptions on $H$ from (CON), (CER) to the following:

• ($\star$)

  $H(x,p)$ is strictly convex in $p$ for any $x\in M$, and there is a superlinear function $\theta:[0,+\infty)\to[0,+\infty)$ such that $H(x,p)\geq\theta(\|p\|)$.

Under the assumption ($\star$), the equi-Lipschitz continuity of $\{T_{t}^{-}\varphi\}_{t\geq\delta}$ follows from the locally Lipschitz property and boundedness of $T_{t}^{-}\varphi$ on $M\times(0,+\infty)$. From the weak KAM point of view, that kind of locally Lipschitz property can be verified by a standard procedure once we have the Lipschitz regularity of minimizers of $T_{t}^{-}\varphi(x)$ (see [7, Lemma 4.6.3]). However, $H$ is only supposed to be continuous in our setting. Then one can not use the method of characteristics to improve regularity of these minimizers. Following [2], we will deal with that issue by using the method of energy estimates. A key ingredient of that method is to establish the Erdmann condition for a non-smooth energy function. More precisely, we obtain the following result, whose proof is given in Appendix A.4.

Let us recall $u_{\max}$ denotes the maximal solution of (E₀), and $u^{+}_{\min}$ denotes its minimal froward weak KAM solution. By Remark 1.3, $u^{+}_{\min}\leq u_{\max}$ on $M$. Both of them play an important role in characterizing the large time behavior of the solution of (CP). By assuming ($\star$) holds, we obtain the following two results.

The rest of this paper is organized as follows. Section 2 gives some preliminaries on $T_{t}^{\pm}$, weak KAM solutions and Aubry sets. In Section 3, a priori estimates on subsolutions of (E₀) are established. The proof of Theorem 1 and a detailed analysis of Example 1.5 are given in Section 4. Theorem 2 and Theorem 3 are proved in Section 5 For the sake of completeness, some auxiliary results are proved in Appendix A.

In this part, we collect some facts on $T_{t}^{\pm}$, weak KAM solutions and Aubry sets. These facts hold under more general assumptions on the dependence of $u$. Consider the evolutionary equation:

$$\left\{\begin{aligned} &\partial_{t}u(x,t)+H(x,u(x,t),Du(x,t))=0,\quad(x,t)\in M\times(0,+\infty).\\ &u(x,0)=\varphi(x),\quad x\in M.\\ \end{aligned}\right.$$

(A0)

and the stationary equation:

$$H(x,u(x),Du(x))=0$$

(B0)

We denote by $(x,u,p)$ a point in $T^{*}M\times\mathbb{R}$, where $(x,p)\in T^{*}M$ and $u\in\mathbb{R}$. Let $H:T^{*}M\times\mathbb{R}\rightarrow\mathbb{R}$ be a continuous Hamiltonian satisfying

• (CON):

  $H(x,u,p)$ is convex in $p$, for any $(x,u)\in M\times\mathbb{R}$;

• (CER):

  $H(x,u,p)$ is coercive in $p$, i.e. $\lim_{\|p\|_{x}\rightarrow+\infty}(\inf_{x\in M}H(x,0,p))=+\infty$;

• (LIP):

  $H(x,u,p)$ is Lipschitz in $u$, uniformly with respect to $(x,p)$, i.e., there exists $\Theta>0$ such that $|H(x,u,p)-H(x,v,p)|\leq\Theta|u-v|$, for all $(x,p)\in\ T^{*}M$ and all $u,v\in\mathbb{R}$.

Correspondingly, one has the Lagrangian associated to $H$:

$$L(x,u,\dot{x}):=\sup_{p\in T^{*}_{x}M}\{\langle\dot{x},p\rangle-H(x,u,p)\}.$$

Due to the absence of superlinearity of $H$, the corresponding Lagrangian $L$ may take the value $+\infty$. Define

$$\text{dom}(L):=\{(x,\dot{x},u)\in TM\times\mathbb{R}\ |\ L(x,u,\dot{x})<+\infty\}.$$

Then $L(x,u,\dot{x})$ satisfies the following properties:

• (LSC):

  $L(x,u,\dot{x})$ is lower semicontinuous, and continuous on the interior of $\textrm{dom}(L)\times\mathbb{R}$;

• (CON):

  $L(x,u,\dot{x})$ is convex in $\dot{x}$, for any $(x,u)\in M\times\mathbb{R}$;

• (LIP):

  $L(x,u,\dot{x})$ is Lipschitz in $u$, uniformly with respect to $(x,\dot{x})$, i.e., there exists $\Theta>0$ such that $|L(x,u,\dot{x})-L(x,v,\dot{x})|\leq\Theta|u-v|$, for all $(x,\dot{x})\in\ \textrm{dom}(L)$ and all $u,v\in\mathbb{R}$.

Following Fathi [7], one can extend the definitions of backward and forward weak KAM solutions of equation (B₀) by using absolutely continuous calibrated curves instead of $C^{1}$ curves.

A forward weak KAM solution of (B₀) can be defined in a similar manner. Similar to [19, Proposition 2.8], one has

The following two results are well known for Hamilton-Jacobi equations independent of $u$. They are also true in contact cases. We will prove them in Appendixes A.1 and A.2. Proposition 2.5 provides some equivalent characterizations of Lipschitz subsolutions. Proposition 2.6 shows that $T^{+}_{t}$ is a ‘weak inverse’ of $T^{-}_{t}$.

The following three results come from [14], which give some connections among the fixed points of $T_{t}^{\pm}$, the lower (resp. upper) half limit, backward (resp. forward) weak KAM solutions and Aubry sets.

In this section, we assume the existence of subsolutions of (E₀) and prove some a priori estimates on subsolutions. The existence of subsolutions will be verified for $c\geq c_{0}$ in Proposition A.6 below.

Let $L(x,\dot{x})$ be the Legendre transformation of $H(x,p)$. Let $T_{t}^{\pm}$ be the Lax-Oleinik semigroups associated to

$$L(x,\dot{x})-\lambda(x)u(x)+c.$$

Similar to [9, Proposition 2.1], one can prove the local boundedness of $L(x,\dot{x})$ in a neighborhood of the zero section of $TM$.

Throughout this paper, we define

$$\mu:=\textrm{diam}(M)/\delta,$$

(3.2)

where $\textrm{diam}(M)$ denotes the diameter of $M$.