[1]\fnmAlejandro \surOrtiz-Bernardin
1]\orgdivComputational and Applied Mechanics Laboratory, Department of Mechanical Engineering, \orgnameUniversidad de Chile, \orgaddress\streetAv. Beauchef 851, \citySantiago, \postcode8370456, \countryChile
2]\orgdivDepartment of Mechanical Engineering, \orgnameUniversidad de La Serena, \orgaddress\streetAv. Benavente 980, \cityLa Serena, \postcode1720170, \countryChile
3]\orgdivDipartimento di Ingegneria “Enzo Ferrari”, \orgnameUniversità degli Studi di Modena e Reggio Emilia, \orgaddress\streetVia Pietro Vivarelli 10, \cityModena, \postcode41125, \countryItaly
A node-based uniform strain virtual element method for elastoplastic solids
Abstract
A recently proposed node-based uniform strain virtual element method (NVEM) is here extended to small strain elastoplastic solids. In the proposed method, the strain is averaged at the nodes from the strain of surrounding linearly precise virtual elements using a generalization to virtual elements of the node-based uniform strain approach for finite elements. The averaged strain is then used to sample the weak form at the nodes of the mesh leading to a method in which all the field variables, including state and history-dependent variables, are related to the nodes and thus they are tracked only at these locations during the nonlinear computations. Through various elastoplastic benchmark problems, we demonstrate that the NVEM is locking-free while enabling linearly precise virtual elements to solve elastoplastic solids with accuracy.
keywords:
Virtual element method, Nodal integration, Strain averaging, Uniform strain, Volumetric locking, Elastoplasticity1 Introduction
Elastoplastic solids demand advanced numerical techniques when using Galerkin-based approaches such as the finite element method (FEM) and the virtual element method (VEM). The need for advanced techniques has its roots in the presence of volumetric locking in the numerical solution due to the volume preserving nature of the plastic strain (plastic incompressibility condition) and in the volume preserving condition that arises when the Poisson’s ratio approaches (elastic incompressibility condition). Whichever is the source of the locking behavior, the standard lowest order elements in general perform poorly in problems that involve volume preserving conditions. In FEM, several approaches to deal with locking effects are found in the literature. An exhaustive review of these approaches is out of the scope of this paper, but we mention the most relevant ones: reduced/selective integration [1], B-bar technique [2, 3], mixed formulations [1], assumed strain methods [4], and nodal integration [5, 6, 7, 8, 9, 10, 11, 12, 13, 14]. Of particular interest for the method proposed in this paper are nodal integration techniques. In these approaches, the Galerkin weak form is sampled at the nodes of the mesh leading to methods in which all the field variables (including state and history-dependent variables) are associated with the nodes.
The VEM is a generalization of the FEM to elements with arbitrary number of edges/faces (convex or nonconvex polytopes) known as virtual elements [15]. In its standard form, the method consists in the construction of an algebraic (exact) representation of the stiffness matrix without computation of basis functions (basis functions are virtual). In this process, a decomposition of the stiffness matrix into a consistency part and a stability part that ensures convergence of the method [16] is realized. The VEM has gained much interest in recent years and nowadays its applications can be found, for instance, in elastic and inelastic solids [17, 18, 19, 20, 21, 22, 23, 24, 25], elastodynamics [26, 27], finite deformations [28, 29, 30, 31, 32, 33, 34, 35, 36], contact mechanics [28, 37, 38], fracture mechanics [39, 40, 41, 42, 43], fluid mechanics [44, 45, 46, 47, 48], geomechanics [49, 50] and topology optimization [34, 51, 52].
In the VEM literature, there are few methods already developed that are suitable for modeling nearly incompressible elastic solids. These are generalizations of some of the above mentioned approaches for FEM. For instance, B-bar formulation [26, 21], mixed formulation [53], enhanced strain formulation [23], hybrid formulation [54], and nonconforming formulations [55, 56, 57]. In small strain elastoplasticity, the VEM literature is very limited. For instance, in Refs. [20, 58] high-order VEM has been used to improve the numerical performance when facing locking effects in elastoplastic solids. A mixed formulation based on a Hu-Washizu functional was adopted in Ref. [25]. Recently, a stabilization-free hybrid virtual element method has been proposed for elastoplastic solids that is locking-free [59].
In this paper, the recently proposed node-based uniform strain virtual element method [60] (NVEM) is extended to small strain elastoplastic solids. In the proposed approach, the strain is averaged at the nodes from the strain of surrounding linearly precise virtual elements using a generalization to virtual elements of the node-based uniform strain approach for finite elements [6]. The nodal strain that results from the averaging process is interpreted as the nodal sample of the strain in the nodal integration of the weak form. Consequently, the nodal strain is also used at the constitutive evaluation level. As in any nodal integration method, the state and history-dependent variables in the NVEM become associated with the nodes. In practice, this means that in nonlinear computations these variables are tracked only at the nodes. This feature can be exploited to avoid mesh remapping of these variables in Lagrangian large deformation simulations with remeshing (see, for instance, Ref. [9]), which is not possible when Gauss integration is used. We do not intend to explore the latter feature in this paper as the focus here is on the small strain regime, which is a necessary intermediate step towards developments in the finite strain regime.
The remainder of this paper is structured as follows. In Section 2, the NVEM for small strain elastoplasticity is developed. The elastoplastic constitutive model used and the stabilization proposed for the NVEM are presented in Section 3. In Section 4, various elastoplastic benchmark problems are considered to assess the performance of the NVEM. The paper ends with a summary and conclusions in Section 5.
2 Node-based uniform strain virtual element method
In this section, the basics of the node-based uniform strain virtual element method (NVEM), which was developed in Ref. [60], is summarized. The method belongs to the Galerkin weak formulation family of methods. In this sense, we consider an elastic body that occupies the open domain and is bounded by the one-dimensional surface whose unit outward normal is . The boundary is assumed to admit decompositions and , where is the Dirichlet boundary and is the Neumann boundary. The closure of the domain is . Let be the displacement field at a point of the elastic body with position vector when the body is subjected to external tractions and body forces . The imposed Dirichlet (essential) boundary conditions are . The displacement field is found such that (weak form)
| (1) |
where denotes the space of admissible displacements and the space of its variations; is the Cauchy stress tensor and is the small strain tensor that is given by
| (2) |
2.1 Virtual element method
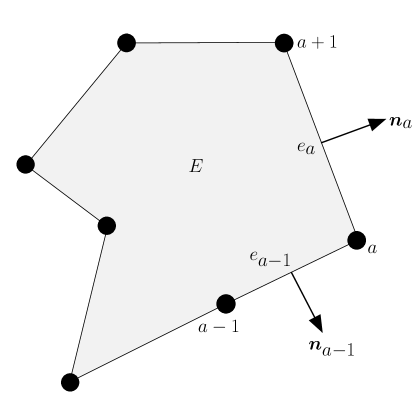
The weak form (1) is the continuous problem. The discrete problem is formulated on a partition of the domain into nonoverlapping elements with arbitrary number of edges (convex or non-convex polygons). This partition is denoted by , where is the maximum diameter of any element in the partition. An element in the partition is denoted by and its boundary by . is the area of the element and its number of edges/nodes. The unit outward normal to the element boundary in the Cartesian coordinate system is denoted by . Fig. 1 depicts an element with seven edges (), where the edge of length and the edge of length are the element edges incident to node , and and are the unit outward normals to these edges, respectively.
Following a standard Galerkin approach, we assume approximations of and on the element, as follows:
| (3) |
where are basis functions that form a partition of unity. A peculiarity of the VEM is that the basis functions are never computed, which is why they are considered virtual. For the method to work, we only need to assume their behavior on the element boundary. For linearly precise VEM approximations, the basis functions on the element boundary are assumed to be
-
piecewise linear (edge by edge),
-
continuous on the element edges,
which means that the basis functions possess the Kronecker-delta property on the element edges, and hence they behave like the one-dimensional hat function.
At the element level, the following discrete local spaces are defined:
The discrete local spaces are assembled to form the following discrete global spaces:
Using the preceding definitions, the discrete version of the weak form (1) reads: find such that
| (4) |
To obtain the discrete weak form for the VEM, we follow the standard VEM literature (see for instance, Ref. [61]). We first define a projection operator onto the space of polynomials of degree 1. To this end, let represent the space of polynomials of degree 1 over the element . The projection operator is defined as:
| (5) |
is then used to split the displacement approximation on the element, as follows:
| (6) |
where is the polynomial part of (of degree 1) and contains its remainder terms. The remainder terms can contain polynomials of order greater than 1 or even nonpolynomial terms. The actual form of the projection is obtained from the orthogonality condition: ,
| (7) |
which, at the element level, gives [22, 62, 63, 64]
| (8) |
where and are the components of the mean of the values that the position vector takes over the vertices of the element; i.e.,
| (9) |
where are the coordinates of node ; and are the components of the mean of the values that the displacement approximation takes over the vertices of the element; i.e.,
| (10) |
In other words, and represent the geometric center of the element and its associated displacement vector, respectively; the terms are components of the element average
| (11) |
and is the component of the element average
| (12) |
where is the skew-symmetric tensor that represents rotations.
2.2 Nodal averaging operator
The VEM as described above is prone to volumetric locking in the limit . Using the virtual element mesh and considering a typical nodal vertex , the NVEM that was proposed in Ref. [60] applies a nodal averaging operator to (13) that precludes volumetric locking without introducing additional degrees of freedom111The nodal averaging operator permits to integrate the weak form integrals directly at the nodes. This results in a total number of incompressiblity constraints equal to the number of nodes in the mesh. If this number divides the total number of displacement equations, two degrees of freedom every one constraint is obtained in two dimensions, which is the optimal ratio to perform well in incompressible and nearly incompressible settings [65].. This leads to a nodal version of (13), as follows: find such that
| (14) |
where the notations , and are introduced as the nodal counterparts of , and , respectively. The construction of the nodal averaging operator is described next.
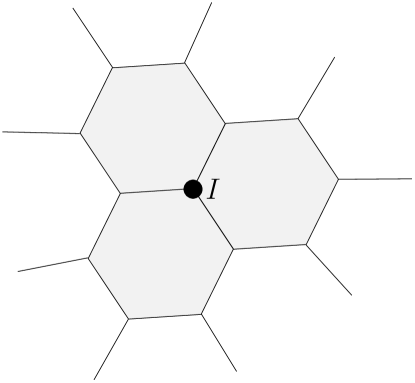
Each node of the mesh is associated with their own patch of virtual elements. The patch for node is denoted by and is defined as the set of virtual elements connected to node (see Fig. 2). Each node of a virtual element in the patch is assigned the area ; that is, the area of an element is uniformly distributed among its nodes. The representative area of node is denoted by and is computed by addition of all the areas that are assigned to node from the elements in ; that is,
| (15) |
Similarly, each node of a virtual element is uniformly assigned the strain . On considering each strain assigned to node from the elements in , the node-based uniform strain is defined as follows:
| (16) |
Since is by definition given at the element level, then from (16) the following nodal averaging operator is proposed:
| (17) |
where denotes evaluation over the element .
2.3 NVEM nodal stiffness matrix and nodal force vector
The NVEM nodal stiffness matrix is developed by substituting the discretizations (3), the projection operator (8) and the nodal averaging operator (17) into the left-hand side of (14) for a node . This gives
| (18) |
where and are column vectors of element nodal displacements and element nodal values associated with , respectively; is the NVEM nodal stiffness matrix given by
| (19) |
where is the constitutive matrix and is the stability matrix both defined in Section 3; and , where is the identity matrix, and and are defined as
| (20) |
where and can be exactly computed on the element boundary using a trapezoidal rule giving the following algebraic expression:
| (21) |
where is the -th component of and is the length of the edge incident to node as defined in Fig. 1;
| (22) |
where
| (23) |
| (24) |
and
| (25) |
Similarly, the NVEM nodal force vector is developed using the right-hand side of (14) for a node , which leads to
| (26) |
where is the column vector of element nodal values associated with , and is the NVEM nodal force vector associated with the body force and external tractions defined as
| (27) |
Regarding the nodal traction force vector in (27), the nodal components are now computed with respect to the one-dimensional domain on the Neumann boundary; that is, the representative nodal area reduces to a representative nodal length , where is an element’s edge located on the Neumann boundary and its length; now represents the set of edges connected to node on the Neumann boundary. Using the preceding definitions, the nodal averaging operator on the Neumann boundary is defined as
| (30) |
where denotes evaluation over the edge . The remainder nodal matrices are then obtained as and , where
| (31) |
and
| (32) |
2.4 NVEM equilibrium equations for elastoplasticity
For linear elastostatics as developed in Ref. [60], the discrete equilibrium equation is obtained by the discretization of (14). This is accomplished by summing (18) and (26) through all the nodes in the domain and invoking the arbitrariness of . This results in the following system of equations:
| (33) |
Eq. (33) is also the discrete equilibrium equation for elastoplasticity when and are nonlinear functions obtained from the elastoplastic constitutive law. As usual, the solution for this problem requires the linearization of (33). Doing this gives
| (34) |
where , , and , which are given in Section 3, are the elastoplastic consistent tangent operator, the stability matrix, and the nonlinear stress, respectively, evaluated at node (by means of the elastoplastic constitutive law) using the node-based uniform strain .
The linearized equilibrium equation (34) is used to solve the equilibrium state at time with a time increment via Newton-Raphson iterations, as follows:
| (35) |
where
| (36) |
3 Elastoplastic constitutive model and stabilization
Within the standard VEM framework, stabilization is one of the key ingredients for convergence of the method. However, in nodal integration, stabilization can make the formulation somewhat stiff in incompressible settings [8]. Therefore, the stabilization in any nodal integration scheme, which includes the NVEM, must be cautiously chosen to not jeopardize its locking-free essence. To deal with this issue, we propose a D-recipe stabilization [66, 67] that uses only a deviatoric term. Firstly, a summary of the constitutive model considered for the elastoplastic solid is given and, secondly, the stabilization for the NVEM is detailed.
3.1 Constitutive model
The strain tensor is split into elastic () and plastic () parts; that is,
| (37) |
The elastic part is governed by the standard linear elastic law, and the plastic part by the von Mises model with mixed linear hardening (for details on this model, see for instance Ref. [68]). The yield function for this model is
| (38) |
where is the backstress tensor, is a function of the accumulated plastic strain and defines the radius of the yield surface, and is the relative stress given by
| (39) |
where is the deviatoric stress. The plastic flow is described by the following associative law:
| (40) |
where is the rate of the plastic strain tensor and is the plastic multiplier.
The mixed linear hardening combines linear isotropic and linear kinematic hardening models. The linear isotropic hardening model is defined by the linear function
| (41) |
where is the initial yield stress and is the linear isotropic hardening modulus. The linear kinematic hardening model describes the evolution law for the backstress as the following linear function:
| (42) |
where is the linear kinematic hardening modulus.
Let and be the subindices that denote the previous and current states, respectively. These subindices are used for labeling the time at which the variables that are involved in the constitutive law are evaluated. Using the preceding notation, the elastoplastic consistent tangent operator (in Voigt notation) for the above model is
| (43) |
where and are the shear modulus and bulk modulus of the material, respectively. Here, we use the three-dimensional constitutive law from where the plain strain state components are extracted. The remainder quantities that appear in (43) are defined as follows:
| (44) |
| (45) |
| (46) |
| (47) |
The strain/stress update is performed as follows:
| (48) |
As previously mentioned in Section 2.4, in the NVEM the constitutive law is evaluated using the nodal strain ; that is, in (36), and .
The above computations of the elastoplastic consistent tangent operator and strain/stress update are part of the implicit elastic predictor/return mapping algorithm for numerical integration of the von Mises model with mixed linear hardening [68]. This algorithm is summarized in Algorithm 1.
3.2 Stabilization
As mentioned before, some precautions must be taken to stabilize the NVEM so that the locking-free behavior of the nodal integration scheme is preserved. Thus, drawing inspiration from one of the possibilities already explored in Ref. [60], the stabilization issue in the NVEM for elastoplastic solids is dealt with a diagonal stability matrix that uses only a deviatoric term, as follows:
| (49) |
where is the deviatoric part of the elastic moduli and is given by
| (50) |
This choice performs very well in a variety of two-dimensional numerical tests and does not introduce any tuning parameter.
4 Numerical examples
In this section, some benchmark tests are conducted to demonstrate the performance of the NVEM in elastoplastic solids simulations. The method is compared with the well-known locking-free 9-node B-bar quadrilateral finite element [3] (FEM Q9 B-bar) as well as with the standard linearly precise virtual element (VEM) and in some cases with the standard 4-node quadrilateral finite element (FEM Q4). All the tests are conducted using the constitutive model described in Section 3.1. Throughout this section, DOF stands for degree(s) of freedom, is the Young’s modulus, is the Poisson’s ratio, is the initial yield stress, and and are the linear isotropic hardening modulus and the linear kinematic hardening modulus, respectively.
4.1 Thick-walled cylinder
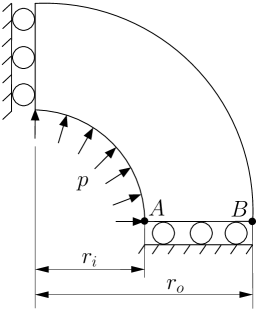
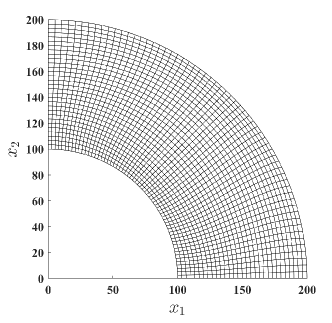
In this test, the ability of the NVEM for solving compressible and nearly incompressible elastoplastic problems is demonstrated. The problem consists of a plane strain (unit thickness) representation of a thick-walled cylinder under internal pressure. The geometry, boundary conditions, and mesh used in this numerical test are shown in Fig. 3, where the internal pressure is MPa, and the internal and external radii are mm and mm, respectively. The material parameters used are the following: MPa, for the compressible case and for the nearly incompressible case, MPa, MPa (perfect plasticity).
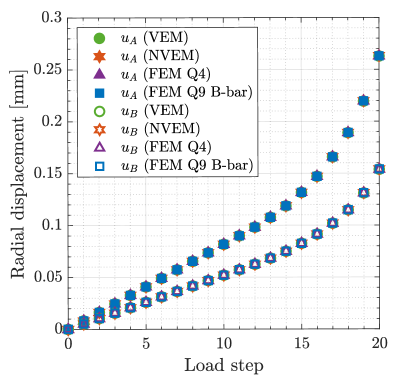
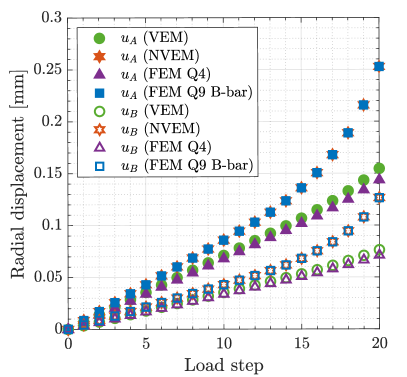
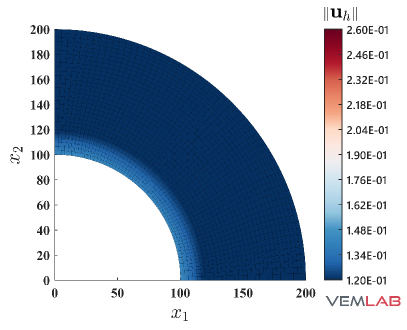
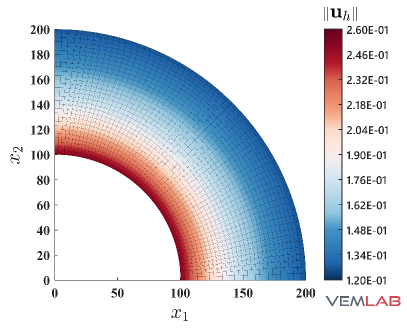
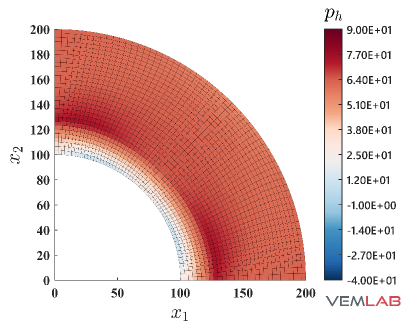
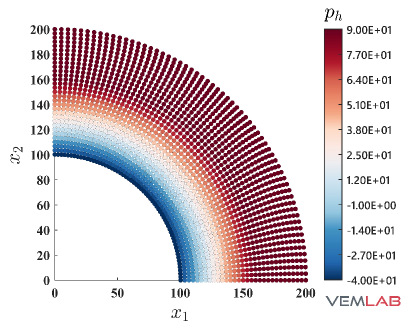
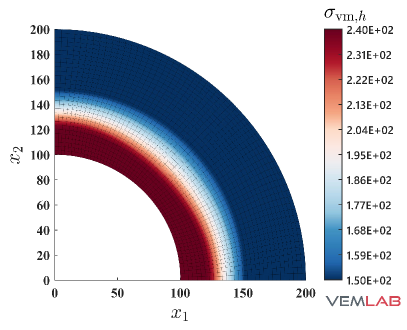
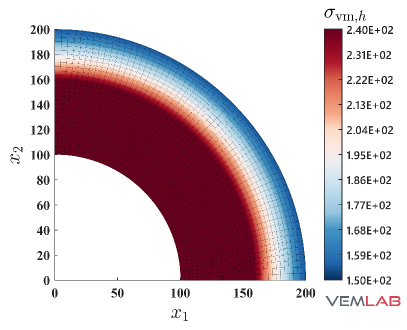
The radial displacement at points and for the compressible and nearly incompressible cases is summarized in Fig. 4 for all the methods. For the compressible case, all the methods match very well (Fig. 4). On the other hand, for the nearly incompressible case (Fig. 4), the NVEM and FEM Q9 B-bar methods still match very well, whereas the VEM and FEM Q4 clearly exhibit a locking behavior since radial displacements are smaller than expected. The same behaviors are observed in the total displacement (Fig. 5), pressure (Fig. 6), and von Mises stress (Fig. 7) field solutions at the last load step for the nearly incompressible case.
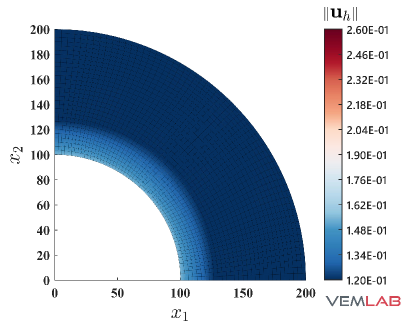
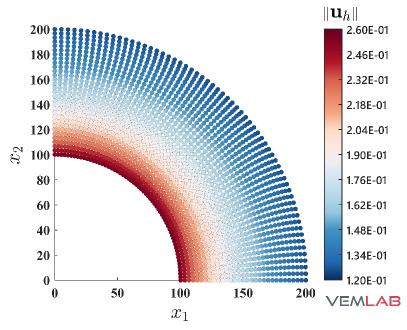
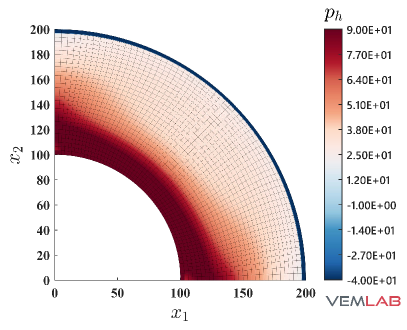
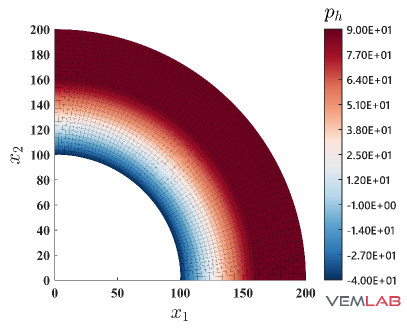
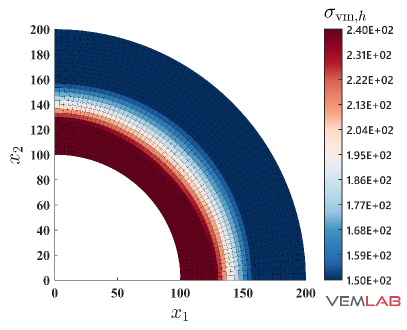
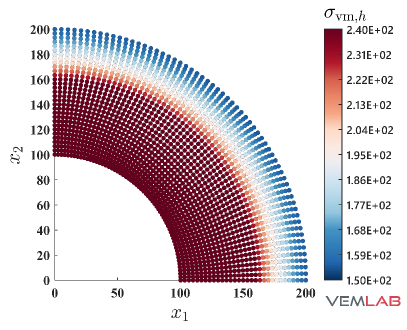
4.2 Cook’s membrane
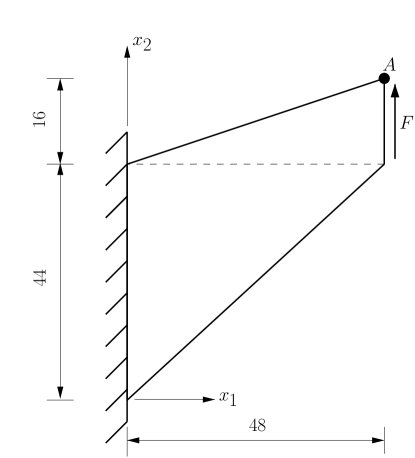
The next example consists of a tapered beam fixed along one end and loaded with a shear force at the other end. It is designed to study the performance of numerical formulations under combined bending and shear when the solid material behaves nearly incompressible. The geometry and boundary conditions are depicted in Fig. 8, where the shear load is N/mm (total shear load of N). The beam has a unit thickness and plane strain condition is assumed. The following material parameters are used: MPa, , MPa, MPa, and MPa. In this test, the performance of the NVEM is compared with the VEM and the FEM Q9 B-bar. Sample meshes used in this test are shown in Fig. 9.
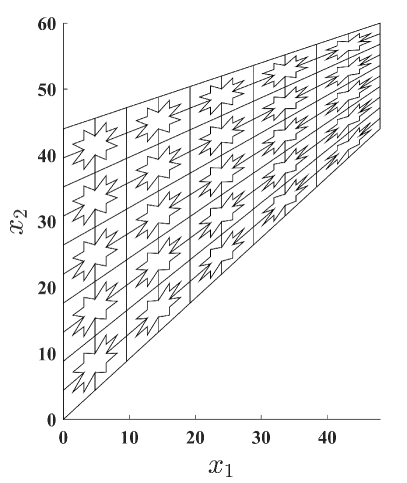
The convergence of the vertical displacement at the tip of the beam (point in Fig. 8) upon mesh refinement is depicted in Fig. 10. As expected, the VEM solution exhibits a severe locking behavior, whereas the NVEM and FEM Q9 B-bar are locking-free and their solutions are in good agreement upon mesh refinement.
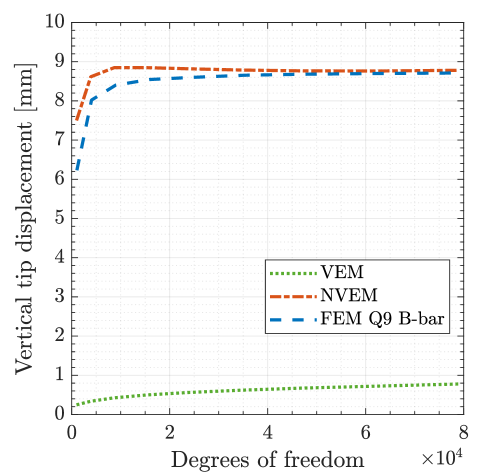
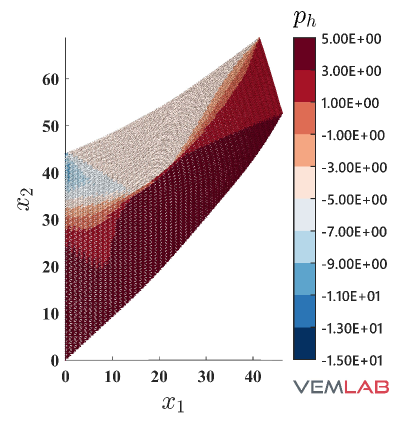
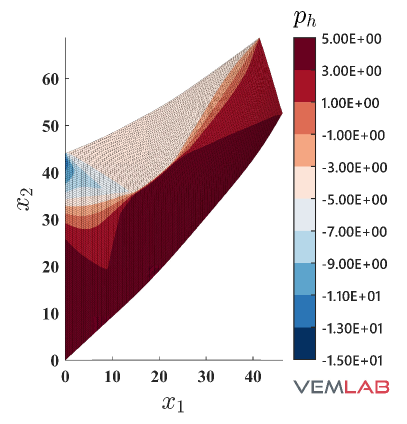
Fig. 11 depicts the pressure field and the von Mises stress field solutions on the most refined mesh for the NVEM and FEM Q9 B-bar approaches. The NVEM plots do not look as smooth as the FEM plots because of the particular shape of the polygonal element used to construct the mesh for the NVEM case (see Fig. 9). Despite this, the solutions are in good agreement.
4.3 Tension problem
In this example, the performance of the NVEM is studied on a pure tension problem. The domain consists of a square of dimensions 100 100 mm2 and unit thickness. Plane strain condition is specified and the following material parameters are used: MPa, , MPa, MPa (perfect plasticity). On the top edge of the domain, a vertical displacement of 0.5 mm is imposed while its lateral movement is restrained. The bottom surface of the domain is fixed. Fig. 12 summarizes the problem definition and presents the mesh used in the analysis.

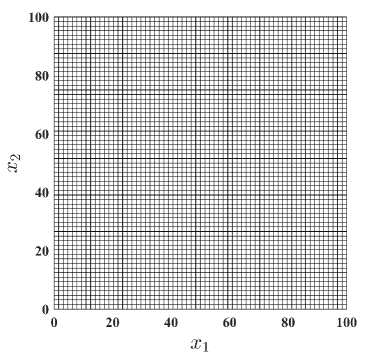
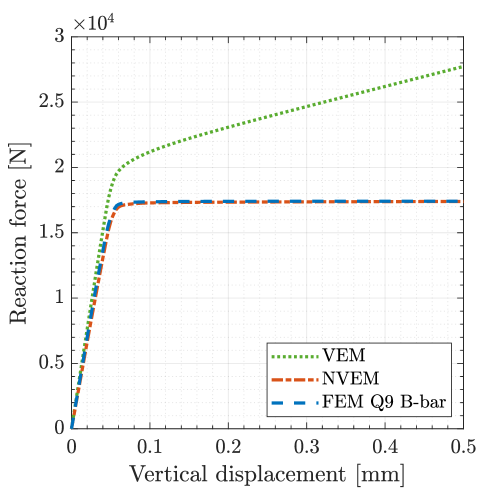
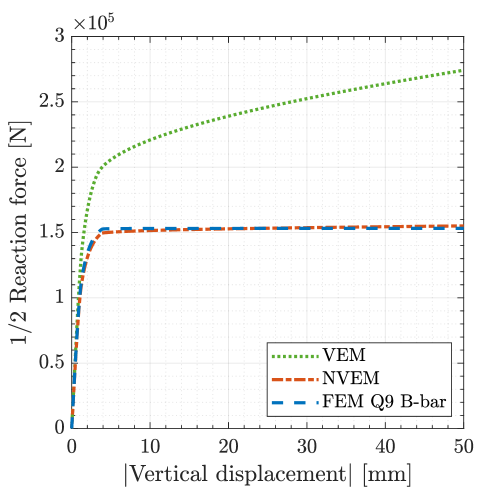
Fig. 13 presents the load-displacement curve, where a coincident limit load is observed for the NVEM and FEM Q9 B-bar approaches. On the other hand, the load-displacement curve for the VEM shows a locking effect both in the elastic and plastic regimes.
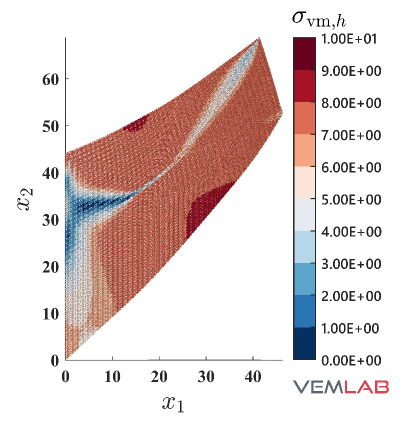
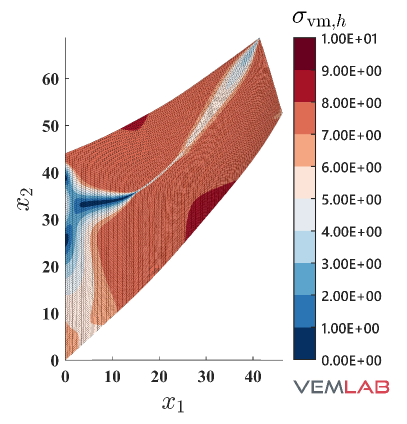
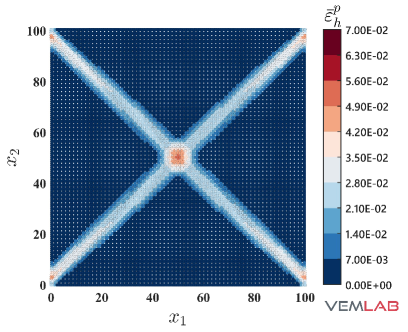
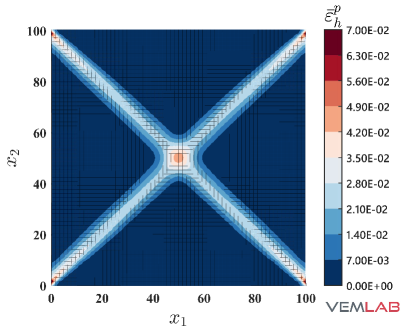
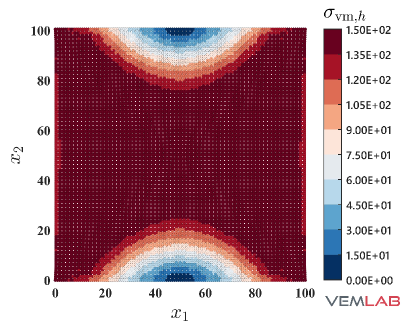
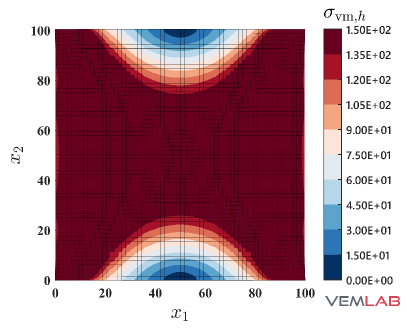
The solutions for the accumulated plastic strain and the von Mises stress are presented in Fig. 14, where once again good agreement is observed between the NVEM and FEM Q9 B-bar methods.
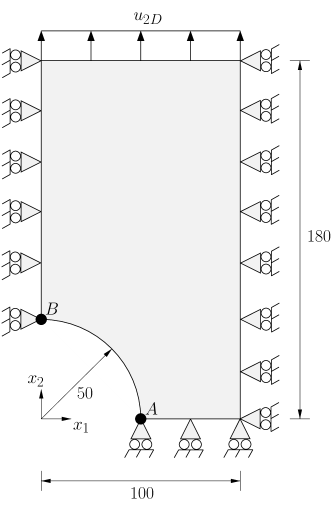
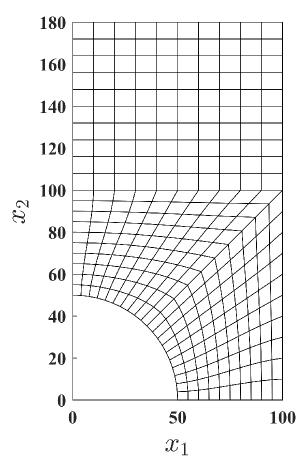
4.4 Perforated plate
In this benchmark problem, a quarter of a perforated plate is considered. The geometry, boundary conditions, and sample mesh are depicted in Fig. 15. The plate has unit thickness and plane strain condition is assumed. The material parameters are set to MPa, , MPa, MPa (perfect plasticity). A vertical displacement mm is applied on the top edge of the plate. On the left, right, and bottom edges of the plate, the translation is restrained in the normal direction to these edges. Therefore, the plate is highly constrained and thus a locking effect is expected for the standard linearly precise VEM. In fact, this is confirmed in the response curve shown in Fig. 16, where the expected limit load is achieved only by the NVEM and the FEM Q9 B-bar in the plastic regime. A pictorial of the accumulated plastic strain and the von Mises stress for the most refined mesh is shown in Fig. 17, where it is observed that the NVEM and FEM Q9 B-bar solutions look very similar.
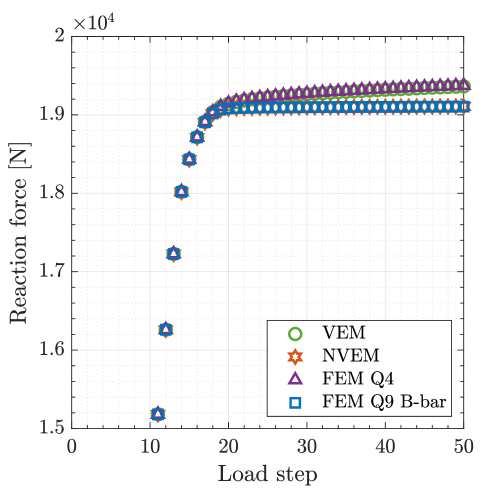
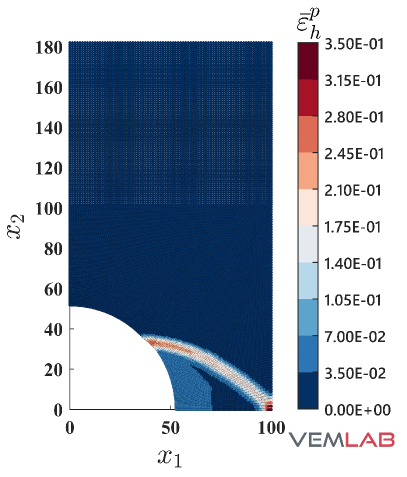
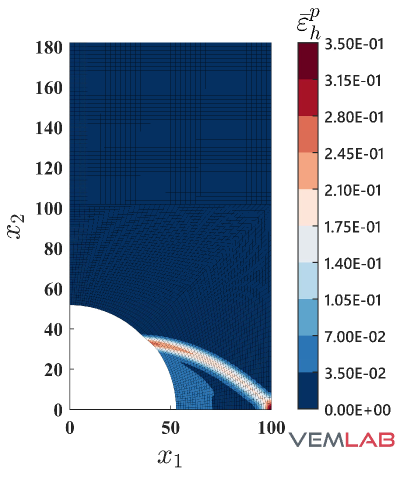
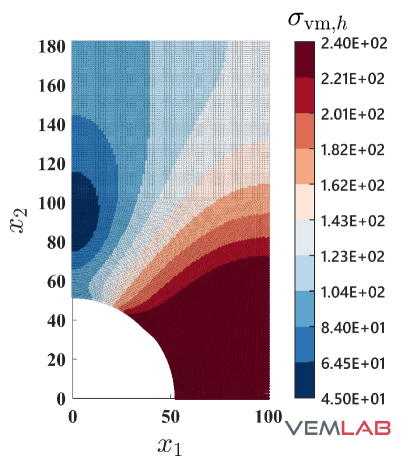
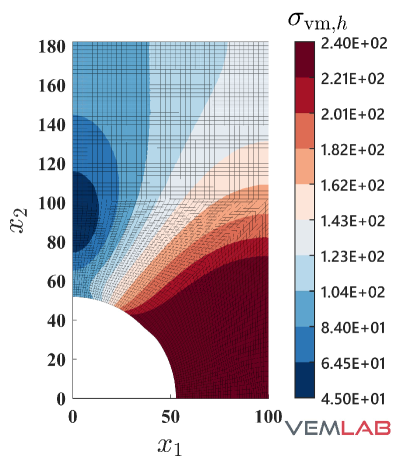
A comparison of the horizontal displacement at point and the vertical displacement at point among the different methods is presented in Table 4.4, where a perfect match to three decimal places is obtained for the NVEM and FEM Q9 B-bar methods.
Displacement comparison for the perforated plate problem Method [mm] [mm] VEM 2.716 1.850 NVEM 2.745 1.855 FEM Q4 2.714 1.849 FEM Q9 B-bar 2.745 1.855
4.5 Prandtl’s punch test
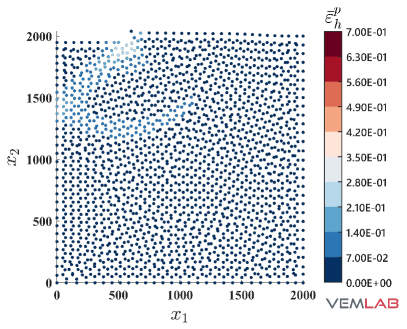
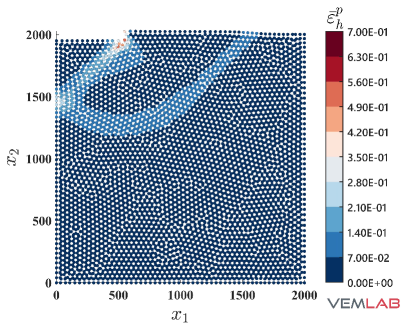
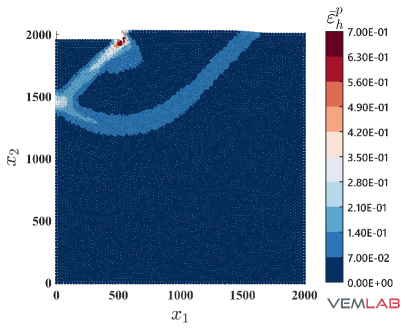
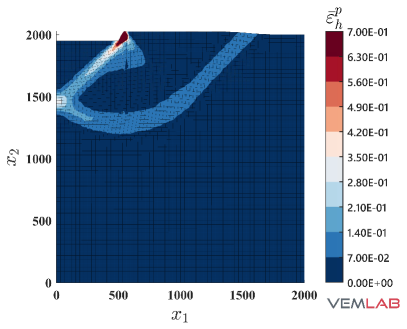
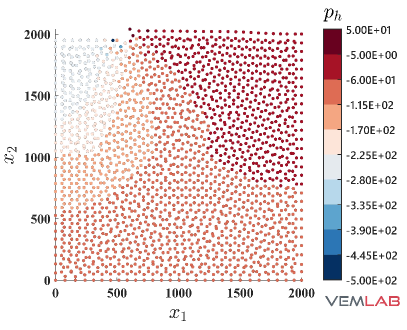
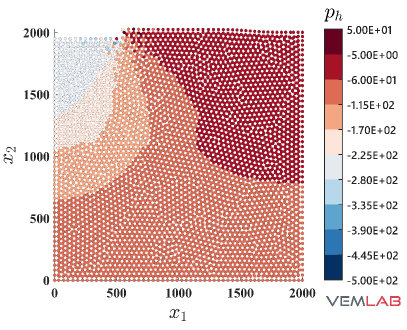
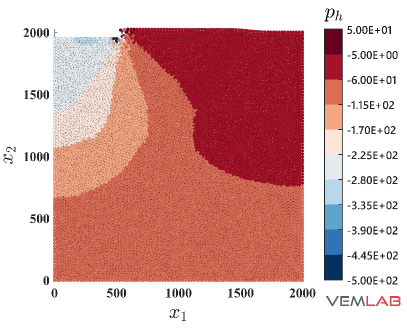
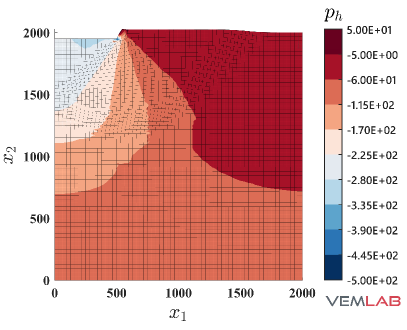
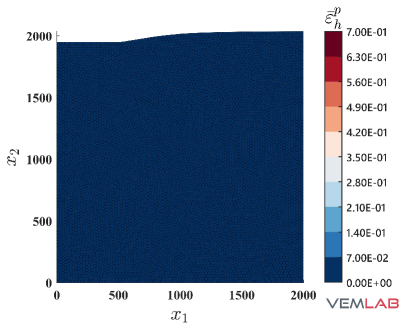
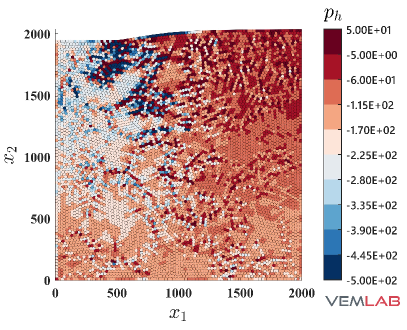
The last benchmark problem is devoted to demonstrate the performance of the NVEM in a highly constrained compression problem. The Prandtl’s punch test [69] is selected for this purpose. The geometry and boundary conditions are shown in Fig. 18, where the punch surface located on the top is horizontally restrained (rough punch) while a downward vertical displacement mm is imposed on it. The dimensions are defined using mm. Because of the symmetry, only half of the domain is considered for discretization. Three polygonal meshes with increasing refinements are considered for the VEM and NVEM (Fig. 19(a)–(c)). The most refined VEM/NVEM mesh (Fig. 19) and the mesh for the FEM Q9 B-bar (Fig. 19) have similar number of DOF. Unit thickness is considered and plane strain condition is assumed with material parameters set to MPa, , MPa, MPa (perfect plasticity). As observed in Fig. 20, a severe locking behavior is obtained for the standard linearly precise VEM in this highly constrained problem. On the other hand, the same figure reports the nearly coincident limit load that is obtained for the NVEM and FEM Q9 B-bar approaches. The accumulated plastic strain is reported on Fig. 21, where similar results are obtained for the NVEM and FEM Q9 B-bar on the meshes with similar number of DOF (Fig. 21 and Fig. 21, respectively). The pressure field is depicted in Fig. 22, where the NVEM and FEM Q9 B-bar solutions look very similar and smooth on the meshes with similar number of DOF (Fig. 22 and Fig. 22, respectively). Just for completeness, the accumulated plastic strain and the pressure field solutions for the linearly precise VEM are shown in Fig. 23, where the severe locking behavior is clearly observed in the oscillations of the pressure field.

5 Summary and conclusions
The node-based uniform strain virtual element method (NVEM) that was recently proposed for compressible and nearly incompressible elasticity [60] has been extended to elastoplastic solids at small strains. In the proposed method, the strain is averaged at the nodes from the strain of surrounding linearly precise virtual elements using a generalization to virtual elements of the node-based uniform strain approach for finite elements [6]. The averaged strain is then used to sample the weak form at the nodes of the mesh leading to a method in which all the field variables, including state and history-dependent variables, are related to the nodes. Consequently, in the nonlinear computations these variables are tracked only at the nodal locations.
Various elastoplastic benchmark problems were conducted to assess the performance of the NVEM. These included a thick-walled cylinder under internal pressure, a combined bending and shear problem (Cook’s membrane), a pure tension problem, a perforated plate subjected to a displacement producing tension, and a highly constrained problem in compression (Prandtl’s punch test). The comparisons with the well-known locking-free 9-node B-bar quadrilateral finite element [3] revealed that the NVEM effectively enables linearly precise virtual elements to solve elastoplastic solids with accuracy and is locking-free. For perfect plasticity, these comparisons also demonstrated that the NVEM is able to capture the expected limit load. Finally, we mention that the present work completes our short term scope for the NVEM development and that its extension to large deformations with remeshing is an undergoing work.
Acknowledgements
This work was performed under the auspices of the Chilean National Fund for Scientific and Technological Development (FONDECYT) through grant ANID FONDECYT No. 1221325 (R.S-V and A.O-B).
References
- \bibcommenthead
- Malkus and Hughes [1978] Malkus, D.S., Hughes, T.J.R.: Mixed finite element methods – reduced and selective integration techniques: a unification of concepts. Computer Methods in Applied Mechanics and Engineering 15(1), 63–81 (1978)
- Hughes [1980] Hughes, T.J.R.: Generalization of selective integration procedures to anisotropic and non-linear media. International Journal for Numerical Methods in Engineering 15(9), 1413–1418 (1980)
- Simo and Hughes [1998] Simo, J.C., Hughes, T.J.R.: Computational Inelasticity. Springer, USA (1998)
- Simo and Rifai [1990] Simo, J.C., Rifai, S.: A class of mixed assumed strain methods and the method of incompatible modes. International Journal for Numerical Methods in Engineering 29(8), 1595–1638 (1990)
- Bonet and Burton [1998] Bonet, J., Burton, A.J.: A simple average nodal pressure tetrahedral element for incompressible and nearly incompressible dynamic explicit applications. Communications in Numerical Methods in Engineering 14(5), 437–449 (1998)
- Dohrmann et al. [2000] Dohrmann, C.R., Heinstein, M.W., Jung, J., Key, S.W., Witkowski, W.R.: Node-based uniform strain elements for three-node triangular and four-node tetrahedral meshes. International Journal for Numerical Methods in Engineering 47(9), 1549–1568 (2000)
- Bonet et al. [2001] Bonet, J., Marriott, H., Hassan, O.: An averaged nodal deformation gradient linear tetrahedral element for large strain explicit dynamic applications. Communications in Numerical Methods in Engineering 17(8), 551–561 (2001)
- Puso and Solberg [2006] Puso, M.A., Solberg, J.: A stabilized nodally integrated tetrahedral. International Journal for Numerical Methods in Engineering 67(6), 841–867 (2006)
- Puso et al. [2008] Puso, M.A., Chen, J.-S., Zywicz, E., Elmer, W.: Meshfree and finite element nodal integration methods. International Journal for Numerical Methods in Engineering 74(3), 416–446 (2008)
- Krysl and Zhu [2008] Krysl, P., Zhu, B.: Locking-free continuum displacement finite elements with nodal integration. International Journal for Numerical Methods in Engineering 76(7), 1020–1043 (2008)
- Broccardo et al. [2009] Broccardo, M., Micheloni, M., Krysl, P.: Assumed-deformation gradient finite elements with nodal integration for nearly incompressible large deformation analysis. International Journal for Numerical Methods in Engineering 78(9), 1113–1134 (2009)
- Castellazzi and Krysl [2012] Castellazzi, G., Krysl, P.: Patch-averaged assumed strain finite elements for stress analysis. International Journal for Numerical Methods in Engineering 90(13), 1618–1635 (2012)
- Krysl and Kagey [2012] Krysl, P., Kagey, H.: Reformulation of nodally integrated continuum elements to attain insensitivity to distortion. International Journal for Numerical Methods in Engineering 90(7), 805–818 (2012)
- Artioli et al. [2014] Artioli, E., Castellazzi, G., Krysl, P.: Assumed strain nodally integrated hexahedral finite element formulation for elastoplastic applications. International Journal for Numerical Methods in Engineering 99(11), 844–866 (2014)
- Beirão da Veiga et al. [2013] Beirão da Veiga, L., Brezzi, F., Cangiani, A., Manzini, G., Marini, L.D., Russo, A.: Basic principles of virtual element methods. Mathematical Models and Methods in Applied Sciences 23(1), 199–214 (2013)
- Cangiani et al. [2015] Cangiani, A., Manzini, G., Russo, A., Sukumar, N.: Hourglass stabilization and the virtual element method. International Journal for Numerical Methods in Engineering 102(3–4), 404–436 (2015)
- Beirão da Veiga et al. [2013] Beirão da Veiga, L., Brezzi, F., Marini, L.D.: Virtual elements for linear elasticity problems. SIAM Journal on Numerical Analysis 51(2), 794–812 (2013)
- Beirão da Veiga et al. [2015] Beirão da Veiga, L., Lovadina, C., Mora, D.: A Virtual Element Method for elastic and inelastic problems on polytope meshes. Computer Methods in Applied Mechanics and Engineering 295, 327–346 (2015)
- Artioli et al. [2017a] Artioli, E., Beirão da Veiga, L., Lovadina, C., Sacco, E.: Arbitrary order 2D virtual elements for polygonal meshes: part I, elastic problem. Computational Mechanics 60(3), 355–377 (2017)
- Artioli et al. [2017b] Artioli, E., Beirão da Veiga, L., Lovadina, C., Sacco, E.: Arbitrary order 2D virtual elements for polygonal meshes: part II, inelastic problem. Computational Mechanics 60(4), 643–657 (2017)
- Park et al. [2021] Park, K., Chi, H., Paulino, G.H.: B-bar virtual element method for nearly incompressible and compressible materials. Meccanica 56(6), 1423–1439 (2021)
- Gain et al. [2014] Gain, A.L., Talischi, C., Paulino, G.H.: On the virtual element method for three-dimensional linear elasticity problems on arbitrary polyhedral meshes. Computer Methods in Applied Mechanics and Engineering 282, 132–160 (2014)
- D’Altri et al. [2021] D’Altri, A.M., de Miranda, S., Patruno, L., Sacco, E.: An enhanced vem formulation for plane elasticity. Computer Methods in Applied Mechanics and Engineering 376, 113663 (2021)
- Tang et al. [2020] Tang, X., Liu, Z., Zhang, B., Feng, M.: A low-order locking-free virtual element for linear elasticity problems. Computers & Mathematics with Applications 80(5), 1260–1274 (2020)
- Cihan et al. [2021] Cihan, M., Hudobivnik, B., Aldakheel, F., Wriggers, P.: 3D mixed virtual element formulation for dynamic elasto-plastic analysis. Computational Mechanics 68(3), 1–18 (2021)
- Park et al. [2020] Park, K., Chi, H., Paulino, G.H.: Numerical recipes for elastodynamic virtual element methods with explicit time integration. International Journal for Numerical Methods in Engineering 121(1), 1–31 (2020)
- Park et al. [2019] Park, K., Chi, H., Paulino, G.H.: On nonconvex meshes for elastodynamics using virtual element methods with explicit time integration. Computer Methods in Applied Mechanics and Engineering 356, 669–684 (2019)
- Wriggers and Rust [2019] Wriggers, P., Rust, W.T.: A virtual element method for frictional contact including large deformations. Engineering Computations 36(7), 2133–2161 (2019)
- De Bellis et al. [2019] De Bellis, M.L., Wriggers, P., Hudobivnik, B.: Serendipity virtual element formulation for nonlinear elasticity. Computers & Structures 223, 106094 (2019)
- Aldakheel et al. [2019] Aldakheel, F., Hudobivnik, B., Wriggers, P.: Virtual elements for finite thermo-plasticity problems. Computational Mechanics 64(5), 1347–1360 (2019)
- Wriggers and Hudobivnik [2017] Wriggers, P., Hudobivnik, B.: A low order virtual element formulation for finite elasto-plastic deformations. Computer Methods in Applied Mechanics and Engineering 327, 459–477 (2017)
- Wriggers et al. [2017] Wriggers, P., Reddy, B.D., Rust, W., Hudobivnik, B.: Efficient virtual element formulations for compressible and incompressible finite deformations. Computational Mechanics 60(2), 253–268 (2017)
- Hudobivnik et al. [2019] Hudobivnik, B., Aldakheel, F., Wriggers, P.: A low order 3D virtual element formulation for finite elasto–plastic deformations. Computational Mechanics 63(2), 253–269 (2019)
- Zhang et al. [2020] Zhang, X.S., Chi, H., Paulino, G.H.: Adaptive multi-material topology optimization with hyperelastic materials under large deformations: A virtual element approach. Computer Methods in Applied Mechanics and Engineering 370, 112976 (2020)
- Chi et al. [2017] Chi, H., Beirão da Veiga, L., Paulino, G.H.: Some basic formulations of the virtual element method (VEM) for finite deformations. Computer Methods in Applied Mechanics and Engineering 318, 148–192 (2017)
- van Huyssteen and Reddy [2020] van Huyssteen, D., Reddy, B.D.: A virtual element method for isotropic hyperelasticity. Computer Methods in Applied Mechanics and Engineering 367, 113134 (2020)
- Wriggers et al. [2016] Wriggers, P., Rust, W.T., Reddy, B.D.: A virtual element method for contact. Computational Mechanics 58(6), 1039–1050 (2016)
- Aldakheel et al. [2020] Aldakheel, F., Hudobivnik, B., Artioli, E., Beirão da Veiga, L., Wriggers, P.: Curvilinear virtual elements for contact mechanics. Computer Methods in Applied Mechanics and Engineering 372, 113394 (2020)
- Aldakheel et al. [2019] Aldakheel, F., Hudobivnik, B., Wriggers, P.: Virtual element formulation for phase-field modeling of ductile fracture. International Journal for Multiscale Computational Engineering 17(2), 181–200 (2019)
- Hussein et al. [2019] Hussein, A., Aldakheel, F., Hudobivnik, B., Wriggers, P., Guidault, P.-A., Allix, O.: A computational framework for brittle crack-propagation based on efficient virtual element method. Finite Elements in Analysis and Design 159, 15–32 (2019)
- Nguyen-Thanh et al. [2018] Nguyen-Thanh, V.M., Zhuang, X., Nguyen-Xuan, H., Rabczuk, T., Wriggers, P.: A Virtual Element Method for 2d linear elastic fracture analysis. Computer Methods in Applied Mechanics and Engineering 340, 366–395 (2018)
- Benedetto et al. [2018] Benedetto, M.F., Caggiano, A., Etse, G.: Virtual elements and zero thickness interface-based approach for fracture analysis of heterogeneous materials. Computer Methods in Applied Mechanics and Engineering 338, 41–67 (2018)
- Artioli et al. [2020] Artioli, E., Marfia, S., Sacco, E.: VEM-based tracking algorithm for cohesive/frictional 2d fracture. Computer Methods in Applied Mechanics and Engineering 365, 112956 (2020)
- Beirão da Veiga et al. [2021] Beirão da Veiga, L., Pichler, A., Vacca, G.: A virtual element method for the miscible displacement of incompressible fluids in porous media. Computer Methods in Applied Mechanics and Engineering 375, 113649 (2021)
- Chen and Wang [2019] Chen, L., Wang, F.: A Divergence Free Weak Virtual Element Method for the Stokes Problem on Polytopal Meshes. Journal of Scientific Computing 78(2), 864–886 (2019)
- Gatica et al. [2018] Gatica, G.N., Munar, M., Sequeira, F.A.: A mixed virtual element method for the Navier–Stokes equations. Mathematical Models and Methods in Applied Sciences 28(14), 2719–2762 (2018)
- Beirão da Veiga et al. [2018] Beirão da Veiga, L., Lovadina, C., Vacca, G.: Virtual elements for the Navier–Stokes problem on polygonal meshes. SIAM Journal on Numerical Analysis 56(3), 1210–1242 (2018)
- Chernov et al. [2021] Chernov, A., Marcati, C., Mascotto, L.: p- and hp- virtual elements for the Stokes problem. Advances in Computational Mathematics 47(2), 24 (2021)
- Andersen et al. [2017] Andersen, O., Nilsen, H.M., Raynaud, X.: Virtual element method for geomechanical simulations of reservoir models. Computational Geosciences 21(5), 877–893 (2017)
- Lin et al. [2020] Lin, S., Zheng, H., Jiang, W., Li, W., Sun, G.: Investigation of the excavation of stony soil slopes using the virtual element method. Engineering Analysis with Boundary Elements 121, 76–90 (2020)
- Gain and Paulino [2015] Gain, A.L., Paulino, G.H.: Bridging art and engineering using Escher-based virtual elements. Structural and Multidisciplinary Optimization 51, 867–883 (2015)
- Chi et al. [2020] Chi, H., Pereira, A., Menezes, I.F.M., Paulino, G.H.: Virtual element method (VEM)-based topology optimization: an integrated framework. Structural and Multidisciplinary Optimization 62(3), 1089–1114 (2020)
- Artioli et al. [2017] Artioli, E., Miranda, S., Lovadina, C., Patruno, L.: A stress/displacement virtual element method for plane elasticity problems. Computer Methods in Applied Mechanics and Engineering 325, 155–174 (2017)
- Dassi et al. [2021] Dassi, F., Lovadina, C., Visinoni, M.: Hybridization of the virtual element method for linear elasticity problems. Mathematical Models and Methods in Applied Sciences 31(14), 2979–3008 (2021)
- Kwak and Park [2022] Kwak, D.Y., Park, H.: Lowest-order virtual element methods for linear elasticity problems. Computer Methods in Applied Mechanics and Engineering 390, 114448 (2022)
- Zhang et al. [2019] Zhang, B., Zhao, J., Yang, Y., Chen, S.: The nonconforming virtual element method for elasticity problems. Journal of Computational Physics 378, 394–410 (2019)
- Yu [2023] Yu, Y.: A lowest-order locking-free nonconforming virtual element method based on the reduced integration technique for linear elasticity problems. Computers & Mathematics with Applications 135, 157–170 (2023)
- Xu et al. [2024] Xu, B.-B., Wang, Y.-F., Wriggers, P.: Stabilization-free virtual element method for 2D elastoplastic problems. International Journal for Numerical Methods in Engineering 125(15), 22 (2024)
- Liguori et al. [2024] Liguori, F.S., Madeo, A., Marfia, S., Garcea, G., Sacco, E.: A stabilization-free hybrid virtual element formulation for the accurate analysis of 2D elasto-plastic problems. Computer Methods in Applied Mechanics and Engineering 431, 117281 (2024)
- Ortiz-Bernardin et al. [2023] Ortiz-Bernardin, A., Silva-Valenzuela, R., Salinas-Fernández, S., Hitschfeld-Kahler, N., Luza, S., Rebolledo, B.: A node-based uniform strain virtual element method for compressible and nearly incompressible elasticity. International Journal for Numerical Methods in Engineering 124(8), 1818–1855 (2023)
- Beirão da Veiga et al. [2014] Beirão da Veiga, L., Brezzi, F., Marini, L.D., Russo, A.: The hitchhiker’s guide to the virtual element method. Mathematical Models and Methods in Applied Sciences 24(08), 1541–1573 (2014)
- Ortiz-Bernardin et al. [2017] Ortiz-Bernardin, A., Russo, A., Sukumar, N.: Consistent and stable meshfree Galerkin methods using the virtual element decomposition. International Journal for Numerical Methods in Engineering 112(7), 655–684 (2017)
- Ortiz-Bernardin et al. [2019] Ortiz-Bernardin, A., Alvarez, C., Hitschfeld-Kahler, N., Russo, A., Silva-Valenzuela, R., Olate-Sanzana, E.: Veamy: an extensible object-oriented C++ library for the virtual element method. Numerical Algorithms 82(4), 1189–1220 (2019)
- Silva-Valenzuela et al. [2020] Silva-Valenzuela, R., Ortiz-Bernardin, A., Sukumar, N., Artioli, E., Hitschfeld-Kahler, N.: A nodal integration scheme for meshfree galerkin methods using the virtual element decomposition. International Journal for Numerical Methods in Engineering 121(10), 2174–2205 (2020)
- Hughes [2000] Hughes, T.J.R.: The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Dover Publications, Inc, Mineola, NY (2000)
- Beirão da Veiga et al. [2017] Beirão da Veiga, L., Dassi, F., Russo, A.: High-order virtual element method on polyhedral meshes. Computers & Mathematics with Applications 74(5), 1110–1122 (2017)
- Mascotto [2018] Mascotto, L.: Ill-conditioning in the virtual element method: Stabilizations and bases. Numerical Methods for Partial Differential Equations 34(4), 1258–1281 (2018)
- de Souza Neto et al. [2008] Souza Neto, E.A., Perić, D., Owen, D.R.J.: Computational Methods for Plasticity: Theory and Applications. John Wiley & Sons Ltd, UK (2008)
- Tan et al. [1989] Tan, T.-M., Li, S., Chou, P.C.: Finite element solution of Prandtl’s flat punch problem. Finite Elements in Analysis and Design 6(2), 173–186 (1989)