A no-go theorem for superpositions of causal orders

Quantum superpositions can be viewed as generalisations of classical probabilities: if classically we can be uncertain between two alternatives, assigning to each a probability, quantumly we should be able to consider a superposition of the two, replacing probabilities with complex amplitudes. Feynman’s sum-over-histories approach famously leverages this intuition [1]. Despite this view, one typically considers superpositions of states, whereas classical probabilities can be assigned to any logical statement. To what extent is it possible to generalise the superposition principle, beyond its original range of applicability? Providing a general, principled answer to this question appears problematic because, unlike classical probabilities, quantum superpositions have no clear interpretation in terms of subjective lack of knowledge.

Of particular interest is the case of causal relations. A main motivation comes from combining the principles of quantum theory and general relativity. In a regime where spacetime itself becomes subject to the laws of quantum mechanics, we expect that causal structure, too, will become nonclassical [2, 3, 4]. A second, more practical, motivation is that quantum causal structures can also be realised experimentally (on a classical spacetime background) [5, 6, 7, 8, 9, 10, 11, 12] possibly leading to an advantage in solving computational and information-theoretic tasks [13, 14, 15, 16, 17, 18, 19, 20, 21].

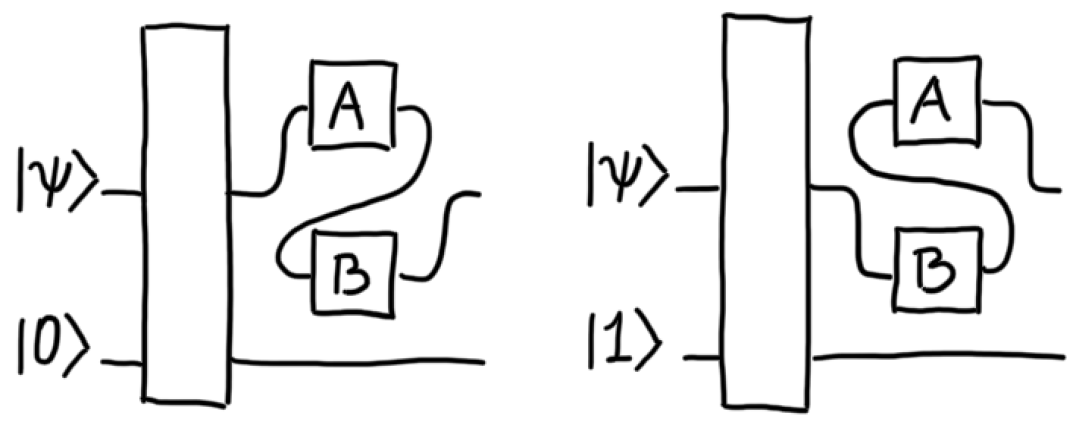
Despite much recent research, the scenarios considered so far do not support a direct interpretation as superpositions of causal orders. The most discussed example is the so-called “quantum switch” [13], Fig. 1, where a control system determines the order in which a set of operations act on a target. Preparing the control in a superposition produces a nonclassical causal structure for the order of operations. Although sometimes colloquially described as a “superposition of causal orders”, the quantum switch is in fact more appropriately interpreted as ‘entanglement’ between causal relations and the control system. Indeed, if the control is discarded, the quantum switch is indistinguishable from a probabilistic mixture of causal orders. Only by measuring the control can one verify the nonclassicality of the order of operations. Probabilistic protocols, where one obtains a superposition of orders through postselection, generally succeed with probability less than one, making them not commensurable with deterministic resources.

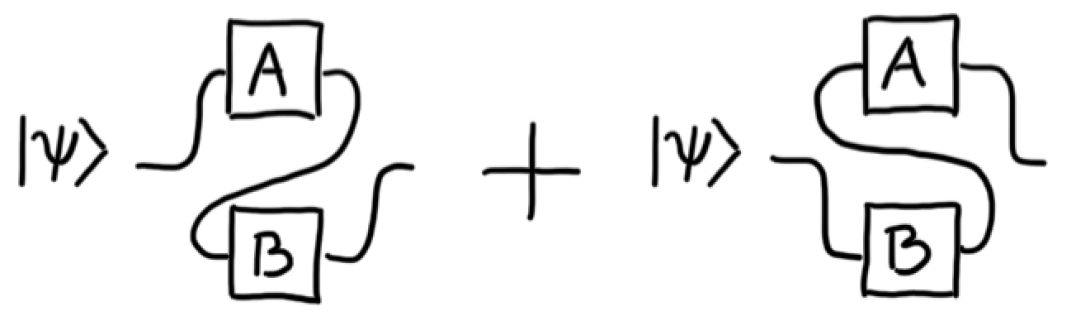
Is a ‘pure’, deterministic superposition of causal orders possible (Fig. 2), not relying on any additional control system? Perhaps, this would provide a novel resource, enabling tasks not achievable by the quantum switch. It might also suggest types of processes arising in a theory of quantum gravity.

Here, we propose a definition of superpositions of causal orders and present a negative result, ruling out the most natural candidates. We show that for unitary, Markovian processes where all systems have equal dimension superpositions of two different causal orders are not possible, in the sense that they do not constitute valid, deterministic processes. In particular, the result applies to simple sequences of operations on a target system—as in the switch—showing that an additional system is necessary for performing such operations in an indefinite causal order. It remains an open question whether a superposition is possible under weaker conditions.

Before considering superpositions of different causal orders, it is useful to look at a simpler case: superpositions of unitary transformations connecting an event in the past—a state preparation—to one in the future—a measurement. Given two unitaries $U_{j}$, $j=0,1$, it is natural to define their superposition as a linear combination $\alpha U_{0}+\beta U_{1}$ for some complex numbers $\alpha$, $\beta$, interpreted as probability amplitudes. However, such a ‘superposition’ is not necessarily a unitary operator. For example, no linear combination of $U_{0}=\mathds{1}$ and $U_{1}=\frac{\sigma_{x}+\mathrm{i}\sigma_{y}}{\sqrt{2}}$ (where $\sigma_{x}$, $\sigma_{y}$, $\sigma_{z}$ denote the Pauli matrices) is unitary, for any complex amplitudes $\alpha\neq 0$, $\beta\neq 0$.

One could interpret arbitrary linear combinations of unitaries in the following way [22]: Introduce the ‘controlled unitary’ $U_{0}\otimes\left[0\right]+U_{1}\otimes\left[1\right]$, which acts on an additional ‘control’ system and where we use the shorthand $\left[\psi\right]=\left|\psi\middle\rangle\middle\langle\psi\right|$. Starting from a state of the form $\left|\psi\right\rangle\left(\alpha\left|0\right\rangle+\beta\left|1\right\rangle\right)$, and postselecting the control on $\left(\left\langle 0\right|+\left\langle 1\right|\right)/\sqrt{2}$, the target system is left into $\left(\alpha U_{0}+\beta U_{1}\right)\left|\psi\right\rangle/\sqrt{2}$, which one can interpret as resulting from a superposition of unitaries. The problem with this interpretation is that the postselection step requires obtaining one out of a set of possible measurement outcomes, which in general only succeeds with some probability that depends on the initial state. As such a probability can be very small, or even vanish, realising a process through postselection can nullify the associated advantages. Furthermore, postselection can induce apparent signalling, making postselected processes unsuitable for studies of causal relations¹¹1For example, one can place bets on a roulette and consider only the winning spins, effectively predicting the roulette’s outcome in each of the postselected spins. This is unlikely to be a remunerative strategy in any casino.. For these reasons, here we are only interested in processes that can be realised without postselection.

We see that, for processes, superposition is not a universal possibility, as it is for states. However, there are unitaries for which superpositions are possible. For example, the Hadamard gate $H:=\frac{\sigma_{x}+\sigma_{z}}{\sqrt{2}}$ is a rightful superposition of $\sigma_{x}$ and $\sigma_{z}$, not requiring any postselection. $H$ is a ubiquitous resource in quantum information and computation, precisely for its ability to convert basis states into superpositions. Therefore, even if we do not expect to be able to superpose arbitrary processes with different causal orders, we can still ask whether any such a superposition is possible.

As we will see, superpositions of causal orders become meaningful for processes connecting more than two events. These can be described conveniently in the so-called “process matrix formalism” [23] (see also other closely related frameworks [24, 25, 26, 27, 28]). A simple example of a multi-event process is one where a sequence of unitaries $U_{1},U_{2},\dots$ connects a set of events at times $t_{1},t_{2},\dots$ At each time $t_{j}$, after unitary $U_{j-1}$ and before unitary $U_{j}$, it is in principle possible to perform arbitrary measurements or transformations on the system. The particular operation taking place at a given time is what we call an ‘event’, while the set of unitaries connecting the events is the ‘process’. More generally, we consider a scenario where the labels that identify possible events are not necessarily associated with time instants (for example, events might be delocalised in time [29, 30] or take place on a nonclassical background [4]). A single ‘event location’ with label $A$ (also referred to as “region”, “party”, or “laboratory”) is therefore identified with the set of possible operations from an input to an output Hilbert space, $\mathcal{H}^{A}_{I}$ and $\mathcal{H}^{A}_{O}$, respectively.

The most general operation [31] is described by a Completely Positive (CP) trace non-increasing map $\mathcal{M}^{A}:A_{I}\rightarrow A_{O}$, where $A_{I,O}\equiv\mathcal{L}(\mathcal{H}^{A}_{I,O})$ are the spaces of linear operators over the respective Hilbert spaces. A deterministic operation, i.e., one that happens with probability one, is CP and trace preserving (CPTP): $\operatorname{tr}\circ\mathcal{M}^{A}=\operatorname{tr}$, where $\operatorname{tr}$ and $\circ$ denote operator trace and function composition, respectively. A collection of CP maps $\{\mathcal{M}^{A}_{a}\}_{a}$, where $a$ labels the measurement outcome, is called an instrument if $\sum_{a}\mathcal{M}^{A}_{a}$ is CPTP, which implies that there is unit probability that at least one of the outcomes will occur. It is convenient to represent CP maps as operators, using a version of the Choi-Jamiołkowksi isomorphism [32, 33], $\mathcal{M}^{A}\mapsto M^{A}\in A_{I}\otimes A_{O}$:

where $\{\left|j\right\rangle\}_{j}$ is a basis of $\mathcal{H}^{A}_{I}$ and ^T denotes transposition.

The local validity of quantum mechanics implies that the joint probability for outcomes $a_{1},\dots,a_{n}$ in regions $A^{1},\dots,A^{n}$ is given by [23, 34]

where $W\in A^{1}\otimes\dots\otimes A^{n}$ is called the process matrix (or simply process) and we use the shorthand $A^{j}\equiv A^{j}_{I}\otimes A^{j}_{O}$. $W$ encodes all information relevant to the possible events, such as initial state, transformations, and causal relations. Positivity of probabilities (and the possibility to extend the local operations to additional systems) implies that the process matrix is positive semidefinite, $W\geq 0$, while normalisation requires

for all CPTP maps $\bar{M}^{A^{1}},\dots,\bar{M}^{A^{n}}$. Crucially, Eq. (3) imposes on $W$ more constraints than the normalisation condition for states, $\operatorname{tr}\rho=1$. Therefore, whereas all positive semidefinite operators represent states (up to normalisation) the same is not true for process matrices. As we will see, it is this constraint that obstructs general superpositions of processes. More general processes, that do not satisfy the linear constraints implied by Eq. (3), can always be realised probabilistically, through postselection [25, 35, 27, 36]. However, as discussed earlier, we are only interested in processes that can be realised without postslection. Therefore, in the following, we will always assume processes to be deterministic (and condition (3) to be satisfied).

The key property of the formalism is that it encodes signalling correlations: a choice of instrument in a region can change the marginal probability for measurement outcomes in another region. We say that a process is causally ordered if there is a permutation $\sigma$ of $n$ elements such that $A^{\sigma(j)}$ cannot signal to any group of parties $\left\{A^{\sigma(k)}\right\}_{k}$ with $\sigma(k)<\sigma(j)$. Conversely, we say that $W$ is incompatible with (the causal order induced by) $\sigma$ if it possible to signal from some $A^{\sigma(j)}$ to a group of parties $\left\{A^{\sigma(k)}\right\}_{k}$, all with $\sigma(k)<\sigma(j)$. We say that two processes $W_{1}$, $W_{2}$ are differently ordered if they are causally ordered relative to permutations $\sigma_{1}$, $\sigma_{2}$, but incompatible with $\sigma_{2}$, $\sigma_{1}$, respectively. We are interested in superpositions of differently ordered processes.

A related concept is that of causally nonseparable process, which formalises the notion of indefinite causal order [23, 37, 38]. A process is causally separable if it is causally ordered or a probabilistic mixture of causally ordered processes. A superposition of differently ordered processes would necessarily be causally nonseparable (because it would be extremal and not causally ordered). However, the existence of locally classical, causally nonseparable processes [39, 40, 41, 42] indicates that the opposite is not true, making causal nonseparability unsuitable to characterise superpositions of causal orders.

Process matrices are a generalisation of density matrices and, as such, cannot be directly superposed. In analogy to states, we can define superpositions for ‘pure’ processes, namely, for rank-1 process matrices, with $W=\left[\omega\right]$ for some process vector $\left|\omega\right\rangle\in\mathcal{H}^{A^{1}}_{I}\otimes\mathcal{H}^{A^{1}}_{O}\otimes\dots$ Given two pure process $\left[\omega_{1}\right]$, $\left[\omega_{2}\right]$, we define their superposition through a linear combination $\left|\omega\right\rangle=\alpha\left|\omega_{1}\right\rangle+\beta\left|\omega_{2}\right\rangle$, with $\alpha,\beta\in\mathbb{C}$, if $\left[\omega\right]$ is a valid process matrix. That is to say, if and only if

If all parties have only input spaces (or, equivalently, if all output spaces are trivial, namely they have dimension 1), the process matrix reduces to a state, and superposition of processes reduces to superposition of states. Another special case is a process that connects a region’s output, $A_{O}$, to another region’s input, $B_{I}$, of equal dimension. In this case, a pure process represents a unitary transformation (see, e.g., Appendix A of Ref. [43]), for which we use the notation

(where $\{\left|j\right\rangle\}_{j}$ is the same basis that defines the Choi-Jamiołkowski isomorphism). Because of the linearity of the representation (5), a ‘superposition of unitary processes’ reduces to the ‘superposition of unitaries’ discussed earlier: $\alpha{|{U_{1}}\rangle\!\rangle}+\beta{|{U_{2}}\rangle\!\rangle}={|{\alpha U_{1}+\beta U_{2}}\rangle\!\rangle}$.

More generally, a pure process defines an isometry from all the output to all the input spaces: if all parties prepare a pure state, they all receive a pure state, related to the prepared ones through an isometry. In the particular case where the total input and output dimensions are equal, the process defines a unitary transformation from outputs to inputs [44]. We will use the term unitary process for such cases²²2Ref. [44] used the term “pure process” for what we call here unitary process..

We are now in a position to discuss superpositions of differently ordered processes. Let us first analyse the quantum switch, to see what type of superposition it represents.

There are two different versions relevant to the present discussion. The first is a tripartite process, where $A^{1}\equiv A$ and $A^{2}\equiv B$ act on a target system, while a third party, $A^{3}\equiv F$ (for “future”), receives the target system resulting from $A$ and $B$’s operations, as well as a control system. In this version, the initial state of the target is set to some fixed state $\left|\psi\right\rangle$, while the control is fixed to $\left|+\right\rangle=\frac{1}{\sqrt{2}}\left(\left|0\right\rangle+\left|1\right\rangle\right)$. The resulting process vector is [43]

where $F_{\textrm{c}}$ and $F_{\textrm{t}}$ respectively denote the control and target subsystems of $F$. Here, $F$ has only input space, while its output is trivial, as no influence from $F$ to $A$ and $B$ is possible.

Expression (6) manifestly represents a superposition of two differently ordered processes, with the target system going first to $A$ and then $B$ or vice versa. However, seen as an isometry, the process maps the two-qubit space ($A_{O}B_{O}$) to the larger four-qubit space ($A_{I}B_{I}F_{\textrm{c}}F_{\textrm{t}}$). This means that the isometry does not describe a ‘pure transformation’, but also the specification of a state. The natural interpretation is that process (6) displays entanglement between the control system $F_{\textrm{c}}$ and the causal order of $A$ and $B$; therefore, it does not represent a superposition of causal orders alone. Indeed, if we trace out the control system, the resulting reduced process is causally separable (i.e., a classical mixture of causally ordered ones) [43, 37].

The second version of the switch features an extra laboratory, $A^{0}\equiv P$ (for ‘past’), where both the control and target systems can be prepared (corresponding to subsystems $P_{\textrm{c}}$, $P_{\textrm{t}}$, respectively). As $P$ does not receive any state, its input space can be taken to be trivial. The resulting unitary process is

This process is the sum of two vectors, each responsible for a different causal order. However, the two vectors do not define individually valid processes, as they are not normalised for arbitrary CPTP maps. Therefore, process (7) does not represent a superposition of processes with different causal orders, but rather describes quantum control of the order of $A$ and $B$.

As mentioned earlier, one can obtain a superposition of valid processes through postselection: By preparing $P_{\mathrm{c}}$ in state $\left|+\right\rangle$ and postselecting $F_{\mathrm{c}}$ in the same state, process (7) reduces to

This, however, is not a valid process vector (nor is it proportional to one), meaning that the probability to get the desired outcome $\left|+\right\rangle$ depends on the operations performed at $A$, $B$ (and it can even vanish, if the operations anticommute). Therefore, $\left|\omega_{\mathrm{post}}\right\rangle$ is not the superposition of orders we were looking for either.

The above observations lead us to the following:

The presence of a past ($P$) and future ($F$) party in the definition follows from the fact that, in a causally ordered process, there must be an initial party, which cannot receive signals from any other, and a final party, which cannot signal to the rest. If the process is unitary, such parties must have trivial input and output space, respectively. As such parties can only be respectively first and last in any causally ordered process, the simplest candidate superposition of orders has to be four-partite, as in the unitary switch (7).

Although we do not know if a superposition of causal orders is possible in general, we can rule it out for the broad class of Markovian processes. These describe evolution from each region to the next, without any memory carried over through an external environment across different steps. A unitary, Markovian process is simply a sequence of unitaries, as in the example discussed in Sec. 3.

A Markovian process matrix is the tensor product of processes describing the individual time evolutions from each region to the next [45, 46, 47]. Therefore, a unitary, Markovian process matrix compatible with the causal order $\sigma$ has the form

where $U_{j}$ are unitary matrices, we identify $A_{O}^{0}\equiv P$, $A_{I}^{n+1}\equiv F$, and we assume that the permutation $\sigma$ leaves first and last parties unchanged, $\sigma(0)=0$, $\sigma(n+1)=n+1$.

Note that, for such a process, each party can always signal to any future one (conditioned on the intermediate parties performing appropriate operations). Therefore, a process of this form compatible with $\sigma$ is necessarily incompatible with any $\sigma^{\prime}\neq\sigma$.

Our core result is that, for the simplest four-partite case, a linear combination of two unitary, Markovian processes with different orders cannot satisfy the process vector normalisation constraints, Eq. (4). In particular, a CPTP map for the output-only space $P$ is an arbitrary density matrix $\rho^{P}\geq 0$, with $\operatorname{tr}\rho^{P}=1$ (describing a state preparation), while the only CPTP map for the input-only space $F$ is $\mathds{1}^{F}$ (describing an arbitrary POVM measurement whose outcome is ignored). For $X=A,B$, a CPTP map is represented by a matrix $\xi^{X_{I}X_{O}}\geq 0$ such that $\operatorname{tr}_{X_{O}}\xi^{X_{I}X_{O}}=\mathds{1}^{X_{I}}$. The technical statement of our result, proved in the Appendix³³3While completing the current manuscript, the author was made aware of related results in Ref. [48]. In particular, Lemma 2 can be deduced from Corollary 5 in Ref. [48], although the consequence as a no go theorem for superpositions of orders is not discussed there. The argument and the proof in the present manuscript were previously presented at [49]., is then as follows:

This result rules out the simplest, most intuitive superpositions of causal orders. In particular, it proves that the control system is necessary for the quantum switch to be a valid process. Note that, because each step is unitary, all input and output spaces must have equal dimension⁴⁴4The unitaries in Eq. (12) imply $d^{P}=d^{A_{I}}$, $d^{A_{O}}=d^{B_{I}}$, and $d^{B_{O}}=d^{F}$, while from Eq. (13) we get $d^{P}=d^{B_{I}}$, $d^{B_{O}}=d^{A_{I}}$, and $d^{A_{O}}=d^{F}$. Taken together, the two sets of equations imply that all dimensions are the same.. This is not guaranteed for arbitrarily many parties. As it turns out, we need the additional assumption of equal dimensions to prove our general result:

We have seen that superpositions of processes with different causal orders are strongly constrained, if we require that the order of events is not correlated with any additional system. In particular, it is not possible to superpose sequences of equal-dimension unitaries connecting events in different orders—arguably the most natural candidate superposition of causal orders. Relaxing the assumptions in the no-go theorem leads to some open possibilities: it is currently unclear whether it is possible to superpose unitary, differently ordered processes that do not satisfy Markovianity or where the local input and output spaces do not have equal dimensions. Another interesting direction is to consider superpositions of more than two processes. Furthermore, it is an intriguing possibility to develop a notion of ‘coherence’ of causal orders that applies to nonpure processes, possibly generalising corresponding resource theories for states [50, 51].