A New Least Squares Parameter Estimator for Nonlinear Regression Equations with Relaxed Excitation Conditions and Forgetting Factor

It has recently been shown [3, 43] that global asymptotic convergence—but not exponential—of the error equation for standard continous-time (CT) gradient estimators is ensured under a strictly weaker condition of generalized PE—see [3, 55] for its definition and [13] for some robustness properties of the algorithm. Unfortunately, this condition is still extremely restrictive to be of practical use. In [7] it is shown that the classical discrete-time (DT) LS algorithm is asymptotically convergent if and only if the regressor $\phi(t)$ satisfies a new excitation property, called weak PE, that is strictly weaker than PE. This result is of limited interest because, on one hand, the definition is extremely technical and difficult to verify in applications. On the other hand, and more importantly, the analysis is limited to standard LS, without forgetting factor or covariance resetting that, as is well-known [16, 48], has a decreasing adaptation gain, loosing its alertness to track parameter variations, which is the main motivation for recursive algorithms. In [29] the underexcited scenario where the Gram matrix of the regressor has a $q_{0}$-dimensional kernel, with $q_{0}\leq q$, is considered. It is shown that incorporating into a CT LS (or gradient) estimator the information of a basis expanding this kernel—the columns of the matrix $N\in\mathbb{R}^{q_{0}\times q}$ in equation (14) or (24) whose columns $v_{i}\in\mathbb{R}^{q},\;i=1,\dots q_{0}$ satisfy equation (4)—it is possible to guarantee consistent estimation to its complementary space. Clearly, if the regressor is PE the dimension $q_{0}$ of the aforementioned kernel is zero and convergence of all the parameters is guaranteed, confirming the well-known result of the PE case. This result is related to the partial convergence property of [48, Theorem 2.7.4] where a similar fact is proven in the context of systems identification in underexcited situations. Although of theoretical interest, the result has little practical relevance because of the impossibilty to compute on-line the matrix $N$ mentioned above. In [10] a slight modification of the DT LS algorithm is proposed to deal with parameter variations in the LPRE, however the main convergence (to a compact set) results still rely on PE assumptions. In [22], an LS version of the well-known I&I estimator [2] is proposed while in [28] a variation of LS that defines a passive operator is proposed.

In [49] an interesting generalization of the classical CT LS with forgetting factor is introduced, where the latter is allowed to be a time varying matrix. See [50] for a similar result in DT. The convergence analysis in both papers still relies on the PE assumption. In the very recent paper [5] a general structure to design and analyze DT LS-like recursive estimators parameterized in terms of some free functions is proposed—see equation (7). A new definition of excitation, called $t^{\star}$-excitation, is given in [5, Definition 1]. Interestingly, this definition involves not only the regressor but also two of the aforementioned functions. A particular choice of these functions yields the classical LS estimator and $t^{\star}$-excitation is equivalent to PE. However, other choices of these free parameters may yield weaker excitation conditions, for instance the choice given in (27). However, this selection has again the problem of driving the adaptation gain to zero, loosing the estimator alertness and it is not clear if there are other choices that do not suffer from this drawback. Another novelty of [5] is that it incorporates a very interesting analysis of robustness to additive disturbances in the LPRE, encrypted in the input-to-state-stability property. The interested reader is referred to [5, 49, 50] for a review of the extensive literature on LS with forgetting factors.

A major breakthrough in the design of recurrent estimators is the proof that it is possible to establish global convergence under the extremely weak assumption of interval excitation²²2It should be pointed out that IE is strictly weaker than the generalized PE of [55], the weak excitation PE property of [7] and the $t^{\star}$-excitation of [5]. (IE) [20]—called initial excitation in [41] and excitation over a finite interval in [52]. To the best of the authors’ knowledge the first estimators where such a result was established are the concurrent and the composite learning schemes reported in [9] and [40], respectively; see [34] for a recent survey on new estimators. These algorithms, which incorporate the monitoring of past data to build a stack of suitable regressor vectors, are closer in spirit to off-line estimators. See also [19, 31] for two early references where a similar idea is explored. As is well-known, the main drawback of off-line estimators is their inability to track parameter variations, which is very often the main objective in applications. This situation motivates the interest to develop bona-fide on-line estimators that relax the PE condition preserving the scheme’s alertness [26].

New on-line estimators relying on the use of the dynamic regressor extension and mixing (DREM) technique with weaker excitation requirements have been recently proposed. DREM was first proposed in [1] for CT and in [4] for DT systems. In Appendix A it is recalled that the main step in the derivation of DREM estimators is the construction of a new extended LPRE $Y(t)=\Phi(t)\theta$, with $Y(t)\in\mathbb{R}^{q}$ and $\Phi(t)\in\mathbb{R}^{q\times q}$ a new square matrix regressor. Two procedures to construct the extended LPRE, reported in [21] and [24], respectively, were originally considered—for the sake of completeness both constructions are reviewed in Appendix A. The final—and critical—mixing step consists of the multiplication of this extended LPRE by the adjugate of $\Phi(t)$.³³3It is interesting to note that this operation was independently reported in [8] in the context of stochastic estimator convergence analysis. Clearly, this operation creates a new scalar LPRE of the form ${\cal Y}_{i}(t)=\Delta(t)\theta_{i},\;i\in\bar{q}$, with ${\cal Y}(t):=\mbox{adj}\{\Phi(t)\}Y(t)$ and $\Delta(t):=\det\{\Phi(t)\}$ a scalar regressor, which is the essential feature of the approach.⁴⁴4In Appendix A DREM is applied to nonlinearly parameterized regression equation (NLPRE) of the form (1), which is also considered in this paper. DREM estimators have been successfully applied in a variety of identification and adaptive control problems, both, theoretical and practical ones, see [34, 38] for an account of some of these results.

The convergence properties of DREM-based estimators clearly depend on the scalar regressor $\Delta(t)$. Due to the scalar nature of $\Delta(t)$, it is clear that the parameter error converges if and only if $\Delta(t)$ is not square integrable (summable for DT systems) and convergence is exponential if and only if $\Delta(t)$ is PE, facts that were proven in [1]. In [14] a DREM-based algorithm using the extended regressor of [21] that ensures convergence in finite-time imposing the IE assumption on $\Delta(t)$ was proposed. An interesting open question was to establish the relation of the excitation of $\Delta(t)$ and the original regressor $\phi(t)$, which was studied in [17] and [55] for the extended regressors of [21] and [24], respectively. The equivalence between PE of $\Delta(t)$ and PE of the original regressor $\phi(t)$ was established for both extended regressors—proving that DREM-based estimators are at least as good as standard gradient or LS schemes for excited LPRE. On the other hand, in [17] it is shown that if $\phi(t)$ is IE then $\Delta(t)$ is also IE for the extended regressor [21], while in [55] it was shown that the scheme of [24] ensures the stronger property that $\Delta(t)$ is bounded away from zero in an open interval $[t_{c},\infty)$ with $t_{c}>0$. Finally, in [38, Proposition 3] a new extended regressor which guarantees exponential convergence under conditions that are strictly weaker than regressor PE was presented.

Three major developments in this line of research reported recently are:

• (i)

  the proposal in [18] and [53] of two new, fully on-line, DREM-based estimators where exponential convergence is established imposing only the IE condition to $\phi(t)$;

• (ii)

  the proof in [53] that IE of the regressor $\phi(t)$ is equivalent to identifiability of the LPRE. It should be recalled that identifiability of a LPRE is the existence of $q$ linearly independent regressor vectors [53, Definition 2] $\phi(t_{i}),\,i\in\bar{q}$, and is a necessary and sufficient condition for the on- or off-line estimation of the parameters [16];

• (iii)

  the proof in [53] that the proposed estimator is applicable also to separable NLPRE of the form (1), provided the mapping ${\cal G}(\theta)$ verifies a monotonicity condition. Estimators for this kind of NLPRE were reported before in [36], but the convergence condition was expressed in terms of the scalar regressor $\Delta(t)$.

The estimators of [18] and [53] rely on the generation of new LPRE using the main idea of generalized parameter estimation based observer (GPEBO), which is a technique to design state observers for state-affine nonlinear systems, first proposed in [32] and latter generalized in [35]. GPEBO translates the problem of state-estimation into one of parameter estimation from a LPRE. The latter is generated exploiting the well-known property [47, Property 4.4] that the trajectories of an LTV system can be expressed as linear combinations of the columns of its fundamental matrix. Besides the addition of the computationally demanding calculation of the fundamental matrix, a potential drawback of GPEBO is that it essentially reconstructs the initial conditions of some error equation, an operation which may adversely affect the robustness of the estimator, [38, Remark 7] and [37], see also [54]. The procedure followed in the construction of the estimator of [18] is first the application of DREM and then invoke GPEBO, hence we refer to it as D+G. On the other hand, the estimator of [53] uses also GPEBO and DREM, but in the opposite order, so we refer to it in the sequel as G+D.

In this paper we provide an alternative to the D+G and G+D estimators that also ensures global exponential convergence under the weak assumption of IE of the original regressor $\phi(t)$. The main features of this new estimator are summarized as follows.

The remainder of the paper is organized as follows. In Section 2 we present the main result of the paper for CT systems, while the DT version is given in Section LABEL:sec3. For the sake of brevity we give both results for the general case of NLPRE, presenting the LPRE case as a corollary. Section 4 is devoted to the derivation of the proposed extended NLPRE applying directly the DREM construction procedure. Section 5 is devoted to the proof of robustness of the new estimator. Simulation results of some examples reported in the literature are given in Section 6 to illustrate the superior performance of the proposed LS+D estimator. The paper is wrapped-up with concluding remarks in Section 7.

Consider the following CT NLPRE

where $y(t)\in\mathbb{R}$, $\phi(t)\in\mathbb{R}^{p}$ and ${\cal G}:\mathbb{R}^{q}\to\mathbb{R}^{p},\;q\leq p$, a smooth mapping verifying the following.

Moreover, assume the regressor $\phi_{k}$ satisfies.

In this section, we use the result of Proposition 2 for the case of LPRE—obviously, in this linear case Assumption A1 and Assumption A3 are automatically satisfied. As a first step we recall [53] that Definition LABEL:def1 and Lemma LABEL:lem1, given for continuous functions, are also valid for sequences.

As a second step notice that for the LPRE case (LABEL:keyide) takes the form

consequently (4eiqrx) now becomes

and the dynamics of the parameter error (LABEL:errequk) is now given by

whose stability is follows immediately from the IE assumption [53, Proposition 2] .

In this section, we consider the case of switched parameters estimation. Whereas the results are presented in DT only, similar results can be formulated for the CT case in a straightforward manner. Rewrite (LABEL:nlprek) as

where $\theta^{*}_{\sigma_{k}}$ denotes the switched unknown parameter vector with $\theta^{*}_{\sigma_{k}}\in\left\{\theta^{*}_{1}\right.$, $\left.\theta^{*}_{2},\ldots,\theta^{*}_{s}\right\}$, $s\in\mathbb{Z}_{>0}$. The switching signal $\sigma_{k}:\mathbb{Z}_{\geq 0}\to\bar{s}$ is a known⁷⁷7Such a scenario arises in several practical control scenarios, when the known switching signal $\sigma_{k}$ characterizes known changes in operation regimes [23]. piecewise-constant function defining the behavior of $\theta^{*}_{\sigma_{k}}$, i.e., $\theta^{*}_{\sigma_{k}}=\theta^{*}_{i}$ when $\sigma_{k}=i$, $i\in\bar{s}$. The known time instants when $\sigma_{k}$ changes its value are further denoted as $t_{r,i}$, $i\in\mathbb{Z}_{\geq 0}$.

The estimator (4eiq), (4eiqr) is not capable of estimating switched parameters as for $\beta<1$ the sequence $z_{k}$ converges to zero, and for $\beta=1$ the LS estimator looses its alertness. To deal with switching parameters, we propose a resetting-based modification of the estimator (4eiq), (4eiqr):

where $\hat{\eta}_{0}=:\eta_{0}\in\mathbb{R}^{p}$, $F_{-1}={1\over f_{0}}I_{p}$, and

Between the reseting instances $t_{r,i}$, the estimator (4eiqrae), (4eiqraf) reproduces the estimator (4eiq), (4eiqr) with $\beta=1$ and thus $z_{k}\equiv 1$. Then, at each reset instance $t_{r,i}$, the matrix $F_{k}$ is reset to its initial condition $F_{-1}$, and the state $\psi_{k}$ saves the value of $\hat{\eta}_{k}$. The state $\psi_{k}$ thus plays the same role as $\eta_{0}$ in (LABEL:keyide), compare (4eiqrafb) and (4eiqr). Following the properties of (4eiq), (4eiqr), the proposed estimator ensures the boundedness of the states and is capable of estimating $\theta^{*}_{\sigma_{k}}$ if the following assumption holds.

Consider the second order stable, CT, linear system described by

or equivalently

where $\theta_{1}$, $\theta_{2}$ and $\theta_{3}$ are unknown parameters. Applying the filter

where ${\mathfrak{p}}:=\frac{d}{dt}$, to both sides of (4eiqragal) and rearranging the terms, we get the LPRE (LABEL:lrect) with

and $\theta:=\mbox{col}(\theta_{1},\,\theta_{2},\,\theta_{3})$.

To carry out the simulations we use the same conditions that [29], that is, we set to zero the initial conditions of the filters, as well as the initial value of the parameter estimation vector ${\hat{\theta}}(0)=0$, $\hat{\eta}(0)=\mbox{col}(0.1,\,0.1,\,0.1)$, $u(t)=5$ and fix $\theta=\mbox{col}(2,3,1)$. Besides, the tuning parameters of the proposed estimator of Corollary LABEL:cor1 were $\alpha=20.3$, $f_{0}=4$, $\beta=0.07$ and $\gamma=700$. In Fig. 1 we appreciate the transient behavior of the estimated parameters, which clearly shows the estimation of the real values. This result should be contrasted with the non-converging behavior of the estimates reported in [29] with the gradient scheme and their modified gradient.

To illustrate the use of the NLPRE (1), we notice that from the proposed values for $\theta$, we have that $\theta_{3}$ can be rewritten as $\theta_{3}=\theta_{2}-\theta_{1}$. Hence, after the application of the filter $H({\mathfrak{p}})$, the system (4eiqragal) can be written as the NLPRE (1) with ${\mathcal{G}}(\theta):=\mbox{col}(\theta_{1},\,\theta_{2},\,\theta_{2}-\theta_{1})$, Thus, using the same initial conditions, estimator gains and verifying Assumption A1 with

and $\rho=1$, we carry out a simulation to estimate only $\theta_{1}$ and $\theta_{2}$ with the estimator of Proposition 1. Fig. 2 shows the transient behavior of the estimated parameters, showing again parameter convergence.

Consider the first order linear system

where ${\mathfrak{q}}$ is the forward-shiff operator and $\theta_{1}$ and $\theta_{2}$ are unknown parameters. After some simple calculations, we have that (4eiqragap) can be written as a LPRE $y_{k}=\phi_{k}^{\top}\theta$ with

To carry out the simulations we have also used the same initial conditions and parameters of [15], that is, $\theta_{1}=0.4$, $\theta_{2}=0.8$, $\theta_{0}=\mbox{col}(0,\,0)$ and the input signal $u_{k}=1$.¹⁰¹⁰10We notice that there is an unfortunate typo in the definition of $u_{k}$ in [15, Example 4]. The tuning gains of the estimator of Corollary 2 were chosen as $\beta=1$, $f_{0}=0.14$, $\gamma=0.4$ and initial conditions ${\hat{\eta}}_{0}=\mbox{col}(1,\,1)$. It is important to note that for this system (4eiqragap), the estimator proposed in [15] only ensures the boundedness of $\hat{\theta}_{i}$, with $i=1,2$ (see Fig. 3 of [15]). This should be contrasted with our estimator, which, as can be seen in Fig. 3, converges to the real value.

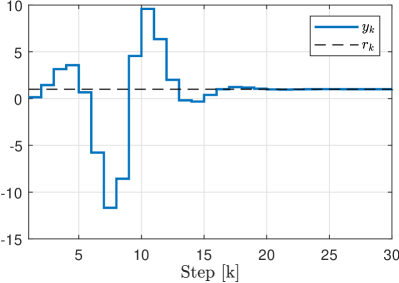
We consider the DT system

which switches for $k\geq k_{c}$ to

Note that for $k\geq k_{c}$ the plant is unstable and not minimum-phase. The initial conditions are $y_{-1}=-0.2$, $y_{-2}=0.4$, and $u_{-1}=u_{-2}=0$, and $k_{c}=50$.

The system can be written in the form (4eiqrad) setting ${\cal G}(\theta^{*}_{\sigma_{k}})=\theta^{*}_{\sigma_{k}}$,

and

which corresponds to $t_{r,0}=0$ and $t_{r,1}=k_{c}$.

In this example, we consider the indirect adaptive poles placement for the reference tracking, where the reference signal is denoted as $r_{k}$. Then the control signal $u$ is given by

where the time-varying coefficients $c_{1,k}$, $c_{2,k}$, $c_{3,k}$, and $c_{4,k}$ are computed based on the current parameter estimate $\hat{\theta}_{k}$ to provide the desired poles and unit gain of the closed-loop system; if for a value of $\hat{\theta}_{k}$ the computations are ill-conditioned, then $u_{k}=0$ is chosen. For this example, the desired poles for this are $e^{-1}$, $e^{-0.5+0.86\sqrt{-1}}$, and $e^{-0.5-0.86\sqrt{-1}}$, and the reference signal is $r_{k}\equiv 1$.

To estimate the parameters, we apply the resetting-based estimator (4eiqrae), (4eiqraf), where we set $f_{0}=0.4$, $\gamma=500$, $\eta_{0}=0$, and $\theta_{0}=\begin{bmatrix}0.1&-0.3&0.5&-0.05\end{bmatrix}$. Note that $\theta_{0}$ cannot be chosen zero as such a choice yields zero input to the system and the regressor $\phi$ is not IE; for a nonzero choice of $\theta_{0}$, the interval excitation is provided by the transients of the plant.

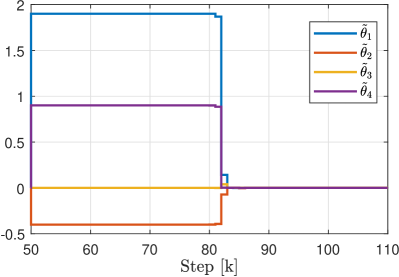
The simulation results are depicted in Fig. 4 for the output signal $y$ and in Fig. 5 for the estimation errors $\tilde{\theta}_{k}=\hat{\theta}_{k}-\theta^{*}_{\sigma_{k}}$. It can be observed that after the switch, parameters estimation errors remain almost constant for approximately $30$ steps, and then quickly converge. Further investigation shows that the regressor $\phi$ is not exciting on this initial interval, and thus the estimation does not progress. As soon as the IE condition is satisfied, the estimates $\hat{\theta}_{k}$ converges to the true value $\theta^{*}_{2}$.