A New Intelligent Reflecting Surface-Aided Electromagnetic Stealth Strategy

Over the past few decades, electromagnetic stealth (ES) technology has attracted significant attention due to its ability to increase the difficulty of radar systems to detect and track stealth targets [1]. As one of the most important techniques to achieve ES, electromagnetic wave absorbing materials (EWAMs) have been widely investigated to enhance electromagnetic wave (EW) absorption efficiency as well as broaden the absorption bandwidth [2, 3]. Generally, existing EWAMs designs mainly focus on studying advanced materials with desired absorbing properties and multi-layer structures containing various materials, which can effectively reduce the reflected EW towards the radar by absorbing a considerable part of the incident electromagnetic energy [4, 5, 6]. However, the performance of these customized EWAMs is limited by various factors, such as coating thickness, incident wave angle, and inherent material properties. Furthermore, with the increasing complexity of battlefield environments, rapid operational changes in the radar signal and targets with high speed can quickly change the angles of the incident waves, resulting in a further serious deterioration of stealth performance. Therefore, there is an urgent need for developing more efficient and intelligent ES strategies to achieve satisfactory stealth performance in fast-changing environments.

Recently, innovative intelligent reflecting surface (IRS) technology has emerged as a tool for improving the performance of wireless systems [7, 8]. Specifically, an IRS is a planar surface composed of a large number of low-cost passive reflecting elements that can independently manipulate the amplitude and/or phase of incident electromagnetic signals. This enables an IRS to adjust the wireless propagation environment in response to rapid variations in the channel conditions. Furthermore, radio-frequency (RF) chains are not required in IRS, thereby reducing the deployment cost and energy consumption. This also facilitates its lightweight fabrication and compact size, opening up new possibilities for achieving improved stealth performance by incorporating IRS as a supplement to EWAMs. Although there are many works on IRS-aided wireless communications [9, 10], only a handful focus on IRS-aided target sensing [11]. While IRS are less effective than EWAMs in absorbing the incident radar energy, their amplitude and phase reconfigurability can be exploited to destructively combine with the residual EWAMs reflection to increase ES performance. This possibility has not been explored before and is the subject of this paper.

Motivated by the above, this work designs a new IRS-aided ES system that enables a target to evade radar detection in highly dynamic environments. From the perspective of anti-radar detection, we formulate an optimization problem that minimizes the received signal-to-noise-ratio (SNR) at the adversarial radar under the modulus constraint of IRS reflection. To address this optimization problem, we derive a semi-closed-form solution by leveraging the Karush-Kuhn-Tucker (KKT) conditions and then obtain the dual variables via solving the dual program. Simulation results are provided to demonstrate the advantages of the proposed IRS-aided ES system compared to various benchmarks.

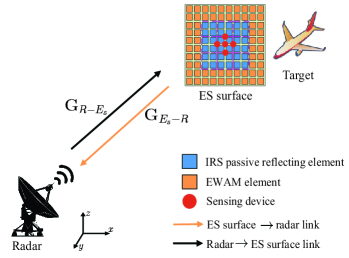
As shown in Fig. 1, we consider an IRS-aided ES system mounted on a moving target (e.g., aircraft), where an IRS is deployed in addition to the EWAM surface for further reducing the target detection probability. Furthermore, we consider a challenging scenario where a monostatic probing radar acts as an opponent that attempts to detect the target. Under this setting, we need to properly design the passive IRS reflection to synergize with the EWAMs, such that the probing signal echoed back from the target to the radar can be effectively mitigated or even eliminated. Without loss of generality, we consider a typical ES surface as a uniform planar array (UPA) that consists of $N_{1}$ IRS elements and $N_{2}$ EWAM elements, with $N\triangleq N_{x}\times N_{z}=N_{1}+N_{2}$ total elements (see Fig. 1). To enable the estimation of the angle-of-arrival (AoA) of the radar probing signal, a cross-shaped sensing array is embedded at the center of the ES surface, which contains $N_{s}=N_{s,x}+N_{s,z}-1$ sensing devices. Moreover, we assume that the monostatic radar system is equipped with a UPA consisting of $M\triangleq M_{x}\times M_{z}$ active antennas for either transmitting the probing signals or receiving the echo signals.

Let $\mathbf{G}_{RE_{w}}^{[t]}\in\mathbb{C}^{N_{2}\times M}$, $\mathbf{G}_{RI}^{[t]}\in\mathbb{C}^{N_{1}\times M}$, and $\mathbf{G}_{RE_{s}}^{[t]}\in\mathbb{C}^{N\times M}$ denote the equivalent baseband channels for the radar$\rightarrow$EWAM surface, radar$\rightarrow$IRS, and radar$\rightarrow$ES surface links at time $t$, respectively.¹¹1For notational convenience, we use subscripts “$R$”, “$I$”, “$E_{w}$”, and “$E_{s}$” to indicate the radar, IRS, EWAM surface, and ES surface, respectively. In a typical military scenario, considering the relatively long distance between the radar and target, the channels between them can be well characterized by the far-field line-of-sight (LoS) model. For convenience, we first define the one-dimensional (1D) steering vector for a symmetrical uniform linear array (ULA) as follows:

where $j=\sqrt{-1}$ denotes the imaginary unit, $\phi$ denotes the constant phase-shift difference between the signals at two adjacent antennas/elements, and $N_{l}$ denotes the number of antennas/elements in the ULA. Since the IRS and EWAM surfaces are centered at the same point and oriented in the same way, they exhibit the same AoA/angle-of-departure (AoD) for the radar signals. We denote the AoA/AoD pairs for the IRS and EWAM as $(\vartheta_{E_{s}}^{[t]},\varphi_{E_{s}}^{[t]})$, and we denote the AoA/AoD pairs for the radar as $(\vartheta_{R}^{[t]},\varphi_{R}^{[t]})$. Accordingly, we let $\bm{a}_{R}(\vartheta_{R}^{[t]},\varphi_{R}^{[t]})$, $\bm{a}_{E_{s}}(\vartheta_{E_{s}}^{[t]},\varphi_{E_{s}}^{[t]})$, $\bm{a}_{I}(\vartheta_{E_{s}}^{[t]},\varphi_{E_{s}}^{[t]})$, and $\bm{a}_{E_{w}}(\vartheta_{E_{s}}^{[t]},\varphi_{E_{s}}^{[t]})$ denote the array response vectors of the radar, ES surface, IRS, and EWAM surface at time $t$, respectively. Under the UPA model, each array response vector is expressed as the Kronecker product of two steering vector functions in the horizontal ($x$-axis) and vertical ($z$-axis) directions. For example, the array response vector at the ES surface can be expressed as

where $\lambda$ denotes the signal wavelength and $\Delta_{E_{s}}$ is the element spacing at the ES surface; the array response vectors at the radar and IRS, i.e., $\bm{a}_{R}\left(\vartheta_{R}^{[t]},\varphi_{R}^{[t]}\right)$ and $\bm{a}_{I}\left(\vartheta_{E_{s}}^{[t]},\varphi_{E_{s}}^{[t]}\right)$ can be similarly defined. Due to the location relationship between the ES surface, IRS, and EWAM shown in Fig. 1, the array response vector at the ES can be decomposed into the array response vectors of the IRS and EWAM surface. More specifically, the relationship between these array response vectors can be described by the following equation:

where

with $a_{n}$ denoting the $n$-th element of $\bm{a}_{E_{s}}(\vartheta_{E_{s}}^{[t]},\varphi_{E_{s}}^{[t]})$. Then, the EWAM array response vector $\bm{a}_{E_{w}}(\vartheta_{E_{s}}^{[t]},\varphi_{E_{s}}^{[t]})$ can be obtained by removing the zero elements of $\tilde{\bm{a}}_{E_{w}}(\vartheta_{E_{s}}^{[t]},\varphi_{E_{s}}^{[t]})$. We assume that the high-speed target moves at a constant speed of $v$, and the channel links are subjected to Doppler frequency. Accordingly, the real-time far-field LoS channels between any two nodes (represented by $X$ and $Y$ for notational simplicity) are modeled as the outer product of array response vectors at their two sides, i.e.,

with $X\in\{I,E_{w},E_{s}\}$ and $Y\in\{R\}$, where $\alpha_{XY}^{[t]}=\frac{\sqrt{\beta}}{d_{XY}^{[t]}}e^{-j2\pi(\frac{d_{XY}^{[t]}}{\lambda}+f_{XY}^{[t]}T_{c})}$ is the corresponding complex-valued path gain between them at time $t$, $\beta$ denotes the reference path gain at a distance of 1 meter (m), $d_{XY}^{[t]}$ denotes the propagation distance between the two nodes at time $t$, and $f_{XY}^{[t]}=\frac{v\cos\varphi_{XY}^{[t]}\cos\vartheta_{XY}^{[t]}}{\lambda}$ is the Doppler frequency, $T_{c}$ is the channel coherence interval. For the purpose of exposition, we assume all the involved LoS channels remain approximately constant during each channel coherence time and that channel reciprocity holds for the uplink and downlink transmission. ²²2 This assumption is practically valid since the target speed $v$ remains constant, and the marginal variations in the geometry-related parameters, i.e., distances and AoDs/AoAs, are negligible. As a result, we have $\mathbf{G}_{XY}^{[t]}=\left(\mathbf{G}_{YX}^{[t]}\right)^{T}$ and $\alpha^{[t]}=\alpha_{XY}^{[t]}=\alpha_{YX}^{[t]}$ with $X\in\{I,E_{w},E_{s}\}$ and $Y\in\{R\}$.

Existing EWAMs may not achieve full EW absorption due to the limitations posed by their physical characteristics, absorption frequency range, structural layout, etc. To characterize the stealth performance of EWAMs, we utilize the absorbing efficiency $p_{n}\in[0,1],n=1,...,N_{2}$ to represent the corresponding absorption capacity. To proceed, we define $\bm{\gamma}=[\gamma_{1}e^{j\psi_{1}},...,\gamma_{N_{2}}e^{j\psi_{N_{2}}}]^{T}\in{\mathbb{C}^{N_{2}\times 1}}$ as the reflection coefficient vector of the EWAM surface, where $\gamma_{n}=\sqrt{1-p_{n}}$ and $\psi_{n}$ respectively represent the amplitude and phase of the $n$-th EWAM element response for $n=1,...,N_{2}$, which can be obtained from offline measurements. Furthermore, we let $\bm{\theta}^{[t]}=\left[\beta_{1}^{[t]}e^{j\varphi_{1}^{[t]}},...,\beta_{N_{1}}^{[t]}e^{j\varphi_{N_{1}}^{[t]}}\right]^{T}\in{\mathbb{C}^{N_{1}\times 1}}$ denote the equivalent tunable reflection coefficients of the IRS at time $t$, where $\beta_{n}^{[t]}\in[0,1]$ and $\varphi_{n}^{[t]}\in[0,2\pi)$ represent the reflection amplitude and phase shift of the $n$-th IRS element, respectively. For the purpose of ES, the IRS reflection is devised to destructively combine with the signals reflected by the EWAM surface to reduce the reflected signal power by the entire ES surface to evade radar detection [12]. As such, the received signals at the radar are composed of two types of echo signals reflected by the IRS and the EWAM surface:

where $\mathbf{\Theta}^{[t]}=\mathrm{diag}\left(\bm{\theta}^{[t]}\right)$ represents the diagonal reflection matrix of the IRS at time $t$, $\mathbf{\Gamma}=\mathrm{diag}\left(\bm{\gamma}\right)$ denotes the diagonal reflection matrix of the EWAM surface, $\mathbf{S}^{[t]}=\left[\mathbf{s}_{1}^{[t]},...,\mathbf{s}_{L}^{[t]}\right]$ represents the transmitted radar waveform at time $t$ satisfying $\mathbb{E}\left[\mathbf{S}^{[t]}({\mathbf{S}^{[t]}})^{H}\right]=\mathbf{I}_{M}$ with $L>M$ representing the number of transmitted samples, and $\mathbf{Z}_{R}^{[t]}\in\mathbb{C}^{M\times L}$ represents an additive white Gaussian noise (AWGN) matrix with independent elements of zero mean and variance $\sigma^{2}$.

The radar detection process during each channel coherence time can be formulated as a binary hypothesis testing problem as follows:

where $\mathcal{H}_{0}$ and $\mathcal{H}_{1}$ represent the absence and presence of a target, respectively. The Neyman-Pearson (NP) criterion is commonly employed for optimal decision-making in the above binary hypothesis test, i.e., $\mathcal{T}(\mathbf{Y}^{[t]})\underset{\mathcal{H}_{0}}{\stackrel{{\scriptstyle\mathcal{H}_{1}}}{{\gtrless}}}\eta$, where $\mathcal{T}(\mathbf{Y}^{[t]})$ is the decision rule based on the received signal $\mathbf{Y}^{[t]}$, and $\eta$ denotes the detection threshold [13]. This criterion aims to maximize the detection probability $P_{d}^{[t]}$, while maintaining a predetermined false alarm probability $P_{fa}^{[t]}$ at time $t$. According to the NP criterion, we have

where $\operatorname{Q}(\cdot)$ denotes the Marcum-Q function. Intuitively, a higher SNR will result in a higher probability of target detection for a given $P_{fa}^{[t]}$. Given the monotonic relationship between the SNR and detection probability in (9), we can reduce $P_{d}^{[t]}$ by decreasing the received SNR at the radar. Thus, we consider SNR as an indicator to evaluate the performance of the IRS-aided ES system. According to (7), the received SNR at the radar can be expressed as

In this section, we present simulation results to demonstrate the performance of the proposed IRS-aided ES system. In particular, we consider two baseline systems for comparison: 1) Random phase shift design, where the IRS phase shifts are randomly generated following a uniform distribution within $[0,2\pi)$; 2) No IRS design, where the ES system works without an IRS by setting the reflection coefficient to $\bm{\theta}^{[t]}=\bm{0}$. In our simulations, we consider that the moving target and probing radar are within the same two-dimensional plane, where the radar is located at the origin point. Under the considered setup, we have $\varphi_{T}^{[t]}=\varphi_{R}^{[t]}=0$ for ease of illustration and only need to focus on the AoAs/AoDs $\left(\vartheta_{T}^{[t]},\vartheta_{R}^{[t]}\right)$.

At the target, the ES surface is composed of a total of $N=N_{1}+N_{2}=70$ elements, with $N_{1}$ and $N_{2}$ to be specified in the following simulations. For the absorbing efficiency of the EWAM surface, we set $p_{1}=...=p_{N_{2}}=p$ for simplicity. Moreover, $\left\{\psi_{n}\right\}_{n=1}^{N_{2}}$ are randomly generated following a uniform distribution within $[0,2\pi)$. Throughout the simulations, each result is attained by independent experiments during a channel coherence time, in which the angles for each experiment are chosen randomly in the region $[-\frac{\pi}{2},\frac{\pi}{2}]$ with a discretization stepsize of $1^{\circ}$.

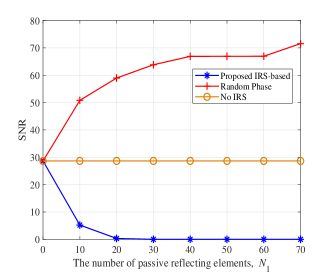
In Fig. 2, we depict the SNR versus the number of passive reflecting elements for $p=0.7$. Several interesting observations are made as follows. First, as the number of IRS elements increases, the received SNR at the radar dramatically decreases due to a higher cancellation of unabsorbed signals at the EWAM surface through tuning the IRS reflection coefficients. Second, the proposed scheme outperforms the no-IRS and random phase shift approaches in terms of the reduction in received SNR. This is because the signals reflected by the IRS and EWAMs are destructively combined in our proposed IRS-aided system to reduce the signal power echoed back to the radar and thus leads to a lower received SNR. Third, the SNR of the random phase shift design increases with the number of IRS elements and far exceeds that of the no IRS and IRS-aided designs. This indicates that if the signals reflected by the IRS are not designed properly to destructively combine with those of the EWAM surface, the ES performance achieved using the IRS is even worse than that without it. Finally, ideal stealth effectiveness, where the SNR reaches the minimum value of $0$, can be achieved when the number of IRS elements exceeds a certain threshold, i.e., in this case $N_{1}\geq 20$.

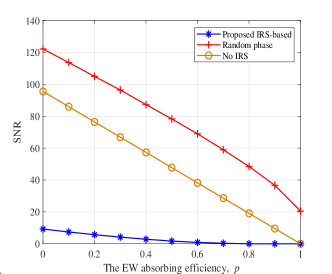
In Fig. 3, we present the received SNR versus the EW absorbing efficiency $p$ assuming an IRS with $N_{1}=20$ elements. It is observed that as the EW absorption efficiency $p$ increases, the SNRs of all the considered ES systems decrease due to the reduced signal power reflected by the EWAM surface. Moreover, the proposed IRS-aided ES system, regardless of the EW absorbing efficiency, outperforms the two baselines in terms of the reduction in received SNR at the radar. In particular, the IRS-aided system can achieve perfect stealth performance, i.e., the received SNR at the radar reaches the minimal value of 0, even when the level of EW absorbing efficiency is not relatively high. This is expected since the tunable elements in the ES surface can collaboratively operate with the EWAM surface for achieving better ES performance.

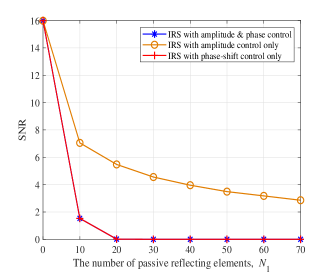
To illustrate the impact of different reflection designs on ES performance, we consider two benchmark approaches: $1)$ IRS with amplitude control only, where each reflecting element can tune the reflection amplitude with a constant phase shift; $2)$ IRS with phase-shift control only, where each reflecting element can tune the phase shift while the reflection amplitude is set to its maximum value of one, i.e., $|\bm{\theta}(n)|=1,\forall n=1,...,N_{1}$. In Fig. 4, we show the received SNR at the radar versus the number of passive reflecting elements at the IRS, with $N_{2}=40$ untunable EWAM elements. It can be seen that the received SNR at the radar for all three IRS reflection designs decreases as the number of passive reflecting elements at the IRS increases. This validates the effectiveness of the proposed IRS-aided ES system for intelligently controlling the IRS to reduce or eliminate the reflected signal power towards the radar. Moreover, an interesting observation is that, regardless of the number of IRS elements, the reflection models involving phase-shift control (i.e., the IRS with reflection amplitude and phase shift control, and the IRS with phase-shift control only) consistently yield identical optimal performance. They both achieve a significantly lower received SNR at the radar compared to the amplitude control only design, owing to their enhanced flexibility. However, using the phase-control-only approach is more challenging to optimize given the non-convex constraints on the IRS element responses.

In this letter, we investigated a new IRS-aided ES system for achieving satisfactory stealth performance by reducing or even eliminating the electromagnetic waves reflected back to a radar system. The problem was formulated as the minimization of the received SNR at the radar, subject to the modulus constraints on the IRS reflection. By exploiting the convexity of the optimization problem, a semi-closed-form solution for optimizing the IRS reflection coefficients was derived based on the KKT conditions. Simulation results demonstrated that the proposed IRS-aided ES system achieves superior stealth performance compared to various baseline ES approaches.