A New Initialization Technique for Reducing the Width of Neural Networks
Bounding the Width of Neural Networks via Coupled Initialization - A Worst Case Analysis
Abstract
A common method in training neural networks is to initialize all the weights to be independent Gaussian vectors. We observe that by instead initializing the weights into independent pairs, where each pair consists of two identical Gaussian vectors, we can significantly improve the convergence analysis. While a similar technique has been studied for random inputs [Daniely, NeurIPS 2020], it has not been analyzed with arbitrary inputs. Using this technique, we show how to significantly reduce the number of neurons required for two-layer ReLU networks, both in the under-parameterized setting with logistic loss, from roughly [Ji and Telgarsky, ICLR 2020] to , where denotes the separation margin with a Neural Tangent Kernel, as well as in the over-parameterized setting with squared loss, from roughly [Song and Yang, 2019] to , implicitly also improving the recent running time bound of [Brand, Peng, Song and Weinstein, ITCS 2021]. For the under-parameterized setting we also prove new lower bounds that improve upon prior work, and that under certain assumptions, are best possible.
1 Introduction
Deep learning has achieved state-of-the-art performance in many areas, e.g., computer vision LeCun et al. (1998); Krizhevsky et al. (2012); Szegedy et al. (2015); He et al. (2016), natural language processing Collobert et al. (2011); Devlin et al. (2018), self-driving cars, games Silver et al. (2016, 2017), and so on. A beautiful work connected the convergence of training algorithms for over-parameterized neural networks to kernel ridge regression, where the kernel is the Neural Tangent Kernel (NTK) Jacot et al. (2018).
The convergence results motivated by NTK mainly require two assumptions: (1) the kernel matrix formed by the input data points has a sufficiently large minimum eigenvalue , which is implied by the separability of the input point set Oymak and Soltanolkotabi (2020), and (2) the neural network is over-parameterized. Mathematically, the latter means that the width of the neural network is a sufficiently large polynomial in the other parameters of the network, such as the number of input points, the data dimension, etc. The major weakness of such convergence results is that the neural network has to be sufficiently over-parameterized. In other words, the over-parameterization is a rather large polynomial, which is not consistent with architectures for neural networks used in practice, cf. Kawaguchi and Huang (2019).
Suppose is the width of the neural network, which is the number of neurons in a hidden layer, and is the number of input data points. In an attempt to reduce the number of neurons for binary classification, a recent work Ji and Telgarsky (2020) has shown that a polylogarithmic dependence on suffices to achieve arbitrarily small training error. Their width, however, depends on the separation margin in the RKHS (Reproducing Kernel Hilbert Space) induced by the NTK. More specifically they show an upper bound of and a lower bound of relying on the NTK technique. Our new analysis in this regime significantly improves the upper bound to .
We complement this result with a series of lower bounds. Without relying on any assumptions we show is necessary. Assuming we need to rely on the NTK technique as in Ji and Telgarsky (2020), we can improve their lower bound to . Finally, assuming we need to rely on a special but natural choice for estimating an expectation by its empirical mean in the analysis of Ji and Telgarsky (2020), which we have adopted in our general upper bound, we can even prove that , i.e., that our analysis is tight. However, in the -dimensional case we can construct a better estimator yielding a linear upper bound of , so the above assumption seems strong for very low dimensions, though it is a seemingly natural method that works in arbitrary dimensions. We also present a candidate hard instance in dimensions which could potentially give a matching lower bound, up to logarithmic factors.
For regression with target variable with we consider a two-layer neural network with squared loss and ReLU as the activation function, which is standard and popular in the study of deep learning. Du et al. (2019c) show that suffices (suppressing the dependence on remaining parameters). Further, Song and Yang (2019) improve this bound to . The trivial information-theoretic lower bound is , since the model has to memorize111Here, by memorize, we mean that the network has zero error on every input point. the input data points arbitrarily well. There remains a huge gap between and . In this work, we improve the upper bound, showing that suffices for gradient descent to get arbitrarily close to training error. We summarize our results and compare with previous work in Table 1.
1.1 Related Work
The theory of neural networks is a huge and quickly growing field. Here we only give a brief summary of the work most closely related to ours.
Convergence results for neural networks with random inputs. Assuming the input data points are sampled from a Gaussian distribution is often done for proving convergence results Zhong et al. (2017b); Li and Yuan (2017); Zhong et al. (2017a); Ge et al. (2018); Bakshi et al. (2019); Chen et al. (2020). A more closely related work is the work of Daniely (2020) who introduced the coupled initialization technique, and showed that hidden neurons can memorize all but an fraction of random binary labels of points uniformly distributed on the sphere. Similar results were obtained for random vertices of a unit hypercube and for random orthonormal basis vectors. In contrast to our work, this reference uses stochastic gradient descent, where the nice assumption on the input distribution gives rise to the factor; however, this reference achieves only an approximate memorization. We note that full memorization of all input points is needed to achieve our goal of an error arbitrarily close to zero, and neurons are needed for worst case inputs. Similarly, though not necessarily relying on random inputs, Bubeck et al. (2020) shows that for well-dispersed inputs, the neural tangent kernel (with ReLU network) can memorize the input data with neurons. However, their training algorithm is neither a gradient descent nor a stochastic gradient descent algorithm, and also their network consists of complex weights rather than real weights. One motivation of our work is to analyze standard algorithms such as gradient descent. In this work, we do not make any input distribution assumptions; therefore, these works are incomparable to ours. In particular, random data sets are often well-dispersed inputs that allow smaller width and tighter concentration, but are hardly realistic. In contrast, we conduct worst case analyses to cover all possible inputs, which might not be well-dispersed in practice.
Convergence results of neural networks in the under-parameterized setting. When considering classification with cross-entropy (logistic) loss, the analogue of the minimum eigenvalue parameter of the kernel matrix is the maximum separation margin (see Assumption 3.1 for a formal definition) in the RKHS of the NTK. Previous separability assumptions on an infinite-width two-layer ReLU network in Cao and Gu (2019b, a) and on smooth target functions in Allen-Zhu et al. (2019a) led to polynomial dependencies between the width and the number of input points. The work of Nitanda et al. (2019) relies on the NTK separation mentioned above and improved the dependence, but was still polynomial.
A recent work of Ji and Telgarsky (2020) gives the first convergence result based on an NTK analysis where the direct dependence on , i.e., the number of points, is only poly-logarithmic. Specifically, they show that as long as the width of the neural network is polynomially larger than and , then gradient descent can achieve zero training loss.
Convergence results for neural networks in the over-parameterized setting. There is a body of work studying convergence results of over-parameterized neural networks Li and Liang (2018); Du et al. (2019c); Allen-Zhu et al. (2019c, b); Du et al. (2019b); Allen-Zhu et al. (2019a); Song and Yang (2019); Arora et al. (2019b, a); Cao and Gu (2019b); Zou and Gu (2019); Du et al. (2019a); Lee et al. (2020); Huang and Yau (2020); Chen and Xu (2020); Brand et al. (2021); Li et al. (2021); Song et al. (2021). One line of work explicitly works on the neural tangent kernel Jacot et al. (2018) with kernel matrix . This line of work shows that as long as the width of the neural network is polynomially larger than , then one can achieve zero training error. Another line of work instead assumes that the input data points are not too “collinear”, where this is formalized by the parameter 222This is also sometimes called the separability of data points. Li and Liang (2018); Oymak and Soltanolkotabi (2020). These works show that as long as the width of the neural network is polynomially larger than and , then one can train the neural network to achieve zero training error. The work of Song and Yang (2019) shows that the over-parameterization suffices for the same regime we consider333Although the title of Song and Yang (2019) is quadratic, is only achieved when the finite sample kernel matrix deviates from its limit in norm only by a constant w.h.p., and the inputs are well-dispersed with constant , i.e., for all . In general, Song and Yang (2019) only achieve a bound of . . Additional work claims that even a linear dependence is possible, though it is in a different setting. E.g., Kawaguchi and Huang (2019) show that for any neural network with nearly linear width, there exists a trainable data set. Although their width is small, this work does not provide a general convergence result. Similarly, Zhang et al. (2021) use a coupled LeCun initialization scheme that also forces the output at initalization to be . This is shown to improve the width bounds for shallow networks below neurons. However, their convergence analysis is local and restricted to cases where it remains unclear how to find globally optimal or even approximate solutions. We instead focus on cases where gradient descent provably optimizes up to arbitrary small error, for which we give a lower bound of .
Other than considering over-parameterization in first-order optimization algorithms, such as gradient descent, Brand et al. (2021) show convergence results via second-order optimization, such as Newton’s method. Their running time also relies on , which is the state-of-the-art width for first-order methods Song and Yang (2019), and it was noted that any improvement to would yield an improved running time bound.
Our work presented in this paper continues and improves those lines of research on understanding two-layer ReLU networks.
Roadmap.
In Section 2, we introduce our problem formulations and present our main ideas. In Section 3, we present our main results. In Section 4, we present a technical overview of our core analysis for the convergence of the gradient descent algorithm in both of our studied regimes and give a hard instance and the intuition behind our lower bounds. In Section 5, we conclude our paper with a summary and some discussion.
2 Problem Formulation and Initialization Scheme
We follow the standard problem formulation Du et al. (2019c); Song and Yang (2019); Ji and Telgarsky (2020). One major difference of our formulation with the previous work is that we do not have a normalization factor in what follows. We note that only removing the normalization does not give any improvement in the amount of over-parameterization required of the previous bounds. The output function of our network is given by
| (1) |
where denotes the ReLU activation function444We note that our analysis can be extended to Lipschitz continuous, positively homogeneous activations., is an input point, are weight vectors in the first (hidden) layer, and are weights in the second layer. We only optimize and keep fixed, which suffices to achieve zero error. Also previous work shows how to extend the analysis to include in the optimization, cf. Du et al. (2019c).
Definition 2.1 (Coupled Initialization).
We initialize the network weights as follows:
-
•
For each , we choose to be a random Gaussian vector drawn from .
-
•
For each , we sample from uniformly at random.
-
•
For each , we choose .
-
•
For each , we choose .
We note this coupled initialization appeared before in Daniely (2020) for analyzing well-spread random inputs on the sphere. The initialization is chosen in such a way as to ensure that for each of the input points, the initial value of the network is . Here we present an independent and novel analysis, where this property is leveraged repeatedly to bound the iterations of the optimization, which yields significantly improved worst case bounds for any input. This is crucial for our analysis, and is precisely what allows us to remove the factor that multiplies the right-hand-side of (1) in previous work. Indeed, that factor was there precisely to ensure that the initial value of the network is small. One might worry that our initialization causes the weights to be dependent. Indeed, each weight vector occurs exactly twice in the hidden layer. We are able to show that this dependence does not cause problems for our analysis. In particular, the minimum eigenvalue bounds of the associated kernel matrix and the separation margin in the NTK-induced feature space required for convergence in previous work can be shown to still hold, since such analyses are loose enough to accommodate such dependencies. Now, we have a similar initialization as in previous work, but since we no longer need a factor in (1), we can show that we can change the learning rate of gradient descent from that in previous work and it no longer needs to be balanced with the initial value, since the latter is . This ultimately allows for us to use a smaller over-parameterization (i.e., value of ) in our analyses. For , we have555Note that ReLU is not continuously differentiable. Slightly abusing notation, one can view as a valid (sub)gradient given in the RHS of (2). This extends to as the RHS of (4) and (5) which yields the update rule (6) commonly used in practice and in related theoretical work, cf. Du et al. (2019c).
| (2) |
independent of the loss function that we aim to minimize.
2.1 Loss Functions
In this work, we mainly focus on two different types of loss functions. The binary cross-entropy (logistic) loss and the squared loss. These loss functions are arguably the most well-studied for binary classification and for regression tasks with low numerical error, respectively.
We are given a set of input data points and corresponding labels, denoted by
We make a standard normalization assumption, as in Du et al. (2019c); Song and Yang (2019); Ji and Telgarsky (2020). In the case of logistic loss, the labels are restricted to . In the case of squared loss, the labels are . In both cases, as in prior work and for simplicity, we assume that 666 We adopt the assumption for a concise presentation, but we note it can be resolved by weaker constant bounds , introducing a constant factor, cf. Du et al. (2019c), or otherwise the data can be rescaled and padded with an additional coordinate to ensure , cf. Allen-Zhu et al. (2019a). , . We also define the output function on input to be . At time , let be the prediction vector, where each is defined to be
| (3) |
For simplicity, we use to denote in later discussion.
We consider the objective function :
where the individual logistic loss is defined as , and the individual squared loss is given by .
For logistic loss, we can compute the gradient55footnotemark: 5 of in terms of
| (4) |
For squared loss, we can compute the gradient55footnotemark: 5 of in terms of
| (5) |
We apply gradient descent to optimize the weight matrix with the following standard update rule,
| (6) |
where determines the step size.
In our analysis, we assume that consists of blocks of Gaussian vectors, where in each block, there are identical copies of the same Gaussian vector. Thus, we have . Ultimately we show it already suffices to set and . We use to denote the -th row of the -th block, where and . When there is no confusion, we also use to denote the -th row of , .
3 Our Results
Our results are summarized and compared to previous work in Table 1. Our first main result is an improved general upper bound for the width of a neural network for binary classification, where training is performed by minimizing the cross-entropy (logistic) loss. We need the following assumption which is standard in previous work in this regime Ji and Telgarsky (2020).
Assumption 3.1 (informal version of Definition C.1 and Assumption C.1).
We assume that there exists a mapping with for all and margin such that
| References | Width | Iterations | Loss function |
| Ji and Telgarsky (2020) | logistic loss | ||
| Our work | logistic loss | ||
| Ji and Telgarsky (2020) | N/A | logistic loss | |
| Our work | N/A | logistic loss | |
| Du et al. (2019c) | squared loss | ||
| Song and Yang (2019) | squared loss | ||
| Our work | squared loss |
Our theorem improves the previous best upper bound of Ji and Telgarsky (2020) from to only . As a side effect, we also remove the dependence of the number of iterations.
Theorem 3.1 (informal version of Theorem E.1).
Given labeled data points in -dimensional space, consider a two-layer ReLU neural network with width . Starting from a coupled initialization (Def. 2.1), for any accuracy , we can ensure the cross-entropy (logistic) training loss is less than when running gradient descent for iterations.
As a corollary of Theorem 3.1, we immediately obtain the same significant improvement from to only for the generalization results of Ji and Telgarsky (2020). To this end, we first extend Assumption 3.1 to hold for any data generating distribution instead of a fixed input data set:
Assumption 3.2.
Ji and Telgarsky (2020) We assume that there exists a mapping with for all and margin such that
for almost all sampled from the data distribution .
By simply replacing the main result, Theorem 2.2 of Ji and Telgarsky (2020) by our Theorem 3.1 in their proof666We note that in Theorem 3.1 we did not bound the distance between the weights at each step compared to the initialization . Since this can be done exactly as in Theorem 2.2 of Ji and Telgarsky (2020), we omit this detail for brevity of presentation., we obtain the following improved generalization bounds with full gradient descent:
Corollary 3.1.
Given a distribution over labeled data points in -dimensional space, consider a two-layer ReLU neural network with width . Starting from a coupled initialization (Def. 2.1), with constant probability over the data samples from and over the random initialization, it holds for an absolute constant that
where denotes the step attaining the smallest empirical risk before iterations.
Corollary 3.2.
Under Assumption 3.2, given , and a uniform random sample of size and it holds with constant probability that where denotes the step attaining the smallest empirical risk before iterations.
We finally note that the improved generalization bound can be further extended exactly as in Ji and Telgarsky (2020) to work for stochastic gradient descent.
Next, we turn our attention to lower bounds. We provide an unconditional linear lower bound, and note that Lemma D.4 yields an lower bound for any loss function, in particular also for squared loss; see Sec. 4.2.
Theorem 3.2 (informal version of Lemma D.4).
There exists a data set in -dimensional space, such that any two-layer ReLU neural network with width necessarily misclassifies at least points.
Next, we impose the same assumption as in Ji and Telgarsky (2020), namely, that separability is possible at initialization of the NTK analysis. Formally, this means that there exists such that no has . Under this condition we improve their lower bound of to :
Theorem 3.3 (informal version of Lemma D.3).
There exists a data set of size in -dimensional space, such that for any two-layer ReLU neural network with width it holds with constant probability over the random initialization of that for any weights there exists at least one index such that .
As pointed out in Ji and Telgarsky (2020) this does not necessarily mean that gradient descent cannot achieve arbitrarily small training error for lower width, but the NTK analysis fails in this case.
An even stronger assumption is that we must rely on the finite dimensional separator in the analysis of Ji and Telgarsky (2020) that mimics the NTK separator in the RKHS achieving a margin of . In this case we can show that our upper bound is indeed tight, i.e., for this natural choice of and the necessity of a union bound over points, we have , which follows from the following lemma.
Lemma 3.4 (informal version of Lemma F.1).
There exists a data set in -dimensional space, such that for the two-layer ReLU neural network with parameter matrix and width , with constant probability there exists an such that .
In fact, this is also the only place in our improved analysis where the width depends on ; everywhere else it only depends on . Our linear upper bound for the -dimensional space gets around this lower bound by defining a different in Lemma F.2:
Lemma 3.5 (follows directly using Lemma F.2 in the analysis of Theorem 3.1).
Given labeled data points in -dimensional space, consider a two-layer ReLU neural network with width . Starting from a coupled initialization (Def. 2.1), for arbitrary accuracy , we can ensure the cross-entropy (logistic) training loss is less than when running gradient descent for iterations.
However, the construction in Lemma F.2 / 3.5 uses a net argument of size to discretize the points on the sphere, and that – already in dimensions – matches the quadratic general upper bound and becomes worse in higher dimensions. It thus remains an open question whether there are better separators in dimensions or if the quadratic lower bound is indeed tight. We also present a candidate hard instance, for which we conjecture that it has an lower bound, up to logarithmic factors, for any algorithm; see Sec. 4.2.
Next, we move on to the analysis of the squared loss. We first state our assumption that is standard in the literature on the width of neural networks, and is necessary to guarantee the existence of an arbitrarily accurate parameterization Du et al. (2019c); Song and Yang (2019).
Assumption 3.3.
Let be the NTK kernel matrix where for each we have that equals
We assume in the following that the smallest eigenvalue of satisfies , for some value .
We state our main result for squared loss as follows:
4 Technical Overview
4.1 Logarithmic Width for Logistic Loss, Upper Bound
The work of Ji and Telgarsky (2020) shows that we can bound the actual logistic loss averaged over gradient descent iterations using any reference parameterization in the following NTK bound:
| (7) |
where . It seems very natural to choose where is a reasonably good separator for the NTK points with bounded norm , meaning that for all it holds that . It thus has the same margin as in the infinite case up to constants. This already implies that the first term of Eq. (7) is sufficiently small when we choose roughly iterations. Now, in order to bound the second term, Ji and Telgarsky (2020) propose to show for every , which is implied if for each index we have that
is sufficiently large. Here, we can leverage the coupled initialization scheme (Def. 2.1) to prove Theorem 3.1: bounding the first term for random Gaussian parameters, this results in roughly the value , but now since for each Gaussian vector there is another identical Gaussian with opposite signs, those simply cancel and we have in the initial state.
To bound the second term, the previous analysis Ji and Telgarsky (2020) relied on a proper scaling with respect to the parameters and , where the requirement that led to a bound of roughly . Using the coupled initialization, however, the terms again cancel in such a way that the scaling does not matter, and in particular does not need to be balanced among the variables. Another crucial insight is that the gradient is entirely independent of the scale of the parameter vectors in . This implies and thus again, notably without any implications for the width of the neural network!
Indeed, the only place in the analysis where the width is constrained by roughly occurs when bounding the contribution of the third term by . This is done exactly as in Ji and Telgarsky (2020) by a Hoeffding bound to relate the separation margin of the finite subsample to the separation margin of the infinite width case, i.e.,
| (8) |
followed by a union bound over all input points.
4.2 Logarithmic Width for Logistic Loss, Lower Bounds
Our assumption on the separation margin is formally defined in Section C where we also give several examples and useful lemmas to bound . Our lower bounds in Section D are based on the following hard instance in dimensions. The points are equally spaced and with alternating labels on the unit circle.
Formally, let be divisible by . We define the alternating points on the circle data set to be , and we put for each .
A natural choice for would send any to its closest point in our data set , multiplied by its label. However, applying Lemma C.2 gives us the following improved mapping, which is even optimal by Lemma C.5: note that for any that is not collinear with any input point, there exists a unique such that . Instead of mapping to the closest input point, in what follows, we map to a point that is nearly orthogonal to ,
More precisely we define by
 |
See Fig. 1 for an illustration. We show in Lemma D.2 that and consequently . Now we can derive our lower bounds under increasingly stronger assumptions as follows:
For the first unconditional bound, Theorem 3.2, we map the input points on the unit circle by contraction to the unit ball and note that by doing so, the labels remain in alternating order. Next we note that the output function of our network restricted to the ball is a piecewise linear function of and thus its gradient can only change in the vertices of the ball or where is orthogonal to one of the parameter vectors , i.e., at most times. Now consider any triple of consecutive points. Since they have alternating labels, the gradient needs to change at least once for each triple. Consequently , improving the conditional lower bound in Ji and Telgarsky (2020). We remark that since the argument only depends on the output function but not on the loss function, Lemma D.4 yields an lower bound for any loss function, in particular also for squared loss.
Now consider any argument that relies on an NTK analysis, where the fist step is to show that for our choice of the width , we have separability at initialization; this is how the argument in Ji and Telgarsky (2020) proceeds. Formally, assume that there exists such that for all , we have . This condition enables us to show an improved lower bound, Theorem 3.3, as follows. Partition our data set into tuples, each consisting of four consecutive points. Now consider the event that there exists a point such that all parameter vectors satisfy
which implies that at least one of the points in is misclassified. To avoid this, it means that our initialization necessarily needs to include, for each divisible by , a vector that hits the areas orthogonal to the cones separating two points out of the quadruple. There are quadruples to hit, each succeeding with probability with respect to the Gaussian measure. This is exactly the coupon collector’s problem, where the coupons are the quadruples, and it is known Erdős and Rényi (1961) that are necessary to collect all items with constant probability, which yields our improved lower bound for this style of analysis. One thus needs a different approach beyond NTK to break this barrier, cf. Ji and Telgarsky (2020).
For the upper bound, Theorem 3.1, we further note that the existence of an NTK separator as above is not sufficient, i.e., we need to construct a separator satisfying the separability condition. Moreover, to achieve a reasonable bound in terms of the margin parameter we also need that achieves a separation margin of . To do so, it seems natural to construct such that for all . Indeed, this is the most natural choice because the resulting separation margin in the finite case is exactly the empirical mean estimator for the infinite case and thus standard concentration bounds (Hoeffing’s bound) yield the necessary proximity of the margins between the two cases, cf. Eq. (8). Let us assume we fix this choice of . This condition enables us to prove a quadratic lower bound, Lemma 3.4, which shows that our analysis of the upper bound is actually tight: for our alternating points on a circle example, the summands have high variance, and therefore Hoeffding’s bound is tight by a matching lower bound Feller (1943). Consequently, , and one would need a different definition of and a non-standard estimation of to break this barrier.
Finally, we conjecture that the quadratic upper bound is actually tight in general. Specifically, we conjecture the following: take random points on the sphere in dimensions and assign random labels . Then the NTK margin is .
If the conjecture is true, we obtain an lower bound for , up to logarithmic factors.777This might be confusing, since we argued before that such data is particularly mild for the squared loss function. This may be due to the different loss functions, but regardless, it does not contradict the bound of Daniely (2020) for the same data distribution in the squared loss regime, since . Indeed, we can round the weights to the nearest vectors in a net of size , which only changes by a constant factor. Then, if we could classify with zero error, we would encode random labels using bits, which implies . We note that Ji and Telgarsky (2020) gave an upper bound for the margin of any data with random labels, but we would need a matching lower bound for this instance in order for this argument to work.
4.3 Polynomial Width for Squared Loss
The high level intuition of our proof of Theorem 3.6 is to recursively prove the following: (1) the weight matrix does not change much, and (2) given that the weight matrix does not change much, the prediction error, measured by the squared loss, decays exponentially.
Given (1) we prove (2) as follows. The intuition is that the kernel matrix does not change much, since the weights do not change much, and it is close to the initial value of the kernel matrix, which is in turn close to the NTK matrix, involving the entire Gaussian distribution rather than our finite sample. The NTK matrix has a lower bound on its minimum eigenvalue by Assumption 3.3. Thus, the prediction loss decays exponentially.
Given (2) we prove (1) as follows. Since the prediction error decays exponentially, one can show that the change in weights is upper bounded by the prediction loss, and thus the change in weights also decays exponentially and the total change is small.
First, we show a concentration lemma for initialization:
Lemma 4.1 (Informal version of Lemma G.1).
Let . Let denote a collection of vectors constructed as in Definition 2.1. We define as follows
Let . If , we have that
holds with probability at least .
Second, we can show a perturbation bound for random weights.
Lemma 4.2 (Informal version of Lemma G.2).
Let . Let denote a collection of weight vectors constructed as in Definition 2.1. For any set of weight vectors that satisfy that for any , , consider the map defined by . Then we have that holds with probability at least .
Next, we have the following lemma (see Section I for a formal proof) stating that the weights should not change too much. Note that the lemma is a variation of Corollary 4.1 in Du et al. (2019c).
Lemma 4.3.
If Eq. (16) holds for , then we have for all
Next, we calculate the difference of predictions between two consecutive iterations, analogous to the term in Fact H.1. For each , we have
where
Here we divide the right hand side into two parts. First, represents the terms for which the pattern does not change, while represents the terms for which the pattern may change. For each , we define the set as
Then we define and as follows
Claim 4.4.
5 Discussion
We present a novel worst case analysis using an initialization scheme for neural networks involving coupled weights. This technique is versatile and can be applied in many different settings. We give an improved analysis based on this technique to reduce the parameterization required to show the convergence of -layer neural networks with ReLU activations in the under-parameterized regime for the logistic loss to , which significantly improves the prior bound. We further introduce a new unconditional lower bound of as well as conditional bounds to narrow the gap in this regime. We also reduce the amount of over-parameterization required for the standard squared loss function to roughly , improving the prior bound, and coming closer to the lower bound. We believe this is a significant theoretical advance towards explaining the behavior of -layer neural networks in different settings. It is an intriguing open question to close the gaps between upper and lower bounds in both the under and over-parameterized settings. We note that the quadratic dependencies arise for several fundamental reasons in our analysis, and are already required to show a large minimum eigenvalue of our kernel matrix, or a large separation margin at initialization. In the latter case we have provided partial evidence of optimality by showing that our analysis has an lower bound, as well as a candidate hard instance for any possible algorithm. Another future direction is to extend our results to more than two layers, which may be possible by increasing by a factor, where denotes the network depth Chen et al. (2019). We note that this also has not been done in earlier work Ji and Telgarsky (2020).
Acknowledgements
We thank the anonymous reviewers and Binghui Peng for their valuable comments. Alexander Munteanu and Simon Omlor were supported by the German Research Foundation (DFG), Collaborative Research Center SFB 876, project C4 and by the Dortmund Data Science Center (DoDSc). David Woodruff would like to thank NSF grant No. CCF-1815840, NIH grant 5401 HG 10798-2, ONR grant N00014-18-1-2562, and a Simons Investigator Award.
References
- Allen-Zhu et al. (2019a) Zeyuan Allen-Zhu, Yuanzhi Li, and Yingyu Liang. Learning and generalization in overparameterized neural networks, going beyond two layers. In Advances in neural information processing systems, pages 6155–6166, 2019a.
- Allen-Zhu et al. (2019b) Zeyuan Allen-Zhu, Yuanzhi Li, and Zhao Song. A convergence theory for deep learning via over-parameterization. In ICML, 2019b.
- Allen-Zhu et al. (2019c) Zeyuan Allen-Zhu, Yuanzhi Li, and Zhao Song. On the convergence rate of training recurrent neural networks. In NeurIPS, 2019c.
- Arora et al. (2019a) Sanjeev Arora, Simon S Du, Wei Hu, Zhiyuan Li, Ruslan Salakhutdinov, and Ruosong Wang. On exact computation with an infinitely wide neural net. In NeurIPS. arXiv preprint arXiv:1904.11955, 2019a.
- Arora et al. (2019b) Sanjeev Arora, Simon S Du, Wei Hu, Zhiyuan Li, and Ruosong Wang. Fine-grained analysis of optimization and generalization for overparameterized two-layer neural networks. In ICML. arXiv preprint arXiv:1901.08584, 2019b.
- Bakshi et al. (2019) Ainesh Bakshi, Rajesh Jayaram, and David P Woodruff. Learning two layer rectified neural networks in polynomial time. In Conference on Learning Theory (COLT), pages 195–268. PMLR, 2019.
- Bernstein (1924) Sergei Bernstein. On a modification of chebyshev’s inequality and of the error formula of laplace. Ann. Sci. Inst. Sav. Ukraine, Sect. Math, 1(4):38–49, 1924.
- Blum et al. (2020) Avrim Blum, John Hopcroft, and Ravi Kannan. Foundations of Data Science. Cambridge University Press, 2020.
- Brand et al. (2021) Jan van den Brand, Binghui Peng, Zhao Song, and Omri Weinstein. Training (overparametrized) neural networks in near-linear time. In ITCS, 2021.
- Bubeck et al. (2020) Sébastien Bubeck, Ronen Eldan, Yin Tat Lee, and Dan Mikulincer. Network size and size of the weights in memorization with two-layers neural networks. In NeurIPS, 2020.
- Cao and Gu (2019a) Yuan Cao and Quanquan Gu. A generalization theory of gradient descent for learning over-parameterized deep relu networks. CoRR, abs/1902.01384, 2019a. URL http://arxiv.org/abs/1902.01384.
- Cao and Gu (2019b) Yuan Cao and Quanquan Gu. Generalization bounds of stochastic gradient descent for wide and deep neural networks. In NeurIPS, pages 10835–10845, 2019b.
- Chen and Xu (2020) Lin Chen and Sheng Xu. Deep neural tangent kernel and laplace kernel have the same rkhs. arXiv preprint arXiv:2009.10683, 2020.
- Chen et al. (2020) Sitan Chen, Adam R. Klivans, and Raghu Meka. Learning deep relu networks is fixed-parameter tractable. arXiv preprint arXiv:2009.13512, 2020.
- Chen et al. (2019) Zixiang Chen, Yuan Cao, Difan Zou, and Quanquan Gu. How much over-parameterization is sufficient to learn deep relu networks? CoRR, abs/1911.12360, 2019. URL http://arxiv.org/abs/1911.12360.
- Chernoff (1952) Herman Chernoff. A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. The Annals of Mathematical Statistics, pages 493–507, 1952.
- Collobert et al. (2011) Ronan Collobert, Jason Weston, Léon Bottou, Michael Karlen, Koray Kavukcuoglu, and Pavel Kuksa. Natural language processing (almost) from scratch. Journal of machine learning research, 12(ARTICLE):2493–2537, 2011.
- Daniely (2020) Amit Daniely. Neural networks learning and memorization with (almost) no over-parameterization. In Advances in Neural Information Processing Systems 33, (NeurIPS), 2020.
- Devlin et al. (2018) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805, 2018.
- Du et al. (2019a) Simon S Du, Kangcheng Hou, Barnabás Póczos, Ruslan Salakhutdinov, Ruosong Wang, and Keyulu Xu. Graph neural tangent kernel: Fusing graph neural networks with graph kernels. arXiv preprint arXiv:1905.13192, 2019a.
- Du et al. (2019b) Simon S Du, Jason D Lee, Haochuan Li, Liwei Wang, and Xiyu Zhai. Gradient descent finds global minima of deep neural networks. In International Conference on Machine Learning (ICML). https://arxiv.org/pdf/1811.03804, 2019b.
- Du et al. (2019c) Simon S Du, Xiyu Zhai, Barnabas Poczos, and Aarti Singh. Gradient descent provably optimizes over-parameterized neural networks. In ICLR. https://arxiv.org/pdf/1810.02054, 2019c.
- Erdős and Rényi (1961) P. Erdős and A. Rényi. On a classical problem of probability theory. Magyar Tud. Akad. Mat. Kutató Int. Közl., 6:215–220, 1961.
- Feller (1943) William Feller. Generalization of a probability limit theorem of cramér. Trans. Am. Math. Soc., 54:361–372, 1943.
- Ge et al. (2018) Rong Ge, Jason D. Lee, and Tengyu Ma. Learning one-hidden-layer neural networks with landscape design. In ICLR, 2018.
- He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR), pages 770–778, 2016.
- Hoeffding (1963) Wassily Hoeffding. Probability inequalities for sums of bounded random variables. Journal of the American Statistical Association, 58(301):13–30, 1963.
- Huang and Yau (2020) Jiaoyang Huang and Horng-Tzer Yau. Dynamics of deep neural networks and neural tangent hierarchy. In International Conference on Machine Learning (ICML), pages 4542–4551. PMLR, 2020.
- Jacot et al. (2018) Arthur Jacot, Franck Gabriel, and Clément Hongler. Neural tangent kernel: convergence and generalization in neural networks. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NeurIPS), pages 8580–8589, 2018.
- Ji and Telgarsky (2020) Ziwei Ji and Matus Telgarsky. Polylogarithmic width suffices for gradient descent to achieve arbitrarily small test error with shallow relu networks. In ICLR, 2020.
- Kawaguchi and Huang (2019) Kenji Kawaguchi and Jiaoyang Huang. Gradient descent finds global minima for generalizable deep neural networks of practical sizes. In 2019 57th Annual Allerton Conference on Communication, Control, and Computing (Allerton), pages 92–99. IEEE, 2019.
- Krizhevsky et al. (2012) Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems, 25:1097–1105, 2012.
- LeCun et al. (1998) Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
- Lee et al. (2020) Jason D Lee, Ruoqi Shen, Zhao Song, Mengdi Wang, and Zheng Yu. Generalized leverage score sampling for neural networks. In NeurIPS, 2020.
- Li et al. (2021) Xiaoxiao Li, Meirui Jiang, Xiaofei Zhang, Michael Kamp, and Qi Dou. Fedbn: Federated learning on non-iid features via local batch normalization. In International Conference on Learning Representations (ICLR). https://openreview.net/forum?id=6YEQUn0QICG, 2021.
- Li and Liang (2018) Yuanzhi Li and Yingyu Liang. Learning overparameterized neural networks via stochastic gradient descent on structured data. In NeurIPS, 2018.
- Li and Yuan (2017) Yuanzhi Li and Yang Yuan. Convergence analysis of two-layer neural networks with ReLU activation. In Advances in neural information processing systems (NIPS), pages 597–607, 2017.
- Nitanda et al. (2019) Atsushi Nitanda, Geoffrey Chinot, and Taiji Suzuki. Gradient descent can learn less over-parameterized two-layer neural networks on classification problems. arXiv preprint arXiv:1905.09870, 2019.
- Oymak and Soltanolkotabi (2020) Samet Oymak and Mahdi Soltanolkotabi. Toward moderate overparameterization: Global convergence guarantees for training shallow neural networks. IEEE Journal on Selected Areas in Information Theory, 1(1):84–105, 2020.
- Silver et al. (2016) David Silver, Aja Huang, Chris J Maddison, Arthur Guez, Laurent Sifre, George Van Den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, et al. Mastering the game of go with deep neural networks and tree search. nature, 529(7587):484–489, 2016.
- Silver et al. (2017) David Silver, Julian Schrittwieser, Karen Simonyan, Ioannis Antonoglou, Aja Huang, Arthur Guez, Thomas Hubert, Lucas Baker, Matthew Lai, Adrian Bolton, et al. Mastering the game of go without human knowledge. nature, 550(7676):354–359, 2017.
- Song and Yang (2019) Zhao Song and Xin Yang. Quadratic suffices for over-parametrization via matrix chernoff bound. arXiv preprint arXiv:1906.03593, 2019.
- Song et al. (2021) Zhao Song, Shuo Yang, and Ruizhe Zhang. Does preprocessing help training over-parameterized neural networks? Advances in Neural Information Processing Systems (NeurIPS), 34, 2021.
- StEx (2011) StEx StEx. How can we sum up sin and cos series when the angles are in arithmetic progression? https://math.stackexchange.com/questions/17966/, 2011. Accessed: 2021-05-21.
- Szegedy et al. (2015) Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, and Andrew Rabinovich. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1–9, 2015.
- Tropp (2015) Joel A Tropp. An introduction to matrix concentration inequalities. Foundations and Trends® in Machine Learning, 8(1-2):1–230, 2015.
- Zhang et al. (2021) Jiawei Zhang, Yushun Zhang, Mingyi Hong, Ruoyu Sun, and Zhi-Quan Luo. When expressivity meets trainability: Fewer than neurons can work. In Advances in Neural Information Processing Systems 34 (NeurIPS), pages 9167–9180, 2021.
- Zhong et al. (2017a) Kai Zhong, Zhao Song, and Inderjit S. Dhillon. Learning non-overlapping convolutional neural networks with multiple kernels. arXiv preprint arXiv:1711.03440, 2017a.
- Zhong et al. (2017b) Kai Zhong, Zhao Song, Prateek Jain, Peter L. Bartlett, and Inderjit S. Dhillon. Recovery guarantees for one-hidden-layer neural networks. In ICML, 2017b.
- Zou and Gu (2019) Difan Zou and Quanquan Gu. An improved analysis of training over-parameterized deep neural networks. In NeurIPS, pages 2053–2062, 2019.
Appendix
Appendix A Probability Tools
In this section we introduce the probability tools that we use in our proofs. Lemma A.1, A.2 and A.3 concern tail bounds for random scalar variables. Lemma A.4 concerns the cumulative density function of the Gaussian distribution. Finally, Lemma A.5 concerns a concentration result for random matrices.
Lemma A.1 (Chernoff bound Chernoff (1952)).
Let , where with probability and with probability , and all are independent. Let . Then
1. , ;
2. , .
Lemma A.2 (Hoeffding bound Hoeffding (1963)).
Let denote independent bounded variables in . Let . Then we have
Lemma A.3 (Bernstein’s inequality Bernstein (1924)).
Let be independent zero-mean random variables. Suppose that almost surely, for all . Then, for all positive ,
Lemma A.4 (Anti-concentration of the Gaussian distribution).
Let , that is, the probability density function of is given by . Then
Lemma A.5 (Matrix Bernstein, Theorem 6.1.1 in Tropp (2015)).
Consider a finite sequence of independent, random matrices with common dimension . Assume that
Let . Let be the matrix variance statistic of the sum:
Then
Furthermore, for all ,
Lemma A.6 (Feller (1943)).
Let be a sum of independent random variables, each attaining values in , and let . Then for all we have
where is some fixed constant.
Appendix B Preliminaries for log width under logistic loss
We consider a set of data points with and labels . The two layer network is parameterized by and as follows: we set the output function
which is scaled by a factor compared to the presentation in the main body to simplify notation, and to be more closely comparable to Ji and Telgarsky (2020). The changed initialization yields initial output of , independent of the normalization, and thus, consistent with the introduction, we could as well omit the normalization here and instead use it only in the learning rate. The main improvement of the network width comes from the fact that the learning rate is no compromise between the right normalization in the initial state and the appropriate progress in the gradient iterations, but can be adjusted to ensure the latter independent of the former. In the output function, denotes the ReLU function for . To simplify notation we set . Further we set to be the logistic loss function. We use a random initialization given in Definition 2.1. Our goal is to minimize the empirical loss of given by
To accomplish this, we use a standard gradient descent algorithm. More precisely for we set
for some step size . Further, it holds that
Moreover, we use the following notation
and
Note that . In particular the gradient is independent of , which will be crucial in our improved analysis.
Appendix C Main assumption and examples
C.1 Main assumption
Here, we define the parameter which was also used in Ji and Telgarsky (2020). Intuitively, determines the separation margin of the NTK. Let be the unit ball in dimensions. We set to be the set of functions mapping from to . Let denote the Gaussian measure on , specified by the Gaussian density with respect to the Lebesgue measure on .
Definition C.1.
Given a data set and a map we set
We say that is optimal if .
We note that always exists since is a set of bounded functions on a compact subset of . We make the following assumption, which is also used in Ji and Telgarsky (2020):
Assumption C.1.
It holds that .
Before we prove our main results we show some properties of to develop a better understanding of our assumption. The following lemma shows that the integral can be viewed as a finite sum over certain cones in . Given we define the cone
Note that and that . Further we set to be the probability that a random Gaussian is an element of and to be the probability measure of random Gaussians restricted to the event that . The following lemma shows that we do not have to consider each mapping in but it suffices to focus on a specific subset. More precisely we can assume that is constant on the cones . In particular this means we can assume for any and scalar and that is locally constant.
Lemma C.2.
Let . Then there exists such that and is constant on for any .
Proof.
Observe that for any distinct the cones and are disjoint since for any the cone containing is given by . Further we have that since any is included in some . Thus for any we have
Hence defining satisfies
and since it follows that for all . ∎
Next we give an idea how the dimension can impact . We show that in the simple case, where can be divided into orthogonal subspaces, such that each data point is an element of one of the subspaces, there is a helpful connection between a mapping and the mapping that induces on the subspaces.
Lemma C.3.
Assume there exist orthogonal subspaces of with such that for each there exists such that . Then the following two statements hold:
Part 1. Assume that for each there exists and such that for all we have
Then for each with there exists with
Part 2. Assume that maximizes the term
and that . Given any vector we denote by the projection of onto . Let . Then for all the mapping maximizes
and it holds that for all . In other words if is optimal for then is optimal for where with the corresponding labels, i.e., .
Proof.
Part 1.
Since applying the projection onto to any point does not change the scalar product of and , i.e., , we can assume that for all we have . Let . We define . Then by orthogonality
Thus it holds that . Further we have for again by orthogonality it holds that
Part 2.
For the sake of contradiction assume that there are and such that
for some . Using Part 1. we can construct a new mapping by using the mappings defined in the lemma for , and exchange by . Also as in Part 1 let for and with . Then we have
Subtracting and multiplying with gives us
Hence it holds that
For any with we have by orthogonality as in Part 1.
Further we have
We conclude again by orthogonality that
and thus contradicts the maximizing choice of . ∎
As a direct consequence we get that the problem of finding an optimal for the whole data set can be reduced to finding an optimal for each subspace.
Corollary C.4.
Assume there exist orthogonal subspaces of with such that for each there exists with . For let denote the data set consisting of all data points where . Then is optimal for if and only if for all the mapping defined in Lemma C.3 is optimal for and where .
Proof.
The following bound for simplifies calculations in some cases of interest. It also gives us a natural candidate for an optimal . Given an instance recall that . We set
| (11) |
We note that is not optimal in general but if instances have certain symmetry properties, then is optimal.
Lemma C.5.
For any subset it holds that
Proof.
By Lemma C.2 there exists an optimal that is constant on for all . For let . Then by using an averaging argument and the Cauchy–Schwarz inequality we get
∎
Finally we give an idea of how two points and their distance impacts the cones and their hitting probabilities.
Lemma C.6.
Let be two points with and . Set . Then for a random Gaussian we have with probability where . Further for any with it holds that .
Proof.
We define . Then since for a random Gaussian it holds that with probability . Since the space spanned by and is -dimensional, we can assume that and are on the unit circle and that and for . Note that is given by where is the length of the arc connecting and on the circle. Since is the Euclidean distance and thus the shortest distance between and we have . Further it holds that
Then is positive on , so is monotonously non-decreasing, and thus and . Consequently for we have that
For the second part we note that for any with we get
by using the Cauchy–Schwarz inequality. ∎
C.2 Example 1: Orthogonal unit vectors
Let us start with a simple example first: let be the -th unit vector. Let , for and otherwise with arbitrary labels. First consider the instance created by the points and for . Then we note that sending any point with to and any other point to is optimal since it holds that . Since the subspaces are orthogonal we can apply Corollary C.4 with vector . Thus the optimal for our instance is .
C.3 Example 2: Two differently labeled points at distance

The next example is a set of two points with and . Let and . Then by Lemma C.6 and . For an illustration see Figure 2.
By Lemma C.2 we can assume that there exists an optimal which is constant on and constant on for , i.e., that for all and for all .
C.4 Example 3: Constant labels
Let be any data set and let be the all s vector. Then for it holds that
Thus we have . We note that is a well-known fact, see Blum et al. (2020). Since we consider only a fixed , we can assume that equals the first standard basis vector . We are interested in the expected projection of a uniformly random unit vector in the same halfspace as .
We give a short proof for completeness: note that with , is a uniformly random unit vector . By Jensen’s inequality we have . Thus, with probability at least it holds that , by a Markov bound. Also, holds with probability at least , since the right hand side is the median of the half-normal distribution, i.e., the distribution of , where . Here denotes the the Gauss error function.
By a union bound over the two events it follows with probability at least that
Consequently and thus
C.5 Example 4: The hypercube
In the following example we use for the -th coordinate of rather than for the -th data point. We consider the hypercube with different labelings. Given we set and .
C.5.1 Majority labels
First we consider the data set and assign if and if . Note that holds if and only if . Let be the constant vector that has all coordinates equal to . Now, if we fix for any , then for all we have that
Hence it follows that
C.5.2 Parity labels
Second we consider the case where . Then we get the following bounds for :
Lemma C.7.
Consider the hypercube with parity labels.
-
1)
If is odd, then .
-
2)
If is even, then .
Proof.
1): First note that the set is a null set with respect to the Gaussian measure . Fix any coordinate . W.l.o.g. let . Given consider the set . Note that is the disjoint union . Further since is even, it holds that . Let and let . W.l.o.g. let . Then we have for exactly one and . Now since we conclude that for all it holds that
and thus we get
Thus by Corollary C.5 it holds that .
2): Consider the set comprising the middle points of the edges, i.e., . Observe that for any and the dot product is an odd integer and thus . Hence, for the cone containing we have .
Now fix and let be the coordinate with . Recall and set . Let be any coordinate other than and consider the pairs where with , and . We denote the union of all those pairs by . The points and have the same entry at coordinate but different labels. Hence it holds that .
Next consider the set of remaining vectors with which is given by . For all with it holds that since the projection of to that results from removing the -th entry of , has Hamming distance to projected to , and vice versa for all with we have that . Hence for it holds that and thus we have
since the number of elements with is the same as the number of elements with . More specifically, it equals the number of points with Hamming distance to the projection of onto , which is since the -th coordinate is fixed and we need to choose coordinates that differ from the remaining coordinates of . Let be the probability that a random Gaussian is in the same cone as for some . Then by symmetry it holds that . ∎
Appendix D Lower bounds for log width
D.1 Example 5: Alternating points on a circle
Next consider the following set of points for divisible by :
and .
Intuitively, defining to send to the closest point of our data set multiplied by its label, gives us a natural candidate for .
However, applying Lemma C.2 gives us a better mapping that also follows from Equation (11), and which is optimal by Lemma C.5:
Define the set
Now, for any there exists a unique such that .
We set .
We define the function by
Observe that for we have
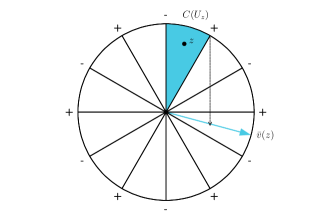
Figure 3 shows how is constructed for . We note that holds almost surely, which in particular implies the optimality of , cf. Equation (11). For computing we need the following lemma.
 |
 |
We found the result in a post on math.stackexchange.com but could not find it in published literature and so we reproduce the full proof from StEx (2011) for completeness of presentation.
Lemma D.1 (StEx (2011)).
For any and it holds that
Proof.
We use to denote the imaginary unit defined by the property . From Euler’s identity we know that and . Then
∎
Lemma D.2.
For all it holds that
Proof.
We set . Note that by symmetry the value of the given integral is the same for all . Thus it suffices to compute for , and note that for this special choice. See Figure 3 for an illustration of the following argument. For a fixed consider the cone . Then and since . Further, for it holds that
and by using the symmetry of we get
Now assume w.l.o.g. that . Further we set and . By using Lemma D.1 and the Taylor series expansion of and we get
when is odd then we have an exact equality. ∎
D.2 Lower Bounds
Lemma D.3.
If then with constant probability over the random initialization of it holds for any weights that for at least one .
Proof.
We set for . Consider the set for with . For any let denote the event that
If there exists such that for all the event is true then at least one of the points is misclassified. To see this, note that there exists such that since the line connecting and crosses the line segment between and . Now let . If the event is true for all then it holds that
and since it must hold for at least one .
Note that is false with probability , namely if is between the point and or between the points and . We denote the union of these areas by . Further these areas are disjoint for different . Now, as we have discussed above, we need at least one to be false for each . This occurs only if for each there exists at least one such that . Let be the minimum number of trials needed to hit every one of the regions . This is the coupon collector’s problem for which it is known Erdős and Rényi (1961) that for arbitrary it holds that as . Thus for sufficiently large and we have
∎
Indeed we can show an even stronger result:
Lemma D.4.
Let . Any two-layer ReLU neural network with width misclassifies more than points of the alternating points on the circle example.
Proof.
Set . Given parameters and consider the function given by . Note that the points do not change their order along the sphere and thus by definition of have alternating labels. Also note that if and only if . Further note that the restriction of to denoted is a piecewise linear function. More precisely the gradient can only change at the points and at points orthogonal to some for . Since for each there are exactly two points on that are orthogonal to this means the gradient changes at most times. Now for divisible by 3 consider the points . If the gradient does not change in the interval induced by and then at least one of the three points is misclassified. Hence if then strictly more than an -fraction of the points is misclassified. ∎
Appendix E Upper bound for log width
We use the following initialization, see Definition 2.1: we set for some natural number . Put where is an appropriate scaling factor to be defined later and for and for . We note that to simplify notations the are permuted compared to Definition 2.1, which does not make a difference. Further note that .
The goal of this section is to show our main theorem:
Theorem E.1.
Given an error parameter and any failure probability , let Then if
and we have with probability at most over the random initialization that , where .
Before proving Theorem E.1 we need some helpful lemmas. Our first lemma shows that with high probability there is a good separator at initialization, similar to Ji and Telgarsky (2020).
Lemma E.1.
If then there exists with for all , and , such that with probability at least it holds simultaneously for all that
Proof.
We define by . Observe that
by assumption. Further since and , we have for . Also by Lemma C.2 we can assume that . Thus
is the empirical mean of i.i.d. random variables supported on with mean . Therefore by Hoeffding’s inequality (Lemma A.2), using it holds that
Applying the union bound proves the lemma. ∎
Lemma E.2.
With probability it holds that for all and
Proof.
By anti-concentration of the Gaussian distribution (Lemma A.4), we have for any
Thus applying the union bound proves the lemma. ∎
Lemma E.3.
For all it holds that
Proof.
Since we have
∎
Further we need the following lemma proved in Ji and Telgarsky (2020).
Lemma E.4 (Lemma 2.6 in Ji and Telgarsky (2020)).
For any and , if then
Consequently, if we use a constant step size for , then
Now we are ready to prove the main theorem:
Proof of Theorem E.1.
With probability at least there exists as in Lemma E.1 and also the statement of Lemma E.2 holds. We set . First we show that for any and any we have . Observe that since for all . Thus for any we have
Consequently we have for .
Next we prove that for any we have . Since for any , the logistic loss satisfies ), and it is sufficient to prove that for any we have
Note that
For the first term we have by Lemma E.3. For the second term we note that . Thus can only hold if which is false for all by Lemma E.2. Hence it holds that
and consequently . It follows for the second term that
Moreover by Lemma E.1 for the third term it follows
Thus since . Consequently it holds that .
Appendix F On the construction of
F.1 Tightness of the construction of
We note that for the construction of used in the upper bound of Lemma E.1 is tight in the following sense: For , the natural estimator of is given by the empirical mean . The following lemma shows that using this estimator, the bound given in Lemma E.1 is tight with respect to the squared dependence on up to a constant factor. In particular we need if we want to use the union bound over all data points.
Lemma F.1.
Fix the choice of for . Then for each there exists an instance and , such that for each it holds with probability at least for an absolute constant that
Proof of Lemma F.1.
Consider Example D.1. Recall that . Choose a sufficiently large , divisible by , such that . Note that the mapping that we constructed, has a high variance since for any , the probability that a random Gaussian satisfies as well as the probability that are equal to . To see this, note that if and in this case is negative with probability . Thus the variance of is at least . Observe that the random variable attains values in . Further the expected value of is , and the variance is at least . Now set and note that holds if and only if . By Lemma D.4 we know that is true for at least one if . Now choosing large enough this implies we only need to show the result for . Hence we can apply Lemma A.6 to and get
for or equivalently which holds if is large enough. ∎
Thus we need that for the given error probability if we construct as in Lemma E.1.
F.2 The two dimensional case (upper bound)
In the following we show how we can improve the construction of in the special case of such that
suffices for getting the same result as in Theorem E.1. We note that the only place where we have a dependence on is in Lemma E.1. It thus suffices to replace it by the following lemma that improves the dependence to in the special case of :
Lemma F.2.
Let be an instance in dimensions. Then there exists a constant such that for with probability there exists with for all , and , such that
for all .
Proof.
The proof consists of three steps. The first step is to construct a net that consists only of ‘large cones of positive volume’ such that for each data point there exists a point whose distance from on the circle is at most : Let and consider the set
Given we define and , where ties are broken arbitrarily. We set . We note that the distance on the circle between two neighboring points in is a multiple of . This implies that for any cone between consecutive points in with we have and . Further note that there are at most cones of this form.
The second step is to construct a separator : Let be optimal for , i.e., . As in Lemma C.2 construct with where is constant for any cone of the form . Using the Chernoff bound (A.1) we get with failure probability at most that the number of points in lies in the interval . Now using and applying a union bound we get that this holds for all cones of the form with failure probability at most . For we define . Since it follows that and consequently . Moreover we have
where we set to be equal to , which is constant for any .
The third step is to prove that is a good separator for : To this end, let and .
If then
Otherwise if then there is exactly one cone with such that and and exactly one cone with such that and . Recall that for . We set . Then it holds that
∎
Appendix G Width under squared loss
G.1 Analysis: achieving concentration
We first present a high-level overview. In Lemma G.1, we prove that the initialization (kernel) matrix is close to the neural tangent kernel (NTK). In Lemma G.2, we bound the spectral norm change of , given that the weight matrix does not change much. In Section H.1 we consider the (simplified) continuous case, where the learning rate is infinitely small. This provides most of the intuition. In Section H.2 we consider the discretized case where we have a finite learning rate. This follows the same intuition as in the continuous case, but we need to deal with a second order term given by the gradient descent algorithm.
The high level intuition of the proof is to recursively prove the following:
-
1.
The weight matrix does not change much.
-
2.
Given that the weight matrix does not change much, the prediction error decays exponentially.
Given (1) we prove (2) as follows. The intuition is that the kernel matrix does not change much, since the weights do not change much, and it is close to the initial value of the kernel matrix, which is in turn close to the NTK matrix (involving the entire Gaussian distribution rather than our finite sample), that has a lower bound on its minimum eigenvalue. Thus, the prediction loss decays exponentially.
Given (2) we prove (1) as follows. Since the prediction error decays exponentially, one can show that the change in weights is upper bounded by the prediction loss, and thus the change in weights also decays exponentially and the total change is small.
G.2 Bounding the difference between the continuous and discrete case
In this section, we show that when the width is sufficiently large, then the continuous version and discrete version of the Gram matrix of the input points are spectrally close. We prove the following Lemma, which is a variation of Lemma 3.1 in Song and Yang (2019) and also of Lemma 3.1 in Du et al. (2019c).
Lemma G.1 (Formal statement of Lemma 4.1).
Let denote a collection of vectors constructed as in Definition 2.1. We define as follows
Let . If , we have that
holds with probability at least .
Proof.
For every fixed pair , is an average of independent random variables, i.e.,
and is the average of all sampled Gaussian vectors:
The expectation of is
Therefore,
For , let . Then is a random function of , and hence, the are mutually independent. Moreover, . By Hoeffding’s inequality (Lemma A.2), we have that for all ,
Setting , we can apply a union bound over and all pairs to get that with probability at least , for all ,
Thus, we have
Hence, if , we have the desired result. ∎
G.3 Bounding changes of when is in a small ball
In this section, we bound the change of when is in a small ball. We define the event
Note this event happens if and only if . Recall that . By anti-concentration of the Gaussian distribution (Lemma A.4), we have
| (12) |
We prove the following perturbation Lemma, which is a variation of Lemma 3.2 in Song and Yang (2019) and Lemma 3.2 in Du et al. (2019c).
Lemma G.2 (Formal version of Lemma 4.2).
Let . Let denote a collection of weight vectors constructed as in Definition 2.1. For any set of weight vectors that satisfy that for any , , consider the map defined by
Then we have that
holds with probability at least .
Proof.
The random variable we care about is
where the last step follows from defining, for each ,
Now consider that are fixed. We simplify to .
Then is a random variable that only depends on .
If events and happen, then
If or happens, then
Thus we have
and
We also have .
Fix and consider . Applying Bernstein’s inequality (Lemma A.3), we get that for all ,
Choosing , we get that
Thus, we have
Next, taking a union bound over such events,
This completes the proof. ∎
Appendix H Analysis: convergence
H.1 The continuous case
We first consider the continuous case, in which the learning rate is sufficiently small. This provides an intuition for the discrete case.
For any , we define the kernel matrix :
We consider the following dynamics of a gradient update:
| (13) |
The dynamics of prediction can be written as follows, which is a simple calculation:
Fact H.1.
Proof.
For each , we have
Lemma H.2.
Suppose for , . Let be defined as Then we have
Proof.
Recall that we can write the dynamics of prediction as
We can calculate the loss function dynamics
Thus we have and that is a decreasing function with respect to .
Using this fact, we can bound the loss by
| (14) |
Now, we can bound the gradient norm. For ,
| (15) | ||||
where the first step follows from Eq. (5) and Eq. (13), the second step follows from the triangle inequality and for and for , the third step follows from the Cauchy-Schwarz inequality, and the last step follows from Eq. (14).
Integrating the gradient, we can bound the distance from the initialization
∎
Lemma H.3.
If . then for all , . Moreover,
Proof.
Assume the conclusion does not hold at time . We argue that there must be some so that .
If , then we can simply take .
Otherwise since the conclusion does not hold, there exists so that
or
Then by Lemma H.2, there exists such that
By Lemma G.2, there exists defined as
Thus at time , there exists satisfying .
By Lemma G.2,
H.2 The discrete case
We next move to the discrete case. The major difference from the continuous case is that the learning rate is not negligible and there is a second order term for gradient descent which we need to handle.
Theorem H.4 (Formal version of Theorem 3.6).
Suppose there are input data points in -dimensional space. Recall that . Suppose the width of the neural network satisfies that
We initialize and as in Definition 2.1, and we set the step size, also called the learning rate, to be
Then with probability at least over the random initialization, we have for that
| (16) |
Further, for any accuracy parameter , if we choose the number of iterations
then
Correctness
We prove Theorem H.4 by induction. The base case is and it is trivially true. Assume for we have proved Eq. (16) to be true. We want to show that Eq. (16) holds for .
From the induction hypothesis, we have the following Lemma (see proof in Section I) stating that the weights should not change too much. Note that the Lemma is a variation of Corollary 4.1 in Du et al. (2019c).
Lemma H.5.
If Eq. (16) holds for , then we have for all
Next, we calculate the difference of predictions between two consecutive iterations, analogous to the term in Fact H.1. For each , we have
where
Here we divide the right hand side into two parts. represents the terms for which the pattern does not change, while represents the terms for which the pattern may change. For each , we define the set as
Then we define and as follows
Define and as
| (17) | ||||
| (18) |
and
Then we have (the proof is deferred to Section I)
Claim H.6.
Choice of and .
Next, we want to choose and such that
| (19) |
If we set and , we have
This implies
holds with probability at least .
Over-parameterization size, lower bound on .
Appendix I Technical claims
| Nt. | Choice | Place | Comment |
|---|---|---|---|
| Lemma G.1 | Data-dependent | ||
| Eq. (19) | Maximal allowed movement of weight | ||
| Lemma H.2 | Actual distance moved of weight, continuous case | ||
| Lemma H.5 | Actual distance moved of weight, discrete case | ||
| Eq. (19) | Step size of gradient descent | ||
| Lemma G.1 | Bounding discrete and continuous | ||
| Lemma G.2 | Bounding discrete and discrete | ||
| Lemma I.2 | |||
| Lemma I.3 | |||
| Lemma I.4 | |||
| Lemma H.3, Claim I.1 | and | ||
| The number of different Gaussian vectors | |||
| Size of each block | |||
I.1 Proof of Lemma H.5
Proof.
We use the norm of the gradient to bound this distance,
where the first step follows from Eq. (6), the second step follows from the expression of the gradient (see Eq. (H.1)), the third step follows from , and , the fourth step follows from the Cauchy-Schwarz inequality, the fifth step follows from the induction hypothesis, the sixth step relaxes the summation to an infinite summation, and the last step follows from .
Thus, we complete the proof. ∎
I.2 Proof of Claim H.6
Proof.
We can rewrite in the following sense
Then, we can rewrite with the notation of and
which means vector can be written as
| (20) |
We can rewrite as follows:
We can rewrite the second term in the above equation in the following sense,
where the third step follows from Eq. (20).
I.3 Proof of Claim I.1
Claim I.1.
For , with probability at least ,
Proof.
Due to the way we choose and , it is easy to see that . Thus
where the last step follows from and .
∎
I.4 Proof of Claim I.2
Claim I.2.
Let . We have that
holds with probability at least .
Proof.
By Lemma G.2 and our choice of , we have . Recall that . Therefore
Then we have
Thus, we complete the proof. ∎
I.5 Proof of Claim I.3
Claim I.3.
Let . We have that
holds with probability .
Proof.
Note that
We thus need an upper bound on . Since , it suffices to upper bound .
For each , we define as follows
For each , , we define
Using Fact I.6, we have .
Fix . Our plan is to use Bernstein’s inequality (Lemma A.3) to upper bound with high probability.
Notice that are mutually independent, since only depends on . Hence from Bernstein’s inequality (Lemma A.3) we have for all ,
By setting , we have
| (21) |
Since we have such copies of the above inequality, it follows that
Hence by a union bound, with probability at least ,
Putting it all together we have
with probability at least .
∎
I.6 Proof of Claim I.4
Claim I.4.
Let . Then we have
with probability at least .
Proof.
Using the Cauchy-Schwarz inequality, we have . We can upper bound in the following way
where the first step follows from the definition of , the fourth step follows from , and the fifth step follows from which holds with probability at least . ∎
I.7 Proof of Claim I.5
Claim I.5.
Let . Then we have
I.8 Proof of Fact I.6
Fact I.6.
Let be defined as in Eq. (10). Then we have
Proof.
We have
where the only inequality follows from . ∎