A new infinite family of 4-regular crossing-critical graphs

All graphs considered here are undirected, finite and simple. For any terminology and definition without explanation, we refer to [2]. For a graph $G$, let $V(G)$ and $E(G)$ denote its vertex set and edge set respectively. For any edge set $E_{0}$ of $G$, let $G\setminus E_{0}$ denote the spanning subgraph of $G$ obtained by deleting all edges in $E_{0}$. In particular, if $E_{0}=e$, then $G\setminus E_{0}$ is written as $G\setminus e$.

For a drawing $D$ of $G$ in the plane, let $cr_{D}(G)$ denote the number of crossings of edges in $D$. The crossing number of $G$, denoted by $cr(G)$, is the minimum value of $cr_{D}(G)$ over all drawings $D$ of $G$ in the plane. A graph $G$ is said to be crossing-critical if $cr(G\setminus e)<cr(G)$ for every edge $e$ of $G$.

The crossing number of a graph is a parameter that measures how far a graph is from a planar graph, and is a classic topological invariant of the graph. Its theory has been widely applied to the repaint and identification of sketch, layout problem in the VLSI in large scale circuit, and the graphical representation of DNA in biology engineering and so on (see [4, 11, 15]).

Computing the crossing number of a graph is an NP-hard problem [5]. For example, $cr(K_{7,11})$ and $cr(K_{13})$ are till unknown. There are still many graph classes whose crossing numbers have not be confirmed (see [8] and [19]). For the initial work about the crossing numbers of the complete bipartite graphs $K_{m,n}$ and complete graphs $K_{n}$, one can refer to [3].

For $K_{m,n}$, Zarankiewicz proposed the followingc conjecture [21]:

$$cr(K_{m,n})=\left\lfloor\frac{m}{2}\right\rfloor\left\lfloor\frac{m-1}{2}\right\rfloor\left\lfloor\frac{n}{2}\right\rfloor\left\lfloor\frac{n-1}{2}\right\rfloor.$$

To date, the conjecture has been verified for $\min\{m,n\}\leq 6$ due to Kleitman [9] and for $m=7$ and $n\leq 10$ due to Woodall [20].

For $K_{n}$, Guy [6] conjectured that

$$cr(K_{n})=\frac{1}{4}\left\lfloor\frac{n}{2}\right\rfloor\left\lfloor\frac{n-1}{2}\right\rfloor\left\lfloor\frac{n-2}{2}\right\rfloor\left\lfloor\frac{n-3}{2}\right\rfloor.$$

Up to now, the conjecture has been verified for $n\leq 12$ by McQuillan and Richter [12]. McQuillan, Pan and Richter [13] has also proved that $cr(K_{13})\neq 217$.

It is even more challenging to determine the crossing numbers of cross-critical graphs. For the extensive literature on infinite families of crossing-critical graphs, we may refer to [1, 7, 17, 18]. Richter and Thomassen [17] constructed an infinite family of 4-regular crossing-critical graphs with crossing number $3$, and posed the following problem.

In this article, we will present a new infinite family of 4-regular crossing-critical graphs $G_{n}$ of order $2n$ and crossing number $cr(G_{n})=n$ for $n\geq 4$.

The graph shown in Figure 1 (a) was called the musical graph by Donald E. Knuth ([10], Problem 133 in p. 44). While many properties of this graph can be easily analyzed, the question “Can it be drawn with fewer than 12 crossings?” was finally settled by Petra Mutzel [14] who used a program to show that the crossing number of this graph is indeed equal to $12$.

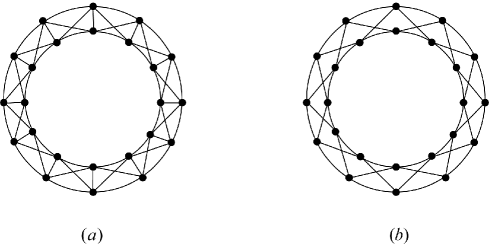
The musical graph, showed in Figure 1 (a), is actually the graph $C_{12}\circ K_{2}$, where $G_{1}\circ G_{2}$, called the lexicographic product of $G_{1}$ and $G_{2}$, is the graph such that

• •

  its vertex set is the cartesian product $V(G_{1})\times V(G_{2})$; and

• •

  any two vertices $(u,u^{\prime})$ and $(v,v^{\prime})$ are adjacent in $G_{1}\circ G_{2}$ if and only if either $u$ is adjacent to $v$ in $G_{1}$ or $u=v$ and $u^{\prime}$ is adjacent to $v^{\prime}$ in $G_{2}$.

Let $M_{n}$ denote the graph $C_{n}\circ K_{2}$. Then $M_{12}$ is the musical graph and Mutzel [14] showed that $cr(M_{12})=12$. Ouyang et al.  [16] extended the conclusion to $cr(M_{n})=n$ for all $n\geq 3$.

Obviously, the result of Theorem 1 implies that $cr(M_{n})=n$ for all $n\geq 4$.

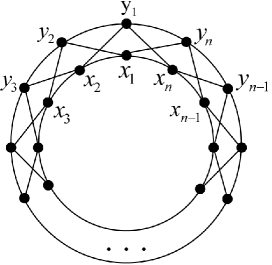
Note that $G_{n}$ is actually the graph with vertex set $\{x_{i},y_{i}:1\leq i\leq n\}$ and edge set

$$\{x_{i}x_{i+1},x_{i}y_{i+1},y_{i}x_{i+1},y_{i}y_{i+1}:i=1,2,\ldots,n\},$$

where $x_{n+1}=x_{1}$ and $y_{n+1}=y_{1}$.

Figure 2, $G_{n}$ is drawn in the plane with $n$ crossings. This indicates that $cr(G_{n})\leq n$.

Proof of Theorem 1: We first show that $cr(G_{n})=n$ for all $n\geq 4$. Note that $G_{4}\cong K_{4,4}$, implying that $cr(G_{4})=cr(K_{4,4})=4$ due to Kleitman [9]. Suppose now that $n\geq 5$ and $cr(G_{k})=k$ holds for $4\leqslant k\leqslant n-1$.

Figure 2 shows that $cr(G_{n})\leq n$. Thus, it suffices to show that $cr_{\phi}(G_{n})\geq n$ in any drawing $\phi$.

For $1\leq i\leq n$, let $L^{i}$ denote the subgraph of $G_{n}$ induced by $\{x_{i},x_{i+1},y_{i},y_{i+1}\}$, where $x_{n+1}=x_{1}$ and $y_{n+1}=y_{1}$. Clearly, $E(L^{i})=\{x_{i}x_{i+1},x_{i}y_{i+1},y_{i}x_{i+1},y_{i}y_{i+1}\}$. For $1\leq i<j\leq n$, $E(L^{i})\cap E(L^{j})=\emptyset$, and $V(L^{i})\cap V(L^{j})\neq\emptyset$ if and only if either $j=i+1$ or $j=n$ and $i=1$.

In the following, let $\gamma_{\phi}(L^{i})$ be number of edges in $E(L^{i})$ which are crossed in $\phi$. We are now going to accomplish the proof by showing the following claims.

Suppose that $\gamma_{\phi}(L^{1})=1$. Clearly, edges in $L^{1}$ do not generate any crossings in $\phi$. Otherwise, $\gamma_{\phi}(L^{1})\geq 2$. This indicates that $cr_{\phi}(L^{1})=0$. Without loss of generality, let $x_{1}y_{2}$ be the only crossing edge in $L^{1}$. We remove the edges $x_{1}y_{2}$ and $x_{2}y_{1}$ from $\phi$ and obtain the restricted drawing $\phi_{1}$ of the subgraph $G_{n}\setminus\{x_{1}y_{2},x_{2}y_{1}\}$ induced by $\phi$. Note that $x_{1}y_{2}$ is a crossing edge, then at least one crossing was reduced by removing these two edges. Thus,

$$cr_{\phi}(G_{n})\geq cr_{\phi_{1}}(G_{n}\setminus\{x_{1}y_{2},x_{2}y_{1}\})+1.$$

In $\phi_{1}$, since $x_{1}x_{2}$ and $y_{1}y_{2}$ are not crossing edges, by contracting both $x_{1}x_{2}$ and $y_{1}y_{2}$, we get a restricted drawing $\phi_{2}$ of $G_{n-1}$ induced by $\phi$. Obviously, the inequality $cr_{\phi_{1}}(G_{n}\setminus\{x_{1}y_{2},y_{1}x_{2}\})\geq cr_{\phi_{2}}(G_{n-1})$ holds. Thus,

	$\displaystyle cr_{\phi}(G_{n})$	$\displaystyle\geq$	$\displaystyle cr_{\phi_{1}}(G_{n}\setminus\{x_{1}y_{2},x_{2}y_{1}\})+1$
		$\displaystyle=$	$\displaystyle cr_{\phi_{2}}(G_{n-1})+1$
		$\displaystyle\geq$	$\displaystyle n-1+1=n.$

Thus, Claim 1 holds.

For any $U\subseteq\{1,2,\ldots,n\}$, let $\overline{U}=\{1,2,\ldots,n\}\setminus U$ and let $E_{U}$ denote the set $\bigcup_{i\in U}E(L^{i})$. For any edge sets $E_{1}$ and $E_{2}$ of $G_{n}$, let $cr_{\phi}(E_{1},E_{2})$ denote the number of crossings in $\phi$ between edges in $E_{1}$ and edges in $E_{2}$.

Since $\gamma_{\phi}(L^{i})\geq 2$ for each $i\in U$, in the drawing $\phi$, there are at least $2|U|$ crossing edges in the edge set $E_{U}$. Each crossing point involves only two crossing edges. Thus, Claim 2 holds.

For any integer $j$ with $0\leq j\leq n+1$, let $\mu(0)=n$, $\mu(n+1)=1$ and $\mu(j)=j$ otherwise.

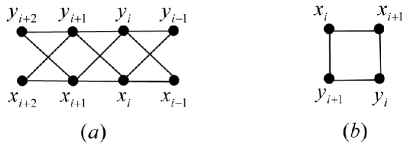
Without loss of generality, assume that $\gamma_{\phi}(L^{i})=0$, where $2\leq i\leq n-1$. We are now going to show that $cr_{\phi}(E(L^{i-1}),E(L^{i+1}))\geq 4$.

By the assumption, there are no crossing edges in $L^{i}$, as shown in Figure 3 (b). Obviously, the subgraph, denoted by $G^{\prime}$, obtained from $G_{n}$ by removing all four vertices in $\{x_{i},x_{i+1},y_{i},y_{i+1}\}$ is connected. Thus, the vertices of $G^{\prime}$ are placed in the same region of $\phi(L^{i})$; otherwise, some edges in $L^{i}$ are crossed. We may assume that all vertices in $G^{\prime}$ are within the finite region of $\phi(L^{i})$, implying that $cr_{\phi}(E(P),E(P^{\prime}))\geq 1$ holds for any pair of vertex-disjoint paths $P$ and $P^{\prime}$ of $G_{n}$, where $P$ joins $x_{i}$ to $y_{i}$ and $P^{\prime}$ joins $x_{i+1}$ to $y_{i+1}$.

There are two edge-disjoint paths $P_{1}$ and $P_{2}$ in $L^{i-1}$ joining $x_{i}$ to $y_{i}$, where $P_{1}=x_{i}x_{i-1}y_{i}$ and $P_{2}=x_{i}y_{i-1}y_{i}$, and two edge-disjoint paths $P_{3}$ and $P_{4}$ in $L^{i+1}$ joining $x_{i+1}$ to $y_{i+1}$, where $P_{3}=x_{i+1}x_{i+2}y_{i+1}$ and $P_{4}=x_{i+1}y_{i+2}y_{i+1}$. Thus,

$$cr_{\phi}(E(P_{k}),E(P_{l}))\geq 1$$

for any $k=1,2$ and $l=3,4$. Therefore,

	$\displaystyle cr_{\phi}(E(L^{i-1}),E(L^{i+1}))$	$\displaystyle=$	$\displaystyle cr_{\phi}(E(P_{1}\cup P_{2}),E(P_{3}\cup P_{4}))$
		$\displaystyle=$	$\displaystyle cr_{\phi}(E(P_{1}),E(P_{3}))+cr_{\phi}(E(P_{1}),E(P_{4}))$
			$\displaystyle+cr_{\phi}(E(P_{2}),E(P_{3}))+cr_{\phi}(E(P_{2}),E(P_{4}))$
		$\displaystyle\geq$	$\displaystyle 4.$

Claim 3 holds.

Let $U_{0}=\{1\leq i\leq n:\gamma_{\phi}(L^{i})=0\}$ and

$$U_{1}=\{1,2,\ldots,n\}\setminus\{\mu(i),\mu(i-1),\mu(i+1):i\in U_{0}\}.$$

Obviously, $U_{1}\subseteq\overline{U_{0}}$ and $3|U_{0}|+|U_{1}|\geq n$.

By Claim 1, the result holds whenever $\gamma_{\phi}(L^{i})=1$ for some $i$ with $1\leq i\leq n$. By Claim 2, the result also holds when $\gamma_{\phi}(L^{i})\geq 2$ for each $i$ with $1\leq i\leq n$. Thus, we need only consider the case that $U_{0}\neq\emptyset$ and $\gamma_{\phi}(L^{i})\geq 2$ for each $i\in\overline{U_{0}}$. Obviously, $\gamma_{\phi}(L^{i})\geq 2$ for each $i\in U_{1}$. It follows that

	$\displaystyle cr_{\phi}(G_{n})$	$\displaystyle\geq$	$\displaystyle cr_{\phi}(E_{U_{1}},E_{U_{1}})+cr_{\phi}\left(E_{U_{1}},E_{\overline{U}_{1}}\right)+\sum_{j\in U_{0}}cr_{\phi}\left(E(L^{\mu(j-1)}),E(L^{\mu(j+1)})\right)$
		$\displaystyle\geq$	$\displaystyle|U_{1}|+4|U_{0}|$
		$\displaystyle\geq$	$\displaystyle n,$

where the second last inequality follows from Claims 2 and 3. Claim 4 holds and thus $cr(G_{n})=n$ for all $n\geq 4$.

We now show that for any $n\geq 4$, $G_{n}$ is crossing-critical. Let $e$ be any edge in $G_{n}$. Without loss of generality, assume that $e$ is an edge in $L^{1}$. If $e\in\{x_{1}y_{2},x_{2}y_{1}\}$, then $G_{n}\setminus e$ has a drawing $D$ obtained from the one in Figure 2 by removing $e$. Note that $cr_{D}(G_{n}\setminus e)=n-1$, implying that $cr(G_{n}\setminus e)\leq n-1$.

If $e\in\{x_{1}x_{2},y_{1}y_{2}\}$, then we consider a new drawing of $G_{n}$ by simply exchanging $x_{2}$ and $y_{2}$. See Figure 4. Similarly, we can obtain a drawing of $G_{n}\setminus e$ in which the crossing number is less than $n$. Thus, $G_{n}$ is crossing-critical for $n\geq 4$. $\Box$

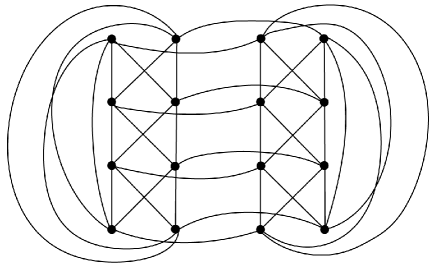
In [17], Richter and Thomassen asked if there are infinitely many 5-regular crossing-critical graphs. Let $H_{n}$ denote the Cartesian product $G_{n}\square K_{2}$, where the Cartesian product $G\square H$ of graphs $G$ and $H$ is the graph such that:

• •

  its vertex set is the Cartesian product $V(G)\times V(H)$; and

• •

  two vertices $(u,v)$ and $(u^{\prime},v^{\prime})$ are adjacent in $G\square H$ if and only if either $u=u^{\prime}$ and $v$ is adjacent to $v^{\prime}$ in $H$, or $v=v^{\prime}$ and $u$ is adjacent to $u^{\prime}$ in $G$.

Clearly, $H_{n}$ is 5-regular. For example, $H_{4}$ is the graph shown in Figure 5. It is readily checked that the graph $H_{n}$ has a drawing $D$ in the plane with $6n$ crossings. We wonder if this drawing is optimal.

Acknowledgments

The first author would like to thank the hospitality of the National Institute of Education, Nanyang Technological University in Singapore, where the work was done.

This work was supported by the National Natural Science Foundation of China (No. 12371346, 12271157, 12371340), the Scientific Research Fund of Hunan Provincial Education Department (No. 22A0637) and the Hunan Provincial Natural Science Foundation of China (No. 2023JJ30178, 2022JJ30028).

Data availability

No data was used for the research described in the article.

Conflict of interest

We claim that there is no conflict of interest in our paper.