A new estimator of resolved molecular gas in nearby galaxies

The sample is selected from the EDGE survey (Bolatto et al., 2017, hereafter B17). The typical angular resolution of EDGE CO maps is 4.5 arcsec, and the typical H₂ surface density sensitivity before deprojecting galaxy inclination is 11 $M_{\odot}$ pc^-2 (B17). Every EDGE galaxy has optical integral field unit (IFU) data from CALIFA, allowing joint studies of the content and kinematics of cold gas (H₂), ionized gas, and stellar populations, all with $\sim$kpc spatial resolution. We processed the CO data for all 126 EDGE galaxies, and as a starting point we selected the 95 galaxies which had at least one detected pixel after smoothing to 6.6 arcsec resolution and regridding the moment-0 maps with 6 arcsec pixels (Section 2.3). We then selected those galaxies with inclinations less than 75 degrees, leaving 83 galaxies. Inclination angles were derived from CO rotation curves where available (B17), and otherwise were taken from the HyperLEDA database (Makarov et al., 2014). Redshifts $z$ (from CALIFA emission lines) and luminosity distances $D_{L}$ were taken from B17. A flat $\Lambda$CDM cosmology was assumed ($h=0.7$, $\Omega_{m}=0.27$, $\Omega_{\Lambda}=0.73$).

We downloaded 2 degree by 2 degree cutouts (pixel size 1.375 arcsec) of WISE 12 µm (W3) flux $F_{\mathrm{W3}}$ and uncertainty for each galaxy from the NASA/IPAC Infrared Science Archive. The background for each galaxy was estimated using the IDL package Software for Source Extraction (SExtractor; Bertin & Arnouts, 1996), with default parameters and with the corresponding W3 uncertainty map as input. The estimated background was subtracted from each cutout. The background-subtracted images were reprojected with 6 arcsec pixels to avoid over-sampling the 6.6 arcsec beam. These maps were originally in units of Digital Numbers (DN), defined such that a W3 magnitude $m_{\mathrm{W3}}$ of 18.0 corresponds to $F_{\mathrm{W3}}=1.0$ DN, or

where the zero-point magnitude $\mathrm{MAGZP}=18.0$ mag. We converted the maps from their original units to flux density in Jy, given by

where the isophotal flux density $S_{0}=31.674$ Jy for the W3 band is from Table 1 of Jarrett et al. (2011). Luminosity in units of $\mathrm{L_{\odot}}$ is given by

where $\Delta\nu=1.1327\times 10^{13}$ Hz is the bandwidth of the 12 µm band (Jarrett et al., 2011), and $D_{L}$ is the luminosity distance. Luminosities were then converted into surface densities $\Sigma(\mathrm{12\>\mu m})$ ($\mathrm{L_{\odot}}$ pc^-2) by

where $i$ is the galaxy inclination, and $A_{\mathrm{pix}}$ is the pixel area in pc².

The uncertainty in each pixel of the rebinned surface density maps is the quadrature sum of the instrumental uncertainty and the 4.5 per cent uncertainty in the zero-point magnitude (Appendix A). Maps for an example galaxy are shown in Figure 1.

The original CO(1-0) datacubes were downloaded from the EDGE website,¹¹1https://mmwave.astro.illinois.edu/carma/edge/bulk/180726/ converted from their native units of K km s^-1 to $\mathrm{Jy\>beam^{-1}\>km\>s^{-1}}$, and then smoothed to a Gaussian beam with FWHM $=6.6$ arcsec using the Common Astronomy Software Applications (CASA; McMullin et al., 2007) task imsmooth to match the WISE resolution. The cubes have a velocity resolution of 20 km s^-1, and span 44 channels (880 km s^-1). Two methods were used to obtain CO integrated intensity (moment-0) maps $S_{\mathrm{CO}}\Delta v$:

1. Method 1:

   an iterative masking technique for improving SNR, described in Sun et al. (2018), shown in Figure 1, and

2. Method 2:

   integrating the flux along the inner 34 channels (680 km s^-1 total). In this “simple” method, the first 5 and last 5 channels were used to compute the root-mean-square (RMS) noise at each pixel.

Method 1 is used for all results in this work, while Method 2 is used as a cross-check and to estimate upper limits for non-detected pixels.

In Method 1 (described in Sun et al., 2018) a mask is generated for the datacube to improve the signal-to-noise of the resulting moment-0 map. A “core mask” is generated by requiring SNR of 3.5 over 2 consecutive channels (channel width of 20 km s^-1), and a “wing mask” is generated by requiring SNR of 2.0 over 2 consecutive channels. The core mask is dilated within the wing mask to generate a “signal mask” which defines detections. Any detected regions that span an area less than the area of the beam are masked. The signal mask is then extended spectrally by $\pm 1$ channels. Method 2 gives a map with lower signal-to-noise, but is useful for computing upper-limits for pixels which are masked in Method 1, and for cross-checking results.

The moment-0 maps were then rebinned with 6 arcsec pixels, and the units were converted to integrated intensity per pixel

where the beam $\mathrm{FWHM}=6.6$ arcsec, and the pixel size $\theta_{\mathrm{pix}}=6$ arcsec.

The total noise variance in each pixel is the sum in quadrature of the instrumental noise which we assume to be the same for both moment-0 map versions, and calibration uncertainty which depends on the moment-0 method (Appendix B). Instrumental noise maps were computed by measuring the RMS in the first five and final five channels at each pixel (Method 2 above). The instrumental noise maps were rebinned (added in quadrature, then square root) into 6 arcsec pixels. To obtain the total noise for each moment-0 map, a calibration uncertainty of 10 per cent (B17) of the rebinned moment-0 map (both versions described above) was added in quadrature with the instrumental uncertainty. The sensitivity of the CO data is worse than that of WISE W3, and so upper limits for undetected pixels are calculated with the second moment-0 map-making method. All pixels detected at less than 3$\sigma$ in CO were assigned an upper limit of 5 times the noise at each pixel.

The CO(1-0) luminosity and noise maps (in units of K km s^-1 pc²) were computed via (Bolatto et al., 2013)

where $z$ is the redshift. The luminosity maps were converted to H₂-mass surface density $\Sigma(\mathrm{H_{2}})$ using a CO-to-H₂ conversion factor $\alpha_{\mathrm{CO}}$

where $i$ is the galaxy inclination angle, and $A_{\mathrm{pix}}$ is the pixel area in pc². In normal star-forming regions a CO-to-H₂ conversion factor of $\alpha_{\mathrm{CO}}=3.2\>\mathrm{M_{\odot}(K\>km\>s^{-1}\>pc^{2})^{-1}}$ (multiply by 1.36 to include helium) is often assumed (Bolatto et al., 2013). We consider both a constant $\alpha_{\mathrm{CO}}$ and a spatially-varying metallicity-dependent $\alpha_{\mathrm{CO}}$ (Section 2.5).

In the third data release (DR3) of the CALIFA survey there are 667 galaxies observed out to at least two effective radii with $\simeq 2.5$ arcsec angular resolution over wavelengths 3700-7500 Å (Sánchez et al., 2012, 2016). The observations were carried out in either a medium spectral resolution mode (“$V_{1200}$,” $R\simeq 1700$, 3700-4200 Å, 484 galaxies) or a low spectral resolution mode (“$V_{500}$,” $R\simeq 850$, 3750-7500 Å, 646 galaxies). Cubes using data from both $V_{1200}$ and $V_{500}$ were made by degrading the spectral resolution of the $V_{1200}$ cube to that of $V_{500}$ and averaging the spectra where their wavelength coverage overlaps, and using only $V_{1200}$ or $V_{500}$ for the remaining wavelength bins between 3700-7140 Å (Sánchez et al., 2016). Combined $V_{1200}+V_{500}$ datacubes and $V_{500}$ datacubes were downloaded from the CALIFA DR3 webpage.²²2https://califaserv.caha.es/CALIFA_WEB/public_html/?q=content/califa-3rd-data-release Of the 95 EDGE galaxies detected in CO, combined $V_{1200}+V_{500}$ datacubes are available for 87 galaxies. $V_{500}$ datacubes were used for the remaining 8 galaxies. We refer to this sample of 8 + 87 galaxies as “Sample A” (Table 1).

The native pixel size of a CALIFA cube is 1 arcsec. The spaxels were stacked into 6 arcsec spaxels to be compared with the WISE and EDGE CO data. Spectral fitting was performed on the stacked spectra using the Penalized Pixel-Fitting (pPXF) Python package (Cappellari, 2017) to obtain 2D maps of emission and absorption line fluxes, equivalent widths, and velocity dispersions, as well as stellar population properties such as stellar mass and light-weighted stellar age. A Kroupa initial mass function (IMF) was assumed (Kroupa & Weidner, 2003).

Line fluxes were corrected for extinction using the Balmer decrement. Stellar mass was measured from the datacubes after subtracting a dust extinction curve using the method of Li et al. (2020). The unattenuated H$\alpha$ emission line flux $F_{\mathrm{H\alpha}}$ is related to the observed (attenuated) flux according to

where the extinction is given by

and $F_{\mathrm{H\alpha,obs.}}$ and $F_{\mathrm{H\beta,obs.}}$ are the observed (attenuated) line fluxes. The star formation rate (SFR) surface density is given by

where the H$\alpha$ luminosity-to-SFR calibration factor $C_{\mathrm{SFR,H\alpha}}=5.3\times 10^{-42}\frac{M_{\odot}\>\mathrm{yr}^{-1}}{\mathrm{erg\>s^{-1}}}$ (Hao et al., 2011; Murphy et al., 2011; Kennicutt & Evans, 2012), $d$ is the luminosity distance in cm, and $A_{\mathrm{pix}}$ is the pixel area in kpc².

The mechanism of gas ionization at each pixel was classified as either star formation (SF), low-ionization emission region (LIER), Seyfert (Sy) or a combination of star formation and AGN (“composite”) on a Baldwin, Phillips, and Terlevich (BPT) diagram (Baldwin et al., 1981). It is important to identify non-starforming regions, especially when estimating SFR from H$\alpha$ flux. BPT classification (Figure 1) was done in the [O iii] $\lambda 5007$/H$\beta$ vs. [N ii] $\lambda 6584$/H$\alpha$ plane using three standard demarcation curves in this space: Eq. 5 of Kewley et al. (2001), Eq. 1 of Kauffmann et al. (2003), and Eq. 3 of Cid Fernandes et al. (2010) (see Figure 7 of Husemann et al., 2013).

The CO-to-H₂ conversion factor $\alpha_{\mathrm{CO}}$ increases slightly with decreasing metallicity (Maloney & Black, 1988; Wilson, 1995; Genzel et al., 2012; Bolatto et al., 2013). At lower metallicities, and consequently lower dust abundance (Draine et al., 2007) and dust shielding, CO is preferentially photodissociated relative to H₂. This process leads to an increase in $\alpha_{\mathrm{CO}}$ (Bolatto et al., 2013).

A metallicity-dependent $\alpha_{\mathrm{CO}}$ equation (Genzel et al., 2012) was calculated at each star-forming pixel (Figure 1)

where $a=12\pm 2$, and $b=-1.30\pm 0.25$. Gas-phase metallicity $12+\log(\mathrm{O/H})$ was computed for the star-forming pixels using

where $p=9.12\pm 0.05$, and $q=0.73\pm 0.10$ (Denicoló et al., 2002). Following other works that have used this $\alpha_{\mathrm{CO}}(Z)$ relation (e.g. Genzel et al., 2015; Tacconi et al., 2018; Bertemes et al., 2018), we consciously choose not to include the uncertainty on $\alpha_{\mathrm{CO}}(Z)$ (which comes from the uncertainties in $a$, $b$, $p$, and $q$) in our analysis, so that the uncertainties on $\log\Sigma(\mathrm{H_{2}})$ only reflect measurement and calibration uncertainties and not systematic uncertainties in the conversion factor.

The metallicity-dependent $\alpha_{\mathrm{CO}}=\alpha_{\mathrm{CO}}(Z)$ (Eq. 18) is our preferred $\alpha_{\mathrm{CO}}$ because it is the most physically accurate. This choice of $\alpha_{\mathrm{CO}}$ has two effects on the sample:

1. 1.

   the exclusion of non-starforming pixels; and

2. 2.

   galaxies that have fewer star-forming pixels with CO detections than a given threshold are removed from the sample.

To assess the impacts of these effects, three $\alpha_{\mathrm{CO}}$ scenarios are considered:

1. 1.

   $\alpha_{\mathrm{CO}}=3.2$, using all pixels (star-forming or not);

2. 2.

   $\alpha_{\mathrm{CO}}=3.2$, only using star-forming pixels; and

3. 3.

   a metallicity-dependent $\alpha_{\mathrm{CO}}=\alpha_{\mathrm{CO}}(Z)$ (Eq. 18).

The impact of only considering star-forming pixels on the total number of pixels and galaxies (Table 1) varies depending on how many pixels per galaxy are required. For example, starting from the 95 galaxies in Sample A (Table 1), if we require at least 4 CO-detected pixels per galaxy, our sample will consist of 83 galaxies and 2059 pixels (Sample B). If we require at least 4 CO-detected star-forming pixels per galaxy (e.g. to apply a metallicity-dependent $\alpha_{\mathrm{CO}}$), we would have to remove 43% of the pixels and 22% of the galaxies from the sample, and would be left with 1168 pixels and 64 galaxies (Sample C). In the analysis that follows, we use Sample C exclusively except for comparison with Sample B in Section 3.1.

Previous work has shown a strong correlation between integrated WISE 12 µm luminosity and CO(1-0) luminosity (Jiang et al., 2015; Gao et al., 2019). To determine if this correlation holds at sub-galaxy spatial scales, we matched the resolution of the EDGE CO maps to WISE W3 resolution and compared surface densities pixel-by-pixel for each galaxy (Figure 2). This comparison indicates that there is a clear correlation between $\Sigma(\mathrm{12\>\mu m})$ and $\Sigma(\mathrm{H_{2}})$, and that within galaxies, the correlation is strong.

To quantify the strength of the correlation per galaxy, the Pearson correlation coefficient between $\log\Sigma(\mathrm{12\>\micron})$ and $\log\Sigma(\mathrm{H_{2}})$ was calculated for each galaxy. The distribution of correlation coefficients across all galaxies was computed separately for each $\alpha_{\mathrm{CO}}$ scenario (Section 2.5; Figure 3). The means for the three distributions are:

1. 1.

   0.79 for $\alpha_{\mathrm{CO}}=3.2$, all pixels included;

2. 2.

   0.79 for $\alpha_{\mathrm{CO}}=3.2$, star-forming pixels only; and

3. 3.

   0.76 for $\alpha_{\mathrm{CO}}(Z)$ (Eq. 18).

These results indicate that there are strong correlations between $\Sigma(\mathrm{12\>\mu m})$ and $\Sigma(\mathrm{H_{2}})$ regardless of the $\alpha_{\mathrm{CO}}$ assumed. A minority of galaxies show poor correlations (4 out of 95 galaxies with correlation coefficients $<0.2$). Reasons for poor correlations include fewer CO-detected pixels, and small dynamic range in the pixels that are detected (e.g. a region covering multiple pixels with uniform surface density).

For comparison, cumulative histograms of the correlation coefficients between $\log\Sigma_{\mathrm{SFR}}$ (Eq. 16) and $\log\Sigma(\mathrm{H_{2}})$ were computed (right panel of Figure 3). The same sets of galaxies and pixels were used as in the left panel of Figure 3, except the “$\alpha_{\mathrm{CO}}=3.2$, all pix.” version is excluded, because $\log\Sigma_{\mathrm{SFR}}$ can only be calculated in star-forming pixels. The mean and median correlation coefficients are lower than those in the left panel of Figure 3. Since the same pixels are used, this suggests a stronger correlation between $\Sigma(\mathrm{12\>\mu m})$ and $\Sigma(\mathrm{H_{2}})$ than between $\Sigma_{\mathrm{SFR}}$ and $\Sigma(\mathrm{H_{2}})$.

The relationship between 12 µm and CO emission resembles the Kennicutt-Schmidt relation, which also shows variation from galaxy to galaxy (Shetty et al., 2013). We model the relationship between $\log\Sigma(\mathrm{12\>\micron})$ and $\log\Sigma(\mathrm{H_{2}})$ with a power-law

To determine whether the 12 µm-CO relation is universal or not, we performed linear fits of $\log\Sigma(\mathrm{H_{2}})$ against $\log\Sigma(12\>\micron)$ for each galaxy with at least 4 CO-detected star-forming pixels (Sample C in Table 1; middle panel of Figure 2). A metallicity-dependent $\alpha_{\mathrm{CO}}$ was used in Figure 2. These fits were performed using LinMix, a Bayesian linear regression code which incorporates uncertainties in both $x$ and $y$ (Kelly, 2007). We repeated the fits for each $\alpha_{\mathrm{CO}}$ (Sec. 2.5) and with $\log\Sigma(\mathrm{H_{2}})$ on the x-axis instead.

For a given galaxy, the best-fit parameters do not vary much depending on the $\alpha_{\mathrm{CO}}$ assumed, provided there are enough pixels to perform the fit even after excluding non-starforming pixels. The fit parameters are also not significantly different if we include upper limits in the fitting. However, we find significant differences in the slope and intercept from galaxy to galaxy, indicating a non-universal resolved relation. The galaxy-to-galaxy variation in best-fit parameters persists for all three $\alpha_{\mathrm{CO}}$ scenarios. The galaxy-to-galaxy variation can be seen in the distribution of slopes and intercepts assuming a metallicity-dependent $\alpha_{\mathrm{CO}}$ for example (Figure 4). The best-fit intercepts span a range of $\simeq 1$ dex ($-0.31$ to $0.87$, median $0.41$), and the slopes range from 0.20 to 2.03, with a median of 1.13. To quantify the significance of the galaxy-to-galaxy variation in best-fit parameters, residuals in the parameters relative to the mean parameters were computed. For example, if the measurement of the slope for galaxy $i$ is $N_{i}\pm\sigma_{N_{i}}$, the residual relative to the average slope over all galaxies $\bar{N}$ is $(N_{i}-\bar{N})/\sigma_{N_{i}}$. Similarly, if the measurement of the intercept for galaxy $i$ is $\log C_{i}\pm\sigma_{\log C_{i}}$, the residual relative to the average intercept over all galaxies $\overline{\log C}$ is $(\log C_{i}-\overline{\log C})/\sigma_{\log C_{i}}$. The residual histograms (Figure 4) show that most of the slopes $N_{i}$ are within $\simeq 1.5\sigma_{N_{i}}$ of $\bar{N}$, but the intercepts show more significant deviations (many beyond $3\sigma_{\log C_{i}}$).

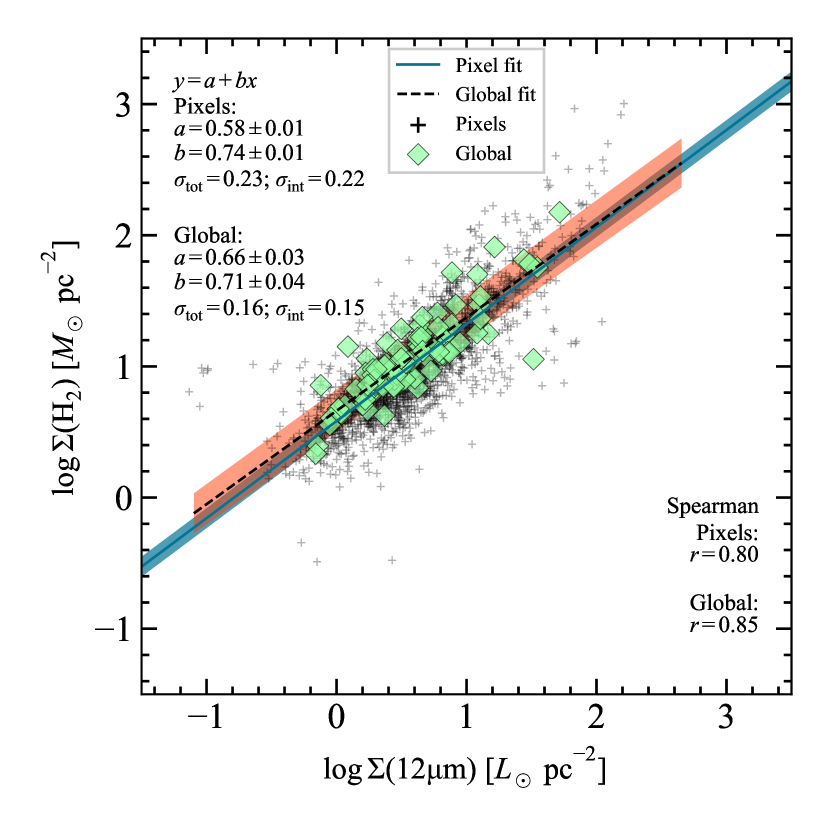
To establish how well-fit all pixels are to a single model, linear fits were done on all CO-detected pixels from all 83 galaxies in Sample B (Table 1) using LinMix (black crosses in Figure 5). The fits were done separately for luminosities ($\log L_{\mathrm{12\>\mu m}}$, $\log L_{\mathrm{CO}}$; left panel of Figure 5) and surface densities ($\log\Sigma(\mathrm{12\>\mu m})$, $\log\Sigma(\mathrm{H_{2}})$; right panel of Figure 5). For completeness, the fits were also done with CO/H₂ on the x-axis (Figure 9). In all cases there are strong correlations (correlation coefficients of $\simeq 0.90$), and good fits (total scatter about the fit $\sigma_{\mathrm{tot}}\simeq 0.19$ dex). By comparing the total scatter $\sigma_{\mathrm{tot}}$ and intrinsic scatter $\sigma_{\mathrm{int}}$ (Appendix C), it is clear that most of the scatter is intrinsic rather than due to measurement and calibration uncertainties. Note that in the right hand panel of Figure 5, ignoring the $\alpha_{\mathrm{CO}}$ uncertainty means that the $\Sigma(\mathrm{H_{2}})$ uncertainty has been underestimated, and therefore the intrinsic scatter $\sigma_{\mathrm{int}}$ (derived from $\sigma_{\mathrm{tot}}$ and the uncertainty on $\Sigma(\mathrm{H_{2}})$, Equation 36) has been overestimated. Also, if we replace $\Sigma(\mathrm{H_{2}})$ with $\Sigma(\mathrm{CO})$, $\sigma_{\mathrm{tot}}$ decreases by only 0.01 dex and $\sigma_{\mathrm{int}}$ does not change, which indicates that the scatter is dominated by that of the 12 µm-CO surface density relationship. Consequently, $\sigma_{\mathrm{int}}$ in the right hand panel of Figure 5 should be interpreted as the intrinsic scatter in the 12 µm-CO surface density relationship.

Similarly, to establish how well-fit all global values are to a single model, linear fits were done on the galaxy-integrated values (green diamonds in Figure 5) for all 83 galaxies in Sample B (Table 1). The results show good fits overall (correlation coefficients of $\simeq 0.90$, scatter about the fit $\sigma_{\mathrm{tot}}\simeq 0.20$ dex). The global values do indeed follow uniform trends (with the exception of one outlier), and the global fits with molecular gas on the x-axis show steeper slopes and smaller y-intercepts than the pixel fits (Figure 5). The global fits with 12 µm on the x-axis show shallower slopes and larger y-intercepts than the pixel fits.

To develop an estimator of $\log\Sigma(\mathrm{H_{2}})$ from $\log\Sigma(\mathrm{12\>\mu m})$ and other galaxy properties, we performed linear regression on all of the star-forming pixels from all galaxies combined. Global properties (from UV, optical, and infrared measurements) and resolved optical properties were included (Table 2). The model is

where each entry of $\vec{y}$ is $\log\Sigma(\mathrm{H_{2}})$ for each pixel of each galaxy (using the metallicity-dependent $\alpha_{\mathrm{CO}}$, Eq. 18), the $\theta$ are the fit parameters, and the sum is over $i$ properties (a combination of pixel properties or global properties). We used ridge regression, implemented in the Scikit-Learn Python package (Pedregosa et al., 2012), which is the same as ordinary least squares regression except it includes a penalty in the likelihood for more complicated models. The penalty term is the sum of the squared coefficients of each parameter $\delta\sum_{i}\theta_{i}^{2}$. The regularization parameter $\delta$ (a scalar) sets the impact of the penalty term. The best value of $\delta$ was determined by cross-validation using RidgeCV. In ridge regression it is important to standardize the data prior to fitting (subtract the sample mean and divide by the standard deviation for all global properties and pixel properties) so that the penalty term is not affected by different units or spreads of the properties. The standardized version of Equation 21 is

Note that it is not necessary to divide $\vec{y}-\mathrm{mean}(\vec{y})$ by $\mathrm{std}(\vec{y})$ because it does not impact the regularization term. After performing ridge regression on the standardized data (which provides $\tilde{\theta_{i}}$), the best-fit coefficients in the original units are given by

The intercept $\theta_{0}$ is given by

Our goal was to identify a combination of properties such that the linear fit of $\log\Sigma(\mathrm{H_{2}})$ vs. these properties (including $\log\Sigma(\mathrm{12\>\mu m})$) was able to reliably predict $\log\Sigma(\mathrm{H_{2}})$. The $\log\Sigma(\mathrm{H_{2}})$-predicting ability of the fit to a given parameter combination was quantified by performing fits with one galaxy excluded, and then measuring the mean-square (MS) error of the prediction for the excluded galaxy (the “testing error”)

where $N_{\mathrm{pix}}$ is the number of pixels for this galaxy, $y_{\mathrm{true}}$ is the true value of $\log\Sigma(\mathrm{H_{2}})$ in each pixel, and $y_{\mathrm{pred}}$ is the predicted value at that pixel using the fit. The RMS error over all test galaxies

was used to decide on a best parameter combination.

To identify the best possible combination of parameters we did the fit separately for all possible combinations with at least one resolved property required in each combination. We did not want to exclude the possibility of parameters other than 12 µm being better predictors of H₂, so we included all combinations even if 12 µm was excluded. To avoid overfitting, we excluded galaxies if the number of CO-detected star-forming pixels minus the number of galaxy properties in the estimator was less than 4 (so there are at least 3 degrees of freedom per galaxy after doing the fit), and only considered models with less than 6 independent variables. We used the metallicity-dependent $\alpha_{\mathrm{CO}}$, so the sample used for these fits was Sample C (Table 1); however, depending on the number of galaxy properties used and the number of CO-detected star-forming pixels, the sample is smaller for some estimators. We require a minimum of 15 galaxies for each estimator.

Here we describe how the pixel selection and fitting method were used to calculate the RMS error for each combination of galaxy properties:

1. 1.

   Generate all possible sets of pixels such that each set has the pixels from one galaxy left out.

2. 2.

   For each set of pixels:

   1. (a)

      Compute $\mathrm{mean}(\vec{x_{i}})$ and $\mathrm{std}(\vec{x_{i}})$ of the resolved and global properties $\vec{x_{i}}$. Use these to standardize the data.

   2. (b)

      Perform the multi-parameter fit on the standardized data, which yields $\tilde{\theta_{i}}$ (Eq. 22).

   3. (c)

      Compute the un-standardized coefficients $\theta_{i}$ (Eq. 23) and zero-point $\theta_{0}$ (Eq. 24).

   4. (d)

      Use these $\theta_{0}$, $\theta_{i}$ to predict $\vec{y}$ of the excluded galaxy (Eq. 21).

   5. (e)

      Tabulate the mean squared-error (Eq. 25).

3. 3.

   Compute the RMS error (Eq. 26) from all of the MS errors. This indicates the ability of this multi-parameter fit to predict new $\vec{y}$. The RMS error for each estimator is shown in Figure 6.

In practical applications outside of this work, not all of the global properties and pixel properties will be available. For this reason, we provide several $\log\Sigma(\mathrm{H_{2}})$ estimators which can be used depending on which data are available. To highlight the relative importance of resolved optical properties vs. 12 µm, the best-performing estimators based on the following galaxy properties are compared:

1. 1.

   all global properties + IFU properties + 12 µm (Table 3),

2. 2.

   all global properties + 12 µm but no IFU properties (Table 4),

3. 3.

   all global properties + IFU properties but no 12 µm (Table 5).

The performance of the estimators was ranked based on their RMS error of predicted $\log\Sigma(\mathrm{H_{2}})$ (Figure 6). The reported estimators are those with the lowest RMS error at a given number of galaxy properties (those corresponding to the stars and squares in Figure 6). We estimated the uncertainty on the coefficients in each estimator by perturbing the 12 µm and H₂ data points randomly according to their uncertainties, redoing the fits 1000 times, and measuring the standard deviation of the parameter distributions.

The lack of points below the green curve in Figure 6 indicates that there is little to be gained by adding IFU data to the estimators with resolved 12 µm (little to no drop in RMS error). The RMS error of the estimator with only resolved $A_{V}$ for example (black circle, upper left) performs significantly worse than the fit with only 12 µm (green square, lower left). Estimators with resolved 12 µm but no IFU data perform better than those with IFU data but no resolved 12 µm. There is also no improvement in predictive accuracy of the estimators using global properties + resolved 12 µm + no IFU data beyond a four-parameter fit (intercept, $\Sigma(12\mathrm{\mu m})$, $\Sigma_{\mathrm{NUV}}$, and global $A_{V}$). The best H₂ estimators all contain $\log\Sigma(\mathrm{12\>\micron})$, which indicates that this variable is indeed the most important for predicting H₂.

For the fits in the opposite direction, $\log\Sigma(\mathrm{H_{2}})$ was found to be the most important for predicting $\mathrm{12\>\micron}$. The best estimators for 1-5 galaxy properties show that if $\log\Sigma(\mathrm{H_{2}})$ is already included, there is essentially no improvement in predictive accuracy (little to no drop in RMS error) when resolved optical IFU data are included as variables in the fitting.

We compared how well these multi-parameter estimators perform relative to the one-parameter estimator from the right panel of Figure 5:

Note that this fit, obtained via Bayesian linear regression (Sec. 3.2) is consistent with the result from ridge regression (first row of Table 3). To compare the performance of each estimator with the fit above, predicted $\log\Sigma(\mathrm{H_{2}})$ for each pixel was computed from the one-parameter fit, and the RMS error (square root of Eq. 25) was computed for each galaxy (Figure 7). Most points lie below the 1:1 relation in Figure 7, indicating that the multi-parameter fits have lower RMS error per pixel than the single-parameter fit.

To establish whether the correlation between global surface densities (12 µm vs H₂) arises from a local correlation between pixel-based surface densities, we computed residuals of the individual pixel measurements from the resolved pixel fit (right panel of Figure 5) with varying surface areas (Figure 8). For each galaxy, contiguous regions of 1, 4, 7 or 9 pixels were used to compute surface densities (the four columns of Figure 8). The contiguous pixels were required to be CO-detected and star-forming, as a metallicity-dependent $\alpha_{\mathrm{CO}}$ was used. Each pixel was used in exactly one surface density calculation for each resolution, so all of the black circles are independent. We found that the scatter diminished as the pixel size approached the whole galaxy size. The total scatter about the individual pixel fit declines as pixel area increases, indicating that the global correlation emerges from the local one.

To determine whether the best-fit relations are biased with respect to any global or resolved properties (Table 2), we performed the following tests for the best-performing H₂ estimators with 1, 2, and 3 parameters from Table 3.

For resolved properties, we plotted the residual in predicted vs. true $\log\Sigma(\mathrm{H_{2}})$ for each pixel versus resolved properties. We computed the Pearson-$r$ between the residuals and the resolved quantities. No significant correlations were found for any of the resolved properties. This indicates that the performance of the estimators is not biased with respect to resolved properties.

For global properties, we plotted the RMS error (Equation 26) for each galaxy versus global properties for that galaxy. We computed the Pearson-$r$ between the RMS error and global quantities. No significant correlations were found for any of the global properties. This indicates that the performance of the estimators is not biased with respect to global properties.

Previous work on the 12 µm-CO relationship has been primarily focused on the total 12 µm luminosity and the total CO luminosity for each galaxy (Jiang et al., 2015; Gao et al., 2019). Our fit of the global CO luminosity versus 12 µm luminosity over the CO-detected area (Figure 5) yields a slope of $0.94\pm 0.04$ and intercept of $0.46\pm 0.38$. Our slope agrees well with Gao et al. (2019) who find $0.98\pm 0.02$, but our intercept is significantly greater than their value of $-0.14\pm 0.18$. Our global CO luminosities are consistent with those reported in B17, which are believed to be accurate estimates of the true total CO luminosities (see Section 3.2 in B17). However, we find that our global 12 µm luminosities (the sum over the CO-detected area) are systematically lower than the true total 12 µm luminosities as measured by the method in Gao et al. (2019). The amount of discrepancy is consistent with the offset in intercept found between this work and Gao et al. (2019). This comparison indicates that 12 µm emission tends to be more spatially extended than CO emission, so by restricting the area to the CO-emitting area, some 12 µm emission is missed, leading to a smaller intercept. The fact that this does not affect the slope indicates that the fraction of 12 µm emission that is excluded by only considering the CO-detected area, is similar from galaxy to galaxy.

When estimating the total CO luminosity in a galaxy, we recommend cross-checking with the Gao et al. (2019) estimators because they take the total 12 µm luminosity as input, whereas our estimators require the 12 µm luminosity over the CO-detected area. Since our total CO luminosities agree with the total CO luminosities presented in B17, it is unlikely that these interferometric measurements significantly underestimate the true total CO luminosities. However, since a comparison of the EDGE total CO luminosities with single-dish measurements for the same sample has not been done, it is not impossible that there is some missing flux.

Our results can be compared to recent work using optical extinction as an estimator of H₂ surface density (Güver & Özel, 2009; Barrera-Ballesteros et al., 2016; Concas & Popesso, 2019; Yesuf & Ho, 2019; Barrera-Ballesteros et al., 2020). We show that resolved 12 µm surface density is better than optical extinction at predicting H₂ surface density by $\simeq 0.1$ dex per pixel (Figure 6). Additionally, a 12 µm estimator does not suffer from a limited dynamic range like $A_{V}$ traced by the Balmer decrement, which is invalid at large extinctions, and where the SNR of the H$\alpha$ and H$\beta$ lines are low. In the recent analysis of EDGE galaxies Barrera-Ballesteros et al. (2020) limit their analysis to $A_{V}<3$ due to the SNR of the H$\beta$ line. Additionally, the correlation between resolved $\Sigma(12\mathrm{\mu m})$ and $\Sigma(\mathrm{H_{2}})$ is stronger than that between $A_{V}$ and $\Sigma(\mathrm{H_{2}})$.

Over the same set of pixels (star forming and CO detected), the correlation between $\log\Sigma(\mathrm{12\>\mu m})$ and $\log\Sigma(\mathrm{H_{2}})$ per galaxy (left panel, Figure 3) is better than the correlation between $\log\Sigma_{\mathrm{SFR}}$ and $\log\Sigma(\mathrm{H_{2}})$ (right panel, Figure 3). This is also apparent from our findings that estimators of $\Sigma($H${}_{2})$ based on $\Sigma(\mathrm{12\>\mu m})$ consistently perform better at predicting $\Sigma(\mathrm{H_{2}})$ than estimators with $\Sigma_{\mathrm{SFR}}$ instead of $\Sigma(\mathrm{12\>\mu m})$ (Section 3.3).

Since we have restricted our analysis to star-forming pixels, the 12 µm emission that we see is likely dominated by the 11.3 µm PAH feature. The underlying continuum emission can arise from warm, very small dust grains heated by AGN. This likely does not dominate the 12 µm emission since most ($\sim 80$ per cent) of the WISE 12 µm emission in star-forming galaxies is from stellar populations younger than 0.6 Gyr (Donoso et al., 2012). However, it is important to rule out any effects of obscured AGN. PAH emission is known to be affected by the presence of an AGN (Diamond-Stanic & Rieke, 2010; Shipley et al., 2013; Jensen et al., 2017; Alonso-Herrero et al., 2020), but there is conflicting evidence on the nature of this relationship. For example, Tommasin et al. (2010) find AGN-dominated and starburst-dominated galaxies have roughly the same 11.3 µm PAH flux, while Murata et al. (2014) and Maragkoudakis et al. (2018) find suppressed PAH emission in starburst galaxies relative to galaxies with AGN. In contrast, Shi et al. (2009) and Shipley et al. (2013) find suppressed PAH emission in AGN compared to non-AGN. If there are any obscured AGN in our sample, they would not be identified as AGN from the BPT method. However, since our pixels are 1 to 2 kpc in size, the impact of an obscured AGN would be restricted to the central pixel of the galaxy. To assess the potential impact of obscured AGN on our results, we redid all of our multiparameter fits with the central pixel of each galaxy masked if it was not already masked based on the BPT classification. We found that the 12 µm-H₂ correlation remains stronger than the SFR-H₂ correlation, and that the fit parameters do not change significantly (they are consistent within the quoted uncertainties). Thus we are confident that AGN do not significantly impact our results.

These results have implications for the connection between emission that is traced by the 12 µm band (mostly PAHs) and CO emission. Exactly how and where PAHs are formed is not currently understood (for a recent review from the Spitzer perspective see Li, 2020), but traditionally PAHs have been modelled to absorb FUV photons through the photoelectric effect and eject electrons into the ISM, which heats the gas (Bakes & Tielens, 1994; Tielens, 2008). Since PAHs are excited by stellar UV photons, PAH emission has been considered as an SFR tracer (e.g. Roussel et al., 2001; Peeters et al., 2004; Wu et al., 2005; Shipley et al., 2016; Cluver et al., 2017; Xie & Ho, 2019; Whitcomb et al., 2020). Although the PAH-SFR connection breaks down at sub-kpc scales (Werner et al., 2004; Bendo et al., 2020), PAH emission is still used as an SFR tracer on global scales for low-redshift galaxies (Kennicutt et al., 2009; Shipley et al., 2016). WISE 12 µm emission has also been examined as a SFR indicator; however its relationship with SFR shows greater scatter than the WISE 22 µm-SFR relationship (Jarrett et al., 2013; Cluver et al., 2017; Leroy et al., 2019). Similar to the 8 µm emission vs. SFR relation Calzetti et al. (2007), the complex relationship between thermal dust, PAH emission and star formation activity adds scatter to the correlations between MIR emission and SFR (Jarrett et al., 2013).

Many studies have also found that there is a tight link between PAHs and the contents of the interstellar medium: molecular gas traced by CO (Regan et al., 2006; Pope et al., 2013; Cortzen et al., 2019), and cold ($T\sim 25$ K) dust, which traces the bulk of the ISM (Haas et al., 2002; Bendo et al., 2008; Jones et al., 2015; Bendo et al., 2020). Milky Way studies have found that PAH emission is enhanced surrounding and suppressed within H ii regions (e.g. Churchwell et al., 2006; Povich et al., 2007). In addition, the PdBI Arcsecond Whirlpool Survey (PAWS; Schinnerer et al., 2013) of cold gas in M51 with cloud-scale resolution ($\sim 40$ pc) found that Spitzer 8 µm PAH emission and CO(1-0) emission are highly correlated in position but not in flux, and that most of the PAH emission appears to be coming from only the surfaces of giant molecular clouds. These results and others such as Sandstrom et al. (2010) suggest that PAHs are either formed in molecular clouds or destroyed in the diffuse ISM, and that the conditions of PAH formation and CO formation are likely similar. The suppression of PAH emission in H ii regions may be due to decreased dust shielding, analogous to how CO emission is reduced in low-metallicity regions, or to changes in how PAHs are formed and/or destroyed (Sandstrom et al., 2013; Li, 2020). It is plausible that our findings support a picture in which PAHs form in molecular clouds or are destroyed in the diffuse ISM; however due to the difference in physical resolution, and the contribution of continuum emission and multiple PAH features to the 12 µm emission, a study focused specifically on 11.3 µm PAH instead of WISE 12 µm would be required. Overall it seems likely that the strength of the 12 µm-H₂ correlation in star-forming regions is due to the combination of the Kennicutt-Schmidt relation and a direct link between the 11.3 µm PAH feature and molecular gas as traced by CO.