A Natural Explanation of the VPOS from Multistate Scalar Field Dark Matter

[43] studied the case of a real SF with mass $m$ and self-interaction $\lambda$, in a thermal bath with temperature $T$. Starting from the SF potential (2.1), it was shown that the characteristic polynomial for this system is given by

$$\omega^{2}=k^{2}c^{2}+m^{2}c^{2}\left(1-\frac{T^{2}}{T_{c}^{2}}\right),$$

(2.2)

where $\omega$ corresponds to the angular frequency of the temporal part of the solution, $k$ to the wave number of the radial part, $c$ is the speed of light and $T_{c}=2m/\sqrt{\lambda}$ is its critical phase-transition temperature.

As the SF in a galaxy halo heats up, the effective mass $m_{\Phi}$ decreases, following the relation

$$m_{\Phi}^{2}=m^{2}\left(1-\frac{T^{2}}{T_{c}^{2}}\right).$$

(2.3)

Consequently, galaxies of different sizes exhibit different effective masses $m_{\Phi}$. For example, if we assume that the mass of the scalar field is $m\sim 10^{-21}\text{ eV}/c^{2}$, which agrees with the constrictions of Lyman alpha observations [51] and of the satellite galaxies of the Milky Way [52], the effective SF mass is of the order of $m_{\Phi}\sim 10^{-24}\text{ eV}/c^{2}$. The halo of such a galaxy remains as a Bose-Einstein condensate, preserving its DM behavior. However, with the increase in temperature, some SFDM particles should occupy excited states, and the effective mass obtained from different observations should be different, solving a current problem found with the Fuzzy DM model [see e.g. 53, 23].

In [43], the finite temperature density profile is obtained as

$$\rho(r)=\sum_{j}\rho_{0}^{j}\frac{\sin^{2}(j\pi r/R)}{(j\pi r/R)^{2}},$$

(2.4)

with $\rho_{0}^{j}$ the central density of the multistate $j$ and $R$ the radius of the whole SFDM configuration. In this case, the multistate SFDM halo is the sum of the same multistates’ functional form with different phases.

The last multistate solution was shown capable of fitting the rotation curves of low and high surface brightness galaxies and the wiggles observed in the rotation curves of some of them [23], the strong gravitational lensing in SFDM halos [54], reproduced successfully the evolution of a dwarf satellite galaxy embedded in the finite temperature SFDM halo in numerical simulations [55] and reproduced the dynamical mass distribution in clusters of galaxies [56].

A disadvantage of this model is that different combinations of ground plus excited states are required to reproduce the observations, which could be explained due to the distinct formation processes of galaxies, groups, and clusters of galaxies, resulting in different numbers of SF particles in diverse states.

For the present article, we start with the following SF potential $V$ at the early stages of the Universe, for a complex SF, $\Phi$:

$$V=\frac{\lambda}{2}\left(\Phi\Phi^{*}-\frac{m^{2}}{\lambda}+\frac{1}{2}T^{2}\right)^{2},$$

(2.5)

which is the same as potential (2.1) plus some gauge terms that depend on the SF mass $m$ and the temperature of the thermal bath $T$. We will denote $\Phi\Phi^{*}:=n$ as the SF number density in what follows. From the first derivative of equation (2.5), we find that this potential has the following two extreme points:

$$\begin{split}\Phi_{1}\Phi_{1}^{*}&=n_{1}=0;\\ \Phi_{2}\Phi_{2}^{*}&=n_{2}=\frac{m^{2}}{\lambda}-\frac{1}{2}T^{2}.\end{split}$$

(2.6)

The second derivative reads

$$V_{,\Phi\Phi^{*}}=\lambda\left(2n-\frac{m^{2}}{\lambda}+\frac{1}{2}T^{2}\right),$$

(2.7)

which takes the value $V_{,\Phi\Phi^{*}}|_{n_{1}}=-m^{2}+\lambda T^{2}/2$ for the first critical point in (2.6), and $V_{,\Phi\Phi^{*}}|_{n_{2}}=m^{2}-\lambda T^{2}/2$ for the second one. If we define:

$$T^{2}_{c}:=\frac{2m^{2}}{\lambda},$$

(2.8)

the values of the second derivative (2.7) read $V_{,\Phi\Phi^{*}}=\pm(\lambda/2)\left(-T_{c}^{2}+T^{2}\right)$. This implies that the first extreme point is a minimum for $T^{2}>T_{c}^{2}$, and it is a maximum for $T^{2}<T_{c}^{2}$. The second extreme point does not exist for $T^{2}>T_{c}^{2}$ (since the corresponding $n_{2}<0$), and it is a double minimum for $T^{2}<T_{c}^{2}$ (see figure 1). That means that $T_{c}$ is the critical temperature where the SSB takes place and the SF potential (2.5) changes from one minimum point to two minima and one maximum point. For the first critical value, $n_{1}=0$, the SF potential takes the value $V(n_{1})=(\lambda/2)\left(-\frac{m^{2}}{\lambda}+\frac{T^{2}}{2}\right)^{2}$, and for the second one, $n_{2}$, the SF potential is $V(n_{2})=0$. Observe that $n=0$ at the critical temperature $T_{c}$.

Now, the effective mass $m_{\Phi}$ of the SF is defined as $m_{\Phi}^{2}:=\left.V_{,\Phi\Phi^{*}}\right|_{\text{min}}$, so we obtain:

$\displaystyle m_{\Phi}^{2}=\left\{\begin{matrix}-m^{2}+\frac{\lambda}{2}T^{2}=\frac{\lambda}{2}(T^{2}-T_{c}^{2})&\text{for}\,\,\,n_{1};\quad T^{2}>T_{c}^{2},\\ \\ m^{2}-\frac{\lambda}{2}T^{2}=\frac{\lambda}{2}(T_{c}^{2}-T^{2})&\text{for}\,\,\,n_{2};\quad T^{2}<T_{c}^{2},\end{matrix}\right.$

(2.9)

therefore $m_{\Phi}^{2}$ is always positive. As in the case of the real SF (equation (2.3)), notice from the last result that the effective mass of the complex SF depends on the temperature $T$ of the SF at the moment the halo collapsed, and the critical temperature $T_{c}$, which depends itself on the mass $m$ and the self-interaction parameter $\lambda$, intrinsic properties of the SF particle. This implies that the effective observed mass will depend on the particular properties of the observed system. Again, this may explain the tensions on the SF mass obtained from the fitting with diverse astrophysical and cosmological observations for the fuzzy DM model [see bellow and e.g. 53, 23].

Now, we study the evolution of the SF with the potential (2.5) and finite temperature, in a FLRW Universe. The SF fulfills the Einstein-Klein-Gordon equations (EKG), $G_{\mu\nu}=\kappa^{2}T_{\mu\nu}$, and $\Box\Phi-\frac{dV}{d\Phi^{*}}=0$, where $G_{\mu\nu}$ is the Einstein tensor, $T_{\mu\nu}$ is the energy-momentum tensor of the SF and $\kappa^{2}:=8\pi G/c^{4}$. If we separate, as usual, the background part from a perturbed fluctuation, $\Phi=\Phi_{0}+\delta\Phi$, the fluctuation $\delta\Phi$ fulfills the following equations:

$$\nabla^{2}\delta\Phi-\ddot{\delta\Phi}-2H\dot{\delta\Phi}+V_{,\Phi_{0}\Phi_{0}^{*}}a^{2}\delta\Phi+V,_{\Phi^{*}_{0}\Phi^{*}_{0}}a^{2}\delta\Phi^{*}-2V,_{\Phi^{*}_{0}}a^{2}\phi+4\dot{\phi}\dot{\Phi}_{0}=0,$$

(2.10)

$$2\nabla^{2}\phi-6H(\dot{\phi}+H\phi)=\kappa^{2}\left[(\dot{\Phi}_{0}\dot{\delta\Phi}^{\ast}+\dot{\Phi}^{\ast}_{0}\dot{\delta\Phi})-2\phi\dot{\Phi}_{0}\dot{\Phi}^{\ast}_{0}+a^{2}\delta V\right],$$

(2.11)

where $H$ is the Hubble parameter, $a$ the scale factor, $\phi$ the Newtonian potential, and $\delta V$ is defined as

$$\delta V:=V,_{\Phi_{0}}\delta\Phi+V,_{\Phi_{0}^{\ast}}\delta\Phi^{\ast}.$$

(2.12)

Equation (2.10) is the KG equation for the perturbation $\delta\Phi$, and equation (2.11) is the Poisson equation.

Now, we aim to study the final formation stage of galactic halos, thus, we constrain our evolution equations to the Newtonian limit, when $\Phi$ is near the minimum of the potential and it starts to oscillate. In this limit, we can neglect the expansion of the Universe, i.e. $H=0$, and the oscillations of the Newtonian gravitational potential are also neglected, i.e. $\dot{\phi}=0$, since the gravitational potential is locally homogeneous at the beginning of the collapse.

For the SF potential (2.5), equations (2.10) and (2.11) read

$$\nabla^{2}\delta\Phi-\ddot{\delta\Phi}+\lambda\left(2n_{0}-\frac{m^{2}}{\lambda}+\frac{1}{2}T^{2}\right)a^{2}\delta\Phi+\lambda\Phi_{0}^{2}a^{2}\delta\Phi^{*}=0,$$

(2.13)

$$\nabla^{2}\phi=\frac{\kappa^{2}}{2}\left[\left(\dot{\Phi}_{0}\dot{\delta\Phi}^{\ast}+\dot{\Phi}^{\ast}_{0}\dot{\delta\Phi}\right)-2\phi\dot{\Phi}_{0}\dot{\Phi}^{\ast}_{0}+a^{2}\lambda\left(\Phi_{0}\Phi_{0}^{*}+\frac{m^{2}}{\lambda}-\frac{1}{2}T^{2}\right)\left(\Phi_{0}\delta\Phi^{*}+\Phi_{0}^{*}\delta\Phi\right)\right].$$

(2.14)

To solve the last equations, we carry out a Madelung transformation [57]:

	$\displaystyle\Phi_{0}$	$\displaystyle=$	$\displaystyle\sqrt{n_{0}}\,e^{i\theta_{0}}=\sqrt{n_{0}}\,e^{i(S_{0}-\omega_{0}t)},$		(2.15)
	$\displaystyle\delta\Phi$	$\displaystyle=$	$\displaystyle R\,e^{i(\theta_{0}+\delta S)}=\sqrt{n}\,e^{i(\theta_{0}-\omega_{0}t+\delta S)},$		(2.16)

where $\Phi$ is decomposed into a density number of the SF $n$ and a phase $S$. We will take perturbations such that if $\phi$ is of the order of $\epsilon$, then $\delta\Phi$, $\delta R$, and $\delta S$ are also of this order, while $n$ is a perturbation of order $\epsilon^{2}$. We will neglect perturbations of order $\epsilon^{2}$ and beyond. With these new variables, equations (2.13) and (2.14) transform into

$$\nabla^{2}R-\ddot{R}+\frac{\lambda}{2}\left(4n_{0}-T^{2}_{c}+T^{2}\right)a^{2}R+\dot{\theta}_{0}^{2}R-i(\dot{\theta}_{0}R^{2}\dot{)}=0,$$

(2.17)

$$\nabla^{2}\phi=\frac{\kappa^{2}}{2}\left[-\left(2\dot{\theta}_{0}^{2}n_{0}+\frac{\dot{n}_{0}^{2}}{2n_{0}}\right)\phi+\frac{\dot{n}_{0}}{\sqrt{n_{0}}}\dot{R}+\left(\lambda(2n_{0}+T_{c}^{2}-T^{2})a^{2}+2\dot{\theta}_{0}^{2}\right)\sqrt{n_{0}}R\right].$$

(2.18)

After the formation of the galaxy halo, the size of the final configuration determines the final temperature $T$.

To solve the last field equations, we perform a separation of variables defining $R:=L_{k}Y_{k}^{j}T_{R}$, where $L_{k}=L_{k}(r)$, $T_{R}=T_{R}(\eta)$ and $Y_{k}^{j}=Y_{k}^{j}(\theta,\varphi)$ are the spherical harmonics polynomials, with $r$ the radial, $\eta$ the temporal, and $\theta$ and $\varphi$ the angular coordinates. The real part of equation (2.17) has the solution

$$R=\sum_{k,j}\frac{J_{k+1/2}(l\,r)}{\sqrt{r}}Y^{j}_{k}T_{R},$$

(2.19)

where $J_{k}=L_{k}\sqrt{r}$ are the Bessel polynomials, and the function $T_{R}$ is a solution of the equation

$$\ddot{T}_{R}+\left(\omega^{2}-2\lambda n_{0}a^{2}-\dot{\theta}_{0}^{2}\right)T_{R}=0,$$

(2.20)

with $l$ an integration constant such that

$$l^{2}=\omega^{2}-\frac{\lambda}{2}\left(T^{2}_{c}-T^{2}\right)a^{2}=\omega^{2}-m_{\Phi}^{2}a^{2},$$

(2.21)

where we used the definition of the SF mass (2.9). The last equation is crucial for what follows. This equation means that $l$ is a parameter that depends on the value of the effective mass $m_{\Phi}$ and the vibration energy $\omega$. We will see that $l$ determines the scale of the galaxy, i.e. the scale $l$ depends strongly on the galaxy we are studying and this scale depends on the temperature and energy with which the galaxy ends after its formation collapse. In other words, the final state of the galaxy determines the temperature of the SFDM, and the scale of the galaxy is determined by the effective mass given by this temperature. By fitting the exact solutions to the rotation curves of galaxies, we can obtain a value for the scale $l$, but unfortunately, we cannot determine the final temperature of the SFDM halo, we can only have the combination $\omega^{2}-m_{\Phi}^{2}a^{2}$. Thus, we can say that equation (2.21) can solve the mass tension between the mass that fits Lyman-$\alpha$ observations and the mass needed to fit rotation curves in galaxies. Let us explain this point a bit further. It has been argued that the mass of the SF $m_{\Phi}$ appears to be different to fit observations of large galaxies, small galaxies, and observations of Lyman-$\alpha$ [31, 58, 59, 60, 61, 62, 63, 64]. It is clear from equation (2.9) that after the turn-around of the galactic halo occurs, the SFDM changes its temperature because it collapses again. Depending on the fluctuation size, environmental conditions, etc., a final SFDM halo temperature will be reached, and hence an effective frequency $\omega$ and the effective SF mass $m_{\Phi}$. There are two possibilities here. The first is that the self-interactions parameter is of order $\lambda\sim 1$, and then if $T\sim T_{c}$, the SFDM mass $m_{\Phi}$ could be the one observed using Lyman-$\alpha$ observations, $m_{\Phi}\sim 10^{-21}$eV, and the effective mass of a medium-sized galaxy given by the equation (2.9) could be $m_{\Phi}\sim 10^{-22}$eV. The second possibility is that the self-interaction parameter $\lambda\ll 1$, as claimed in [50]. In that case, $T^{2}/T_{c}^{2}\sim 0$ and it is sufficient that $m_{\Phi}\sim\omega$ for the scale $l$ to fit well to any galaxy. In other words, equation (2.21) can relieve the mass tension of the SFDM model, and the scale $l$ of a galaxy is determined not only by the mass $m_{\Phi}$ but also by the parameter $\omega$.

For equation (2.18), we can expand the Newtonian potential as $\phi=pT_{p}Y^{j}_{k}$, where again $p=p(r)$, $T_{p}=T_{p}(\eta)$ and $Y_{k}^{j}=Y_{k}^{j}(\theta,\varphi)$. Such an equation transforms into

$$\frac{1}{r^{2}}\left(r^{2}p_{,r}\right)_{,r}+\left(\Omega_{1}^{2}-\frac{k(k+1)}{r^{2}}\right)p=\Omega_{2}^{2}L_{k},$$

(2.22)

whose solution is

$$p=\sum_{k,j}\left(\frac{J_{k+1/2}(\Omega_{1}\,r)}{\sqrt{r}}+\Omega_{2}^{2}p_{0}\frac{J_{k+1/2}(l\,r)}{\sqrt{r}(\Omega_{1}^{2}-l^{2})}\right)$$

(2.23)

where $p_{0}$ is an integration constant. It can be seen that solution (2.23) is well behaved even at $\Omega_{1}=l$. Functions $\Omega_{i}=\Omega_{i}(\eta)$ are defined as

$$\Omega_{1}^{2}=\frac{\kappa^{2}}{2}\left(2\dot{\theta}_{0}^{2}n_{0}+\frac{\dot{n}_{0}^{2}}{2n_{0}}\right)=\kappa^{2}\dot{\Phi}_{0}\dot{\Phi}_{0}^{*},$$

(2.24)

$$\Omega_{2}^{2}=\frac{\kappa^{2}}{2}\left[\frac{\dot{n}_{0}}{\sqrt{n_{0}}}\frac{\dot{T}_{R}}{T_{p}}+\left(\lambda(2n_{0}+T_{c}^{2}-T^{2})a^{2}+2\dot{\theta}_{0}^{2}\right)\sqrt{n_{0}}\frac{T_{R}}{T_{p}}\right].$$

(2.25)

One interesting solution is when

$$T_{p}=\frac{\kappa^{2}}{2}\left[\frac{\dot{n}_{0}}{\sqrt{n_{0}}}{\dot{T}_{R}}+\left(\lambda(2n_{0}+T_{c}^{2}-T^{2})a^{2}+2\dot{\theta}_{0}^{2}\right)\sqrt{n_{0}}{T_{R}}\right],$$

(2.26)

in that case $\Omega_{2}=1$. Notice that the time dependence of the equations is due to the expansion of the Universe, which is too slow compared to the movements of the galaxies. Therefore, if we assume that such functions of the background are almost constant in time, as a good approximation we can set all these functions as constant. Thus, we can consider $\Omega_{1}$ and $\Omega_{2}$ as constants. In that case, equation (2.22) can be solved analytically. Furthermore, equation (2.20) for the time evolution of function $R$ is $T_{R}=T_{0}\exp(i(\omega^{2}-2\lambda n_{0}a^{2}-\dot{\theta}_{0}^{2})\eta)$, and the density number $n$ reduce to

$$n=\sum_{k,j}\frac{J^{2}_{k+1/2}(l\,r)}{r}Y^{j}_{k}Y^{*j}_{k},$$

(2.27)

where we have used the orthogonal properties of the spherical harmonic functions.

From equation (2.19), using the orthogonality of functions $Y^{j}_{k}$, we can define the complex function $R_{k}$ as

$$R_{k}=\frac{J_{k+1/2}(l\,r)}{\sqrt{r}}\exp(i\omega_{k}\eta).$$

(2.28)

For the ground state ($k=0$) and the first excited state ($k=1$), we have the following exact solutions:

$$R_{0}=\frac{J_{1/2}(lr)}{\sqrt{r}}\exp(i\omega_{0}\eta)=R_{00}\frac{\sin x}{x}\exp(i\omega_{0}\eta),$$

(2.29)

$$R_{1}=\frac{J_{3/2}(lr)}{\sqrt{r}}\exp(i\omega_{1}\eta)=R_{10}\left(\frac{\sin x}{x^{2}}-\frac{\cos x}{x}\right)\exp(i\omega_{1}\eta),$$

(2.30)

where we have defined $x:=lr$, and $R_{00}$ and $R_{10}$ are constants.

See figure 2 for a 3D representation of the spherical ground state, the first excited state, and the sum of these two states of the SFDM. The main result of this work is that we obtained, in an analytical way, a spherical ground state, as expected, and a first excited state with a two-lobe shape towards the north and south of the center of the configuration. This structure is like that of the hydrogen atom, called a gravitational atom. The two-lobe structure can explain why satellite galaxies in MW-like galaxies are not distributed spherically, but rather along a north-south line, which has been called VPOS. This behavior has not only been observed in the Milky Way [6, 7], but also in Andromeda [8, 9] and Centaurus A [10, 11]. In this way, our result has the potential to explain this anisotropic distribution of satellite galaxies. Additionally, we tested the model with the distribution of satellites in 6 other galaxies reported in [65].

This behavior, with a significant number of particles in excited states, while still maintaining the Bose-Einstein condensate nature of the halo, is essential for understanding the implications of the multistate SFDM model for galaxy formation and the large-scale structure of the Universe. It offers a mechanism for accommodating the observed stability of galaxies and their structures while accounting for the deviations in the effective mass due to temperature effects.

Now, from (2.29) and (2.30), the physical densities are given by $\rho_{k}(r)=R_{k}(r)R_{k}^{*}(r)$, and we define $\rho_{0}:=R_{00}^{2}$ and $\rho_{1}:=R_{10}^{2}$, with the constants $\rho_{0}$, the central density of the ground state, and $\rho_{1}$, the corresponding maximum density of the first excited state (see figure 3):

$$\rho_{0}(r)=\rho_{0}\frac{\sin^{2}x}{x^{2}},$$

(2.31)

$$\rho_{1}(r)=\rho_{1}\left(\frac{\sin x}{x^{2}}-\frac{\cos x}{x}\right)^{2}.$$

(2.32)

Notice that the density of the ground state (2.31) is of the same form as in the case of the real SF solution (equation (2.4)), for $j=1$ and $l=\pi/R$. In our case, the value $R=\pi/l$ defines the radius of the first minima of the ground state (see figure 3). In [43], the authors defined $R$ as the radius of the SFDM halo. However, in this work, since there is still contribution to the mass beyond the first minimum, as seen in figure 3, we define the maximum radius of every SF state, $R_{i}^{\text{max}}$, such that

$$\rho_{i}(R_{i}^{\text{max}})=200\rho_{c},$$

(2.33)

for $i=0,1$, where $\rho_{c}$ is the critical density of the Universe.

Another difference with the previous work [43], is that the SFDM states in the case of the real SF are all centered at r=0, only their wavelength decreases and their amplitude changes, being all spherically symmetric. In that case, all the excited states share the definition of the radius $R$ of the halo. In the present work, for the complex SF, the second excited state has a different functional form, which gives it the two-lobe shape, with $\rho_{1}(0)=0$ and its maximum density outside $r=0$ (see figure 3).

The corresponding masses of both states, $M_{i}(r)=4\pi\int\rho_{i}(r)r^{2}\text{d}r$, are given by :

$$M_{0}(r)=\frac{2\pi\rho_{0}}{l^{3}}\left(x-\cos x\sin x\right),$$

(2.34)

$$M_{1}(r)=\frac{2\pi\rho_{1}}{l^{3}}\left(\frac{\cos(2x)}{x}-\frac{1}{x}+\cos x\sin x+x\right).$$

(2.35)

From now on, we will denote the resulting density profiles as multistate SFDM (mSFDM). For the densities and masses, we have 3 free parameters only, $\rho_{0}$, $\rho_{1}$ and $l$. In the next section, we explain how we fit these functions to the rotation curves of the galaxies we are interested in, to obtain the halo configurations.

For the bulge in the MW, we use the exponential-sphere model. In this case, the volume mass density $\rho_{b}$ is an exponential function of the radius $r$ with a scale radius $h_{b}$, as follows [67]:

$$\rho_{b}(r)=\rho_{b,0}e^{-r/h_{b}},$$

(3.2)

with $\rho_{b,0}$ the central bulge density. The corresponding mass enclosed on a sphere of radius $r$ is

$$M_{b}(r)=m_{b}\left[1-e^{-y}\left(1+y+\frac{y^{2}}{2}\right)\right],$$

(3.3)

where $y:=r/h_{b}$, while the total mass of the bulge, $m_{b}$, is

$$m_{b}=\int_{0}^{\infty}4\pi r^{2}\rho_{b}(r)\text{d}r=8\pi h_{b}^{3}\rho_{b,0}.$$

(3.4)

The bulge rotation curve is

$$v_{b}(r)=\sqrt{\frac{GM_{b}(r)}{r}}.$$

(3.5)

For the galactic discs, we use the exponential Freeman model for the surface mass density [68]:

$$\Sigma_{d}(r)=\Sigma_{d,0}e^{-r/h_{d}},$$

(3.6)

where $\Sigma_{d,0}$ is the central density and $h_{d}$ is the scale radius. The total mass is given by $m_{d}=2\pi\Sigma_{d,0}h_{d}^{2}$. The corresponding rotation curve is given by

$$v_{d}(r)=\sqrt{4\pi Gy^{2}\Sigma_{d,0}h_{d}\left[I_{0}(y)K_{0}(y)-I_{1}(y)K_{1}(y)\right]},$$

(3.7)

where $y:=r/(2h_{d})$, and $I_{i}$ and $K_{i}$ (for $i=0,1$) are the modified Bessel functions.

For the Milky Way, we use the rotation velocities data reported in [67], obtained for the values at the Sun radius $(R_{0},V_{0})=(8.0\text{ kpc},238\text{ km/s})$. Data are reported between 0.29 and 1280 kpc. However, we use the data from 0.564 to 64.5 kpc, since the errors at larger radii are huge. For simplicity, we avoid the innermost region, where the supermassive black hole Sgr A* is dominant, and where it has been found a massive central core (or second bulge) inside 0.1 kpc [see e.g. 81].

The initial values for the MCMC method are taken from those reported in [82]: For the exponential bulge $m_{b}=(1.652\pm 0.083)\times 10^{10}M_{\odot}$ and $h_{b}=(522\pm 37)$ pc; for the exponential disc $m_{d}=(3.41\pm 0.41)\times 10^{10}M_{\odot}$ and $h_{d}=(3.19\pm 0.35)$ kpc. The total mass of the Milky Way, including the DM halo up to $\sim 150$ kpc, has been estimated to be $\sim 3\times 10^{11}M_{\odot}$ [67]. We did not take into account the gas contribution.

For Andromeda, we exclude the central region from the analysis, because of the large surface density of baryons and a possible adiabatic contraction there [see 72, and references therein]. As the bulge is the most important contribution in that region, we do not fit such a component, we use only an exponential disc, starting from 8.5 kpc.

We use the data reported in [72]. Following that work, the disc luminosity $L_{d}$ used to obtain the mass parameter $m_{d}$ is $2.1\times 10^{10}L_{\odot}$. In their analysis, the authors vary the disc mass-to-light ratios between 2.5 and 8 $M_{\odot}/L_{\odot}$. For the best fitting $\Lambda$CDM model, they obtained $(M/L)_{d}=5.0M_{\odot}/L_{\odot}$, concentration parameter $C=12.0$, and length-scale $h_{d}=4.5$ kpc (this parameter varies between 4.5 and 6.1 kpc), for an exponential disc. The total bulge + disc mass in that work is $1.3\times 10^{11}M_{\odot}$, and the dark NFW halo is $1.2\times 10^{12}M_{\odot}$.

According to the last values, we use as initial numbers for the MCMC method: $m_{d}=(5.25-16.8)\times 10^{10}M_{\odot}$ and $h_{d}=4.5$ kpc. For simplicity, we did not take into account the gas mass contribution.

Centaurus A (NGC 5128) is an active galactic nucleus, with a supermassive black hole at its center ejecting relativistic jets emitting in X-ray and radio wavelengths. It is a peculiar galaxy since it is in collision with another spiral galaxy. For the analysis, we exclude the innermost region and the region where the bulge is dominant, thus we fit an exponential disc with the mSFDM halo.

We use the rotation curve obtained in [73], with ATCA 21-cm line observations of the neutral hydrogen (HI). The HI kinematics shows that the galaxy has a regularly rotating, warped main disc (for $r<6$ kpc). No bar or bulge is necessary to reproduce the HI kinematics. The total extent of the HI disc is $\sim 7.5$ kpc in radius, and its total mass is $4.9\times 10^{8}M_{\odot}$.

In [65], the authors analyzed observations from Subaru/Hyper Suprime-Cam of satellite galaxies around 9 Milky Way-like galaxies located outside of the Local Group. After screening to eliminate false positives, they identified 51 dwarf satellite galaxies within the virial radius of the host galaxies.

The study found that the average luminosity function of the satellite galaxies is consistent with that of the Milky Way satellites, though the luminosity function of each host galaxy varies significantly. They also found that more massive host galaxies tend to have a larger number of satellites. The physical properties of the satellites, such as the size-luminosity relation, were consistent with those of the Milky Way satellites.

However, there was a notable difference in the spatial distribution. The satellite galaxies outside the Local Group showed no signs of concentration or alignment, unlike the MW satellites, which are more concentrated around the host galaxy and exhibit significant alignment.

The study concluded that this difference in spatial distribution might represent a peculiarity of the Milky Way satellites and further research is required to understand the origin of this trend, considering that the observation was focused on relatively massive satellites with $M_{V}<-10$.

Despite not observing a clear alignment of satellites in those galaxies, we used their reported observations to test the SFDM model with two quantum states and see if there is any indication of a distribution around the atom-like structure of the SF model. While the absence of a pronounced alignment of satellite galaxies might suggest that the model’s atom-like structure is not immediately evident, exploring this possible implication of the model is relevant.

Thus, we fit the rotation curves of 6 of the 9 galaxies we found to obtain the best parameters of the model, with a mSFDM halo.

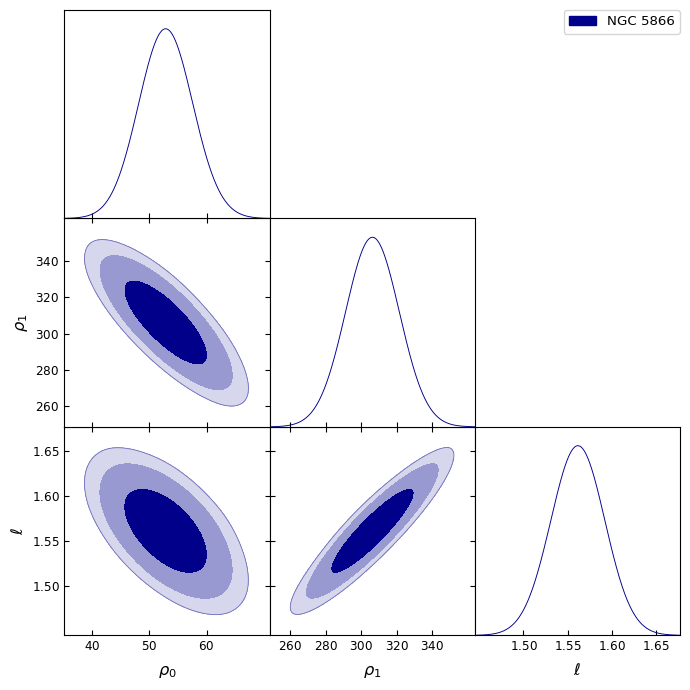
The rotation curve and the data for NGC 2950 are taken from [74]. The line-of-sight velocity data for NGC 3437 are taken from [77], from which we made the interpolation between the approaching and the receding parts of the galaxy to obtain the rotation curve and errors we used in the present work. The position-velocity map for NGC 3338 is taken from [76], from which we obtained the rotation curve and errors used in this work. The rotation velocities for NGC 3245 and NGC 7332 are taken from [75] and [79], respectively. For NGC 5866 the rotation velocities are taken from [78], from which we interpolated between the approaching and the receding parts of the galaxy.

The best-fit parameters, obtained for the exponential bulge and disc, and the ground and first excited states of the mSFDM halo, are listed in table 2.

In figure 4, we show the best-fit MW rotation curve up to 64.5 kpc and the densities of the ground and first excited states of the mSFDM configuration. We cut the DM contribution as defined in (2.33). The posterior distributions for the 7 free parameters are also shown in this figure.

In table 3, we compare the maximum radius of the mSFDM configuration, with the virial radius reported in [82]. Both radii, $R_{0}^{\text{max}}$ and $R_{1}^{\text{max}}$, are around 0.3 and 0.5 times the virial radius, respectively. With this result, the two-lobe structure, originating in the center of the Milky Way and orthogonal to its plane, would enclose around 53 of 61 satellites listed in [83].

The best-fit parameters for Andromeda for an exponential disc and mSFDM halo are listed in table 2. In figure 5, we show the best-fit M31 rotation curve up to 36.5 kpc and the densities of the ground and first excited states. We also show the posterior distributions for the 5 free parameters.

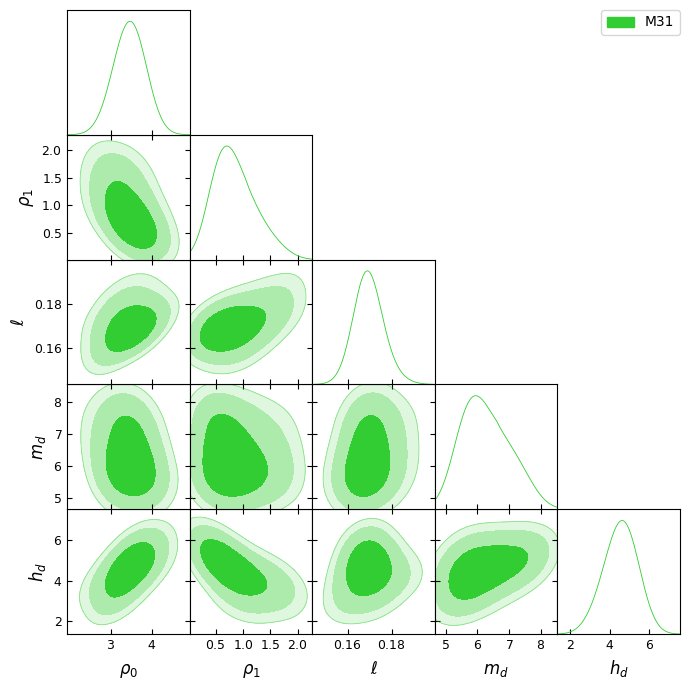
In table 3, we show the maximum radii of both mSFDM states, the ground and the first excited states, and the virial radius reported in [72]. Such radii are around 0.75 and 0.5 times the virial radius, respectively. With this result, the two-lobe structure, originating in the center of Andromeda and orthogonal to its plane, would enclose 10 of 18 satellites listed in [84].

The best-fit parameters, obtained from the MCMC method for an exponential disc and mSDFM halo, are listed in table 2. Figure 6 shows the resulting best-fit rotation curve and the behavior of the SF densities. Notice that the best-fit rotation curve agrees well with the observations. We also show the resulting posterior distributions for the 5 free parameters.

In table 3, we show the maximum radii of both mSFDM states, the ground and the first excited states, and the virial radius reported in [85]. Such radii are around 0.7 and 0.4 times the virial radius, respectively. With this result, the two-lobe structure, originating in the center of Centaurus A and orthogonal to its plane, would enclose 15 of 31 satellites (5 with velocity measurements and 10 without velocities), and mainly the whole structure of 1239 planetary nebulae reported in [10] (see the central squared region of figure 1 in that work).

For these galaxies, we used a mSFDM halo and only for NGC 3437 we included an exponential disc to better fit the data. The results of these fits are presented in table 2. Figures 8-10 show the best-fit rotation curves for each galaxy, and the figures reproduced from [65] for NGC 3338, 3437, 5866 and 7332, show the central galaxy and the confirmed and tentative satellites within the virial radius of each galaxy. We superposed with yellow solid circles the resulting two-lobe structure (the excited state) from our best fits for the host galaxies, with radius $R_{\text{max}}^{1}$ (see table 3).

Although the alignment in all the galaxies in [65] is not clear, in some cases it would be possible to explain that dwarf galaxies are found within the gravitational potential traced by the two-lobe structure of the first excited state, as in NGC 3338 (the galaxies near the center), two dwarf galaxies in NGC 3437 near the center, about 7 satellite galaxies in NGC 5866, and one or two galaxies around NGC 7332. The corresponding figures for NGC 2950 and NGC 3245 can be found in [86]; in these cases, for NGC 2950 it is possible to find 3 galaxies inside the gravitational potential of the lobes, and in NGC 3245 about 6 galaxies.

The whole analysis in this Section confirms that the mSFDM model with two states is capable of accurately describing the rotation curves of the galaxies under study. The fact that all galaxies were well-fitted with the same number of parameters further supports the robustness and universality of the model in capturing the essential features of the observed rotation curves.

This is a significant advantage over the finite temperature model with real SF presented in [43], which required various combinations of ground plus excited states to reproduce different observations [43, 56, 23]. In the present model, with a complex SF and by using the spherical ground state and the two-lobe first excited state only, it is possible to reproduce all the rotation curves of the studied galaxies. In other words, with the spherical structure of the ground state and the two-lobe structure of the first excited state, it is sufficient to reproduce the observations and also explain the gravitational potential responsible for aligning the satellite galaxies as observed in MW, M31, and CenA, and possibly the galaxies in [65].