A Multi-Spatial, Multi-Temporal, Semi-Analytical Model for Bathymetry, Water Turbidity and Bottom Composition using Multispectral Imagery
Abstract
In this paper we introduce a semi-analytical model for bathymetry, water turbidity and bottom composition; which is primarily based on the physics-based model, HOPE, of Lee et al [14][15]. Unlike the model of Lee, which was originally designed to use hyperspectral imagery, our model is specifically designed to use multispectral satellite imagery. In particular, we adapt to the greatly decreased spectral resolution by introducing temporal and spatial assumptions on the depth and water turbidity. We validate the extensions to the Lee et al model with a 260 case study in the area of the Murion Islands off Western Australia, where we compare the atmospherically-corrected LANDSAT-8 derived bathymetry against a 2011 single-beam sonar survey by Transport Western Australia. The model validates well against the single-beam sonar survey, with , a mean absolute error of 1.37 m and a mean relative error of 9.24%. This indicates the model could be widely applicable to LANDSAT-8 imagery.
Keywords: Remote sensing, satellite-derived bathymetry, multispectral imagery,
radiative transfer models, LANDSAT-8.
| symbol | description | units |
|---|---|---|
| remote sensing reflectance (RRS) | ||
| subsurface remote sensing reflectance | ||
| phytoplankton absorption coefficient at 440 nm | ||
| absorption coefficient of gelbstoff and detritus at 440 nm | ||
| backscattering coefficient of particles at 440 nm | ||
| bottom albedo at 550 nm | ||
| bottom depth | m | |
| spectrally-constant offset | ||
| absorption coefficient | ||
| backscattering coefficient | ||
| attenuation coefficient | ||
| bottom albedo spectrum normalised to 550 nm | ||
| subsurface solar zenith angle | rad | |
| subsurface viewing angle from nadir | rad |
1 Introduction
The origins of marine remote sensing by satellite date to the early 1970s with the launch of LANDSAT 1
and the seminal research of Polcyn & Cousteau [1][4]. In 1975, NASA and Jacques
Cousteau used multispectral imagery from LANDSAT 1 and in situ measurements of water clarity and
sea floor reflectance to estimate the bathymetry in the Bahamas and off the eastern coast of Florida. They
concluded that with optimal conditions, satellite-derived depths could be reliably modelled up to a depth of 22 m.
Polcyn initially used a single band to estimate the depth, where the band attenuation coefficient and
bottom reflectance was measured at the same time as the satellite image acquisition. Later Polcyn generalised
this method to a depth estimate based on the ratio of two bands.
As the field measurements were taken at a single location, these depth estimates assumed constant
water turbidity and bottom reflectance across the entire satellite scene.
In 1978, Lyzenga [6] introduced an empirical multi-band method to estimate the
bathymetry. Like the ratio method of Polcyn, this method assumed constant water turbidity and
bottom type. The Lyzenga method is outlined in Section 4.1. In 2006, Lyzenga
et al refined this method [24].
Since the turn of the century, physics-based radiative transfer models have existed to
simultaneously estimate depth, water turbidity and bottom reflectance from hyperspectral
imagery. A detailed summary and inter-comparison at two sites of a number of key models
is given in Dekker et al [33].
The original model of Lee et al [14][15], HOPE (Hyperspectral Optimisation
Process Exemplar), assumed a single benthic substratum (sand). Lee et al [16]
subsequently generalised this to two benthic substratum - sand and seagrass, where the two
were delineated by way of an empirical relationship prior to the model inversion. The HOPE
model originally used the SOLVER tool (within Microsoft Excel) as the optimisation routine.
Subsequently, HOPE used the Levenberg-Marquardt and B2NLS optimisation
algorithms [27].
In 2004, Klonowski et al [20][26] made extensions to the model of Lee et al
to classify bottom spectra in Jurien Bay, Western Australia. Modifications were made to the model of
Chlorophyll-a concentrations, based on measurements in Cockburn Sound. This model included a
parameterisation for three bottom spectra - sand, Hallophylla (green leafy seagrass) and Sargassum
(brown seaweed). This model used the Levenburg-Marquardt optimisation scheme.
In 2005, Mobley et al [23] used the radiative transfer numerical model, HydroLight,
to construct lookup tables for spectrum matching of hyperspectral imagery. This model is
known as CRISTAL (Comprehensive Reflectance Inversion based on Spectrum matching and TAble
Lookup) [33].
In 2006, Wettle et al [25][29] developed a semi-analytical model, SAMBUCA (Semi-Analytical
Model for Bathymetry, Un-mixing, and Concentration Assessment), based on the Lee et al model, HOPE.
This model incorporates a different parameterisation for the absorption and backscatter
coefficients to HOPE, which is in line with field data measurement protocols used by the CSIRO.
This model used the Simplex optimisation scheme.
In 2009, Hedley et al [28] implemented an efficient lookup table inversion scheme
for radiative transfer models using adaptive lookup trees (ALUT). This model was more efficient
than optimisation-based models and had comparable accuracy in bathymetric retrievals.
In 2014, Gege [19] used the shallow water parameterisation of the RRS by Albert and
Mobley [18] to implement the WASI (Water Colour Simulator) model. This parameterisation
is an alternative to the model of Lee et al. This model uses the simplex optimisation scheme.
In 2018, Hedley et al [35] examined the use of the Sentinel-2 satellite to monitor
coral reefs. It was found that the Sentinel-2 data can be used within a physics-based model to
monitor coral reefs and retrieve bathymetric estimations with comparable performance to WorldView-2.
In this paper we detail the development of the photic model, an extension of the Lee et al [14][15][16] semi-analytical model for use with multispectral imagery. In particular, for the LANDSAT-8 and Sentinel-2 satellites. These satellites have greatly decreased spectral resolution in comparison to airborne hyperspectral sensors, however they have regular global coverage in coastal areas and their datasets are freely available. Given this availability, we are motivated to see if we can apply semi-analytical models accurately and efficiently to these datasets.
In section 2 we recap the hyperspectral model of Lee et al [14][15][16],
along with extensions to include multiple bottom types by Gege [19] and
Wettle et al [25]. We follow Wettle et al [25] and use
both the root-mean-square and spectral angle mapper error in our error metric.
In section 3 we introduce spatial and temporal extensions to the Lee et al model.
In section 4 we detail how the model is inverted to yield stable depth, water turbidity and
bottom reflectance estimates.
In section 5 we detail an iterative modelling framework, where model parameters are
estimated and subsequently refined to improve their retrieval.
In section 6 we give a detailed case study where we validate the photic model against single-beam sonar data in the area of the Murion Island Marine Management Area.
2 The Model for Hyperspectral Imagery
Our modelling approach for hyperspectral imagery directly follows the model of Lee et
al [14][15][16], with additions to include multiple bottom
spectra as given in the model of Gege [19] and the spectral angle mapper
(SAM) in the spectral matching error metric as given in the model of Wettel et
al [25]. We will now briefly describe the model.
The remote-sensing reflectance (RRS), , is defined at the ratio of the water leaving radiance to downwelling irradiance just above the surface. The RRS over optically shallow water is controlled by a number of factors, including absorption properties, scattering properties, the bottom albedo, bottom depth and solar elevation. We begin by relating the RRS above the surface, , to the subsurface RRS, which is given by
where is a spectrally-constant offset. The subsurface RRS, , is expressed as a linear combination of subsurface RRS from the water column, , and the subsurface RRS from the bottom reflectance, .
| (2.1) |
Where is the subsurface RRS for optically deep water. and are the path elongation for photons from the water column and from the bottom respectively. is the subsurface solar zenith angle and is the subsurface viewing angle from nadir. is the bottom albedo. is the bottom depth. is the attenuation coefficient, which is given by
| (2.2) |
where is the absorption coefficient and is the backscattering
coefficient.
For the subsurface RRS of optically deep water, Lee et al [14][15][16] used the model of Gordon et al [8]
where
The path elongation factors are given by
The inherent optical properties, & are given by
where is the absorption coefficients of pure water as given in Pope &
Fry [12], is the absorption coefficients for phytoplankton
pigments, is the absorption coefficients for gelbstoff and detrius,
is the backscattering coefficient for pure seawater as given in
Morel [3], is the backscattering coefficient of
suspended particles.
For an -band spectrum the model above has equations (one for each ), each
with 4 unknowns – .
Thus, there are unknowns and equations, and consequently finding solutions
to this system requires establishing additional relationships.
Lee et al estimated the spectral shape of with a single parameter, , which represents the phytoplankton absorption coefficient at 440 nm, ie.
| (2.3) |
where , was modelled by Lee [10]. We use this model for ,
however we derived the parameterisation of , from a dataset sourced
from the CSIRO [21] (See Appendix A).
The spectral shape for the absorption of gelbstoff and detritus, is expressed with the parameter and is given by
The parameter S is in the range – .
The spectral shape for the backscattering coefficient of suspended particles, is expressed with the parameter and is given by
where is estimated by the empirical relationship
Finally, for bottom types, the bottom albedo is parameterised with and we write as , where
| (2.4) |
where is the bottom albedo of a given bottom type as
estimated from field measurements and normalised to 550 nm, and the specify the fraction
of each bottom type. This is based on the parameterisations used in Gege [19] and
Wettle et al [25].
Our model can estimate bottom reflectance using (2.4), however if the
model is required to delineate between a large number of bottom spectra then we are better to
adopt the iterative method of Wettle et al [25]. In this formulation, we iterate over
all individual bottom spectra, then over all pairs of bottom spectra. The spectra or pair of
spectra best matching the input RRS is then representative of the bottom composition. It is worth
noting that this method is significantly slower due to the combinatorial nature of exhaustively
iterating through all the pairs.
With this parameterisation we reduce the number of unknowns which influence the RRS spectrum to , , , , , , , , and . Thus if we have independent channels it should be possible to determine a unique solution to the system of equations. However due to the presence of noise the best we can do is seek to minimise the difference between the modelled RRS, , and the measured RRS, . Following Lee et al [14][15][16], we define the RRS RMS relative error, , as
| (2.5) |
Wettle et al [25] included the Spectral Angle Mapper (SAM) within the error metric
where in both and the term is dependent on the parameters , , , , , , , , , , , , and . We will describe the full error metric used in photic in the following section.
3 Extensions to the Model for Multispectral Imagery
Lee et al [17] found that 15 equispaced spectral bands covering the
400–800 nm range are adequate for most coastal and oceanic remote sensing
applications. The satellite imagery of LANDSAT 8 and Sentinel-2 have significantly
fewer spectral bands in this range, however we would still like to apply the
semi-analytical model to these vast and freely available datasets. Previously
Dekker et al [34] has applied the SAMBUCA [25] model to
QuickBird multispectral satellite imagery.
We now describe two extensions to the semi-analytical model to increase its applicability to multispectral imagery.
3.1 Spatial extension
A reasonable assumption to make for medium to high resolution satellite imagery is constant
water turbidity within a spatial region around a given pixel. Klonowski et al [20]
used a constant , and throughout an entire scene for bottom type classification
using hyperspectral imagery.
If we define a spatial region, , around a given pixel, then we (simultaneously) model pixels. Within this region we constrain , , and to be (spatially) static, while , , , , , , , , may vary.

Thus, we may represent the non-static parameters within each region as
| (3.1) | ||||
Additionally, in many instances it is reasonable to constrain the variance of H within the spatial region. That is, a constraint of the form with . Where and is the standard deviation and mean of H respectively. (Alternatively, can be dependent on depth.) The error metric we use in photic for the continuity of H is given by
| (3.2) |
3.2 Temporal extension
We can further increase the spectral data available to the model by using a time series of
satellite scenes. For LANDSAT-8 and Sentinel-2 scenes, a large number of scenes are
available and most are usable for our purposes.
We assume continuity of the seabed over time. Thus, across multiple scenes the depth, , is static up to tidal effects. For scenes, it is assumed we know the tidal corrections , , , to a common datum, such that
We further assume the bottom reflectance is constant over time. This may be a more tenuous
assumption than our other assumptions, for example for some coral reefs or seagrass beds.
Thus, the temporal constraints are , , , , , , , and are constant, while allowing the water turbidity to vary over time - , , (and ), which we represent as
| (3.3) | ||||
These constraints complement the spatial constraints, in that previously , , , , , , , , could vary spatially, while , , are spatially static.
3.3 The multi-spatial, multi-temporal, error metric
We will now combine the spatial and temporal extensions into a single error metric for our model. As before, let be the number of satellite scenes and the size of the spatial region around the spectra we are modelling. Then denote and to be the measured and modelled RRS at spatial location (for ) and scene (for ) for wavelength, , respectively. Then the RMS error across all scenes and the entire region is given by
| (3.4) |
similarly, the SAM error is given by
| (3.5) |
where H, , , , , ,
, , are given in (3.1), and P,
G, X, are given in (3.3). We denote
as shorthand for
.
We have three error metrics - the RMS error (3.4), the SAM error (3.5), and the continuity of H error (3.2). We combine these into a final, weighted, error metric for our model,
| (3.6) |
where and . In photic, we experimentally
found and balances both terms in the error metric.
In this formulation of the model, we have parameters for H; parameters for , , , ; parameters for , , , ; and parameters for P, G, X, . In total, we have
parameters to determine.
These spatial and temporal extensions to the model of Lee et al greatly increase data used in the spectral matching. Below we compare the number of measured spectra (assuming we use the LANDSAT 8 satellite with the coastal, blue, green and red spectral bands) across each scene and region to the number of unknown parameters in our model, where the number of bottom types, is 2.
A common setting for our modelling is , and , which is highlighted above.
4 Inverting the Model
We will now detail how we invert (2.1) to obtain estimates for P, G, X, , , , , H, , , , and by finding a (global) minimum of .
4.1 Initial depth estimate
Lee et al [15] used m as an initial depth estimate and subsequently
used an estimate of [33]. Starting the model inversion at a
reasonable depth estimate was a technique used by Albert et al [22].
If reliable depth profiles are known, then initial, and often accurate, depth estimates can be obtained using an empirical method [4][6][24]. Closely following the model of Lyzenga et al [24] - the empirical depth, , for a -band spectrum is given by
where and .
The subsurface RRS of optically deep waters is estimated using the method of Lyzenga
et al [24]. We compute both the mean subsurface RRS of optically deep
water, , and the standard deviation of the subsurface
RRS of optically deep water, in each
band. It is worth noting that this is a scene-wide estimate.
The attenuation coefficients are estimated using the blue and green spectral bands
then interpolate across spectra and water types from a table of spectral attenuation
coefficients for different coastal and oceanic water types to directly estimate the
attenuation coefficients and the water type [5][13]. Again,
it is worth noting that this is a scene-wide estimate.
Consider soundings , we begin by generating weights for each soundings such that
where . This weighting scheme prevents frequently occurring depths from skewing the subsequence fitting. We construct a weighted, root-mean-square, relative error metric, , such that
where is shorthand for
at the spatial location
of the sounding, .
To find the minima of , we use multiple iterations of the
simplex algorithm [2], each with a pseudo-randomly generated initial
simplex. This random initialisation with multiple iterations helps prevent the
optimisation from settling in a local minimum.
With multiple scenes, the depths from each scene from the empirical algorithm can be synthesised into a single depth estimate by way of a temporal median across all modelled scenes (once we account for tidal variations). Alternatively, a weighted mean can be used. In this case, the weights are inversely proportional to the final of each scene.
4.2 Ordering pixels by spectral angle
It would be natural within a computer implementation to model the pixels in a column- or row-major order. However in photic, pixels within the modelling domain are sorted by spectral angle above the deep water mean (via the SAM). The spatial indices of the pixels are stored so we can return the modelling results to their original location. The model starts with the pixels closest to the mean deep water spectrum. We will subsequently see why this ordering is favourable to our modelling.
4.3 Initial estimates for P, G, X and
The initial estimates closely follows Lee et al [15]. Without any knowledge of field samples, the initial parameterisation of P, G, X and is given by
where is the average over the spectra in the region. We call this
parameterisation a cold start, as previously modelled pixels with similar spectra have
not guided the current starting point.
Alternatively, as the pixels are sorted by their SAM from the deep water mean RRS, if the current region of pixels being modelled is within a model-defined threshold of the previously modelled pixel, then we hot start the model with the previous optimal parameterisation for P, G, X and . This significantly reduces the number of iterations before convergence.
4.4 Initial estimates for B and q
The initial estimate of follows the HOPE model of Lee et al [33]. We arbitrarily set , which corresponds to equal proportions of each bottom type. Unlike the initialisation of P, G, X and , we do not hot start B and q; as this would make assumptions on the continuity of the bottom reflectance.
4.5 The optimisation approach
With our initial estimation of all parameters (both spatially and temporally) in (2.1), we
now seek the parameterisation which minimises our error metric, . photic
uses the simplex algorithm [2] to perform the optimisation. This algorithm is
derivative free and converges quickly if a reasonable starting point (simplex) is chosen.
When the model is cold started and an initial estimate for H is not given, then we perform
multiple optimisations with starting points at the following depths 0.1, 0.5, 1.0, 1.5, 2.0, 3.0,
4.0, 5.0, 6.0, 8.0, 10.0, 12.5, 15.0, 17.5, 20.0, 25.0, 30.0 m. This is computationally expensive,
but rare as most pixels are hot-started.
photic can also take a range for each parameter. Within the simplex optimisation each parameter is constrained to be within its user-defined range. These ranges could come from local knowledge or from physical measurements from the modelling domain.
4.6 The dynamic lookup table approach
Modelling large areas using the optimisation approach requires significant computing resources.
One way to decrease this computational burden is the inclusion of a small, dynamic, lookup table
(LUT) which is searched prior to running the optimisation approach. If the match between the
current pixel and spectra in the LUT (in the sense of the SAM between the two spectra) is
below a model-defined threshold then the LUT is used and the optimisation approach is skipped.
Whenever a pixel is modelled with the optimisation approach, if is below a
model-defined threshold then the result of this modelling is stored in the LUT along with a
timestamp. When a new entry is stored in the LUT, the oldest entry is discarded (overwritten).
In photic the LUT is deliberately small, with only 256 entries. This way searching
the LUT is fast, however the LUT should still contain many spectra relevant to the current
pixel being modelled as the pixels are sorted prior to modelling.
In photic the threshold on entering a modelled pixel to the LUT is initially
, but can be adaptively modified. The
threshold cannot exceed (where the units of is
relative percentage error). This prevents poorly modelled pixels from further degrading
pixels within the modelling domain.
Using a dynamic LUT in conjunction with sorting the spectra results in significant speed improvements. Generally, more than 95% of pixels are modelled using the LUT. The LUT can model in excess of , which is at least three orders of magnitude faster than the optimisation approach.
4.7 An example inversion
As a detailed example of the model, we give a breakdown of the optimisation process for and . The spectra are taken from the case study in section 6, for scenes LC81150752018058LGN00 and LC81150752019253LGN00. The location of these spectra are 114.361135E, 21.676824S and from the sounding data the water depth is 14.9 m LAT. The bottom of atmosphere RRS spectra for each scene and region is given in the table below.


In summary, the model required 1043 iterations to converge to a model error of . The derived parameters were
| P | |||
| G | |||
| X | |||
| B | |||
| H |
Thus, the model-derived depth is 16.47 m.
5 Iterative Estimation of Depth, Water Turbidity and Bottom Composition
5.1 The first approximation
In the first approximation to the inversion, we model all individual scenes, pairs of scenes, 3-tuples of scenes and 4-tuples of scenes. In each of these modelling iterations, all parameters P, G, X, , , , , , , , , H and are estimated by the model and stored for subsequent use.
5.2 Depth averaging
If reliable depth profiles are not known, then we take the median of all iterations of the singletons, pairs, 3- and 4-tuples from the first approximation above. We use a weighted median, where the weight is proportional to the number of scenes in the model. That is, proportional to .
5.3 Aligning , with known depth profiles
If reliable depth profiles are known, then the model-derived depths, , can be
aligned with these profiles. This technique, for a single scene, was used
by Ohlendorf et al [32, Figure 9. Depth validation at Rottnest
Island, 2005] as a post processing step to the model inversion.
From the model-derived depths, , we construct a single depth , such that
where . We construct the same weighting scheme as used in the empirical method - consider soundings , we begin by generating weights for each soundings such that
where . We construct a weighted, root-mean-square, relative error metric, , such that
where is shorthand for at the spatial location of the sounding, .
To find the minima of , we use the simplex algorithm [2] with an
initial simplex of for all . If the model is well calibrated,
then we expect this starting point to be close to the minima.
5.4 Averaging
5.5 Deriving bottom types
We perform an additional optimisation iteration to improve the accuracy of the unmixing of
multiple bottom types. In this modelling iteration we use the previously estimated
P, G, X, , , , ,
H and . However, P, G, X and
are constant. We use the values of , ,
, as an initialisation for subsequent modelling.
We begin by expressing 2.1 in terms of , which we term with parameters , , , ,
where
and the corresponding unmixed , which we term is given by
Then we use the averaged (or aligned) depths as H across all subsequent model iterations. The
values of P, G, X, are averaged across all previous
modelling iterations from 5.1 for each scene. If noise is present in these datasets
then we apply a median filter, prior to computing .
In this modelling iteration we keep P, G, X, H,
static and optimise only for , , , ,
, , , . As previously, we assume the bottom
spectra do not change over time, this allows us to simultaneously model multiple scenes. We index
the scenes, with .
The error metric for the unmixing is given by
where
and
where is shorthand for and is shorthand for .
5.6 Depth error estimate
Obtaining a realistic depth error estimate requires accounting for uncertainties in both
the model inputs and the model itself.
We estimate the sensor noise by computing the RRS standard deviation in optically deep
water. The model then adds (or subtracts) random noise within the threshold of the
estimated sensor noise. The corresponding standard deviation of the resulting depths
over many trials is the depth error estimate.
We can further account for errors in the model, bottom reflectance, absorption and backscattering spectra by scaling the depth error estimate, if reasonable upper bounds on the error estimates of these quantities are known.
6 Case Study – Murion Island Marine Management Area
As a small exemplar case study we modelled a 260 region to the south of North Murion Island, including Sunday Island, Combe Reef and Exmouth Reef; which are off the Pilbara Coast in Western Australia. This area is part of the Murion Island Marine Management Area. It is also an important area for commercial marine traffic.

A single-beam sonar survey was conducted in 2011 by Transport WA. Within the spatial
domain of this case study there are 53 194 sonar measurements, the majority of
which are between depths of 12 and 22 m. This survey is approximately 32 km by 9.5 km.
The satellite imagery used for this study was from the LANDSAT 8 satellite. The scenes from this satellite are in size at a horizontal resolution of approximately 30 m. The USGS provides open access to the entire archive of LANDSAT imagery dating back to 1972. In total, 4 scenes were selected for modelling
| study ID | scene ID |
|
|
date |
|
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | LC81150752015210LGN02 | 115 | 75 | 2015-07-29 | 38.86∘ | ||||||
| 2 | LC81150752018058LGN00 | 115 | 75 | 2018-02-27 | 55.22∘ | ||||||
| 3 | LC81150752018266LGN00 | 115 | 75 | 2018-09-23 | 54.85∘ | ||||||
| 4 | LC81150752019253LGN00 | 115 | 75 | 2019-09-10 | 50.68∘ |
Atmospheric correction and sun glint correction was performed with ACOLITE [36].

The bottom types used in this study were sand, seagrass and coral. Unfortunately, these
spectra were not collected from the study site and at best can only be used as
approximate representative samples.
Depth soundings used for the initial depth estimation were digitised from chart WA 900 - Point
Murat to North Murion Island. The empirical model (see section 4.1) performed
well, with a mean relative error of 15% and a mean absolute error of 1.74 m.
photic was parameterised with , , . In total,
we modelled 15 combinations of these 4 scenes. Where the combinations of modelled scenes,
by study ID, were [1], [2], [3], [4], [1,2], [1,3], [1,4], [2,3], [2,4], [3,4],
[1,2,3], [1,2,4], [1,3,4], [2,3,4], [1,2,3,4]. The final depth was taken as the spatial
median of the 15 modelling iterations.
All 15 model iterations of photic ran sequentially in 5 hours. The lookup table
accounted for modelling the majority of the points. Without the lookup table the modelling
would have taken around two weeks (running sequentially on a single core).
In the scatter plot below a vertical correction of -0.75 m was applied to the model-derived bathymetry. This accounts for tidal variations and a correction to the vertical datum of the sonar data.

The regression analysis between the sonar survey and the LANDSAT-derived bathymetry shows good agreement, with , , the least squares line of best fit was , the mean absolute error was 1.17 m, and the mean relative error was 7.52%. Furthermore, below we give a summary of the absolute and relative errors.
|
|
|---|
The LANDSAT-derived bathymetry correlates well with the single-beam sonar
data. While it is difficult to compare studies in different regions, the
regression analysis suggests our model-derived bathymetry has similar
performance to other physics-based, model-derived
bathymetry [32][30]. We do not, however see
LANDSAT 8 or Sentinel-2 data competing with hyperspectral data in terms
of accuracy of bathymetric retrieval.
In the following graphic we display the key model-derived datasets and the model derived parameterisation of P, G and X.
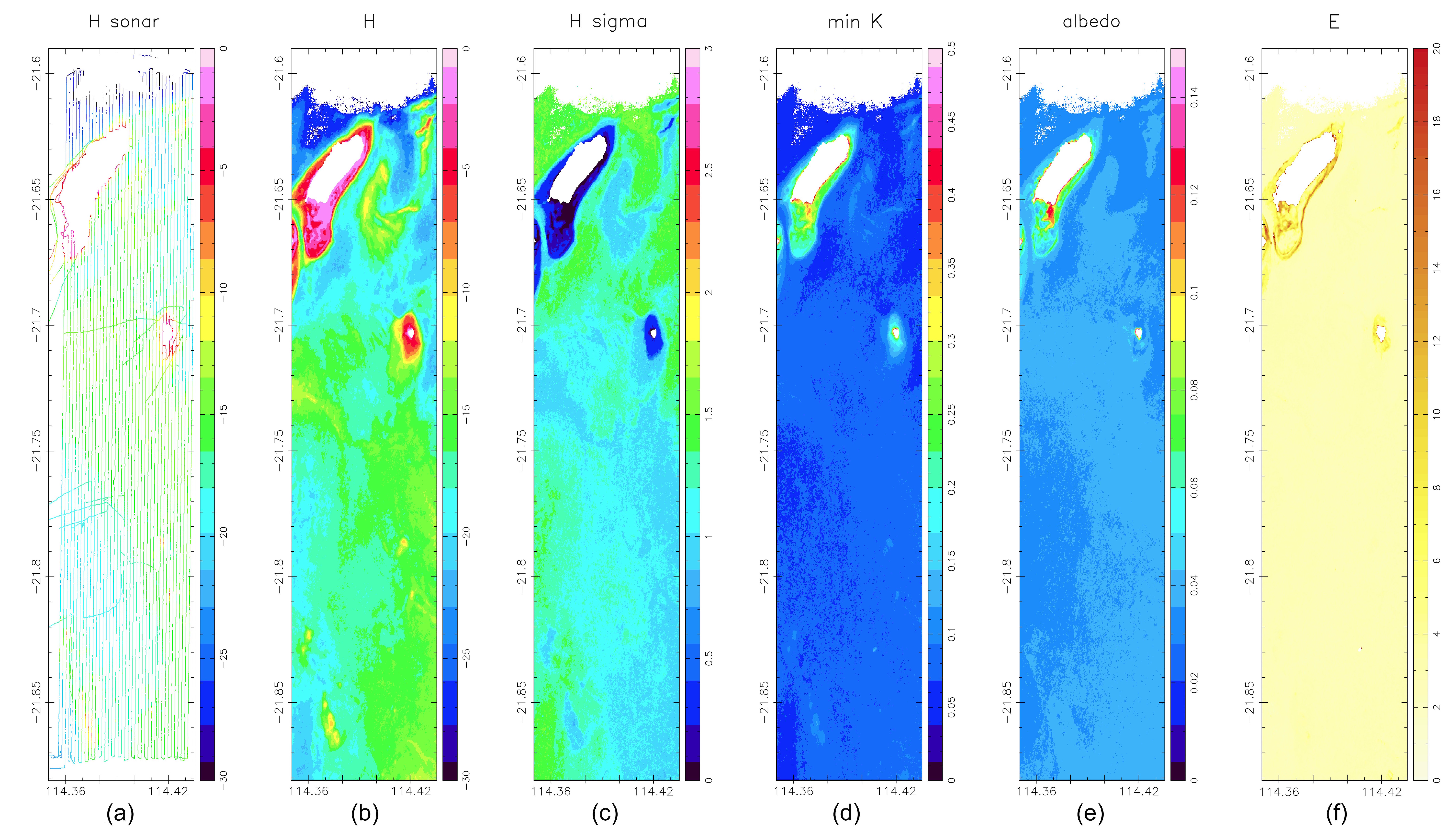


It is of interest to see the increase in in a band to the south of
North Murion Island (plot (f) above). This coincides with a sharp drop-off in depth
and consequently is can be explained by the model trying to minimise both the RRS error
and the depth continuity error (3.2). As the RRS error is significantly higher
weighted than the depth continuity error, the model will favour the minimisation of the
RRS error in such cases. Otherwise, the average error is well below 5%, which is
expected.
The range of H-sigma is reasonable, as this estimate does not include uncertainties
introduced in the estimation of the bottom spectra, atmospheric correction,
and core assumptions within the original model of Lee et al.
When interpreting the range of the mean, minimum attenuation coefficient it must be
considered that the 4 scenes were selected amongst over 100 scenes for their
minimal water turbidity.
One region where upon visual inspection the model-derived bathymetry performs poorly is directly east of North Murion Island. Below we have plotted the sonar data over the model-derived bathymetry. This may be due to a shift in the seabed in the 9 years since the sonar survey was conducted (unlikely) or due to poorly estimating the bottom reflectance in this area (likely).

By way of comparison, we modelled each scene individually with the spatial and temporal extensions removed (, ). We also removed the initial depth estimates and the lookup table. The resulting model-derived bathymetry clearly shows instabilities in the optimisation scheme with so few data points to perform the fit.

7 Conclusions & Future Work
In this paper we have shown that multispectral imagery can be used successfully within a
physics-based. We have made temporal and spatial extensions to the model of Lee et al
[14][15][16], which increase the stability and accuracy
of depth retrievals when using low spectral resolution satellites like LANDSAT 8 or
Sentinel-2.
Further work is underway to sort the spectra into clusters, where in each cluster only a small fraction of the spectra require modelling due to their spectral similarity.
References
- [1] F.C. Polcyn, W.L. Brown, I.J. Sattinger, “The Measurement of Water Depth by Remote Sensing Techniques”, Spacecraft Oceanography Project, US Naval Oceanographic Office, Washington DC, 1970
- [2] R. O’Neil, “Algorithm AS 47: Function Minimization Using a Simplex Procedure”, Journal of the Royal Statistical Society. Series C (Applied Statistics), vol. 20, no. 3, pp. 338–345, 1971
- [3] A. Morel, “Optical properties of pure water and pure sea waters”, Optical Aspects of Oceanography, N. G. Jerlov and E. S.Nielsen, eds. Academic, pp. 1–24, 1974
- [4] F.C. Polcyn, “NASA/COUSTEAU OCEAN BATHYMETRY EXPERIMENT - Remote Bathymetry Using High Gain LANDSAT data”, NASA, Goddard Space Fligh Center, 1976
- [5] N. Jerlov, “Optical Oceanography”, 1968
- [6] D.R. Lyzenga, “Passive remote sensing techniques for mapping water depth and bottom features”, Applied Optics, vol. 17, no. 3, pp. 379–383, 1978
- [7] https://science.nasa.gov/missions/geosat
- [8] H.R. Gordon et al, “A semianalytical radiance model of ocean color”, Journal of Geophysical Research, vol. 93, pp. 10909–10942, 1988
- [9] S. Maritorena, A. Morel, B. Gentili, “Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo”, American Society of Limnology and Oceanography, vol. 39, no. 7, pp. 1689–1703, 1994
- [10] Z. P. Lee, “Visible-infrared remote-sensing model and applications for ocean waters”, Ph.D. dissertation, Department of Marine Science, University of South Florida, 1994
- [11] A. Lawler, “Sea-Floor Data Flow From Postwar Era”, Science, vol. 270, issue 5237, pp. 727, November 1995
- [12] R. Pope, E. Fry, “Absorption spectrum 380–700 nm of pure waters: II. Integrating cavity measurements”, Applied Optics, vol. 36, pp. 8710–8723, 1997
- [13] Y. Morel, L.T. Lindell, “PASSIVE MULTISPECTRAL BATHYMETRY MAPPING OF NEGRIL SHORES, JAMAICA”, Fifth International Conference on Remote Sensing for Marine and Coastal Environments, San Diego, California, October 1998
- [14] Z. Lee et al, “Hyperspectral remote sensing for shallow waters. I. A semianalytical model”, Applied Optics, vol. 37, no. 27, pp. 6329–6338, 1998
- [15] Z. Lee et al, “Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization”, Applied Optics, vol. 38, no. 18, pp. 3831–3843, 1999
- [16] Z. Lee et al, “Properties of the water column and bottom derived from Airborne Visible Infrared Imaging Spectrometer (AVIRIS) data”, Journal of Geophysical Research, vol. 106, no. C6, pp. 11639–11651, June 2001
- [17] Z. Lee, K.L. Carder, “Effect of spectral band numbers on the retrieval of water column and bottom properties from ocean color data”, Applied Optics, vol. 41, no. 12, pp. 2191–2201, April 2002
- [18] A. Albert, C.D. Mobley, “An analytical model for subsurface irradiance and remote sensing reflectance in deep and shallow case-2 waters”, Optics Express, vol. 11, no. 22, pp. 2873–2890, 2003
- [19] P. Gege, “The water color simulator WASI: an integrating software tool for analysis and simulation of optical in situ spectra”, Computers & Geosciences, vol. 30, pp. 523–532, 2004
- [20] W.M. Klonowski, L.J. Majewski, P.R.C.S. Fearns, L.A. Clementson, M.J. Lynch, 2004. “Bottom type classification using hyperspectral imagery”, Proceedings Ocean Optics XVII (CDROM), 2004
- [21] R. Babcock, L. Clementson, Bunbury Deployment 2003–2005: absorption-phytoplankton data, Integrated Marine Observing System (IMOS), https://portal.aodn.org.au/, CSIRO, 2003–2005
- [22] A. Albert, P. Gege, “Inversion of irradiance and remote sensing reflectance in shallow water between 400 and 800 nm for calculations of water and bottom properties”, APPLIED OPTICS, vol. 45, no. 10, pp. 2331–2343, April 2006
- [23] C.D. Mobley et al, “Interpretation of hyperspectral remote-sensing imagery by spectrum matching and look-up tables”, Applied Optics, vol. 44, no. 17, pp. 3576–3592, 2005
- [24] D.R. Lyzenga, N.P. Malinas, F.J. Tanis, “Multispectral Bathymetry Using a Simple Physically Based Algorithm”, IEEE Transactions on Geoscience and Remote Sensing, vol. 44, no. 8, 2006
- [25] M. Wettle, V.E. Brando, “SAMBUCA Semi-Analytical Model for Bathymetry, Un-mixing, and Concentration Assessment”, CSIRO Land and Water Science Report 22/06, July 2006
- [26] W.M. Klonowski, P.R.C.S. Fearns, M.J. Lynch, “Retrieving key benthic cover types and bathymetry from hyperspectral imagery”, Journal of Applied Remote Sensing, vol. 1, 011505, 2007
- [27] Z. Lee, “Test, Evaluate, and Characterize a Remote-Sensing Algorithm for Optically-Shallow Waters”, Geosystems Research Institute, Northern Gulf Institute, Mississippi State University, Stennis Space Center, 2009
- [28] J. Hedley, C. Roelfsema, S. Phinn, “Efficient radiative transfer model inversion for remote sensing applications”, Remote Sensing of the Environment, vol. 133, issue 11, pp. 2527–2532, November 2009
- [29] V.E. Brando, J.M. Anstee, M. Wettle, A.G. Dekker, S.R. Phinn, C. Roelfsema, “A physics based retrieval and quality assessment of bathymetry from suboptimal hyperspectral data”, Remote Sensing of the Environment, vol. 113, issue 4, pp. 755–770, 2009
- [30] S. Sagar, M. Wettle, “Mapping the fine-scale shallow water bathymetry of the Great Barrier Reef using ALOS AVNIR-2 data”, OCEANS 2010 IEEE - Sydney
- [31] Z. Lee, “Global Shallow-Water Bathymetry From Satellite Ocean Color Data”, EOS, vol. 91, no. 46, 16 November 2010
- [32] S. Ohlendorf, A. Muller, T. Heege, S. Cerdeira-Estrada, H.T. Kobryn, “Bathymetry mapping and sea floor classification using multispectral satellite data and standardized physics-based data processing”, Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions, Prague, September 2011
- [33] A. Dekker et al, “Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments”, Limnology and Oceanography: Methods, vol. 9, pp. 396–425, 2011
- [34] A.G. Dekker, S. Sagar, V.E. Brando, D. Hudson, “Bathymetry from satellites for hydrographic purposes”, Shallow Survey 2012, Wellington, New Zealand, February 2012
- [35] J.D. Hedley, et al, “Coral reef applications of Sentinel-2: Coverage, characteristics, bathymetry and benthic mapping with comparison to Landsat 8”, Remote Sensing of Environment, vol. 216, pp. 598–614.
- [36] Q. Vanhellemont, “Adaptation of the dark spectrum fitting atmospheric correction for aquatic applications of the Landsat and Sentinel-2 archives”, Remote Sensing of Environment, vol. 225, pp. 175–192, 2019. (https://doi.org/10.1016/j.rse.2019.03.010)
- [37] OpenStreetMap contributors, https://www.openstreetmap.org/
Appendix A Appendix
From the model of Lee for , we derived (using least-squares, non-linear optimisation) and using a dataset collected by the CSIRO in 2003–2005 near Bunbury, Western Australia [21]. This dataset comprised 71 measurements and collected in depths ranging from 1.5 to 20 m.
| 400 | 0.69322 | 0.01035 | 520 | 0.32875 | 0.00617 | 640 | 0.24139 | 0.02122 |
|---|---|---|---|---|---|---|---|---|
| 405 | 0.80506 | 0.01868 | 525 | 0.30033 | 0.00753 | 645 | 0.25922 | 0.02508 |
| 410 | 0.89891 | 0.02278 | 530 | 0.27633 | 0.00874 | 650 | 0.26483 | 0.02589 |
| 415 | 0.96392 | 0.02497 | 535 | 0.25874 | 0.01065 | 655 | 0.27135 | 0.02374 |
| 420 | 0.99268 | 0.02371 | 540 | 0.23621 | 0.01005 | 660 | 0.31442 | 0.02326 |
| 425 | 1.00392 | 0.01841 | 545 | 0.21342 | 0.00897 | 665 | 0.40322 | 0.02714 |
| 430 | 1.02963 | 0.01381 | 550 | 0.19724 | 0.00975 | 670 | 0.49153 | 0.03177 |
| 435 | 1.03967 | 0.00750 | 555 | 0.18247 | 0.01048 | 675 | 0.52301 | 0.03344 |
| 440 | 1.0 | 0.0 | 560 | 0.16819 | 0.01044 | 680 | 0.46490 | 0.02943 |
| 445 | 0.90067 | -0.01143 | 565 | 0.15781 | 0.01023 | 685 | 0.33078 | 0.01968 |
| 450 | 0.79228 | -0.02292 | 570 | 0.15495 | 0.01076 | 690 | 0.19484 | 0.01007 |
| 455 | 0.74203 | -0.02655 | 575 | 0.15478 | 0.01080 | 695 | 0.11332 | 0.00577 |
| 460 | 0.74870 | -0.02273 | 580 | 0.15795 | 0.01102 | 700 | 0.07804 | 0.00588 |
| 465 | 0.76773 | -0.01590 | 585 | 0.16251 | 0.01104 | 705 | 0.05617 | 0.00477 |
| 470 | 0.77611 | -0.00746 | 590 | 0.16427 | 0.01054 | 710 | 0.04426 | 0.00401 |
| 475 | 0.76177 | -0.00132 | 595 | 0.16247 | 0.01027 | 715 | 0.03844 | 0.00414 |
| 480 | 0.72663 | -0.00007 | 600 | 0.16094 | 0.01062 | 720 | 0.03209 | 0.00361 |
| 485 | 0.68161 | -0.00094 | 605 | 0.16188 | 0.01104 | 725 | 0.02705 | 0.00333 |
| 490 | 0.63211 | -0.00109 | 610 | 0.16489 | 0.01075 | 730 | 0.02090 | 0.00253 |
| 495 | 0.57497 | -0.00056 | 615 | 0.17238 | 0.01088 | 735 | 0.02198 | 0.00528 |
| 500 | 0.51537 | 0.00073 | 620 | 0.17878 | 0.01073 | 740 | 0.01671 | 0.00383 |
| 505 | 0.45850 | 0.00244 | 625 | 0.18479 | 0.01090 | 745 | 0.00866 | 0.00191 |
| 510 | 0.40764 | 0.00391 | 630 | 0.19970 | 0.01329 | 750 | 0.01262 | 0.00288 |
| 515 | 0.36526 | 0.00529 | 635 | 0.21805 | 0.01636 |
Below we compare our derived , with the original parameterisation of Lee [10] and Lee et al [14] against 12 of the collected samples.

