A Masked Segmental Language Model for Unsupervised Natural Language Segmentation
Abstract
We introduce a Masked Segmental Language Model (MSLM) for unsupervised segmentation. Segmentation remains an important preprocessing step both for languages where “words” or other linguistic units (like morphemes) are not clearly delineated by whitespace, as well as for continuous speech data, where there is often no meaningful pause between words. Near-perfect supervised methods have been developed for use in resource-rich languages such as Chinese, but many of the world’s languages are both morphologically complex, and have no large dataset of “gold” segmentations. To solve this problem, we propose a new type of Segmental Language Model for use in both unsupervised and lightly supervised segmentation tasks. The MSLM is built on a span-masking transformer architecture, harnessing the power of a bidirectional masked context and attention. In a series of experiments, our model outperforms Recurrent SLMs on Chinese in segmentation quality, and performs similarly to the recurrent model on English. We conclude by discussing the challenges posed by segmentation in differing natural language settings.
1 Introduction
Outside of the orthography of English and languages with similar writing systems, natural language is not usually overtly segmented into meaningful units. Many languages, like Chinese, are written with no spaces in between characters, and Chinese Word Segmentation remains an active field of study (e.g. Tian et al., 2020). Running speech is also usually highly fluent with no meaningful pauses existing between “words” like in orthography.
Tokenization schemes for powerful modern language models have now largely been passed off to greedy information-theoretic algorithms like Byte-Pair Encoding (Sennrich et al., 2016) and the subsequent SentencePiece (Kudo and Richardson, 2018), which create subword vocabularies of a desired size by iteratively joining commonly co-occuring units. However, these segmentations are usually not sensical to human readers: for instance, twice is sometimes modeled as tw + ice, even though a human would know twice is not related to ice. Given the current performance of models using BPE-type tokenization, the nonsensical nature of these segmentations does not necessarily seem to inhibit the success of neural models.
Nevertheless, BPE does not necessarily help in situations where knowing a sensical segmentation of linguistic-like units is important, such as attempting to model the ways in which children acquire language (Goldwater et al., 2009), segmenting free-flowing speech (Kamper et al., 2016; Rasanen and Blandon, 2020), creating linguistic tools for morphologically complex languages (Moeng et al., 2021), or studying the structure of an endangered language with few or no current speakers (Dunbar et al., 2020).
In this paper, we present a new unsupervised model for robust segmentation. While near-perfect supervised models have been developed for resource-rich languages like Chinese, most of the world’s languages do not have large corpora of training data (Joshi et al., 2020). Especially for morphologically complex languages, large datasets containing “gold” segmentations into units like morphemes are very rare. To solve this problem we propose a type of Segmental Language Model (Sun and Deng, 2018; Kawakami et al., 2019), based on the powerful neural transformer architecture (Vaswani et al., 2017).
Segmental Language Models (SLMs) produce strong language models that can also be used for unsupervised segmentation that correlates with units like words and morphemes (Kawakami et al., 2019). SLMs can be considered a form of character or open-vocabulary language model in which the input is a sequence of characters, and the sequence is modeled as a latent series of segments comprised of one or more characters.
In departure from previous SLMs, we present a Masked Segmental Language Model (MSLM), built on the transformer’s powerful ability to mask out and predict spans of input characters, and embracing a fully bidirectional modeling context with attention. As far as we are aware, we are the first to introduce a non-recurrent architecture for segmental modeling, and conduct comparisons to recurrent baselines across two standard word-segmentation datasets in Chinese and English, with the hope of expanding to more languages and domains (such as speech) in future work.
In Section 2, we overview baselines in unsupervised segmentation as well as other precursors to the Segmental Language Model. In Section 3, we provide a formal characterization of SLMs in general, as well as the architecture and modeling assumptions that make the MSLM distinct. In Section 4, we present the experiments conducted in this study using both recurrent and masked SLMs, and in Sections 5-6 we show that the MSLM outperforms its recurrent counterpart on Chinese segmentation, and performs similarly to the recurrent model on English. These results demonstrate the power of MSLMs. Section 7 lays out directions for future work.
2 Related Work
Segmentation Techniques and SLM Precursors
An early application of machine learning to unsupervised segmentation is Elman (1990), who shows that temporal surprisal peaks of RNNs provide a useful heuristic for inferring word boundaries. Subsequently, Minimum Description Length (MDL) (Rissanen, 1989) was widely used. The MDL model family underlies well-known segmentation tools such as Morfessor (Creutz and Lagus, 2002) and other notable works on unsupervised segmentation (de Marcken, 1996; Goldsmith, 2001).
More recently, Bayesian models inspired by child language acquisition have proved some of the most accurate in terms of their ability to model word boundaries. Some of the best examples are Hierarchical Dirichlet Processes (Teh et al., 2006), e.g. those applied to natural language by Goldwater et al. (2009), as well as Nested Pitman-Yor (Mochihashi et al., 2009; Uchiumi et al., 2015). However, Kawakami et al. (2019) notes most of these do not adequately account for long-range dependencies in the same capacity as modern neural language models.
Segmental Language Models follow a variety of recurrent models proposed for finding hierarchical structure in sequential data. Influential among these are Connectionist Temporal Classification (Graves et al., 2006), Sleep-Wake Networks (Wang et al., 2017), Segmental RNNs (Kong et al., 2016), and Hierarchical Multiscale Recurrent Neural Networks (Chung et al., 2017).
In addition, SLMs draw heavily from character and open-vocabulary language models. For example, Kawakami et al. (2017) and Mielke and Eisner (2019) present open-vocabulary language models in which words are represented either as atomic lexical units, or built out of characters. While the hierarchical nature and dual-generation strategy of these models did influence SLMs (Kawakami et al., 2019), both assume that word boundaries are available during training, and use them to form word embeddings from characters on-line. In contrast, SLMs usually assume no word boundary information is available in training.
Segmental Language Models
The next section has a more technical description of SLMs; here we give an short overview of other related work. The term Segmental Language Model seems to be jointly due to Sun and Deng (2018) and Kawakami et al. (2019). Sun and Deng (2018) demonstrate strong results for Chinese Word Segmentation using an LSTM-based SLM and greedy decoding, competitive with and sometimes exceeding state of the art for the time. This study tunes the model for segmentation quality on a validation set, which we will call a “lightly supervised” setting (Section 4.3).
Kawakami et al. (2019) use LSTM-based SLMs in a strictly unsupervised setting in which the model is only trained to optimize language-modeling performance on the validation set, and is not tuned on segmentation quality. Here they report that “vanilla” SLMs give sub-par segmentations unless combined with one or more regularization techniques, including a character -gram “lexicon” and length regularization.
Finally, Wang et al. (2021) very recently introduce a bidirectional SLM based on a Bi-LSTM. They show improved results over the unidirectional SLM of Sun and Deng (2018), test over more supervision settings, and include novel methods for combining decoding decisions over the forward and backward directions. This study is most similar to our own work, though transformer-based SLMs utilize a bidirectional context in a qualitatively different way, and do not require an additional layer to capture the reverse context.
3 Model
3.1 Recurrent SLMs
A schematic of the original Recurrent SLM can be found in Figure 1. Within an SLM, a sequence of symbols or time-steps x can further be modeled as a sequence of segments y, which are themselves sequences of the input time-steps, such that the concatenation of segments .
SLMs are broken into two levels: a Context Encoder and a Segment Decoder. The Segment Decoder estimates the probability of the character in the segment starting at index , , as:
where the indices for are . The Context Encoder encodes information about the input sequence up to index . The hidden encoding is
Finally, the Context Encoder “feeds” the Segment Decoder: the initial character of a segment beginning at is decoded using (transformations of) the encoded context as initial states ( and are single feed-forward layers):
For inference, the probability of a segment (starting at index and of length ) is modeled as the log probability of generating with the Segment Decoder given the left context . Note that the probability of a segment is not conditioned on other segments / segmentation choice, but only on the unsegmented input timeseries. Thus, the probability of the segment is
where is the end-of-segment symbol.
The probability of a sentence is thus modeled as the marginal probability over all possible segmentations of the input, as in equation (1) below (where is the set of all possible segmentations of an input x). However, since there are possible segmentations, directly marginalizing is intractable. Instead, dynamic programming over a forward-pass lattice can be used to recursively compute the marginal as in (2) given the base condition that . The maximum-probability segmentation can then be read off of the backpointer-augmented lattice through Viterbi decoding.
| (1) | ||||
| (2) |

3.2 New Model: Masked SLM
We present a Masked Segmental Language Model, which leverages a non-directional transformer as the Context Encoder. This reflects recent advances in bidirectional (Schuster and Paliwal, 1997; Graves and Schmidhuber, 2005; Peters et al., 2018) and adirectional architectures in language modeling (Devlin et al., 2019). Such modeling contexts are also psychologically plausible: Luce (1986) shows that in acoustic perception, most words need some following context to be recognizable.
A key difference between our model and standard, transformer-based Masked Language Models like BERT is that the latter predict single tokens based on the rest, while for SLMs we are interested in predicting a segment of tokens based on all other tokens outside the segment. For instance, to predict the three-character segment starting at , the distribution to be modeled is .
There are some recent pre-training techniques for transformers, such as MASS (Song et al., 2019) and BART (Lewis et al., 2020), that mask out spans to be predicted. One key difference between our model and these approaches is that while the pre-training data for large transformer models is usually large enough that only about 15% of training tokens are masked, we will always want to estimate the generation probability for every possible segment of x. Since the usual method for masking requires replacing the masked token(s) with a special symbol, only one span can be predicted with each forward pass. However, in each sequence there are possible segments, so replacing each one with a mask token and recovering it would require as many forward passes.
These design considerations motivate our Segmental Transformer Encoder, and the Segmental Attention Mask around which it is based. For each forward pass of this encoder, an encoding is generated for every possible starting position in x for a segment of up to length . The encoding at timestep corresponds to every possible segment whose first timestep is at index . Thus with maximum segment length of and total sequence length , the encoding at each index will approximate
This encoder leverages an attention mask designed to condition predictions only on indices that are not part of the segment to be predicted. An example of this mask with is shown in Figure 2. For max segment length , the mask is given by:

This solution is similar to that of Shin et al. (2020), developed independently and concurrently with the present work, which uses a custom attention mask to “autoencode” each position in the sequence without the need to input a special mask token. One key difference is that their masking scheme is used to predict single tokens, rather than spans. In addition, their mask runs directly along the diagonal of the attention matrix, rather than being offset. This means that to preserve self-masking in the first layer, the Queries are the “pure” positional embeddings, rather than a transformation of the input sequence.
To prevent information leaking “from under the mask”, our encoder uses a different configuration in its first layer than in subsequent layers. In the first layer, Queries, Keys, and Values are all learned from the original input encodings. In subsequent layers, the Queries come from the hidden encodings output by the previous layer, while Keys and Values are learned directly from the original encodings. If Queries and Keys or Queries and Values both come from the previous layer, information can leak from positions that are supposed to be masked for each respective query position. Shin et al. (2020) come to a similar solution to preserve their auto-encoder masking.
The encodings learned by the segmental encoder can then be input to an SLM decoder in exactly the same way as previous models (Figure 3).

To tease apart the role of attention in a transformer and the encoder’s adirectional context modeling assumption, we additionally define a Directional Masked Segmental Language Model, which uses a directional mask instead of the span masking type. Using the directional mask, the encoder is still completely attention-based, but the language modeling context is strictly “directional”, in that positions are only allowed to attend over a monotonic “leftward” context (Figure 4).
Finally, to add positional information to the encoder, we use static sinusoidal encodings (Vaswani et al., 2017) and additionally employ a linear mapping to the concatenation of the original and positional embeddings to learn the ratio at which to add the two together.
4 Experiments
Our experiments assess SLMs across three dimensions: (1) network architecture and language modeling assumptions, (2) evaluation metrics, specifically segmentation quality and language-modeling performance, and (3) supervision setting (if and where gold segmentation data is available).
4.1 Architecture and Modeling
To analyze the importance of the self-attention architecture versus the bidirectional conditioning context, we test SLMs with three different encoders: the standard R(ecurrent)SLM based on an LSTM, the M(asked)SLM introduced in 3.2 with a segmental or “cloze” mask, and a D(irectional)MSLM, with a “causal” or directional mask. The RSLM is thus (+recurrent context, +directional), the DMSLM is (-recurrent context, +directional), and the MSLM is (-recurrent context, -directional).
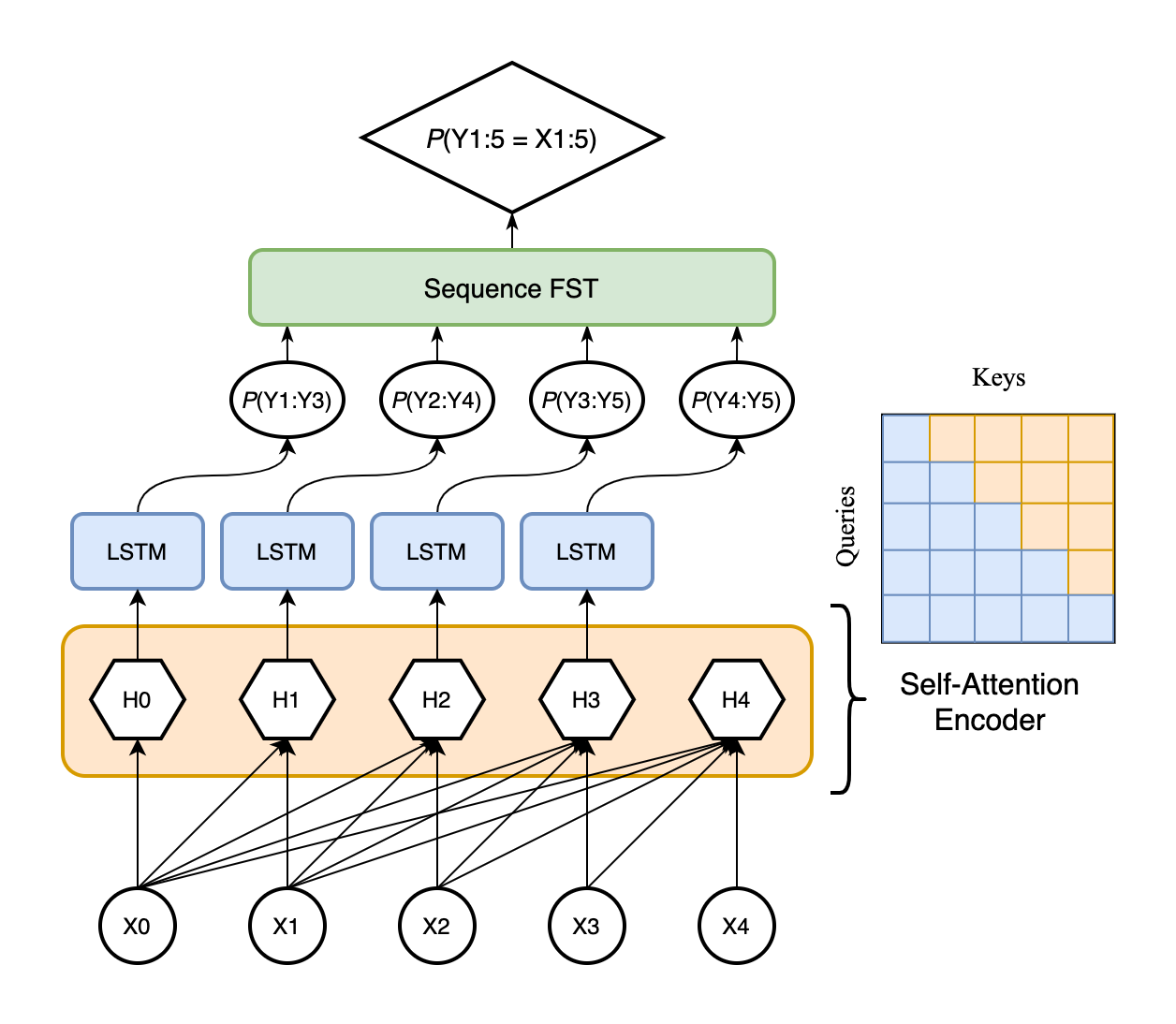
For all models, we use an LSTM for the segment decoder, as a control and because the decoded sequences are relatively short and may not benefit as much from an attention model. See also Chen et al. (2018) for hybrid models with transformer encoders and recurrent decoders.
4.2 Evaluation Metrics
Part of the motivation for SLMs is to create strong language models that can also be used for segmentation (Kawakami et al., 2019). Because of this, we report both segmentation quality and language modeling performance.
For segmentation quality, we get the word-F1 score for each corpus using the script from the SIGHAN Bakeoff (Emerson, 2005). Following Kawakami et al. (2019), we report this measure over the entire corpus. For language modeling performance, we report the average Bits Per Character (bpc) loss over the test set.
4.3 Supervision Setting
Because previous studies have used SLMs both in “lightly supervised” settings (Sun and Deng, 2018) and totally unsupervised ones (Kawakami et al., 2019), and because we expect SLMs to be deployed in either use case, we test both. For all model types, we conduct a hyperparameter sweep and select both the configuration that maximizes the validation segmentation quality (light supervision) and the one that minimizes the validation bpc (unsupervised).
4.4 Datasets
We evaluate our SLMs on two datasets used in Kawakami et al. (2019). For each, we use the same training, validation, and test split. The sets were chosen to represent two relatively different writing systems: Chinese (PKU) and English (PTB). Statistics for each are in Table 1. One striking difference between the two writing systems can be seen in the character vocabulary size: phonemic-type writing systems like English have a much smaller vocabulary of tokens, with words being built out of longer sequences of characters that are not meaningful on their own.
| Corpus | PKU | PTB |
|---|---|---|
| Tokens/Characters | 1.93M | 4.60M |
| Words | 1.21M | 1.04M |
| Lines | 20.78k | 49.20k |
| Avg. Characters per Word | 1.59 | 4.44 |
| Character Vocabulary Size | 4508 | 46 |
Peking University Corpus (PKU)
PKU has been used as a Chinese Word Segmentation benchmark since the International Chinese Word Segmentation Bakeoff (Emerson, 2005). One minor change we make to this dataset is to tokenize English, number, and punctuation tokens using the module from Sun and Deng (2018), to make our results more comparable to theirs. Unlike them, we do not pre-split sequences on punctuation.
Penn Treebank (PTB)
4.5 Parameters and Trials
For all models, we tune among six learning rates on a single random seed. After the parameter sweep, the configuration that maximizes validation segmentation quality and the one that minimizes validation bpc are run over an additional four random seeds. All models are trained using Adam (Kingma and Ba, 2015) for 8192 steps.
All models have one encoder layer and one decoder layer, as well as an embedding and hidden size of 256. The transformer-based encoder has a number of trainable parameters less than or equal to the number in the LSTM-based encoder.111592,381 trainable parameters in the former, 592,640 in the latter
One important parameter for SLMs is the maximum segment length . Sun and Deng (2018) tune this as a hyperparameter, with different values for fitting different Chinese segmentation standards more or less well. In practice, this parameter can be chosen empirically to be an upper bound on the maximum segment length one expects to find, so as to not rule out long segments. We follow Kawakami et al. (2019) in choosing for Chinese and for English. For a more complete characterization of our training procedure, see Appendix A.222The code used to build SLMs and conduct these experiments can be found at https://github.com/cmdowney88/SegmentalLMs
5 Results
5.1 Chinese
| Dataset | Model | Tuned on Gold | Unsupervised | ||
|---|---|---|---|---|---|
| F1 Mean / Median | BPC | F1 Mean / Median | BPC | ||
| PKU | RSLM | 61.2 3.6 / 60.2 | 5.67 0.01 | 59.4 1.9 / 58.7 | 5.63 0.01 |
| DMSLM | 72.2 2.0 / 72.7 | 6.08 0.31 | 62.9 2.6 / 63.4 | 5.67 0.03 | |
| MSLM | 72.3 0.7 / 72.6 | 5.85 0.12 | 62.9 2.8 / 64.1 | 5.56 0.01 | |
| PTB | RSLM | 77.4 0.7 / 77.6 | 2.10 0.04 | 75.7 2.6 / 76.2 | 1.96 0.00 |
| DMSLM | 70.6 6.4 / 73.3 | 2.36 0.07 | 67.9 10.6 / 73.8 | 2.27 0.04 | |
| MSLM | 71.1 5.6 / 73.6 | 2.39 0.06 | 69.3 5.6 / 71.5 | 2.27 0.01 | |
For PKU (Table 2), Masked SLMs yield better segmentation quality in both the lightly-supervised and unsupervised settings, though the advantage in the former setting is much larger (+12.4 median F1). The Directional MSLM produces similar quality segmentations to the MSLM, but it has worse language modeling performance in both settings (+0.23 bpc for lightly supervised and +0.11 bpc for unsupervised); the RSLM produced the second-best bpc in the unsupervised setting.
The RSLM gives the best bpc in the lightly-supervised setting. However for this setting, the strict division of the models that maximize segmentation quality and those that minimize bpc can be misleading. In between these two configurations, many have both good segmentation quality and low bpc, and if the practitioner has gold validation data, they will be able to pick a configuration with the desired tradeoff.
In addition, there is some evidence that “undershooting” the objective in the unsupervised case with a slightly lower learning rate may lead to more stable segmentation quality. The unsupervised MSLM in the table was trained at rate 2e-3, and achieved 5.625 bpc (validation). An MSLM trained at rate 1e-3 achieved only a slightly worse bpc (5.631) and resulted in better and more stable segmentation quality (69.4 2.0 / 70.4).
5.2 English
Results for English (PTB) can also be found in Table 2. By median, results remain comparable between the recurrent and transformer-based models, but the RSLM yields better segmentation performance in both settings (+4.0 and +4.7 F1). However, both types of MSLM are slightly more susceptible to random seed variation, causing those means to be skewed slightly lower. The DMSLM seems more susceptible than the MSLM to outlier performance based on random seeds, as evidenced by its large standard deviation. Finally, the RSLM gives considerably better bpc performance in both settings (-0.29 and -0.31 bpc).
6 Analysis and Discussion
6.1 Error Analysis
We conduct an error analysis for our models based on the total Precision and Recall scores for each (using the character-wise binary classification task, i.e. word-boundary vs no word-boundary).
As can be seen in Table 3, all model types trained on Chinese have a Precision that approaches 100%, meaning almost all boundaries that are inserted are true boundaries. On first glance the main difference in the unsupervised case seems to be the RSLM’s relatively higher Recall. However, the higher Precision of both MSLM types seems to be more important for the overall segmentation performance.333This table also shows that though character-wise segmentation quality (i.e. classifying whether a certain character has a boundary after it) is a useful heuristic, it does not always scale in a straightforward manner to word-wise F1 like is traditionally used (e.g. by the SIGHAN script). In the lightly-supervised case, the MSLM variants learn to trade off a small amount of Precision for a large gain in Recall, allowing them to capture more of the true word boundaries in the data. Given different corpora have different standards for the coarseness of Chinese segmentation, this reinforces the need for studies on a wider selection of datasets.
Because the English results (also in Table 3) are similar between supervision settings, we only show the unsupervised variants. Here, the RSLM shows a definitive advantage in Recall, leading to overall better performance. The transformer-based models show equal or higher Precision, but tend to under-segment, i.e. produce longer words. Example model segmentations for PTB can be found in Table 4. Some intuitions from our error analysis can be seen here: the moderate Precision of these models yields some false splits like be + fore and quest + ion, but all models also seem to pick up some valid morphological splits not present in the gold standard (e.g. +able in questionable). Predictably, rare words with uncommon structure remain difficult to segment (e.g. asbestos).
| Dataset | Model | Avg. Word Length | Precision | Recall |
|---|---|---|---|---|
| PKU | Gold | 1.59 | - | - |
| RSLM (unsup.) | 1.93 0.02 | 98.2 0.1 | 80.8 0.6 | |
| DMSLM (unsup.) | 1.99 0.04 | 98.6 0.1 | 78.5 1.8 | |
| MSLM (unsup.) | 2.00 0.05 | 98.5 0.1 | 78.1 1.9 | |
| RSLM (sup.) | 1.92 0.02 | 98.2 0.1 | 81.3 0.7 | |
| DMSLM (sup.) | 1.83 0.04 | 97.5 0.5 | 84.6 1.5 | |
| MSLM (sup.) | 1.83 0.01 | 97.6 0.1 | 84.5 0.4 | |
| PTB | Gold | 4.44 | - | - |
| RSLM (unsup.) | 4.02 0.08 | 86.1 1.9 | 95.5 0.1 | |
| DMSLM (unsup.) | 4.27 0.17 | 85.4 5.4 | 88.9 4.6 | |
| MSLM (unsup.) | 4.29 0.12 | 86.2 1.5 | 89.5 3.5 |
| Examples | |
|---|---|
| Gold | we ’re talking about years ago before anyone heard of asbestos having any questionable… |
| RSLM Median | we’re talking about years ago be fore any one heard of as best os having any question able |
| DMSLM Median | we’re talking about years ago be fore any one heard of as bestos having any quest ion able |
| MSLM Median | we’re talking about years ago be fore any one heard of as bestos having any quest ion able |
6.2 Discussion
For Chinese, the transformer-based SLM exceeds the recurrent baseline for segmentation quality, by a moderate amount for the unsupervised setting, and by a large amount when tuned on gold validation segmentations. The MSLM also gives stronger language modeling. Given the large vocabulary size for Chinese, it is intuitive that the powerful transformer architecture may make a difference in this difficult language-modeling task. Further, though the DMSLM achieves similar segmentation quality, the bidirectional context of the MSLM does seem to be the source of the best bpc modeling performance.
In English, on the other hand, recurrent SLMs seem to retain a slight edge. By median, segmentation quality remains fairly similar between the three model types, but the RSLM holds a major language-modeling advantage in our experiments. Our main hypothesis for the disparity in modeling performance between Chinese and English comes down to the nature of the orthography for each. As noted before, Chinese has a much larger character vocabulary. This is because in Chinese, almost every character is a morpheme itself (i.e. it has some meaning). English, on the other hand, has a roughly phonemic writing system, e.g. the letter c has no inherent meaning outside of a context like cat.
Intuitively, it is easy to see why this might pose a limitation on transformers. Without additive or learned positional encodings, they are essentially adirectional. In English, cat is a completely different context than act, but this might be difficult to model for an attention model without robust positional information. To try to counteract this, we added dynamic scaling to our static positional encodings, but without deeper networks or more robust positional information, the discrepancy in character-based modeling for phonemic systems may remain.
7 Conclusion
This study constitutes strong proof-of-concept for the use of Masked Segmental Language Models in unsupervised segmentation and/or character modeling, with several open avenues to extend their utility. To close, we lay out directions for future work with MSLMs, including extension to more languages and domains, applications to deep modeling, and regularization techniques.
The most obvious next step is using MSLMs to model more segmentation datasets. As mentioned previously, the criteria for what defines a “word” in Chinese are not agreed upon, and so more experiments are warranted using corpora with different standards. Prime candidates include the Chinese Penn Treebank (Xue et al., 2005), as well as those included in the SIGHAN segmentation bakeoff: Microsoft Research, City University of Hong Kong, and Academia Sinicia (Emerson, 2005).
The Chinese and English sets examined here are also relatively formal orthographic datasets. An eventual use of SLMs may be in speech segmentation, but a smaller step in that direction could be using phonemic transcript datasets like the Brent Corpus, also used in Kawakami et al. (2019), which consists of phonemic transcripts of child-directed English speech (Brent, 1999). SLMs could also be applied to the orthographies of more typologically diverse languages, such as ones with complicated systems of morphology (e.g. Swahili, Turkish, Hungarian, Finnish).
Further, though we have only experimented with shallow models here, one of the main advantages of transformers is their ability to scale to deep models due to their short derivational chains. That being so, extending segmental models to “deep” settings may be more feasible using MSLMs than RSLMs.
Lastly, Kawakami et al. (2019) propose regularization techniques for SLMs due to low segmentation quality from their “vanilla” models. They report good findings using a character -gram “lexicon” in conjunction with expected segment length regularization based on Eisner (2002) and Liang and Klein (2009). Both techniques are implemented in our codebase, and we have tested them in pilot settings. Oddly, neither has given us any gain in performance over our “vanilla” models tested here. A more exhaustive hyperparameter search with these methods for both kinds of models may produce a future benefits as well.
In conclusion, the present study shows strong potential for the use of MSLMs. They show particular promise for writing systems with a large inventory of semantic characters (e.g. Chinese), and we believe that they could be stable competitors of recurrent models in phonemic-type writing systems if the relative weakness of positional encodings in transformers can be mitigated.
References
- Brent (1999) Michael R. Brent. 1999. An Efficient, Probabilistically Sound Algorithm for Segmentation and Word Discovery. Machine Learning, 34:71–105.
- Chen et al. (2018) Mia Xu Chen, Orhan Firat, Ankur Bapna, Melvin Johnson, Wolfgang Macherey, George Foster, Llion Jones, Mike Schuster, Noam Shazeer, Niki Parmar, Ashish Vaswani, Jakob Uszkoreit, Lukasz Kaiser, Zhifeng Chen, Yonghui Wu, and Macduff Hughes. 2018. The Best of Both Worlds: Combining Recent Advances in Neural Machine Translation. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 76–86, Melbourne, Australia. Association for Computational Linguistics.
- Chung et al. (2017) J. Chung, Sungjin Ahn, and Yoshua Bengio. 2017. Hierarchical Multiscale Recurrent Neural Networks. In 5th International Conference on Learning Representations, ICLR 2017, Conference Track Proceedings, Toulon, France.
- Creutz and Lagus (2002) Mathias Creutz and Krista Lagus. 2002. Unsupervised Discovery of Morphemes. In Proceedings of the ACL-02 Workshop on Morphological and Phonological Learning, pages 21–30. Association for Computational Linguistics.
- de Marcken (1996) Carl de Marcken. 1996. Linguistic Structure as Composition and Perturbation. In 34th Annual Meeting of the Association for Computational Linguistics, pages 335–341, Santa Cruz, California, USA. Association for Computational Linguistics.
- Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 4171–4186, Minneapolis, Minnesota. Association for Computational Linguistics.
- Dunbar et al. (2020) Ewan Dunbar, Julien Karadayi, Mathieu Bernard, Xuan-Nga Cao, Robin Algayres, Lucas Ondel, Laurent Besacier, Sakriani Sakti, and Emmanuel Dupoux. 2020. The Zero Resource Speech Challenge 2020: Discovering discrete subword and word units. In Proceedings of INTERSPEECH 2020.
- Eisner (2002) Jason Eisner. 2002. Parameter Estimation for Probabilistic Finite-State Transducers. In Proceedings of the 40th Annual Meeting of the Association for Computational Linguistics, pages 1–8, Philadelphia, Pennsylvania, USA. Association for Computational Linguistics.
- Elman (1990) Jeffrey L. Elman. 1990. Finding structure in time. Cognitive Science, 14(2):179–211.
- Emerson (2005) Thomas Emerson. 2005. The Second International Chinese Word Segmentation Bakeoff. In Proceedings of the Fourth SIGHAN Workshop on Chinese Language Processing.
- Goldsmith (2001) John Goldsmith. 2001. Unsupervised Learning of the Morphology of a Natural Language. Computational Linguistics, 27(2):153–198.
- Goldwater et al. (2009) Sharon Goldwater, Thomas L. Griffiths, and Mark Johnson. 2009. A Bayesian framework for word segmentation: Exploring the effects of context. Cognition, 112(1):21–54.
- Graves et al. (2006) Alex Graves, Fernández Santiago, Faustino Gomez, and Jürgen Schmidhuber. 2006. Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA.
- Graves and Schmidhuber (2005) Alex Graves and Jürgen Schmidhuber. 2005. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. In Neural Networks, volume 18, pages 602–610. Pergamon.
- Joshi et al. (2020) Pratik Joshi, Sebastin Santy, Amar Budhiraja, Kalika Bali, and Monojit Choudhury. 2020. The State and Fate of Linguistic Diversity and Inclusion in the NLP World. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 6282–6293, Online. Association for Computational Linguistics.
- Kamper et al. (2016) Herman Kamper, Aren Jansen, and Sharon Goldwater. 2016. Unsupervised word segmentation and lexicon discovery using acoustic word embeddings. IEEE/ACM Transactions on Audio, Speech and Language Processing, 24(4):669–679.
- Kawakami et al. (2017) Kazuya Kawakami, Chris Dyer, and Phil Blunsom. 2017. Learning to Create and Reuse Words in Open-Vocabulary Neural Language Modeling. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1492–1502, Vancouver, Canada. Association for Computational Linguistics.
- Kawakami et al. (2019) Kazuya Kawakami, Chris Dyer, and Phil Blunsom. 2019. Learning to Discover, Ground and Use Words with Segmental Neural Language Models. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 6429–6441, Florence, Italy. Association for Computational Linguistics.
- Kingma and Ba (2015) Diederik Kingma and Jimmy Ba. 2015. Adam: A Method for Stochastic Optimization. In 3rd International Conference on Learning Representations, ICLR 2015, Conference Track Proceedings, San Diego, CA, USA.
- Kong et al. (2016) Lingpeng Kong, Chris Dyer, and Noah A Smith. 2016. Segmental Recurrent Neural Networks. In 4th International Conference on Learning Representations, ICLR 2016, Conference Track Proceedings, San Juan, Puerto Rico.
- Kudo and Richardson (2018) Taku Kudo and John Richardson. 2018. SentencePiece: A simple and language independent subword tokenizer and detokenizer for Neural Text Processing. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, pages 66–71, Brussels, Belgium. Association for Computational Linguistics.
- Lewis et al. (2020) Mike Lewis, Yinhan Liu, Naman Goyal, Marjan Ghazvininejad, Abdelrahman Mohamed, Omer Levy, Veselin Stoyanov, and Luke Zettlemoyer. 2020. BART: Denoising Sequence-to-Sequence Pre-training for Natural Language Generation, Translation, and Comprehension. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 7871–7880, Online. Association for Computational Linguistics.
- Liang and Klein (2009) Percy Liang and Dan Klein. 2009. Online EM for Unsupervised Models. In Proceedings of Human Language Technologies: The 2009 Annual Conference of the North American Chapter of the Association for Computational Linguistics, pages 611–619, Boulder, Colorado. Association for Computational Linguistics.
- Luce (1986) Paul A. Luce. 1986. A computational analysis of uniqueness points in auditory word recognition. Perception & Psychophysics, 39(3):155–158.
- Mielke and Eisner (2019) Sabrina Mielke and Jason Eisner. 2019. Spell Once, Summon Anywhere: A Two-Level Open-Vocabulary Language Model. Proceedings of the AAAI Conference on Artificial Intelligence, 33(01):6843–6850. Number: 01.
- Mikolov et al. (2013) Tomas Mikolov, Kai Chen, G. Corrado, and J. Dean. 2013. Efficient Estimation of Word Representations in Vector Space. In 1st International Conference on Learning Representations, ICLR 2013, Workshop Track Proceedings, Scottsdale, AR, USA.
- Mikolov et al. (2010) Tomas Mikolov, Martin Karafiát, Lukas Burget, Jan Cernocký, and Sanjeev Khudanpur. 2010. Recurrent neural network based language model. volume 2, pages 1045–1048.
- Mochihashi et al. (2009) Daichi Mochihashi, Takeshi Yamada, and Naonori Ueda. 2009. Bayesian Unsupervised Word Segmentation with Nested Pitman-Yor Language Modeling. In Proceedings of the Joint Conference of the 47th Annual Meeting of the ACL and the 4th International Joint Conference on Natural Language Processing of the AFNLP, pages 100–108, Suntec, Singapore. Association for Computational Linguistics.
- Moeng et al. (2021) Tumi Moeng, Sheldon Reay, Aaron Daniels, and Jan Buys. 2021. Canonical and Surface Morphological Segmentation for Nguni Languages. ArXiv.
- Peters et al. (2018) Matthew Peters, Mark Neumann, Mohit Iyyer, Matt Gardner, Christopher Clark, Kenton Lee, and Luke Zettlemoyer. 2018. Deep Contextualized Word Representations. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long Papers), pages 2227–2237, New Orleans, Louisiana. Association for Computational Linguistics.
- Rasanen and Blandon (2020) O. Rasanen and M. A. Cruz Blandon. 2020. Unsupervised Discovery of Recurring Speech Patterns using Probabilistic Adaptive Metrics. In Proceedings of INTERSPEECH 2020.
- Rissanen (1989) Jorma Rissanen. 1989. Stochastic Complexity in Statistical Inquiry, volume 15 of Series in Computer Science. World Scientific, Singapore.
- Schuster and Paliwal (1997) Mike Schuster and Kuldip K. Paliwal. 1997. Bidirectional recurrent neural networks. IEEE Transactions on Signal Processing, 45(11):2673–2681.
- Sennrich et al. (2016) Rico Sennrich, Barry Haddow, and Alexandra Birch. 2016. Neural Machine Translation of Rare Words with Subword Units. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), pages 1715–1725, Berlin, Germany. Association for Computational Linguistics.
- Shin et al. (2020) Joongbo Shin, Yoonhyung Lee, Seunghyun Yoon, and Kyomin Jung. 2020. Fast and Accurate Deep Bidirectional Language Representations for Unsupervised Learning. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 823–835, Online. Association for Computational Linguistics.
- Song et al. (2019) K. Song, X. Tan, Tao Qin, Jianfeng Lu, and T. Liu. 2019. MASS: Masked Sequence to Sequence Pre-training for Language Generation. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA.
- Sun and Deng (2018) Zhiqing Sun and Zhi-Hong Deng. 2018. Unsupervised Neural Word Segmentation for Chinese via Segmental Language Modeling. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pages 4915–4920, Brussels, Belgium. Association for Computational Linguistics.
- Teh et al. (2006) Yee Whye Teh, Michael I. Jordan, Matthew J. Beal, and David M. Blei. 2006. Hierarchical Dirichlet Processes. Journal of the American Statistical Association, 101(476):1566–1581.
- Tian et al. (2020) Yuanhe Tian, Yan Song, Fei Xia, Tong Zhang, and Yonggang Wang. 2020. Improving Chinese Word Segmentation with Wordhood Memory Networks. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, pages 8274–8285, Online. Association for Computational Linguistics.
- Uchiumi et al. (2015) Kei Uchiumi, Hiroshi Tsukahara, and Daichi Mochihashi. 2015. Inducing Word and Part-of-Speech with Pitman-Yor Hidden Semi-Markov Models. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), pages 1774–1782, Beijing, China. Association for Computational Linguistics.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Lukasz Kaiser, and Ilia Polosukhin. 2017. Attention is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA. Neural Information Processing Systems Foundation.
- Wang et al. (2017) Chong Wang, Yining Wang, Po-Sen Huang, Abdelrahman Mohamed, Dengyong Zhou, and Li Deng. 2017. Sequence Modeling via Segmentations. In Proceedings of the 34th International Conference on Machine Learning, volume 70 of Proceedings of Machine Learning Research, pages 3674–3683, International Convention Centre, Sydney, Australia. PMLR.
- Wang et al. (2021) L. Wang, Zongyi Li, and Xiaoqing Zheng. 2021. Unsupervised Word Segmentation with Bi-directional Neural Language Model. ArXiv.
- Xue et al. (2005) Nianwen Xue, Fei Xia, Fu-Dong Chiou, and Martha Palmer. 2005. The Penn Chinese TreeBank: Phrase Structure Annotation of a Large Corpus. Natural Language Engineering, 11(2):207–238.
Appendix A Training Details
A.1 Data
The datasets used here are sourced from Kawakami et al. (2019), and can be downloaded at https://s3.eu-west-2.amazonaws.com/k-kawakami/seg.zip. Our PKU data is tokenized slightly differently, and all data used in our experiments can be found in our project repository (url redacted).
A.2 Architecture
A dropout rate of 0.1 is applied leading into both the encoder and the decoder. Transformers use 4 attention heads and a feedforward size of 509 (chosen to come out less than or equal to the number of parameters in the standard LSTM). This also includes a 512-parameter linear mapping to learn the combination proportion of the word and sinusoidal positional embeddings. The dropout within transformer layers is 0.15.
A.3 Initialization
Character embeddings are initialized using CBOW (Mikolov et al., 2013) on the given training set for 32 epochs, with a window size of 5 for Chinese and 10 for English. Special tokens like <eoseg> that do not appear in the training corpus are randomly initialized. These pre-trained embeddings are not frozen during training.
A.4 Training
For PKU, the learning rates swept are {6e-4, 7e-4, 8e-4, 9e-4, 1e-3, 2e-3}, and for PTB we use {6e-4, 8e-4, 1e-3, 3e-3, 5e-3, 7e-3}. For Chinese, we found a linear warmup for 1024 steps was useful, followed by a linear decay. For English, we apply simple linear decay from the beginning. Checkpoints are taken every 128 steps. A gradient norm clip threshold of 1.0 is used. Mini-batches are sized by number of characters rather than number of sequences, with a size of 8192 (though this is not always exact since we do not split up sequences). The five random seeds used are {2, 3, 5, 8, 13}.
Each model is trained on an Nvidia Tesla M10 GPU with 8GB memory, with the average per-batch runtime of each model type listed in Table 5.
| Model | s / step | |
|---|---|---|
| PKU | PTB | |
| RSLM | 2.942 | 2.177 |
| DMSLM | 2.987 | 2.190 |
| MSLM | 2.988 | 2.200 |
A.5 Optimal Hyperparameters
The optimal learning rate for each model type, dataset, and supervision setting are listed in the Table 6. Parameters are listed by the validation objective they optimize: segmentation MCC or language-modeling BPC.
| Dataset | Model | by MCC | by BPC |
|---|---|---|---|
| PKU | RSLM | 6e-4 | 9e-4 |
| DMSLM | 6e-4 | 2e-3 | |
| MSLM | 6e-4 | 2e-3 | |
| PTB | RSLM | 7e-3 | 3e-3 |
| DMSLM | 1e-3 | 8e-4 | |
| MSLM | 1e-3 | 6e-4 |