A lower bound for the first eigenvalue of a minimal hypersurface in the sphere

Let $\mathbb{S}^{m+1}$ denote the unit sphere in $\mathbb{R}^{m+2}$. and $\Sigma$ a closed embedded hypersurface within $\mathbb{S}^{m+1}$. The eigenvalues of the Laplacian operator $\triangle$ on $\Sigma$ form a discrete set of non-negative real numbers. We denote by $\lambda_{1}(\Sigma)$ the first nonzero eigenvalue. It is well known that $\Sigma$ is minimal if and only if all coordinate functions in $\mathbb{R}^{m+2}$ restricted on $\Sigma$ are eigenfunctions corresponding to eigenvalues $m$. This implies that $\lambda_{1}(\Sigma)\leq m$.

On the other hand, it is interesting and important to find the sharp lower bound of $\lambda_{1}$ for minimal hypersurfaces in $\mathbb{S}^{m+1}$. Yau [11] conjectured that $\lambda_{1}(\Sigma)=m$. Choi and Wang [3] proved that $\lambda_{1}(\Sigma)\geq\frac{m}{2}$. This estimate was later refined in [1] by Barros-Bessa who gave the lower bound

Many progress has been made towards proving Yau’s conjecture after Choi-Wang’s paper (see for instance [1], [5], [9], [4], and [12]). Despite an extensive literature relating to the study of $\lambda_{1}(\Sigma)$ under additional assumptions on $\Sigma$, (1.1) has remained the strongest explicit lower bound that is known to hold for a general embedded minimal hypersurface in $\mathbb{S}^{n+1}$. The new estimate that we obtain in this work depends on the geometry of $\Sigma$ as we explain in detail next.

Given $x\in\Sigma$, let $|A|(x):=\left(\sum\limits_{i=1}^{m}k_{i}^{2}(x)\right)^{1/2},$ where $k_{1}(x),\ldots,k_{m}(x)$ are the principal curvatures of $\Sigma$ in $x$ with respect to $\nu(x)$. We call $|A|$ the norm of the second fundamental form $A_{\nu}$ and we define $\Lambda:=\max\limits_{\Sigma}|A|$. It is known (see [8]) that in the case $\Lambda\leq\sqrt{m}$, then $\lambda_{1}(\Sigma)=m$. Therefore our contribution concerns only the case $\Lambda>\sqrt{m}$.

Precisely, we prove

The rest of the paper is divided into two sections.

In Section 2, we recall the Reilly’s formula and reformulate a result in [1]. We also give a lower bound for $\lambda_{1}(\Sigma)$ in terms of the Rayleigh quotient of its harmonic extension. Namely

where

and $u$ is a solution to

where the bars in the expressions above refer to operations in the ambient sphere. Here, $\varphi$ is an eigenfunction of the Laplacian $\triangle$ associated to the eigenvalue $\lambda_{1}(\Sigma)$ and $\Omega$ is a component of $\mathbb{S}^{m+1}-\Sigma$ which is chosen appropriately. We call $u$ the harmonic extension of $\varphi$ to $\Omega$. Then we prove Theorem 1.1 assuming the validity of an appropriate estimate for $Q$.

In Section 3 we make a quick review of the normal exponential map and we prove the estimate

which may be considered as an inverse Poincaré type inequality, i.e. $C_{2}$ is an upper estimate for $Q$. We finish the paper by comparing our estimate with the one in [5].

It is important to note that, as in [5], we also use Reilly’s formula and an upper bound of the mean curvature of the parallel surfaces to $\Sigma$. However, we provide an upper bound of $|\overline{\nabla}u|_{L^{2}(\Omega)}^{2}$ that depends only on the geometry of $\Sigma$, via an elementary result on harmonic extensions.

We need to point out that our techniques can be improved and generalized in order to obtain an estimate for the first eigenvalue of a minimal surface embedded in an ambient of bounded sectional curvature. However, the sharp bound can only be achieved by proving that $Q=m+1$. Further work will be part of the PhD thesis of the second author. In fact, this work was in preparation before we had access to [5].

In this section we will review Reilly’s formula and give a lower bound for the nonzero first eigenvalue $\lambda_{1}(\Sigma)$ in terms of the Rayleigh quotient of the harmonic extension of the corresponding eigenfunction. As a consequence, we will prove our main result, Theorem 1.1, assuming the inequality (1.3) which will be explicitly stated in Theorem 3.10.

From now on, $\Sigma$ will denote a closed embedded hypersurface of $\mathbb{S}^{m+1}$. It follows that $\Sigma$ divides the sphere into two components $\Omega_{1}$ and $\Omega_{2}$, where $\partial\Omega_{1}=\partial\Omega_{2}=\Sigma$ (see [3]). Set $\nu$ as the unit normal of $\Sigma$ pointing outward to $\Omega_{1}$ ($-\nu$ as the unit normal of $\Sigma$ and pointing outward to $\Omega_{2}$) and $A_{\nu}$ the second fundamental form of $\Sigma$ with respect to $\nu$.

Let $\varphi\in C^{\infty}(\Sigma)$. We can assume, without loss of generality, it satisfies the property

and denote $\Omega:=\Omega_{1}$. Otherwise we can choose $\Omega=\Omega_{2}.$ Let us denote all the functions of class $C^{2}$ that extend the function $\varphi$ over $\overline{\Omega}$ as $C^{2}_{\varphi}(\overline{\Omega})$. The following equation is known as Reilly’s formula (see [7]).

The following corollary follows from (2.1) by using that $|\overline{\nabla}^{2}u|^{2}\geq\frac{1}{m+1}(\overline{\triangle}u)^{2}$.

The following result is proven by Barros and Bessa in [1]. We include here a simpler proof.

Next we obtain a first estimate for $\lambda_{1}(\Sigma)$ which is a corollary of Barros-Bessa’s theorem.

Next we prove Theorem 1.1 assuming Theorem 3.10.

Proof of Theorem 1.1.

It is well known that when $\Lambda\leq\sqrt{m}$, $\Sigma$ is either a great sphere $\mathbb{S}^{n}$ or a Clifford torus and so $\lambda_{1}(\Sigma)=m$. Therefore, we can now assume that $\Lambda\geq\sqrt{m}$. Let $\varphi\in C^{\infty}(\Sigma)$ be the eigenfunction corresponding to the first nonzero eigenvalue $\lambda_{1}(\Sigma)$ and $u\in C^{2}_{\varphi}(\overline{\Omega})$ its harmonic extension to $\Omega$ as before. It follows from Theorem 3.10 that $Q<4(12\Lambda+m+11)^{2}+1.$ Therefore we have from (2.11) that

On the other hand, since for all $0\leq x<1$,

we can consider $x=(m+1)Q^{-1}$ in (2.14) and deduce from Theorem 3.10 that

The proof is then complete.

$\square$

The aim of this section is to prove an inverse Poincaré-type inequality in Theorem 3.10. To do that we recall first some preliminary results concerning the normal exponential map.

In what follows $N\Sigma:=\{(x,v):\,x\in\Sigma,v\in T_{x}^{\bot}\Sigma\}$ will denote the normal bundle of $\Sigma$, $U\Sigma:=\{(x,v)\in N\Sigma:\,|v|=1\}$ will denote the normal unit bundle of $\Sigma$ and $\textrm{exp}^{\bot}:N\Sigma\to\mathbb{S}^{m+1}$ defined by $\textrm{exp}^{\bot}(x,v):=\exp_{x}(v)$ will denote the normal exponential map on $\Sigma$. Such map is well defined in $\Sigma$ since $\Sigma$ is embedded with compact closure on the sphere $\mathbb{S}^{m+1}$ (see for instance [6] ). Let $\theta_{\Sigma}:N\Sigma\to\mathbb{R}$ denote the Jacobian determinant of the normal exponential map $\textrm{exp}^{\bot}$. On the other hand, let $\Phi_{t}:\Sigma\to\mathbb{S}^{m+1}$ be defined by $\Phi_{t}(x):=\textrm{exp}^{\bot}(x,t\nu(x))$ and

From Proposition 2.1 in [5], if we define $k_{\textrm{max}}:=\max\limits_{\Sigma,i}|k_{i}|$ and

we have

Similarly, we have

Defining $\textrm{minfoc}(\Sigma):=\min\{t_{\ast},t^{\ast}\}$, we have that

The following lemma correspond to Lemma 10.9 in [6].

The proof of the following Lemma is straightforward from Lemma 8.1 in [6] and the definition of $\theta_{\Sigma}$.

Given $\varphi\in C^{\infty}(\Sigma)$, we define $\widetilde{\varphi}(\Phi_{t}(x)):=\varphi(x)$. The function $\widetilde{\varphi}$ is called the normal extension of $\varphi$ and it is well defined in the set

Next we are going to construct a transition function wich will be a key technical tool in the proof of our main result. For any $a<b$ we define

where the function $g:\mathbb{R}\to[0,1]$ is defined by

It follows that

1. (1)

   $g(t)\geq 0$ $\forall t\in\mathbb{R}.$

2. (2)

   $g(t)=0$ $\forall t\in(-\infty,0].$

3. (3)

   $\lim\limits_{t\to 0^{+}}g(t)=0$ and $\lim\limits_{t\to 1^{-}}g(t)=1$.

4. (4)

   The function $g^{\prime}(t)=\dfrac{e^{\frac{1}{t(1-t)}}(1-2t+2t^{2})}{(e^{\frac{1}{t-t}}+e^{\frac{1}{t}})^{2}(t-1)^{2}t^{2}},$ is such that $0<g^{\prime}(t)\leq 2$, for all $t\in(0,1)$ and $\lim\limits_{t\to 0^{+}}g^{\prime}(t)=\lim\limits_{t\to 1^{-}}g^{\prime}(t)=0.$

For $t\in[a,b],$ it follows from (3.6) that

Therefore

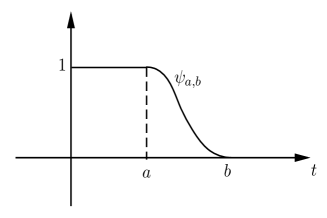
In particular, if we denote $\overline{\psi}_{\rho,c}:=\psi_{a,b}$ for the special choices $a=\frac{b}{c}$ for some $c>1$, and $b=\rho T_{\Sigma}$ for some $0<\rho<1$, we have that