A Lagrangian with $E_{8}\times E_{8}$ symmetry for the standard model and pre-gravitation I.
- The bosonic Lagrangian, and a theoretical derivation of the weak mixing angle -

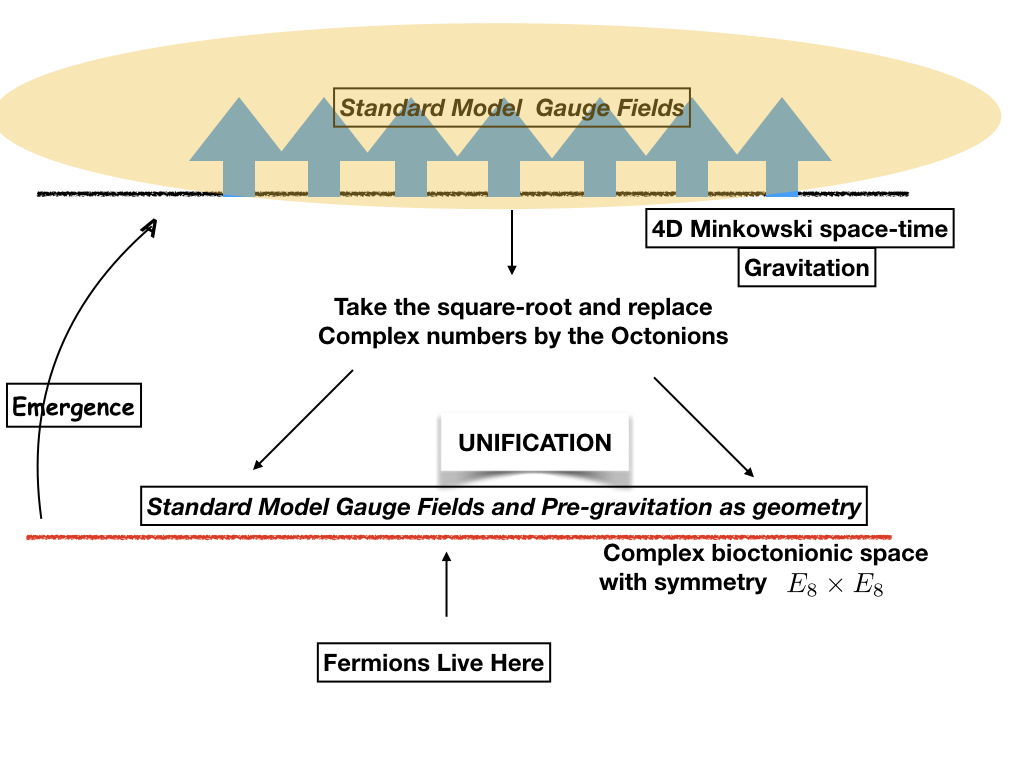
In a recent work [1] we have proposed the unbroken $E_{8}\times E_{8}$ symmetry as the symmetry for unification of the standard model and pre-gravitation. Amongst many noteworthy features, one is that the 248 fundamental rep of $E_{8}$ is also its adjoint rep. This is appropriate for our theory in which a priori the fundamental degrees of freedom are neither bosonic nor fermionic, as will see below. The two $E_{8}$ branch as follows, after the $E_{8}\times E_{8}$ symmetry is broken:

	$\displaystyle E_{8}\rightarrow SU(3)_{Eucsp}\times E_{6}\rightarrow SU(3)_{Eucsp}\times SU(3)_{genL}\times SU(3)_{color}\times SU(2)_{L}\times U(1)_{Y}$
	$\displaystyle E_{8}\rightarrow SU(3)_{spacetime}\times E_{6}\rightarrow SU(3)_{spacetime}\times SU(3)_{genR}\times SU(3)_{grav}\times SU(2)_{R}\times U(1)_{g}$		(1)

The branching naturally induces separation of space-time-matter into space-time and matter (see Lagrangian below). The first $E_{8}$ branches into $SU(3)_{Eucsp}\times E_{6}$, and the 8D real rep of this $SU(3)$ is mapped on to an 8D vector space, this being the eight directions of an octonion $O$ (one real direction and seven imaginary). The absolute squared magnitude of the octonion has Euclidean signature and this space is equivalent to 10D Euclidean space $SO(10)$. The accompanying $E_{6}$ describes three generations of left-handed quarks and leptons of the standard model, and their anti-particles, and twelve gauge bosons of the standard model $SU(3)_{c}\times SU(2)_{L}\times U(1)_{Y}$ and four Higgs boson degrees of freedom (most likely a charged Higgs).

The second $E_{8}$ branches into $SU(3)_{spacetime}\times E_{6}$, with the 8D real rep of $SU(3)_{spacetime}$ this time mapped to the split octonion part $O^{\prime}$ (please see below for details) of a split bioctonion $O\oplus\omega O^{\prime}$ ($\omega$ being the split complex number). The absolute squared magnitude of $\omega O^{\prime}$ has Lorentzian signature and this octonionic space corresponds to 10D spacetime $SO(1,9)$. The associated $E_{6}$ describes three generations of right-handed quarks and leptons of the standard model (including sterile neutrinos), and their antiparticles, and twelve newly introduced gauge bosons describing the pre-gravitational symmetry $SU(3)_{grav}\times SU(2)_{R}\times U(1)_{g}$ and the standard model Higgs.

Between them, the two $E_{8}$, after symmetry breaking, give a picture akin to ‘fibre bundle describing gauge fields on spacetime’. Only, now the fibre bundle as well as spacetime have higher dimensions, and are defined on a bioctonionic spinor space. The endeavour is to build on earlier preliminary work and construct a Lagrangian which describes the original symmetry and its breaking, and to recover the observed 4D universe with standard model fields living on it. As an application, in the present paper we deduce the low energy asymptotic value of the weak mixing angle. A key idea is that quantum systems (such as an electron in flight) in fact obey the unbroken $E_{8}\times E_{8}$ symmetry, even at low energies, and the symmetry appears broken because of the measurements we choose to make. We will also see that it is not possible to determine the value of the mixing angle without first unifying the standard model with pre-gravitation; nor without working on a higher dimensional spinor spacetime. The same was seen earlier for the derivation of the low energy fine structure constant as well as the mass ratios.

An octonion is made of one real unit and seven imaginary units $e_{i}^{2}=-1$ for i = 1, 2,…, 7. Just as for the quaternions, the imaginary units of an octonion anti-commute. The multiplication of octonions is prescribed by a diagram known as the Fano plane (Fig. 2)

There are seven quaternionic subsets in the Fano plane, these are given by the three sides of the triangle, the three altitudes, and the circle. Multiplication of points lying along a quaternionic subset in cyclic order (as per the arrow) is given by $e_{i}e_{j}=e_{k}$, whereas $e_{j}e_{i}=-e_{k}$.

A split bioctonion $O_{sb}\equiv O\oplus\omega\tilde{O}$ is made from a pair of octonions as follows [6]

$$O_{sb}=(1,e_{1},e_{2},e_{3},e_{4},e_{5},e_{6},e_{8})\oplus\omega(1,-e_{1},-e_{2},-e_{3},-e_{4},-e_{5},-e_{6},-e_{8})$$

(2)

where $\tilde{O}$ is the octonionic conjugate of $O$, and $\omega$ is the equivalent of a split complex number, but made from the octonions themselves, as is seen in the context of the Clifford algebra $Cl(7)$ [6]. The fundamental degree of freedom in the octonionic theory is a 2-brane, also referred to as an ‘atom of space-time-matter’, or an aikyon. It is defined by a pair of matrices $\widetilde{Q}_{1}$ and $\widetilde{Q}_{2}$ which have complex Grassmann numbers as their entries. Each of the two matrices has sixteen matrix-valued coordinate components, one for each of the sixteen directions of the above bioctonion. The action principle for the 2-brane is given by [4, 7]

$$\frac{S}{\hbar}=\int\frac{d\tau}{\tau_{Pl}}\;{\cal L}\qquad;\qquad\mathcal{L}=\frac{L_{p}^{2}}{2L^{2}}Tr\biggl{[}\biggr{.}\dot{\widetilde{Q}}_{1}^{\dagger}\;\dot{\widetilde{Q}}_{2}\biggr{]}$$

(3)

where $\tau$ is Connes time [8] and $L^{2}$ is the fundamental area of the 2-brane, in units of Planck area $L_{p}^{2}$. This is the only parameter in the theory to begin with, and its value is also fixed by the octonion algebra. Thus there are no free or fine tuned constants in the theory. Coupling constants and all other parameters of the standard model should emerge upon symmetry breaking, from the octonion algebra / geometry. We note that this Lagrangian is scale-invariant and assumed invariant under an unbroken $E_{8}\times E_{8}$ symmetry. Scale invariance is broken when this symmetry breaks, which is also Left-Right symmetry breaking as we will see below.

This matrix-valued Lagrangian dynamics is not to be quantised; rather it is a pre-quantum dynamics from which quantum field theory is emergent. This is as per the theory of trace dynamics [9, 10, 11]. Additionally, our theory is also a pre-spacetine dynamics, from which 4D curved spacetime and classical macroscopic objects are emergent [4]. Therefore, gravitation, as well as quantum theory, are regarded as emergent phenomena.

An atom of space-time-matter is an elementary particle, say an electron, along with all the fields it produces. Of course the particle is fermionic and the produced fields are bosonic, but at the level of $\widetilde{Q}_{1}$ and $\widetilde{Q}_{2}$ one does not make a distinction between the bosonic aspect and the fermionic aspect. That distinction is introduced by noting that a Grassmann number can always be written as the sum of a Grassmann even part and a Grassmann odd part. Hence a matrix $\widetilde{Q}$ can be written as a sum of two matrices: $Q=Q_{B}+Q_{F}$, with the first one made from even-grade Grassmann numbers and called bosonic part, and the second one made from odd-grade Grassmann numbers and called fermionic.

Our universe is fundamentally made of enormously many aikyons, each having its own copy of $E_{8}\times E_{8}$ symmetry. Entanglement of sufficiently many aikyons localises their fermionic aspect, giving rise to macroscopic objects in the universe, and the emergence of 4D curved spacetime and classical gauge fields. Quantum degrees of freedom, i.e. those aikyons which are not critically entangled, continue to obey $E_{8}\times E_{8}$ symmetry and are described precisely by the Lagrangian dynamics outlined below, or approximately, by the laws of quantum field theory on the emergent 4D spacetime. In the latter formalism, we lose the explanation for the origin of the standard model symmetries and for values of its parameters, because the memory of the underlying $E_{8}\times E_{8}$ symmetry is lost. The emergence of the classical theory is facilitated by the spectral action principle [12, 13] which relates the eigenvalues of the Dirac operator (on which the present dynamics is based) to the action principle of the classical theory (gravitation and gauge fields and their matter sources).

Hence we define bosonic and fermionic degrees of freedom as follows

$$\dot{\widetilde{Q}}_{1}^{\dagger}\equiv\dot{\widetilde{Q}}_{B}^{\dagger}+\frac{L_{p}^{2}}{L^{2}}\beta_{1}\dot{\widetilde{Q}}_{F}^{\dagger}\ ;\qquad\dot{\tilde{Q}}_{2}\equiv\dot{\widetilde{Q}}_{B}+\frac{L_{p}^{2}}{L^{2}}\beta_{2}\dot{\widetilde{Q}}_{F}$$

(4)

and use this expansion in the Lagrangian. Here $\beta_{1}$ and $\beta_{2}$ are two unequal odd-grade Grassmann numbers introduced so as to keep the Lagrangian bosonic, and the constant $L_{p}^{2}/L^{2}$ is essential for obtaining the correct classical limit of the theory. The bosonic matrix and the fermionic matrix each have sixteen components over the sixteen directions of the bioctonion, and the Yang-Mills coupling constant $\alpha$ is now introduced as follows

$$\dot{\widetilde{Q}}_{B}=\frac{1}{L}(i\alpha q_{B}+L\dot{q}_{B})\ ;\qquad\dot{\widetilde{Q}}_{F}=\frac{1}{L}(i\alpha q_{F}+L\dot{q}_{F})$$

(5)

The introduction of $\alpha/L$ is an important step in the theory; it breaks the scale invariance of the original Lagrangian (3). The introduction of $L$ is essential for matching dimension of the undotted terms with that of the dotted terms. The dotted terms are defined only over the conjugated octonionic part $\tilde{O}$ of the split bioctonion and hence have eight matrix-valued coordinate components; these are related to pre-gravitation. The undotted parts are defined over the part ${O}$ of the split bioctonion and hence also have eight matrix-valued components; these are related to the standard model $SU(3)_{c}\times SU(2)_{L}\times U(1)_{Y}$. Pre-gravitation is $SU(3)_{grav}\times SU(2)_{R}\times U(1)_{g}$. In the split bioctonion, since the part $\omega\tilde{O}$ is interpreted as the parity reversal of $\tilde{O}$, and since $SU(2)_{L}$ and $SU(2)_{R}$ are chiral symmetries, the introduction of the standard model and of pre-gravitation breaks Left-Right symmetry and also breaks $E_{8}\times E_{8}$ symmetry. The breaking of scale invariance also helps understand why general relativity obeys equivalence principle, whereas standard model forces do not; the latter depend on $L$.

In terms of these variables, the Lagrangian can be written as

$$\qquad\mathcal{L}=\frac{L_{p}^{2}}{2L^{2}}Tr\biggl{[}\biggr{.}\left\{\frac{1}{L}(i\alpha q_{B}+L\dot{q}_{B})^{\dagger}+\frac{L_{p}^{2}}{L^{2}}\beta_{1}.\frac{1}{L}(i\alpha q_{F}+L\dot{q}_{F})^{\dagger}\right\}\times\left\{\frac{1}{L}(i\alpha q_{B}+L\dot{q}_{B})+\frac{L_{p}^{2}}{L^{2}}\beta_{2}.\frac{1}{L}(i\alpha q_{F}+L\dot{q}_{F})\right\}\biggr{]}$$

(6)

When the brackets are opened out, there are 1024 terms. Another useful way to write the Lagrangian is to define the dynamical variables

$$q^{\dagger}_{1}=q_{B}^{\dagger}+\frac{L_{P}^{2}}{L^{2}}\beta_{1}q^{\dagger}_{F}\qquad;\qquad q_{2}=q_{B}+\frac{L_{P}^{2}}{L^{2}}\beta_{2}q_{F}$$

(7)

which gives

	$\displaystyle{\cal L}$	$\displaystyle=\frac{L_{P}^{2}}{2L^{2}}\;Tr\left[\left(\dot{q}_{1}^{\dagger}+\frac{i\alpha}{L}q_{1}^{\dagger}\right)\times\left(\dot{q}_{2}+\frac{i\alpha}{L}q_{2}\right)\right]$		(8)
		$\displaystyle=\frac{L_{P}^{2}}{2L^{2}}\;Tr\left[\dot{q}_{1}^{\dagger}\dot{q}_{2}-\frac{\alpha^{2}}{L^{2}}q_{1}^{\dagger}q_{2}+\frac{i\alpha}{L}q_{1}^{\dagger}\dot{q}_{2}+\frac{i\alpha}{L}\dot{q}_{1}^{\dagger}q_{2}\right]$

We can expand each of these four terms inside of the trace Lagrangian by using the definitions of $q_{1}$ and $q_{2}$:

	$\displaystyle\dot{q}_{1}^{\dagger}\dot{q}_{2}$	$\displaystyle=\dot{q}_{B}^{\dagger}\dot{q}_{B}+\frac{L_{P}^{2}}{L^{2}}\dot{q}_{B}^{\dagger}\beta_{2}\dot{q}_{F}+\frac{L_{P}^{2}}{L^{2}}\beta_{1}\dot{q}_{F}^{\dagger}\dot{q}_{B}+\frac{L_{P}^{4}}{L^{4}}\beta_{1}\dot{q}_{F}^{\dagger}\beta_{2}\dot{q}_{F}$		(9)
	$\displaystyle q_{1}^{\dagger}q_{2}$	$\displaystyle=q_{B}^{\dagger}{q}_{B}+\frac{L_{P}^{2}}{L^{2}}q_{B}^{\dagger}\beta_{2}{q}_{F}+\frac{L_{P}^{2}}{L^{2}}\beta_{1}q_{F}^{\dagger}{q}_{B}+\frac{L_{P}^{4}}{L^{4}}\beta_{1}q_{F}^{\dagger}\beta_{2}{q}_{F}$
	$\displaystyle q_{1}^{\dagger}\dot{q}_{2}$	$\displaystyle=q_{B}^{\dagger}\dot{q}_{B}+\frac{L_{P}^{2}}{L^{2}}q_{B}^{\dagger}\beta_{2}\dot{q}_{F}+\frac{L_{P}^{2}}{L^{2}}\beta_{1}q_{F}^{\dagger}\dot{q}_{B}+\frac{L_{P}^{4}}{L^{4}}\beta_{1}q_{F}^{\dagger}\beta_{2}\dot{q}_{F}$
	$\displaystyle\dot{q}_{1}^{\dagger}q_{2}$	$\displaystyle=\dot{q}_{B}^{\dagger}{q}_{B}+\frac{L_{P}^{2}}{L^{2}}\dot{q}_{B}^{\dagger}\beta_{2}{q}_{F}+\frac{L_{P}^{2}}{L^{2}}\beta_{1}\dot{q}_{F}^{\dagger}{q}_{B}+\frac{L_{P}^{4}}{L^{4}}\beta_{1}\dot{q}_{F}^{\dagger}\beta_{2}{q}_{F}$

This form of the Lagrangian displays terms for the bosonic variables (gauge fields), the interaction part of the action, and terms bilinear in fermionic varaibles. The goal of the present series of papers is to investigate if this Lagrangian, expanded over the split bioctonionic space, describes the standard model as well as general relativity, possibly with some additional departures from currently known theory. In the present paper, starting with the next section, we write out in detail the bosonic part of the Lagrangian, and interpret it.

The equations of motion in this Lagrangian dynamics can be worked out from (8) and are given by [7]

$$\ddot{q}_{1}^{\dagger}=-\frac{\alpha^{2}}{L^{2}}\;{q}_{1}^{\dagger}\;;\qquad\ddot{q}_{2}=-\frac{\alpha^{2}}{L^{2}}\;{q}_{2}$$

(10)

and are discussed in a little more detail in [7]. Different particles are different vibrations of the 2-brane obeying these equations. In particular, the Dirac equation for three fermion generations arises as the eigenvalue equation for the constant matrices arising in the solution to these oscillator equations. Its symmetry group in ten dimensions is in fact $E_{6}$ which is also the automorphism group of the complexified exceptional Jordan algebra [14, 15]. When restricted to the Hermitean sector, we get the exceptional Jordan algebra, whose automorphism group is $F_{4}$ and which solves the eigenvalue problem for given values of quantised electric charge, and reveals a derivation of mass ratios [2, 3].

Note that in the Lagrangian (8) the cross-terms, i.e. the ones proportional to $i\alpha$, do not contribute to the equations of motion, with their contribution cancelling out. These cross terms form a total time derivative, and hence their time integral gives a boundary term, but there is no reason why the boundary term should vanish. Thus its time dependence is determined by the equations of motion. Remarkably, as we will see below, these cross-terms describe the $SU(2)_{L}\times SU(2)_{R}$ symmetry of electroweak - pregravitation sector, suggesting that the sector $SU(3)_{c}\times SU(3)_{grav}$ [which comes from the fully dotted first two terms] determines the weak-pregrav sector, as if there is a gauge-gravity duality, with $SU(3)_{grav}$ actually belonging to gauge sector, and the weak force belonging to the gravity sector.

In our theory, the $E_{8}\times E_{8}$ symmetry breaking is also left-right symmetry breaking, and it is clearly also the electroweak symmetry breaking. Thus we have the inescapable conclusion that prior to the EW breaking quantum gravity and unification come in play, and therefore that a de Sitter like scale-invariant cosmic expansion resets the Planck scale to the EW scale. This partly solves the hierarchy problem (effective Planck scale = EW scale), though of course it remains to be understood why the Higgs has the particular mass it does. Furthermore, since we have noted from the outset that description of matter fields on a spinor spacetime does not involve going to higher energies, we are compelled to note that the said symmetry breaking must be manifest even at currently studied low energies. This can be understood if the symmetry breaking process is the quantum-to-classical transition, which is precipitated whenever sufficiently many atoms of space-time-matter are entangled, resulting in the localisation of fermions and emergence of 4D classical spacetime. Quantum systems do not live in 4D spacetime; they live in the space having $E_{8}\times E_{8}$ symmetry, at all energies. Therefore the (non-commuting) extra dimensions are never to be compactified. Only classical systems live in 4D (compactification without compactification) and arrive here dynamically. Energy scale is not the key, but the degree of entanglement is. In the very early universe the energy scale is important, but only indirectly so. When the very early universe undergoing a de Sitter like scale-invariant expansion becomes cool enough to allow critical entanglement for the quantum-to-classical transition to take place, the $E_{8}\times E_{8}$ symmetry is broken. What remains to be proved is that the freeze-out happens somewhere between 100 GeV and a TeV, and to find the exact value of this transition energy scale.

Our Lagrangian is over a sixteen dimensional split bi-octonionic space ($O\oplus\omega\tilde{O}$)

$$\mathscr{L}=\frac{L_{p}^{2}}{2L^{2}}Tr(\dot{\widetilde{Q}}_{1}^{\dagger}\dot{\widetilde{Q}}_{2})$$

(11)

where

$$\dot{\widetilde{Q}}_{1}^{\dagger}=\dot{\widetilde{Q}}_{B}^{\dagger}+\frac{L_{p}^{2}}{L^{2}}\beta_{1}\dot{\widetilde{Q}}_{F}^{\dagger}\ ;\qquad\dot{\widetilde{Q}}_{2}=\dot{\widetilde{Q}}_{B}+\frac{L_{p}^{2}}{L^{2}}\beta_{2}\dot{\widetilde{Q}}_{F}$$

(12)

Each matrix has sixteen components, and

$$\dot{\widetilde{Q}}_{B}=\frac{1}{L}(i\alpha q_{B}+L\dot{q}_{B})\ ;\qquad\dot{\widetilde{Q}}_{F}=\frac{1}{L}(i\alpha q_{F}+L\dot{q}_{F})$$

(13)

The bosonic terms of the Lagrangian are:

$$\mathscr{L}_{bosonic}=\frac{L_{p}^{2}}{L^{4}}\left(\alpha^{2}q_{B}^{\dagger}q_{B}+L^{2}\dot{q}_{B}^{\dagger}\dot{q}_{B}-i\alpha Lq_{B}^{\dagger}\dot{q}_{B}+i\alpha L\dot{q}_{B}^{\dagger}q_{B}\right)$$

(14)

and these four terms can respectively be expanded as follows:

The first of these terms has a coefficient ${L_{p}^{2}\alpha^{2}/L^{4}}$ as per Eqn. (14) above.

	$\displaystyle q_{B}^{\dagger}q_{B}=$	$\displaystyle(q_{B0}e_{0}-q_{B1}^{\dagger}e_{1}-q_{B2}^{\dagger}e_{2}-q_{B3}^{\dagger}e_{3}-q_{B4}^{\dagger}e_{4}-q_{B5}^{\dagger}e_{5}-q_{B6}^{\dagger}e_{6}-q_{B8}^{\dagger}e_{8})\times$
		$\displaystyle(q_{B0}e_{0}+q_{B1}e_{1}+q_{B2}e_{2}+q_{B3}e_{3}+q_{B4}e_{4}+q_{B5}e_{5}+q_{B6}e_{6}+q_{B8}e_{8})$
	$\displaystyle=$
		$\displaystyle q_{B0}^{2}+q_{B1}^{\dagger}q_{B1}+q_{B2}^{\dagger}q_{B2}+q_{B3}^{\dagger}q_{B3}+q_{B4}^{\dagger}q_{B4}+q_{B5}^{\dagger}q_{B5}+q_{B6}^{\dagger}q_{B6}+q_{B8}^{\dagger}q_{B8}$
	$\displaystyle-\$	$\displaystyle(q_{B1}^{\dagger}e_{1}+q_{B2}^{\dagger}e_{2}+q_{B3}^{\dagger}e_{3}+q_{B4}^{\dagger}e_{4}+q_{B5}^{\dagger}e_{5}+q_{B6}^{\dagger}e_{6}+q_{B8}^{\dagger})q_{B0}$
	$\displaystyle+\$	$\displaystyle q_{B0}(q_{B1}e_{1}+q_{B2}e_{2}+q_{B3}e_{3}+q_{B4}e_{4}+q_{B5}e_{5}+q_{B6}e_{6}+q_{B8}e_{8})$
	$\displaystyle+\$	$\displaystyle(-q_{B2}^{\dagger}q_{B4}+q_{B4}^{\dagger}q_{B2}-q_{B3}^{\dagger}q_{B8}+q_{B8}^{\dagger}q_{B3}-q_{B5}^{\dagger}q_{B6}+q_{B6}^{\dagger}q_{B5})e_{1}$
	$\displaystyle\ +\$	$\displaystyle(-q_{B4}^{\dagger}q_{B1}+q_{B1}^{\dagger}q_{B4}-q_{B3}^{\dagger}q_{B5}+q_{B5}^{\dagger}q_{B3}-q_{B6}^{\dagger}q_{B8}+q_{B8}^{\dagger}q_{B6})e_{2}$
	$\displaystyle+\$	$\displaystyle(-q_{B4}^{\dagger}q_{B6}+q_{B6}^{\dagger}q_{B4}-q_{B5}^{\dagger}q_{B2}+q_{B2}^{\dagger}q_{B5}-q_{B8}^{\dagger}q_{B1}+q_{B1}^{\dagger}q_{B8})e_{3}$
	$\displaystyle+\$	$\displaystyle(-q_{B1}^{\dagger}q_{B2}+q_{B2}^{\dagger}q_{B1}-q_{B6}^{\dagger}q_{B3}+q_{B3}^{\dagger}q_{B6}-q_{B5}^{\dagger}q_{B8}+q_{B8}^{\dagger}q_{B5})e_{4}$
	$\displaystyle+\$	$\displaystyle(-q_{B2}^{\dagger}q_{B3}+q_{B3}^{\dagger}q_{B2}-q_{B6}^{\dagger}q_{B1}+q_{B1}^{\dagger}q_{B6}-q_{B8}^{\dagger}q_{B4}+q_{B4}^{\dagger}q_{B8})e_{5}$
	$\displaystyle+\$	$\displaystyle(-q_{B1}^{\dagger}q_{B5}+q_{B5}^{\dagger}q_{B1}-q_{B8}^{\dagger}q_{B2}+q_{B2}^{\dagger}q_{B8}-q_{B3}^{\dagger}q_{B4}+q_{B4}^{\dagger}q_{B3})e_{6}$
	$\displaystyle+\$	$\displaystyle(-q_{B1}^{\dagger}q_{B3}+q_{B3}^{\dagger}q_{B1}-q_{B2}^{\dagger}q_{B6}+q_{B6}^{\dagger}q_{B2}-q_{B4}^{\dagger}q_{B5}+q_{B5}^{\dagger}q_{B4})e_{8}$		(15)

This term has a coefficient ${L_{p}^{2}/L^{2}}$ as per Eqn. (14) above.

	$\displaystyle\dot{q}_{B}^{\dagger}\dot{q}_{B}=$	$\displaystyle(\dot{q}_{B0}e_{0}-\dot{q}_{B1}^{\dagger}e_{1}-\dot{q}_{B2}^{\dagger}e_{2}-\dot{q}_{B3}^{\dagger}e_{3}-\dot{q}_{B4}^{\dagger}e_{4}-\dot{q}_{B5}^{\dagger}e_{5}-\dot{q}_{B6}^{\dagger}e_{6}-\dot{q}_{B8}^{\dagger}e_{8})\times$
		$\displaystyle(\dot{q}_{B0}e_{0}+\dot{q}_{B1}e_{1}+\dot{q}_{B2}e_{2}+\dot{q}_{B3}e_{3}+\dot{q}_{B4}e_{4}+\dot{q}_{B5}e_{5}+\dot{q}_{B6}e_{6}+\dot{q}_{B8}e_{8})$
	$\displaystyle=$
		$\displaystyle\dot{q}_{B0}^{2}+\dot{q}_{B1}^{\dagger}\dot{q}_{B1}+\dot{q}_{B2}^{\dagger}\dot{q}_{B2}+\dot{q}_{B3}^{\dagger}\dot{q}_{B3}+\dot{q}_{B4}^{\dagger}\dot{q}_{B4}+\dot{q}_{B5}^{\dagger}\dot{q}_{B5}+\dot{q}_{B6}^{\dagger}\dot{q}_{B6}+\dot{q}_{B8}^{\dagger}\dot{q}_{B8}$
	$\displaystyle+\$	$\displaystyle\dot{q}_{B0}(\dot{q}_{B1}e_{1}+\dot{q}_{B2}e_{2}+\dot{q}_{B3}e_{3}+\dot{q}_{B4}e_{4}+\dot{q}_{B5}e_{5}+\dot{q}_{B6}e_{6}+\dot{q}_{B8}e_{8})$
	$\displaystyle+\$	$\displaystyle(-\dot{q}_{B1}^{\dagger}e_{1}-\dot{q}_{B2}^{\dagger}e_{2}-\dot{q}_{B3}^{\dagger}e_{3}-\dot{q}_{B4}^{\dagger}e_{4}-\dot{q}_{B5}^{\dagger}e_{5}-\dot{q}_{B6}^{\dagger}e_{6}-\dot{q}_{B8}^{\dagger}e_{8})\dot{q}_{B0}$
	$\displaystyle+\$	$\displaystyle(-\dot{q}_{B2}^{\dagger}\dot{q}_{B4}+\dot{q}_{B4}^{\dagger}\dot{q}_{B2}-\dot{q}_{B3}^{\dagger}\dot{q}_{B8}+\dot{q}_{B8}^{\dagger}\dot{q}_{B3}-\dot{q}_{B5}^{\dagger}\dot{q}_{B6}+\dot{q}_{B6}^{\dagger}\dot{q}_{B5})e_{1}$
	$\displaystyle+\$	$\displaystyle(-\dot{q}_{B4}^{\dagger}\dot{q}_{B1}+\dot{q}_{B1}^{\dagger}\dot{q}_{B4}-\dot{q}_{B3}^{\dagger}\dot{q}_{B5}+\dot{q}_{B5}^{\dagger}\dot{q}_{B3}-\dot{q}_{B6}^{\dagger}\dot{q}_{B8}+\ \dot{q}_{B8}^{\dagger}\dot{q}_{B6})e_{2}$
	$\displaystyle+\$	$\displaystyle(-\dot{q}_{B4}^{\dagger}\dot{q}_{B6}+\dot{q}_{B6}^{\dagger}\dot{q}_{B4}-\dot{q}_{B5}^{\dagger}\dot{q}_{B2}+\dot{q}_{B5}^{\dagger}\dot{q}_{B2}-\dot{q}_{B8}^{\dagger}\dot{q}_{B1}+\dot{q}_{B1}^{\dagger}\dot{q}_{B8})e_{3}$
	$\displaystyle+\$	$\displaystyle(-\dot{q}_{B1}^{\dagger}\dot{q}_{B2}+\dot{q}_{B2}^{\dagger}\dot{q}_{B1}-\dot{q}_{B4}^{\dagger}\dot{q}_{B6}+\dot{q}_{B6}^{\dagger}\dot{q}_{B3}-\dot{q}_{B5}^{\dagger}\dot{q}_{B8}+\dot{q}_{B8}^{\dagger}\dot{q}_{B5})e_{4}$
	$\displaystyle+\$	$\displaystyle(-\dot{q}_{B2}^{\dagger}\dot{q}_{B3}+\dot{q}_{B3}^{\dagger}\ dot{q}_{B2}-\dot{q}_{B6}^{\dagger}\dot{q}_{B1}+\dot{q}_{B1}^{\dagger}\dot{q}_{B6}-\dot{q}_{B8}^{\dagger}\dot{q}_{B4}+\dot{q}_{B4}^{\dagger}\dot{q}_{B8})e_{5}$
	$\displaystyle+\$	$\displaystyle(-\dot{q}_{B1}^{\dagger}\dot{q}_{B5}+\dot{q}_{B5}^{\dagger}\dot{q}_{B1}-\dot{q}_{B8}^{\dagger}\dot{q}_{B2}+\dot{q}_{B2}^{\dagger}\dot{q}_{B8}-\dot{q}_{B3}^{\dagger}\dot{q}_{B4}+\dot{q}_{B4}^{\dagger}\dot{q}_{B3})e_{6}$
	$\displaystyle+\$	$\displaystyle(-\dot{q}_{B1}^{\dagger}\dot{q}_{B3}+\dot{q}_{B3}^{\dagger}\dot{q}_{B1}-\dot{q}_{B2}^{\dagger}\dot{q}_{B6}+\dot{q}_{B6}^{\dagger}\dot{q}_{B2}-\dot{q}_{B4}^{\dagger}\dot{q}_{B5}+\dot{q}_{B5}^{\dagger}\dot{q}_{B4})e_{8}$		(16)

These terms have a coefficient $-i{L_{p}^{2}\alpha/L^{3}}$ as per Eqn. (14) above.

	$\displaystyle\left(q_{B}^{\dagger}\dot{q}_{B}-\dot{q}_{B}^{\dagger}q_{B}\right)=$	$\displaystyle\omega(\dot{q}_{B0}q_{B0}-q_{B0}\dot{q}_{B0}-\dot{q}_{B1}^{\dagger}q_{B1}+q_{B1}^{\dagger}\dot{q}_{B1}-\dot{q}_{B2}^{\dagger}q_{B2}+q_{B2}^{\dagger}\dot{q}_{B2}-\dot{q}_{B3}^{\dagger}q_{B3}+q_{B3}^{\dagger}\dot{q}_{B3}$
	$\displaystyle-\$	$\displaystyle\dot{q}_{B4}^{\dagger}q_{B4}+q_{B4}^{\dagger}\dot{q}_{B4}-\dot{q}_{B5}^{\dagger}q_{B5}+q_{B5}^{\dagger}\dot{q}_{B5}-\dot{q}_{B6}^{\dagger}q_{B6}+q_{B6}^{\dagger}\dot{q}_{B6}-\dot{q}_{B8}^{\dagger}q_{B8}+q_{B8}^{\dagger}\dot{q}_{B8})$
	$\displaystyle+\$	$\displaystyle(\dot{q}_{B1}^{\dagger}q_{B0}-\dot{q}_{B4}^{\dagger}q_{B2}+\dot{q}_{B2}^{\dagger}q_{B4}-\dot{q}_{B6}^{\dagger}q_{B5}+\dot{q}_{B5}^{\dagger}q_{B6}-\dot{q}_{B8}^{\dagger}q_{B3}+\dot{q}_{B3}^{\dagger}q_{B8}+q_{B1}^{\dagger}\dot{q}_{B0}+q_{B4}^{\dagger}\dot{q}_{B2}-q_{B2}^{\dagger}\dot{q}_{B4}$
		$\displaystyle+q_{B6}^{\dagger}\dot{q}_{B5}-q_{B5}^{\dagger}\dot{q}_{B6}+q_{B8}^{\dagger}\dot{q}_{B3}-q_{B3}^{\dagger}\dot{q}_{B8})\omega e_{1}$
	$\displaystyle+\$	$\displaystyle(\dot{q}_{B2}^{\dagger}q_{B0}-\dot{q}_{B1}^{\dagger}q_{B4}+\dot{q}_{B4}^{\dagger}q_{B1}-\dot{q}_{B5}^{\dagger}q_{B3}+\dot{q}_{B3}^{\dagger}q_{B5}-\dot{q}_{B8}^{\dagger}q_{B6}+\dot{q}_{B6}^{\dagger}q_{B8}+q_{B2}^{\dagger}\dot{q}_{B0}+q_{B1}^{\dagger}\dot{q}_{B4}-q_{B4}^{\dagger}\dot{q}_{B1}$
		$\displaystyle+q_{B5}^{\dagger}\dot{q}_{B3}-q_{B3}^{\dagger}\dot{q}_{B5}+q_{B8}^{\dagger}\dot{q}_{B6}-q_{B6}^{\dagger}\dot{q}_{B8})\omega e_{2}$
	$\displaystyle+\$	$\displaystyle(\dot{q}_{B3}^{\dagger}q_{B0}-\dot{q}_{B1}^{\dagger}q_{B8}+\dot{q}_{B8}^{\dagger}q_{B1}-\dot{q}_{B2}^{\dagger}q_{B5}+\dot{q}_{B5}^{\dagger}q_{B2}-\dot{q}_{B6}^{\dagger}q_{B4}+\dot{q}_{B4}^{\dagger}q_{B6}+q_{B3}^{\dagger}\dot{q}_{B0}+q_{B1}^{\dagger}\dot{q}_{B8}-q_{B8}^{\dagger}\dot{q}_{B1}$
		$\displaystyle+q_{B2}^{\dagger}\dot{q}_{B5}-q_{B5}^{\dagger}\dot{q}_{B2}+q_{B6}^{\dagger}\dot{q}_{B4}-q_{B4}^{\dagger}\dot{q}_{B6})\omega e_{3}$
	$\displaystyle+\$	$\displaystyle(\dot{q}_{B4}^{\dagger}q_{B0}-\dot{q}_{B2}^{\dagger}q_{B1}+\dot{q}_{B1}^{\dagger}q_{B2}-\dot{q}_{B3}^{\dagger}q_{B6}+\dot{q}_{B6}^{\dagger}q_{B3}-\dot{q}_{B8}^{\dagger}q_{B5}+\dot{q}_{B5}^{\dagger}q_{B8}+q_{B4}^{\dagger}\dot{q}_{B0}+q_{B2}^{\dagger}\dot{q}_{B1}-q_{B1}^{\dagger}\dot{q}_{B2}$
		$\displaystyle+q_{B3}^{\dagger}\dot{q}_{B6}-q_{B6}^{\dagger}\dot{q}_{B3}+q_{B8}^{\dagger}\dot{q}_{B5}-q_{B5}^{\dagger}\dot{q}_{B8})\omega e_{4}$
	$\displaystyle+\$	$\displaystyle(\dot{q}_{B5}^{\dagger}q_{B0}-\dot{q}_{B1}^{\dagger}q_{B6}+\dot{q}_{B6}^{\dagger}q_{B1}-\dot{q}_{B3}^{\dagger}q_{B2}+\dot{q}_{B2}^{\dagger}q_{B3}-\dot{q}_{B4}^{\dagger}q_{B8}+\dot{q}_{B8}^{\dagger}q_{B4}+q_{B5}^{\dagger}\dot{q}_{B0}+q_{B1}^{\dagger}\dot{q}_{B6}-q_{B6}^{\dagger}\dot{q}_{B1}$
		$\displaystyle+q_{B3}^{\dagger}\dot{q}_{B2}-q_{B2}^{\dagger}\dot{q}_{B3}+q_{B4}^{\dagger}\dot{q}_{B8}-q_{B8}^{\dagger}\dot{q}_{B4})\omega e_{5}$
	$\displaystyle+\$	$\displaystyle(\dot{q}_{B6}^{\dagger}q_{B0}-\dot{q}_{B5}^{\dagger}q_{B1}+\dot{q}_{B1}^{\dagger}q_{B5}-\dot{q}_{B2}^{\dagger}q_{B8}+\dot{q}_{B8}^{\dagger}q_{B2}-\dot{q}_{B4}^{\dagger}q_{B3}+\dot{q}_{B3}^{\dagger}q_{B4}+q_{B6}^{\dagger}\dot{q}_{B0}+q_{B5}^{\dagger}\dot{q}_{B1}-q_{B1}^{\dagger}\dot{q}_{B5}$
		$\displaystyle+q_{B2}^{\dagger}\dot{q}_{B8}-q_{B8}^{\dagger}\dot{q}_{B2}+q_{B4}^{\dagger}\dot{q}_{B3}-q_{B3}^{\dagger}\dot{q}_{B4})\omega e_{6}$
	$\displaystyle+\$	$\displaystyle(\dot{q}_{B8}^{\dagger}q_{B0}-\dot{q}_{B3}^{\dagger}q_{B1}+\dot{q}_{B1}^{\dagger}q_{B3}-\dot{q}_{B6}^{\dagger}q_{B2}+\dot{q}_{B2}^{\dagger}q_{B6}-\dot{q}_{B5}^{\dagger}q_{B4}+\dot{q}_{B4}^{\dagger}q_{B5}+q_{B8}^{\dagger}\dot{q}_{B0}+q_{B3}^{\dagger}\dot{q}_{B1}-q_{B1}^{\dagger}\dot{q}_{B3}$
		$\displaystyle+q_{B6}^{\dagger}\dot{q}_{B2}-q_{B2}^{\dagger}\dot{q}_{B6}+q_{B5}^{\dagger}\dot{q}_{B4}-q_{B4}^{\dagger}\dot{q}_{B5})\omega e_{8}$		(17)