A joint reconstruction and lambda tomography regularization technique for energy-resolved X-ray imaging
\ddmmyyyydate \currenttime
Abstract.
We present new joint reconstruction and regularization techniques inspired by ideas in microlocal analysis and lambda tomography, for the simultaneous reconstruction of the attenuation coefficient and electron density from X-ray transmission (i.e., X-ray CT) and backscattered data (assumed to be primarily Compton scattered). To demonstrate our theory and reconstruction methods, we consider the “parallel line segment” acquisition geometry of [54], which is motivated by system architectures currently under development for airport security screening. We first present a novel microlocal analysis of the parallel line geometry which explains the nature of image artefacts when the attenuation coefficient and electron density are reconstructed separately. We next introduce a new joint reconstruction scheme for low effective (atomic number) imaging () characterized by a regularization strategy whose structure is derived from lambda tomography principles and motivated directly by the microlocal analytic results. Finally we show the effectiveness of our method in combating noise and image artefacts on simulated phantoms.
1. Introduction
In this paper we introduce new joint reconstruction and regularization techniques based on ideas in microlocal analysis and lambda tomography [13, 14] (see also [32] for related work). We consider the simultaneous reconstruction of the attenuation coefficient and electron density from joint X-ray CT (transmission) and Compton scattered data, with particular focus on the parallel line segment X-ray scanner displayed in figures 1 and 2. The acquisition geometry in question is based on a new airport baggage scanner currently in development, and has the ability to measure X-ray CT and Compton data simultaneously. The line segment geometry was first considered in [54], where injectivity results are derived in Compton Scattering Tomography (CST). We provide a stability analysis of the CST problem of [54] here, from a microlocal perspective. The scanner depicted in figure 1 consists of a row of fixed, switched, monochromatic fan beam sources (), a row of detectors () to measure the transmitted photons, and a second (slightly out of plane) row of detectors () to measure Compton scatter. The detectors are assumed to energy-resolved, a common assumption in CST [35, 51, 41, 43, 55], and the sources are fan-beam (in the plane) with opening angle (so there is no restriction due to cropped fan-beams).
The attenuation coefficient relates to the X-ray transmission data by the Beer-Lambert law, [31, page 2] where is the photon intensity measured at the detector, is the initial source intensity and is the attenuation coefficient at energy . Here is a line through and , with arc measure . Hence the transmission data determines a set of integrals of over lines, and the problem of reconstructing is equivalent to inversion of the line Radon transform with limited data (e.g., [31, 33]). Note that we need not account for the energy dependence of in this case as the detectors are energy-resolved, and hence there are no issues due to beam-hardening. See figure 1.
When the attenuation of the incoming and scattered rays is ignored, the Compton scattered intensity in two-dimensions can be modelled as integrals of over toric sections [35, 51, 55]
| (1.1) |
where is the Compton scattered intensity measured at a point on . A toric section is the union of two intersecting circles of the same radii (as displayed in figure 2), and is the arc measure on . The recovery of is equivalent to inversion of the toric section Radon transform [34, 35, 51, 55]. See figure 2. See also [41, 43] for alternative reconstruction methods. We now discuss the approximation made above to neglect the attenuative effects from the CST model. When the attenuation effects are included, the inverse scattering problem becomes nonlinear [42]. We choose to focus on the analysis of the idealised linear case here, as this allows us to apply the well established theory on linear Fourier Integral Operators (FIO) and microlocal analysis to derive expression for the image artefacts. Such analysis will likely give valuable insight into the expected artefacts in the nonlinear case. The nonlinear models and their inversion properties are left for future work.
The line and circular arc Radon transforms with full data, are known [35, 30] to have inverses that are continuous in some range of Sobolev norms. Hence with adequate regularization we can reconstruct an image free of artefacts. With limited data however [31, 51], the solution is unstable and the image wavefront set (see Definition 2.2) is not recovered stably in all directions. We will see later in section 3 through simulation that such data limitations in the parallel line geometry cause a blurring artefact over a cone in the reconstruction. There may also be nonlocal artefacts specific to the geometry (as in [55]), which we shall discover later in section 3 in the geometry of figure 2.
The main goal of this paper is to combine limited datasets in X-ray CT and CST with new lambda tomography regularization techniques, to recover the image edges stably in all directions. We focus particularly on the geometry of figure 1. In lambda tomography the image reconstruction is carried out by filtered backprojection of the Radon projections, where the filter is chosen to emphasize boundaries. This means that the jump singularities in the lambda reconstruction have the same location and direction to those of the target function, but the smooth parts are undetermined. A common choice of filter is a second derivative in the linear variable [7, 43]. The application of the derivative filter emphasizes the singularities in the Radon projections, and this is a key idea behind lambda tomography [13, 14, 52], and the microlocal view on lambda CT (e.g., [7, 39, 43]). The regularization penalty we propose aims to minimize the difference for some , where denotes the Radon line transform. Therefore, with a full set of Radon projections, the lambda penalties enforce a similarity in the locations and direction of the image singularities (edges) of and . Further for is equivalent to taking derivatives of the object (this operation is continuous of positive order in Sobolev scales), and hence its inverse is a smoothing operation, which we expect to be of aid in combatting the measurement noise. In addition, the regularized inverse problem we propose is linear (similarly to the Tikhonov regularized inverse [21, page 99]), which (among other benefits of linearity) allows for the fast application of iterative least squares solvers in the solution.
The literature considers joint image reconstruction and regularization in for example, [1, 19, 40, 46, 47, 6, 50, 12, 20, 11, 48, 10, 45, 4]. See also the special issue [3] for a more general review of joint reconstruction techniques. In [12] the authors consider the joint reconstruction from Positron Emission Tomography (PET) and Magnetic Resonance Imaging (MRI) data and use a Parallel Level Set (PLS) prior for the joint regularization. The PLS approach (first introduced in [10]) imposes soft constraints on the equality of the image gradient location and direction, thus enforcing structural similarity in the image wavefront sets. This follows a similar intuition to the “Nambu” functionals of [48] and the “cross-gradient” methods of [16, 17] in seismic imaging, the latter of which specify hard constraints that the gradient cross products are zero (i.e. parallel image gradients). The methods of [12] use linear and quadratic formulations of PLS, denoted by Linear PLS (LPLS) and Quadratic PLS (QPLS). The LPLS method will be a point of comparison with the proposed method. We choose to compare with LPLS as it is shown to offer greater performance than QPLS in the experiments conducted in [12].
In [20] the authors consider a class of techniques in joint reconstruction and regularization, including inversion through correspondence mapping, mutual information and Joint Total Variation (JTV). In addition to LPLS, we will compare against JTV as the intuition of JTV is similar to that of lambda regularization (and LPLS), in the sense that a structural similarity is enforced in the image wavefronts. Similar to standard Total Variation (TV), which favours sparsity in the (single) image gradient, the JTV penalties (first introduced in [45] for colour imaging) favour sparsity in the joint gradient. Thus the image gradients are more likely to occur in the same location and direction upon minimization of JTV. The JTV penalties also have generalizations in colour imaging and vector-valued imaging [4].
In [54] the authors introduce a new toric section transform in the geometry of figure 2. Here explicit inversion formulae are derived, but the stability analysis is lacking. We aim to address the stability of in this work from a microlocal perspective. Through an analysis of the canonical relations of , we discover the existence of nonlocal artefacts in the inversion, similarly to [55]. In [40] the joint reconstruction of and is considered in a pencil beam scanner geometry. Here gradient descent solvers are applied to nonlinear objectives, derived from the physical models, and a weighted, iterative Tikhonov type penalty is applied. The works of [6] improve the wavefront set recovery in limited angle CT using a partially learned, hybrid reconstruction scheme, which adopts ideas in microlocal analysis and neural networks. The fusion with Compton data is not considered however. In our work we assume an equality in the wavefront sets of and (in a similar vein to [47]), and we investigate the microlocal advantages of combining Compton and transmission data, as such an analysis is lacking in the literature.
The remainder of this paper is organized as follows. In section 2, we recall some definitions and theorems from microlocal analysis. In section 3 we present a microlocal analysis of and explain the image artefacts in the reconstruction. Here we prove our main theorem (Theorem 3.2), where we show that the canonical relation of is 2–1. This implies the existence of nonlocal image artefacts in a reconstruction from toric section integral data. Further we find explicit expressions for the nonlocal artefacts and simulate these by applying the normal operations to a delta function. In section 4 we consider the microlocal artefacts from X-ray (transmission) data. This yields a limited dataset for the Radon transform, whereby we have knowledge the line integrals for all which intersect and (see figure 1). We use the results in [5] to describe the resulting artifacts in the X-ray CT reconstruction. In section 5, we detail our joint reconstruction method for the simultaneous reconstruction of and . Later in section 5.4 we present simulated reconstructions of and using the proposed methods and compare against JTV [20] and LPLS [12] from the literature. We also give a comparison to a separate reconstruction using TV.
2. Microlocal definitions
We next provide some notation and definitions. Let and be open subsets of . Let be the space of smooth functions compactly supported on with the standard topology and let denote its dual space, the vector space of distributions on . Let be the space of all smooth functions on with the standard topology and let denote its dual space, the vector space of distributions with compact support contained in . Finally, let be the space of Schwartz functions, that are rapidly decreasing at along with all derivatives. See [44] for more information.
Definition 2.1 ([25, Definition 7.1.1]).
For a function in the Schwartz space , we define the Fourier transform and its inverse as
| (2.1) |
We use the standard multi-index notation: if is a multi-index and is a function on , then
If is a function of then and are defined similarly.
We identify cotangent spaces on Euclidean spaces with the underlying Euclidean spaces, so we identify with .
If is a function of then we define , and and are defined similarly. We let .
The singularities of a function and the directions in which they occur are described by the wavefront set [9, page 16]:
Definition 2.2.
Let Let an open subset of and let be a distribution in . Let . Then is smooth at in direction if exists a neighbourhood of and of such that for every and there exists a constant such that
| (2.2) |
The pair is in the wavefront set, , if is not smooth at in direction .
This definition follows the intuitive idea that the elements of are the point–normal vector pairs above points of where has singularities. For example, if is the characteristic function of the unit ball in , then its wavefront set is , the set of points on a sphere paired with the corresponding normal vectors to the sphere.
The wavefront set of a distribution on is normally defined as a subset the cotangent bundle so it is invariant under diffeomorphisms, but we will continue to identify and consider as a subset of .
Definition 2.3 ([25, Definition 7.8.1]).
We define to be the set of such that for every compact set and all multi–indices the bound
holds for some constant . The elements of are called symbols of order .
Note that these symbols are sometimes denoted .
Definition 2.4 ([26, Definition 21.2.15]).
A function is a phase function if , and is nowhere zero. A phase function is clean if the critical set is a smooth manifold with tangent space defined by .
By the implicit function theorem the requirement for a phase function to be clean is satisfied if has constant rank.
Definition 2.5 ([26, Definition 21.2.15] and [27, Section 25.2]).
Let and be open subsets of . Let be a clean phase function. In addition, we assume that is nondegenerate in the following sense:
| and are never zero. |
The critical set of is
The canonical relation parametrised by is defined as
| (2.3) |
Definition 2.6.
Let and be open subsets of . A Fourier integral operator (FIO) of order is an operator with Schwartz kernel given by an oscillatory integral of the form
| (2.4) |
where is a clean nondegenerate phase function and is a symbol. The canonical relation of is the canonical relation of defined in (2.3).
This is a simplified version of the definition of FIO in [8, Section 2.4] or [27, Section 25.2] that is suitable for our purposes since our phase functions are global. For general information about FIOs see [8, 27, 26].
Definition 2.7.
Let be the canonical relation associated to the FIO . Then we let and denote the natural left- and right-projections of , and .
Because is nondegenerate, the projections do not map to the zero section. If a FIO satisfies our next definition, then (or if does not map to ) is a pseudodifferential operator [18, 37].
Definition 2.8.
Let be a FIO with canonical relation then (or ) satisfies the semi-global Bolker Assumption if the natural projection is an embedding (injective immersion).
3. Microlocal properties of translational Compton transforms
Here we present a microlocal analysis of the toric section transform in the translational (parallel line) scanning geometry. Through an analysis of two separate limited data problems for the circle transform (where the integrals over circles with centres on a straight line are known) and using microlocal analysis, we show that the canonical relation of the toric section transform is 2–1. The analysis follows in a similar way to the work of [55]. We discuss the nonlocal artefacts inherent to the toric section inversion in section 3.1, and then go on to explain the artefacts due to limited data in section 3.2.
We first define our geometry and formulate the toric section transform of [54] in terms of functions, before proving our main microlocal theory.
Let and define the set of points to be scanned as
Note that controls the depth of the scanning tunnel as in figures 1 and 2. Let
then for , and , we define the circles and their centers
| (3.1) |
Note that is the radius of the circle . The union of the reflected circles is called a toric section. Let be the electron charge density. To define the toric section transform we first introduce two circle transforms
| (3.2) |
Now we have the definition of the toric section transform [54]
| (3.3) |
where denotes the arc element on a circle and .
We express in terms of delta functions as is done for the generalized Funk-Radon transforms studied by Palamodov. [36]
| (3.4) |
Note that the factor in front of the integrals comes about using the change of variables formula and that . So the toric section transform is the sum of two FIO’s with phase functions
for . Our distributions are supported away from the intersection points of and , and hence we can consider the microlocal properties of and separately to describe the microlocal properties of .
Proposition 3.1.
For , the circle transform is an FIO or order with canonical relation
| (3.5) | ||||
Furthermore satisfies the semi-global Bolker assumption for .
Proof.
First, one can check that and both satisfy the restrictions in Definition 2.6 so is a FIO. Using this definition again and the fact that its symbol is order zero [37], one sees that it has order .
A straightforward calculation using Definition 2.5 shows that the canonical relation of is as given in (3.5). Note that we have absorbed a factor of into in this calculation. Global coordinates on are given by
| (3.6) | ||||
| where |
because . Recall that is given in (3.1).
We now show that satisfies the semiglobal Bolker assumption by finding a smooth inverse in these coordinates to the projection . Let . We solve for and in the equation . Then, and are known as are
| (3.7) |
A straightforward linear algebra exercise shows that the unique solutions for and are
| (3.8) |
This gives a smooth inverse to on the image and finishes the proof. ∎
Because satisfies the Bolker Assumption, the composition , where is the diagonal in . Hence in a reconstruction from circular integral data with centres on a line we would not expect to see image artefacts for functions supported in unless one uses a sharp cutoff on the data.
The canonical relation of can be written as the disjoint union since for any .
For convenience, we will sometimes label the coordinate in (3.6) as it is associated with and if it is associated with .
Theorem 3.2.
For , the projection is bijective onto the set
| (3.9) |
In addition, is two-to one onto .
Proof.
Let and let and . If for either or , then by (3.5) since . For the rest of the proof, assume is in the set given by (3.9)
We will now describe the preimage of in . The covector is conormal to a unique circle centered on , and its center is on the line through and parallel . If the center has coordinates , then a calculation shows that is given by
| (3.10) |
Using this calculation, one sees that the radius of the circle and coordinate are given by
| (3.11) |
and the coordinate is given by
| (3.12) |
A straightforward calculation shows that
| (3.13) |
This gives the coordinates (3.6) on and shows that is injective with smooth inverse.
The abstract adjoint cannot be composed with for , because the support of can be unbounded in , even for and is not defined for such distributions. Therefore, we introduce a smooth cutoff function. Choose and let be a smooth compactly supported function equal to one for and define
| (3.14) |
for all because our bound on introduces a bound on so the integral is over a bounded set for each .
3.1. The nonlocal artefacts
Now, we can state our next theorem, which describes the artifacts that can be added to the reconstruction using the normal operator, .
Theorem 3.3.
Therefore, recovers most singularities of , as indicated in the first term in (3.15), but it adds two sets of nonlocal singularities, as given by and . Note that, even if and are both elliptic above a covector , artifacts caused by other points could mask singularities of that “should” be visible in .
Proof.
Let . By the Hörmander-Sato Lemma [25, Theorem 8.2.13] We have the expansion
| (3.17) | ||||
The first term in brackets in (3.17) is . This proves the first part of the inclusion (3.15).
We now analyze the other two terms to define the functions and finish the proof. Let . First, consider .111For convenience, we will abbreviate the set theoretic composition by . Using the calculations in the proof of Theorem 3.2 one sees that is given by
| (3.18) |
where we have taken these from the proof of Theorem 3.2. To find we calculate the composition of the covector described in (3.18) with . Note that the values of and are the same in both calculations and are given by (3.18). After using (3.8) and that , one sees that
| (3.19) | ||||
where and are given in (3.18) and is calculated using the expression (3.8) with .
Note that the function is defined for only some ; for example if the argument for the square root defining is negative, then is not defined and the point will not generate artifacts in .
A similar calculation shows for that
| (3.20) | ||||
where
Note that the function is not defined for all , and other points do not generate artifacts. This is for the same reason as for . ∎
Remark 3.4.
The artefacts caused by a singularity of are as strong as the reconstruction of that singularity. To see this, first note that each smooths of order one in Sobolev scale since it an FIO of order [24, Theorem 4.3.1].
The visible singularities in the reconstruction come from the compositions and since these are pseudodifferential operators of order . The artefacts come from the “cross” compositions and , and they are FIO of order . Therefore, since the terms that preserve the real singularities of , , , are also of order , smooths each singularity of by one order in Sobolev scale and the composition (corresponding to the artifact , if defined at this covector) can create an artefact from that singularity that are also one order smoother than that singularity, and similarly with the composition .
Second, our results are valid, not only for the normal operator but for any filtered backprojection method where is a pseudodifferential operator. This is true since pseudodifferential operators have canonical relation and they do not move singularities, so our microlocal calculations are the same. If has order , then decreases the Sobolev order of each singularity of by order in Sobolev norm and can create an artefact from that singularity of the same order.
3.2. Artifacts for due to limited data
In practice we do not have access to for all (or ) and , and will have knowledge of and for some (see figures 1 and 2) and maximum radius .
We now evaluate which wavefront directions will be visible from this limited data. Let us consider the pair and let be the angle of from the vertical as depicted in figure 2. Then and
Let be defined by
| (3.21) |
(noting that we only consider such that ). Then the maximum directional coverage of the singularities (wavefront set) at a given which are resolved by the Compton data are described by the open cone of
| (3.22) |
and the opening angle of the cone depends on the depth of (i.e. ). See figure 2. The cone illustrated corresponds to the case when .
In all of our numerical experiments, we set the tunnel height as and the detector line width is . We let be large enough to penetrate the entire scanning tunnel (up to the line as highlighted in figures 1 and 2), so as to imply a unique reconstruction [55]. Specifically we set the maximum radius and simulate for and . Further the densities considered are represented on ( pixel grid) in the reconstructions shown. The machine design considered is such that for any we have the maximal directional coverage in allowed for the limited (see figure 7). With the exception of the horizontal bar phantom depicted in figure 14, all objects considered for reconstruction are approximately in this region.






To demonstrate the artefacts, we apply a discrete form of to a delta function. We have the expansion
| (3.23) |
Using equations (3.18), (3.19), and (3.20) one can show for that the backprojection operators , can be written
| (3.24) |
Note that we are not restricting to but we are restricting to , and hence the cutoff function of equation 3.14 is equal to one on the bounds of integration.
Now, let be a delta function at . We calculate the artifacts
| (3.25) |
where , and . Similarly
| (3.26) |
where , and . Hence the only contributions to the backprojection from and are on the following sets:
| (3.27) |
where and and
| (3.28) |
where and . This means that all artifacts will be in these sets. Note that besides the artifacts shown in figure 4(e) and 4(f) there are limited data artifacts caused by circles meeting of radius (figures 4(a)-4(c)) and these are of higher strength in Sobolev norm.






To simulate a function discretely we assign a value of 1 to nine neighbouring pixels in a 200–200 grid (which will represent ) and set all other pixel values to zero. Letting our discrete delta function be denoted by , we approximate , where is the discrete form of . For comparison we show images of
a characteristic function on the set , and the artefacts induced by and . Here is the discrete form of , for . See figure 3. For example, in figure 3(b) we see a butterfly wing type artefact in . This is due to the limited and data inherent to our acquisition geometry (there are unresolved wavefront directions). In the image of figure 3(c) we see artefacts appearing on the set as shown in figure 3(d). This is as predicted by our theory. The artefacts induced by the in this case lie outside the scanning region (), and hence they are not observed in the reconstruction. See figures 3(e) and 3(f). In figure 4 the artefact curves intersect in the top left and right-hand corners respectively. See figures 4(e) and 4(f). In this case the artefacts are observed faintly in the reconstructions (their magnitude is small compared to the delta function), and it is unclear whether they align with our predictions.





To show the artefacts induced by the more clearly, we repeat the analysis above using filtered backprojection, and a second derivative filter . That is we show images of . Note that is applied in the variable (the torus radius). The application of derivative filters is a common idea in lambda tomography [13, 14], and is known to highlight the image contours (singularities or edges) in the reconstruction [43, Theorem 3.5]. See figure 5. As the artefacts induced by appeared to be largely outside the scanning region () in our previous simulations, we have increased the scanning region size to , to show more the effects of the in the observed reconstruction. Here suppresses the artefacts due to limited data, and the artefacts appear as additional contours in the reconstruction. The observed artefacts appear most clearly in figures 5(b) and 5(e), and align exactly with our predictions in figures 5(c) and 5(f).
Remark 3.5.
With precise knowledge of the locations of the artefacts induced by the we can assist in the design of the proposed parallel line scanner. That is we can choose , and the scanning tunnel size to minimize the presence of the nonlocal artefacts in the reconstruction (i.e., those from ). Such advice would be of benefit to our industrial partners in airport screening to remove the concern for nonlocal artefacts in the image reconstruction of baggage. Indeed the machine dimensions we have chosen seem to be suitable as the artefacts appear largely outside the reconstruction space (see figures 3 and 4).
4. The transmission artefacts
The detector row collects Compton (back) scattered data, which determines for a range of and , where is the electron charge density. The forward detector array collects transmission (standard X-ray CT) data, which determine a set of straight line integrals over the attenuation coefficient , for some photon energy . The data is limited to the set of lines which intersect (the source array) and . This limited data can cause artefacts in the X-ray reconstruction, and we will analyze these artefacts using the theory in [5]. Let be the line parameterized by a rotation and a directed distance from the origin . Here and is the line containing and perpendicular to .
In the scanning geometry of this article, the set of X-ray transmitters is the segment between and and the set of X-ray detectors, , is the segment between and as in figure 1. For this reason, the cutoff in the sinogram space is described by the set
| (4.1) |
The characteristic function of appears as a skewed diamond shape in sinogram space.
To illustrate the added artifacts inherent in this incomplete data problem, we simulate reconstructions of delta functions with transmission CT data on . That is, we apply the backprojection operator to functions, where denotes for . See figure 6.



By the theory in [5], artefacts caused by the incomplete data occur on lines for in the boundary of . Each delta function in Figure 6 is at a point for some with , so the lines that meet the support of the delta function, that are in the boundary of must also contain either or . This is true because and are mirror images about the line and .
Furthermore, by symmetry (the functions are on the center line of the scanning region), these artifact lines will be reflections of each other in the vertical line . This is illustrated in our reconstructions in Figure 6. The opening angle of the cone in the delta reconstructions decreases (fewer wavefront set directions are stably resolved) as we translate to the right on the line .
Example 4.1.
We now use these ideas to analyze the visible wavefront directions for the joint problem. Let be the square between and and let , the center of . We consider wavefronts at points which is a square centered at and the region in which our simulated reconstructions are done.
By (4.1), lines in the data set must intersect both and , so lines through in the data set are all lines through that are more vertical than the diagonals of . Because visible wavefront directions are normal to lines in the X-ray CT data set [38], the wavefront directions which are resolved lie in the horizontal open cone between normals to these diagonals. Therefore, they are in the cone
which is shown in figure 1.
An analysis of the singularities that are visible by the Compton data was done in section 3.2. For the point , the angle defined by (3.21) gives and the cone of visible directions given by (3.22) is the vertical cone with angles from the vertical between and since the parameter . A calculation shows that and this implies and we have a full resolution of the image singularities at .

However, for points near the bottom , there are invisible singularities that are not visible from either the Compton or X-ray data. For example, the vertical direction is not normal to any circle in the Compton data set at any point for . Figure 7 shows the points for which all wavefront directions are visible at those points (yellow color–roughly for points for ) and near the bottom of the reconstruction region, there are more missing directions.
5. A joint reconstruction approach and results
In this section we detail our joint reconstruction scheme and lambda tomography regularization technique, and show the effectiveness of our methods in combatting the artefacts observed and predicted by our microlocal theory. We first explain the physical relationship between and , which will be needed later in the formulation of our regularized inverse problem.
5.1. Relating and
The attenuation coefficient and electron density satisfy the formula [53, page 36]
| (5.1) |
where denotes the electron cross section, at energy . Here denotes the effective atomic number. In the proposed application in airport baggage screening (among many other applications such as medical CT) we are typically interested in the materials with low effective . Hence we consider the materials with in this paper. For large enough and , is approximately constant as a function of . Equivalently and are approximately proportional for low and high by equation 5.1. See figure 8. We see a strong correlation between and when keV and , and even more so when is increased to MeV. The sample of materials considered consists of 153 compounds (e.g. wax, soap, salt, sugar, the elements) taken from the NIST database [29]. In this case for some is approximately constant and we have .


5.2. Lambda regularization; the idea
In sections 3 and 4 we discovered that the and data provide complementary information regarding the detection and resolution of edges in an image. More specifically the line integral data resolved singularities in an open cone with central axis and the toric section integral data resolved singularities in a cone with central axis . So the overlapping cones give a greater coverage of than when considered separately. In figures 3, 4 and 6, this theory was later verified through reconstructions of a delta functions by (un)filtered backprojection.
For a further example, let us consider a more complicated phantom than a delta function, one which is akin to densities considered later for testing our joint reconstruction and lambda regularization method. In figure 9 we have presented reconstructions of an image phantom (with no noise) from (transmission data–middle figure) using FBP, and from (Compton data–right figure) by an application of (a contour reconstruction). In the reconstruction from Compton data, we see that the image singularities are well resolved in the vertical direction (), and conversely in the horizontal direction () in the reconstruction from transmission data. In the middle picture (reconstruction from ), the visible singularities of the object are tangent to lines in the data set (normal wavefront set) and the artifacts are along lines at the end of the data set that are tangent to boundaries of the objects. In the right-hand reconstruction from Compton data, the visible boundaries are tangent to circles in the data set and the streaks are along circles at the end of the data set. Note that the visible boundaries in each picture complement each other and together, image the full objects. This is all as predicted by the theory of sections 3 and 4 (and is consistent with the theory in [5] and [15]) and highlights the complementary nature of the Compton and transmission data in their ability to detect and resolve singularities.
Given the complementary edge resolution capabilities of and , and given the approximate linear relationship between and , we can devise a joint linear least squares reconstruction scheme with the aim to recover the image singularities stably in all directions in the and images simultaneously.



To this end we employ ideas in lambda tomography and microlocal analysis.
Let and let denote the hyperplane Radon transform of , where is as defined in section 4. The Radon projections detect singularities in in the direction (i.e. the elements ). Applying a derivative filter , for some , increases the strength of the singularities in the direction by order in Sobolev scale.




Given , we aim to enforce a similarity in and through the addition of the penalty term to the least squares solution. Note that we are integrating over all directions in to enforce a full directional similarity in and . Specifically in our case , and we aim to minimize the quadratic functional
| (5.2) |
where denotes a discrete, limited data Radon operator, is the discrete form of the full data Radon operator, is the discrete form of the toric section transform, is known transmission data and is the Compton scattered data. Here is a regularization parameter which controls the level of similarity in the image wavefront sets. The lambda regularizers enforce the soft constraint that (since for ), but with emphasis on the location, direction and magnitude of the image singularities in the comparison.
| TV | JLAM | JTV | LPLS | |
|---|---|---|---|---|
| -score | TV | JLAM | JTV | LPLS |
|---|---|---|---|---|
| JLAM | JTV | LPLS | |
|---|---|---|---|
| JLAM | JTV | LPLS | |
|---|---|---|---|
Further we expect the lambda regularizers to have a smoothing effect given the nature of as a differential operator (i.e. the inverse is a smoothing operation). Hence we expect to also act as a smoothing parameter. The weighting is included so as to give equal weighting to the transmission and scattering datasets in the inversion. We denote the joint reconstruction method using lambda tomography regularizers as “JLAM”. A common choice for in lambda tomography applications is [7, 43] (hence the name “lambda regularizers”).
| Density | Attenuation , keV | |
|---|---|---|
|
TV |
 |
 |
|
JLAM |
 |
 |
|
JTV |
 |
 |
|
LPLS |
 |
 |
With complete X-ray data, the application of a Lambda term yields this [31, Example 9], so the singularities of are preserved and emphasized by order in Sobolev scale, so they will dominate the Lambda reconstruction. Hence choosing is sufficient for a full recovery of the image singularities. Since the singularities are dominant in the lambda term, they are matched accurately in (5.2). Indeed we have already seen the effectiveness of such a filtering approach in recovering the image contours earlier in the right hand of figure 9. We find that setting here works well as a regularizer on synthetic image phantoms and simulated data with added pseudo random noise, as we shall now demonstrate. We note that the derivative filters for are also worth exploration but we leave such analysis for future work.
5.3. Proposed testing and comparison to the literature
To test our reconstruction method, we first consider two test phantoms, one simple and one complex (as in [55]). See figure 11. The phantoms considered are supported on , the region in figure 7 in which there is full wavefront coverage from joint X-ray and Compton scattered data. The simple density phantom consists of a Polyvinyl Chloride (PVC) cuboid and an Aluminium sphere with an approximate density ratio of 1:2 (PVC:Al). The complex density phantom consists of a water ellipsoid, a Sulfur ellipsoid, a Calcium sulfate () right-angled-triangle and a thin film of Titanium dioxide () in the shape of a cross. The density ratio of the materials which compose the complex phantom is approximately 1:2:3:4 (:S::). The density values used are those of figure 8 taken from the NIST database [28], and the background densities () were set to the density of dry air (near sea level). The corresponding attenuation coefficient phantoms are simulated similarly. The materials considered are widely used in practice. For example is used in the production of plaster of Paris and stucco (a common construction material) [57], and is used in the making of decorative thin films (e.g. topaz) and in pigmentation [56, page 15].
To simulate data we set
| (5.3) |
and add a Gaussian noise
| (5.4) |
for some noise level , where is the length of and is a vector of length of draws from . For comparison we present separate reconstructions of and using Total Variation (TV regularizers). That is we will find
| (5.5) |
to reconstruct and
| (5.6) |
for , where and is a regularization parameter. We will denote this method as “TV”. In addition we present reconstructions using the state-of-the-art joint reconstruction and regularization techniques from the literature, namely the Joint Total Variation (JTV) methods of [20] and the Linear Parallel Level Sets (LPLS) methods of [12]. To implement JTV we minimize
| (5.7) |
where as before, and
| (5.8) |
where is an additional hyperparameter included so that the gradient of is defined at zero. This allows one to apply techniques in smooth optimization to solve (5.7).
| Density | Attenuation , keV | |
|---|---|---|
|
TV |
 |
 |
|
JLAM |
 |
 |
|
JTV |
 |
 |
|
LPLS |
 |
 |
To implement LPLS we minimize
| (5.9) |
where
| (5.10) |
where and for . The JTV and LPLS penalties seek to impose soft constraints on the equality of the image wavefront sets of and . For example setting in the calculation of yields
| (5.11) |
where is the angle between and . Hence (5.11) is minimized for the gradients which are parallel (i.e. when ), and thus using as regularization serves to enforce equality in the image gradient direction and location (i.e. when is small, the gradient directions are approximately equal).
We wish to stress that the comparison with JTV and LPLS is included purely to illustrate the potential advantages (and disadvantages) of the lambda regularizers when compared to the state-of-the-art regularization techniques. Namely is the improvement in image quality due to joint data, lambda regularizers or are they both beneficial? We are not claiming a state-of-the-art performance using JLAM, but our results show JLAM has good performance, and it is numerically easier to implement, requiring only least squares solvers. There are two hyperparameters ( and ) to be tuned in order to implement JTV and LPLS, which is more numerically intensive (e.g. using cross validation) in contrast to JLAM with only one hyperparameter (). Moreover the LPLS objective is non-convex [12, appendix A], and hence there are potential local minima to contend with, which is not an issue with JLAM, being a simple quadratic objective.
| TV | JLAM | JTV | LPLS | |
|---|---|---|---|---|
| -score | TV | JLAM | JTV | LPLS |
|---|---|---|---|---|
| JLAM | JTV | LPLS | |
|---|---|---|---|
| JLAM | JTV | LPLS | |
|---|---|---|---|
To minimize (5.2), we store the discrete forms of , and as sparse matrices and apply the Conjugate Gradient Least Squares (CGLS) solvers of [22, 23] (specifically the “IRnnfcgls” code) with non-negativity constraints (since the physical quantities and are known a-priori to be nonnegative). To solve equations (5.5) and (5.6) we apply the heuristic least squares solvers of [22, 23] (specifically the “IRhtv” code) with TV penalties and non-negativity constraints. To solve (5.7) and (5.9) we apply the codes of [12], modified so as to suit a Gaussian noise model (a Poisson model is used in [12, equation 3]). The relative reconstruction error is calculated as , where is the ground truth image and is the reconstruction. For all methods compared against we simulate data and added noise as in equations (5.3) and (5.4), and the noise level added for each simulation is ( noise). We choose for each method such that is minimized for a noise level of . That is we are comparing the best possible performance of each method. We set for JTV and LPLS to the values used on the “lines2” data set of [12]. We do not tune to the best performance (as with ) so as to give fair comparison between TV, JLAM, JTV and LPLS. After the optimal hyperparameters were selected, we performed 100 runs of TV, JLAM, JTV and LPLS on both phantoms for 100 randomly selected sets of materials. That is, for 100 randomly chosen sets of values from figure 8 and the NIST database, with the NIST values corresponding to the nonzero parts of the phantoms. We present the mean () and standard deviation () relative errors over 100 runs in the left-hand of tables 2 and 4 for the simple and complex phantom respectively. The results are given in the form for each method. In addition to the relative error , we also provide metrics to measure the structural accuracy of the results. Specifically we will compare -scores on the image gradient and support, as is done in [49, 2]. The gradient -score [2] measures the wavefront set reconstruction accuracy, and the support -score [49, page 5] (see DICE score) is a measure of the geometric accuracy. That is, the support -score checks whether the reconstructed phantoms are the correct shape and size. The -score takes values on . For this metric, values close to one indicate higher performance, and conversely for values close to zero. Similarly to , we present the -scores of the randomized tests in the form , where and are the mean and standard deviation -scores respectively. In all tables, the support -scores are labelled by and , and by and for the gradient -scores.
5.4. Results and discussion
See figure 11 for image reconstructions of the simple phantom using TV, JLAM, JTV and LPLS, and see table 1 for the corresponding and -score values. See table 2 for the and values calculated over 100 randomized simple phantom reconstructions. For the complex phantom, see figure 12 for image reconstructions, and table 3 for the and -score values. See table 4 for and . In the separate reconstruction of (using method TV) we see a blurring of the ground truth image edges (wavefront directions) in the horizontal direction and there are artefacts in the reconstruction due to limited data, as predicted by our microlocal theory. In the TV reconstruction of we see a similar effect, but in this case we fail to resolve the wavefront directions in the vertical direction due to limited line integral data. This is as predicted by the theory of section 4 and [5].


In section 3 we discovered the existence also of nonlocal artefacts in the reconstruction, which were induced by the mappings . However these were found to lie largely outside the imaging space unless the singularity in question were such that is close to the detector array (see figures 3 and 4). Hence why we do not see the effects of the in the phantom reconstructions, as the phantoms are bounded sufficiently away from the detector array. The added regularization may smooth out such artefacts also, which was found to be the case in [55].
Using the joint reconstruction methods (i.e. JLAM, JTV and LPLS) we see a large reduction in the image artefacts in and , since with joint data we are able to stably resolve the image singularities in all directions. The improvement in and the -score is also significant, particularly in the reconstruction. Thus it seems that the joint data is the greater contributor (over the regularization) to the improvement in the image quality, as the approaches with joint data each perform well.
| Density | Attenuation , keV | |
|---|---|---|
|
TV |
 |
 |
|
JLAM |
 |
 |
|
JTV |
 |
 |
|
LPLS |
 |
 |
Upon comparison of JLAM, JTV and LPLS, the metrics are significantly improved when using JTV and LPLS over JLAM, but the image quality and -scores are highly comparable. This indicates that, while the noise in the reconstruction is higher using JLAM, the recovery of the image edges and support is similar using JLAM, JTV and JLAM. As theorized, the lambda regularizers were successful in preserving the wavefront sets of and . However there is a distortion present in the nonzero parts of the JLAM reconstruction. This is the most notable difference in JLAM and JTV/LPMS, and is likely the cause of the discrepancy. So while the edge preservation and geometric accuracy of JLAM is of a high quality (and this was our goal), the smoothing properties of JLAM are not up to par with the state-of-the-art currently. We note however that the JTV and LPLS objectives are nonlinear (with LPLS also non-convex) and require significant additional machinery (e.g. in the implementation of the code of [12] used here) in the inversion when compared to JLAM, which is a straight forward implementation of linear least squares solvers.
| TV | JLAM | JTV | LPLS | |
|---|---|---|---|---|
| -score | TV | JLAM | JTV | LPLS |
|---|---|---|---|---|
| JLAM | JTV | LPLS | |
|---|---|---|---|
| JLAM | JTV | LPLS | |
|---|---|---|---|
5.5. Reconstructions with limited data
The simple and complex phantoms considered thus far are supported within (the yellow region of figure 7) so as to allow for a full wavefront coverage in the reconstruction. To investigate what happens when the object is supported outside of , we present additional reconstructions of an Aluminium bar phantom with support towards the bottom (close to ) of the reconstruction space. See figure 13. In this case we have limited data and the full wavefront coverage is not available with the combined X-ray and Compton data sets. Image reconstructions of the Al bar phantom are presented in figure 14, and the corresponding and -score values are displayed in table 5. See table 4 for the and values corresponding to the randomized bar phantom reconstructions. In this case and were calculated from reconstructions of 153 bar phantoms (we used 100 runs previously), replacing the Al density value of figure 13 with one of each NIST value considered (153 in total). The reconstruction processes and hyperparameter selection applied here were exactly the same as for the simple and complex phantom. In this case we see artefacts in the Compton reconstruction along curves which follow the shape of the boundary of , and the X-ray artefacts constitute a vertical blurring as before. The error when using JLAM, JTV and LPLS is more comparable in this example (compared to tables 1 and 3), particularly in the case of the phantom. The image quality and -scores are again similar as with the simple and complex phantom examples. All joint reconstruction methods were successful in removing the image artefacts observed in the separate reconstructions, and thus can offer satisfactory image quality under the constraints of limited data. However this is only a single test of the capabilities of JLAM, JTV and LPLS with limited data and we leave future work to conclude such analysis.
6. Conclusions and further work
Here we have introduced a new joint reconstruction method “JLAM” for low effective imaging (), based on ideas in lambda tomography. We considered primarily the “parallel line segment” geometry of [54], which is motivated by system architectures for airport security screening applications. In section 3 we gave a microlocal analysis of the toric section transform , which was first proposed in [54] for a CST problem. Explicit expressions were provided for the microlocal artefacts and verified through simulation. Section 4 explained the X-ray CT artefacts using the theory of [5]. Following the theory of sections 3 and 4, we detailed the JLAM algorithm in section 5. Here we conducted simulation testing and compared JLAM to separate reconstructions using TV, and to the nonlinear joint inversion methods, JTV [20] and LPLS [12] from the literature. The joint inversion methods considered (i.e. JLAM, JTV and LPLS) were successful in preserving the image contours in the reconstruction, as predicted. However the smoothing applied by JLAM was not as effective as JTV and LPLS, and we saw a distortion in the JLAM reconstruction (see figures 11 and 12). JTV and LPLS were thus shown to offer better performance than JLAM, with LPLS producing the best results overall. The advantages of JLAM over JTV and LPLS are in the fast, linear inversion, and the reduction in tuning parameters (one for JLAM, two for JTV/LPLS). Given the linearity of JLAM, the ideas of JTV and LPLS can be easily integrated with lambda regularization to modify the objectives of the literature and improve further the edge resolution of the reconstruction. To preserve the linearity of JLAM we could also combine JLAM with a Tikhonov regularizer. This may help smooth out the distortion observed in the JLAM reconstruction. We leave such ideas for future work.
Acknowledgements
We would like to thank the journal reviewers for their helpful comments and insight towards this article, particularly in regards to the simulation study. This material is based upon work supported by the U.S. Department of Homeland Security, Science and Technology Directorate, Office of University Programs, under Grant Award 2013-ST-061-ED0001. The views and conclusions contained in this document are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of the U.S. Department of Homeland Security. The work of the second author was partially supported by U.S. National Science Foundation grant DMS 1712207. The authors thank the referees for thorough reviews and thoughtful comments that improved the article.
References
- [1] A. Aghasi, I. Mendoza-Sanchez, E. L. Miller, C. A. Ramsburg, and L. M. Abriola. A geometric approach to joint inversion with applications to contaminant source zone characterization. Inverse problems, 29(11):115014, 2013.
- [2] H. Andrade-Loarca, G. Kutyniok, and O. Öktem. Shearlets as feature extractor for semantic edge detection: The model-based and data-driven realm. arXiv preprint arXiv:1911.12159, 2019.
- [3] S. R. Arridge, M. Burger, and M. J. Ehrhardt. Preface to special issue on joint reconstruction and multi-modality/multi-spectral imaging. Inverse Problems, 36(2):020302, 2020.
- [4] P. Blomgren and T. F. Chan. Color tv: total variation methods for restoration of vector-valued images. IEEE Transactions on Image Processing, 7(3):304–309, 1998.
- [5] L. Borg, J. Frikel, J. S. Jørgensen, and E. T. Quinto. Analyzing reconstruction artifacts from arbitrary incomplete x-ray ct data. SIAM Journal on Imaging Sciences, 11(4):2786–2814, 2018.
- [6] T. A. Bubba, G. Kutyniok, M. Lassas, M. Maerz, W. Samek, S. Siltanen, and V. Srinivasan. Learning the invisible: A hybrid deep learning-shearlet framework for limited angle computed tomography. Inverse Problems, 2019.
- [7] A. S. Denisyuk. Inversion of the generalized Radon transform. In Applied problems of Radon transform, volume 162 of Amer. Math. Soc. Transl. Ser. 2, pages 19–32. Amer. Math. Soc., Providence, RI, 1994.
- [8] J. J. Duistermaat. Fourier integral operators, volume 130 of Progress in Mathematics. Birkhäuser, Inc., Boston, MA, 1996.
- [9] J. J. Duistermaat and L. Hormander. Fourier integral operators, volume 2. Springer, 1996.
- [10] M. J. Ehrhardt and S. R. Arridge. Vector-valued image processing by parallel level sets. IEEE Transactions on Image Processing, 23(1):9–18, 2013.
- [11] M. J. Ehrhardt and M. M. Betcke. Multicontrast mri reconstruction with structure-guided total variation. SIAM Journal on Imaging Sciences, 9(3):1084–1106, 2016.
- [12] M. J. Ehrhardt, K. Thielemans, L. Pizarro, D. Atkinson, S. Ourselin, B. F. Hutton, and S. R. Arridge. Joint reconstruction of PET-MRI by exploiting structural similarity. Inverse Problems, 31(1):015001, dec 2014.
- [13] A. Faridani, D. Finch, E. L. Ritman, and K. T. Smith. Local tomography, II. SIAM J. Appl. Math., 57:1095–1127, 1997.
- [14] A. Faridani, E. L. Ritman, and K. T. Smith. Local tomography. SIAM J. Appl. Math., 52:459–484, 1992.
- [15] J. Frikel and E. T. Quinto. Artifacts in incomplete data tomography with applications to photoacoustic tomography and sonar. SIAM J. Appl. Math., 75(2):703–725, 2015.
- [16] L. A. Gallardo and M. A. Meju. Joint two-dimensional dc resistivity and seismic travel time inversion with cross-gradients constraints. Journal of Geophysical Research: Solid Earth, 109(B3), 2004.
- [17] L. A. Gallardo and M. A. Meju. Joint two-dimensional cross-gradient imaging of magnetotelluric and seismic traveltime data for structural and lithological classification. Geophysical Journal International, 169(3):1261–1272, 2007.
- [18] V. Guillemin and S. Sternberg. Geometric Asymptotics. American Mathematical Society, Providence, RI, 1977.
- [19] H. E. Guven, E. L. Miller, and R. O. Cleveland. Multi-parameter acoustic imaging of uniform objects in inhomogeneous soft tissue. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 59(8):1700–1712, 2012.
- [20] E. Haber and M. H. Gazit. Model fusion and joint inversion. Surveys in Geophysics, 34(5):675–695, 2013.
- [21] P. C. Hansen. Rank-deficient and discrete ill-posed problems: numerical aspects of linear inversion, volume 4. Siam, 2005.
- [22] P. C. Hansen. Regularization Tools version 4.0 for Matlab 7.3. Numer. Algorithms, 46(2):189–194, 2007.
- [23] P. C. Hansen and J. S. Jø rgensen. AIR Tools II: algebraic iterative reconstruction methods, improved implementation. Numer. Algorithms, 79(1):107–137, 2018.
- [24] L. Hörmander. Fourier Integral Operators, I. Acta Mathematica, 127:79–183, 1971.
- [25] L. Hörmander. The analysis of linear partial differential operators. I. Classics in Mathematics. Springer-Verlag, Berlin, 2003. Distribution theory and Fourier analysis, Reprint of the second (1990) edition [Springer, Berlin].
- [26] L. Hörmander. The analysis of linear partial differential operators. III. Classics in Mathematics. Springer, Berlin, 2007. Pseudo-differential operators, Reprint of the 1994 edition.
- [27] L. Hörmander. The analysis of linear partial differential operators. IV. Classics in Mathematics. Springer-Verlag, Berlin, 2009. Fourier integral operators, Reprint of the 1994 edition.
- [28] J. Hubbell. Photon cross sections, attenuation coefficients and energy absorption coefficients. National Bureau of Standards Report NSRDS-NBS29, Washington DC, 1969.
- [29] J. H. Hubbell and S. M. Seltzer. Tables of x-ray mass attenuation coefficients and mass energy-absorption coefficients 1 kev to 20 mev for elements z= 1 to 92 and 48 additional substances of dosimetric interest. Technical report, National Inst. of Standards and Technology-PL, Gaithersburg, MD (United …, 1995.
- [30] W. A. Kalender. X-ray computed tomography. Physics in Medicine & Biology, 51(13):R29, 2006.
- [31] V. P. Krishnan and E. T. Quinto. Microlocal analysis in tomography. Handbook of mathematical methods in imaging, pages 1–50, 2014.
- [32] A. K. Louis. Combining Image Reconstruction and Image Analysis with an Application to Two-Dimensional Tomography. SIAM J. Img. Sci., 1:188–208, 2008.
- [33] F. Natterer. The mathematics of computerized tomography. Classics in Mathematics. Society for Industrial and Applied Mathematics (SIAM), New York, 2001.
- [34] S. J. Norton. Compton scattering tomography. Journal of applied physics, 76(4):2007–2015, 1994.
- [35] V. Palamodov. An analytic reconstruction for the compton scattering tomography in a plane. Inverse Problems, 27(12):125004, 2011.
- [36] V. P. Palamodov. A uniform reconstruction formula in integral geometry. Inverse Problems, 28(6):065014, 2012.
- [37] E. T. Quinto. The dependence of the generalized Radon transform on defining measures. Trans. Amer. Math. Soc., 257:331–346, 1980.
- [38] E. T. Quinto. Singularities of the X-ray transform and limited data tomography in and . SIAM J. Math. Anal., 24:1215–1225, 1993.
- [39] E. T. Quinto and O. Öktem. Local tomography in electron microscopy. SIAM J. Appl. Math., 68:1282–1303, 2008.
- [40] H. Rezaee, B. Tracey, and E. L. Miller. On the fusion of compton scatter and attenuation data for limited-view x-ray tomographic applications. arXiv preprint arXiv:1707.01530, 2017.
- [41] G. Rigaud. Compton scattering tomography: feature reconstruction and rotation-free modality. SIAM J. Imaging Sci., 10(4):2217–2249, 2017.
- [42] G. Rigaud. 3d compton scattering imaging: study of the spectrum and contour reconstruction. arXiv preprint arXiv:1908.03066, 2019.
- [43] G. Rigaud and B. N. Hahn. 3d compton scattering imaging and contour reconstruction for a class of radon transforms. Inverse Problems, 34(7):075004, 2018.
- [44] W. Rudin. Functional analysis. McGraw-Hill Book Co., New York, 1973. McGraw-Hill Series in Higher Mathematics.
- [45] G. Sapiro and D. L. Ringach. Anisotropic diffusion of multivalued images with applications to color filtering. IEEE transactions on image processing, 5(11):1582–1586, 1996.
- [46] O. Semerci, N. Hao, M. E. Kilmer, and E. L. Miller. Tensor-based formulation and nuclear norm regularization for multienergy computed tomography. IEEE Transactions on Image Processing, 23(4):1678–1693, 2014.
- [47] O. Semerci and E. L. Miller. A parametric level-set approach to simultaneous object identification and background reconstruction for dual-energy computed tomography. IEEE transactions on image processing, 21(5):2719–2734, 2012.
- [48] N. Sochen, R. Kimmel, and R. Malladi. A general framework for low level vision. IEEE transactions on image processing, 7(3):310–318, 1998.
- [49] A. A. Taha and A. Hanbury. Metrics for evaluating 3d medical image segmentation: analysis, selection, and tool. BMC medical imaging, 15(1):29, 2015.
- [50] B. H. Tracey and E. L. Miller. Stabilizing dual-energy x-ray computed tomography reconstructions using patch-based regularization. Inverse Problems, 31(10):105004, 2015.
- [51] T.-T. Truong and M. K. Nguyen. Compton scatter tomography in annular domains. Inverse Problems, 2019.
- [52] E. Vainberg, I. A. Kazak, and V. P. Kurozaev. Reconstruction of the internal three-dimensional structure of objects based on real-time integral projections. Soviet Journal of Nondestructive Testing, 17:415–423, 1981.
- [53] N. Wadeson. Modelling and correction of Scatter in a switched source multi-ring detector x-ray CT machine. PhD thesis, The University of Manchester (United Kingdom), 2011.
- [54] J. Webber and E. Miller. Compton scattering tomography in translational geometries. Technical report, Tufts University, 2019.
- [55] J. Webber and E. T. Quinto. Microlocal analysis of a Compton tomography problem. SIAM Journal on Imaging Sciences, 2020. to appear.
- [56] J. Winkler. Titanium Dioxide: Production, Properties and Effective Usage 2nd Revised Edition. Vincentz Network, 2014.
- [57] F. Wirsching. Calcium sulfate. Ullmann’s encyclopedia of industrial chemistry, 2000.
Appendix A Generating the plots of figure 8
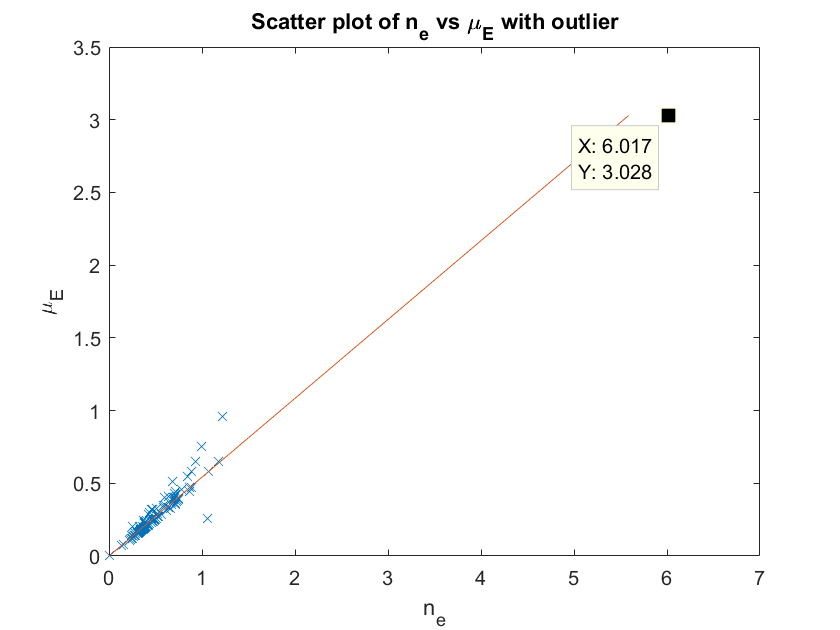
The generation of the plots of figure 8 is explained in more detail here. We will explain the generation of the plot for keV. Refer to figure 15. We first plotted for keV against for all materials in the NIST database [28] with effective less than 20. This is the left hand plot of figure 15. The set of materials with effective was
where is the electron cross section. We noticed a large outlier (coal, or amorphous Carbon) which corrupts the correlation in our favour, and hence we chose to remove the material from consideration in simulation. The outlier is highlighted in the left hand plot. After the outlier was removed we noticed a number of materials located at the origin (with negligible attenuation coefficient and density, such as air) in the middle scatter plot of figure 15. As such materials again bias the correlation and plot standard deviation in our favour, these were removed to produce the left hand plot of figure 8 in the right hand of figure 15. The same points were removed in the generation of the right hand plot of figure 8 also, for MeV.