A generalization of Cardy’s and Schramm’s formulae
Abstract
We study critical site percolation on the triangular lattice. We find the difference of the probabilities of having a percolation interface to the right and to the left of two given points in the scaling limit. This generalizes both Cardy’s and Schramm’s formulae. The generalization involves a new interesting discrete analytic observable and an unexpected conformal mapping.
Keywords: percolation, O(1) model, hypergeometric function, crossing probability
2020 MSC: 60K35, 30C30, 33C05, 81T40, 82B43
1 Introduction
Percolation is an archetypical model of phase transition, used to describe many natural phenomena, from the spread of epidemics to a liquid seeping through a porous medium. It was introduced by Broadbent and Hammersley [1] but appeared even earlier in the problem section of the American Mathematical Monthly [20].
In the simplest setup of Bernoulli percolation, vertices (sites) or edges (bonds) of a graph are independently declared open or closed with probabilities and correspondingly; the resulting model is called site or bond percolation correspondingly. Connected clusters of open sites (or bonds) are then studied. For example, one can ask how the probability of having an open cluster connecting two sets depends on . Despite simple formulation, the model approximates physical phenomena quite well and exhibits a very complicated behavior.
There is an extensive theory, see e.g. [5], but still there are many open questions. For instance, it is not known whether probability of having an infinite open cluster containing origin in depends continuously on .
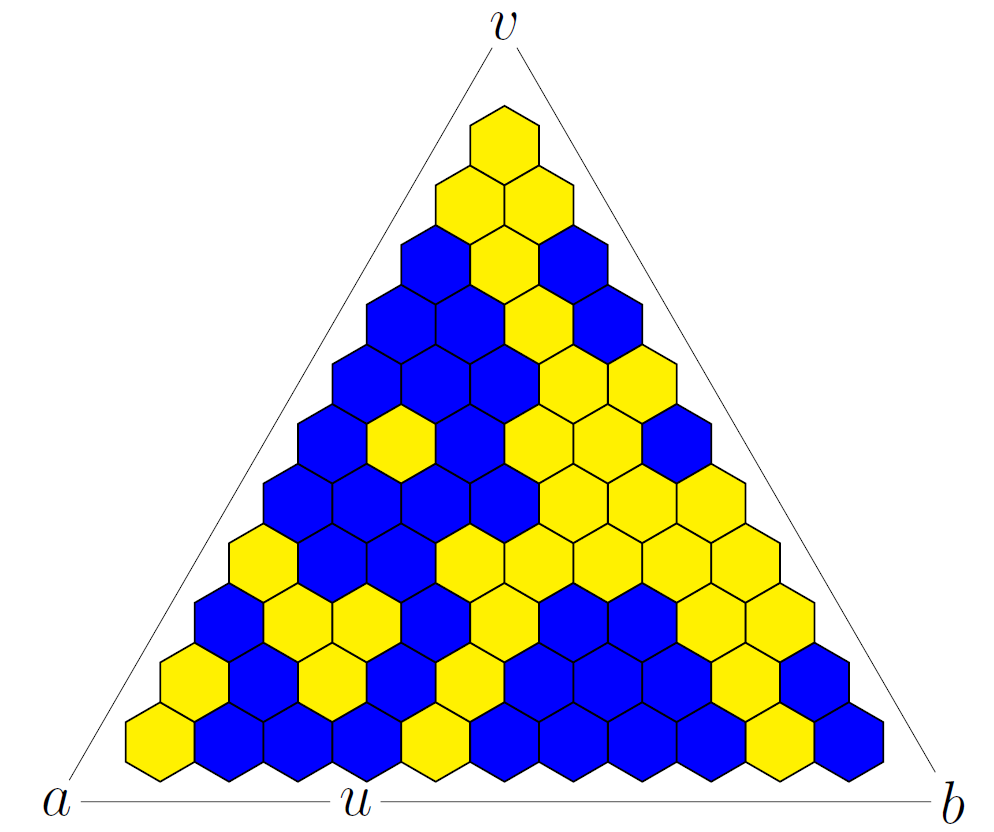
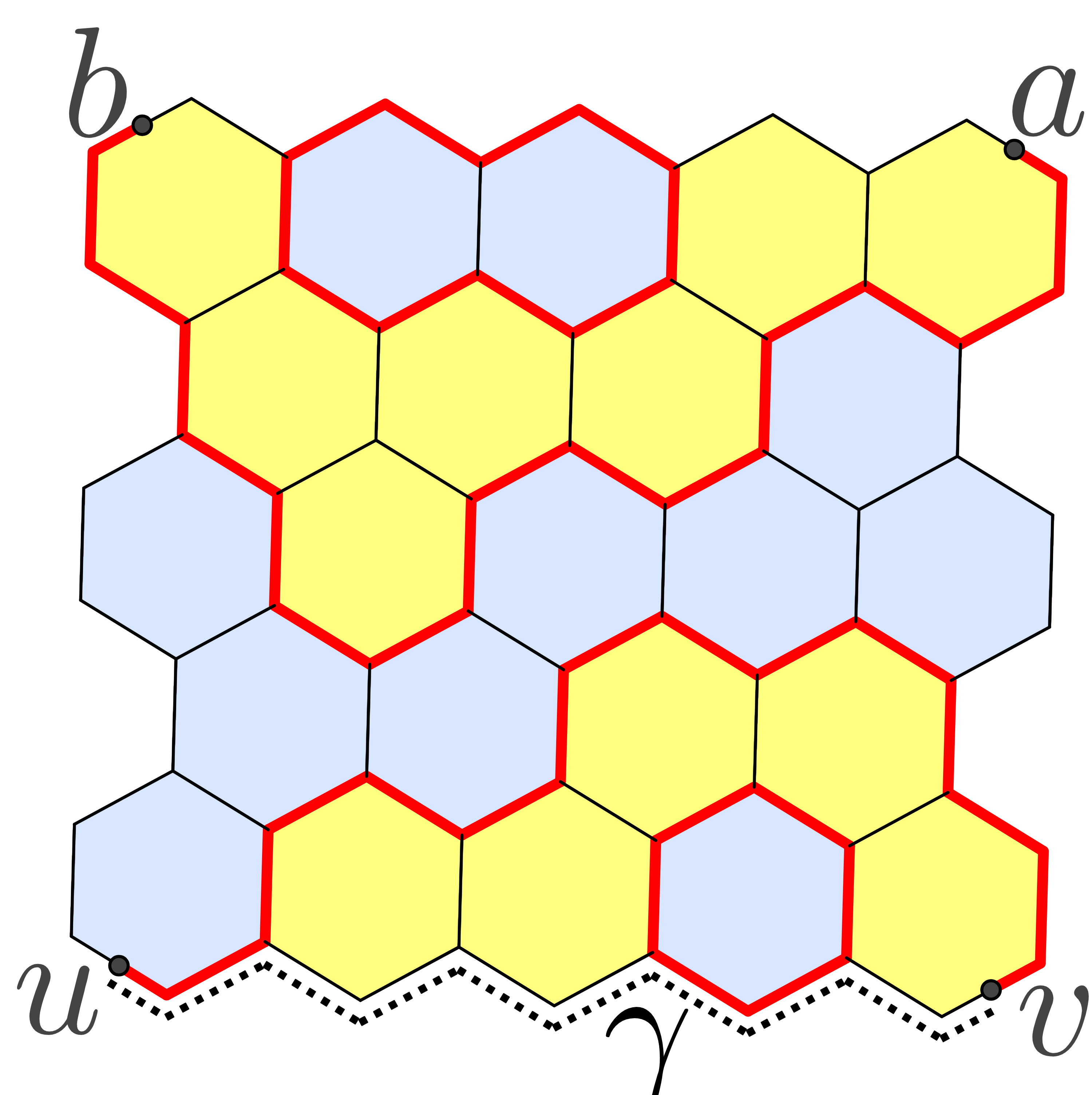
In contrast, planar models are fairly well understood. We will study critical site percolation on the triangular lattice, which by duality can be represented as a random coloring of faces (plaquettes) on the hexagonal lattice; see Figure 1, where open and closed hexagons are represented by blue and yellow colors. For this model, it is known that the critical value is equal to , which was first proved by Kesten using duality; see [5]. This means in particular that when one takes a topological rectangle (i.e. a domain with four marked boundary points) and superimposes a mesh lattice, the crossing probability (i.e. the probability of the existence of an open crossing between the chosen opposite sides) tends to when and to when as . The same argument shows that for the crossing probability is nontrivial, and in 1992 physicist J. Cardy suggested an exact formula for its scaling limit as as a hypergeometric function of the conformal modulus (see Corollary 2.3). The formula is expected to hold for any critical percolation, but so far it was proved only for the model under consideration by the third author [16, 18, 9] by establishing discrete holomorphicity of certain observables.
Henceforth one can connect [17] scaling limits of percolation interfaces between open and closed clusters to Schramm’s SLE(6) curve [13, 14] and deduce many properties, e.g. the values of critical exponents and dimensions [19].
This leaves open the question of how far one can go with purely discrete techniques. For example, in the critical Ising model much can be learned from similar observables without alluding to SLE [6, 3], as is the case for the Uniform Spanning Tree [7, §11.2]. Cf. an elementary example in [12].
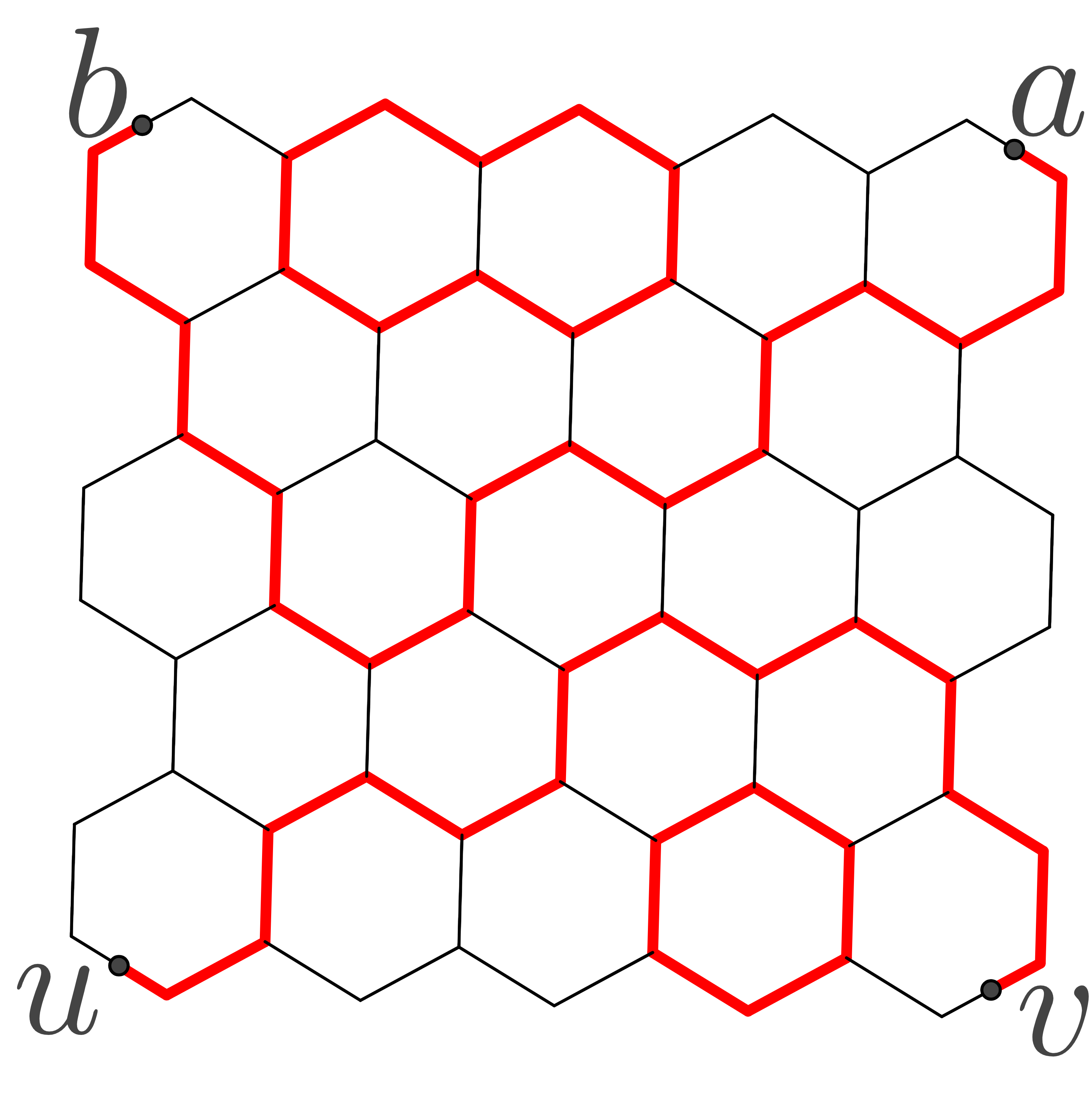
In this paper, we introduce a new percolation observable, which allows us to prove new results and give new proofs to old ones, which beforehand required an SLE limit (see Corollary 2.4). In particular, we find the difference of the probabilities of having a percolation interface to the right and to the left of two given points in the scaling limit (see Figure 2 and Theorem 2.1).
Remarkably, the observable we introduce here is nothing more than a natural generalization of the observable from [9] which itself is just equal to the observable from [16]. However, it seems that getting to the new observable directly from [16] was not as straightforward (and so took a while). It is worth noting that our construction admits further generalizations, at least to the problem with six disorders instead of four [8] and that some appearing functions bear resemblance to modular forms discussed by P. Kleban and D. Zagier [10].
Organization of the paper. In §2 and §3 we state main and auxiliary results respectively. In §4 and Appendix A we prove conceptual and technical ones respectively.
 |
 |
2 Statement
Let us introduce a few definitions to state our result precisely (see Figure 2).
Consider a hexagonal lattice on the complex plane formed by hexagons with side . Let be a domain bounded by a closed smooth curve (that is, is the image of a periodic map with nonzero derivative). A lattice approximation of the domain is the maximal-area connected component of the union of all the hexagons lying inside (if such a connected component is not unique, then we choose any of them). Mark two distinct boundary points and two other points . Their lattice approximations are the midpoints of sides of the hexagons of , closest to respectively (if the closest midpoint is not unique, then we choose any of them). Clearly, . We allow but disallow the coincidence of any other pair among .
The percolation model on is the uniform measure on the set of all the colorings of hexagons of in two colors, say, blue and yellow. Introduce the Dobrushin boundary condition: in addition, paint the hexagons outside bordering upon the clockwise arc of between and blue, and the ones bordering upon the counterclockwise arc yellow (the ones bordering upon and are paint both colors). For the whole coloring, the interface is the oriented simple broken line going from to along the sides of the hexagons of such that all the hexagons bordering upon from the left are blue and all the hexagons bordering upon from the right are yellow.
The interface splits the union of the sides of the hexagons of into connected components. Let (respectively, ) be the probability that and belong to the same component lying to the left (respectively, to the right) from .
Our main result expresses those probabilities in terms of certain conformal mappings. Let be a conformal mapping of onto the upper half-plane (continuously extended to ) taking and to and respectively. Let be the conformal mapping of onto the interior of the rhombus with the vertices , continuously extended to the points and having fixed points . See Figure 3.
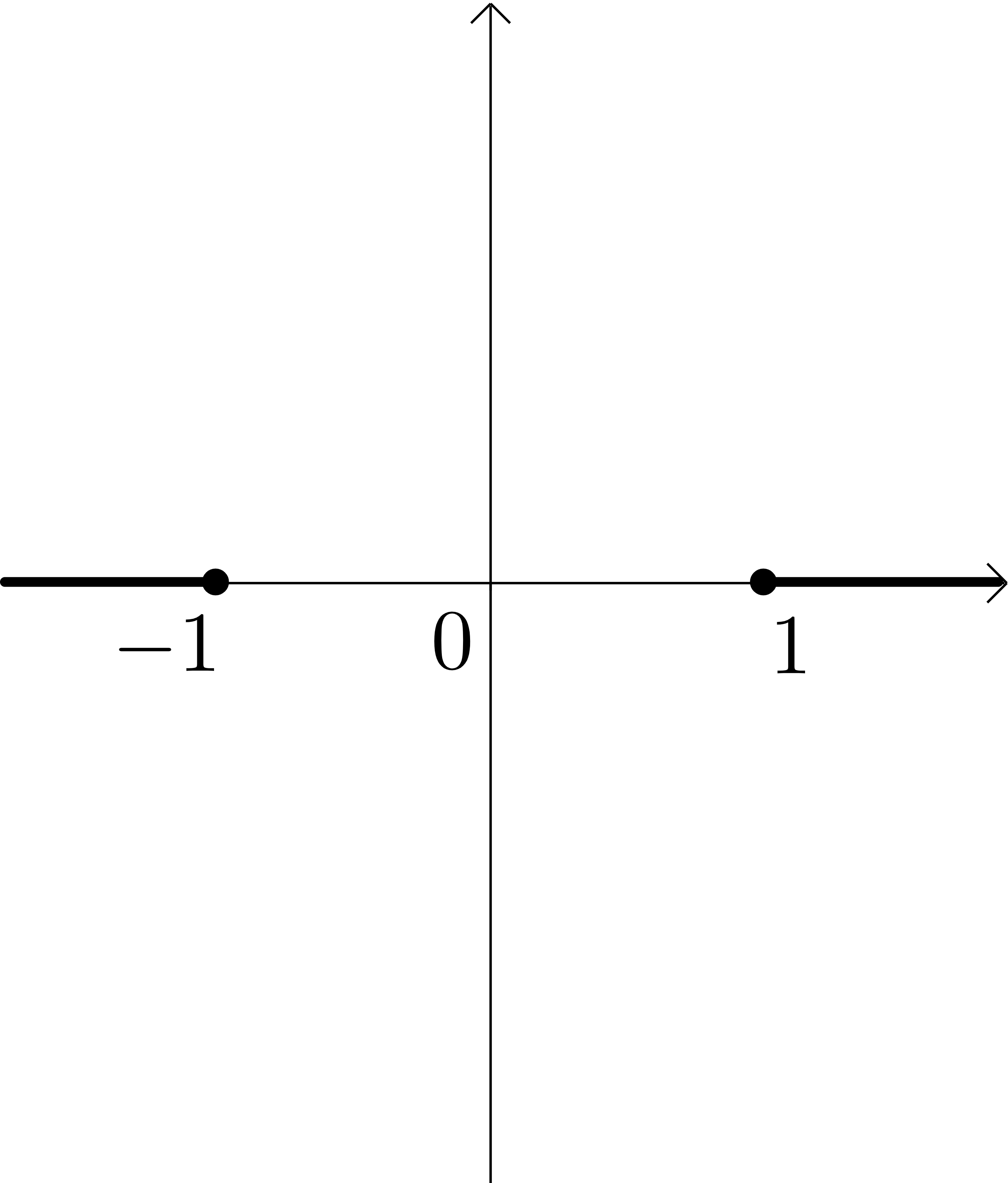
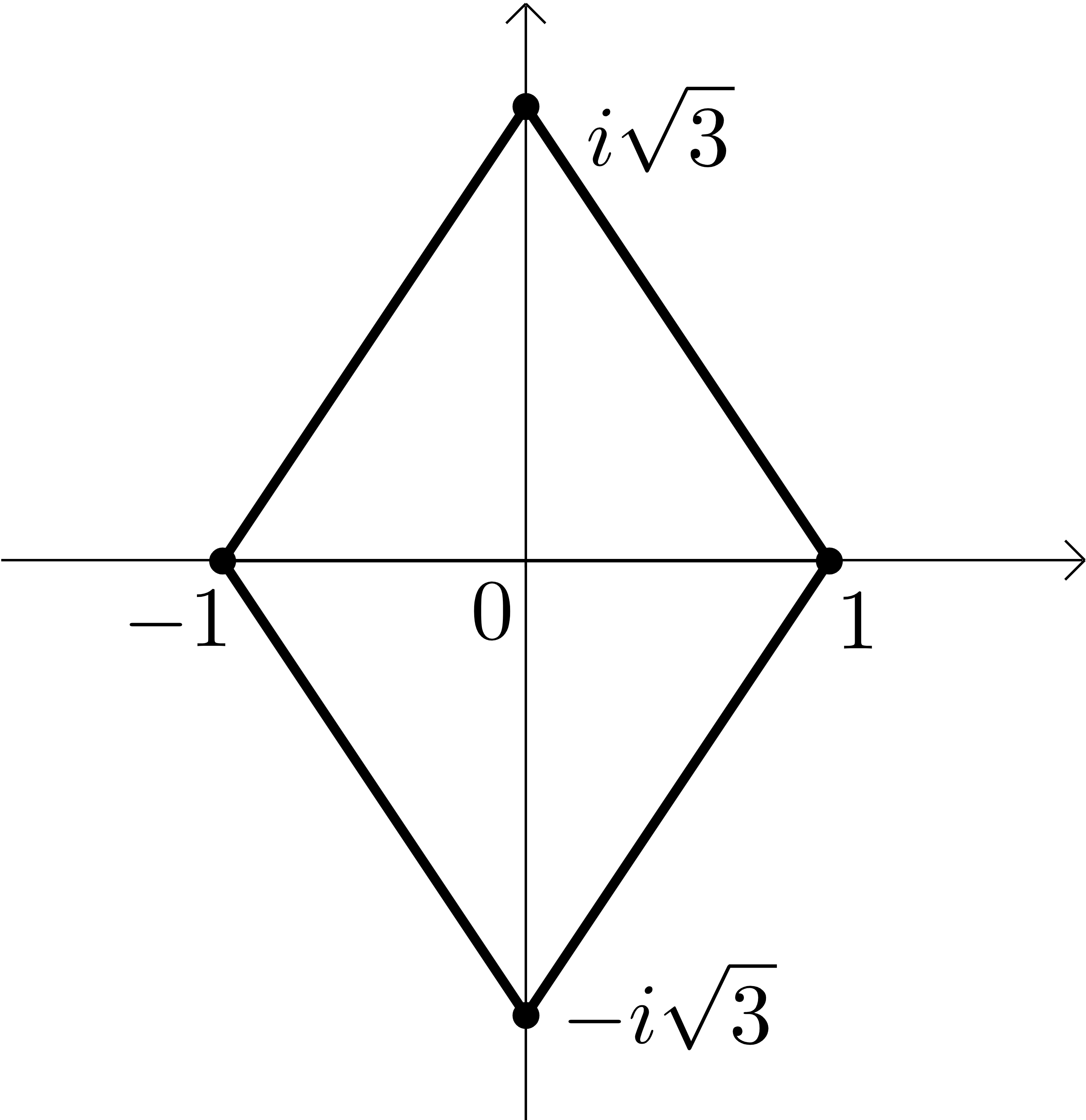
Theorem 2.1.
Let be a lattice approximation of a domain with two marked distinct boundary points and two other points such that is a closed smooth curve. Then
| (1) |
Here if both and belong to the counterclockwise (respectively, clockwise) boundary arc of , then the value of the mapping in (1) is understood as continuously extended from the lower (respectively, upper) half-plane. There is an explicit formula for the mapping .
Proposition 2.2.
We have
| (2) |
Remark.
The real part of has a probabilistic meaning as well; see Theorem 3.2 below.
Remark.
The smoothness of is not really a restriction. Using the methods of [9], one can generalize this result to a Jordan domain (and even an arbitrary bounded simply-connected domain , if is understood as the set of prime ends of and converges to in the Caratheodory sense). However, the message of the paper can be seen already in the simplest particular case .
Remark.
For the theorem gives Cardy’s formula for the crossing probability, and for it gives Schramm’s formula for the surrounding probability. The crossing probability is the probability that some connected component of the union of blue hexagons of has common points with both arcs and of (which means just a blue crossing between the arcs). The surrounding (or right-passage) probability is the probability that belongs to a connected component of the complement bordering upon the interface from the left (which means surrounding of by the interface and the clockwise boundary arc ).
Corollary 2.3 (Cardy’s formula).
[2, Eq. (8)] Let be a lattice approximation of a domain bounded by a closed smooth curve with four distinct marked points lying on the boundary in the counterclockwise order . Then
| (3) |
where is the conformal mapping of onto the equilateral triangle with the vertices (continuously extended to ) taking to the respective vertices.
Corollary 2.4 (Schramm’s formula).
[14, Theorem 1] Let be a lattice approximation of the unit disk with two distinct marked boundary points . Then
| (4) |
While the proof of Theorem 2.1 is similar to the proof of Cardy’s formula from [9], the proof of Schramm’s formula by means of Theorem 2.1 is essentially new, and we think is simpler than the original one. Originally, Schramm’s formula was stated as a corollary of the weak convergence of interfaces to SLE(6), itself deduced from Cardy’s formula [16]; but actually, it is rather technical to deduce the convergence of surrounding probabilities from the latter weak convergence.
3 Preliminaries
Theorem 2.1 is deduced from a more general result, interesting in itself. Let us introduce some notation, state the main result in full strength, and state lemmas used in the proof, giving proofs in the next sections. Throughout this section we assume that the assumptions of Theorem 2.1 hold, we omit the superscript so that mean respectively (everywhere except Theorem 3.2, Lemmas 3.8–3.9, and other explicitly indicated places), and assume that are pairwise distinct. Remarkably, although we take in the proof of Schramm’s formula at the very end, here we need .
In what follows a hexagon is a hexagon of the lattice approximation . A midpoint is a midpoint of a side of a hexagon. A half-side is a segment joining a midpoint with an endpoint of the same side. A broken line is a simple broken line (possibly closed) consisting of half-sides, viewed as a subset of the plane. A broken line is such a broken line with distinct endpoints and . A loop configuration with disorders at (or just loop configuration for brevity) is a disjoint union of several broken lines, with exactly two being non-closed and having the endpoints at and all the other ones being closed. It is easy to see (see, for instance, [9, §1.2]) that the number of loop configurations equals the number of colorings of hexagons in two colors. See Figure 4.
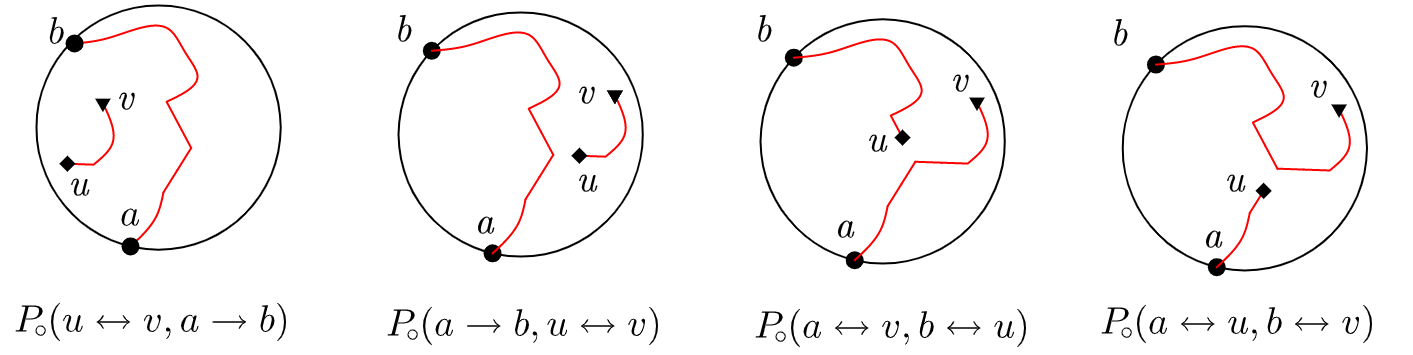
Denote by the fraction of loop configurations containing a broken line (and hence another broken line as well). Define analogously. See Figure 5.
Now consider loop configurations containing a broken line . The broken line (which we always orient from to ) divides the polygon into connected components, each bordering upon either from the right or from the left. We say that those connected components lie to the right and to the left from respectively. Denote by the fraction of loop configurations containing broken lines and such that lies to the right from . Define analogously. Beware the different meaning of notations and .
We have decomposed the set of all loop configurations into subsets (called link patterns) depending on the arrangement of broken lines with the endpoints (see Figure 5).
The parafermionic observable is the complex-valued function on the set of pairs of midpoints, distinct from and , given by the formula
The following lemma and theorem, being the main result in full strength, will imply Theorem 2.1.
Lemma 3.1.
For any distinct midpoints we have and . Hence .
The latter automatically holds for as well.
Theorem 3.2 (Continuum limit of the parafermionic observable).
Let be a lattice approximation of a domain with two marked distinct boundary points and two other points such that is a closed smooth curve. Then
| (5) |
The proof of this theorem uses the following properties of the parafermionic observable.
Lemma 3.3 (Conjugate antisymmetry).
The function is conjugate-antisymmetric, i.e.,
Lemma 3.4 (Discrete analyticity).
Let be a common vertex of hexagons. Let be the midpoints of their common sides in the counterclockwise order. Then for each midpoint we have
| (6) |
Corollary 3.5 (Cauchy’s formula).
Let with be a closed broken line with the vertices at the centers of hexagons such that the hexagons centered at and share a side for each . Denote by the midpoint of the side . Assume that lie outside . Then the discrete integral of along the contour defined by the formula
vanishes.
Denote by the straight-line segment with the endpoints .
Lemma 3.6 (Boundary values).
Take distinct midpoints . Let us go around counterclockwise and write the order of these points. Then
| (7) |
By the inradius of a closed bounded domain with three marked points we mean the minimal radius of a disk such that no two points among belong to the same connected component of . For instance, if is the triangle with the vertices then the inradius of equals the usual inradius of the triangle, i.e. the radius of the inscribed circle. We are going to apply the following two lemmas to .
Lemma 3.7 (Uniform Hölderness).
There exist such that for any distinct midpoints of a lattice approximation of an arbitrary bounded simply-connected domain and any broken line we have
where is the inradius of . The same inequality remains true, if we allow and set , .
Remark.
Here cannot be replaced by in general, e.g., for .
Lemma 3.8 (Geometry of a lattice approximation).
Let be a lattice approximation of the domain with three distinct marked points and two more marked points such that is a closed smooth curve. Then there exist not depending on such that:
-
1.
;
-
2.
and can be joined by a broken line of diameter less than ;
-
3.
the inradius of is greater than .
Remark.
The ratio can be arbitrarily large for a triangle with a small angle at its vertex . Using this observation, one can construct a Jordan domain such that is unbounded.
Lemma 3.9 (Solution of the resulting boundary-value problem).
Let be a domain bounded by a closed smooth curve. Then the right-hand side of (5) (continuously extended to all except for ) is the unique function in that is:
-
1.
conjugate-antisymmetric in ;
-
2.
analytic in and continuous in for each ; and
-
3.
satisfies boundary conditions (7) (with understood as points of rather than ).
Remark.
The lemma is easily generalized to an arbitrary bounded simply-connected domain, if is understood as the set of prime ends.
4 Proofs
Proof of Lemma 3.1.
Fix distinct midpoints , , , . Let us construct a bijection between the loop configurations containing broken lines and , the former to the left from the latter, and the colorings of hexagons such that and can be joined by a broken line lying to the left from the interface. For that purpose, for each possible interface of such colorings, fix such a broken line , so that depends only on the interface but not a particular coloring.
Take a loop configuration containing broken lines , and let us construct a coloring with the interface . Perform the symmetric difference of the loop configuration and the fixed broken line (and take the topological closure). We get a disjoint union of closed broken lines and just one non-closed broken line . The desired coloring is then determined by the following two conditions:
-
1.
two hexagons with a common side have different colors if and only if the side is contained in the resulting union;
-
2.
the hexagon containing the midpoint is blue, if and only if the half-side of starting at goes counterclockwise around the boundary of the hexagon.
Clearly, this gives the desired bijection. See Figure 4.
A similar bijection shows that the total number of loop configurations equals the total number of colorings [9, §1.2]. Thus . Analogously, . ∎
Proof of Lemma 3.3.
This is a direct consequence of the definition because and . ∎
Proof of Lemma 3.4.
(Cf. [9, Proof of Lemma 4]) Rewrite (6) in the form
| (8) |
where denotes the number of loop configurations containing broken lines and etc.
We group loop configurations with respectively in triples such that any two loop configurations in a same triple differ by two half-sides adjacent to . See Figure 6. Each triple contributes zero to the left-hand side of (8). Indeed, if the loop configurations in a triple belong to the same link pattern (as in Figure 6 to the top and to the middle), then the contributions of the loop configurations to (8) are proportional to , , , hence sum up to zero. If the loop configurations in a triple do not belong to the same link pattern (as in Figure 6 to the bottom), then up to a cyclic permutation of and a permutation of , they contain the broken lines , , and respectively, the latter lying to the left from . Up to overall minus sign, such loop configurations contribute , , respectively to (8), again summing up to zero. This proves (8), and hence (6). ∎
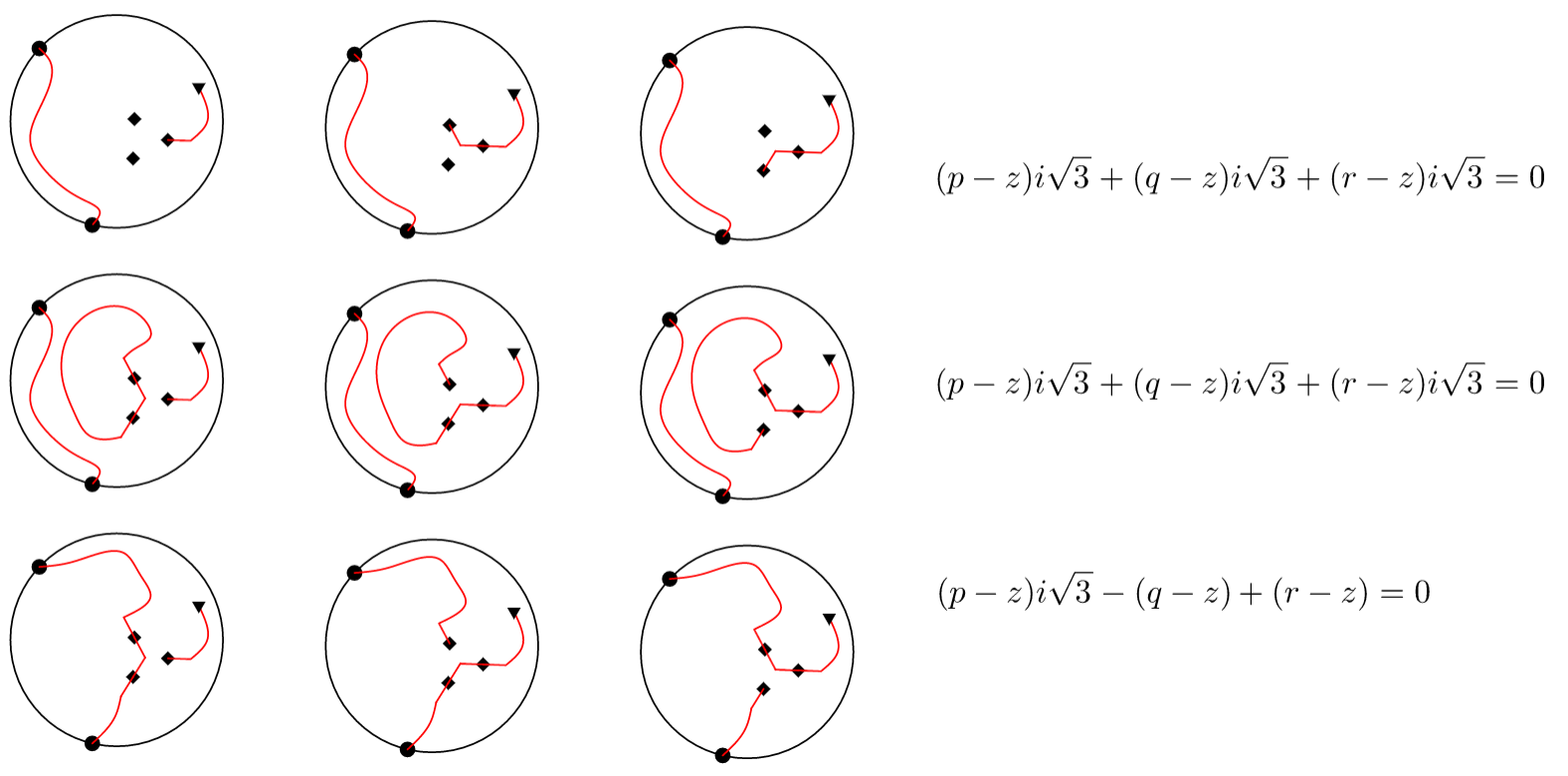
Proof of Corollary 3.5.
For a counterclockwise triangular contour , the corollary follows from (6) because , where is the vertex enclosed by the contour. Since any closed broken line can be tiled by triangular contours and the discrete integration is additive with respect to contour, the corollary follows. ∎
Proof of Lemma 3.6.
Since each loop configuration belongs to exactly one of the four link patterns, it follows that
If the order of the points is , then no loop configurations containing disjoint broken lines and are possible. Neither loop configurations containing a broken line to the right from are possible. Hence in this case and thus
The other orders are considered analogously. ∎
Proof of Theorem 3.2.
Step 1: piecewise linear extension of . Fix and consider the function on the set of all midpoints . Set and . Extend the function to the centers, vertices and side midpoints of all the hexagons intersecting (not just contained in ) by the formula , i.e., set the value at a given point to be the same as at an arbitrary closest midpoint . Then extend the function linearly to each triangle spanned by adjacent vertex, side midpoint, and center of a hexagon. Finally, restrict the function to . We get a continuous piecewise-linear function .
Step 2: extraction of a converging subsequence . By the definition, , hence is uniformly bounded.
Since is smooth, by Lemmas 3.7–3.8 is uniformly Hölder in . Indeed, the lemmas imply
for all . This gives the Hölder condition for . Applying this inequality for a triangle spanned by adjacent vertex, side midpoint, and hexagon center, we get inside the triangle for some not depending on . This implies the Hölder condition for .
Then by the Arzelà–Ascoli theorem, there is a continuous function and a subsequence such that uniformly in . Hence,
| (9) |
Step 3: analyticity of the limit . Take an arbitrary triangular contour such that is outside of . Let be the closed broken line with the vertices at the centers of the hexagons of of maximal enclosed area contained inside . Then is outside for sufficiently small . Approximating an integral by a sum, applying (9) and Corollary 3.5, we get
Thus , and by Morera’s theorem is analytic in . Since is continuous in the whole , by the removable singularity theorem it follows that is analytic in the whole .
Step 4: boundary values of the limit . Let us show that the function satisfies boundary conditions (7) (with understood as points of rather than midpoints). Indeed, if the order of the points on is, say, , then the order of on is the same for sufficiently small . By Lemma 3.6 we have . By (9), as well.
Step 5: identification of the limit . Recall that the function depends on the parameter as well, and write . By Lemma 3.3 and (9) it follows that the function is conjugate-antisymmetric for . Then by Lemma 3.9 the function coincides with the right-hand side of (5). Thus the limit function is uniquely determined by , and thus does not depend on the choice of the converging subsequence . Hence convergence (9) holds for the initial sequence , not just a subsequence. We have arrived at (5). ∎
Remark.
Step 2 is the only one where the smoothness of the boundary is essentially used. For more general domains, this step is more technical; see [9, §5].
Let us show that Cardy’s and Schramm’s formulae are indeed particular cases of this result.
Proof of Corollary 2.3.
Apply Theorem 2.1. Since the counterclockwise order of the marked points on is , it follows that and for sufficiently small . Clearly, . Hence the crossing probability tends to the right-hand side of (1) as .
It remains to prove that the right-hand sides of (1) and (3) are equal for , i.e. for each . Here the left-hand side is the Schwarz triangle function that conformally maps the upper half-plane onto the equilateral triangle with the vertices and takes to the respective vertices [11, Ch. VI, §5]. By the definition and a symmetry argument, is the conformal mapping of the lower half-plane onto the same triangle, with the images of and interchanged. Since a conformal mapping onto a domain is determined by the images of three boundary points, it follows that the images of each under the two conformal mappings are symmetric with respect to the bisector of the angle with the vertex . Since for each the imaginary part of the symmetric point equals , it follows that the right-hand sides of (1) and (3) are equal. ∎
Remark.
Proof of Corollary 2.4.
Apply Theorem 2.1 for , , and . We have
as because the probability that the interface intersects the -neighborhood of the origin tends to . (The latter well-known fact is actually reproved in the proof of Lemma 3.7 in the appendix.) Thus by (1) we get
Here
because the value is the cross-ratio of the points , the value is the cross-ratio of their -images, and the linear-fractional mapping extended to preserves cross-ratios. Together with Proposition 2.2, this gives (4). ∎
Acknowledgements
The work is supported by the Swiss NSF, ERC Advanced Grants 340340 and 741487, National Center of Competence in Research (NCCR SwissMAP), and Theoretical Physics and Mathematics Advancements Foundation “Basis” grant 21-7-2-19-1. Section 3 was written entirely under the support of Russian Science Foundation grant 19-71-30002. Appendix A was written entirely under the support of the Ministry of Science and Higher Education of the Russian Federation (agreement no. 075-15-2022-287).
The authors are grateful to I. Benjamini, O. Feldheim, G. Kozma, I. Novikov for useful discussions.
Appendix A Proofs of technical lemmas
Proof of Lemma 3.7.
The lemma follows from the sequence of inequalities to be explained below:
Here we use the following notation:
-
•
is the fraction of loop configurations with disorders at such that both non-closed broken lines have common points with . Those loop configurations are called tripod in what follows.
-
•
is the fraction of loop configurations with disorders at such that the only non-closed broken line has common points with . Those loop configurations are called bipod in what follows. Loop configurations with disorders at are defined analogously to the ones with disorders at .
-
•
and are the lattice approximations of the disks centered at of radii and respectively (the factor of guarantees that for ).
-
•
is the probability that there is a crossing between and in a coloring of , i.e. a connected component of the union of the hexagons of the same color having common points with both and .
-
•
and are the constants from the Russo–Seymour–Welsh inequality [9, Proposition 8].
We assume that , otherwise there is nothing to prove.
Step 1: the first inequality. The symmetric difference with the broken line does not change the link pattern of a loop configuration unless both non-closed broken lines in the configuration have common points with . Thus each pair of non-tripod loop configurations with the symmetric difference contributes zero to . Each tripod loop configuration contributes at most times the probability of the configuration, which gives the first inequality.
Step 2: the second inequality. Let us prove that, say, . In what follows we are not going to use that , hence the same argument will prove that and .
It suffices to construct an injection from the set of tripod loop configurations to bipod ones.
Take a tripod loop configuration. Denote by the connected parts of the broken lines from respectively to the first intersection point with . Fix a broken line (not necessary from the loop configuration) having no common points with neither nor (possibly except the endpoints and ). Such a broken line exists, e.g., the union of and the part of from to will work. But we fix so that it depends only on and but not on the tripod loop configuration itself. Then the symmetric difference with gives the required injection, implying the second inequality.
Step 3: the third inequality. Choose two points from , say, and , belonging to the same connected component of . Such a pair of points exists by the definition of the inradius . Join and by a fixed broken line outside .
It suffices to construct an injection from the set of bipod loop configurations to the set of colorings with a crossing between and .
Take a bipod loop configuration. Perform its symmetric difference with the fixed broken line (and take the closure). We get a disjoint union of closed broken lines. The resulting union determines a coloring of the hexagons (by condition 1 from the proof of Lemma 3.1 and the requirement that the hexagon containing is painted blue), which we assign to the initial loop configuration.
At least one of the resulting closed broken lines has common points with both and , hence with both and , otherwise the symmetric difference of and the union of all the resulting closed broken lines would not connect with . The hexagons bordering upon that closed broken line from inside have the same color. Thus the constructed coloring has a crossing, which implies the third inequality.
Step 4: the fourth inequality. Notice that removing the hexagons outside the ring between and does not affect the probability of a crossing, and adding hexagons inside the ring (not contained in initially) can only increase this probability. This way the third inequality reduces to the Russo–Seymour–Welsh inequality for a ring [9, Proposition 8].
This concludes the proof for . Otherwise, the argument is analogous, only some loop configurations contain fewer disorders. ∎
Proof of Lemma 3.8.
For an open square with side length and a real number denote by the square with side length having the same center and side directions. By the implicit function theorem and a compactness argument, we can choose and open squares such that
-
1.
is covered by (in particular, each has side length at least );
-
2.
for each either or the intersection has a form for some function with and , where the coordinate axes pass through the center of and are parallel to the sides.
Take . Then each hexagon of the lattice contained in is contained in some by condition 1, all the hexagons in form a connected polygon by condition 2, and the union of such polygons for all is connected. So, the union of hexagons of the lattice contained in is connected and hence coincides with . Set and let us prove properties 1–3 stated in the lemma.
Property 1. If then there is nothing to prove. Otherwise take any . Then for some . The distance between and is at most (because by condition 2 the point belongs to a hexagon contained in , hence to ). Thus .
Property 2. If or then there is nothing to prove. Otherwise and for some . It suffices to join and by a broken line of length at most . If does not intersect , then there is a broken line of length at most . If does intersect , then consider the points and . Then the three segments , , and of total length are contained in . Hence and can be joined by a broken line of length at most .
Property 3. Join by curves having no common points besides the endpoints. The domain enclosed by the curves has a positive inradius . Decompose each curve into arcs of diameter at most . For each arc , the points and are -close to and (property 1) and can be joined by a broken line of diameter at most (property 2). Thus can be joined by three broken lines (possibly having common points), -close to . Hence the inradius of is greater than for (and greater than for all ). ∎
Proof of Lemma 3.9.
Existence. Let us prove the right-hand side of (5) has all the properties listed in the lemma. Denote so that the right-hand side equals .
Property 1: conjugate-antisymmetry. We have for all , because the four conformal mappings have the same domain, the same image, and the same images of . Since interchanging and takes to , the right-hand side of (5) is conjugate-antisymmetric.
Property 2: analyticity and continuity. For fixed , the right-hand side of (5) is analytic in and continuous in because only if both belong to the counterclockwise arc of or both belong to the clockwise arc (see the convention right after Theorem 2.1).
Property 3: boundary values. If the order of the points on is , then . Then by the convention right after Theorem 2.1, the value is understood as continuously extended from the first coordinate quadrant. Since for all , it follows that maps the first quadrant to the triangle with the vertices , maps onto itself, and takes the positive imaginary semi-axis to . By the boundary correspondence principle, . The other orders of are considered analogously. We arrive at (7).
Uniqueness. Let us prove that each function satisfying the conditions of the lemma, coincides with the right-hand side of (5). Consider the following cases:
Case 1: . For fixed , the function is analytic in , continuous in , and takes the arcs , , of to the segments , , respectively (where the sign depends on the clockwise order of , , along ). By the argument principle, it follows that such function is unique, hence it coincides with the right-hand side of (5) for .
Case 2: and . By the conjugate antisymmetry, we have . The latter coincides with the right-hand side of (5) by Case 1 and by conjugate antisymmetry of the right-hand side of (5).
Case 3: and . By the continuity, the values for determined in Case 2 uniquely determine the values and .
Case 4: . For fixed , the function is analytic in and continuous in . Thus the boundary values (determined in Cases 2–3) uniquely determine the function . Thus coincides with the right-hand side of (5) for all . ∎
Proof of Proposition 2.2.
We use well-known properties of the Schwarz triangle functions [11, Ch. VI,§5].
The Schwarz triangle function maps the upper half-plane onto the equilateral triangle with the vertices , and takes to the respective vertices. The composition maps the half-plane onto the triangle with the vertices , and takes to the respective vertices. It also takes to by symmetry because conformal mapping is uniquely determined by the images of three points. The Schwarz reflection principle shows that the same composition maps onto the interior of the rhombus.
The Schwarz triangle function maps the upper half-plane onto the right triangle with the vertices , and takes to the respective vertices. The precomposition with the mapping takes the first quadrant to the same triangle. Applying the Schwarz reflection principle, we see that the same composition maps onto the interior of the rhombus, and are fixed. ∎
References
- [1] S. Broadbent, J. Hammersley, Percolation processes: I. Crystals and mazes. Math. Proc. Camb. Philos. Soc. 53:3 (1957) 629–641.
- [2] J.L. Cardy. Critical percolation in finite geometries, J. Phys. A, 25(4):L201–L206, 1992.
- [3] D. Chelkak, C. Hongler, K. Izyurov, Conformal invariance of spin correlations in the planar Ising model, Ann. Math. (2015), 1087–1138.
- [4] H. Duminil-Copin, Parafermionic observables and their applications to planar statistical physics models, volume 25 of Ensaios Mateáticos [Mathematical Surveys]. Sociedade Brasileira de Matemática, Rio de Janeiro, 2013.
- [5] G. Grimmett, Percolation, Vol. 321 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Springer-Verlag, Berlin, second edition, 1999.
- [6] C. Hongler and S. Smirnov, The energy density in the planar Ising model, Acta Math., 211:2 (2013) 191–225.
- [7] R. Kenyon, Spanning forests and the vector bundle Laplacian, Ann. Prob. 39:5 (2011) 1983–2017.
- [8] M. Khristoforov and V. Kleptsyn, Smirnov’s observable and link pattern probabilities in percolation, in preparation.
- [9] M. Khristoforov, S. Smirnov, Percolation and O(1) loop model, preprint, 2021, \urlhttps://arxiv.org/abs/2111.15612.
- [10] P. Kleban, D. Zagier, Crossing probabilities and modular forms, J. Stat. Phys. 113 (2003) 431–454.
- [11] Z. Nehari, Conformal mapping, New York: Dover Publications, 1975.
- [12] I. Novikov, Percolation of three fluids on a honeycomb lattice, Monatsh Math 199, 611-626 (2022), \urlhttps://arxiv.org/abs/1912.01757.
- [13] O. Schramm, Scaling limits of loop-erased random walks and uniform spanning trees, Isr. J. Math. 118 (2000), 221–288. \urlhttps://arxiv.org/abs/math/9904022
- [14] O. Schramm, A percolation formula, Electron. Comm. Probab. 6 (2001) 115–120.
- [15] S. Sheffield and D.B. Wilson, Schramm’s proof of Watts’ formula, Ann. Probab. 39:5 (2011), Memorial Issue for Oded Schramm 1961–2008, 1844–1863.
- [16] S. Smirnov, Critical percolation in the plane: Conformal invariance, Cardy’s formula, scaling limits. C. R. Math. Acad. Sci. Paris, 333(3):239-244, 2001.
- [17] S. Smirnov, Critical percolation and conformal invariance. In: XIVth International Congress on Mathematical Physics: Lisbon, 2003.
- [18] S. Smirnov, Critical percolation in the plane, 2009, \urlhttps://arxiv.org/abs/0909.4499.
- [19] S. Smirnov, W. Werner, Critical exponents for two-dimensional percolation, Math. Res. Lett. 8:6 (2001), 729–744.
- [20] De Volson Wood, Problem, Amer. Math. Monthly 1 (1894), p. 99.
Mikhail Khristoforov
Saint Petersburg University
mikhail.khristoforov @ gmailcom
Mikhail Skopenkov
King Abdullah University of Science and Technology &
HSE University (Faculty of Mathematics) &
Institute for Information Transmission Problems of the Russian Academy of Sciences
mikhail.skopenkov @ gmailcom \urlhttps://users.mccme.ru/mskopenkov/
Stanislav Smirnov
Université de Genève, Genève 4, Switzerland &
Saint Petersburg University
&
Skolkovo Institute of Science and Technology
[email protected]