A finite element method for Electrowetting on Dielectric
Abstract
We consider the problem of electrowetting on dielectric (EWoD). The system involves the dynamics of a conducting droplet, which is immersed in another dielectric fluid, on a dielectric substrate under an applied voltage. The fluid dynamics is modeled by the two-phase incompressible Navier-Stokes equations with the standard interface conditions, the Navier slip condition on the substrate and a contact angle condition which relates the dynamic contact angle and the contact line velocity, as well as the kinematic condition for the evolution of the interface. The electric force acting on the fluid interface is modeled by the Maxwell’s equations in the domain occupied by the dielectric fluid and the dielectric substrate. We develop a numerical method for the model based on its weak form. This method combines the finite element method for the Navier-Stokes equations on a fixed bulk mesh with a parametric finite element method for the dynamics of the fluid interface, and the boundary integral method for the electric force along the fluid interface. Numerical examples are presented to demonstrate the accuracy and convergence of the numerical method, the effect of various physical parameters on the interface profile and other interesting phenomena such as the transportation of droplet driven by applied non-uniform electric potential difference.
keywords:
Electrowetting, moving contact lines, two-phase flows, the finite element methodAMS:
74M15, 76D05, 76T10, 76M10, 76M151 Introduction
Since the pioneer work of Lippmann [23] on electro-capillarity, it has been found that applied electric fields have a great effect on the wetting behavior of small charged droplets. This phenomenon is referred to as electrowetting and has received much attention in recent years [27, 44, 7]. In the device of electro-wetting on dielectric (EWoD), a dielectric film is placed on the substrate to separate the droplet and the electrode to avoid electrolytic decomposition [4] (see Fig. 1 for the set-up of EWoD). EWoD has found many applications in various fields, such as adjustable lenses [20], electronic displays [18], lab-on-a-chip devices [31, 8], suppressing coffee strain effects [15], etc.
The static problem of EWoD has been extensively studied in recent years, for example, in Refs. [19, 6, 38, 5, 28, 25, 37, 16, 11, 12, 13] and many others. These work has revealed the structure of the static interface profile. It was found that the electric force does not contribute to the force balance at the contact line, therefore the local static contact angle still satisfies the Young-Dupré equation
| (1) |
where , and are the surface tension coefficients of the fluid-fluid and fluid-solid interfaces. On the other hand, the divergent electric force incurs a large curvature and causes a significant deformation of the fluid interface in a small neighborhood of the contact line. The contact angle of the interface outside this small region, called the apparent contact angle and denoted by , is well characterized by the Lippmann equation [32, 6, 13]
| (2) |
where is the applied voltage, and are the permittivity and thickness of the dielectric substrate, respectively. Except in the extreme case of contact angle saturation, this equation also matches experimental results quite well for different types of droplets and insulators, and wide range of and (see [39, 40, 26] for example).
In this work, we consider the dynamical problem of EWoD. Because of its importance in industrial applications, a lot of efforts have been devoted to this problem and some numerical methods have been proposed in recent years. These include Lattice Boltzmann methods [9, 22, 36], molecular dynamics simulations [14, 21], the level set method [41, 17], the phase-field approach [24, 16, 30], and others [8, 29, 10], etc. Here, we develop a finite element method for EWoD based on our earlier work on moving contact lines [43].
The model we use in this work for EWoD is based on the contact line model developed by Ren et al. [33, 35, 34]. It contains the incompressible Navier-Stokes equations for the two-phase fluid dynamics, the Navier slip condition on the substrate and a dynamic contact angle condition at the contact line. On the fluid interface, besides the viscous stress and the curvature force, the electric force also contributes to the force balance thus the interface conditions. We assume that the electric charging time is negligible compared to the time scale of the fluid motion, therefore model the electrostatic potential using the Maxwell’s equation [13].
Based on the previous work for two-phase fluid dynamics [3] and moving contact lines [43], we develop a finite element method for the EWoD model. The method couples the finite element method for the incompressible Navier-Stokes equations and a semi-implicit parametric finite element method for the evolution of the fluid interface. We use unfitted mesh such that the discretization of the moving fluid interface is decoupled from the fixed bulk mesh. Besides, the electric force on the fluid interface is computed by using the boundary integral method. The numerical method obeys a similar energy law as the continuum model when the electric field is absent, which is a desired property for the numerical method.
This paper is organzied as follows. In section 2, we present the EWoD model and its dimensionless form. In section 3, we develop the numerical method based on a weak form of the continuum model, and present the full discretized scheme for the Navier-Stokes equations, the dynamics of the fluid interface, and the electric force on the fluid interface. In section 4, we present numerical examples to demonstrate the convergence and accuracy of the numerical method, the effect of the various physical parameters on the interface profiles, as well as the wetting dynamics driven by non-uniform electric potential. Finally, we draw the conclusion in section 5.

2 The mathematical model
We consider the EWoD problem in the 2d space as shown in Fig. 1(a). In this setup, a conductive liquid droplet (shaded in blue), is immersed in another dielectric fluid such as vapor or oil, and deposited on a thin dielectric substrate/insulator (shaded in orange), below which we place an electrode (shaded in gray). Between the electrode and the droplet, we apply a voltage difference, which generates electric fields and influences the wetting behavior of the charged droplet.
The corresponding mathematical setup is shown in Fig. 1(b). We consider the system in a bounded domain and use the Cartesian coordinates, where the fluid-insulator interface is on the -axis. For simplicity, we assume the periodic structure along -direction for the system, and moreover, another electrode is placed on the top . The domain is composed of three regions, the conducting droplet, the dielectric fluid, and the dielectric substrate, which are labeled as , , and , respectively. The fluid interface is denoted by the open curve , which intersects with the flat insulator at two contact points, labeled as and . and represent the corresponding fluid-insulator interfaces, and is the insulator-electrode interface.
Some relevant parameters are defined as follows: and are the density and viscosity of fluid , respectively; is permittivity of the dielectric medium in (); denotes the surface tension of the fluid interface , and denotes the surface tension of the fluid-solid interface . Furthermore, we denote by the unit normal vector on pointing to fluid 2, and and the unit normal and tangent vector on respectively.
2.1 Governing equations for the fluid dynamics
The mathematical model is an extension of the contact line model proposed by Ren et al. [33, 35, 34] to include the contribution of electric field in EWoD. It consists of the two-phase incompressible Navier-Stokes equations for the fluid dynamics and the Maxwell’s equation for the electrostatic potential.
First we consider the two-phase fluid dynamics in the domain . Let be the fluid velocity and be the pressure. The dynamic of the system is governed by the standard incompressible Navier-Stokes equations in ,
| (3a) | ||||
| (3b) | ||||
where is the viscous stress with .
On the fluid interface , we have the following conditions
| (4a) | ||||
| (4b) | ||||
| (4c) | ||||
where denotes the jump from fluid 1 to fluid 2, is the identity matrix, is the curvature of the fluid interface , is the electrostatic potential, and denotes the normal velocity of the fluid interface. Equation (4a) states the fluid velocity is continuous across the interface. Equation (4b) states that the tangential stress is continuous across the interface and the normal stress jump is balanced by the curvature force together with the electric force . Equation (4c) is the kinetic condition for the interface, where the fluid interface evolves according to the local fluid velocity.
At the lower solid wall , the fluid velocity satisfies the no-penetration condition and the Navier boundary condition
| (5a) | ||||
| (5b) | ||||
where is the friction coefficient of fluid at the wall, and is the slip velocity of the fluids.
At the contact points and , the dynamic contact angles, denoted by and respectively, depend on the contact line velocity [33, 35],
| (6a) | ||||
| (6b) | ||||
where is the equilibrium contact angle satisfying the Young’s relation (1), and is the friction coefficient of the fluid interface at the contact line. The contact line velocity is determined by the slip velocity of the fluids: . The contact angle condition (6) is a force balance at the contact point: the Young stress resulted from the deviation of the dynamic contact angle from the equilibrium angle is balanced by the friction force. Note that the electric force does not contribute to the force balance at the contact line.
Furthermore, we use the no-slip boundary condition on the upper wall and the periodic boundary conditions along .
2.2 Governing equations for the electrostatic field
The applied voltage induces electrostatic fields in the fluid region and the dielectric substrate , where the electric potential, denoted by , satisfies the Laplace equation,
| (7) |
On the interface and at the top/bottom electrode , the electric potential satisfies the Dirichlet boundary conditions
| (8a) | |||
| (8b) | |||
where is the imposed voltage difference. Since there is no free charge density across the interface between the dielectric fluid and the dielectric substrate, we have
| (9) |
where denotes the jump from to , in and in . Furthermore, the periodic boundary condition is prescribed along .
2.3 Nondimensionlization
Next we present the above governing equations and the boundary/interface conditions in their dimensionless form. By choosing and as the characteristic length and velocity respectively, we rescale the physical quantities as
We define the Reynolds number , the Capillary number , the slip length , the Weber number and the parameter as
| (10) |
where measures the relative strength of the electric force compared to the surface tension at the fluid interface.
For ease of presentation, we will drop the hats on the dimensionless parameters and variables. In the dimensionless form, the governing equations for the fluid dynamics in read
| (11a) | |||
| (11b) | |||
where is the stress tensor. These equations are supplemented with the following boundary/interface conditions:
-
(i)
The interface conditions on :
(12a) (12b) (12c) (12d) where denotes the fluid interface, is the arc length parameter with being at the left contact point.
-
(ii)
The condition for the dynamic contact angles:
(13a) (13b) -
(iii)
The boundary conditions on :
(14) -
(iv)
The no-slip condition on
(15) -
(v)
Periodic boundary conditions on :
(16)
The governing equations for the electric field potential in read
| (17) |
subject to the following boundary conditions:
-
(i)
The Dirichlet Boundary conditions on , , and :
(18a) (18b) -
(ii)
The interface condition on :
(19) -
(iii)
Periodic boundary conditions on :
(20) where is the unit outward normal to on .
Equations (11) and (17) together with the boundary/interface conditions (12)-(16) and (18)-(20) form the complete model for the problem of EWoD. For this dynamical system, we define the total energy as
| (21) |
where and are the total arc length of and , respectively. The four terms represents the kinetic energy of the fluids, the interfacial energy at the solid wall, the interfacial energy of the fluid interface and the electrical energy, respectively. The dynamical system obeys the energy dissipation law
| (22) |
where the three terms represent the viscous dissipation in the bulk fluid with being the Frobenius norm, the dissipation at the solid wall due to the friction and the dissipation at the contact points, respectively. Details for the derivation of (22) are provided in the Appendix A.
3 The numerical method
The numerical method consists of a finite element method for the fluid dynamics, a parametric finite element method for the dynamics of the fluid interface, and the boundary integral method for the electric field. The numerical method is based on a weak formulation for the EWoD model, which we will present first.
3.1 Weak formulation
To propose the weak formulation for equations (11)-(16), we define the function space for the pressure and the velocity, respectively as
| (23a) | ||||
| (23b) | ||||
with the -inner product on
| (24) |
We parameterize the fluid interface as , where , and corresponding to the left and and right contact points, respectively. We define the function spaces for the interface curvature and the interface as
| (25a) | |||
| (25b) | |||
equipped with the -inner product on
| (26) |
Taking the inner product of (11a) with then using the boundary/interface conditions in (12)-(16) and , we obtain [3, 43]
| (27) |
where with being the characteristic function. With the special treatment of the inertia term in (27), the numerical scheme enjoys the discrete stability for the fluid kinetic energy in the absence of electric field. This will be discussed later in section 3.4. For the viscous term, integrating by parts then applying the boundary/interface conditions yields
| (28) |
where , , and .
Equation (12c) for the curvature can be rewritten as . Taking the inner product of it with on then applying integration by parts yields
| (29) |
where we have used the fact that , , and the dynamic contact angle conditions in (13).
Combining these results, we obtain the weak formulation for the dynamic system (11)-(16) as follows: Given the initial fluid velocity and the interface , find the fluid velocity , the pressure , the fluid interface , and the curvature such that
| (30a) | ||||
| (30b) | ||||
| (30c) | ||||
| (30d) | ||||
Eq. (30a) is obtained from Eq. (27) and Eq. (3.1). Eq. (30b) results from the incompressibility condition (11b). Eq. (30c) is obtained from the kinetic condition (12d). Eq. (30d) is obtained from (29).
The above system (30a)-(30d) is an extension of the weak formulation introduced in Ref. [3] for two-phase flows and Ref. [43] for moving contact lines. In the current problem for EWoD, we have the additional term for the electric force in (30a). The electric force is obtained from solving (17)-(20).
3.2 Finite element discretization
We solve equations (30a)-(30d) for and on the fluid domain and for and on the reference domain using the finite element method on unfitted meshes. To that end, we uniformly partition the time domain as with , , and the reference domain as with , and . We approximate the function spaces and by the finite element spaces
| (31a) | |||
| (31b) | |||
where denotes the space of the polynomials of degree at most 1 over . Denote by the numerical approximation to the fluid interface at . Then are polygonal curves consisting of ordered line segments. The unit tangential vector and normal vector of are constant vectors on each interval with possible jumps at the nodes , and they can be easily computed as
| (32) |
where , and denotes the counter-clockwise rotation by degrees.
Let be a triangulation of the bounded domain , and
| (33a) | |||
| (33b) | |||
where , and denotes the space of polynomials of degree on . Let and denote the finite element spaces for the numerical solutions for the velocity and pressure, respectively. In this work, we choose them as
| (34) |
which satisfies the inf-sup stability condition [1, 43]
| (35) |
where and denote the and -norm on respectively, and is a constant.

In the simulation, the partition of the reference domain for the interface and the triangulation of the fluid domain are both fixed in time. As a result, the triangulation of is decoupled from the discretization of the interface , thus may not fit the interface, i.e. the line segments comprising of are in general not the boundaries of the elements in . At , the interface divides into two sub-domains, and . Correspondingly, we split into three disjoint subsets: being the set of elements in , being the set of elements in , and being the set of elements that intersect with the interface (see Fig. 2 for an illustration). The splitting can be easily done by using a recursive algorithm as follows:
-
(1)
First form by locating all elements that intersect with .
-
(2)
Locate one element in , for example, the one that contains the point with coordinate , and set .
-
(3)
Check all neighbours of the elements in . If a neighbor is not in , then add it to .
The last step is repeated until no element can be added to . This gives the set . The rest of the elements not belonging to form the set .
Denote by , and the numerical approximations of the density , the viscosity and the friction coefficient at , respectively. We define and as
where , . Similarly, we denote by and the boundary of and at the lower wall respectively, and define at the lower wall as
| (36) |
where is the boundary of at the lower wall, and and are the two contact line points.
The finite element method is given as follows. First we partition the time domain , the reference domain for the interface and the fluid domain as described above. Let and be the initial interface and velocity field, respectively. For , we compute , , , and by solving the linear system
| (37a) | ||||
| (37b) | ||||
| (37c) | ||||
| (37d) | ||||
Here, , , , and , . The electric force in (37) is computed by solving equations (17)-(20) in the domain ; its computation will be presented in section 3.3. In (37d), the derivative is taken with respect to the arc length of : , and similarly for . At the first time step, we set .
In the numerical method, the inner product is approximated by using either the trapezoidal rule, denoted by , or the Simpson’s rule, denoted by . Since we are using unfitted mesh, the interface intersects with the bulk mesh. Denote by the set, in ascending order, of both the -values of the intersecting points and the mesh points of the reference interval , . Then the inner products involving interface and bulk quantities are approximated by the Simpson’s rule on the mesh ,
| (38) |
and the inner products involving only quantities on the interface are simply approximated by the trapezoidal rule on the mesh ,
| (39) |
where , are the one-sided limits of at , and similarly for .

3.3 Computation of the electric force
The electric force on the fluid interface is computed by solving Eqs. (17)-(20) using the boundary integral method. Without loss of generality, we assume that satisfies the Laplace equation on a domain with boundary . Denote the directional derivative of in the outward normal direction of the boundary by , where is the outward unit normal vector on . For any point lies on the smooth part of , we have the boundary integral equation
| (40) |
where is the Green function for the Laplace equation in , and .
Eq. (40) can be used to compute and/or its derivative on the boundary . To that end, we partition then approximate it by a collection of line segments: . We further approximate and by constants on each line segment: and on , . Denote by the mid-point of the line segment . It lies on a smooth part of the approximation boundary . Then we can apply Eq. (40) to and obtain
| (41) |
where
| (42) |
For the current problem, we apply the boundary integral method to the domain and the domain separately. A discretization of the boundary of the two domains is shown in Fig. 3. Eq. (41) is applied at each discrete point. These equations, together with the prescribed Dirichlet boundary conditions and , the periodic boundary conditions , , and , as well as the interface conditions and on form a system of linear algebraic equations for and at the discrete points. After the linear system is solved, is used to compute the electric force: on .
3.4 Properties of the numerical method
For the numerical method (37)-(37d), we can show that it yields a unique solution. Furthermore, in the special case when the electric force is absent, the numerical method is unconditionally energy stable. We make the following assumptions on the interface , ,
-
i)
the interface does not intersect with itself;
-
ii)
the parameterization is such that , and
-
iii)
the first and last segments of are not parallel to the -axis.
These assumptions particularly imply that the mesh points on do not merge, and the dynamic contact angle is not 0 or .
Theorem 3.1 (Existence and Uniqueness).
Theorem 3.2 (Unconditional Energy Stability).
The three summation terms in (44) correspond to the energy dissipation due to the viscous stress in the bulk, the friction force on the wall and the contact line friction, respectively.
The above theorems are extensions of the previous work by Barrett et al. [3] to problems with moving contact lines. In another related work [43], similar results were obtained for moving contact lines but on fitted meshes. There the energy stability only holds locally in time due to the required interpolation of the velocity and density between the fitted meshes at each time step. Here the global energy stability of the discrete system is established on the unfitted mesh. The proof of the theorems is similar to that in Ref. [43] and is provided in the Appendix B and C.
The discrete scheme (37c)-(37d) introduces an implicit tangential velocity for the mesh points along the fluid interface such that they tend to be uniformly distributed according to the arc length in long time [2, 42]. In our numerical experiments presented below, no re-meshing for the fluid interface is needed during the simulation.
4 Numerical results
In this section, we present some numerical results for EWoD obtained using the proposed numerical method. We first test the accuracy and convergence of the boundary integral method for the computation of the electric force on a given fluid interface in section 4.1. Then we test the convergence of the numerical method (37)-(37d) using the example of a spreading droplet in section 4.2. Subsequently, we examine the effect of the different parameters in the model on the equilibrium interface profiles in section 4.3. Finally, in section 4.4 the numerical method is applied to the spreading and migration dynamics of a droplet on various substrates.
Unless otherwise stated, we will choose , , , , , , , , , and the initial velocity in the numerical examples. The computational domain occupied by the fluids is .
4.1 Convergence test for the electric force

The electrostatic potential satisfies the Maxwell’s equations in the domain . This is outside the domain , which has a wedge-like geometry with an open angle at the contact points . The open angle is equal to the contact angle. In this geometry, the electric force in the vicinity of the contact point behaves as [6]
| (45) |
where is the distance to the contact point, and is related to the contact angle and satisfies
| (46) |
In particular, we have when .
To assess the performance of the boundary integral method for the current problem, we compute the electric force along a given interface. The interface is the semi-circle of radius centered at . The thickness of the dielectric substrate is . The numerical results are shown in Fig. 4. In the two upper panels, we plot the electric force along the interface. The different curves are obtained using different mesh sizes for (left) and (right). It is evident that the electric force exhibits a singular behavior at the contact points: the force at the contact point (more precisely, the force at half grid point away from the contact point) keeps increasing as the mesh is refined.
To further examine the singular structure, we depict the log-log plot of the electric force against the arc-length in the lower-left panel of the figure. It can be seen that the electric force behaves as as the contact line is approached. This is in good agreement with the the theoretical prediction of Eqs. (45)-(46), which is shown as the straight lines with slope for and for . These lines fit the numerical results very well.
To examine the convergence of the numerical solution as the mesh is refined, we compute the relative error defined as
| (47) |
where denotes the numerical solution obtained with mesh size . The error for different mesh sizes is shown in the lower-right panel of Fig. 4. As expected, the error decreases as the mesh is refined. In this simulation, we used the uniform mesh along the interface. In practice, one may use local mesh refinement near the contact point to obtain more accurate solutions.
4.2 Convergence test for contact line dynamics

We assess the performance of the numerical method (37)-(37d) for the contact line dynamics by carrying out simulations under different mesh sizes. We consider the spreading dynamics of a droplet. Initially the fluid interface is given by a semi-circle with center and radius . The equilibrium contact angle of the droplet is . The thickness of the dielectric substrate is , and the permittivities are and .
We use uniform mesh (see Fig. 2), and denote the mesh size in the bulk by and the mesh size on the reference domain of the interface by . In the boundary integral method, all the boundaries and interfaces are discretized into line segments; for example, the fluid-solid interface is also discretized into line segments. Different values of and will be used in the mesh refinement for the convergence test. For simplicity, we shall fix the discretization of the outer boundaries.
The evolution of the (left) contact point is shown in Fig. 5 for (upper-left panel) and (upper-right panel), respectively. In both cases, we can observe the convergence of the contact line dynamics as the mesh and the time step are refined. In the lower panels of the same figure, we plot the time history of the contact angle. Similar convergence can also be observed.
| order | order | order | ||||
|---|---|---|---|---|---|---|
| 2.16E-3 | - | 3.38E-4 | - | 3.11E-4 | - | |
| 6.28E-4 | 1.78 | 7.51E-5 | 2.17 | 1.50E-4 | 1.05 | |
| 1.70E-4 | 1.88 | 1.77E-5 | 2.09 | 4.82E-5 | 1.64 | |
| 4.33E-5 | 1.97 | 4.14E-6 | 2.10 | 1.36E-5 | 1.82 | |
| order | order | order | ||||
|---|---|---|---|---|---|---|
| 7.12E-2 | - | 2.00E-1 | - | 3.79E-1 | - | |
| 3.54E-2 | 1.01 | 1.40E-1 | 0.51 | 3.11E-1 | 0.29 | |
| 1.77E-2 | 1.00 | 9.74E-2 | 0.52 | 2.27E-1 | 0.45 | |
| 8.90E-3 | 0.99 | 6.61E-2 | 0.55 | 1.53E-1 | 0.57 | |
Next we examine the conservation of area for the droplet. The finite element space for the pressure given in (34) contains piecewise constant functions, which ensures the local mass conservation particularly over each element. Besides, by choosing in (30b) and in (30c), we can establish the mass conservation law within the weak form as
| (48) |
Therefore in this and the following simulations, we further enrich the pressure space with the basis function , the characteristic function over the domain occupied by the droplet. This helps preserving the area of the droplet [3]. In addition, the pressure jump across the interface can be captured with this function. In practical numerical implementations, the new contribution of the single basis function to (37) and (37b) can be written in terms of the integrals over as
| (49) |
In Table. 1, we present the relative area change of the droplet at . At this time the droplet has evolved close to the steady state. Here, is defined as
| (50) |
where is the area of the droplet at time . From the table, we observe that the droplet area is well-preserved. As the mesh is refined, the area change converges to zero with order close to 2.
After the droplet reaches the steady state, the theoretical value of the contact angle should converge to the equilibrium angle . In table 2, we present , the deviation of the contact angle from this equilibrium angle at , obtained with different mesh sizes. We observe that in all three cases for the different values of , the contact angle indeed converges to the equilibrium angle. When , i.e. in the absence of electric field, the convergence order is close to 1; however, the order is reduced to about 0.5 for .
The order of convergence for the contact angle can be understood as follows. Denote by and the numerical solution for the interface and its curvature at the steady state, respectively. Then from (37d), we have
| (51) |
By choosing in (51), where is the piecewise linear function taking the value 1 at and 0 at all other nodes, we obtain
| (52) |
where is the first component of , and is the contact angle of . This yields
| (53) |
where . On the other hand, the interface condition implies that the curvature of the fluid interface has the same singular structure as the electric field at the contact point. Therefore, we have , and consequently
| (54) |
where and are constants independent of the mesh size . When , we have and the curvature is constant along the interface at the steady state, therefore the convergence order of the contact angle is 1. On the other hand, in the presence of the electric field, we have , and the convergence order is lowered. In the current example, we have from Eq. (46), thus , which is consistent with the numerical results.
4.3 Equilibrium interface profiles

In this example, we investigate the influence of the various model parameters, such as , and , on the equilibrium profile of the fluid interface. The fluid interface of the droplet is initially given by a semi-circle with centre and radius . The equilibrium contact angle of the droplet is . The fluid domain is discretized into triangles with vertices, and the fluid interface is discretized into elements. The time step is .
The numerical results are shown in Fig. 6. The left panel shows the equilibrium profiles of the interface for different values of , and . Comparing with the interface profile when (i.e. in the absence of electric field), we see that the electric force flattens the interface and make the droplet spread.
A more quantitative assessment of the effect of the electric force is shown in the right panel, where we plot against for different values of and . The apparent contact angle is computed by fitting the interface by a circular arc using the apex of the interface and the given area of the droplet. From the numerical results, we observe that the ratio plays the dominant role here; more specifically, increases linearly with with the slope close to 1. In contrast, the permittivity of the fluid outside the droplet, , has little effect on the interface profile. This is in good agreement with the Lippmann equation (2). In terms of the dimensionless parameters, Eq. (2) reads
| (55) |
The contact angle computed using this equation is also shown in the figure, and good agreement with the numerical results can be observed. The discrepancy might be due to the finite system size, the effect of the boundary conditions, or the finite value of and . After all, the Lippmann equation is an asymptotic result which is derived in the limit of and [13].

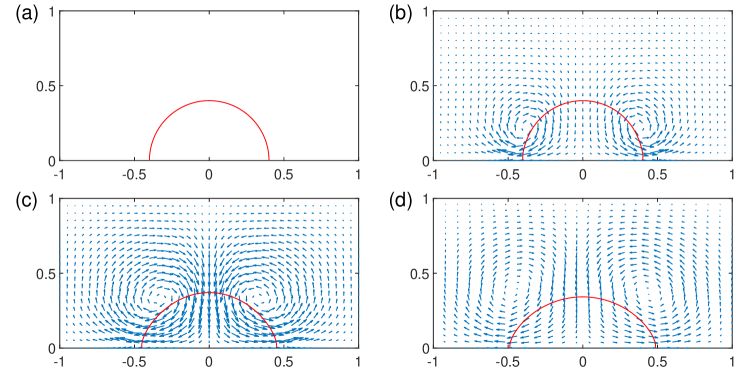

4.4 Applications
We investigate the detailed dynamics of a droplet on dielectric substrates driven by the electric force. We consider a hydrophilic case with the contact angle and a hydrophobic case with the contact angle . The initial configuration of the system and the discretizations of the computational domain and the interface are the same as those in the previous example. Several snapshots of the interface profile are shown in Fig. 7 for the hydrophilic case and in Fig. 8 for the hydrophobic case. Also shown in the figures are the respective velocity field. We observe that vortices are generated near the contact points, driving the droplet to spread on the substrate.
In Fig. 9, we plot the loss of the total energy (left panel) and the kinetic energy of the fluids (right panel) as functions of time. The total energy, as given in Eq. (21), consists of the kinetic energy, the interfacial energies and the electrostatic energy. We observe that the total energy of the discrete system decays in time, a desired property of the numerical method.

In the last example, we simulate the migration of a droplet on a substrate with non-uniform electrostatic potential prescribed on the boundary. The non-uniform potential mimics an array of electrodes placed below the substrate that is used to transport the droplet in experiments. The electrostatic potential on the lower boundary of the substrate is given as . Other parameters are chosen as , , , and . The initial interface of the droplet is given by a semi-ellipse as . Numerical results for the interface profile and the velocity field are shown in Fig. 10. We observe that the droplet first de-wets the substrate to form a near-circular shape with contact angle close to . In this stage, the dynamics is mainly driven by the surface tension. Afterwards, the electric force plays dominant role, and it drives the droplet to migrate from the right to the left.
5 Conclusions
In this work, we presented a hydrodynamic model for electrowetting on dielectric based on the earlier work on moving contact lines, and developed an efficient numerical method for the model. The numerical method combines a semi-implicit parametric finite element method for the dynamics of the fluid interface and the finite element method for the Navier-Stokes equations as well as the boundary integral method for the electric field. We proved that the numerical method admits a unique solution. In the case without the electric field, we showed that the numerical method obeys a similar energy law as the continuum model.
In the numerical experiments, we assessed the accuracy and convergence of the numerical method and investigated the effect of the different physical parameters on the interface dynamics and its equilibrium profile. Numerical results for the equilibrium profile of the interface agree well with the predictions of the Lippmann equation.
The numerical solution for the electric force exhibits a singular structure near the contact point that is consistent with theoretical results. This singularity incurs large curvature of the interface near the contact point, which deteriorates the convergence order of the numerical solution, particularly the convergence of the contact angle to the equilibrium angle.
In this work, we focused on simulations in two dimensions. The numerical method can be readily extended to three-dimensional problems. This will be left to our future work.
Acknowledgement
The work was partially supported by Singapore MOE RSB grant, Singapore MOE AcRF grants (No. R-146-000-267-114, No. R-146-000-285-114) and NSFC grant (No. 11871365).
Appendix A Energy law for the continuum model
The total energy for the EWoD model (3)-(9) in its original dimension form reads
| (56) |
Integrating by parts and using the electrostatic potential equation in (7) as well as the boundary conditions for , we can transform the electrical energy in (56) into expressions only involving line integrals over and . This gives the following alternative form of the total energy
| (57) |
which can be used to compute the discrete electrical energy in view of the boundary integral method in (41). The dynamic system obeys the energy dissipation law
| (58) |
We show the proof of (58). The dissipation of the fluid kinetic energy is
| (59) |
where we have used the divergence free condition in (3b), the interface conditions in (4a)-(4b), the boundary condition (5), the no-slip boundary condition on the upper wall and the periodic boundary conditions along .
Denote by the outward unit normal vector on the boundary of and . Differentiating the electrical energy yields
| (61) |
where the first equality results from the Reynolds transport theorem, the second equality is obtained from (7), the third equality comes from the divergence theorem, and for the last equality, we have used the boundary conditions in (8)-(9), the periodic boundary condition along as well as the fact that
| (62) |
Combining Eqs. (59)-(61), we obtain the energy dissipation law in (58). In terms of the dimensionless variables defined in section 2.3, the energy law in (58) gives Eq. (22) (scaled by ).
Appendix B Proof of Theorem 3.1
It suffices to show that the corresponding homogeneous system has only zero solution. By noting that electric force in (37) is explicitly evaluated on , thus we can consider solving the following homogeneous system for such that
| (63a) | ||||
| (63b) | ||||
| (63c) | ||||
| (63d) | ||||
where , , and and .
Taking , , and , then combining these equations yields
| (64) |
By Korn’s inequality, we have
| (65) |
thus we immediately obtain . We also have by noting . Substituting into Eq. (63d), we obtain
| (66) |
Denote . Choosing in (66) as
| (67) |
and by noting the norm in (39), we obtain
| (68) |
which implies from the assmuptions i)–iii). We then substitute and into (63) and obtain
| (69) |
Using the stability condition in (35), we consequently obtain . This shows that the homogeneous linear system (63) - (63d) has only the zero solution. Thus, the numerical scheme (37)-(37d) admits a unique solution.
Appendix C Proof of Theorem 3.2
Setting , , and in Eqs. (37)-(37d), noting and then combining these equations yield
| (70) |
It is easy to see that the following inequalities hold:
| (71) | |||
| (72) |
Using (71) and (72) in (70) and noting , , we immediately obtain Eq. (43). Replacing by in Eq. (43) and by summarising up for from to , we obtain the global discrete energy dissipation law (44).
References
- [1] M. Agnese and R. Nürnberg, Fitted finite element discretization of two-phase Stokes flow, Int J Numer Methods Fluids., 82 (2016), pp. 709–729.
- [2] J. W. Barrett, H. Garcke, and R. Nürnberg, A parametric finite element method for fourth order geometric evolution equations, J. Comput. Phys., 222 (2007), pp. 441–467.
- [3] J. W. Barrett, H. Garcke, and R. Nürnberg, A stable parametric finite element discretization of two-phase Navier–Stokes flow, J. Sci. Comput., 63 (2015), pp. 78–117.
- [4] B. Berge, Electrocapillarité et mouillage de films isolants par l’eau, Comptes Rendus de L’Academie des Sciences Paris, Serie, II, 317 (1993), pp. 157–163.
- [5] M. Bienia, M. Vallade, C. Quilliet, and F. Mugele, Electrical-field-induced curvature increase on a drop of conducting liquid, Europhys. Lett., 74 (2006), 103.
- [6] J. Buehrle, S. Herminghaus, and F. Mugele, Interface profiles near three-phase contact lines in electric fields, Phys. Rev. Lett., 91 (2003), 086101.
- [7] L. Chen and E. Bonaccurso, Electrowetting - from statics to dynamics, Adv. Colloid Interface Sci., 210 (2014), pp. 2–12.
- [8] S. K. Cho, H. Moon, and C.-J. Kim, Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits, J. Microelectromechanical. Syst., 12 (2003), pp. 70–80.
- [9] L. Clime, D. Brassard, and T. Veres, Numerical modeling of electrowetting processes in digital microfluidic devices, Comput & Fluids, 39 (2010), pp. 1510–1515.
- [10] L. Corson, N. Mottram, B. Duffy, S. Wilson, C. Tsakonas, and C. Brown, Dynamic response of a thin sessile drop of conductive liquid to an abruptly applied or removed electric field, Phys. Rev. E, 94 (2016), 043112.
- [11] L. T. Corson, C. Tsakonas, B. R. Duffy, N. J. Mottram, I. C. Sage, C. V. Brown, and S. K. Wilson, Deformation of a nearly hemispherical conducting drop due to an electric field: Theory and experiment, Phys. Fluids, 26 (2014), 122106.
- [12] D. Crowdy, Exact solutions for the static dewetting of two-dimensional charged conducting droplets on a substrate, Phys. Fluids, 27 (2015), 061705.
- [13] H. Cui and W. Ren, Interface profile near the contact line in electro-wetting on dielectric, SIAM J. Appl. Math., 80 (2020), pp. 402–421.
- [14] C. D. Daub, D. Bratko, K. Leung, and A. Luzar, Electrowetting at the nanoscale, J. Phys. Chem. C, 111 (2007), pp. 505–509.
- [15] H. B. Eral, D. M. Augustine, M. H. Duits, and F. Mugele, Suppressing the coffee stain effect: how to control colloidal self-assembly in evaporating drops using electrowetting, Soft Matter, 7 (2011), pp. 4954–4958.
- [16] M. Fontelos, G. Grün, U. Kindelan, and F. Klingbeil, Numerical simulation of static and dynamic electrowetting, J. Adhes. Sci. Technol., 26 (2012), pp. 1805–1824.
- [17] Y. Guan, B. Li, and L. Xing, Numerical investigation of electrowetting-based droplet splitting in closed digital microfluidic system: Dynamics, mode, and satellite droplet, Phys. Fluids, 30 (2018), 112001.
- [18] R. A. Hayes and B. J. Feenstra, Video-speed electronic paper based on electrowetting, Nature, 425 (2003), 383.
- [19] H. K. Kang, How electrostatic fields change contact angle in electrowetting, Langmuir, 18 (2002), pp. 10318–10322.
- [20] S. Kuiper and B. Hendriks, Variable-focus liquid lens for miniature cameras, Appl. Phys. Lett., 85 (2004), pp. 1128–1130.
- [21] A. Kutana and K. Giapis, Atomistic simulations of electrowetting in carbon nanotubes, Nano. Lett., 6 (2006), pp. 656–661.
- [22] H. Li and H. Fang, Lattice Boltzmann simulation of electrowetting, Euro. Phys. J. Special Topics, 171 (2009), pp. 129–133.
- [23] G. Lippmann, Relations entre les phénomènes électriques et capillaires, PhD thesis, Gauthier-Villars Paris, France:, 1875.
- [24] H.-W. Lu, K. Glasner, A. Bertozzi, and C.-J. Kim, A diffuse-interface model for electrowetting drops in a Hele-Shaw cell, J. Fluid. Mech., 590 (2007), pp. 411–435.
- [25] J. Monnier, P. Witomski, P. Chow-Wing-Bom, and C. Scheid, Numerical modeling of electrowetting by a shape inverse approach, SIAM J. Appl. Math., 69 (2009), pp. 1477–1500.
- [26] H. Moon, S. K. Cho, R. L. Garrell, and C.-J. C. Kim, Low voltage electrowetting-on-dielectric, J. Appl. Phys., 92 (2002), pp. 4080–4087.
- [27] F. Mugele and J.-C. Baret, Electrowetting: from basics to applications, J. Phys. Condens. Matter, 17 (2005), R705.
- [28] F. Mugele and J. Buehrle, Equilibrium drop surface profiles in electric fields, J. Phys. Condens. Matter, 19 (2007), 375112.
- [29] M. M. Nahar, G. S. Bindiganavane, J. Nikapitiya, and H. Moon, Numerical modeling of 3D electrowetting droplet actuation and cooling of a hotspot, in Proceedings of the 2015 COMSOL Conference, Boston, MA, USA, 2015, pp. 7–9.
- [30] R. H. Nochetto, A. J. Salgado, and S. W. Walker, A diffuse interface model for electrowetting with moving contact lines, Math. Mod. Meth. Appl. Sci., 24 (2014), pp. 67–111.
- [31] M. G. Pollack, A. D. Shenderov, and R. B. Fair, Electrowetting-based actuation of droplets for integrated microfluidics, Appl. Phys. Lett., 2 (2002), pp. 96–101.
- [32] C. Quilliet and B. Berge, Electrowetting: a recent outbreak, Curr. Opin. Colloid Interface Sci., 6 (2001), pp. 34–39.
- [33] W. Ren and W. E, Boundary conditions for the moving contact line problem, Phys. Fluids, 19 (2007), 022101.
- [34] W. Ren and W. E, Derivation of continuum models for the moving contact line problem based on thermodynamic principles, Commun. Math. Sci., 9 (2011), pp. 597–606.
- [35] W. Ren, D. Hu, and W. E, Continuum models for the contact line problem, Phys. Fluids, 22 (2010), 102103.
- [36] É. Ruiz-Gutiérrez and R. Ledesma-Aguilar, Lattice-Boltzmann simulations of electrowetting phenomena, Langmuir, 35 (2019), pp. 4849–4859.
- [37] C. Scheid and P. Witomski, A proof of the invariance of the contact angle in electrowetting, Math. Comput. Model., 49 (2009), pp. 647–665.
- [38] B. Shapiro, H. Moon, R. L. Garrell, and C.-J. C. Kim, Equilibrium behavior of sessile drops under surface tension, applied external fields, and material variations, J. Appl. Phys., 93 (2003), pp. 5794–5811.
- [39] M. Vallet, M. Vallade, and B. Berge, Limiting phenomena for the spreading of water on polymer films by electrowetting, Eur. Phys. J. B, 11 (1999), pp. 583–591.
- [40] H. Verheijen and M. Prins, Reversible electrowetting and trapping of charge: model and experiments, Langmuir, 15 (1999), pp. 6616–6620.
- [41] S. W. Walker and B. Shapiro, Modeling the fluid dynamics of electrowetting on dielectric (EWOD), J. Microelectromech. Syst., 15 (2006), pp. 986–1000.
- [42] Q. Zhao, W. Jiang, and W. Bao, An energy-stable parametric finite element method for simulating solid-state dewetting, (2020), arXiv:2003.01677 [math.NA].
- [43] Q. Zhao and W. Ren, An energy-stable finite element method for the simulation for moving contact lines in two-phase flows, J. Comput. Phys., 417 (2020), doi:10.1016/j.jcp.2020.109582.
- [44] Y.-P. Zhao and Y. Wang, Fundamentals and applications of electrowetting, Rev. Adhes. Adhes., 1 (2013), pp. 114–174.