A Distribution Free Conditional Independence Test with Applications to Causal Discovery
Abstract
This paper is concerned with test of the conditional independence. We first establish an equivalence between the conditional independence and the mutual independence. Based on the equivalence, we propose an index to measure the conditional dependence by quantifying the mutual dependence among the transformed variables. The proposed index has several appealing properties. (a) It is distribution free since the limiting null distribution of the proposed index does not depend on the population distributions of the data. Hence the critical values can be tabulated by simulations. (b) The proposed index ranges from zero to one, and equals zero if and only if the conditional independence holds. Thus, it has nontrivial power under the alternative hypothesis. (c) It is robust to outliers and heavy-tailed data since it is invariant to conditional strictly monotone transformations. (d) It has low computational cost since it incorporates a simple closed-form expression and can be implemented in quadratic time. (e) It is insensitive to tuning parameters involved in the calculation of the proposed index. (f) The new index is applicable for multivariate random vectors as well as for discrete data. All these properties enable us to use the new index as statistical inference tools for various data. The effectiveness of the method is illustrated through extensive simulations and a real application on causal discovery.
Key words : Conditional independence, mutual independence, distribution free.
1 Introduction
Conditional independence is fundamental in graphical models and causal inference (Jordan, 1998). Under multinormality assumption, conditional independence is equivalent to the corresponding partial correlation being 0. Thus, partial correlation may be used to measure conditional dependence (Lawrance, 1976). However, partial correlation has low power in detecting conditional dependence in the presence of nonlinear dependence. In addition, it cannot control Type I error when the multinormality assumption is violated. In general, testing for conditional independence is much more challenging than for unconditional independence (Zhang et al., 2011; Shah and Peters, 2020).
Recent works on test of conditional independence have focused on developing omnibus conditional independence test without assuming specific functional forms of the dependencies. Linton and Gozalo (1996) proposed a nonparametric conditional independence test based on the generalization of empirical distribution function, and proposed using bootstrap to obtain the null distribution of the proposed test. This diminishes the computational efficiency. Other approaches include measuring the difference between conditional characteristic functions (Su and White, 2007), the weighted Hellinger distance (Su and White, 2008), and the empirical likelihood (Su and White, 2014). Although these authors established the asymptotical normality of the proposed test under conditional independence, the performance of their proposed tests relies heavily on consistent estimate of the bias and variance terms, which are quite complicated in practice. The asymptotical null distribution may perform badly with a small sample. Thus, the authors recommended obtaining critical values of the proposed tests by a bootstrap. This results in heavy computation burdens. Huang (2010) proposed a test of conditional independence based on the maximum nonlinear conditional correlation. By discretizing the conditioning set into a set of bins, the author transforms the original problem into an unconditional testing problem. Zhang et al. (2011) proposed a kernel-based conditional independence test, which essentially tests for zero Hilbert-Schmidt norm of the partial cross-covariance operator in the reproducing kernel Hilbert spaces. The test also required a bootstrap to approximate the null distribution. Wang et al. (2015) introduced the energy statistics into the conditional test and developed the conditional distance correlation based on Székely et al. (2007), which can also be linked to kernel-based approaches. But the test statistics requires to compute high order U–statistics and therefore suffers heavy computation burden, which is of order for a sample with size . Runge (2018) proposed a non-parametric conditional independence testing based on the information theory framework, in which the conditional mutual information was estimated directly via combining the -nearest neighbor estimator with a nearest-neighbor local permutation scheme. However, the theoretical distribution of the proposed test is unclear.
In this paper, we develop a new methodology to test conditional independence and propose conditional independence tests that are applicable for continuous or discrete random variables or vectors. Let , and be three continuous random variables. We are interested in testing whether and are statistically independent given :
Here we focus on random variables for simplicity. We will consider test of conditional independence for random vectors in Section 3. To begin with, we observe that with Rosenblatt transformation (Rosenblatt, 1952), i.e., , and , is equivalent to the mutual independence of , and . Thus we convert a conditional independence test into a mutual independence test, and any technique for testing mutual independence can be readily applied. For example, Chakraborty and Zhang (2019) proposed the joint distance covariance to test mutual independence and Drton et al. (2020) constructed a family of tests with maxima of rank correlations in high dimensions. However, these mutual independence tests do not consider the intrinsic properties of , and . This motivates us to develop a new index to measure the mutual dependence. We show that the index has a closed form, which is much simpler than that of Chakraborty and Zhang (2019). In addition, it is symmetric, invariant to strictly monotone transformations, and ranges from zero to one, and is equal to zero if and only if , and are mutually independent. Based on the index , we further proposed tests of conditional independence. We would like to further note a recent work proposed by Zhou et al. (2020), who suggested to simply test whether and are independent. However, this is not fully equivalent to the conditional independence test and it is unclear what kind of power loss one might have.
The proposed tests have several appealing features. (a) The proposed test is distribution free in the sense that its limiting null distribution does not depend on unknown parameters and the population distributions of the data. The fact that both and are independent of makes the test statistic -consistent under the null hypothesis without requiring under-smoothing. In addition, even though the test statistic depends on , and , which needs to be estimated nonparametrically, we show that the test statistic has the same asymptotic properties as the statistics where true , and are directly available. This leads to a distribution free test statistic when further considering that and are uniformly distributed. Although some tests in the literature are also distribution free, the asymptotic distributions are either complicated to estimate (e.g., Su and White, 2007) or rely on the Gaussian process, which is not known how to simulate (e.g., Song, 2009) and would require a wild bootstrap method to determine the critical values. Compared with existing ones, the limiting null distribution of the proposed test depends on , and only, and the critical values can be easily obtained by a simulation-based procedure. (b) The proposed test has nontrivial power against all fixed alternatives. The population version of the test statistic ranges from zero to one and equals zero if and only if conditional independence holds. Unlike many testing procedures that are weaker than that for conditional independence (e.g., Song, 2009), the equivalence between conditional independence and mutual independence guarantees that the newly proposed test has nontrivial power against all fixed alternatives. (c) The proposed test is robust since it is invariant to strictly monotone transformations and thus, it is robust to outliers. Furthermore, , and all have bounded support, and therefore it is suitable for handling heavy-tailed data. (d) The proposed test has low computational cost. It is a –statistic, and direct calculation requires only computational complexity. (e) It is insensitive to tuning parameters involved in the test statistics. The test statistics are –consistent under the null hypothesis without under-smoothing, and is hence much less sensitive to the bandwidth. The proposed index is extended to continuous random vectors and discrete data in Section 3. All these properties enable us to use the new conditional independence test for various data.
The rest of this paper is organized as follows. In Section 2 we first show the equivalence between conditional independence and mutual independence. We propose a new index to measure the mutual dependence, and derive desirable properties of the proposed index in Section 2.1. We propose an estimator for the new index in Section 2.2. The asymptotic distributions of the proposed estimator under the null hypothesis, global alternative, and local alternative hypothesis are derived in Section 2.2. We extend the new index to the multivariate and discrete cases in Section 3. We conduct numerical comparisons and apply the proposed test to causal discovery in directed acyclic graphs in Section 4. Some final remarks are given in Section 5. We provide some additional simulation results as well as all the technical proofs in the appendix.
2 Methodology
To begin with, we establish an equivalence between conditional independence and mutual independence. In this section, we focus on the setting in which , and are continuous univariate random variables, and the problem of interest is to test . Throughout this section, denote , and . The proposed methodology is built upon the following proposition.
Proposition 1
Suppose that and are both univariate and have continuous conditional distribution functions for every given value of , and is a continuous univariate random variable. Then if and only if and are mutually independent.
We provide a detailed proof of Proposition 1 in the appendix. Essentially, it establishes an equivalence between the conditional independence of and the mutual independence among , and under the conditions in Proposition 1. Therefore, we can alleviate the hardness issue of conditional independence testing (Shah and Peters, 2020) by restricting the distribution family of the data such that , and can be estimated sufficiently well using samples. As shown in our theoretical analysis, we further impose certain smoothness conditions on the conditional distributions of as varies in the support of . This distribution family is also considered in Neykov et al. (2020) to develop a minimax optimal conditional independence test. We discuss the extension of Proposition 1 to multivariate and discrete data in Section 3.
According to Proposition 1, any techniques for testing mutual independence among three random variables can be readily applied for conditional independence testing problems. For example, Chakraborty and Zhang (2019) proposed the joint distance covariance and Patra et al. (2016) developed a bootstrap procedure to test mutual independence with known marginals. However, a direct application of these metrics may not be a good choice because it ignores the fact that the variables , and are all uniformly distributed, as well as and . Next, we discuss how to develop a new mutual independence test while considering these intrinsic properties of .
2.1 A mutual independence test
In this section, we propose to characterize the conditional dependence of and given through quantifying the mutual dependence among , and . Although our proposed test is based on the distance between characteristics functions, our proposed test is much simpler and has different asymptotic distribution as well as different convergence rate from the conditional distance correlation proposed by Wang et al. (2015). Let be an arbitrary positive weight function and , , , and be the characteristic functions of , , and , respectively. Then
| , and are mutually independent | ||||
where for a complex-valued function and is the conjugate of . By choosing to be the joint probability density function of three independent and identically distributed standard Cauchy random variables, the integration in the above equation has a closed form,
| (1) |
where , , are four independent copies of . Here the choice of the weight function is mainly for the convenient analytic form of the integration. Different from the distance correlation (Székely et al., 2007), our integration exists without any moment conditions on the data, which is more widely applicable. Furthermore, with the fact that and , (1) boils down to
| (2) |
where and are defined as
Recall that , and are uniformly distributed on . With further calculations based on (2), we obtain a normalized index and define it as to measure the mutual dependence:
| (3) | |||||
where . Several appealing properties of the proposed index are summarized in Theorem 1.
Theorem 1
Suppose that the conditions in Proposition 1 are fulfilled. The index defined in (3) has the following properties:
(1) , holds if and only if . Furthermore, if or , then .
(2) The index is symmetric conditioning on . That is, .
(3) For any strictly monotone transformations , and , .
The step-by-step derivation of and proof of Theorem 1 are presented in the appendix. Property (1) indicates that the index ranges from zero to one, equals zero when the conditional independence holds, and is equal to one if is a strictly monotone transformation of conditional on . Property (2) shows that the index is a symmetric measure of conditional dependence. Property (3) illustrates that the index is invariant to any strictly monotone transformation. In fact, is not only invariant to marginal strictly monotone transformations, but also invariant to strictly monotone transformations conditional on . For example, it can be verified that .
2.2 Asymptotic properties
In this section, we establish the asymptotic properties of the sample version of the proposed index under the null and alternative hypothesis. Consider independent and identically distributed samples , . To estimate the proposed index , we apply kernel estimator for the conditional cumulative distribution function. Specifically, define
where , is a kernel function, and is the bandwidth. Besides, we use empirical distribution function to estimate the cumulative distribution function, i.e., . The sample version of the index, denoted by , is thus given by
One can also obtain a normalized index , which is a direct normalization based on (1) without considering and :
The corresponding moment estimator is
Although at the population level, those two statistics and exhibit different properties at the sample level. This is because considers the fact that and . But on the other hand, is only a regular mutual independence test statistic, where , , and are exchangeable. When , under Conditions 1-4 listed below, is of order , while is of order because of the bias caused by nonparametric estimation. Note that is the order of kernel functions and equal to 2 when using regular kernel functions such as Gaussian and epanechnikov kernels. This indicates that is essentially consistent without under-smoothing while typically requires under-smoothing. In addition, our statistic has the same asymptotic properties as if and are observed, but does not. See Figure 1 for a numerical comparison between the empirical null distributions of the two statistics.
We next study the asymptotical behaviors of the estimated index, , under both the null and the alternative hypotheses. The following regularity conditions are imposed to facilitate our subsequent theoretical analyses. In what follows, we derive the limiting distribution of under the null hypothesis in Theorem 2.
Condition 1. The univariate kernel function is symmetric about zero and Lipschitz continuous. In addition, it satisfies
Condition 2. The bandwidth satisfies , and .
Condition 3. The probability density function of , denoted by is bounded away from to infinity.
Condition 4. The th derivatives of , and with respect to are locally Lipschitz-continuous.
Theorem 2
Suppose that Conditions 1-4 hold and the conditions in Proposition 1 are fulfilled. Under the null hypothesis,
in distribution, where , are independent chi-square random variables with one degree of freedom, and s, are eigenvalues of
That is, there exists orthonormal eigenfunction such that
The proof of Theorem 2 is given in the appendix. To understand the asymptotic distributions intuitively, we showed in the proof that can be approximated by degenerate V-statistics, i.e.,
and . By the spectral decomposition,
Therefore, which converges in distribution to the weighted sum of independent chi squared distributions provided in Theorem 2 because is asymptotically standard normal (Korolyuk and Borovskich, 2013). Moreover, the s, are real numbers associated with the distribution of , and , all of which follow uniform distributions on . In addition, , and are mutually independent under the null hypothesis. This indicates that the proposed test statistic is essentially distribution free under the null hypothesis. Therefore, we suggest a simulation procedure to approximate the null distribution and decide the critical value. The simulation procedure can be independent of the original data and hence greatly improved the computation efficiency. In what follows, we describe the simulation-based procedure in detail to decide the critical value .
-
1.
Generate , independently from mutually independent standard uniform distributions;
-
2.
Compute the statistic based on , , i.e.,
(4) -
3.
Repeat Steps 1-2 for times and set to be the upper quantile of the estimated obtained from the randomly simulated samples.
Because has the same distribution as that of under the null hypothesis, it is straightforward that this simulation-based procedure can provide a valid approximation of the asymptotic null distribution of when is large. The consistency of this procedure is guaranteed by Theorem 3.
Theorem 3
Under Conditions 1-4, it follows that
in distribution, where , are independent variables, and , are the same as that of Theorem 2.
Next, we study the power performance of the proposed test under two kinds of alternative hypotheses, under which the conditional independence no longer holds. We first consider the global alternative, denoted by , we have
We then consider a sequence of local alternatives, denoted by ,
The asymptotical properties of the test statistics under the global alternative and local alternatives are given in Theorem 4, whose proof is in the appendix. Theorem 4 shows that the proposed test can consistently detect any fixed alternatives as well as local alternatives at rate .
Theorem 4
Suppose that Conditions 1-4 hold and the conditions in Proposition 1 are fulfilled. Under , when ,
in distribution, where , and are defined in (7)-(10) in the appendix, respectively.
Under ,
in distribution, where stands for a complex-valued Gaussian random process with mean function and covariance function defined in (11) in the appendix, and is the joint probability density function of three independent and identically distributed standard Cauchy random variables.
3 Extensions
3.1 Multivariate continuous data
The methodology developed in Section 2 assumes that all the variables are univariate. In this section, we generalize the proposed index to the multivariate case. Let , and be continuous random vectors. More specifically, all elements of , and are continuous random variables. Define for the cumulative distribution function of given and for the cumulative distribution function of given for . Similar notation apply for and . Denote , , ,
Further denote , , . Similar to test of conditional independence for random variables, we first establish an equivalence between the conditional independence and the mutual independence of , and , which is stated in Theorem 5.
Theorem 5
Assume that all the conditional cumulative distribution functions used in constructing , and are continuous for every given values, then if and only if , and are mutually independent.
The proof of Theorem 5 is illustrated in the appendix. Theorem 5 established an equivalence between the conditional independence and the mutual independence among , and . It is notable that when are relatively large, may be difficult to estimate because of the curse of dimensionality. In this paper, we mainly focus on the low dimensional case. Next, we develop the mutual independence test among , and . Similar as the univariate case, we set the weight function to be the joint density of independent and identically distributed standard Cauchy random variables. We may further derive the closed form expression of
where and are two independent copies of . Moreover,
and is the norm. Then is nonnegative and equals zero if and only if . By estimating consistently at the sample level, the resulting test is clearly consistent. To implement the test, it is still required to study the asymptotic distributions under the conditional independence using independent and identically distributed samples , . We also apply kernel estimator for the conditional cumulative distribution functions when estimating and . Specifically, we estimate with
where are , , , , or , when estimating , and , respectively. The sample version of is given by
where is an independent copy of , and further calculations yield that is equal to
We next study the asymptotical behaviors of under the null hypothesis in Theorem 6, whose proof is given in the appendix. We begin by providing some regularity conditions for the multivariate data.
Condition . The bandwidth satisfies , , and .
Condition . The probability density function of the random vector , , , , and , , are all bounded away from to infinity.
Condition . The th derivatives of , and with respect to are locally Lipschitz-continuous, where can be any one of , , , , or , .
Theorem 6
Suppose that Conditions 1 and - hold and the conditions in Theorem 5 are fulfilled. Under the null hypothesis,
in distribution, where , are independent chi-square random variables with one degree of freedom, and s, are eigenvalues of
That is, there exists orthonormal eigenfunction such that
3.2 Discrete data
In this section, we discuss the setting in which , and are univariate discrete random variables. Specifically, we apply transformations in Brockwell (2007) to obtain and . Define , , , and . We further let and be two independent and identically distributed random variables, and apply the transformations
According to Brockwell (2007), both and are uniformly distributed on . In addition, and . In the following proposition, we establish the equivalence between the conditional independence and the mutual independence.
Theorem 7
For discrete random variables , and , if and only if and are mutually independent.
4 Numerical Validations
4.1 Conditional independence test
In this section, we investigate the finite sample performance of the proposed methods. To begin with, we illustrate that the null distribution of is indeed distribution free as if , and can be observed, and is insensitive to the bandwidth of the nonparametric kernel. In comparison, the null distribution of does not enjoy such properties. To facilitate the analysis, let and , where , and are independent and identically distributed. We consider three scenarios where , , are independently drawn from normal distribution , uniform distribution , and exponential distribution , respectively. It is clear that and are conditionally independent given . The sample size is set to be 100.
The simulated null distributions based on and are depicted in Figure 1. The estimated kernel density curves of based on 1000 repetitions are shown in Figure 1(a), where the reference curve is generated by the simulation-based statistic defined in (4). Clearly all the estimated density curves are close to the reference, indicating that limiting null distribution of the estimated index is indeed distribution free as if no kernel estimation is involved. In comparison, we apply the same simulation settings for and plot the null distributions in Figure 1(b), from which it can be seen that the involved estimation of and significantly influences the null distribution of . To show the insensitivity of the choice of the bandwidth, we set the bandwidths to be , where 1, and 2, respectively, and is the bandwidth obtained by the rule of thumb. The estimated kernel density curves of and based normal distributions with 1000 repetitions, together with the reference curve, are shown in Figure 1(c) and (d), from which we can see that the null distributions of almost remain the same for all choices of the bandwidths, implying that our test is insensitive to the bandwidth of the nonparametric kernel. However, the null distributions of can be dramatically influenced when the bandwidth changes.
Next, we perform the sensitivity analysis under the alternative hypothesis using Models M2 - M6, which will be listed shortly. We fix the sample size and set the significance level . To inspect how the power performance is varied with the choice of the bandwidth, we set the bandwidths to be , where is the bandwidth obtained by the rule of thumb and increase from 0.5 to 1.5 step by 0.1. The respective empirical powers are charted in Table 1, from which we can see that the test is the most powerful when is around 1. Therefore, we advocate using the rule of thumb (i.e., ) to decide the bandwidth in practice.
 |
 |
|
| (a) | (b) | |
 |
 |
|
| (c) | (d) |
| 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| M2 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| M3 | 0.957 | 0.962 | 0.98 | 0.977 | 0.975 | 0.971 | 0.972 | 0.968 | 0.955 | 0.960 | 0.956 |
| M4 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| M5 | 0.999 | 1.000 | 0.997 | 0.998 | 0.999 | 0.997 | 0.995 | 0.997 | 0.999 | 0.997 | 0.997 |
| M6 | 0.999 | 0.999 | 0.999 | 1.000 | 0.999 | 0.999 | 0.996 | 1.000 | 0.999 | 1.000 | 1.000 |
We compare our proposed conditional independence test (denoted by “CIT”) with some popular nonlinear conditional dependence measure. They are, respectively, the conditional distance correlation (Wang et al., 2015, denoted by “CDC”), conditional mutual information (Scutari, 2010, denoted by “CMI”), and the KCI.test (Zhang et al., 2011, denoted by “KCI”). We conduct 500 replications for each scenario. The critical values of the CIT are obtained by conducting 1000 simulations. We first consider the following models with random variable . In (M1), . This model is designed for examining the empirical Type I error rate. While (M2)(M6) are designed for examining the power of the proposed test of conditional independence. Moreover, for M1 - M3, we generate , and independently from . For M4 - M6, we let , and generate , independently to investigate the power of the methods under heavy tailed distributions.
M1: , .
M2: , .
M3: , .
M4: , .
M5: , .
M6: , .
The empirical sizes for M1 and powers for the other five models at the significance levels and 0.1 are depicted in Table 2. In our simulation, we consider two sample sizes and . Table 2 indicates that the empirical sizes of all the tests are all very close to the level , which means that the Type I error can be controlled very well. As for the empirical power performance of models M2M6, the proposed test outperforms other tests for both normal data and heavy tailed data, especially when .
Test M1 M2 M3 M4 M5 M6 50 0.05 CIT 0.056 1.000 0.572 1.000 0.954 0.888 CDC 0.050 0.886 0.338 0.837 0.881 0.473 CMI 0.048 0.380 0.070 0.829 0.898 0.448 KCI 0.038 0.884 0.250 0.191 0.048 0.010 0.1 CIT 0.098 1.000 0.712 1.000 0.974 0.938 CDC 0.134 0.970 0.562 0.934 0.930 0.642 CMI 0.088 0.484 0.132 0.854 0.912 0.485 KCI 0.088 0.968 0.344 0.323 0.145 0.042 100 0.05 CIT 0.048 1.000 0.960 1.000 1.000 0.997 CDC 0.066 0.998 0.694 0.918 0.971 0.624 CMI 0.054 0.402 0.070 0.877 0.904 0.424 KCI 0.040 1.000 0.444 0.371 0.095 0.020 0.1 CIT 0.112 1.000 0.998 1.000 1.000 0.999 CDC 0.158 1.000 0.834 0.974 0.985 0.745 CMI 0.098 0.496 0.124 0.902 0.926 0.455 KCI 0.088 1.000 0.598 0.513 0.199 0.057
We next examine the finite sample performance of the tests when is two-dimensional random vector, i.e., . M7 is designed for examining the size since . Five conditional dependent model M8–M12 are designed to examine the power of the tests. Similar as M1-M6, we generate , , and independently from in each of the following model.
M7: , .
M8: , .
M9: , .
M10: , .
M11: , .
M12: , .
Test M7 M8 M9 M10 M11 M12 50 0.05 CIT 0.046 0.672 0.906 0.686 0.440 0.788 CDC 0.052 0.408 0.850 0.054 0.128 0.134 CMI 0.072 0.426 0.192 0.392 0.118 0.300 KCI 0.046 0.030 0.088 0.026 0.662 0.248 0.1 CIT 0.092 0.792 0.948 0.798 0.582 0.874 CDC 0.126 0.670 0.976 0.194 0.298 0.264 CMI 0.120 0.506 0.292 0.500 0.210 0.386 KCI 0.098 0.092 0.190 0.074 0.820 0.492 100 0.05 CIT 0.048 0.936 0.998 0.936 0.664 0.988 CDC 0.084 0.890 1.000 0.920 0.972 0.306 CMI 0.044 0.412 0.164 0.392 0.126 0.300 KCI 0.044 0.038 0.172 0.028 0.990 0.358 0.1 CIT 0.104 0.958 1.000 0.966 0.766 0.996 CDC 0.168 0.978 1.000 0.986 0.992 0.456 CMI 0.128 0.486 0.240 0.460 0.194 0.390 KCI 0.090 0.092 0.358 0.108 0.998 0.608
Lastly, we study the finite sample performance of the tests when , and are all multivariate. Specifically, , , . M13 is designed to examine the size of the tests, while M14 -M18 are designed to study the powers. We generate , , , and independently from for each model in M13-M18.
M13: , .
M14: , .
M15: , .
M16: , .
M17: , .
M18: , .
Simulation results of models M7M12 and models M13M18 are summarized in Tables 3 and 4, respectively, from which it can be seen that the proposed method outperforms all other tests in terms of type I error and power. Furthermore, the numerical results seem to indicates that when the conditional set is large, the conditional mutual information and the kernel based conditional test tend to have relatively low power. The conditional distance correlation has high power but suffers huge computational burden.
Test M13 M14 M15 M16 M17 M18 50 0.05 CIT 0.05 1.000 1.000 1.000 0.363 0.986 CDC 0.019 0.022 0.984 0.304 0.120 0.833 CMI 0.01 0.582 0.812 0.205 0.082 0.020 KCI 0.036 0.036 0.047 0.042 0.052 0.688 0.1 CIT 0.100 1.000 1.000 1.000 0.564 0.997 CDC 0.092 0.064 1.000 0.733 0.262 0.939 CMI 0.028 0.6 0.915 0.294 0.170 0.054 KCI 0.086 0.081 0.099 0.083 0.118 0.886 100 0.05 CIT 0.026 1.000 1.000 1.000 0.873 1 CDC 0.048 0.032 1.000 0.965 0.38 0.999 CMI 0.004 0.498 1.000 0.211 0.218 0.036 KCI 0.044 0.042 0.052 0.05 0.068 0.999 0.1 CIT 0.077 1.000 1.000 1.000 0.965 1.000 CDC 0.127 0.13 1.000 1.000 0.567 1.000 CMI 0.013 0.523 1.000 0.338 0.378 0.077 KCI 0.087 0.077 0.102 0.091 0.119 1.000
4.2 Application to causal discovery
In this section, we consider a real application of conditional independence test in causal discovery of directed acyclic graphs. For a directed acyclic graph , the nodes corresponds to a random vector , and the set of edges do not form any directed cycles. Two vertices and are d-separated by a subset of vertices if every path between them is blocked by . One may refer to Wasserman (2013) for a formal definition. Denote the joint distribution of by . The joint distribution is said to be faithful with respect to a graph if and only if for any , and any subset ,
One of the most famous algorithms for recovering the graphs satisfying the faithfulness assumption is the PC–algorithm (Spirtes et al., 2000; Kalisch and Bühlmann, 2007). The algorithm could recover the graph up to its Markov equivalence class, which are sets of graphs that entail the same set of (conditional) independencies. The performance of the PC–algorithm relies heavily on the (conditional) independence tests because small mistakes at the beginning of the algorithm may lead to a totally different directed acyclic graph (Zhang et al., 2011). One of the most popular approach for testing conditional independence is the partial correlation, under the assumption that the joint distribution follows Gaussian distribution and the nodes relationship is linear (Kalisch and Bühlmann, 2007). Conditional mutual information (Scutari, 2010) is another possible option. Zhang et al. (2011) proposed a kernel-based conditional independence test for causal discovery in directed acyclic graphs. In this section, we demonstrate how the proposed conditional independence index can be applied for causal discovery in real data. Additional simulation results are relegated into the appendix.
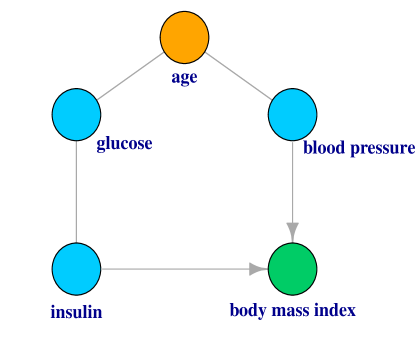
We analyze a real data set originally from the National Institute of Diabetes and Digestive and Kidney Diseases (Smith et al., 1988). The dataset consists of serval medical predictor variables for the outcome of diabetes. We are interested in the causal structural of five variables: age, body mass index, 2-hour serum insulin, plasma glucose concentration and diastolic blood pressure. After removing the missing data, we obtain samples. The PC–algorithm is applied to examine the causal structure of the five variables based on the four different conditional independence measures. We implement the causal algorithms by the R package pcalg (Kalisch et al., 2012). The estimated causal structure are shown in Figure 2. The proposed test gives the same estimated graph as the partial correlation, since the data is approximately normally distributed. To interpret the graph, note that age is likely to affect the diastolic blood pressure. The plasma glucose concentration level is also likely to be related to age. This is confirmed by the causal findings of (a), (b) and (c) in Figure 2. Besides, serum insulin has plausible causal effects on body mass index, and is also related to plasma glucose concentration. The causal relationship between age and blood pressure is not confirmed in part (c), the test of conditional mutual information. This is not a surprise given the high false positive rate reported in Table 5 in the appendix. The kernel based conditional independence is a little conservative and is not able to detect some of the possible edges. To further illustrate the robustness of the proposed test, we make a logarithm transformation on the data, and apply the same procedure again. The estimated causal structures are reported in Figure 3. We observe that the proposed test results in the same estimated structure as the original data, which echos property (4) in Theorem 1, i.e., the proposed test is invariant with respect to monotone transformations. However, the partial correlation test yields more false positives, since the normality assumption is violated.

 (a)
(b)
(a)
(b)

 (c)
(d)
(c)
(d)

 (a)
(b)
(a)
(b)

 (c)
(d)
(c)
(d)
5 Discussions
In this paper we developed a new index to measure conditional dependence of random variables and vectors. The calculation of the estimated index requires low computational cost. The test of conditional independence based on the newly proposed index has nontrivial power against all fixed and local alternatives. The proposed test is distribution free under the null hypothesis, and is robust to outliers and heavy-tailed data. Numerical simulations indicate that the proposed test is more powerful than some existing ones. The proposed test is further applied to directed acyclic graphs for causal discovery and shows superior performance.
6 Technical Proofs
6.1 Proof of Proposition 1
For , define quantile function for as
Similarly, we can define , the quantile function for , for . Since and have continuous conditional distribution functions for every given value of , it follows that when and ,
This implies that is equivalent to . In addition, conditional on , is uniformly distributed on , which does not depend on the particular value of , indicating . That is, . Similarly, . Thus, the conditional independence together with and implies that
Thus, , and are mutually independent.
On the other hand, the mutual independence immediately leads to the conditional independence . Therefore, the conditional independence is equivalent to the mutual independence of , and . We next show that the mutual independence of , and is equivalent to mutual independence of , and .
Define for . If , and are mutually independent, then
holds for all and . On the other hand, if , and are mutually independent, it follows that
holds for all and . Thus, the mutual independence of , and is equivalent to the mutual independence of , and . This completes the proof.
6.2 Proof of Theorem 1
We start with the derivation of the index . , and are mutually independent if and only if
| (5) |
for arbitrary positive weight function . We now show that the proposed index is proportional to the integration in (5) by choosing to be the joint probability density function of three independent and identically distributed standard Cauchy random variables.
With some calculation and Fubini’s theorem, we have
According to the property of characteristic function for standard Cauchy distribution, we have
Then by choosing , i.e., the joint density function of three i.i.d. standard Cauchy distributions, we have
| (6) | ||||
Furthermore, with the fact that and , (6) is equal to
where and are defined as
Now we calculate the normalization constant . It follows by the Cauchy-Schwarz inequality that
where the equality holds if and only if holds with probability 1, where (because is nonnegative). Recall that , and are all uniformly distributed on , further calculations give us
This, together with the normalization constant , yield the expression of the index . Subsequently, the properties of the index can be established.
(1) holds obviously. It equals only when , , are mutual independent, which is equivalent to the conditional independence . holds obviously according to the derivation of the index . The equality holds if and only if . Because , we have . If or , it is easy to check . This completes the proof of Part (1).
(2) This property is trivial according to the definition of .
(3) For strictly monotone transformations , we have when is strictly increasing, equals , while when is strictly decreasing, it equals . It can be easily verified that , then we have no matter whether is strictly increasing or decreasing. Similarly, let , we obtain that . It is clear that equals either or , implying . Therefore, we have
and it is true that .
6.3 Proof of Theorem 2
For simplicity, we denote by and . We write as
With Taylor’s expansion, when and , we have
where , and are defined to be each row in an obvious way. Similarly, we expand as
As for , we have
Therefore, it follows that
We first show that is of order . In fact,
Under the null hypothesis, , and are mutually independent, it is easy to verify that , and hence
Then for each fixed , we have
Thus, is clearly of order because . Now we deal with .
Under the null hypothesis, because , is uniformly distributed, we have . Thus, the corresponding U-statistic of the equation above is second order degenerate. In addition, when any two of are identical, we have
Then the summations associated with any two of the are identical is of order . Therefore, . It remains to deal with . Similarly, the corresponding U-statistic of
is second order degenerate and hence we obtain that .
Next, we show . Recall that
Similar to dealing with , we have . We now evaluate .
Because under the null hypothesis, , it follows that for each ,
and the first term of is of order because and . In addition, for each ,
is degenerate and hence the second term of is also of order because , indicating . Similarly, we have . Thus it follows that .
Finally, we show that . Or equivalently, we show that and are all of order , where
We first show that , where
Without loss of generality, we only show that . Calculate
Thus, when and ,
where the last equality holds due to equations (2)-(3) of section 5.3.4 in Serfling (2009) and the fact that . Therefore, since
when the th derivatives of and with respect to are locally Lipschitz-continuous, is clearly of order by noting that the summation in the last display is degenerate.
Next, we consider , where
We first show that . It follows that
Because . For each ,
is of order . Then because . For , . By expanding the , , , in as U statistics and apply the same technique as showing and , it follows immediately that is of order . Thus is of order .
For and , we only show that is of order , for simplicity. Recall that is defined as
The summations associated with either or are of order following similar reasons as showing , and that associated with are of order similar to dealing with . As a result, is of order .
For , we have
We only show that because the other terms are similar. Calculate
Then the summations associated with either or are of order similar to dealing with , and that associated with or are of order similar to the second term of .
To sum up, we have shown that
where the right hand side is essentially a first order degenerate V-statistics. Thus by applying Theorem 6.4.1.B of Serfling (2009),
where , are independent random variables, and , are the corresponding eigenvalues of . It is worth mentioning that the kernel is positive definite and hence all the s are positive. Therefore, the proof is completed.
6.4 Proof of Theorem 3
Since we generate , independently from uniform distribution, it is quite straightforward that and are mutually independent. In addition, we can write as
which clearly converges in distribution to , where , are independent random variables, and , are the eigenvalues of , implying , for , and hence the proof is completed.
6.5 Proof of Theorem 4
We use the same notation as the proof in Theorem 2. With Taylor’s expansion, when and , we have
Therefore, we have
We deal with the four terms, respectively. For , by applying Lemma 5.7.3 and equation (2) in section 5.3.1 of Serfling (2009), we have
| (7) | |||||
Next, we deal with . Recall that
By applying Lemma 5.7.3 and equation (2) in section 5.3.1 of Serfling (2009) again, we can obtain that
| (8) | |||||
where is an independent copy of .
It remains to deal with and . equals
By definition, we have and hence it can be verified that
Denote . Thus,
Thus when and , we have
| (9) | |||||
Following similar arguments, we can show that
| (10) | |||||
To sum up, it is shown that could be written as
where and are defined in (7)-(10), respectively. Thus the asymptotic normality follows.
Under the local alternative, we have and it is easy to verify that , and are mutually independent. With Taylor’s expansion, we have
where . Then we can write as
With the same arguments as that in deriving in the proof of Theorem 2, we have .
Now we deal with . For ease of notation, we write as in the remaining proof. By decomposing as , we have
is clearly of order because for each fixed ,
is also of order because for each ,
is degenerate.
Then we deal with the last quantity, , where
We simplify first. According to the proof of Theorem 2, we have
As we can see, is of order . Then we can derive that
It can be verified that
And
is of order and is only a function of , which is independent of . Substituting this into , we have
Then is clearly of order by noting that the conditional expectation of the above display is of order while the unconditional expectation is zero.
Next, we deal with . It is straightforward that
Similar to dealing with , we can show that
Then is of order because and
is also with the expectation being zero. Similar as before, we can show that
Now we show that . Because , we have
Similar to dealing with , we can obtain that .
Combining these results together, we have
Then we can verify that can be written as
It is clear that the empirical process
converges in distribution to a complex valued gaussian process with mean function
and covariance function given by
| (11) |
Therefore, by employing empirical process technology, we can derive that
Hence we conclude the proof for local alternatives.
6.6 Proof of Theorem 5
Firstly, is equivalent to . According to Proposition 4.6 of Cook (2009), it is also equivalent to
Following similar arguments for proving the equivalence between and in the proof of Proposition 1, the above conditional independence series are equivalent to
According to the proof of Proposition 1, we know that is equivalent to for . Hence the conditional independence series hold if and only if
Then by applying Proposition 4.6 of Cook (2009) again, we know that is equivalent to . Furthermore, with the same arguments for dealing with , we can obtain that it is additionally equivalent to . Besides, with the fact that and , we can get the conditional independence is equivalent to the mutual independence of , and . Therefore, the proof is completed by following similar arguments with the proof of Proposition 1.
6.7 Proof of Theorem 6
Following the proof of Theorem 2, we denote by , and . Then we have
Therefore, can be written as
With Taylor’s expansion, when , , under conditions and , we have
where denotes the -th Kronecker power of the matrix , and
In addition, we can expand as
Therefore, by the definition of , we have
where and are defined obviously. Similarly, when , and , we can expand as
and it follows that
Then following similar arguments in the proof of Theorem 2, we have , and are all of order and equals . Combing these results, we have
where the right hand side is a first order degenerate V statistics. Thus by applying Theorem 6.4.1.B of Serfling (2009),
where , are independent random variables, and , are the corresponding eigenvalues of . Therefore, the proof is completed.
6.8 Proof of Theorem 7
It suffices to show that if and only if because is equivalent to and are mutually independent under and .
We only show that if and only if , because similar arguments will yield that it is also equivalent to . It is quite straightforward that implies . While when , we have for each , and in the corresponding support,
Substituting into the above equation, with some straight calculation, the left hand side is
Because is standard uniformly distributed, we obtain
where is the cumulative distribution function of a standard uniformly distributed random variable. Now assume that conditional on , the support of is , where . Therefore, when , the expectation in the above equation is
The expectation equals . That is, .
When , we can calculate the expectation as
Since we have shown that , with the fact that the expectation equals , we can get .
Similarly, we can obtain that , . Consequently, we have for all and in their support. That is, . Therefore, the proof is completed.
7 Additional Simulations Results
We consider the directed acyclic graph with 5 nodes, i.e., , and only allow directed edge from and for . Denote the adjacency matrix . The existence of the edge follows a Bernoulli distribution, and we set , for . When , we replace with independent realizations of a uniform random variable. The value of the first random variable is randomly sampled from some distribution . Specifically,
The value of the next nodes is
for . All random errors are independently sampled from the distribution . We consider two scenarios, where follows either normal distribution or uniform distribution . We compare our proposed conditional independence test (denoted by “CIT”) with other popular conditional dependence measure. They are, respectively, the partial correlation conditional mutual information (Scutari, 2010, denoted by “CMI”), and the KCI.test (Zhang et al., 2011, denoted by “KCI”). We set the sample size , 100, 200 and . The true positive rate and false positive rate for the four different tests are reported in Tables 5, from which we can see that as the sample size increases, the true positive rate of the proposed method steadily grows, and the proposed method outperforms the other tests, while the false positive rate remains under control with slightly decrease.
| Samples | 50 | 100 | 200 | 300 | 50 | 100 | 200 | 300 |
|---|---|---|---|---|---|---|---|---|
| Tests | ||||||||
| true positive rate | false positive rate | |||||||
| CIT | 0.555 | 0.658 | 0.734 | 0.789 | 0.117 | 0.112 | 0.107 | 0.103 |
| PCR | 0.479 | 0.489 | 0.546 | 0.589 | 0.101 | 0.110 | 0.130 | 0.135 |
| CMI | 0.472 | 0.530 | 0.604 | 0.590 | 0.097 | 0.127 | 0.143 | 0.150 |
| KCI | 0.360 | 0.516 | 0.592 | 0.634 | 0.072 | 0.135 | 0.144 | 0.168 |
| Tests | ||||||||
| true positive rate | false positive rate | |||||||
| CIT | 0.468 | 0.587 | 0.734 | 0.736 | 0.070 | 0.099 | 0.095 | 0.113 |
| PCR | 0.469 | 0.526 | 0.588 | 0.545 | 0.111 | 0.129 | 0.140 | 0.140 |
| CMI | 0.497 | 0.568 | 0.566 | 0.633 | 0.103 | 0.127 | 0.138 | 0.149 |
| KCI | 0.386 | 0.458 | 0.523 | 0.564 | 0.082 | 0.099 | 0.123 | 0.122 |
References
- Brockwell (2007) Brockwell, A. (2007). “Universal residuals: A multivariate transformation.” Statistics & Probability Letters, 77(14), 1473–1478.
- Chakraborty and Zhang (2019) Chakraborty, S. and Zhang, X. (2019). “Distance metrics for measuring joint dependence with application to causal inference.” Journal of the American Statistical Association, 114(528), 1638–1650.
- Cook (2009) Cook, R.D. (2009). Regression graphics: ideas for studying regressions through graphics, volume 482. John Wiley & Sons.
- Drton et al. (2020) Drton, M., Han, F., and Shi, H. (2020). “High dimensional independence testing with maxima of rank correlations.” The Annals of Statistics, To Appear.
- Huang (2010) Huang, T.M. (2010). “Testing conditional independence using maximal nonlinear conditional correlation.” The Annals of Statistics, 38(4), 2047–2091.
- Jordan (1998) Jordan, M.I. (1998). Learning in Graphical Models, volume 89. Springer Science & Business Media.
- Kalisch and Bühlmann (2007) Kalisch, M. and Bühlmann, P. (2007). “Estimating high-dimensional directed acyclic graphs with the pc-algorithm.” Journal of Machine Learning Research, 8, 613–636.
- Kalisch et al. (2012) Kalisch, M., Mächler, M., Colombo, D., Maathuis, M.H., and Bühlmann, P. (2012). “Causal inference using graphical models with the r package pcalg.” Journal of Statistical Software, 47(11), 1–26.
- Korolyuk and Borovskich (2013) Korolyuk, V.S. and Borovskich, Y.V. (2013). Theory of U-statistics, volume 273. Springer Science & Business Media.
- Lawrance (1976) Lawrance, A. (1976). “On conditional and partial correlation.” The American Statistician, 30(3), 146–149.
- Linton and Gozalo (1996) Linton, O. and Gozalo, P. (1996). “Conditional independence restrictions: Testing and estimation.” Cowels Foundation Discussion Paper.
- Neykov et al. (2020) Neykov, M., Balakrishnan, S., and Wasserman, L. (2020). “Minimax optimal conditional independence testing.” arXiv preprint arXiv:2001.03039.
- Patra et al. (2016) Patra, R.K., Sen, B., and Székely, G.J. (2016). “On a nonparametric notion of residual and its applications.” Statistics & Probability Letters, 109, 208–213.
- Rosenblatt (1952) Rosenblatt, M. (1952). “Remarks on a multivariate transformation.” The Annals of Mathematical Statistics, 23(3), 470–472.
- Runge (2018) Runge, J. (2018). “Conditional independence testing based on a nearest-neighbor estimator of conditional mutual information.” In “Proceeding of International Conference on Artificial Intelligence and Statistics,” pages 938–947.
- Scutari (2010) Scutari, M. (2010). “Learning bayesian networks with the bnlearn r package.” Journal of Statistical Software, Articles, 35(3), 1–22. ISSN 1548-7660. doi:10.18637/jss.v035.i03.
- Serfling (2009) Serfling, R.J. (2009). Approximation Theorems of Mathematical Statistics. John Wiley & Sons.
- Shah and Peters (2020) Shah, R.D. and Peters, J. (2020). “The hardness of conditional independence testing and the generalised covariance measure.” Annals of Statistics, 48(3), 1514–1538.
- Smith et al. (1988) Smith, J.W., Everhart, J., Dickson, W., Knowler, W., and Johannes, R. (1988). “Using the adap learning algorithm to forecast the onset of diabetes mellitus.” In “Proceedings of the Annual Symposium on Computer Application in Medical Care,” page 261. American Medical Informatics Association.
- Song (2009) Song, K. (2009). “Testing conditional independence via rosenblatt transforms.” The Annals of Statistics, 37(6B), 4011–4045.
- Spirtes et al. (2000) Spirtes, P., Glymour, C.N., and Scheines, R. (2000). Causation, prediction, and search. MIT press.
- Su and White (2007) Su, L. and White, H. (2007). “A consistent characteristic function-based test for conditional independence.” Journal of Econometrics, 141(2), 807–834.
- Su and White (2008) Su, L. and White, H. (2008). “A nonparametric hellinger metric test for conditional independence.” Econometric Theory, 24(4), 829–864.
- Su and White (2014) Su, L. and White, H. (2014). “Testing conditional independence via empirical likelihood.” Journal of Econometrics, 182(1), 27–44.
- Székely et al. (2007) Székely, G.J., Rizzo, M.L., and Bakirov, N.K. (2007). “Measuring and testing dependence by correlation of distances.” The Annals of Statistics, 35(6), 2769–2794.
- Wang et al. (2015) Wang, X., Pan, W., Hu, W., Tian, Y., and Zhang, H. (2015). “Conditional distance correlation.” Journal of the American Statistical Association, 110(512), 1726–1734.
- Wasserman (2013) Wasserman, L. (2013). All of Statistics: A Concise Course in Statistical Inference. Springer Science & Business Media.
- Zhang et al. (2011) Zhang, K., Peters, J., Janzing, D., and Schölkopf, B. (2011). “Kernel-based conditional independence test and application in causal discovery.” In “Proceedings of the Twenty-Seventh Conference on Uncertainty in Artificial Intelligence,” UAI’11, pages 804–813. AUAI Press.
- Zhou et al. (2020) Zhou, Y., Liu, J., and Zhu, L. (2020). “Test for conditional independence with application to conditional screening.” Journal of Multivariate Analysis, 175, 104557.