A dissimilarity measure for semidirected networks
Abstract
Semidirected networks have received interest in evolutionary biology as the appropriate generalization of unrooted trees to networks, in which some but not all edges are directed. Yet these networks lack proper theoretical study. We define here a general class of semidirected phylogenetic networks, with a stable set of leaves, tree nodes and hybrid nodes. We prove that for these networks, if we locally choose the direction of one edge, then globally the set of directed paths starting by this edge is stable across all choices to root the network. We define an edge-based representation of semidirected phylogenetic networks and use it to define a dissimilarity between networks, which can be efficiently computed in near-quadratic time. Our dissimilarity extends the widely-used Robinson-Foulds distance on both rooted trees and unrooted trees. After generalizing the notion of tree-child networks to semidirected networks, we prove that our edge-based dissimilarity is in fact a distance on the space of tree-child semidirected phylogenetic networks.
Index Terms:
phylogenetic, admixture graph, Robinson-Foulds, tree-child, -representation, ancestral profileI Introduction
Historical relationships between species, virus strains or languages are represented by phylogenies, which are rooted graphs, in which the edge direction indicates the flow of time going forward. Semidirected phylogenetic networks are to rooted networks what undirected trees are to rooted trees. They appeared recently, following studies showing that the root and the direction of some edges in the network may not be identifiable, from various data types [28, 3]. Consequently, several methods to infer phylogenies from data aim to estimate semidirected networks, rather than fully directed networks, such as SNaQ [28], NANUQ [1], admixtools2 [23], poolfstat [11], NetRAX [22], and PhyNEST [18].
The theoretical identifiability of semidirected networks is receiving increased attention [12, 24, 33, 2] but graph theory is still at an early stage for this type of network [but see 21]. In particular, adapted distance and dissimilarity measures are lacking, as are tools to test whether two phylogenetic semidirected networks are isomorphic. These tools are urgently needed for applications. For example, when an inference method is evaluated using simulations, its performance is quantified by how often the inferred network matches the true network used to simulate data, or how similar the inferred network is to the true network. Tools for semidirected networks would also help summarize a posterior sample of networks output by Bayesian inference methods. Even for a basic summary such as the posterior probability of a given topology, we need to decide which semidirected networks are isomorphic, in a potentially very large posterior sample of networks.
Unless additional structure is assumed, current methods appeal to a naive strategy that considers all possible ways to root semidirected networks, and then use methods designed for directed networks, e.g. to check if the candidate rooted networks are isomorphic or to minimize a dissimilarity between the two rooted networks across all possible root positions.
In this work, we first generalize the notion of semidirected phylogenetic networks in which edges are either of tree type or hybrid type, such that any edge can be directed or undirected. We relax the constraint of a single root (of unknown position). Multi-rooted phylogenetic networks were recently introduced, although for directed networks, to represent the history of closely related and admixed populations [29] or distant groups of species that exchanged genes nonetheless [14, 15]. Our general definition requires care to define a set of leaves consistent across all compatible directed phylogenetic networks.
For these semidirected networks, we define an edge-based “-representation” , extending the node-based -representation, denoted here as , by Cardona et al. [7]. The “ancestral profile” of a rooted network contain the same information as the node-based representation , that is: the number of directed paths from each node to each leaf [5]. So our edge-based representation also extends the notion of ancestral profile to semidirected networks, in which ancestral relationships are unknown between some nodes because the root is unknown. Briefly, ’s information for an edge depends on whether the edge direction is known or implicitly constrained by the direction of other edges in the network. For example, if is a semidirected tree and an edge is explicitly or implicitly directed, then associates the edge to the cluster of taxa below it. If instead the edge direction depends on the unknown placement of the root(s), then associates the edge to the bipartition of the taxa obtained by deleting the edge from the semidirected tree. If has reticulations, uses -vectors to generalize the notion of clusters, storing the number of directed paths from a given node to each taxon. Our extension associates a directed edge to the -vector of its child node, and an undirected edge to two -vectors: one for each direction that the edge can take. To handle and distinguish semidirected networks with multiple roots, also associates each root to a -vector, well-defined even when the exact root position(s) are unknown. We then define a dissimilarity measure between semidirected networks.
Our network representation can be calculated in polynomial time, namely where is the number of leaves and is the number of edges. The associated network dissimilarity can then be calculated in time. It provides the first dissimilarity measure adapted to semidirected networks (without iteratively network re-rooting) that can be calculated in polynomial time. Linz and Wicke [21] also recently considered semidirected networks (with a single root of unknown position). They showed that “cut edge transfer” rearrangements, which transform one network into another, define a finite distance on the space of level-1 networks with a fixed number of hybrid nodes. This distance is NP-hard to compute, however, because it extends the subtree prune and regraft (SPR) distance on unrooted trees [13].
Finally, we generalize the notion of tree-child networks to semidirected networks, and prove that is a true distance on the subspace of tree-child semidirected networks, extending the result of [7] to semidirected networks using an edge-based representation. On trees, this dissimilarity equals the widely used Robinson-Foulds distance between unrooted trees [27]. We provide concrete algorithms to construct from a given semidirected network, and to reconstruct the network from .
As a proper distance, can decide in polynomial time if two tree-child semidirected networks are isomorphic. For rooted phylogenetic networks, the isomorphism problem is polynomially equivalent to the general graph isomorphism problem, even if restricted to tree-sibling time-consistent rooted networks [8]. As semidirected networks include single-rooted networks, the graph isomorphism problem for semidirected networks is necessarily more complex. The general graph isomorphism problem was shown to be of subexponential complexity [4] but is not known to be solvable in polynomial time. Therefore, there is little hope of finding a dissimilarity that can be computed in polynomial time, and that is a distance for general semidirected phylogenetic networks. Hence, dissimilarities like offer a balance between computation time and the extent of network space in which it can discriminate between distinct networks.
II Basic definitions for semidirected graphs
For a graph we denote its vertex set as and its edge set as . The subgraph induced by a subset of vertices is denoted as , and the edge-induced subgraph is denoted as for a subset .
We use the following terminology for a directed graph . For a node , its in-degree is denoted as and out-degree as . Its total degree is . We may omit when no confusion is likely. For , we write if there exists a directed path . A node is a leaf if ; is an internal node otherwise. We denote the set of leaves as . A node is a root if ; a tree node if ; and a hybrid node otherwise. We denote the set of tree nodes as and the set of hybrid nodes as . An edge is a tree edge if is a tree node; a hybrid edge otherwise. We denote the set of tree edges as and the set of hybrid edges as . A descendant of is any node such that . A tree path is a directed path consisting only of tree edges. A tree descendant leaf of is any leaf such that there exists a tree path . An elementary path in is a directed path such that the first node has out-degree in and all intermediate nodes have in-degree and out-degree in . In the remainder, we use “path” to mean “directed path” for brevity, unless otherwise specified.
We now extend these notions to semidirected graphs.
Definition 1 (semidirected graph).
A semidirected graph is a tuple , where is the set of vertices, and is the set of edges, being the set of undirected edges and the set of directed edges.
Undirected edges in are denoted as for some , instead of the standard notation of for brevity. Directed edges in are denoted as for some , implying the direction from to , with referred to as the parent of the edge, and as its child. A directed graph is a semidirected graph with no undirected edges: .
For , denotes the number of directed edges with as their child, the number of directed edges with as their parent, the number of undirected edges in incident to , and . We may omit when no confusion is likely. Furthermore, . is binary if or for all nodes. is bicombining if for all hybrid nodes.
A semidirected graph is compatible with another semidirected graph if can be obtained from by directing some undirected edges in .
The contraction of , denoted as , is the directed graph obtained by contracting every undirected edge in . It is well defined, as it can be viewed as the quotient graph of under the partition that groups nodes connected by a series of undirected edges. For , is defined as the node in which gets contracted into.
In a semidirected graph , a node is a root if it only has outgoing edges. It is a tree node if . Otherwise, is called a hybrid node. The set of tree nodes is denoted as or and the set of hybrid nodes as or . A tree edge is an undirected edge, or a directed edge whose child is a tree node. A hybrid edge is a directed edge whose child is a hybrid node. We denote the set of tree edges as or and the set of hybrid edges as or .
A semidirected cycle is a semidirected graph if its undirected edges can be directed so that it becomes a directed cycle. A semidirected graph is acyclic if it does not contain a semidirected cycle. We refer to directed acyclic graphs as DAGs and to semidirected acyclic graphs as SDAGs.
Next, we define a more stringent notion of compatibility to maintain the classification of nodes and edges as being of tree versus hybrid type, illustrated in Figs. 1 and 2.
Definition 2 (phylogenetically compatible, rooted partner, network).
An SDAG is phylogenetically compatible with another SDAG if is compatible with and . A rooted partner of is a DAG that is phylogenetically compatible with . A multi-root semidirected network, or network for short, is an SDAG that admits a rooted partner.
Note that if SDAG is phylogenetically compatible with SDAG , then and . Note also the rooted partner of a binary network may not be binary by the typical definition for rooted networks, since the root can have degree instead of .
Not all SDAGs are networks (see Fig. 1 for an example). We are interested in networks rather than general SDAGs, because a network can represent evolutionary history up to “rerooting”, as captured by its rooted partners. Fig. 1 gives an example network (, top) and 2 of its 4 rooted partners (bottom).

Traditionally, phylogenetic trees and networks are connected and with a single root [30]. We consider here a broader class of graphs, allowing for multiple connected components and multiple roots per connected component. We also allow for non-simple graphs, that is, for multiple parallel edges between the same two nodes and , directed and in the same direction for the graph to be acyclic. With a slight abuse of notation, we keep referring to each parallel edge as . Self-loops are not allowed as they would cause the graph to be cyclic. The term “rooted partner” was introduced by Linz and Wicke [21] in the context of traditional semidirected phylogenetic networks in which the set of directed edges is precisely the set of hybrid edges, and for which a rooted partner has a single root.
We will use the following results frequently. The first one is trivial.
Proposition 1.
Let be an SDAG phylogenetically compatible with SDAG . Then .
Proposition 2.
Let be a network, and the semidirected graph obtained from by undirecting some of the tree edges of . Then is a network, and is phylogenetically compatible with .
Proof.
Let be the set of tree edges in that are undirected to obtain . We first consider the case when consists of a single edge . We shall establish the following claims:
-
1.
is a network;
-
2.
the edges of in retain their type (undirected, tree, or hybrid);
-
3.
is phylogenetically compatible with .
For claim 1, suppose for contradiction that is not an SDAG. Then there exists in a semidirected cycle which contains . Let be a rooted partner of , and the subgraph made of the corresponding edges in . Since cannot be a directed cycle, there exist two hybrid edges and in . Both are also directed in by phylogenetic compatibility. Because they are hybrid edges, they are distinct from , so they are directed in and . This contradicts being a semidirected cycle, showing that is an SDAG. Since it also admits as a rooted partner, is a network.
Claim 2 follows from the observation that the types of nodes (tree vs hybrid) in stays the same. Claim 3 follows from claim 2.
If contains multiple edges, then we iteratively undirect one edge at a time. By the previous argument, the resulting graph at each step is a network with which is phylogenetically compatible, because phylogenetic compatibility is transitive. Hence is a network and is phylogenetically compatible with it. ∎
The next definition is motivated by the fact that phylogenies are inferred from data collected at leaves, which are known entities with labels (individuals, populations, or species), whereas non-leaf nodes are inferred and unlabeled.
Definition 3 (unrooted, rooted and ambiguous leaves).
A node in a network is a rooted leaf in if is a leaf in every rooted partner of ; and an unrooted leaf if it is a leaf in some rooted partner . We denote the set of rooted leaves and unrooted leaves as and respectively. An ambiguous leaf is a node in .

Clearly, . If is directed, then . As we will see later in 12, an ambiguous leaf is of degree 1 in the undirected graph obtained by undirecting all edges in , hence a leaf in the traditional sense. In Fig. 2 for example, is an ambiguous leaf in but a rooted leaf in .
In Section III we make no assumption regarding and . But to extend -vectors to semidirected graphs in Section IV, we will need a stable set of leaves across rooted partners. For a vector of distinct labels , an -DAG is a DAG whose leaves are bijectively labeled by . To extend this definition we impose below, but we will see (after 12) that this requirement is less stringent than it appears.
Definition 4 (leaf-labeled network).
A network is labeled in and called an -network, if and is bijectively labeled by elements of . The leaf set of an -network is defined as .
For example, in Fig. 2 is an -network with , while is not because . is a -network.
A rooted partner of an -network must be an -DAG: since generally, we have that and can inherit the labels in .
Our main result concerns the class of tree-child graphs. If is a DAG, it is tree-child if every internal node of has at least one child that is a tree node [16]. Equivalently, is tree-child if every non-leaf node in has a tree descendant leaf [7]. We extend this notion to semidirected networks, illustrated in Fig. 2.
Definition 5 (semidirected tree-child).
A network is weakly tree-child if one of its rooted partners is tree-child. It is strongly tree-child, or simply tree-child, if all its rooted partners are tree-child.
Since a DAG is a network with a single rooted partner, is strongly and weakly tree-child if and only if it is tree-child as a DAG. In Fig. 2, is weakly but not strongly tree-child: of its 3 rooted partners, only one is tree-child. Later in 11, we provide a characterization easy to check without enumerating rooted partners.
III Properties of semidirected acyclic graphs
Proposition 3.
A semidirected graph is acyclic if and only if the undirected graph induced by its undirected edges consists of trees only (i.e. is a forest), and is acyclic.
Proof.
Let be a semidirected graph. Suppose that is not a forest. Then there exists a compatible directed graph of which contains a cycle that exists in a compatible directed graph of , therefore is not acyclic. Next suppose that contains a cycle . Then there exists a compatible directed graph of which contains a cycle such that is obtained from after contracting edges in that correspond to undirected edges in , and so is not acyclic.
Now suppose the graph induced by is a forest and that is acyclic. If is not acyclic, then by definition there exists a compatible directed graph that contains a cycle . Since is acyclic, must contract into a single node in . This implies that contains undirected edges only, hence is contained in , a contradiction. Therefore is acyclic. ∎
In a network , a semidirected path from to is a sequence of nodes , such that for , either or is an edge in . On we define if there is a semidirected path from to , and the associated equivalence relation: if and . In Fig. 2, in and . Also so in , but not in . On equivalence classes, becomes a partial order, with which we can define the following.
Definition 6 (undirected components, root components, directed part).
In a network , an undirected component is the subgraph induced by an equivalence class under . A root component of is an undirected component that is maximal under . A root component is trivial if it consists of a single node. The set of edges and nodes that are not in a root component is called the directed part of . We denote the set of nodes in the directed part as and the set of edges . We also denote the set of nodes in root components and the set of edges .
The directed part of is generally not a subgraph: it may contain an edge but not one of its incident nodes. In Fig. 2, edges in the directed part are those in black (tree edges) and blue (hybrid edges). Edges in root components are in brown. In , is adjacent to the directed part, but is not in . has a trivial root component: . The following result justifies the name given to the equivalence classes.
Proposition 4.
For nodes in a network , if and only if there is an undirected path between and .
Proof.
Consider and connected by an undirected path. Since this path does not contain any directed edge, clearly, and , hence .
Now suppose . By definition, there exists a semidirected path from to and a semidirected path from to . If then all edges in these paths must be shared and undirected. This is because is acyclic, in case and have distinct edges incident to and . Then, there is an undirected path between and as claimed. Otherwise, there exists and such that is the concatenation of semidirected paths ; from to not containing any for ; and . Then, the concatenation of with forms a semidirected cycle. Since is acyclic, this case cannot occur. ∎
We now characterize undirected components as the undirected trees in the forest induced by ’s undirected edges.
Proposition 5.
Let be a network and the graph induced by the undirected edges of . Then is a forest where:
-
1.
each tree corresponds to an undirected component of , and has at most one node with ;
-
2.
the root components of are exactly the trees without such nodes, and they contain tree nodes only.
Proof.
By 3, is a forest. By 4, each tree in is an undirected component. If a tree in had more than one node with , it would be impossible to direct the edges in without making one of them hybrid, contradicting the existence of a rooted partner of .
For the second claim, let be a tree in . Note that implies that and ’s equivalence class is not maximal under . So if is maximal under , then all nodes in have , which implies that is a tree node. Conversely, if is not maximal, then there exist nodes in , in a different tree of , and a semidirected path from to containing a directed edge. Taking the last directed edge on this path gives a node in with . ∎
Lemma 6.
Let be a network and a rooted partner of . Let . If in , then .
Proof.
Let in . Then in . By Definition 6, in as well. Therefore, belongs to the same root component as , hence . ∎
Proposition 7.
Let be a network. Let and be rooted partners of . Then edges in have the same direction in and .
Proof.
Let be an undirected component of that is not a root component. We need to show that ’s edges have the same direction in and . By 5, is an undirected tree in , and has exactly one node with an incoming edge in . Then must be the root of in both and , for and to be phylogenetically compatible with , which completes the proof. ∎
Definition 7 (root choice function).
Let be a network, and be the set of root components of . A root choice function of is a function such that for a root component , . In other words, chooses a node for each root component.
Conceptually, a semidirected network represents uncertainty about the root(s) position. Next, we show that to resolve uncertainty, exactly 1 node from each root component must be chosen as root, and this choice can be made independently across root components. In other words, root choice functions are in one-to-one correspondence with rooted partners. As a result, all rooted partners have the same number of roots: the number of root components. In Fig. 1, has 2 root components each with 2 nodes, hence rooted partners.
Proposition 8.
Given a root choice function of a network , there exists a unique rooted partner of such that the set of roots in is the image of . Conversely, given any rooted partner of , there exists a unique root choice function such that .
Proof.
Let be a rooted partner of . For a root choice function , let be the graph compatible with obtained by directing edges in as they are in , and away from in any root component (which is possible by 5). is a DAG because is acyclic. To prove that is phylogenetically compatible with (and hence a rooted partner), we need to show that . Since all edges in incident to both and are directed from to , they have the same direction in and . Therefore nodes in and edges in are of the same type in and (and ). Furthermore, by construction and 5, all edges in remain of tree type in both and . Hence is a rooted partner of . Finally, the root set of is the image of because a root component’s root is a root of the full network (from for any ) and because cannot contain any root of (by 5 again).
To prove that is unique, let be a rooted partner of whose set of roots is the image of . By 7, edges in have the same direction in and . For a root component , because is an undirected tree in , rooted by the same in both and . Therefore .
Let be a rooted partner of . By 5 and phylogenetic compatibility, must have exactly one root in each root component . Define such that is this root of in . By the arguments above, cannot have any root in , and then . ∎
We can define the following thanks to 7:
Definition 8 (network completion).
The completion of a network is the semidirected graph obtained from by directing every undirected edge in its directed part, as it is in any rooted partner of . More precisely, let be a rooted partner of . We direct as in if . A network is complete if .
Proposition 9.
For a network , is a network and phylogenetically compatible with .
Proof.
Remark 1.
Propositions 5 and 8 yield practical algorithms. Finding the root components requires only traversing the network , tracking the forest of undirected components, and which nodes have nonzero in-degree. Computing then consists in directing the edges away from such a node in each tree of , if one exists. In particular, in a single traversal of we can construct a rooted partner , record the roots of , record the edges of that were in root components of , and for each such edge record the corresponding root. To do this, for each tree in that is a root component, we arbitrarily choose and record a node as root, direct the edges in away from , record these edges as belonging to a root component of , and for all these edges record as the corresponding root. We then direct the rest of the undirected edges the same way as when computing the completion. We shall use this in Algorithm 1 later.
With as many directed edges as can be possibly implied by the directed edges in , is the network that we are generally interested in. We define phylogenetic isomorphism between networks based on their completion.
Definition 9 (network isomorphism).
-networks and are phylogenetically isomorphic, denoted by , if and are isomorphic as semidirected graphs, with an isomorphism that preserves the leaf labels.
In Fig. 2 for example, is complete, but is not. and are not phylogenetically isomorphic, because the edge incident to remains undirected in the completion . is not phylogenetically compatible with or , and not phylogenetically isomorphic to either.
Lemma 10.
Let be a complete network. There exists a directed edge in if and only if .
Proof.
Using , we can now decide if a network is weakly or strongly tree-child in a single traversal, thanks to the following.
Proposition 11.
Let be a complete network, its set of root components, and the set of nodes that form trivial root components. For , let be the set of nodes in adjacent to with and without a tree-child in . is weakly (resp. strongly) tree-child if and only if every non-leaf node in has a tree child in ; and for every , (resp. ).
If is a DAG, then is the full node set and we simply recover the tree-child definition. Recall that children are defined using directed edges only. For example, take in Fig. 1. In the edges incident to and are directed; remains undirected and forms a root component (). but , because is incident to exactly 1 undirected edge and 2 outgoing hybrid edges. By 11, is weakly tree-child. Indeed, its partners rooted at are tree-child (e.g. Fig. 1 bottom left) but its partners rooted at are not (e.g. bottom right). The proof below shows that, more generally, a weakly tree-child network has at most one ‘problematic’ node in each root component, and this node must serve as root for a rooted partner to be tree-child.
Proof of 11.
We first characterize which rooted partners are tree-child. Suppose that is complete, and that every non-leaf node in has a tree child in . For a root choice function , we claim that the rooted partner is tree-child if and only if for every . To prove this claim, consider a node in . If is in then has the same children in as in any rooted partner, so its tree child in is also its tree child in . Otherwise, is in some , is non-trivial and . If , then at least one of its neighbor in is its tree child in . If and is not adjacent to , then and is a leaf in or its unique neighbor is its tree child in . If has a tree child in , then is also its tree child in . Otherwise, . Let be its unique neighbor in . If then is the parent of in , has the same children in as in , so has no tree child in (by definition of ). If then is a child of in , and since is a tree node (because ) has a tree child in . Overall, we get that is tree-child if and only if any node in any is a root, which proves the claim.
For the first direction of 11, suppose that is complete and weakly tree-child. If is a non-leaf node in , then has the same children in as in any rooted partner, so has a tree child in . Also, we can apply our claim. Since is tree-child for some , by our claim we get which implies that for each . Suppose further that is strongly tree-child. If for some then is nontrivial, we can choose for which is not tree-child, a contradiction. This proves the first direction.
For the second direction, assume that every non-leaf node in has a tree child in and (resp. ) for every . Then admits at least one tree-child rooted partner (setting such that for any with ) and is weakly tree-child. Further, if for all , then is tree-child for any root choice function , and is strongly tree-child. ∎
Finally, we characterize unambiguous leaves quickly.
Lemma 12.
In a network , is an ambiguous leaf if and only if , , and .
Proof.
Let be an ambiguous leaf. Then . By 7, is in so . Finally, if , then is isolated, and a rooted leaf. If , then in any rooted partner one of the incident edges is directed away from , and is never a leaf. Therefore .
Conversely, let be incident to exactly one edge, . By 8, we can find a rooted partner where is a non-leaf root as well as a rooted partner where is a root and is a leaf. Hence is an ambiguous leaf. ∎
Remark 2.
We argue that requiring for to be an -network is reasonable in practice. By 12, an ambiguous leaf is in a root component and incident to only one undirected edge. The ambiguity is whether becomes a leaf or a root in a rooted partner. In practice, one knows which nodes are supposed to be leaves, with a label and data [10, 25]. Then one can, for each root component, either direct all incident edges to ambiguous leaves towards them, making them rooted leaves (as in Fig. 2, compare and ), or pick one ambiguous leaf to serve as root for that component (as in , Fig. 2) and direct edges accordingly, turning the remaining ambiguous leaves into rooted leaves. This yields a network with . By 5, this can be done in where is the number of edges.
IV Vectors and Representations
Formally a multiset is a tuple , where is a set and : gives the multiplicity. We consider two multisets and to be the same if , , and . To simplify notations, we use to denote a multiset by enumerating each element as many times as its multiplicity. For example, contains with multiplicity 2 and with multiplicity 1. For brevity, we identify a multiset with the set if , e.g. . We adopt the standard notion of sum and difference for multisets. The symmetric difference between multisets is defined as .
In what follows, we consider a vector of distinct labels , whose order is arbitrary but fixed, as it will determine the order of coordinates in all vectors and representations. For an -DAG and for node , the -vector of is defined as the tuple where is the number of labels in and is the number of paths in from to the leaf with the label in . As in [7], the partial order between -vectors is the coordinatewise order. Namely, for and , if for all . If and then and are incomparable. The node-based -representation of from [7], denoted as , is defined as the multiset . Algorithm 1 in [7] computes recursively in post-order thanks to the following property, which is a slight extension of Lemma 4 in [7] allowing for parallel edges by summing over child edges instead of child nodes.
Lemma 13.
Let be a DAG and a node in . Then
We will make frequent use of the following result, whose original proof easily extends to DAGs with parallel edges thanks to 13. It is an extension of Lemma 5 of [7] stating the assumption used in the proof by [7], which is weaker than requiring a tree-child DAG.
Lemma 14.
Let be an -DAG and two nodes in .
-
1.
If there exists a path , then .
-
2.
If and if has a tree descendant leaf, then there exists a path .
-
3.
If and if has a tree descendant leaf, then are connected by an elementary path.
Other results in [7] similarly hold when parallel edges are allowed, such as their Theorem 1 on tree-child networks (which must be non-binary if they have parallel edges).
The rest of the section is organized as follows. In part IV-A we define the edge-based -representation for -networks, with Algorithm 1 to compute it. Part IV-B presents properties of this -representation for tree-child networks, and part IV-C describes how to reconstruct a complete tree-child -network from its edge-based -representation. The networks in Fig. 3 are used as examples throughout.
IV-A Edge-based -representation
We first extend the notion of -vectors to nodes in the directed part of an -network.
Proposition 15.
Let be an -network, and . Then the set of directed paths starting at , and consequently , are the same for any rooted partner of .
Using the proposition above, the following is well-defined.
Definition 10 (-vector of a node in the directed part).
Let be an -network and any rooted partner of . For , we define .
In Fig. 3 for example, is in the directed part of . Applying 13 recursively on , and their parent in , we get with leaf order given by . All 3 hybrid edges have the same -vector in : .
Proof of 15.
Let be a rooted partner of . Let (), where , be a directed path starting at in . We claim are all in : Otherwise, we can find such that and . Since , either or is in . By 4, this implies either or , a contradiction. Therefore any directed paths from in lies entirely in . The conclusion then follows from 7. ∎
Now we turn to root components. Here the -vector for a node is not well-defined as it varies depending on the rooted partner. It turns out that if locally we choose the direction of an edge , say , then globally the set of directed paths from across all rooted partners are the same, and consequently the -vector of is fixed. We now formalize this.
Proposition 16.
Let be an -network with . Then the set of directed paths starting at , and consequently , are the same for any rooted partner of where is directed as , and there always exists such a rooted partner.
Using this proposition, we can define the following.
Definition 11 (directional -vector).
Let be an -network, , and any rooted partner of where is directed as . We call the directional -vector of , and write it as , or if is clear in the context.
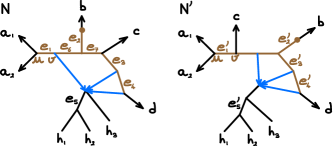
In Fig. 3 for example, is in the root component of , with directional -vectors: and . In , has these same directional -vectors.
Before the proof we establish a lemma.
Lemma 17.
Let be a network with an edge in some root component. Let be the semidirected graph obtained from by directing as . Then is a network phylogenetically compatible with .
Proof.
Let be a rooted partner of where is a root. Let be the set of edges that are directed in but not in . By phylogenetic compatibility, consists of tree edges only. also contains .
Since from we get back if we undirect all the edges in , by 2, is phylogenetically compatible with . Then and is phylogenetically compatible with . ∎
In the next lemma and definition, we associate each root component (rather than a node or edge) to a -vector.
Lemma 18.
Let be an -network, and a root component of . Then the -vector is independent of the root choice function . Furthermore, if is an edge in , this -vector is equal to .
With this lemma we define the following:
Definition 12 (root -vector).
Let be an -network and a root component of . The root -vector of is defined as where is any root choice function of . We write it as or if is clear from context.
In Fig. 3, has one root component (in brown), with . The root component of has the same root -vector.
Proof of 18.
The claims obviously hold when is trivial. Now consider non-trivial and distinct nodes in . Let (resp. ) be a rooted partner of where (resp. ) is a root. To prove the first claim, we show that by constructing a bijection between and , where () is the set of directed paths from to in , for an arbitrary but fixed leaf of . Suppose , where is the last node such that lies in . We can modify to a new path by changing the subpath to , the unique tree path between and in . By 6, the subpath only contain edges in . Then by 7, . Obviously, is a bijection whose inverse is the map from to constructed by symmetry, proving the first claim.
For the second claim, let be an edge in and , , , and as before. Let be the set of directed paths from to in , such that is the coordinate value for in . Define similarly. We can partition where paths in contain , and paths in do not. It is easily verified that , and that prepending to a path gives a bijection . Since is arbitrary, we get . ∎
We are now ready to define the edge-based -representation of an -network, and an algorithm to compute it.
Definition 13 (edge-based -representation).
Let be a complete -network. To edge of we associate a set , called the edge -vector set of the edge , as follows:
- •
-
•
For , using 11 we define .
Let be the set of root components of , then the edge-based -representation of , denoted by , is defined as the multiset
with from 12 and a tag value indicating a root -vector. For an -network , is defined as .
In Fig. 3 for example, contains 19 -vector sets: 9 in , 3 in , 6 in and 1 in , using notations as in Algorithm 1. contains the unidirectional -vector sets from the 8 edges incident to the leaves, such as for the edge to , and from . is from the hybrid edges: with multiplicity 3. has only 1 element: . Finally, contains the bidirectional -vector sets from the 6 edges in the root component(s). For example, contributes See the Appendix for the other 5.

18 together with 5 yields the following Algorithm 1 to compute the edge-based -representation of an -network with leaves. As discussed in Remark 1, line 1 in Algorithm 1 takes a single traversal of and time. Computing the node-based -representation by Algorithm 1 in [7] takes time. The remaining steps iterate over edges and take time, giving an overall complexity of .
-
•
the set of roots in
-
•
: the function that maps a node in a root component of to the root of in
-
•
the set of edges in that corresponds to
-
•
Compared to the node-based representation , has two features. Unsurprisingly, each undirected edge (whose direction is not resolved by completion) is represented as bidirectional using two -vectors. This is similar to the representation of edges in unrooted trees, as bipartitions of . The second feature is the inclusion of a -vector for each root component, which may seem surprising. For a non-trivial root component , is redundant with information from for any in , by 18. The purpose of including the root -vectors in is to keep information from trivial root components, for networks with multiple roots. Without this information, cannot discriminate simple networks with multiple roots when one or more root component is trivial, as illustrated in Fig. 4.
Networks with a unique and non-trivial root component correspond to standard phylogenetic rooted networks, with uncertainty about the root location. For these networks, we could use edge -vectors only: , that is, omit in Algorithm 1. Indeed, the root -vector of the unique root component is redundant with of any edge in . For this class of standard networks, then, our results below also hold using the simplified definition of .
IV-B Properties for tree-child networks
We will use the following results to reconstruct a tree-child network from its edge-based -representation. First we characterize when and how -vectors are comparable.
Proposition 19.
Let and be distinct nontrivial root components of a strongly tree-child -network . Then directional -vectors from and from are incomparable to one another.
Proof.
Let and . Suppose for contradiction that . Let be a rooted partner of in which and are roots. Then and . Since is tree-child, there exists a path in by 14 (possibly up to relabeling if ) Since is a tree edge in , by Lemma 1 in [7], contains or is contained in . Both cases imply that (using that is a root for the first case), a contradiction. ∎
Proposition 20.
In a weakly tree-child -network, different root components have incomparable root -vectors.
Proof.
Lemma 21.
Let be a strongly tree-child -network. Suppose are two (not necessarily distinct) edges in root component of such that the undirected tree path from to in contains and . Then:
-
1.
,
-
2.
is incomparable to ,
-
3.
is incomparable to .
Proof.
Let (resp. ) be a rooted partner of with (resp. ) as a root. For part 1, by 14, we have .
For part 2, by symmetry, it suffices to show that . Let be the neighbors of besides . Then by 15 if , or 16 if . Then by 13 we have .
First, suppose for contradiction that . Then for each , , and since is tree-child there exists a path in by 14. As is a root in and not contained in these paths, are hybrid nodes. Then does not have a tree child in , a contradiction.
Now suppose instead , then for all . If for some , then is the only neighbor of other than . By 14, and are connected by an elementary path in , which is impossible as both have as a parent. Therefore for all , which leads to a contradiction by the argument above.
Part 3 follows from part 2 using that for any by 18. ∎
Next, we relate edges with identical directional -vectors.
Lemma 22.
Let be a strongly tree-child -network, and a fixed -vector. If we direct all edges with as , then these edges form a directed path. If the path is nonempty, we denote the first node as .
Proof.
Let . Take and in . By 19, they are in the same root component , so there is an undirected path in connecting and . By applying 21 multiple times and permuting labels if necessary, we may assume is of the form with . For a rooted partner of with a root, we have , which implies by 14 there is an elementary path in from to . By 6, this path lies in . But since induces a forest, this elementary path must be the part of the path . Therefore all the intermediate nodes in have and . Furthermore, if and are consecutive nodes in , then because . Therefore all edges in are in , and form a directed path when directed as in the statement.
Now take an undirected path of edges in , of maximum length, and let one of its edges. To show that contains all the edges in , take . By the previous argument, and are connected by a tree path . Also by the previous argument, all intermediate nodes in and in have . Since cannot extend by definition of , must be contained in , therefore is in as claimed. ∎
Finally, the next result was proved for orchard DAGs, which include tree-child DAGs [9, Proposition 10]. We restrict its statement to hybrid nodes here, because we allow networks to have in and out degree-1 nodes.
Lemma 23.
Let be a tree-child -DAG. Let be distinct hybrid nodes in . Then .
IV-C Reconstructing a complete tree-child network
To reconstruct a complete tree-child network from its edge-based -representation, Algorithm 2 will first construct for a rooted partner from . Then Algorithm 3 will use to undirect some edges in and recover .
Continuing with in Fig. 3 (left), is given in the Appendix. Algorithm 2 starts with for edges incident to leaves and (in black in Fig. 3). , for the unique -vector shared by all 3 hybrid edges in . has a single element because has a single root component, so the loop on line 5 has a single iteration and all elements in satisfy (from edges in brown in Fig. 3). On line 6, has 12 elements (see the Appendix). We can arbitrarily pick , which corresponds to directed rightward. Then for the partner of rooted at the node incident to and (see Fig. A7).
Proof of correctness for Algorithm 2.
As and have the same rooted partners and , we may assume to be complete.
Let be a root choice function such that , where is the function on line 8 and is defined in 22. By 18 and 20, is well-defined. Let . We shall show that Algorithm 2, with as input, produces the output .
Consider partitioning into the following sets:
-
is a tree node in the directed part of ,
-
is a hybrid node,
-
is a root in ,
-
in a root component of , but not a root in .
We will establish for the multisets in the algorithm (), to conclude the proof.
For , 23 implies that for distinct in . Therefore . By the definition of hybrid edges, is equal to , which implies .
For , by 18 and 20, the -vectors of the roots in are the same as the root -vectors, and are all distinct. Hence .
For , let be the set of edges in that corresponds to . Consider the map that associates to its parent edge in . It is well-defined because excludes the roots of , root components only contain tree nodes (5) and by 10. Furthermore, the map is a bijection. Therefore we have .
is constructed in Algorithm 2 by taking a -vector from the pair and , for each undirected edge in each root component. Let be the root component that contains and let . Then equals but no other root -vector by 20, so is considered at exactly one iteration of the loop on line 9. Next we need to show that on line 10, exactly one -vector gets chosen, and is where .
From 22, let be the root of in and such that . Since is a root in and , the tree path in from to contains . If also contains , then and by 21, so line 10 defines as claimed. If does not contain , then the tree path from to contains and , so by 21 is incomparable to and . Further, by the choice and 22. Therefore line 10 defines , which concludes the proof. ∎
Given from in Fig. 3 and from Algorithm 2 (Fig. A7), contains 6 -vectors (see the Appendix) so 6 edges in are undirected to obtain . One of them has multiplicity 1 in but corresponds to an elementary path of 2 edges in adjacent to . On this path, only is undirected by Algorithm 3.
Proof of correctness of Algorithm 3.
Let denote the set of edges in that corresponds to edges in . It suffices to show that line 6 undirects all edges in and no other. Obviously, line 2 defines . Suppose consists of elements with multiplicities . We know that exactly consists of edges whose children have -vector , for . Thus we only need to show that for each , the first edges in are in . By 6, if an edge is not in , then all edges below it are also not in . Therefore along the path , edges in must come first before any edge not in , which finishes the proof. ∎
The following theorem derives directly from Theorem 1 in [7] to reconstruct from , and the application of Algorithms 2 and 3.
Theorem 1.
Let and be strongly tree-child -networks. Then if and only if and are phylogenetically isomorphic.

, and .
V The edge-based -distance
Definition 14 (edge-based -distance).
Let and be -networks. The edge-based -dissimilarity between and is defined as
For example, in Fig. 6. For the networks in Fig. 3, due to non-matching -vector sets for edges and in and the 3 unlabelled tree edges in . (see Fig. 3 and the Appendix for details).
We are now ready to state our main theorem, which justifies why we may refer to as a distance.

Theorem 2.
For a vector of leaf labels , is a distance on the class of (complete) strongly tree-child -networks.
Proof.
From the properties of the symmetric difference, is a dissimilarity in the sense that is it symmetric, non-negative, and satisfies the triangle inequality. It remains to show that satisfies the separation property. Let and be tree-child -networks. If then and by 1, . ∎
For unrooted trees, the -vector of each undirected edge encodes the bipartition on associated with the edge, hence agrees with the Robinson-Foulds distance on unrooted trees.
On rooted trees, agrees with . Indeed, if is a directed tree or forest on , then each non-root node has a unique parent edge with element in ; and each root forms to a trivial root component with element in .
However, does not generally extend . For example, consider the rooted networks in Fig. 6. They have the same representation, hence . However, their representations differ, due to edges with the same vector (1 path to only) but different tags (tree edge in versus hybrid edge in ). Hence can distinguish these networks: .
We can compute using a variant of Algorithm 3 in [7]. Specifically, we first group the elements of () by their type: of the form , , , or . Then it suffices to equip a total order and apply Algorithm 3 in [7] to each group, then add the distances obtained from the 4 groups. For the first 3 types we can simply use the lexical order on the -vector . For the last type, we may compare two elements by comparing the lexically smaller -vector first and then the larger one, to obtain a total order within the group.
As in [7], with computed and sorted, the above takes time where . Taking into account computing and sorting , computing takes time.
This complexity can also be expressed in terms of the number of leaves and root components, thanks to the following straightforward generalization of Proposition 1 in [7], allowing for multiple root components.
Proposition 24.
Let be a tree-child -network with leaves and root components.
Then
.
A node is called elementary
if it is a tree node and either
, or .
If has no elementary nodes
then
where , and .
Proof.
Since is an -network, it has no ambiguous leaves, and the elementary nodes in are the tree nodes of out-degree 1 in any rooted partner. By considering a rooted partner, we may assume that is a DAG with roots, and follow the proof of Proposition 1 in [7]. Their arguments remain valid for the bounds on and when has roots, and when the removal of all but 1 parent hybrid edges at each hybrid node gives a forest instead of a tree. To bound we enumerate the parent edges of each node: then use the previous bounds. ∎
Therefore, as long as and are bounded and there are no elementary nodes, for example in binary tree-child networks with a single root component, then . Consequently, computing on one such network or computing on two such networks takes time.
VI Conclusion and extensions
For rooted networks, the node-based representation , or equivalently the ancestral profile, is known to provide a distance between networks beyond the class of tree-child networks, such as the class of semibinary tree-sibling time-consistent networks [6] and stack-free orchard binary networks [5], a class that includes binary tree-child networks. Orchard networks can be characterized as rooted trees with additional “horizontal arcs” [32]. They were first defined as cherry-picking networks: networks that can be reduced to a single edge by iteratively reducing a cherry or a reticulated cherry [17]. A cherry is a pair of leaves with a common parent. A reticulated cherry is a pair of leaves such that the parent of is a tree node and the parent of is a hybrid node with as a parent hybrid edge. Reducing the pair means removing taxon if is a cherry or removing hybrid edge if is a reticulated cherry, and subsequently suppressing and if they are of degree 2. Cherries and reticulated cherries are both well-defined on the class of semidirected networks considered here, because leaves are well-defined (stable across rooted partners), each leaf is incident to a single tree edge, and hybrid nodes / edges are well-defined. A stack is a pair of hybrid nodes connected by a hybrid edge, and a rooted network is stack-free if it has no stack. As hybrid edges are well-defined on our general class of networks, the concepts of stacks and stack-free networks also generalize directly. Therefore, we conjecture that for semidirected networks, our edge-based representation and the associated dissimilarity also separate distinct networks well beyond the tree-child class, possibly to stack-free orchard semidirected networks.
To discriminate distinct orchard networks with possible stacks, Cardona et al. [9] introduced an “extended” node-based -representation of rooted phylogenetic networks. In this representation, the -vector for each node is extended by one more coordinate, , counting the number of paths from to a hybrid node (any hybrid node). On rooted networks, adding this extension allows to distinguish between any two orchard networks, even if they contain stacks (but assumed binary, without parallel edges and without outdegree-1 tree nodes in [9]). For semidirected networks, we conjecture that the edge-based representation can also be extended in the same way, and that this extension may provide a proper distance on the space of semidirected orchard networks.
Phylogenetic networks are most often used as metric networks with edge lengths and inheritance probabilities. Dissimilarities are needed to compare metric networks using both their topologies and edge parameters. For trees, extensions of the RF distance, which extends, are widely used. They can be expressed using edge-based -vectors as
| (1) |
where is the length in tree of the edge corresponding to the -vector , considered to be if is absent from . The weighted RF distance uses [26] and the branch score distance uses [20]. If all weights are 1 for , then (1) boils down to the RF distance when restricted to trees (either rooted or unrooted), and to our dissimilarity on semidirected phylogenetic networks more generally. For networks with edge lengths, (1) could be used to extend , where is defined as the length of edge in as it is for trees. A root -vector could be assigned weight , because in standard cases, such as for networks with a single root component, the root -vector(s) carry redundant information.
Alternatively, using inheritance probabilities could be useful to capture the similarity between a network having a hybrid edge with inheritance very close to and a network lacking this edge. To this end, we could modify -vectors. Recall that [7] defined with equal to the number of paths from to taxon in a directed network . We could generalize to be a function of these paths, possibly reflecting inheritance probabilities. For example, we could use the weight of a path , defined as . These weights sum to 1 over up-down paths between and [33], although not over the directed paths from to . The weights of the paths could then be normalized before calculating their entropy and then define . The original definition corresponds to giving all paths equal weight . This extension carries over from directed to semidirected networks because we proved here that the set of directed paths from an edge to is independent of the root choice, given a fixed admissible direction assigned to , as shown in Propositions 15 and 16. With this extension, -vectors are in the continuous space instead of . To use them in a dissimilarity between networks and , we could use non-trivial distance between -vectors (such as the or norm) then get the score of an optimal matching between -vectors in and . Searching for an optimal matching would increase the computational complexity of the dissimilarity, but would remain polynomial using the Hungarian algorithm [19].
To reduce the dependence of on the number of taxa in the two networks, should be normalized by a factor depending on only. This is particularly useful to compare networks with different leaf labels, by taking the dissimilarity between the subnetworks on their shared leaves. Ideally, the normalization factor is the diameter of the network space, that is, the maximum distance over all networks and in a subspace of interest. For the subspace of unrooted trees on leaves, this is [30]. Future work could study the diameter of other semidirected network spaces, such as level-1 or tree-child semidirected networks (which have or fewer hybrid nodes, 24) or orchard semidirected networks (whose number of hybrids is unbounded).
To compare semidirected networks on leaf set and on leaf set with a non-zero dissimilarity if , one idea is to consider the subnetworks and on their common leaf set then use a penalized dissimilarity:
for some constant . This dissimilarity may not satisfy the triangle inequality, which might be acceptable in some contexts. For example, consider as input a set of semidirected networks with on leaf set , and consider the full leaf set . We may then seek an -network that minimizes some criterion, such as
| (2) |
When is constrained to be an unrooted tree, input networks are unrooted trees and when is the RF distance using pruned to , this is the well-studied RF supertree problem [31]. When the input trees are further restricted to be on 4 taxa, (2) is the criterion used by ASTRAL [34]. The very wide use of ASTRAL and its high accuracy points to the impact of distances that are fast to calculate, such as our proposed .
Acknowledgements
This work was supported in part by the National Science Foundation (DMS 2023239) and by a H. I. Romnes faculty fellowship to C.A. provided by the University of Wisconsin-Madison Office of the Vice Chancellor for Research with funding from the Wisconsin Alumni Research Foundation.
References
- Allman et al. [2019] Elizabeth S. Allman, Hector Baños, and John A. Rhodes. NANUQ: a method for inferring species networks from gene trees under the coalescent model. Algorithms for Molecular Biology, 14(1), 2019. doi: 10.1186/s13015-019-0159-2.
- Ané et al. [2024] Cécile Ané, John Fogg, Elizabeth S. Allman, Hector Baños, and John A. Rhodes. Anomalous networks under the multispecies coalescent: theory and prevalence. Journal of Mathematical Biology, 88:29, 2024. doi: 10.1007/s00285-024-02050-7.
- Baños [2019] Hector Baños. Identifying species network features from gene tree quartets under the coalescent model. Bulletin of Mathematical Biology, 81(2):494–534, 2019. doi: 10.1007/s11538-018-0485-4.
- Babai [2016] László Babai. Graph isomorphism in quasipolynomial time. arXiv, 2016. doi: 10.48550/arXiv.1512.03547.
- Bai et al. [2021] Allan Bai, Péter L. Erdős, Charles Semple, and Mike Steel. Defining phylogenetic networks using ancestral profiles. Mathematical Biosciences, 332:108537, 2021. doi: 10.1016/j.mbs.2021.108537.
- Cardona et al. [2008] Gabriel Cardona, Mercè Llabrés, Francesc Rosselló, and Gabriel Valiente. A distance metric for a class of tree-sibling phylogenetic networks. Bioinformatics, 24(13):1481–1488, 2008. doi: 10.1093/bioinformatics/btn231.
- Cardona et al. [2009] Gabriel Cardona, Francesc Rosselló, and Gabriel Valiente. Comparison of tree-child phylogenetic networks. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 6(4):552–569, 2009. doi: 10.1109/tcbb.2007.70270.
- Cardona et al. [2014] Gabriel Cardona, Mercè Llabrés, Francesc Rosselló, and Gabriel Valiente. The comparison of tree-sibling time consistent phylogenetic networks is graph isomorphism-complete. The Scientific World Journal, 2014:254279, 2014. doi: 10.1155/2014/254279.
- Cardona et al. [2024] Gabriel Cardona, Joan Carles Pons, Gerard Ribas, and Tomás Martínez Coronado. Comparison of orchard networks using their extended -representation. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 21(3):501–507, 2024. doi: 10.1109/TCBB.2024.3361390.
- Felsenstein [2004] Joseph Felsenstein. Inferring Phylogenies. Sinauer Associates, Sunderland, Massachusetts, 2004. ISBN 0878931775. doi: 10.1086/383584.
- Gautier et al. [2022] Mathieu Gautier, Renaud Vitalis, Laurence Flori, and Arnaud Estoup. f-statistics estimation and admixture graph construction with pool-seq or allele count data using the R package poolfstat. Molecular Ecology Resources, 22(4):1394–1416, 2022. doi: 10.1111/1755-0998.13557.
- Gross et al. [2021] Elizabeth Gross, Leo van Iersel, Remie Janssen, Mark Jones, Colby Long, and Yukihiro Murakami. Distinguishing level-1 phylogenetic networks on the basis of data generated by Markov processes. Journal of Mathematical Biology, 83(3):32, 2021. doi: 10.1007/s00285-021-01653-8.
- Hickey et al. [2008] Glenn Hickey, Frank Dehne, Andrew Rau-Chaplin, and Christian Blouin. SPR distance computation for unrooted trees. Evolutionary Bioinformatics, 4:EBO.S419, 2008. doi: 10.4137/EBO.S419.
- Huber et al. [2022] Katharina T. Huber, Vincent Moulton, and Guillaume E. Scholz. Forest-based networks. Bulletin of Mathematical Biology, 84:119, 2022. doi: 10.1007/s11538-022-01081-9.
- Huber et al. [2025] Katharina T. Huber, Leo van Iersel, Vincent Moulton, and Guillaume E. Scholz. Is this network proper forest-based? Information Processing Letters, 187:106500, 2025. doi: 10.1016/j.ipl.2024.106500.
- Huson et al. [2010] Daniel H. Huson, Regula Rupp, and Celine Scornavacca. Phylogenetic Networks: Concepts, Algorithms and Applications. Cambridge University Press, Cambridge, 2010. doi: 10.1017/CBO9780511974076.
- Janssen and Murakami [2021] Remie Janssen and Yukihiro Murakami. On cherry-picking and network containment. Theoretical Computer Science, 856:121–150, 2021. doi: 10.1016/j.tcs.2020.12.031.
- Kong et al. [2022] Sungsik Kong, David L. Swofford, and Laura S. Kubatko. Inference of phylogenetic networks from sequence data using composite likelihood. bioRxiv, 2022. doi: 10.1101/2022.11.14.516468.
- Kuhn [1955] Harold W. Kuhn. The hungarian method for the assignment problem. Naval Research Logistics Quarterly, 2(1-2):83–97, 1955. doi: 10.1002/nav.3800020109.
- Kuhner and Felsenstein [1994] M K Kuhner and J Felsenstein. A simulation comparison of phylogeny algorithms under equal and unequal evolutionary rates. Molecular Biology and Evolution, 11(3):459–468, 1994. doi: 10.1093/oxfordjournals.molbev.a040126.
- Linz and Wicke [2023] Simone Linz and Kristina Wicke. Exploring spaces of semi-directed level-1 networks. Journal of Mathematical Biology, 87(70), 2023. doi: 10.1007/s00285-023-02004-5.
- Lutteropp et al. [2022] Sarah Lutteropp, Celine Scornavacca, Alexey M Kozlov, Benoit Morel, and Alexandros Stamatakis. NetRAX: accurate and fast maximum likelihood phylogenetic network inference. Bioinformatics, 38(15):3725–3733, 2022. doi: 10.1093/bioinformatics/btac396.
- Maier et al. [2023] Robert Maier, Pavel Flegontov, Olga Flegontova, Ulaş Işıldak, Piya Changmai, and David Reich. On the limits of fitting complex models of population history to f-statistics. eLife, 12:e85492, 2023. doi: 10.7554/eLife.85492.
- Martin et al. [2023] Samuel Martin, Vincent Moulton, and Richard M. Leggett. Algebraic invariants for inferring 4-leaf semi-directed phylogenetic networks. bioRxiv, 2023. doi: 10.1101/2023.09.11.557152.
- Neureiter et al. [2022] Nico Neureiter, Peter Ranacher, Nour Efrat-Kowalsky, Gereon A. Kaiping, Robert Weibel, Paul Widmer, and Remco R. Bouckaert. Detecting contact in language trees: a Bayesian phylogenetic model with horizontal transfer. Humanities and Social Sciences Communications, 9(1):205, 2022. doi: 10.1057/s41599-022-01211-7.
- Robinson and Foulds [1979] D. F. Robinson and L. R. Foulds. Comparison of weighted labelled trees. In A. F. Horadam and W. D. Wallis, editors, Combinatorial Mathematics VI, pages 119–126, Berlin, Heidelberg, 1979. Springer Berlin Heidelberg. ISBN 978-3-540-34857-3.
- Robinson and Foulds [1981] D.F. Robinson and L.R. Foulds. Comparison of phylogenetic trees. Mathematical Biosciences, 53(1):131–147, 1981. doi: doi.org/10.1016/0025-5564(81)90043-2.
- Solís-Lemus and Ané [2016] Claudia Solís-Lemus and Cécile Ané. Inferring phylogenetic networks with maximum pseudolikelihood under incomplete lineage sorting. PLOS Genetics, 12(3):e1005896, 2016. doi: 10.1371/journal.pgen.1005896.
- Soraggi and Wiuf [2019] Samuele Soraggi and Carsten Wiuf. General theory for stochastic admixture graphs and f-statistics. Theoretical Population Biology, 125:56–66, 2019. doi: 10.1016/j.tpb.2018.12.002.
- Steel [2016] Mike Steel. Phylogeny: Discrete and Random Processes in Evolution. Society for Industrial and Applied Mathematics, Philadelphia, PA, 2016. doi: 10.1137/1.9781611974485.
- Vachaspati and Warnow [2017] Pranjal Vachaspati and Tandy Warnow. Fastrfs: fast and accurate Robinson-Foulds supertrees using constrained exact optimization. Bioinformatics, 33(5):631–639, 2017. doi: 10.1093/bioinformatics/btw600.
- van Iersel et al. [2022] Leo van Iersel, Remie Janssen, Mark Jones, and Yukihiro Murakami. Orchard networks are trees with additional horizontal arcs. Bulletin of Mathematical Biology, 84:76, 2022. doi: 10.1007/s11538-022-01037-z.
- Xu and Ané [2023] Jingcheng Xu and Cécile Ané. Identifiability of local and global features of phylogenetic networks from average distances. Journal of Mathematical Biology, 86(1):12, 2023. doi: 10.1007/s00285-022-01847-8.
- Zhang et al. [2018] Chao Zhang, Maryam Rabiee, Erfan Sayyari, and Siavash Mirarab. ASTRAL-III: polynomial time species tree reconstruction from partially resolved gene trees. BMC Bioinformatics, 19(Suppl 6):153, 2018. doi: 10.1186/s12859-018-2129-y.
[Example edge-based -representation]
Let . In Fig. 3 left, is an -network. In -vectors, leaves are ordered as in . Following notations in Algorithm 1, where the multisets () partition the -vector sets based on their type (uni/bidirectional) and tags (, or ).
contains the -vector sets of tree edges in the directed part (in black in Fig. 3), which are here the pendent edges (incident to leaves) and :
| {((1,0,0,0,0, 0,0,0), :t)}, | # pendent to a_1 |
contains the -vector sets of hybrid edges (in blue in Fig. 3):
| {((0,0,0,0,0, 1,1,1), :h)}, |
contains a single -vector set, because has only 1 root component:
| {((1,1,1,1,1, 3,3,3), :r)} ⟆ . |
contains the bidirectional -vector sets of edges in the root component (in brown in Fig. 3):
| {((1,1,0,0,0, 0,0,0), :t), ((0,0,1,1,1, 3,3,3), :t)}, | # e_1 |
Now we reconstruct from , following notations from Algorithm 2 and Algorithm 3.
contains the -vectors from those in , corresponding to the tree nodes in the directed part:
| (1,0,0,0,0, 0,0,0), (0,0,0,1,0, 0,0,0), (0,0,0,0,0, 0,1,0), |
contains the hybrid node’s -vector (in the directed part):
| (0,0,0,0,0, 1,1,1) } . |
contains a single root -vector:
contains all directional -vectors of all edges in the root component corresponding to :
| (1,1,0,0,0, 0,0,0), (0,0,1,0,0, 0,0,0), (1,1,1,1,0, 1,1,1), |
After arbitrarily choosing , contains a subset of directional -vectors:
| (1,1,0,0,0, 0,0,0), (0,0,1,0,0, 0,0,0), (0,0,0,0,1, 2,2,2), |

Fig. A7 shows , the rooted partner such that . Algorithm 3 starts by obtaining :
| {((1,0,0,0,0, 0,0,0), :t)}, {((0,0,1,0,0, 0,0,0), :t)}, |
Then contains the -vectors of elements that are in but not in :
| (1,1,0,0,0, 0,0,0), (0,0,1,0,0, 0,0,0), |
For , has multiplicity 2 in , corresponding to an elementary path of 2 edges: and the pendent edge incident to . As has multiplicity 1 in , only (in ) is undirected to obtain . The other elements in also have multiplicity 1. Each one corresponds to a single edge in (labeled in brown in Fig. A7) and is undirected to obtain .