A curious identity in connection with saddle-point method and Stirling’s formula

The two uses above (with $z=re^{i\theta}$ or $z=R(1+it)$) of the saddle-point method for coefficient integrals of the form

for some contour $\mathscr{C}$ are standard in the combinatorial literature and are reminiscent of the difference between moments and factorial moments in probability; the corresponding saddle-point equations are given by

respectively. Often the question is which one to choose and is better (numerically or in some other sense)? For example, take $f(z)=e^{e^{z}-1}$ (Bell numbers [22, A000110]); then we found both uses in the literature:

The question of whether to use $r$ or $R$ in (14) is partly answered in [9, p. 555, footnote]: “the choice being often suggested by computational convenience.” Odlyzko in [20, p. 1184] also commented that the use of $r$ is slightly preferred because the manipulation of the other version is less elegant.

Apart from computational convenience, the numerical advantages of the expansion (9) over (7) are visible because they have the same sequence of coefficients and $(n+1)^{-m}$ is always smaller than $n^{-m}$; see also [4] for Stirling’s original expansion in decreasing powers of $n+\frac{1}{2}$. Although the numerical difference is minor for most practical uses, the same question can naturally be raised more generally for functions $f$ whose Taylor coefficients are amenable to saddle-point method (for example, exponential of Hayman admissible functions; see [21]). Indeed, such a numerical difference was already observed in the 1960s by Harris and Schoenfeld in their study of idempotent elements in symmetric semigroups [10] where $f(z)=e^{ze^{z}}$. Based on numerical calculations, they found that the saddle-point approximation

is “considerably better than the approximation”

Surprisingly, this is the only paper we found where such a numerical comparison between the two versions of saddle-point method was made.

In the same paper [10], Harris and Schoenfeld also argued that the reason that (15) outperforms (16) is (we change their notations to ours) “because the derivation of (15) uses a contour which passes through the saddle point of a certain integral for $a_{n}/n!$. However, Hayman’s proof of the formula yielding (16) employs a contour passing through $r=r(n)=R(n-1)$ and it therefore misses the saddle point at $R$ by $R(n)-R(n-1)\sim 1/n$.”

However, such a comparison is not quite right. In fact, the use of $r$ or $R$ in each case, after the change of variables, is optimally guided by the saddle-point principle, and thus different choices of integration contour will result in different expansions with different asymptotic scales. As we will see below in § 2.3, while the dominant term in (15) is better than that in (16) under the absolute difference measure, the use of more terms in the corresponding asymptotic expansions may change the scenario, and which expansion is numerically more precise depends on the number of terms used.

In this section, we first consider the two versions of the saddle-point method for general $f$, and then give succinct expressions for the coefficients in the corresponding asymptotic expansions. Then we discuss some examples, highlighting briefly their numerical differences.

Consider

where $\phi$ is analytic at zero. For simplicity we will simply assume that asymptotic expansions can be derived by the saddle-point method, instead of formulating general theorems for asymptotic expansions whose conditions are often very messy to the extent that in many practical cases, their justifications are not much different from working out the saddle-point method from scratch; see e.g. [11, 17, 21, 29]. In this way, we focus on the formal aspects of the coefficients and the differences between the two expansions, referring all technical details or justification to standard references such as [11, 17, 29] or [9, § VIII.5]. Then we have the following two different asymptotic expansions.

• •

  The change of variables $z\mapsto re^{i\theta}$ (integration on a circle): let

  $\displaystyle\kappa_{j}(r)$

  $\displaystyle:=j![s^{j}]\bigl{(}{-ns+\phi(re^{s})}\bigr{)}\qquad(j=1,2,\dots),$

  where $\kappa_{1}(r)=0$ or $r\phi^{\prime}(r)=n$. Also $\kappa_{2}(r)=r\phi^{\prime}(r)+r^{2}\phi^{\prime\prime}(r)$. Then under proper conditions

  $\displaystyle a_{n}\sim\frac{r^{-n}e^{\phi(r)}}{\sqrt{2\pi\kappa_{2}(r)}}\sum_{m\geqslant 0}c_{m}(r)\kappa_{2}(r)^{-m},$

  where

  $\displaystyle c_{m}(r):=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-\frac{1}{2}t^{2}}[y^{m}]\exp\biggl{(}{\sum_{j\geqslant 3}\frac{\kappa_{j}(r)}{j!\kappa_{2}(r)}(it)^{j}y^{\frac{1}{2}j-1}}\biggr{)}{\,\rm d}t.$

  Alternatively, by the same analysis as above for Stirling’s formula, we also have

  $\displaystyle c_{m}(r)=g_{2m}(r)\frac{(-1)^{m}(2m)!}{m!2^{m}},$

  (17)

  where

  $$g_{m}(r)=[v^{m}]\biggl{(}{\frac{\frac{1}{2}\kappa_{2}(r)v^{2}}{\phi(re^{v})-\phi(r)-r\phi^{\prime}(r)v}}\biggr{)}^{\frac{1}{2}(m+1)}.$$

  In particular (with $\kappa_{j}=\kappa_{j}(r)$),

  	$\displaystyle c_{1}(r)$	$\displaystyle=\frac{3\kappa_{2}\kappa_{4}-5\kappa_{3}^{2}}{24\kappa_{2}^{2}},$
  	$\displaystyle c_{2}(r)$	$\displaystyle=-\frac{24\kappa_{2}^{3}\kappa_{6}-168\kappa_{2}^{2}\kappa_{3}\kappa_{5}-105\kappa_{2}^{2}\kappa_{4}^{2}+630\kappa_{2}\kappa_{3}^{2}\kappa_{4}-385\kappa_{3}^{4}}{1152\kappa_{2}^{4}}.$

• •

  The change of variables $z\mapsto R(1+it)$ (integration on a vertical line): let

  	$\displaystyle\lambda_{j}(R)$	$\displaystyle=j![s^{j}]\bigl{(}{-(n+1)\log(1+s)+\phi(R(1+s))}\bigr{)}$
  		$\displaystyle=(-1)^{j}(j-1)!R\phi^{\prime}(R)+j![s^{j}]\phi(R(1+s)),$

  where $R\phi^{\prime}(R)=n+1$. Note that $\lambda_{2}(t)=\kappa_{2}(t)$. Then under proper conditions

  $\displaystyle a_{n}\sim\frac{R^{-n}e^{\phi(R)}}{\sqrt{2\pi\lambda_{2}(R)}}\sum_{m\geqslant 0}d_{m}(R)\lambda_{2}(R)^{-m},$

  where

  $\displaystyle d_{m}(R):=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-\frac{1}{2}t^{2}}[y^{m}]\exp\biggl{(}{\sum_{j\geqslant 3}\frac{\lambda_{j}(r)}{j!\lambda_{2}(r)}(it)^{j}y^{\frac{1}{2}j-1}}\biggr{)}{\,\rm d}t.$

  Alternatively, we also have

  $\displaystyle d_{m}(R)=h_{2m}(R)\frac{(-1)^{m}(2m)!}{m!2^{m}},$

  (18)

  where

  $$h_{m}(R)=[y^{m}]\biggl{(}{\frac{\frac{1}{2}\lambda_{2}(R)y^{2}}{\phi(R(1+y))-\phi(R)-R\phi^{\prime}(R)\log(1+y)}}\biggr{)}^{\frac{1}{2}(m+1)}.$$

  In particular, (with $\lambda_{j}=\lambda_{j}(R)$)

  	$\displaystyle d_{1}(R)$	$\displaystyle=\frac{3\lambda_{2}\lambda_{4}-5\lambda_{3}^{2}}{24\lambda_{2}^{2}},$
  	$\displaystyle d_{2}(R)$	$\displaystyle=-\frac{24\lambda_{2}^{3}\lambda_{6}-168\lambda_{2}^{2}\lambda_{3}\lambda_{5}-105\lambda_{2}^{2}\lambda_{4}^{2}+630\lambda_{2}\lambda_{3}^{2}\lambda_{4}-385\lambda_{3}^{4}}{1152\lambda_{2}^{4}},$

  the expressions differing from $c_{1}(r)$ and $c_{2}(r)$ by replacing all $\kappa_{j}(r)$ by $\lambda_{j}(R)$.

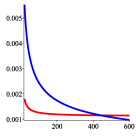
We begin with Harris and Schoenfeld’s example $\phi(z)=ze^{z}$ [10] and let $a_{n}:=n![z^{n}]e^{ze^{z}}$, the number of idempotent mappings from a set of $n$ elements into itself; see also [22, A000248]. Asymptotic expansions by saddle-point method can be justified either by checking the Harris-Schoenfeld admissibility conditions as in [10] or by showing that $ze^{z}$ is a Hayman admissible function (see [12, 21, 9]). We then compute the absolute differences between the true values and the two asymptotic expansions with varying number of terms:

where $r>0$ solves $r(r+1)e^{r}=n$, $R>0$ solves $R(r+1)e^{R}=n+1$, and $\kappa_{2}$ and the coefficients $c_{m}$ and $d_{m}$ can be computed by (17) and (18), respectively, with $\phi(z)=ze^{z}$. Note that $g(2m)\kappa_{2}(r)^{-m}$ grows in the order $n^{-m}(\log n)^{m}$ for $m=0,1,\dots$.

From Figure 1, we see that while (15) is numerically better than its circular counterpart (16) (or $M=0$. as already observed in [10]), more terms in the asymptotic expansions show that both expansions are indeed comparable, and their numerical performance depends on the number of terms used.

We also observed a very similar pattern (as Figure 1) for Bell numbers when $\phi(z)=e^{z}-1$; see [22, A000110].

In the case of $\phi(z)=\frac{z}{1-z}$, $a_{n}:=n![z^{n}]e^{z/(1-z)}$ enumerates the number of partitions of $\{1,\dots,n\}$ into any number of ordered subsets; see [22, A000262]. Justification of an asymptotic expansion is straightforward and similar to integer partition problems.

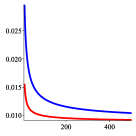One sees that the circular version is numerically better except for $M=0$.

Finally, consider the case $\phi(z)=z+\frac{1}{2}z^{2}$, whose coefficients (times $n!$) enumerate the number of self-inverse permutations on $n$ elements; see [22, A000085]. Since all coefficients of $\phi(z)$ are positive, an asymptotic expansion by saddle-point method is possible by known results of Moser and Wyman in the 1950s [17]; see also [20]. In this case, we plot the difference $\Delta_{n,M}^{(c)}-\Delta_{n,M}^{(v)}$ because the two curves are too close to be distinguishable.

In summary, we clarified here the often unclear situation of which version of the saddle-point contour to choose, and provided concrete examples for a more detailed comparison, from both analytic and numerical viewpoints. Such a clarification will be of instructional value, in addition to its own methodological interests.