A Comprehensive Survey and Taxonomy on Single Image Dehazing Based on Deep Learning
Abstract.
With the development of convolutional neural networks, hundreds of deep learning based dehazing methods have been proposed. In this paper, we provide a comprehensive survey on supervised, semi-supervised, and unsupervised single image dehazing. We first discuss the physical model, datasets, network modules, loss functions, and evaluation metrics that are commonly used. Then, the main contributions of various dehazing algorithms are categorized and summarized. Further, quantitative and qualitative experiments of various baseline methods are carried out. Finally, the unsolved issues and challenges that can inspire the future research are pointed out. A collection of useful dehazing materials is available at https://github.com/Xiaofeng-life/AwesomeDehazing.
1. Introduction
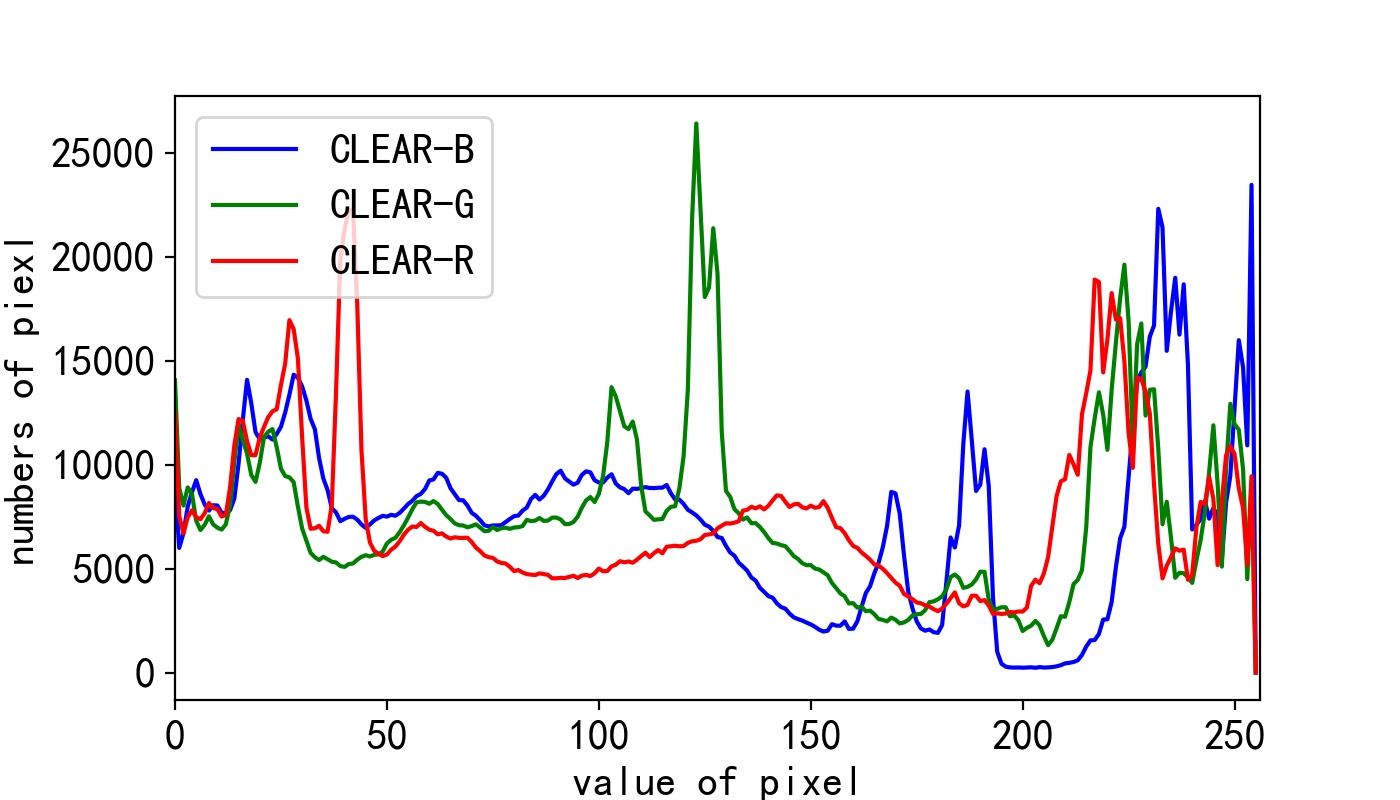
Due to the absorption by floating particles contained in the hazy environment, the quality of the image captured by the camera will be reduced. The phenomenon of image quality degradation in hazy weather has a negative impact on photography work. The contrast of the image will decrease and the color will shift. Meantime, the texture and edge of objects in the scene will become blurred. As shown in Fig. 1, there is an obvious difference between the pixel histograms of hazy and haze-free images. For computer vision tasks such as object detection and image segmentation, low-quality inputs can degrade the performance of the models trained on haze-free images.
Therefore, many researchers try to recover high-quality clear scenes from hazy images. Before deep learning was widely used in computer vision tasks, image dehazing algorithms had mainly relied on various prior assumptions (He et al., 2010) and atmospheric scattering model (ASM) (McCartney, 1976). The processing flow of these statistical rule based methods has good interpretability. However, they may exhibit shortcomings when facing complex real world scenarios. For example, the well-known dark channel prior (He et al., 2010) (DCP, best paper of CVPR 2009) cannot handle regions containing sky well.
Inspired by deep learning, (Ren et al., 2016; Cai et al., 2016; Ren et al., 2020) combine ASM and convolutional neural network (CNN) to estimate the parameters of the ASM. Quantitative and qualitative experimental results show that deep learning can help the prediction of these parameters in a supervised way.
Following this, (Qin et al., 2020; Liu et al., 2019a; Liang et al., 2019; Zhang et al., 2022c; Zheng et al., 2021) have demonstrated that end-to-end supervised dehazing networks can be implemented independently of the ASM. Thanks to the powerful feature extraction capability of CNN, these non-ASM-based dehazing algorithms can achieve comparable accuracy as ASM-based algorithms.
ASM-based and non-ASM-based supervised algorithms have shown impressive performance. However, they often require synthetic paired images that are inconsistent with real world hazy images. Therefore, recent research focus on methods that are more suitable to the real world dehazing task. (Cong et al., 2020; Golts et al., 2020; Li et al., 2020b) explore unsupervised algorithms that do not require synthetic data while other studies (Li et al., 2020a; An et al., 2022; Chen et al., 2021b; Zhang and Li, 2021) propose semi-supervised algorithms that exploit both synthetic paired data and real world unpaired data.


(a) A clear image (c) A hazy image

(b) Histogram for (a) (d) Histogram for (c)
With the rapid development in this area, hundreds of dehazing methods have been proposed. To inspire and guide the future research, a comprehensive survey is urgently needed. Some papers have attempted to partially review the recent development of the dehazing research. For example, (Singh and Kumar, 2019; Li et al., 2017b; Xu et al., 2015) gives a summary of the non-deep learning dehazing methods, including depth estimation, wavelet, enhancement, filtering, but lacks of research on recent CNN-based methods. Parihar et al. (Parihar et al., 2020) provides a survey about supervised dehazing models, but it does not pay enough attention to the latest explorations of semi-supervised and unsupervised methods. Banerjee et al. (Banerjee and Chaudhuri, 2021) introduce and group the existing nighttime image dehazing methods, however, the methods of daytime are rarely analyzed. Gui et al. (Gui et al., 2021) briefly classify and analyze supervised and unsupervised algorithms, but does not summarize the various recently proposed semi-supervised methods. Unlike existing reviews, we give a comprehensive survey on the supervised, semi-supervised and unsupervised daytime dehazing models based on deep learning.

| Category | Key Idea | Methods | ||
| Supervised | Learning of |
|
||
| Joint learning of and |
|
|||
| Non-explicitly embedded ASM |
|
|||
| Generative adversarial network |
|
|||
| Level-aware | LAP-Net (Li et al., 2019b), HardGAN (Deng et al., 2020) | |||
| Multi-function fusion | DMMFD (Deng et al., 2019) | |||
| Transformation and decomposition of input | GFN (Ren et al., 2018a), MSRL-DehazeNet (Yeh et al., 2019), DPDP-Net (Yang et al., 2019), DIDH (Shyam et al., 2021) | |||
| Knowledge distillation | KDDN (Hong et al., 2020), KTDN (Wu et al., 2020), SRKTDN (Chen et al., 2021a), DALF (Fang et al., 2021) | |||
| Transformation of colorspace | AIP-Net (Wang et al., 2018a), MSRA-Net (Sheng et al., 2022), TheiaNet (Mehra et al., 2021), RYF-Net (Dudhane and Murala, 2019b) | |||
| Contrastive learning | AECR-Net (Wu et al., 2021) | |||
| Non-deterministic output | pWAE (Kim et al., 2021), DehazeFlow (Li et al., 2021b) | |||
| Retinex model | RDN (Li et al., 2021c) | |||
| Residual learning | GCA-Net(Chen et al., 2019c), DRL (Du and Li, 2018), SID-HL (Xiao et al., 2020), POGAN (Du and Li, 2019) | |||
| Frequency domain |
|
|||
| Joint dehazing and depth estimation |
|
|||
| Detection and segmentation with dehazing | LEAAL (Li et al., 2020c), SDNet (Zhang et al., 2022a), UDnD (Zhang et al., 2020g) | |||
| End-to-end CNN |
|
|||
| Semi-supervised | Pretrain backbone and fine-tune | PSD (Chen et al., 2021b), SSDT (Zhang and Li, 2021) | ||
| Disentangled and reconstruction | DCNet (Chen et al., 2021c), FSR (Liu et al., 2021), CCDM (Zhang et al., 2020f) | |||
| Two-branches training | DAID (Shao et al., 2020), SSID (Li et al., 2020a), SSIDN (An et al., 2022) | |||
| Unsupervised | Unsupervised domain translation |
|
||
| Learning without haze-free images | Deep-DCP (Golts et al., 2020) | |||
| Unsupervised image decomposition | Double-DIP (Gandelsman et al., 2019) | |||
| Zero-shot learning | ZID (Li et al., 2020b), YOLY (Li et al., 2021a) |
1.1. Scope and Goals of This Survey
This survey does not cover all themes of dehazing research. We focus our attention on deep learning based algorithms that employ monocular daytime images. This means that we will not discuss in detail about non-deep learning dehazing, underwater dehazing (Wang et al., 2021b, 2017; Li et al., 2016), video dehazing (Ren et al., 2018b), hyperspectral dehazing (Mehta et al., 2020), nighttime dehazing (Zhang et al., 2020a, 2017a, 2014), binocular dehazing (Pang et al., 2020), etc. Therefore, when we refer to “dehazing” in this paper, we usually mean deep learning based algorithms whose input data satisfies four conditions: single frame image, daytime, monocular, on the ground. In summary, there are three contributions to this survey as follows.
-
•
Commonly used physical models, datasets, network modules, loss functions and evaluation metrics are summarized.
-
•
A classification and introduction of supervised, semi-supervised, and unsupervised methods is presented.
-
•
According to the existing achievements and unsolved problems, the future research directions are prospected.
1.2. A Guide for Reading This Survey
Section 2 introduces physical model ASM, synthetic & generated & real world datasets, loss functions, basic modules commonly used in dehazing networks and evaluation metrics for various algorithms. Section 3 provides a comprehensive discussion of supervised dehazing algorithms. A review of semi-supervised and unsupervised dehazing methods is in Section 4 and Section 5, respectively. Section 6 presents quantitative and qualitative experimental results for three categories of baseline algorithms. Section 7 discusses the open issues of dehazing research.
A critical challenge for a logical and comprehensive review of dehazing research is how to properly classify existing methods. In the classification of Table 1, there are several items that need to be pointed out as follows.
-
•
The DCP is validated on the dehazing task, and the inference process utilizes ASM. Therefore, those methods that utilize DCP are considered to be ASM-based.
-
•
This survey treat the knowledge distillation based supervised dehazing network as a supervised algorithm rather than a weakly supervised/semi-supervised algorithm.
-
•
Supervised dehazing methods using total variation loss or GAN loss are still classified as supervised.
Here we give the notational conventions for this survey. Unless otherwise specified, all symbols have the following meanings: means hazy image; denotes haze-free image. stands for transmission map; in , and is pixel location. The subscript “” denotes “reconstructed”, such as is the reconstructed hazy image. The subscript “” refers to the prediction output. According to (Gandelsman et al., 2019), atmospheric light may be regarded as a constant or a non-uniform matrix . In this survey, atmospheric light is uniformly denoted as . In addition, many papers give the proposed algorithm an abbreviated name, such as GFN (Ren et al., 2018a) (gated fusion network for single image dehazing). For readability, this survey uses abbreviations as references to these papers. For a small amount of papers that do not give a name for their algorithms, we designate the abbreviated name according to the title of the corresponding paper.
2. Related Work
The commonalities of dehazing algorithms are mainly reflected in four aspects. First, the modeling of the network relies on physical model ASM or is completely based on neural networks. Second, the dataset used for training the network needs to contain transmission map, atmospheric light value, or paired supervision information. Third, the dehazing networks employ different kinds of basic modules. Fourth, different kinds of loss functions are used for training. Based on these four factors, the researchers designed a variety of effective dehazing algorithms. Thus, this section introduces ASM, datasets, loss functions, and network architecture modules. In addition, how to evaluate the dehazing results is also discussed in this section.
2.1. Modeling of the Dehazing Process
Haze is a natural phenomenon that can be approximately explained by ASM. McCartney (McCartney, 1976) first proposed the basic ASM to describe the principles of haze formation. Then, Narasimhan (Narasimhan and Nayar, 2003) and Nayar (Nayar and Narasimhan, 1999) extended and developed the ASM that is currently widely used. The ASM provides a reliable theoretical basis for the research of image dehazing. Its formula is
| (1) |
where is the pixel location and means the global atmospheric light. In different papers, may be referred to as airlight or ambient light. For ease of understanding, is noted as atmospheric light in this survey. For the dehazing methods based on ASM, is usually unknown. stands for the hazy image and denotes the clear scene image. For most dehazing models, is the input and is the desired output. The means the medium transmission map which is defined as
| (2) |
where and stands for the atmosphere scattering parameter and the depth of , respectively. Thus, the is determined by , which can be used for the synthesis of hazy image. If the and can be estimated, the haze-free image can be obtained by the following formula:
| (3) |
The imaging principle of ASM is shown in Fig. 2. It can be seen that the light reaching the camera from the object is affected by the particles in the air. Some works use ASM to describe the formation process of haze, and the parameters included in the atmospheric scattering model are solved in an explicit or implicit way. As shown in Table 1, ASM has a profound impact on dehazing research, including supervised (Ren et al., 2016; Cai et al., 2016; Li et al., 2017a; Zhang and Patel, 2018), semi-supervised (Li et al., 2020a; Liu et al., 2021; Chen et al., 2021b), and unsupervised algorithms (Li et al., 2021a; Golts et al., 2020).
2.2. Datasets for Dehazing Task
| Dataset | type | Nums | I/O | P/NP |
|---|---|---|---|---|
| D-HAZY (Ancuti et al., 2016) | Syn | 1400+ | I | P |
| HazeRD (Zhang et al., 2017b) | Syn | 15 | O | P |
| I-HAZE (Ancuti et al., 2018b) | HG | 35 | I | P |
| O-HAZE (Ancuti et al., 2018c) | HG | 45 | O | P |
| RESIDE (Li et al., 2019c) | S&R | 10000+ | I&O | P&NP |
| Dense-Haze (Ancuti et al., 2019a) | HG | 33 | O | P |
| NH-HAZE (Ancuti et al., 2020a) | HG | 55 | O | P |
| MRFID (Liu et al., 2020a) | Real | 200 | O | P |
| BeDDE (Zhao et al., 2020) | Real | 200+ | O | P |
| 4KID (Zheng et al., 2021) | Syn | 10000 | O | P |
For computer vision tasks such as object detection, image segmentation, and image classification, accurate ground-truth labels can be obtained with careful annotation. However, sharp, accurate and pixel-wise labels (i.e., paired haze-free images) for hazy images in natural scenes are almost impossible to obtain. Currently, there are mainly two approaches for obtaining paired hazy and haze-free images. The first way is to obtain synthetic data with the help of ASM, such as the D-HAZY (Ancuti et al., 2016), HazeRD (Zhang et al., 2017b) and RESIDE (Li et al., 2019c). By selecting different parameters for ASM, researchers can easily obtain hazy images with different haze densities. Four components are needed to synthesize a hazy image: a clear image, a depth map corresponding to the content of the clear image, atmospheric light and atmosphere scattering parameter . Thus, we can divide the synthetic dataset into two stages. In the first stage, clear images and corresponding depth maps are needed to be collected in pairs. In order to ensure that the synthesized haze is as close as possible to the real world haze, the depth information must be sufficiently accurate. Fig. 3 shows the clear image and corresponding depth map in the NYU-Depth dataset (Silberman et al., 2012). In the second stage, atmospheric light and atmosphere scattering parameter are designated as fixed values or randomly selected. The commonly used D-HAZY (Ancuti et al., 2016) dataset is synthesized when both and are . Several researches choose different and in order to increase the diversity of the synthesized images and thus improve the generalization ability of the trained model. For example, MSCNN (Ren et al., 2016) sets and . Fig. 4 shows the corresponding hazy image when takes different values.


(a) A clear image (b) Depth for the clear image






The second way is to generate the hazy image by using a haze generator, such as I-HAZE (Ancuti et al., 2018b), O-HAZE (Ancuti et al., 2018c), Dense-Haze (Ancuti et al., 2019a) and NH-HAZE (Ancuti et al., 2020a). The well-known competition New Trends in Image Restoration and Enhance (NTIRE 2018-2020) dehazing challenge (Ancuti et al., 2018a, 2019b, 2020b) are based on these generated datasets. Fig. 5 shows four pairs of hazy and haze-free examples contained in the datasets simulated by the haze generator. The images in Fig. 5 (a) are from indoor scenes, while (b), (c) and (d) are all pictured at outdoor views. There are differences in the pattern of haze in these three outdoor datasets. The haze in (b) and (c) is evenly distributed throughout the entire image, while the haze in (d) are non-homogeneous in the whole scenes. In addition, the density of haze in (c) is significantly higher than that in (b) and (d). These datasets with different characteristics provide useful insights for the design of dehazing algorithms. For example, in order to remove the high density of haze in Dense-Haze, it is necessary to design dehazing models with stronger feature extraction and recovery capabilities.








(a) Indoor Haze (b) Outdoor Haze (c) Dense Haze (d) Non-Homogeneous Haze
The main advantage of synthetic and generated haze is that it alleviates the difficulty during data acquisition. However, the hazy images synthesized based on ASM or generated by haze generator cannot perfectly simulate the formation process of real world haze. Therefore, there is an inherent difference between the synthetic and real world data. Several researches have noticed the problems of artificial data and tried to construct real world datasets, such as MRFID (Liu et al., 2020a) and BeDDE (Zhao et al., 2020). However, due to the high costs and difficulties of data collection, the current real world datasets do not contain enough examples as the synthetic dataset, like RESIDE (Li et al., 2019c). To facilitate the comparison of different datasets, we summarize the characteristics of various datasets in Table 2.
2.3. Network Block
CNNs are widely used in current deep learning based dehazing networks. Commonly adopted modules are standard convolution, dilated convolution, multi-scale fusion, feature pyramid, cross-layer connection and attention. Usually, multiple basic blocks are formed into a dehazing network. In order to facilitate the understanding of the principles of different dehazing algorithms, the basic blocks commonly used in network architectures are summarized as follows.
-
•
Standard convolution: It is shown that using standard convolution in a sequential connection way to build neural networks is effective. Therefore, standard convolution are often used in dehazing models (Li et al., 2017a; Ren et al., 2016; Sharma et al., 2020; Zhang et al., 2020e) together with other blocks.
-
•
Dilated convolution: Dilated convolution can increase the receptive field while keeping the size of the convolution kernel unchanged. Studies (Chen et al., 2019c; Zhang et al., 2020c; Zhang and He, 2020; Lee et al., 2020b; Yan et al., 2020) have shown that dilated convolution can improve the performance of global feature extraction. Moreover, fusing convolution layers with different dilation rates can extract features from different receptive fields.
-
•
Multi-scale fusion: CNNs with multi-scale convolution kernels have been proven effective in extracting features in a variety of visual tasks (Szegedy et al., 2015). By using convolution kernels at different scales and fusing the extracted feature together, dehazing methods (Wang et al., 2018a; Tang et al., 2019; Dudhane et al., 2019; Wang et al., 2020) have demonstrated that the fusion strategy can obtain the multi-scale details that are useful for image restoration. In the process of feature fusion, a common way is to spatially concatenate or add output features obtained by convolution kernels of different sizes.
-
•
Feature pyramid: In the research of digital image processing, the image pyramid can be used to obtain information of different resolutions. The dehazing network based on deep learning (Zhang et al., 2020e; Zhang and Patel, 2018; Zhang et al., 2018b; Singh et al., 2020; Zhao et al., 2021a; Yin et al., 2020; Chen et al., 2019a) uses this strategy in the middle layer of the network to extract multiple scales of space and channel information.
-
•
Cross-layer connection: In order to enhance the information exchange between different layers and improve the feature extraction ability of the network, cross-layer connections are often used in CNNs. There are mainly three types of cross-layer connections used in dehazing networks, which are residual connection (Zhang et al., 2020g; Qu et al., 2019; Hong et al., 2020; Liang et al., 2019; Chen et al., 2019d) proposed by ResNet (He et al., 2016), dense connection (Zhu et al., 2018; Zhang et al., 2022a; Dong et al., 2020a; Chen and Lai, 2019; Guo et al., 2019a; Li et al., 2019a) designed by DenseNet (Huang et al., 2017), and skip connection (Zhao et al., 2021a; Dudhane et al., 2019; Yang and Zhang, 2022; Lee et al., 2020b) inspired by U-Net (Ronneberger et al., 2015).
-
•
Attention in dehazing: The attention mechanism has been successfully applied in the research of natural language processing. Commonly used attention blocks in computer vision include channel attention and spatial attention. For the feature extraction and reconstruction process of 2D image, channel attention can emphasize the useful channels of the feature map. This unequal feature map processing strategy allows the model to focus more on effective feature information. The spatial attention mechanism focuses on the differences in the internal location regions of the feature map, such as the distribution of haze on the entire map. By embedding the attention module in the network, several dehazing methods (Liang et al., 2019; Chen et al., 2019d; Liu et al., 2019a; Qin et al., 2020; Yin et al., 2020; Lee et al., 2020b; Yan et al., 2020; Dong et al., 2020c; Yan et al., 2020; Zhang et al., 2020e; Yin et al., 2021; Metwaly et al., 2020; Wang et al., 2021d) have achieved excellent dehazing performance.
2.4. Loss Function
This section introduces the commonly adopted loss functions in supervised, semi-supervised and unsupervised dehazing models, which can be used for transmission map estimation, clear image prediction, hazy image reconstruction, atmospheric light regression, etc. Several algorithms use multiple losses in combination to obtain better dehazing performance. A detailed classification and summary of the loss functions used by different dehazing methods is presented in Table 3. In the loss function introduced below, and denote the predicted value and ground truth value, respectively.
2.4.1. Fidelity Loss
The widely used pixel-wise loss functions for dehazing research are L1 loss and L2 loss, which are defined as follows:
| (4) |
| (5) |
2.4.2. Perceptual Loss
The research on image super resolution (Ledig et al., 2017; Wang et al., 2018b) and style transfer (Johnson et al., 2016) indicates that the attributes of the human visual system in the process of perceptual evaluation is not fully reflected by L1 or L2 loss. Meanwhile, L2 loss may lead to over-smooth outputs (Ledig et al., 2017). Recent researches use pre-trained classification neural networks to calculate the perceptual loss in the feature space. The most commonly used pre-training model is VGG (Simonyan and Zisserman, 2015), and some of its layers are used to calculate the distance between the predicted image and the reference image in the feature space, i.e.,
| (6) |
where represents the number of features selected for calculation; means the index of feature map; denotes the pretrained VGG. During the calculation of perceptual loss and network optimization, the parameters of VGG are always frozen.
2.4.3. Structure Loss
As a metric of the dehazing methods, Structural Similarity (SSIM) (Wang et al., 2004) is also used as a loss function in the optimization process. Studies (Dong et al., 2020a; Yu et al., 2020) have shown that SSIM loss can improve the structural similarity during image restoration. MS-SSIM (Wang et al., 2003) introduces multi-scale evaluation into SSIM, which is also used as a loss function by the dehazing algorithms, i.e.,
| (7) |
| (8) |
2.4.4. Gradient Loss
Gradient loss, also known as edge loss, is used to better restore the contour and edge information of the haze-free image. The edge extraction can be implemented as Laplacian operator, Canny operator, and so on. For example, SA-CGAN (Sharma et al., 2020) uses the Laplacian of Gaussian with standard deviation to perform quadratic differentiation on the two-dimensional image :
| (9) |
where means pixel location and is calculated for both and , respectively. Then, regression objective functions such as L1 and L2 are used for the calculation of gradient loss.
2.4.5. Total Variation Loss
Total variation (TV) loss (Rudin et al., 1992) can be used to smooth image and remove noise. The training objective is to minimize the following function:
| (10) |
where and represent the horizontal and vertical coordinates, respectively. It can be seen from the formula that the TV loss can be added to networks trained in an unsupervised manner without using ground-truth .
| Loss Function | Algorithms |
|---|---|
| L1 | (Mondal et al., 2018; Chen et al., 2019b; Deng et al., 2019; Liang et al., 2019; Yin et al., 2019; Dong and Pan, 2020; Chen et al., 2020; Yan et al., 2020; Qin et al., 2020; Hong et al., 2020; Li et al., 2020d; Zhang et al., 2020b; Zhao et al., 2021a; Park et al., 2020; Shin et al., 2022; Zhang et al., 2022a) |
| L2 | (Li et al., 2017a; Pang et al., 2018; Zhu et al., 2018; Zhang et al., 2018a; Guo et al., 2019b; Morales et al., 2019; Chen et al., 2019d; Yang et al., 2019; Tang et al., 2019; Dong et al., 2020b; Zhang et al., 2020d; Yin et al., 2020; Zhang et al., 2021b, a, 2022c; Huang et al., 2021; Sheng et al., 2022) |
| SSIM | (Dong et al., 2020a; Yu et al., 2020; Metwaly et al., 2020; Wei et al., 2020; Singh et al., 2020; Li et al., 2020e; Jo and Sim, 2021; Shyam et al., 2021; Zhao et al., 2021a) |
| MS-SSIM | (Sun et al., 2021; Guo et al., 2019a; Cong et al., 2020; Yu et al., 2021; Fu et al., 2021) |
| Perceptual | (Sim et al., 2018; Pang et al., 2018; Zhu et al., 2021; Zhang et al., 2022c; Wang et al., 2021c; Deng et al., 2020; Liu et al., 2019a; Hong et al., 2020; Qu et al., 2019; Chen and Lai, 2019; Li et al., 2019a; Chen et al., 2019d; Singh et al., 2020; Dong et al., 2020a; Shyam et al., 2021; Engin et al., 2018) |
| TV Loss | (Das and Dutta, 2020; Li et al., 2020a; Shao et al., 2020; Huang et al., 2019; Wang et al., 2021c; He et al., 2019) |
| Gradient | (Zhang and Patel, 2018; Zhang et al., 2019a, 2020b, 2020e; Yin et al., 2020; Zhang et al., 2022b; Li et al., 2021c; Dudhane et al., 2019; Yin et al., 2021) |
2.5. Image Quality Metrics
Due to the presence of haze, the saturation and contrast of the image are reduced, and color of the image is distorted by the uncertainty mode. To measure the difference between the dehazed image and the ground truth haze-free image, objective metrics are needed to evaluate the results obtained by various dehazing algorithms.
Most papers use Peak Signal-to-Noise Ratio (PSNR) (Huynh-Thu and Ghanbari, 2008) and SSIM (Wang et al., 2004) to evaluate the image quality after dehazing. The computation of PSNR needs to use the formula (11) to obtain the mean square error (MSE):
| (11) |
where and respectively represent two images to be evaluated. and are their height and width, that is, the dimensionalities of and should be strictly the same. The pixel position index of the image is represented by and . Then, the PSNR can be obtained by logarithmic calculation as following:
| (12) |
where equals for -bit images. SSIM is based on the correlation between human visual perception and structural information, and its formula is defined as following:
| (13) |
where , , and represent the mean and variance of and , respectively; is the covariance between two variables; and are constants used to ensure numerical stability.
Since haze can cause the color of scenes and objects to change, some works use CIEDE2000 (Sharma et al., 2005) as an assessment of the degree of color shift. PSNR, SSIM and CIEDE belong to full-reference evaluation metrics, which means that a clear image corresponding to a hazy image must be used as a reference. However, real world pairs of hazy and haze-free images are difficult to keep exactly the same in content. For example, the lighting and objects in the scene may change before and after the haze appears. Therefore, in order to maintain the accuracy of the evaluation process, it is necessary to synthesize the corresponding hazy image with a clear image (Min et al., 2019).
In addition to the full-reference metric PSNR, SSIM and CIEDE, the recent works (Li et al., 2020c, 2019c) utilizes the no-reference metrics SSEQ (Liu et al., 2014) and BLIINDS-II (Saad et al., 2012) to evaluate dehazed images without ground truth. No-reference metric is of crucial value for real world dehazing evaluation. Nevertheless, the evaluation of current dehazing algorithms are usually conducted on datasets with pairs of hazy and haze-free images. Since the full-reference metric is more suitable for paired datasets, it is more widely used than the no-reference metric.
3. Supervised Dehazing
Supervised dehazing models usually require different types of supervisory signals to guide the training process, such as transmission map, atmospheric light, haze-free image label, etc. Conceptually, supervised dehazing methods can be divided into ASM-based and non-ASM-based ones. However, there may be overlaps in this way, since both ASM-based and non-ASM-based algorithms may entangle with other computer vision tasks such as segmentation, detection, and depth estimation. Therefore, this section categorizes supervised algorithms according to their main contributions, so that the techniques that prove valuable for dehazing research are clearly observed.
3.1. Learning of
According to the ASM, the dehazing process can be divided into three parts: transmission map estimation, atmospheric light prediction, and haze-free image recovery. MSCNN (Ren et al., 2016) proposes the following three steps for solving ASM: (1) use CNN to estimate the transmission map , (2) adopt statistical rules to predict atmospheric light , and (3) solve by and jointly. MSCNN adopts a multi-scale convolutional model for transmission map estimation and optimizes it with L2 loss. In addition, can be obtained by selecting darkest pixels in corresponding the one with the highest intensity in (He et al., 2010). Thus the clear image can be obtained by
| (14) |
Different papers may use different statistical priors to estimate , but the strategies they use for dehazing are similar to MSCNN. ABC-Net (Wang et al., 2020) uses the max pooling operation to obtain maximum value from each channel of . SID-JPM (Huang et al., 2018) filters each channel of a RGB input image by a minimum filter kernel. Then the maximum value of each channel is used as the estimated . LAPTN (Liu et al., 2018) also applies the minimum filter together with the maximum filter for the prediction of . These methods generally do not require atmospheric light annotations, but need paired of hazy images and transmission maps.
3.2. Joint Learning of and
Instead of using convolutional networks and statistical priors jointly to estimate the physical parameters of ASM, some works implement the prediction of physical parameters entirely through CNN. DCPDN (Zhang and Patel, 2018) estimates the transmission map through a pyramid densely connected encoder-decoder network, and uses a symmetric U-Net to predict the atmospheric light . In order to improve the edge accuracy of the transmission map, DCPDN has designed a hybrid edge-preserving loss, which includes L2 loss, two-directional gradient loss, and feature edge loss.
DHD-Net (Xie et al., 2020) designs a segmentation-based haze density estimation algorithm, which can segment dense haze areas and divide the global atmosphere light candidate areas. HRGAN (Pang et al., 2018) utilizes a multi-scale fused dilated convolutional network to predict , and employs a single-layer convolutional model to estimate . PMHLD (Chen et al., 2020) uses a patch map generator and refine the network for transmission map estimation, and utilizes VGG-16 for atmospheric light estimation. It is worth noting that if using regression training to obtain , the ground truth labels are generally required.
3.3. Non-explicitly Embedded ASM
ASM can be incorporated into CNN in a reformulated or embedded way. AOD-Net (Li et al., 2017a) founds that the end-to-end neural network can still be used to solve the ASM without directly using ground truth and . According to the original ASM, the expression of is
| (15) |
AOD-Net proposes , which has no actual physical meaning, as an intermediate parameter describing and . is defined as
| (16) |
where equals . According to the ASM theory, can be uniquely determined by as
| (17) |
AOD-Net considers that the non-joint transmission map and atmospheric light prediction process may produce accumulated errors. Therefore, independent estimation of can reduce the systematic error. FAMED-Net (Zhang and Tao, 2020) extends this formulation in a multi-scale framework and utilizes fully point-wise convolutions to achieve fast and accurate dehazing performance. DehazeGAN (Zhu et al., 2018) incorporates the idea of differentiable programming into the estimation process of and . Combined with a reformulated ASM, DehazeGAN also implements an end-to-end dehazing pipeline. PFDN (Dong and Pan, 2020) embeds ASM in the network design and proposes a feature dehazing unit, which removes haze in a well-designed feature space rather in the raw image space. It is instructive that ASM can still help the dehazing task for non-explicit parameter estimation.

3.4. Generative Adversarial Networks
Generative adversarial networks have an important impact on dehazing research. In general, supervised dehazing networks that rely on paired data can use adversarial loss as an auxiliary supervisory signal. Adversarial loss (Gui et al., 2022) can be seen as two parts: the training objective of the generator is to generate images that the discriminator considers to be real. The optimization purpose of the discriminator is to distinguish the generated image from the real image contained in the dataset as possible as it could. For dehazing task, the effect of the adversarial loss is to make the generated image closer to the real one, which is beneficial for the optimization of the haze-free and transmission map (Zhang et al., 2019a), as shown in Fig. 6.
Inspired by patchGAN (Isola et al., 2017), which can better preserve high-frequency information, DH-GAN (Sim et al., 2018), RI-GAN (Dudhane et al., 2019) and DehazingGAN (Zhang et al., 2020c) use patches instead of a single value as the output of the discriminator. Several works explore joint training mechanisms of multiple discriminators, such as EPDN (Qu et al., 2019) and PGC-UNet (Zhao et al., 2021a). Discriminator is used to guide the generator on a fine scale, while discriminator helps the generator to produce a global realistic output on a coarse scale. In order to realize the joint training of the two discriminators, EPDN downsamples the input image of by a factor of as the input of . The adversarial loss is
| (18) |
where the form of adversarial loss is the same as the single GAN. The exploration of GAN brings plug-and-play tools to supervised algorithms. Since the training of the discriminator can be done in an unsupervised manner, the quality of the dehazed images can be improved without the requirement of extra labels. However, the training of GAN sometimes suffers from instability and non-convergence, which may bring certain additional difficulties to the training of the dehazing network.
3.5. Level-aware
According to the scattering theory, the farther the scene is from the camera, the more aerosol particles pass through. This means that areas within a single hazy image that are farther from the camera have higher densities of haze. Therefore, LAP-Net (Li et al., 2019b) proposes that the algorithm should consider the difference in haze density inside the image. Through multi-stage joint training, LAP-Net implements an easy-to-hard model that focuses on a specific haze density level by a stage-wise loss
| (19) |
where represents the transmission map prediction network with parameter in stage . In the first stage, the transmission map prediction network is responsible for estimating the case with mild haze. In the second and subsequent stages, the prediction result of the previous stage and the hazy image are used as joint input for processing higher haze density.
The density of haze may be related to conditions such as temperature, wind, altitude, and humidity. Thus, the formation of haze should be space-variant and non-homogeneous. Based on this observation, HardGAN (Deng et al., 2020) argues that estimating the transmission map for dehazing may be inaccurate. By encoding the atmospheric brightness as matrix and pixel-wise spatial information as matrix for -th channel of the input , HardGAN designs the control function of atmospheric brightness and spatial information as
| (20) |
where and denote the mean and standard deviation for , respectively. After obtaining and , HardGAN uses a linear model to fuse them for recovering haze-free image
| (21) |
where is calculated by the intermediate feature map of HardGAN via using instance normalization followed by a sigmoid layer, and denotes element-wise product.
3.6. Multi-function Fusion
DMMFD (Deng et al., 2019) designs a layer separation and fusion model for improving learning ability, including reformulated ASM, multiplication, addition, exponentiation and logarithmic decomposition:
| (22) |
where stands for layers in the network; and are the atmospheric light and transmission map estimated by the feature extraction network, respectively. , , , and can be used as four independent haze-layer separation models. It is based on the assumption that the input hazy image can be separated into a haze-free layer and another layer , denoted as . The final dehazing result is obtained by weighted fusion of the intermediate outputs , , , and by five learned attention maps , , , and as
| (23) |
Through ablation studies, DMMFD has demonstrated that the fusion of multiple layers can improve the quality of the scene restoration process.
3.7. Transformation and Decomposition of Input
GFN (Ren et al., 2018a) proposes two observations on the influence of haze. First, under the influence of atmospheric light, the color of a hazy image may be distorted to some extent. Second, due to the existence of scattering and attenuation phenomena, the visibility of objects far away from the camera in the scene will be reduced. Therefore, GFN uses three enhancement strategies to process the original hazy image and use them as inputs to the dehazing network together. The white balanced input is obtained from the gray world assumption. The contrast enhanced input is composed of average luminance value and the control factor , as following:
| (24) |
where . By using the the nonlinear gamma correction, the used to enhance the visibility of the can be obtained by
| (25) |
where , and . The final dehazing image is determined by the combination of three inputs, where , and are confidences map for fusion process:
| (26) |
MSRL-DehazeNet (Yeh et al., 2019) decomposes the hazy image into low frequency and high frequency as the base component and the detail component , respectively. The basic component can be thought as the main content of the image, while the high frequency component denotes the edge and texture. Therefore, the dehazed image can be obtained by the dehazing function of the basic component and the enhancement function of the detail component. The whole process can be represented by a linear model as following:
| (27) |
DIDH (Shyam et al., 2021) decomposes both the input hazy image and the predicted haze-free image to obtain , , and , where and denotes Gaussian and Laplacian filter, respectively. By fusing the decomposed data with the pre-decomposition data as the input of the discriminator, DIDH can improve the quality of the image generated by the adversarial training process. With the help of the discriminators and , the dehazing network can be optimized in an adversarial way.
Compared with conventional data augmentation, such as rotation, horizontal or vertical mirror symmetry, and random cropping, the transformation and decomposition of the input is a more efficient strategy for the usage of hazy images.

3.8. Knowledge Distillation
Knowledge distillation (Gou et al., 2021) provides a strategy to transfer the knowledge learned by the teacher network to the student network, which has been applied in high-level computer vision tasks like object detection and image classification (Wang et al., 2019). Recent work (Hong et al., 2020) presents three challenges for applying knowledge distillation to the dehazing task. First, what kind of teacher task can help the dehazing task. Second, how the teacher network helps the dehazing network during training. Third, which similarity measure between teacher task and student task should be chosen. Fig. 7 shows the knowledge distillation strategy adopted by various dehazing algorithms. Different methods may use different numbers and locations of output features to compute feature loss.
KDDN (Hong et al., 2020) designs a process-oriented learning mechanism, where the teacher network is an auto-encoder for high-quality haze-free image reconstruction. When training the dehazing network, the teacher network assists in feature learning, and optimizes . Therefore, the teacher task and the student task proposed by KDDN are two different tasks. In order to make full use of the feature information learned by the teacher network and help the training of the dehazing network. KDDN uses feature matching loss and haze density aware loss by a linear transformation function , which are represented by (28) and (29), respectively.
| (28) |
| (29) |
where represents the -th layer of the teacher network, and the corresponding represents the -th layer of the student network; is obtained by the normalization operation. KDDN can be trained without real transmission map, replaced by the residual between hazy and haze-free images.
KTDN (Wu et al., 2020) is jointly trained using a teacher network and a dehazing network with the same structure. Through feature level loss, the prior knowledge possessed by the teacher network can be transferred to the dehazing network. SRKTDN (Chen et al., 2021a) uses ResNet18 pre-trained on ImageNet (with classification layers removed) as the teacher network, transferring many statistical experiences to the Res2Net101 encoder for dehazing. DALF (Fang et al., 2021) integrates dual adversarial training into the training process of knowledge distillation to improve the imitation ability of the student network to the teacher network. Applying knowledge distillation to dehazing networks provides a new and efficient way to introduce external prior knowledge.
3.9. Transformation of Colorspace
The input data of the dehazing network are usually three channel color images in RGB mode. By calculating the mean square error of hazy and haze-free images in RGB space and YCrCb space on the Dense-Haze dataset, Bianco et al. (Bianco et al., 2019) find that haze shows obvious numerical differences in the two spaces. The error values for the red, green and blue channels in RGB space are very close. However, in the YCrCb space, the error value of the luminance channel is significantly larger than that of the blue and red chroma components. AIP-Net (Wang et al., 2018a) performs a similar error comparison of color space transformation on synthetic datasets and obtained the same conclusion as (Bianco et al., 2019). Quantitative results (Wang et al., 2018a; Bianco et al., 2019) obtained by training the dehazing network in the YCrCb color space show that RGB space is not the only effective color mode for deep learning based dehazing methods. Furthermore, TheiaNet (Mehra et al., 2021) comprehensively analyzes the performance obtained by training the dehazing model in RGB, YCrCb, HSV and LAB color spaces. Experiments (Singh et al., 2020; Sheng et al., 2022; Chen et al., 2021a; Dudhane and Murala, 2019b) show that converting images from RGB space to other color spaces for model training is an effective scheme.
3.10. Contrastive Learning
In the process of training a non-ASM-based supervised dehazing network, a common way is to use the hazy image as the input of the network and expect to obtain a clear image. In this process, the clear image is used as a positive example to guide the optimization of the network. By designing pairs of positive and negative examples, AECR-Net provides a new perspective for treating hazy and haze-free images. Specifically, the clear image and the dehazed image are taken as a positive sample pair, while the hazy image and the dehazed image are taken as a negative sample pair. According to contrastive learning (Khosla et al., 2020), , and can be regarded as anchor, positive and negative, respectively. For the pre-trained model , the dehazing loss can be regarded as the sum of the reconstruction loss and the regularization term, as following:
| (30) |
where represents the output feature of the -th layer of the pre-trained model; is the weight ratio between the image reconstruction loss and the regularization term; is weight factor for feature output; is the dehazing network. AECR-Net provides a universal contrastive regularization strategy for existing methods without adding extra parameters.
3.11. Non-deterministic Output
Dehazing methods based on deep learning usually set the optimization objective to obtain a single dehazed image. By introducing 2-dimensional latent tensors, pWAE (Kim et al., 2021) can generate different styles of dehazed images, which extends the general training purpose. pWAE proposes dehazing latent space and style latent space for dehazing, and applies the mean function and standard deviation function to perform the transformation of the space:
| (31) |
A natural question is how to adjust the magnitude of the spatial mapping to control the degree of style transformation. pWAE uses linear module to adjust the weight between the dehazed image and the style information. By controlling , different degrees of stylized dehazed images corresponding to the style image can be obtained.
DehazeFlow (Li et al., 2021b) proposes that the dehazing task itself is ill-posedness, so it is unreliable to learn a model with deterministic one-to-one mapping. With a conditional normalizing flow network, DehazeFlow can compute the conditional distribution of clear images from a given hazy image. Therefore, it can learn a one-to-many mapping and obtain different dehazing results in the inference stage. The non-deterministic output (Kim et al., 2021; Li et al., 2021b) brings interpretable flexibility to the dehazing algorithm. Since the visual evaluation criteria of individual human beings are inherently different, one-to-many dehazing mapping provides more options for photographic work.
3.12. Retinex Model
Non-deep learning based research (Galdran et al., 2018) demonstrates the duality between Retinex and image dehazing. Apart from the already widely used ASM, recent work (Li et al., 2021c) explores the combination of Retinex model and CNN for dehazing. Retinex theory proposes that the image can be regarded as the element-wise product of the reflectance image and the illumination map . Assuming the reflectance is illumination invariant, the relationship between hazy and haze-free image can be modeled by a retinex-based decomposition model as following:
| (32) |
where means the multiplication in an element-wise way. can be seen as absorbed and scattered light caused by haze, which is determined by the ratio of the hazy image illumination map and natural illumination map .
Compared with ASM, which has been proven to be reliable, Retinex has a more compact physical form and fewer parameters to be estimated, but is not widely combined with CNN for dehazing, yet.
3.13. Residual Learning
Rather than directly learning the mapping from hazy to haze-free image, several methods argue that the residual learning method can reduce the learning difficulty of the network. The dehazing methods based on residual learning is performed at the image level. GCANet (Chen et al., 2019c) uses the residual {} between haze-free and hazy images as the optimization objective. DRL (Du and Li, 2018), SID-HL (Xiao et al., 2020) and POGAN (Du and Li, 2019) believe that the way of residual learning is related to ASM, and the relationship can be obtained by reformulated ASM:
| (33) |
where can be interpreted as a structural error term. By predicting nonlinear signal-dependent degradation , a clear image can be obtained.
3.14. Frequency Domain
The dehazing methods based on CNN usually use down-sampling and upsampling for feature extraction and clear image reconstruction, and this process less considers the frequency information contained in the image. There are currently two approaches to combine frequency analysis and dehazing networks. The first is to embed the frequency decomposition function into the convolutional network, and the second is to use frequency decomposition as a constraint for loss computation. For a given image, one low-frequency component and three high-frequency components can be obtained by wavelet decomposition. Wavelet U-net (Yang and Fu, 2019) uses discrete wavelet transform (DWT) and inverse discrete wavelet transform (IDWT) to facilitate high quality restoration of edge information in a clear image. Through the 1D scaling function and the wavelet function , the 2D wavelets low-low (LL), low-high (LH), high-low (HL) and high-high (HH) are calculated as follows
| (34) |
where and represent the horizontal and vertical coordinates, respectively. MsGWN (Dong et al., 2020c) uses Gabor wavelet decomposition for feature extraction and reconstruction. By setting different degree values, the feature extraction module of MsGWN can obtain frequency information in different directions. EMRA-Net (Wang et al., 2021d) uses Haar wavelet decomposition as a downsampling operation instead of nearest downsampling and strided-convolution to avoid the loss of image texture details. By embedding wavelet analysis into convolutional network or loss function, recent studies (Yang et al., 2020; Dharejo et al., 2021; Fu et al., 2021) have shown that 2D wavelet transform can improve the recovery of high-frequency information in the wavelet domain. These works successfully apply wavelet theory and neural networks to dehazing tasks.
Besides, TDN (Liu et al., 2020b) introduces the Fast Fourier transform (FFT) loss as a constraint in the frequency domain. With the help of supervised training on amplitude and phase, the visual perceptual quality of images is improved without any additional computation in the inference stage.
3.15. Joint Dehazing and Depth Estimation
The scattering particles in the hazy environment will affect the accuracy of the depth information collected by the LiDAR equipment. S2DNet (Hambarde and Murala, 2020) proves that high-quality depth estimation algorithms can help the dehazing task. According to ASM, it can be known that the transmission map and the depth map have a negative exponential relationship . Based on this physical dependency, SDDE (Lee et al., 2020a) uses four decoders to integrate estimates of atmospheric light, clear image, transmission map, and depth map into an end-to-end training pipeline. In particular, SDDE proposes a depth-transmission consistency loss based on the observation that the standard deviation value () of the transmission map and the depth map pair should tend to zero:
| (35) |
where and represent the predicted transmission map and depth map, respectively. Aiming at better dehazing, TSDCN-Net (Cheng and Zhao, 2021) designs a cascaded network for two-stage methods with depth information prediction. Quantitative experimental results (Yang and Zhang, 2022) show that this joint estimation method can improve the accuracy of dehazing task.
3.16. Segmentation and Detection with Dehazing
Existing experiments (Li et al., 2017a) show that the existence of image haze may cause various problems in detection algorithms, such as missing targets, inaccurate localizations and unconfident category prediction. Recent work (Sakaridis et al., 2018) has shown that haze also brings difficulties to semantic scene understanding. As a preprocessing module for high-level computer vision tasks, the dehazing process is usually separated from high-level computer vision tasks.
Li et al. (Li et al., 2017a) jointly optimize the object detection algorithm and AOD-Net, and the result proves that the dehazing algorithm can promote the detection task. LEAAL (Li et al., 2020c) proposes that fine-tuning the parameters of the object detector during joint training may lead to a detector biased towards the haze-free images generated by the pretrained dehazing network. Different from the fine-tuning operation of Li et al. (Li et al., 2017a), LEAAL uses object detection as an auxiliary task for dehazing and the parameters of the object detector are not fully updated during the training process.
UDnD (Zhang et al., 2020g) takes advantage of each other by jointly training a dehazing network and a dense-aware multi-domain object detector. The object detection network is trained by adopting the classification and localization terms used by Region Proposal Network and Region of Interest. The multi-task training approach used by UDnD can consider the reduced inter-domain gaps and the remained intra-domain gaps for different density levels.
Recent work has explored performing dehazing and high-level computer vision tasks simultaneously without using ASM. SDNet (Zhang et al., 2022a) combines semantic segmentation and dehazing into a unified framework in order to use semantic prior as a constraint for the optimization process. By embedding the predictions of the segmentation map into the dehazing network, SDNet performs a joint optimization of pixel-wise classification loss and regression loss. The classification loss is
| (36) |
where is the total number of pixels; is the class prediction at position ; denotes the ground truth semantic annotation.
(Zhang et al., 2022a, 2020g; Li et al., 2020c) show that segmentation and detection can be performed by embedding with dehazing networks. The way of joint dehazing task and high-level vision task may reduce the computational load to a certain extent by sharing the learned features, which can expand the goal of dehazing research.
3.17. End-to-end CNN
The “end-to-end” CNN stands for the non-ASM-based supervised algorithms, which usually consist of well-designed neural networks that take a single hazy image as input and a haze-free image as output. Networks based on different ideas are adopted, which are summarized as follows.
The end-to-end dehazing networks have an important impact on the entire dehazing field, proving that numerous deep learning models are beneficial to the dehazing task.
4. Semi-supervised Dehazing
Compared with the research on supervised methods, semi-supervised dehazing (Zhao et al., 2021b; Chen et al., 2021b) algorithms have received relatively less attention. An important advantage of semi-supervised methods is the ability to utilize both labeled and unlabeled datasets. Therefore, compared to the fully supervised dehazing model, the semi-supervised dehazing model can alleviate the requirement of paired hazy and haze-free images. For dehazing task, labeled datasets are usually synthetic or artificially generated, while unlabeled datasets usually contain real world hazy images. According to the analysis of the dataset in Section 2, there are inherent differences between synthetic data and real world data. Therefore, semi-supervised algorithms usually have the ability to mitigate the gaps between synthetic domain and the real domain.
Fig. 8 shows the principles of various semi-supervised dehazing models, where the network is a schematic diagram.

(a) Pretrain and finetune (b) Disentangled and reconstruction (c) Two branches training
4.1. Pretrain Backbone and Finetune
PSD (Chen et al., 2021b) proposes a domain adaptation method that can be extended by existing models. It first uses a powerful backbone network for pre-training to obtain a base model suitable for synthetic data. Then the fine-tuning of the real domain in an unsupervised manner is applied to the well-trained network, thereby improving the generalization ability of the model to real world hazy images. To achieve fine-tuning in the real domain, PSD combines DCP loss, Bright Channel Prior (BCP) (Wang et al., 2013) loss and Contrast Limited Adaptive Histogram Equalization (CLAHE) loss together. BCP loss and CLAHE loss are
| (37) |
| (38) |
where represents the transmission map estimated by BCP and is the predicted output of the network. is the hazy image reconstructed by CLAHE and other physical parameters.
During fine-tuning, the model may forget the useful knowledge it learned during the pre-training phase. Therefore, PSD proposes a feature-level constraint, which is achieved by calculating the feature map difference between the fine-tuning network and the pre-trained network. By feeding the synthetic data and real data into the fine-tuning network and the pre-trained network, respectively, four feature maps can be obtained: , , , and . Then, the loss for preventing knowledge forgetting can be calculated as
| (39) |
As shown in Fig. 8(a), supervised pre-training is performed first, and then the dehazing network is fine-tuned in an unsupervised form.
SSDT (Zhang and Li, 2021) uses the encoder-decoder network for pre-training in the form of domain translation. After pre-training, two encoders and one decoder are selected to obtain the holistic dehazing network . Then, is fine-tuned with synthetic hazy images and real world hazy images. The two-stage method described above needs to ensure that the pre-training process can meet the accuracy requirements, otherwise it may bring accumulated errors to the fine-tuning process.
4.2. Disentangled and Reconstruction
From the perspective of dual learning, the dehazing task and the haze generation task can be able to assist each other. Based on this assumption, DCNet (Chen et al., 2021c) proposes a dual-task cycle network that jointly utilizes labeled dataset and unlabeled dataset by dehazing network and haze generation network . The total loss is combine by dehazing loss and reconstruction loss , that is , as
| (40) |
where and are regularizing hyper-parameter; equals when the comes from the labeled dataset , and equals otherwise. As shown in Fig. 8 (b), the predicted haze-free image is first obtained by the left network, and then the hazy image is reconstructed by the right network.
Liu et al. (Liu et al., 2021) use a disentangled image dehazing network (DID-Net) and a disentangled-consistency mean-teacher network (DMT-Net) to combine labeled and unlabeled data. DID-Net is responsible for disentangling the hazy image into a haze-free image, the transmission map, and the global atmospheric light. DMT-Net is used to jointly exploit the labeled synthetic data and unlabeled real world data through disentangled consistency loss. The supervised loss consists of four terms: haze-free image prediction , transmission map prediction , atmospheric light prediction , and hazy image reconstruction :
| (41) |
where stands for ground-truth, is the prediction of the first stage, and is the prediction of the second stage. The supervised loss is the weighted sum of the above four losses, that is . For unlabeled data, consistency loss is used to constrain the teacher network and the student network :
| (42) |
where the subscript , , and denote the results predicted in second stage. Thus, the loss for the unlabeled dataset is . The final loss function of the semi-supervised framework consists of a supervised loss on the labeled dataset and a consistency loss on the unlabeled dataset , that is .
CCDM (Zhang et al., 2020f) designs a color-constrained dehazing model that can be extended to a semi-supervised framework, which is achieved by the reconstruction of hazy images, the smoothing loss of and , etc. Experiments (Liu et al., 2021; Zhang et al., 2020f; Chen et al., 2021c) show that the reconstruction of hazy images can provide effective supervisory signals in an unsupervised manner, which is instructive for semi-supervised frameworks.
4.3. Two-branches Training
SSID (Li et al., 2020a) designs an end-to-end network that integrates a supervised learning branch and an unsupervised learning branch. The training process of SSID uses both the labeled dataset and the unlabeled dataset by the following process:
| (43) |
where consists of a supervised part and an unsupervised part . The supervised loss composed of L2 loss and perceptual loss is used to ensure that the predicted image and its corresponding ground truth image are as close as possible, which is the same as the supervised dehazing algorithm. A combination of total variation loss and dark channel loss is used for unsupervised training. As shown in Fig. 8(c), supervised training and unsupervised training are performed in a shared weight manner.
SSIDN (An et al., 2022) also combines supervised and unsupervised training processes. Supervised training is used to learn the mapping from hazy to haze-free images. With dark channel prior and bright channel prior (Wang et al., 2013) guiding the training process, the unsupervised branch incorporates the estimation of the transmission map and atmospheric light.
The DAID (Shao et al., 2020) adopts a domain adaptation model to jointly train multi-subnetworks. The and are the image translation modules used for the translation between the synthetic domain and the real domain, where and stand for real domain and synthetic domain, respectively. By using an image-level discriminator and a feature-level discriminator , the adversarial loss of the translation process can be calculated. In order to ensure that the content of images are maintained during the translation process, DAID uses cycle consistency loss to constrain the translation network. Furthermore, identity mapping loss is also used in the conversion process to restrict the identity of the image generation process in two domains. The training of the dehazing network is a combination of unsupervised and supervised processes. The supervised process minimizes the loss to make the dehazed image closer to the corresponding haze-free image :
| (44) |
Then, the total variation loss and dark channel loss are used as unsupervised losses. For the training of the dehazing network , there is also a combination of supervised loss and unsupervised loss. With the help of domain transformation and unsupervised loss, DAID can effectively reduce the gap between the synthetic domain and the real domain.
5. Unsupervised Dehazing
The supervised and semi-supervised dehazing methods have achieved excellent performance on public datasets. However, the training process requires paired data (i.e. hazy images and haze-free images / transmission maps), which are difficult to obtain in the real world. For outdoor scenes containing grass, water or moving objects, it is difficult to guarantee that two images taken under hazy and clear weather have exactly the same content. If the haze-free labels are not accurate enough, the accuracy of dehazed images will be reduced. Therefore, (Engin et al., 2018; Dudhane and Murala, 2019a; Liu et al., 2020a; Wei et al., 2021) explore dehazing algorithms in an unsupervised way.

(a) Between two domains (b) Among multi-domains (c) Without target (d) Zero-shot
5.1. Unsupervised Domain Transfer
In the study of image style transfer and image-to-image translation, CycleGAN (Zhu et al., 2017) is proposed, which provides a way for learning the bidirectional mapping functions between two domains. Inspired by CycleGAN, (Engin et al., 2018; Dudhane and Murala, 2019a; Liu et al., 2020a) are designed for unsupervised transformation of hazy and haze-free / transmission domains. The Cycle-Dehaze (Engin et al., 2018) contains two generators and , which are used to learn the mapping from hazy domain to haze-free domain and the reverse mapping, respectively. As shown in Fig. 9 (a), the hazy and haze-free images are translated to each other by two generators. By sampling and from the hazy domain and the haze-free domain , the Cycle-Dehaze uses the perceptual metric (denoted as ) to obtain the cyclic perceptual consistency loss:
| (45) |
The overall loss function of Cycle-Dehaze is composed of cyclic perceptual consistency loss and Cycle-GAN’s loss function, which can alleviate the requirement of paired data. CDNet (Dudhane and Murala, 2019a) also adopts a cycle-consistent adversarial approach for unsupervised dehazing network training. Unlike Cycle-Dehaze, CDNet embeds ASM into the network architecture for estimating transmission map, which enables it to acquire physical parameters while restoring haze-free images. E-CycleGAN (Liu et al., 2020a) adds ASM and a priori statistical law to estimate atmospheric light on the basis of CycleGAN, which allows it to perform independent parameter estimation for sky regions.
USID (Huang et al., 2019) introduces the concept of haze mask and constant bias , which can obtain the reformulated ASM as
| (46) |
By combining with cycle consistent loss, USID also removes the requirement of an explicit paired haze/depth data in an unsupervised multi-task learning manner. In order to decouple content and haze information, USID-DR (Liu, 2019) designs a content encoder and a haze encoder embedded in CycleGAN. This decoupling approach can enhance feature extraction and reconstruction during cycle consistent training. USID-DR proposes that making the output of the encoder conform to the Gaussian distribution by latent regression loss can improve the quality of hazy image synthesis process, thereby improving the overall dehazing performance. DCA-CycleGAN (Mo et al., 2022) utilizes the dark channel to build the input and generates the attention for handling the nonhomogeneous haze. These CycleGAN-based methods demonstrate that unsupervised hazy and haze-free image domain transformation can achieve the same performance as supervised algorithms from both ASM-based and non-ASM-based perspectives.
For the dehazing task, the haze density in hazy images can be very different. Most supervised, semi-supervised and unsupervised dehazing methods hold the view that hazy images and haze-free images should be treated as two domains, without considering the density among different examples. Recent work (Jin et al., 2020) proposes that it is an important issue to apply the haze density information to the unsupervised training process, thereby improving the generalization ability of the dehazing model to images with different densities of haze. An unsupervised conditional disentangle network, called UCDN (Jin et al., 2020), is designed by incorporating conditional information into the training process of CycleGAN. Further, DHL-Dehaze (Cong et al., 2020) analyzes multiple haze density levels of hazy images, and proposes that the difference in haze density should be fully utilized in the dehazing procedure. Compared to UCDN which contains four submodules, DHL-Dehaze has only two networks to train. The idea of DHL-Dehaze is based on the research of multi-domain image-to-image translation. As shown in Fig. 9(b), the images , and of different densities can be transformed to other domains, where can be explained as the haze-free domain. The training of DHL-Dehaze consists of a adversarial process and a classification process. By sampling with corresponding density labels , the classification loss and adversarial loss in the source domain can be obtained by (47) and (48):
| (47) |
| (48) |
In order to generate the images of the target domain, the labels of target domain are required. DHL-Dehaze sends and into the multi-scale generator (MST) together, and obtains new images with the same attributes as :
| (49) |
Then, the classification loss and adversarial loss of the target domain image can be obtained by using (50) and (51):
| (50) |
| (51) |
It is worth noting that UCDN and DHL-Dehaze do not use the hazy and haze-free images of the same scene for supervision, but apply the density of haze as the supervisory information for the training process.
The training of unsupervised domain transformation algorithms is more difficult than that of supervised algorithms. The convergence of GAN-based domain transformation algorithms is difficult to determine, which may lead to over-enhanced images.
5.2. Learning without Haze-free Images
The training process of CycleGAN-based methods and DHL-Dehaze does not require paired data, which has greatly reduced the difficulty of data collection. Further, Deep-DCP (Golts et al., 2020) proposes to use only hazy image for training process. The strategy of domain translation dehazing algorithms is to learn the mapping relationship between hazy and haze-free / transmission domains, while the main idea of Deep-DCP is to minimize the DCP (He et al., 2010) energy function. According to statistical assumption, the transmission map can be estimated in an unsupervised way. Based on the estimated transmission map and soft matting, the energy function can be obtained, where is the parameters for tuning. Thus, the goal of training is to minimize the energy function:
| (52) |
As shown in Fig. 9(c), the network can automatically learn the mapping from hazy to haze-free images without requiring target domain labels.
5.3. Unsupervised Image Decomposition
Double-DIP (Gandelsman et al., 2019) proposes an unsupervised hierarchical decoupling framework based on the observation that the internal statistics of a mixed layer is more complex than the single layer that composes it. Suppose is a linear sum of independent random variables and . From a statistical point of view, the entropy of is larger than its independent components, that is, . Based on this, Double-DIP proposes the loss for image layer decomposition:
| (53) |
where represents the reconstruction loss of the hazy image, is the exclusion loss between the two DIPs, and is the regularization loss used to obtain the continuous and smooth transmission map.
5.4. Zero-Shot Learning for Dehazing
Data-driven unsupervised dehazing methods have achieved impressive performance. Unlike those models that require sufficient data to perform network training, ZID (Li et al., 2020b) proposes a neural network dehazing process that only requires a single example. ZID has further reduced the dependence of the parameter learning process on data by combining the advantages of unsupervised learning and zero-shot learning. Three sub-networks (J-Net), (T-Net) and (A-Net) are used to estimate the , and , respectively. By the reconstruction process, the hazy image can be disentangled by minimizing loss:
| (54) |
where is reconstructed hazy image, and denotes -norm. The disentangled atmospheric light and Kullback-Leibler divergence are used to obtain the atmospheric light as shown in the following formula:
| (55) |
where is the loss for and initial hint value is automatically learned from data. It should be noted that in ZID is not the same as in ASM; stands for Gaussian distribution; is learned from input . The unsupervised channel loss used in J-Net is for the decomposing process of the haze-free image . The is calculated based on the dark channel, and the formula is , where denotes color channel and stands for local patch of the J-Net output. The purpose of is to enhance the stability of the model and make and smooth. The overall loss function of ZID is
| (56) |
YOLY (Li et al., 2021a) uses three joint disentanglement subnetworks for clear image and physical parameter estimation, enabling unsupervised and untrained haze removal. As shown in Fig. 9(d), ZID and YOLY can learn the mapping from hazy to haze-free image using a single unlabeled example.
The limitation of the zero-shot algorithm is that the generalization ability is limited, and the network must be retrained for each unseen example to get good dehazing performance.
6. Experiment and Performance Analysis
This section provides quantitative and qualitative analysis of the dehazing performance of the baseline supervised, semi-supervised and unsupervised algorithms. The training examples used in the experiments are the indoor data ITS and outdoor data OTS from RESIDE (Li et al., 2019c). In order to accurately compare the dehazed images and the real clear images, the indoor and outdoor images included in the SOTS provided by RESIDE are used as the test set. Aiming at ensuring the fairness and representativeness of the experimental results, 10 representative algorithms are selected for comparison:
- •
-
•
semi-supervised: SSID (Li et al., 2020a).
- •
The framework used for the algorithm implementation is PyTorch, and the running platform is NVIDIA Tesla V100 32 GB (2 GPUs). Except for the zero-shot ZID, all algorithms use a batch size of 8 in the training phase. For the ITS and OTS datasets, the training epochs are set according to (Qin et al., 2020) and (Liu et al., 2019a), respectively. For the supervised dehazing methods, four loss function strategies are adopted, including L1, L2, L1 + P, L2 + P, where P denotes the perceptual loss. For semi-supervised and unsupervised methods, the loss functions follow the settings in the respective papers. In the experiment, we first compared the convergence curves of different supervised algorithms when they were set to 0.001, 0.0005 or 0.0002, and selected the value with the best convergence effect as the best learning rate. After the training process, the loss values of all supervised models have stably converged. For semi-supervised and unsupervised algorithms, the learning rates used are those recommended in the corresponding papers.
In order to ensure as few interference factors as possible in the experiments, the following strategies are not used in the experiments: (1) pre-training, (2) dynamic learning rate adjustment, (3) larger batch size, and (4) data augmentation. Therefore, the quantitative results obtained in the following experiments may be a little lower than the best results provided in the papers corresponding to the various algorithms.
Tables 4 and 5 show the PSNR/SSIM values obtained on the indoor and outdoor test sets of various algorithms on RESIDE SOTS, where the highest values are shown in bold. It can be concluded that FFA-Net achieves the best performance on the indoor test set, with the highest PSNR and SSIM. The best performance among different algorithms on the outdoor test set is achieved by different methods. It can be also seen from Tables 4 and 5 that the perceptual loss has a certain effect on the performance of the model, but it is not obvious.
Figure 10 and Figure 11 show the visual results achieved by the supervised, semi-supervised and unsupervised algorithms, respectively, where the loss function used by the supervised algorithms is the L1 loss. The visual results show that the dehazed images obtained by the supervised algorithms are closer to the real images in terms of color and detail than the semi-supervised/unsupervised algorithms.
| Config | L1 | L1 + P | L2 | L2 + P |
|---|---|---|---|---|
| AODNet | 0.839/19.375 | 0.841/19.454 | 0.851/19.576 | 0.839/19.388 |
| 4kDehazing | 0.932/23.881 | 0.949/26.569 | 0.928/23.370 | 0.928/23.353 |
| DMMDF | 0.959/30.585 | 0.960/30.383 | 0.961/30.631 | 0.961/30.725 |
| FFA-Net | 0.983/32.730 | 0.983/32.536 | 0.978/32.224 | 0.978/32.178 |
| GCA-Net | 0.924/25.044 | 0.930/25.638 | 0.917/24.716 | 0.909/24.714 |
| GridDehazeNet | 0.962/25.671 | 0.962/25.655 | 0.935/22.940 | 0.940/23.052 |
| MSBDN | 0.955/28.341 | 0.955/28.562 | 0.941/27.237 | 0.937/25.662 |
| SSID | 0.814/20.959 | |||
| Cycle-Dehaze | 0.810/18.880 | |||
| ZID | 0.835/19.830 | |||
| Config | L1 | L1 + P | L2 | L2 + P |
| AODNet | 0.913/23.613 | 0.917/23.683 | 0.912/23.253 | 0.916/23.488 |
| 4kDehazing | 0.963/28.476 | 0.964/28.473 | 0.958/28.103 | 0.950/27.546 |
| DMMDF | 0.905/25.805 | 0.963/30.237 | 0.963/30.535 | 0.965/30.682 |
| FFA-Net | 0.921/27.126 | 0.925/27.299 | 0.913/28.176 | 0.920/28.441 |
| GCA-Net | 0.953/27.784 | 0.949/27.559 | 0.946/27.20 | 0.943/27.273 |
| GridDehazeNet | 0.964/28.296 | 0.964/28.388 | 0.963/27.807 | 0.963/27.766 |
| MSBDN | 0.962/29.944 | 0.963/30.277 | 0.964/29.843 | 0.956/28.782 |
| SSID | 0.840/20.905 | |||
| Cycle-Dehaze | 0.861/20.347 | |||
| ZID | 0.633/13.520 | |||












(a) hazy (b) 4kDehazing (c) AODNet (d) DMMFD (e) FFA-Net (f) GCA-Net












(g) GridDehazeNet (h) MSBDN (i) SSID (j) Cycle-Dehaze (k) ZID (l) clear
For a fair comparison of the computational speed of the baseline methods, the zero-shot-based ZID and high-resolution-based 4kDehazing are excluded. Fig. 12 shows the average time for each algorithm that run 1000 times with PyTorch framework. It can be seen that AODNet is the fastest, and can achieve real-time effects for inputs of different sizes. FFA-Net is the slowest, taking more than 0.3 seconds to process the input.












(a) hazy (b) 4kDehazing (c) AODNet (d) DMMFD (e) FFA-Net (f) GCA-Net












(g) GridDehazeNet (h) MSBDN (i) SSID (j) Cycle-Dehaze (k) ZID (l) clear

7. Challenges and Opportunities
For image dehazing task, the current supervised, semi-supervised and unsupervised methods have achieved good performance. However, there are problems that still exist and open issues that should be explored in the future research. Next, we will discuss these challenges.
7.1. More Effective ASM
The current ASM has been proved to be suitable for describing the formation process of haze by many supervised, semi-supervised and unsupervised dehazing methods. However, recent work (Ju et al., 2021) finds that the intrinsic limitation of ASM will cause a dim effect in the image after dehazing. By adding a new parameter, an enhanced ASM (EASM) (Ju et al., 2021) is proposed. Improvements to ASM will have an important impact on the dehazing performance of existing methods that rely on ASM. Therefore, it is worth exploring a more accurate model of the haze formation process.
7.2. Shift between the Real Domain and Synthetic Domain
The current training process of dehazing models generally requires sufficient data. Since it is difficult to collect pairs of hazy and haze-free images in the real world, the synthesized data is needed by dehazing task. However, there are inherent differences between the synthesized hazy image and the real world hazy image. In order to solve the domain shift problem, the following three directions are worth exploring.
-
•
The haze synthesized based on ASM cannot completely simulate the formation of haze in the real world, so we can attempt to design a more realistic hazy image synthesis algorithm to compensate for the difference between domains.
-
•
By introducing domain adaptation, semi-supervised and unsupervised methods into network design, experiments show that these algorithms can perform well in real world dehazing task.
-
•
Recent work (MRFID/BeDDE) collected some real world paired data, but they did not contain as many examples as RESIDE. It is challenging to build a large-scale real world dataset that can be used for a large-capacity CNN-based dehazing model.
7.3. Computational Efficiency and New Metrics
The dehazing models are often used as a preprocessing module for high-level computer vision tasks. For example, the lightweight AOD-Net is applied to object detection task. There are three issues that should be considered in the application of the dehazing model.
-
•
In order to help follow-up tasks, the dehazing model should ensure that the dehazed image is of high quality.
-
•
The inference speed of the model must be fast enough to meet the real-time requirement.
-
•
Several end devices with small storage are sensitive to the number of parameters of the dehazing model.
Therefore, we need to balance quantitative performance, inference time and the number of parameters. High-quality dehazed image with high PSNR and SSIM are the main goals of the current research. FAMED-Net (Zhang and Tao, 2020) discusses the computational efficiency of 14 models, which shows that several algorithms with excellent performance may be very time and memory consuming. Dehazing algorithms based on deep learning usually require the use of graphical computing units for model training and deployment. In real world applications, the forward inference speed of an algorithm is an important evaluation metric. 4kDehazing (Zheng et al., 2021) explores fast dehazing of high-resolution input, which takes only ms ( fps) to process a 4K () image on a single Titan RTX GPU. Future research can try to design a new evaluation metric that can comprehensively consider the dehazing quality, running speed and model size.
7.4. Perceptual Loss
The pre-trained model trained on a large-scale dataset can be used to calculate the perceptual loss. As shown in Table 3, many dehazing models use the perceptual loss obtained by VGG16 or VGG19 as a part of the overall loss to improve the quality of the final result. Thus, a natural question is, can the perceptual loss be the same as the L1/L2 loss as a general loss for image dehazing task? Alternatively, is there a more efficient and higher quality way to compute the perceptual loss? For example, is it a better solution to obtain perceptual loss by other pre-trained models? Currently, there is no comprehensive study on the relationship between perceptual loss and dehazing task.
7.5. How Dehazing Methods Affect High-level Computer Vision Tasks
Many dehazing algorithms have been validated on high-level computer vision tasks, such as image segmentation and object detection. Experiments show that these dehazing methods can promote the performance of high-level computer vision tasks under hazy conditions. However, the recent study (Pei et al., 2018) has shown that several dehazing algorithms may be ineffective for image classification, although their dehazing ability has been proven. The experimental results (Pei et al., 2018) on synthetic and real hazy data show that several well-designed dehazing models have little positive effect on the performance of the classification model, and sometimes may reduce the classification accuracy to some extent.
Besides, domain adaptation and generalization methods have been proposed to deal with high-level computer vision tasks such as object detection (Wang et al., 2022, 2021a) and semantic segmentation (Zhang et al., 2019b; Gao et al., 2021) in bad weather conditions including haze, which can be treated as mitigating the side effect of haze in the feature space by aligning hazy image features with those clean ones. It will be an interesting research topic to investigate and reduce the influence of haze on high-level computer vision tasks both at image-level (i.e., dehazing) and feature-level (i.e., domain adaptation).
7.6. Prior Knowledge and Learning Model
Before deep learning was widely used in image dehazing task, image-based prior statistical knowledge was an important part for guiding the dehazing process. Now, extensive work has shown that deep learning techniques can effectively remove haze from images independently of physical model. At the same time, several recent studies have found that prior statistical knowledge can be used for semi-supervised (Li et al., 2020a) and unsupervised (Golts et al., 2020) network training. Effective prior knowledge can reduce the model’s dependence on data to a certain extent and improve the generalization ability of the model. However, there is currently no evidence which statistical priors are always valid. Therefore, the general prior knowledge that can be used for the CNN-based dehazing algorithm is worth verifying.
8. Conclusion
This paper provides a comprehensive survey of deep learning-based dehazing research. First, the commonly used physical model, high-quality datasets, general loss functions, effective network modules and evaluation metrics are summarized. Then, supervised, semi-supervised and unsupervised dehazing studies are classified and analyzed from different technical perspectives. Moreover, quantitative and qualitative dehazing performance of various baselines are discussed. Finally, we discuss several valuable research directions and open issues.
Acknowledgements.
This work was supported in part by the grant of the National Science Foundation of China under Grant 62172090, 62172089; Alibaba Group through Alibaba Innovative Research Program; CAAI-Huawei MindSpore Open Fund. All correspondence should be directed to Xiaofeng Cong and Yuan Cao. Dr Jing Zhang is supported by ARC research project FL-170100117.Appendix A What is not discussed in this survey
We noticed that several papers’ formulation description and open source code may not be consistent. In particular, loss functions not provided in several papers are used in the training code. In this case, we use the loss functions provided in the paper as a guide, regardless of the code implementation. Further, several public papers that have not yet been published formally are not covered in this survey, such as those on arxiv, since their content may be changed in the future.
References
- (1)
- An et al. (2022) Shunmin An, Xixia Huang, Le Wang, Linling Wang, and Zhangjing Zheng. 2022. Semi-Supervised image dehazing network. The Visual Computer 38, 6 (2022), 2041–2055.
- Ancuti et al. (2016) Cosmin Ancuti, Codruta O Ancuti, and Christophe De Vleeschouwer. 2016. D-hazy: A dataset to evaluate quantitatively dehazing algorithms. In International Conference on Image Processing. 2226–2230.
- Ancuti et al. (2018a) Cosmin Ancuti, Codruta O Ancuti, and Radu Timofte. 2018a. Ntire 2018 challenge on image dehazing: Methods and results. In Conference on Computer Vision and Pattern Recognition Workshops. 891–901.
- Ancuti et al. (2018b) Cosmin Ancuti, Codruta O Ancuti, Radu Timofte, and Christophe De Vleeschouwer. 2018b. I-HAZE: a dehazing benchmark with real hazy and haze-free indoor images. In International Conference on Advanced Concepts for Intelligent Vision Systems. 620–631.
- Ancuti et al. (2019a) Codruta O Ancuti, Cosmin Ancuti, Mateu Sbert, and Radu Timofte. 2019a. Dense-Haze: A Benchmark for Image Dehazing with Dense-Haze and Haze-Free Images. In International Conference on Image Processing. 1014–1018.
- Ancuti et al. (2020a) Codruta O. Ancuti, Cosmin Ancuti, and Radu Timofte. 2020a. NH-HAZE: An Image Dehazing Benchmark with Non-Homogeneous Hazy and Haze-Free Images. In Conference on Computer Vision and Pattern Recognition Workshops. 1798–1805.
- Ancuti et al. (2018c) Codruta O Ancuti, Cosmin Ancuti, Radu Timofte, and Christophe De Vleeschouwer. 2018c. O-HAZE: a dehazing benchmark with real hazy and haze-free outdoor images. In Conference on Computer Vision and Pattern Recognition Workshops. 754–762.
- Ancuti et al. (2019b) Codruta O Ancuti, Cosmin Ancuti, Radu Timofte, Luc Van Gool, Lei Zhang, and Ming-Hsuan Yang. 2019b. NTIRE 2019 Image Dehazing Challenge Report. In Conference on Computer Vision and Pattern Recognition Workshops. 2241–2253.
- Ancuti et al. (2020b) Codruta O Ancuti, Cosmin Ancuti, Florin-Alexandru Vasluianu, and Radu Timofte. 2020b. NTIRE 2020 Challenge on NonHomogeneous Dehazing. In Conference on Computer Vision and Pattern Recognition Workshops. 2029–2044.
- Banerjee and Chaudhuri (2021) Sriparna Banerjee and Sheli Sinha Chaudhuri. 2021. Nighttime Image-Dehazing: A Review and Quantitative Benchmarking. Archives of Computational Methods in Engineering 28 (2021), 2943–2975.
- Bianco et al. (2019) Simone Bianco, Luigi Celona, Flavio Piccoli, and Raimondo Schettini. 2019. High-resolution single image dehazing using encoder-decoder architecture. In Conference on Computer Vision and Pattern Recognition Workshops. 1927–1935.
- Cai et al. (2016) Bolun Cai, Xiangmin Xu, Kui Jia, Chunmei Qing, and Dacheng Tao. 2016. Dehazenet: An end-to-end system for single image haze removal. IEEE Transactions on Image Processing 25, 11 (2016), 5187–5198.
- Chen et al. (2019c) Dongdong Chen, Mingming He, Qingnan Fan, Jing Liao, Liheng Zhang, Dongdong Hou, Lu Yuan, and Gang Hua. 2019c. Gated Context Aggregation Network for Image Dehazing and Deraining. In Winter Conference on Applications of Computer Vision. 1375–1383.
- Chen and Lai (2019) Rongsen Chen and Edmund M-K Lai. 2019. Convolutional Autoencoder For Single Image Dehazing.. In International Conference on Image Processing. 4464–4468.
- Chen et al. (2019a) Shuxin Chen, Yizi Chen, Yanyun Qu, Jingying Huang, and Ming Hong. 2019a. Multi-scale adaptive dehazing network. In Conference on Computer Vision and Pattern Recognition Workshops. 2051–2059.
- Chen et al. (2021a) Tianyi Chen, Jiahui Fu, Wentao Jiang, Chen Gao, and Si Liu. 2021a. SRKTDN: Applying Super Resolution Method to Dehazing Task. In Conference on Computer Vision and Pattern Recognition. 487–496.
- Chen et al. (2019b) Wei-Ting Chen, Jian-Jiun Ding, and Sy-Yen Kuo. 2019b. PMS-Net: Robust Haze Removal Based on Patch Map for Single Images. In Conference on Computer Vision and Pattern Recognition. 11673–11681.
- Chen et al. (2020) Wei-Ting Chen, Hao-Yu Fang, Jian-Jiun Ding, and Sy-Yen Kuo. 2020. PMHLD: patch map-based hybrid learning DehazeNet for single image haze removal. IEEE Transactions on Image Processing 29 (2020), 6773–6788.
- Chen et al. (2019d) Xuesong Chen, Haihua Lu, Kaili Cheng, Yanbo Ma, Qiuhao Zhou, and Yong Zhao. 2019d. Sequentially refined spatial and channel-wise feature aggregation in encoder-decoder network for single image dehazing. In International Conference on Image Processing. 2776–2780.
- Chen et al. (2021b) Zeyuan Chen, Yangchao Wang, Yang Yang, and Dong Liu. 2021b. PSD: Principled Synthetic-to-Real Dehazing Guided by Physical Priors. In Conference on Computer Vision and Pattern Recognition. 7180–7189.
- Chen et al. (2021c) Zhihua Chen, Yu Zhou, Ping Li, Xiaoyu Chi, Lei Ma, and Bin Sheng. 2021c. DCNet: Dual-Task Cycle Network for End-to-End Image Dehazing. In International Conference on Multimedia and Expo. 1–6.
- Cheng and Zhao (2021) Lu Cheng and Li Zhao. 2021. Two-Stage Image Dehazing with Depth Information and Cross-Scale Non-Local Attention. In International Conference on Big Data. 3155–3162.
- Cong et al. (2020) Xiaofeng Cong, Jie Gui, Kai-Chao Miao, Jun Zhang, Bing Wang, and Peng Chen. 2020. Discrete Haze Level Dehazing Network. In ACM International Conference on Multimedia. 1828–1836.
- Das and Dutta (2020) Sourya Dipta Das and Saikat Dutta. 2020. Fast deep multi-patch hierarchical network for nonhomogeneous image dehazing. In Conference on Computer Vision and Pattern Recognition Workshops. 482–483.
- Deng et al. (2020) Qili Deng, Ziling Huang, Chung-Chi Tsai, and Chia-Wen Lin. 2020. Hardgan: A haze-aware representation distillation gan for single image dehazing. In European Conference on Computer Vision. 722–738.
- Deng et al. (2019) Zijun Deng, Lei Zhu, Xiaowei Hu, Chi-Wing Fu, Xuemiao Xu, Qing Zhang, Jing Qin, and Pheng-Ann Heng. 2019. Deep multi-model fusion for single-image dehazing. In International Conference on Computer Vision. 2453–2462.
- Dharejo et al. (2021) Fayaz Ali Dharejo, Yuanchun Zhou, Farah Deeba, Munsif Ali Jatoi, Muhammad Ashfaq Khan, Ghulam Ali Mallah, Abdul Ghaffar, Muhammad Chhattal, Yi Du, and Xuezhi Wang. 2021. A deep hybrid neural network for single image dehazing via wavelet transform. Optik 231 (2021), 166462.
- Dong et al. (2020b) Hang Dong, Jinshan Pan, Lei Xiang, Zhe Hu, Xinyi Zhang, Fei Wang, and Ming-Hsuan Yang. 2020b. Multi-scale boosted dehazing network with dense feature fusion. In Conference on Computer Vision and Pattern Recognition. 2157–2167.
- Dong et al. (2020c) Hang Dong, Xinyi Zhang, Yu Guo, and Fei Wang. 2020c. Deep multi-scale gabor wavelet network for image restoration. In International Conference on Acoustics, Speech and Signal Processing. 2028–2032.
- Dong and Pan (2020) Jiangxin Dong and Jinshan Pan. 2020. Physics-based feature dehazing networks. In European Conference on Computer Vision. 188–204.
- Dong et al. (2020a) Yu Dong, Yihao Liu, He Zhang, Shifeng Chen, and Yu Qiao. 2020a. FD-GAN: Generative Adversarial Networks with Fusion-Discriminator for Single Image Dehazing. In AAAI Conference on Artificial Intelligence. 10729–10736.
- Du and Li (2018) Yixin Du and Xin Li. 2018. Recursive deep residual learning for single image dehazing. In Conference on Computer Vision and Pattern Recognition Workshops. 730–737.
- Du and Li (2019) Yixin Du and Xin Li. 2019. Recursive image dehazing via perceptually optimized generative adversarial network (POGAN). In Conference on Computer Vision and Pattern Recognition Workshops. 1824–1832.
- Dudhane and Murala (2019a) Akshay Dudhane and Subrahmanyam Murala. 2019a. Cdnet: Single image de-hazing using unpaired adversarial training. In Winter Conference on Applications of Computer Vision. 1147–1155.
- Dudhane and Murala (2019b) Akshay Dudhane and Subrahmanyam Murala. 2019b. RYF-Net: Deep fusion network for single image haze removal. IEEE Transactions on Image Processing 29 (2019), 628–640.
- Dudhane et al. (2019) Akshay Dudhane, Harshjeet Singh Aulakh, and Subrahmanyam Murala. 2019. Ri-gan: An end-to-end network for single image haze removal. In Conference on Computer Vision and Pattern Recognition Workshops. 2014–2023.
- Engin et al. (2018) Deniz Engin, Anil Genç, and Hazim Kemal Ekenel. 2018. Cycle-dehaze: Enhanced cyclegan for single image dehazing. In Conference on Computer Vision and Pattern Recognition Workshops. 825–833.
- Fang et al. (2021) Zhengyun Fang, Ming Zhao, Zhengtao Yu, Meiyu Li, and Yong Yang. 2021. A guiding teaching and dual adversarial learning framework for a single image dehazing. The Visual Computer (2021), 1–13.
- Fu et al. (2021) Minghan Fu, Huan Liu, Yankun Yu, Jun Chen, and Keyan Wang. 2021. DW-GAN: A Discrete Wavelet Transform GAN for NonHomogeneous Dehazing. In Conference on Computer Vision and Pattern Recognition Workshops. 203–212.
- Galdran et al. (2018) Adrian Galdran, Aitor Alvarez-Gila, Alessandro Bria, Javier Vazquez-Corral, and Marcelo Bertalmío. 2018. On the duality between retinex and image dehazing. In Conference on Computer Vision and Pattern Recognition. 8212–8221.
- Gandelsman et al. (2019) Yosef Gandelsman, Assaf Shocher, and Michal Irani. 2019. “Double-DIP”: Unsupervised Image Decomposition via Coupled Deep-Image-Priors. In Conference on Computer Vision and Pattern Recognition. 11026–11035.
- Gao et al. (2021) Li Gao, Jing Zhang, Lefei Zhang, and Dacheng Tao. 2021. Dsp: Dual soft-paste for unsupervised domain adaptive semantic segmentation. In ACM International Conference on Multimedia. 2825–2833.
- Golts et al. (2020) Alona Golts, Daniel Freedman, and Michael Elad. 2020. Unsupervised Single Image Dehazing Using Dark Channel Prior Loss. IEEE Transactions on Image Processing 29 (2020), 2692–2701.
- Gou et al. (2021) Jianping Gou, Baosheng Yu, Stephen J Maybank, and Dacheng Tao. 2021. Knowledge distillation: A survey. International Journal of Computer Vision 129, 6 (2021), 1789–1819.
- Gui et al. (2021) Jie Gui, Xiaofeng Cong, Yuan Cao, Wenqi Ren, Jun Zhang, Jing Zhang, and Dacheng Tao. 2021. A Comprehensive Survey on Image Dehazing Based on Deep Learning. In International Joint Conference on Artificial Intelligence. 4426–4433.
- Gui et al. (2022) Jie Gui, Zhenan Sun, Yonggang Wen, Dacheng Tao, and Jieping Ye. 2022. A review on generative adversarial networks: Algorithms, theory, and applications. IEEE Transactions on Knowledge and Data Engineering (2022).
- Guo et al. (2019a) Tiantong Guo, Venkateswararao Cherukuri, and Vishal Monga. 2019a. Dense ‘123’ color enhancement dehazing network. In Conference on Computer Vision and Pattern Recognition Workshops. 2131–2139.
- Guo et al. (2019b) Tiantong Guo, Xuelu Li, Venkateswararao Cherukuri, and Vishal Monga. 2019b. Dense scene information estimation network for dehazing. In Conference on Computer Vision and Pattern Recognition Workshops. 2122–2130.
- Guo and Monga (2020) Tiantong Guo and Vishal Monga. 2020. Reinforced depth-aware deep learning for single image dehazing. In International Conference on Acoustics, Speech and Signal Processing. 8891–8895.
- Hambarde and Murala (2020) Praful Hambarde and Subrahmanyam Murala. 2020. S2dnet: Depth estimation from single image and sparse samples. IEEE Transactions on Computational Imaging 6 (2020), 806–817.
- He et al. (2010) Kaiming He, Jian Sun, and Xiaoou Tang. 2010. Single image haze removal using dark channel prior. IEEE Transactions on Pattern Analysis and Machine Intelligence 33, 12 (2010), 2341–2353.
- He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep residual learning for image recognition. In Conference on Computer Vision and Pattern Recognition. 770–778.
- He et al. (2019) Linyuan He, Junqiang Bai, and Meng Yang. 2019. Feature aggregation convolution network for haze removal. In International Conference on Image Processing. 2806–2810.
- Hong et al. (2020) Ming Hong, Yuan Xie, Cuihua Li, and Yanyun Qu. 2020. Distilling Image Dehazing With Heterogeneous Task Imitation. In Conference on Computer Vision and Pattern Recognition. 3462–3471.
- Huang et al. (2017) Gao Huang, Zhuang Liu, Laurens Van Der Maaten, and Kilian Q Weinberger. 2017. Densely connected convolutional networks. In Conference on Computer Vision and Pattern Recognition. 4700–4708.
- Huang et al. (2019) Lu-Yao Huang, Jia-Li Yin, Bo-Hao Chen, and Shao-Zhen Ye. 2019. Towards unsupervised single image dehazing with deep learning. In International Conference on Image Processing. 2741–2745.
- Huang et al. (2021) Pengcheng Huang, Li Zhao, Runhua Jiang, Tao Wang, and Xiaoqin Zhang. 2021. Self-filtering image dehazing with self-supporting module. Neurocomputing 432 (2021), 57–69.
- Huang et al. (2018) Yimin Huang, Yiyang Wang, and Zhixun Su. 2018. Single image dehazing via a joint deep modeling. In International Conference on Image Processing. 2840–2844.
- Huynh-Thu and Ghanbari (2008) Quan Huynh-Thu and Mohammed Ghanbari. 2008. Scope of validity of PSNR in image/video quality assessment. Electronics letters 44, 13 (2008), 800–801.
- Isola et al. (2017) Phillip Isola, Jun-Yan Zhu, Tinghui Zhou, and Alexei A Efros. 2017. Image-to-image translation with conditional adversarial networks. In Conference on Computer Vision and Pattern Recognition. 1125–1134.
- Jin et al. (2020) Yizhou Jin, Guangshuai Gao, Qingjie Liu, and Yunhong Wang. 2020. Unsupervised conditional disentangle network for image dehazing. In International Conference on Image Processing. 963–967.
- Jo and Sim (2021) Eunsung Jo and Jae-Young Sim. 2021. Multi-Scale Selective Residual Learning for Non-Homogeneous Dehazing. In Conference on Computer Vision and Pattern Recognition Workshop. 507–515.
- Johnson et al. (2016) Justin Johnson, Alexandre Alahi, and Li Fei-Fei. 2016. Perceptual losses for real-time style transfer and super-resolution. In European Conference on Computer Vision. 694–711.
- Ju et al. (2021) Mingye Ju, Can Ding, Wenqi Ren, Yi Yang, Dengyin Zhang, and Y Jay Guo. 2021. Ide: Image dehazing and exposure using an enhanced atmospheric scattering model. IEEE Transactions on Image Processing 30 (2021), 2180–2192.
- Khosla et al. (2020) Prannay Khosla, Piotr Teterwak, Chen Wang, Aaron Sarna, Yonglong Tian, Phillip Isola, Aaron Maschinot, Ce Liu, and Dilip Krishnan. 2020. Supervised contrastive learning. In Neural Information Processing Systems. 18661–18673.
- Kim et al. (2021) Guisik Kim, Sung Woo Park, and Junseok Kwon. 2021. Pixel-wise Wasserstein Autoencoder for Highly Generative Dehazing. IEEE Transactions on Image Processing 30 (2021), 5452–5462.
- Ledig et al. (2017) Christian Ledig, Lucas Theis, Ferenc Huszár, Jose Caballero, Andrew Cunningham, Alejandro Acosta, Andrew Aitken, Alykhan Tejani, Johannes Totz, Zehan Wang, et al. 2017. Photo-realistic single image super-resolution using a generative adversarial network. In Conference on Computer Vision and Pattern Recognition. 4681–4690.
- Lee et al. (2020a) Byeong-Uk Lee, Kyunghyun Lee, Jean Oh, and In So Kweon. 2020a. CNN-Based Simultaneous Dehazing and Depth Estimation. In International Conference on Robotics and Automation. 9722–9728.
- Lee et al. (2020b) Yean-Wei Lee, Lai-Kuan Wong, and John See. 2020b. Image Dehazing With Contextualized Attentive U-NET. In International Conference on Image Processing. 1068–1072.
- Li et al. (2021a) Boyun Li, Yuanbiao Gou, Shuhang Gu, Jerry Zitao Liu, Joey Tianyi Zhou, and Xi Peng. 2021a. You only look yourself: Unsupervised and untrained single image dehazing neural network. International Journal of Computer Vision 129, 5 (2021), 1754–1767.
- Li et al. (2020b) Boyun Li, Yuanbiao Gou, Jerry Zitao Liu, Hongyuan Zhu, Joey Tianyi Zhou, and Xi Peng. 2020b. Zero-Shot Image Dehazing. IEEE Transactions on Image Processing 29 (2020), 8457–8466.
- Li et al. (2017a) Boyi Li, Xiulian Peng, Zhangyang Wang, Jizheng Xu, and Dan Feng. 2017a. AOD-Net: All-in-One Dehazing Network. In International Conference on Computer Vision. 4780–4788.
- Li et al. (2019c) Boyi Li, Wenqi Ren, Dengpan Fu, Dacheng Tao, Dan Feng, Wenjun Zeng, and Zhangyang Wang. 2019c. Benchmarking Single-Image Dehazing and Beyond. IEEE Transactions on Image Processing 28, 1 (2019), 492–505.
- Li et al. (2019a) Chongyi Li, Chunle Guo, Jichang Guo, Ping Han, Huazhu Fu, and Runmin Cong. 2019a. PDR-Net: Perception-inspired single image dehazing network with refinement. IEEE Transactions on Multimedia 22, 3 (2019), 704–716.
- Li et al. (2016) Chongyi Li, Jichang Guo, Runmin Cong, Yanwei Pang, and Bo Wang. 2016. Underwater image enhancement by dehazing with minimum information loss and histogram distribution prior. IEEE Transactions on Image Processing 25, 12 (2016), 5664–5677.
- Li et al. (2021b) Hongyu Li, Jia Li, Dong Zhao, and Long Xu. 2021b. DehazeFlow: Multi-scale Conditional Flow Network for Single Image Dehazing. In ACM International Conference on Multimedia. 2577–2585.
- Li et al. (2020e) Hui Li, Qingbo Wu, King Ngi Ngan, Hongliang Li, and Fanman Meng. 2020e. Region adaptive two-shot network for single image dehazing. In International Conference on Multimedia and Expo. 1–6.
- Li et al. (2020a) Lerenhan Li, Yunlong Dong, Wenqi Ren, Jinshan Pan, Changxin Gao, Nong Sang, and Ming-Hsuan Yang. 2020a. Semi-Supervised Image Dehazing. IEEE Transactions on Image Processing 29 (2020), 2766–2779.
- Li et al. (2021c) Pengyue Li, Jiandong Tian, Yandong Tang, Guolin Wang, and Chengdong Wu. 2021c. Deep Retinex Network for Single Image Dehazing. IEEE Transactions on Image Processing 30 (2021), 1100–1115.
- Li et al. (2020d) Runde Li, Jinshan Pan, Min He, Zechao Li, and Jinhui Tang. 2020d. Task-oriented network for image dehazing. IEEE Transactions on Image Processing 29 (2020), 6523–6534.
- Li et al. (2020c) Yuenan Li, Yuhang Liu, Qixin Yan, and Kuangshi Zhang. 2020c. Deep Dehazing Network With Latent Ensembling Architecture and Adversarial Learning. IEEE Transactions on Image Processing 30 (2020), 1354–1368.
- Li et al. (2019b) Yunan Li, Qiguang Miao, Wanli Ouyang, Zhenxin Ma, Huijuan Fang, Chao Dong, and Yining Quan. 2019b. LAP-Net: Level-aware progressive network for image dehazing. In International Conference on Computer Vision. 3276–3285.
- Li et al. (2017b) Yu Li, Shaodi You, Michael S Brown, and Robby T Tan. 2017b. Haze visibility enhancement: A survey and quantitative benchmarking. Computer Vision and Image Understanding 165 (2017), 1–16.
- Liang et al. (2019) Xiao Liang, Runde Li, and Jinhui Tang. 2019. Selective Attention network for Image Dehazing and Deraining. In ACM Multimedia Asia. 1–6.
- Liu et al. (2020b) Jing Liu, Haiyan Wu, Yuan Xie, Yanyun Qu, and Lizhuang Ma. 2020b. Trident dehazing network. In Conference on Computer Vision and Pattern Recognition Workshops. 430–431.
- Liu et al. (2014) Lixiong Liu, Bao Liu, Hua Huang, and Alan Conrad Bovik. 2014. No-reference image quality assessment based on spatial and spectral entropies. Signal processing: Image communication 29, 8 (2014), 856–863.
- Liu (2019) Qian Liu. 2019. Unsupervised Single Image Dehazing Via Disentangled Representation. In International Conference on Video and Image Processing. 106–111.
- Liu et al. (2018) Risheng Liu, Xin Fan, Minjun Hou, Zhiying Jiang, Zhongxuan Luo, and Lei Zhang. 2018. Learning aggregated transmission propagation networks for haze removal and beyond. IEEE Transactions on Neural Networks and Learning Systems 30, 10 (2018), 2973–2986.
- Liu et al. (2020a) Wei Liu, Xianxu Hou, Jiang Duan, and Guoping Qiu. 2020a. End-to-End Single Image Fog Removal Using Enhanced Cycle Consistent Adversarial Networks. IEEE Transactions on Image Processing 29 (2020), 7819–7833.
- Liu et al. (2019a) Xiaohong Liu, Yongrui Ma, Zhihao Shi, and Jun Chen. 2019a. GridDehazeNet: Attention-Based Multi-Scale Network for Image Dehazing. In International Conference on Computer Vision. 7313–7322.
- Liu et al. (2019b) Yang Liu, Jinshan Pan, Jimmy Ren, and Zhixun Su. 2019b. Learning deep priors for image dehazing. In International Conference on Computer Vision. 2492–2500.
- Liu et al. (2021) Ye Liu, Lei Zhu, Shunda Pei, Huazhu Fu, Jing Qin, Qing Zhang, Liang Wan, and Wei Feng. 2021. From Synthetic to Real: Image Dehazing Collaborating with Unlabeled Real Data. In ACM International Conference on Multimedia. 50–58.
- McCartney (1976) Earl J McCartney. 1976. Optics of the atmosphere: scattering by molecules and particles. Physics Bulletin (1976), 1–421.
- Mehra et al. (2021) Aryan Mehra, Pratik Narang, and Murari Mandal. 2021. TheiaNet: Towards fast and inexpensive CNN design choices for image dehazing. Journal of Visual Communication and Image Representation 77 (2021), 103137.
- Mehta et al. (2020) Aditya Mehta, Harsh Sinha, Pratik Narang, and Murari Mandal. 2020. Hidegan: A hyperspectral-guided image dehazing gan. In Conference on Computer Vision and Pattern Recognition Workshops. 212–213.
- Metwaly et al. (2020) Kareem Metwaly, Xuelu Li, Tiantong Guo, and Vishal Monga. 2020. Nonlocal channel attention for nonhomogeneous image dehazing. In Conference on Computer Vision and Pattern Recognition Workshops. 452–453.
- Min et al. (2019) Xiongkuo Min, Guangtao Zhai, Ke Gu, Yucheng Zhu, Jiantao Zhou, Guodong Guo, Xiaokang Yang, Xinping Guan, and Wenjun Zhang. 2019. Quality evaluation of image dehazing methods using synthetic hazy images. IEEE Transactions on Multimedia 21, 9 (2019), 2319–2333.
- Mo et al. (2022) Yaozong Mo, Chaofeng Li, Yuhui Zheng, and Xiaojun Wu. 2022. DCA-CycleGAN: Unsupervised Single Image Dehazing Using Dark Channel Attention Optimized CycleGAN. Journal of Visual Communication and Image Representation 82 (2022), 103431.
- Mondal et al. (2018) Ranjan Mondal, Sanchayan Santra, and Bhabatosh Chanda. 2018. Image dehazing by joint estimation of transmittance and airlight using bi-directional consistency loss minimized FCN. In Conference on Computer Vision and Pattern Recognition Workshops. 920–928.
- Morales et al. (2019) Peter Morales, Tzofi Klinghoffer, and Seung Jae Lee. 2019. Feature forwarding for efficient single image dehazing. In Conference on Computer Vision and Pattern Recognition Workshops. 2078–2085.
- Narasimhan and Nayar (2003) Srinivasa G Narasimhan and Shree K Nayar. 2003. Contrast restoration of weather degraded images. IEEE Transactions on Pattern Analysis and Machine Intelligence 25, 6 (2003), 713–724.
- Nayar and Narasimhan (1999) Shree K Nayar and Srinivasa G Narasimhan. 1999. Vision in bad weather. In International Conference on Computer Vision. 820–827.
- Pang et al. (2020) Yanwei Pang, Jing Nie, Jin Xie, Jungong Han, and Xuelong Li. 2020. BidNet: Binocular Image Dehazing Without Explicit Disparity Estimation. In Conference on Computer Vision and Pattern Recognition. 5930–5939.
- Pang et al. (2018) Yanwei Pang, Jin Xie, and Xuelong Li. 2018. Visual haze removal by a unified generative adversarial network. IEEE Transactions on Circuits and Systems for Video Technology 29, 11 (2018), 3211–3221.
- Parihar et al. (2020) Anil Singh Parihar, Yash Kumar Gupta, Yash Singodia, Vibhu Singh, and Kavinder Singh. 2020. A comparative study of image dehazing algorithms. In International Conference on Communication and Electronics Systems. 766–771.
- Park et al. (2020) Jaihyun Park, David K Han, and Hanseok Ko. 2020. Fusion of heterogeneous adversarial networks for single image dehazing. IEEE Transactions on Image Processing 29 (2020), 4721–4732.
- Pei et al. (2018) Yanting Pei, Yaping Huang, Qi Zou, Yuhang Lu, and Song Wang. 2018. Does Haze Removal Help CNN-based Image Classification?. In European Conference on Computer Vision. 697–712.
- Qin et al. (2020) Xu Qin, Zhilin Wang, Yuanchao Bai, Xiaodong Xie, and Huizhu Jia. 2020. FFA-Net: Feature Fusion Attention Network for Single Image Dehazing. In AAAI Conference on Artificial Intelligence. 11908–11915.
- Qu et al. (2019) Yanyun Qu, Yizi Chen, Jingying Huang, and Yuan Xie. 2019. Enhanced Pix2pix Dehazing Network. In Conference on Computer Vision and Pattern Recognition. 8152–8160.
- Ren et al. (2016) Wenqi Ren, Si Liu, Hua Zhang, Jinshan Pan, Xiaochun Cao, and Ming-Hsuan Yang. 2016. Single image dehazing via multi-scale convolutional neural networks. In European Conference on Computer Vision. 154–169.
- Ren et al. (2018a) Wenqi Ren, Lin Ma, Jiawei Zhang, Jinshan Pan, Xiaochun Cao, Wei Liu, and Ming-Hsuan Yang. 2018a. Gated Fusion Network for Single Image Dehazing. In Conference on Computer Vision and Pattern Recognition. 3253–3261.
- Ren et al. (2020) Wenqi Ren, Jinshan Pan, Hua Zhang, Xiaochun Cao, and Ming-Hsuan Yang. 2020. Single image dehazing via multi-scale convolutional neural networks with holistic edges. International Journal of Computer Vision 128, 1 (2020), 240–259.
- Ren et al. (2018b) Wenqi Ren, Jingang Zhang, Xiangyu Xu, Lin Ma, Xiaochun Cao, Gaofeng Meng, and Wei Liu. 2018b. Deep video dehazing with semantic segmentation. IEEE Transactions on Image Processing 28, 4 (2018), 1895–1908.
- Ronneberger et al. (2015) Olaf Ronneberger, Philipp Fischer, and Thomas Brox. 2015. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-assisted Intervention. 234–241.
- Rudin et al. (1992) Leonid I Rudin, Stanley Osher, and Emad Fatemi. 1992. Nonlinear total variation based noise removal algorithms. Physica D: nonlinear phenomena 60, 1-4 (1992), 259–268.
- Saad et al. (2012) Michele A Saad, Alan C Bovik, and Christophe Charrier. 2012. Blind image quality assessment: A natural scene statistics approach in the DCT domain. IEEE transactions on Image Processing 21, 8 (2012), 3339–3352.
- Sakaridis et al. (2018) Christos Sakaridis, Dengxin Dai, Simon Hecker, and Luc Van Gool. 2018. Model adaptation with synthetic and real data for semantic dense foggy scene understanding. In European Conference on Computer Vision. 687–704.
- Shao et al. (2020) Yuanjie Shao, Lerenhan Li, Wenqi Ren, Changxin Gao, and Nong Sang. 2020. Domain Adaptation for Image Dehazing. In Conference on Computer Vision and Pattern Recognition. 2805–2814.
- Sharma et al. (2005) Gaurav Sharma, Wencheng Wu, and Edul N Dalal. 2005. The CIEDE2000 color-difference formula: Implementation notes, supplementary test data, and mathematical observations. Color Research & Application: Endorsed by Inter-Society Color Council, etc 30, 1 (2005), 21–30.
- Sharma et al. (2020) Prasen Sharma, Priyankar Jain, and Arijit Sur. 2020. Scale-aware conditional generative adversarial network for image dehazing. In Winter Conference on Applications of Computer Vision. 2355–2365.
- Sheng et al. (2022) Jiechao Sheng, Guoqiang Lv, Gang Du, Zi Wang, and Qibin Feng. 2022. Multi-scale residual attention network for single image dehazing. Digital Signal Processing 121 (2022), 103327.
- Shin et al. (2022) Joongchol Shin, Hasil Park, and Joonki Paik. 2022. Region-Based Dehazing via Dual-Supervised Triple-Convolutional Network. IEEE Transactions on Multimedia 24 (2022), 245–260.
- Shyam et al. (2021) Pranjay Shyam, Kuk-Jin Yoon, and Kyung-Soo Kim. 2021. Towards Domain Invariant Single Image Dehazing. In AAAI Conference on Artificial Intelligence. 9657–9665.
- Silberman et al. (2012) Nathan Silberman, Derek Hoiem, Pushmeet Kohli, and Rob Fergus. 2012. Indoor segmentation and support inference from rgbd images. In European Conference on Computer Vision. 746–760.
- Sim et al. (2018) Hyeonjun Sim, Sehwan Ki, Jae-Seok Choi, Soomin Seo, Saehun Kim, and Munchurl Kim. 2018. High-resolution image dehazing with respect to training losses and receptive field sizes. In Conference on Computer Vision and Pattern Recognition Workshops. 912–919.
- Simonyan and Zisserman (2015) K. Simonyan and A. Zisserman. 2015. Very Deep Convolutional Networks for Large-Scale Image Recognition. In International Conference on Learning Representations. 1–14.
- Singh et al. (2020) Ayush Singh, Ajay Bhave, and Dilip K Prasad. 2020. Single image dehazing for a variety of haze scenarios using back projected pyramid network. In European Conference on Computer Vision. 166–181.
- Singh and Kumar (2019) Dilbag Singh and Vijay Kumar. 2019. A comprehensive review of computational dehazing techniques. Archives of Computational Methods in Engineering 26, 5 (2019), 1395–1413.
- Sun et al. (2021) Lexuan Sun, Xueliang Liu, Zhenzhen Hu, and Richang Hong. 2021. WFN-PSC: weighted-fusion network with poly-scale convolution for image dehazing. In ACM International Conference on Multimedia in Asia. 1–7.
- Szegedy et al. (2015) Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, and Andrew Rabinovich. 2015. Going deeper with convolutions. In Conference on Computer Vision and Pattern Recognition. 1–9.
- Tang et al. (2019) Guiying Tang, Li Zhao, Runhua Jiang, and Xiaoqin Zhang. 2019. Single Image Dehazing via Lightweight Multi-scale Networks. In International Conference on Big Data. 5062–5069.
- Wang et al. (2018a) Anna Wang, Wenhui Wang, Jinglu Liu, and Nanhui Gu. 2018a. AIPNet: Image-to-image single image dehazing with atmospheric illumination prior. IEEE Transactions on Image Processing 28, 1 (2018), 381–393.
- Wang et al. (2020) Cong Wang, Yuexian Zou, and Zehan Chen. 2020. ABC-NET: Avoiding Blocking Effect & Color Shift Network for Single Image Dehazing Via Restraining Transmission Bias. In International Conference on Image Processing. 1053–1057.
- Wang et al. (2021c) Juan Wang, Chang Ding, Minghu Wu, Yuanyuan Liu, and Guanhai Chen. 2021c. Lightweight multiple scale-patch dehazing network for real-world hazy image. KSII Transactions on Internet and Information Systems 15, 12 (2021), 4420–4438.
- Wang et al. (2021d) Jixiao Wang, Chaofeng Li, and Shoukun Xu. 2021d. An ensemble multi-scale residual attention network (EMRA-net) for image Dehazing. Multimedia Tools and Applications (2021), 29299–29319.
- Wang et al. (2019) Tao Wang, Li Yuan, Xiaopeng Zhang, and Jiashi Feng. 2019. Distilling Object Detectors With Fine-Grained Feature Imitation. In Conference on Computer Vision and Pattern Recognition. 4928–4937.
- Wang et al. (2021a) Wen Wang, Yang Cao, Jing Zhang, Fengxiang He, Zheng-Jun Zha, Yonggang Wen, and Dacheng Tao. 2021a. Exploring Sequence Feature Alignment for Domain Adaptive Detection Transformers. In ACM International Conference on Multimedia. 1730–1738.
- Wang et al. (2022) Wen Wang, Jing Zhang, Wei Zhai, Yang Cao, and Dacheng Tao. 2022. Robust Object Detection via Adversarial Novel Style Exploration. IEEE Transactions on Image Processing 31 (2022), 1949–1962.
- Wang et al. (2018b) Xintao Wang, Ke Yu, Shixiang Wu, Jinjin Gu, Yihao Liu, Chao Dong, Yu Qiao, and Chen Change Loy. 2018b. Esrgan: Enhanced super-resolution generative adversarial networks. In European Conference on Computer Vision. 63–79.
- Wang et al. (2021b) Yang Wang, Yang Cao, Jing Zhang, Feng Wu, and Zheng-Jun Zha. 2021b. Leveraging Deep Statistics for Underwater Image Enhancement. ACM Transactions on Multimedia Computing, Communications, and Applications 17, 3s (2021), 1–20.
- Wang et al. (2017) Yang Wang, Jing Zhang, Yang Cao, and Zengfu Wang. 2017. A deep CNN method for underwater image enhancement. In IEEE International Conference on Image Processing. 1382–1386.
- Wang et al. (2013) Yinting Wang, Shaojie Zhuo, Dapeng Tao, Jiajun Bu, and Na Li. 2013. Automatic local exposure correction using bright channel prior for under-exposed images. Signal processing 93, 11 (2013), 3227–3238.
- Wang et al. (2004) Zhou Wang, Alan C Bovik, Hamid R Sheikh, Eero P Simoncelli, et al. 2004. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing 13, 4 (2004), 600–612.
- Wang et al. (2003) Zhou Wang, Eero P Simoncelli, and Alan C Bovik. 2003. Multiscale structural similarity for image quality assessment. In Asilomar Conference on Signals, Systems & Computers. 1398–1402.
- Wei et al. (2020) Haoran Wei, Qingbo Wu, Hui Li, King Ngi Ngan, Hongliang Li, and Fanman Meng. 2020. Single Image Dehazing via Artificial Multiple Shots and Multidimensional Context. In International Conference on Image Processing. 1023–1027.
- Wei et al. (2021) Pan Wei, Xin Wang, Lei Wang, and Ji Xiang. 2021. SIDGAN: Single Image Dehazing without Paired Supervision. In International Conference on Pattern Recognition. 2958–2965.
- Wu et al. (2020) Haiyan Wu, Jing Liu, Yuan Xie, Yanyun Qu, and Lizhuang Ma. 2020. Knowledge transfer dehazing network for nonhomogeneous dehazing. In Conference on Computer Vision and Pattern Recognition Workshops. 478–479.
- Wu et al. (2021) Haiyan Wu, Yanyun Qu, Shaohui Lin, Jian Zhou, Ruizhi Qiao, Zhizhong Zhang, Yuan Xie, and Lizhuang Ma. 2021. Contrastive Learning for Compact Single Image Dehazing. In Conference on Computer Vision and Pattern Recognition. 10551–10560.
- Xiao et al. (2020) Jinsheng Xiao, Mengyao Shen, Junfeng Lei, Jinglong Zhou, Reinhard Klette, and HaiGang Sui. 2020. Single image dehazing based on learning of haze layers. Neurocomputing 389 (2020), 108–122.
- Xie et al. (2020) Liangru Xie, Hao Wang, Zhuowei Wang, and Lianglun Cheng. 2020. DHD-Net: A Novel Deep-Learning-based Dehazing Network. In International Joint Conference on Neural Networks. 1–7.
- Xu et al. (2015) Yong Xu, Jie Wen, Lunke Fei, and Zheng Zhang. 2015. Review of video and image defogging algorithms and related studies on image restoration and enhancement. IEEE Access 4 (2015), 165–188.
- Yan et al. (2020) Lan Yan, Wenbo Zheng, Chao Gou, and Fei-Yue Wang. 2020. Feature Aggregation Attention Network for Single Image Dehazing. In International Conference on Image Processing. 923–927.
- Yang et al. (2019) Aiping Yang, Haixin Wang, Zhong Ji, Yanwei Pang, and Ling Shao. 2019. Dual-Path in Dual-Path Network for Single Image Dehazing. In International Joint Conference on Artificial Intelligence. 4627–4634.
- Yang and Zhang (2022) Fei Yang and Qian Zhang. 2022. Depth aware image dehazing. The Visual Computer 38, 5 (2022), 1579–1587.
- Yang and Fu (2019) Hao-Hsiang Yang and Yanwei Fu. 2019. Wavelet u-net and the chromatic adaptation transform for single image dehazing. In International Conference on Image Processing. 2736–2740.
- Yang et al. (2020) Hao-Hsiang Yang, Chao-Han Huck Yang, and Yi-Chang James Tsai. 2020. Y-net: Multi-scale feature aggregation network with wavelet structure similarity loss function for single image dehazing. In International Conference on Acoustics, Speech and Signal Processing. 2628–2632.
- Yeh et al. (2019) Chia-Hung Yeh, Chih-Hsiang Huang, and Li-Wei Kang. 2019. Multi-scale deep residual learning-based single image haze removal via image decomposition. IEEE Transactions on Image Processing 29 (2019), 3153–3167.
- Yin et al. (2019) Jia-Li Yin, Yi-Chi Huang, Bo-Hao Chen, and Shao-Zhen Ye. 2019. Color transferred convolutional neural networks for image dehazing. IEEE Transactions on Circuits and Systems for Video Technology 30, 11 (2019), 3957–3967.
- Yin et al. (2020) Shibai Yin, Yibin Wang, and Yee-Hong Yang. 2020. A novel image-dehazing network with a parallel attention block. Pattern Recognition 102 (2020), 107255.
- Yin et al. (2021) Shibai Yin, Xiaolong Yang, Yibin Wang, and Yee-Hong Yang. 2021. Visual Attention Dehazing Network with Multi-level Features Refinement and Fusion. Pattern Recognition 118 (2021), 108021.
- Yu et al. (2020) Mingzhao Yu, Venkateswararao Cherukuri, Tiantong Guo, and Vishal Monga. 2020. Ensemble dehazing networks for non-homogeneous haze. In Conference on Computer Vision and Pattern Recognition Workshops. 450–451.
- Yu et al. (2021) Yankun Yu, Huan Liu, Minghan Fu, Jun Chen, Xiyao Wang, and Keyan Wang. 2021. A Two-branch Neural Network for Non-homogeneous Dehazing via Ensemble Learning. In Conference on Computer Vision and Pattern Recognition Workshops. 193–202.
- Zhang and Patel (2018) He Zhang and Vishal M Patel. 2018. Densely connected pyramid dehazing network. In Conference on Computer Vision and Pattern Recognition. 3194–3203.
- Zhang et al. (2018b) He Zhang, Vishwanath Sindagi, and Vishal M Patel. 2018b. Multi-scale single image dehazing using perceptual pyramid deep network. In Conference on Computer Vision and Pattern Recognition Workshops. 902–911.
- Zhang et al. (2019a) He Zhang, Vishwanath Sindagi, and Vishal M Patel. 2019a. Joint transmission map estimation and dehazing using deep networks. IEEE Transactions on Circuits and Systems for Video Technology 30, 7 (2019), 1975–1986.
- Zhang et al. (2017a) Jing Zhang, Yang Cao, Shuai Fang, Yu Kang, and Chang Wen Chen. 2017a. Fast haze removal for nighttime image using maximum reflectance prior. In Conference on Computer Vision and Pattern Recognition. 7418–7426.
- Zhang et al. (2014) Jing Zhang, Yang Cao, and Zengfu Wang. 2014. Nighttime haze removal based on a new imaging model. In International Conference on Image Processing. 4557–4561.
- Zhang et al. (2020a) Jing Zhang, Yang Cao, Zheng-Jun Zha, and Dacheng Tao. 2020a. Nighttime dehazing with a synthetic benchmark. In ACM International Conference on Multimedia. 2355–2363.
- Zhang et al. (2022b) Jingang Zhang, Wenqi Ren, Shengdong Zhang, He Zhang, Yunfeng Nie, Zhe Xue, and Xiaochun Cao. 2022b. Hierarchical Density-Aware Dehazing Network. IEEE Transactions on Cybernetics 52, 10 (2022), 11187–11199.
- Zhang and Tao (2020) Jing Zhang and Dacheng Tao. 2020. FAMED-Net: A Fast and Accurate Multi-Scale End-to-End Dehazing Network. IEEE Transactions on Image Processing 29 (2020), 72–84.
- Zhang and Li (2021) Kuangshi Zhang and Yuenan Li. 2021. Single image dehazing via semi-supervised domain translation and architecture search. IEEE Signal Processing Letters 28 (2021), 2127–2131.
- Zhang et al. (2019b) Qiming Zhang, Jing Zhang, Wei Liu, and Dacheng Tao. 2019b. Category anchor-guided unsupervised domain adaptation for semantic segmentation. In Neural Information Processing Systems. 433–443.
- Zhang and He (2020) Shengdong Zhang and Fazhi He. 2020. DRCDN: learning deep residual convolutional dehazing networks. The Visual Computer 36 (2020), 1797–1808.
- Zhang et al. (2020b) Shengdong Zhang, Fazhi He, and Wenqi Ren. 2020b. NLDN: Non-local dehazing network for dense haze removal. Neurocomputing 410 (2020), 363–373.
- Zhang et al. (2020c) Shengdong Zhang, Fazhi He, and Wenqi Ren. 2020c. Photo-realistic dehazing via contextual generative adversarial networks. Machine Vision and Applications 31 (2020), 1–12.
- Zhang et al. (2020d) Shengdong Zhang, Fazhi He, Wenqi Ren, and Jian Yao. 2020d. Joint learning of image detail and transmission map for single image dehazing. The Visual Computer 36, 2 (2020), 305–316.
- Zhang et al. (2022a) Shengdong Zhang, Wenqi Ren, Xin Tan, Zhi-Jie Wang, Yong Liu, Jingang Zhang, Xiaoqin Zhang, and Xiaochun Cao. 2022a. Semantic-aware dehazing network with adaptive feature fusion. IEEE Transactions on Cybernetics (2022).
- Zhang et al. (2018a) Shengdong Zhang, Wenqi Ren, and Jian Yao. 2018a. Feed-Net: Fully End-to-End Dehazing. In International Conference on Multimedia and Expo. 1–6.
- Zhang et al. (2020f) Shengdong Zhang, Yue Wu, Yuanjie Zhao, Zuomin Cheng, and Wenqi Ren. 2020f. Color-constrained dehazing model. In Conference on Computer Vision and Pattern Recognition Workshops. 870–871.
- Zhang et al. (2021a) Xiaoqin Zhang, Runhua Jiang, Tao Wang, and Wenhan Luo. 2021a. Single Image Dehazing via Dual-Path Recurrent Network. IEEE Transactions on Image Processing 30 (2021), 5211–5222.
- Zhang et al. (2022c) Xiaoqin Zhang, Jinxin Wang, Tao Wang, and Runhua Jiang. 2022c. Hierarchical feature fusion with mixed convolution attention for single image dehazing. IEEE Transactions on Circuits and Systems for Video Technology 32, 2 (2022), 510–522.
- Zhang et al. (2021b) Xiaoqin Zhang, Tao Wang, Wenhan Luo, and Pengcheng Huang. 2021b. Multi-level fusion and attention-guided CNN for image dehazing. IEEE Transactions on Circuits and Systems for Video Technology 31, 11 (2021), 4162–4173.
- Zhang et al. (2020e) Xiaoqin Zhang, Tao Wang, Jinxin Wang, Guiying Tang, and Li Zhao. 2020e. Pyramid Channel-based Feature Attention Network for image dehazing. Computer Vision and Image Understanding 197-198 (2020), 103003.
- Zhang et al. (2017b) Yanfu Zhang, Li Ding, and Gaurav Sharma. 2017b. HazeRD: An outdoor scene dataset and benchmark for single image dehazing. In International Conference on Image Processing. 3205–3209.
- Zhang et al. (2020g) Zhengxi Zhang, Liang Zhao, Yunan Liu, Shanshan Zhang, and Jian Yang. 2020g. Unified Density-Aware Image Dehazing and Object Detection in Real-World Hazy Scenes. In Asian Conference on Computer Vision. 119–135.
- Zhao et al. (2021a) Dong Zhao, Long Xu, Lin Ma, Jia Li, and Yihua Yan. 2021a. Pyramid Global Context Network for Image Dehazing. IEEE Transactions on Circuits and Systems for Video Technology 31, 8 (2021), 3037–3050.
- Zhao et al. (2020) Shiyu Zhao, Lin Zhang, Shuaiyi Huang, Ying Shen, and Shengjie Zhao. 2020. Dehazing Evaluation: Real-World Benchmark Datasets, Criteria, and Baselines. IEEE Transactions on Image Processing 29 (2020), 6947–6962.
- Zhao et al. (2021b) Shiyu Zhao, Lin Zhang, Ying Shen, and Yicong Zhou. 2021b. RefineDNet: A Weakly Supervised Refinement Framework for Single Image Dehazing. IEEE Transactions on Image Processing 30 (2021), 3391–3404.
- Zheng et al. (2021) Zhuoran Zheng, Wenqi Ren, Xiaochun Cao, Xiaobin Hu, Tao Wang, Fenglong Song, and Xiuyi Jia. 2021. Ultra-High-Definition Image Dehazing via Multi-Guided Bilateral Learning. In Conference on Computer Vision and Pattern Recognition. 16180–16189.
- Zhu et al. (2021) Hongyuan Zhu, Yi Cheng, Xi Peng, Joey Tianyi Zhou, Zhao Kang, Shijian Lu, Zhiwen Fang, Liyuan Li, and Joo-Hwee Lim. 2021. Single-image dehazing via compositional adversarial network. IEEE Transactions on Cybernetics 51, 2 (2021), 829–838.
- Zhu et al. (2018) Hongyuan Zhu, Xi Peng, Vijay Chandrasekhar, Liyuan Li, and Joo-Hwee Lim. 2018. DehazeGAN: When Image Dehazing Meets Differential Programming. In International Joint Conference on Artificial Intelligence. 1234–1240.
- Zhu et al. (2017) Jun-Yan Zhu, Taesung Park, Phillip Isola, and Alexei A Efros. 2017. Unpaired image-to-image translation using cycle-consistent adversarial networks. In International Conference on Computer Vision. 2223–2232.