A comparison between Avila-Gouëzel-Yoccoz norm and Teichmüller norm

Weixu Su and Shenxing Zhang Weixu Su: School of Mathematics, Sun Yat-sen University, Guangzhou 510275, China [email protected] Shenxing, Zhang: School of Mathematical Sciences, Fudan University, Shanghai 200433, China [email protected]

Abstract.

We give a comparison between the Avila-Gouëzel-Yoccoz norm and the Teichmüller norm on the principal stratum of holomorphic quadratic differentials.

Keywords: Avila-Gouëzel-Yoccoz norm; quadratic differentials; Teichmüller norm.

MSC2020: 30F30, 30F60.

1. Introduction

Let $X$ be a compact Riemann surface of genus $g$ . A holomorphic quadratic differential $q$ on $X$ is a tensor given locally by an expression $q=q(z)dz^{2}$ where $z$ is a conformal coordinate on $X$ and $q(z)$ is holomorphic. Such a (nonzero) quadratic differential $q$ defines a flat metric $|q|^{1/2}$ on $X$ . This metric has conical singularities at zeroes of $q$ . Its area is defined by

\|q\|=\int_{X}|q(z)||dz|^{2}.

Fix $g\geq 2$ and let $\mathcal{P}_{g}$ be the principal stratum of the moduli space of quadratic differentials, consisting of isomorphism classes of holomorphic quadratic differentials $(X,q)$ with $4g-4$ distinct simple zeroes.

There is a Finsler metric on $\mathcal{P}_{g}$ called AGY metric, which was introduced by Avila-Gouëzel-Yoccoz [2, §2.2.2]. This norm plays an important role in the study of Teichmüller flow. See [1, 2, 4].

Let $\mathcal{M}_{g}$ be the moduli space of Riemann surfaces of genus $g$ . Let $\pi:\mathcal{P}_{g}\to\mathcal{M}_{g}$ be the natural projection, defined by $\pi(X,q)=X$ . In the note, we consider the derivative of $\pi$ and compare the AGY norm with the Teichmüller norm.

Recently, Kahn-Wright [6] derived a comparison between the Hodge norm (another important norm on $\mathcal{P}_{g}$ ) and the Teichmüller norm. Our research is motivated by their work.

For each $(X,q)\in\mathcal{P}_{g}$ , there is a canonical double cover $\rho:\hat{X}\to X$ , ramified at the odd zeros of $q$ , such that $\rho^{*}q$ is the square of an Abelian differential $\omega$ on $\hat{X}$ . See [3] or [7, §2] for details. The Abelian differential $\omega$ is a $-1$ eigenvector for the holomorphic involution $\tau:\hat{X}\to\hat{X}$ that permutes the sheets of the double cover, that is,

\tau^{*}\omega=-\omega.

We can identify the tangent space of $\mathcal{P}_{g}$ at $(X,q)$ as $H^{1}_{-1}(\hat{X},\mathbb{C})$ , the $-1$ eigenspace for the action of $\tau$ on the cohomology group $H^{1}(\hat{X},\mathbb{C})$ .

Every element of $H^{1}(\hat{X},\mathbb{C})$ can be represented uniquely by a harmonic one-form. Consequently, there is a natural decomposition of $H^{1}_{-1}(\hat{X},\mathbb{C})$ into $H_{-1}^{1,0}(\hat{X})\oplus H_{-1}^{0,1}(\hat{X}).$ Note that the kernel of $D\pi$ is $H_{-1}^{1,0}(\hat{X})$ . See Theorem 2.1 below.

We consider $\eta\in H_{-1}^{0,1}(\hat{X})$ and compare the AGY norm of $\eta$ with the Teichmüller norm of $D\pi(\eta)$ . The main result is

Theorem 1.1.

Let $(X,q)\in\mathcal{P}_{g}$ with area $\|q\|=1$ . Let $\rho:\hat{X}\to X$ be the canonical double cover such that $\rho^{*}q=\omega^{2}$ . Then for any $\eta\in H_{-1}^{0,1}(\hat{X})$ , we have

(1)

\frac{r}{2\sqrt{2}}\ {\|\eta\|_{\mathrm{AGY}}}\leq{\|D\pi(\eta)\|_{\mathrm{Teich}}}\leq\frac{8}{\sqrt{\pi}r}\|\eta\|_{\mathrm{AGY}},

where $2r$ is the shortest length of saddle connections on $(\hat{X},\omega)$ .

Remark 1.2.

Note that the area of $\omega$ is $2$ .

The paper has the following structure. In §2, we present some basic properties of quadratic differentials. The upper bound in (1) is proved in §3, where we use the Delaunay triangulation of quadratic differential to construct quasiconformal maps with explicit Beltrami differentials. In §4, we give an upper bound of the AGY norm in terms of the Hodge norm, and then we derive the lower bound in (1) from Kahn-Wright[6, Theorem 1.4].

2. Preliminaries

2.1. The moduli space of quadratic differentials

Let $g\geq 2$ . We denote by $\mathcal{M}_{g}$ the moduli space of compact Riemann surfaces of genus $g$ . For $X\in\mathcal{M}_{g}$ , the cotangent space of $\mathcal{M}_{g}$ at $X$ is canonically identified with the space $Q(X)$ of holomorphic quadratic differentials on $X$ . We define the $L^{1}$ -norm on $Q(X)$ by

\|q\|=\int_{X}|q|.

A tangent vector of $\mathcal{M}_{g}$ at $X$ is represented by a Beltrami differential $\mu$ . There is a natural pairing between quadratic differentials and Beltrami differentials given by

\langle\mu,q\rangle=\int_{X}\mu q.

The Teichmüller norm of $\mu$ is defined by

\|\mu\|_{\mathrm{Teich}}=\sup_{\|q\|=1}\operatorname{Re}\ \langle\mu,q\rangle.

This gives the infinitesimal form of the Teichmüller metric on $\mathcal{M}_{g}$ .

Let $\mathcal{Q}_{g}$ be the moduli space of quadratic differentials, consisting of pairs $(X,q)$ where $X$ is a compact Riemann surface of genus $g$ and $q$ is a holomorphic quadratic differential on $X$ . The moduli space $\mathcal{Q}_{g}$ has a stratified structure: given a positive integral vector $\kappa=\left(\kappa_{1},\cdots,\kappa_{n}\right)$ with $\sum\kappa_{i}=4g-4$ , we let $\mathcal{Q}_{g}(\kappa)\subset\mathcal{Q}_{g}$ be the set of quadratic differentials $(X,q)$ where $q$ has $n$ zeros of order $\kappa_{1},\cdots,\kappa_{n}$ .

In the paper, our study is mainly restricted on the principal stratum, consisting of those quadratic differentials all of whose zeros are simple. We denote the principal stratum by $\mathcal{P}_{g}$ . This stratum is both open and dense in $\mathcal{Q}_{g}$ .

2.2. Canonical double cover

Let $\mathcal{Q}_{g}(\kappa)$ be a stratum of quadratic differentials. Given $(X,q)\in\mathcal{Q}_{g}(\kappa)$ , let $\rho:\hat{X}\to X$ be the canonical double cover such that the pull-back $\rho^{*}q$ becomes the square of an Abelian differential $\omega$ on $\hat{X}$ . Let $\tau:\hat{X}\to\hat{X}$ be the involution that permutes the sheets of the double cover. By the construction, $\tau^{*}\omega=-\omega$ .

Let $\Sigma$ be the set of zeros of $\omega$ . Denote by $H^{1}_{-1}(\hat{X},\Sigma,\mathbb{C})$ the $-1$ eigenspace for the action of $\tau$ on the relative homology group $H^{1}(\hat{X},\Sigma,\mathbb{C})$ . Note that the relative cohomology class of $\omega$ is an element of $H^{1}_{-1}(\hat{X},\Sigma,\mathbb{C})$ . A neighborhood of $\omega$ in $H^{1}_{-1}(\hat{X},\Sigma,\mathbb{C})$ gives a local chart of $q$ in the stratum, via the period mapping.

In the following, we shall identify the tangent space at $(X,q)$ with the cohomology $H^{1}_{-1}(\hat{X},\Sigma,\mathbb{C})$ . If $(X,q)\in\mathcal{P}_{g}$ , then $q$ has no zeros of even order. In this case, since $\Sigma$ is the set of fixed points of $\tau$ , we have

H^{1}_{-1}(\hat{X},\Sigma,\mathbb{C})\cong H^{1}_{-1}(\hat{X},\mathbb{C}).

Thus each element of $H^{1}_{-1}(\hat{X},\mathbb{C})$ can be uniquely represented by a harmonic $1$ -form.

The following result describes the tangent map of $\pi:\mathcal{P}_{g}\to\mathcal{M}_{g}$ in terms of the period coordinates. It is proved by Kahn-Wright [6, Corollary 1.2].

Theorem 2.1.

Consider the projection $\pi:\mathcal{P}_{g}\to\mathcal{M}_{g}$ . Let $(X,q)\in\mathcal{P}_{g}$ and let $\eta$ be a harmonic $1$ -form on $\hat{X}$ that represents an element of $H^{1}_{-1}(\hat{X},\mathbb{C})$ . Then for any $\phi\in Q(X)$ , we have

\langle D\pi(\eta),\phi\rangle=\frac{1}{2}\int_{\hat{X}}\rho^{*}(\phi)\frac{\eta^{0,1}}{\omega},

where $\eta^{0,1}$ is the anti-holomorphic part of $\eta$ .

2.3. The AGY norm.

The AGY norm is defined by Avila-Gouëzel-Yoccoz [2] on any stratum of Abelian differentials.

With the notations in §2.2, we consider the Abelian differential $\omega$ as an element of $H^{1}(\hat{X},\Sigma,\mathbb{C})$ . A saddle connection of $\omega$ is a geodesic segment for the flat metric defined by $|\omega|$ joining two zeros of $\omega$ and not passing any zero in its interior. Each saddle connection $\gamma$ gives rise to an element $[\gamma]$ of the homology $H_{1}(\hat{X},\Sigma,\mathbb{C})$ . And the set of saddle connections generates the the homology $H_{1}(\hat{X},\Sigma,\mathbb{C})$ . Denote by $\left\{\gamma_{j}\right\}$ the set of saddle connections on $\omega$ .

For any $[\eta]\in H^{1}(\hat{X},\Sigma,\mathbb{C})$ , its AGY norm is defined by

\|\eta\|_{\mathrm{AGY}}=\sup_{\gamma_{j}}\frac{\left|\int_{\gamma_{j}}\eta\right|}{\left|\int_{\gamma_{j}}\omega\right|},

where the supremum is taken over all saddle connections.

Avila-Gouëzel-Yoccoz [2, §2.2.2] showed that the AGY norm is continuous and induces a complete metric on each stratum.

3. The upper bound

In this section, we give an upper bound of $\|D\pi(\eta)\|_{\mathrm{Teich}}$ in terms of $\|\eta\|_{\mathrm{AGY}},$ for any $\eta\in H^{1}_{-1}(\hat{X},\mathbb{C})$ . The idea is to triangulate the surface and compute the Beltrami differentials of maps that are affine on each triangle. We remark that the proof applies to any other stratum of quadratic differentials or Abelian differentials.

3.1. Delaunay triangulation

Given a quadratic differential $(X,q)$ , there is an associated flat metric (with conical singularities) on $X$ , defined by $|q|^{1/2}$ . Denote by $\Sigma$ the set of zeros of $q$ . For any $x\in X$ , let $d(x,\Sigma)$ be the minimal $|q|^{1/2}$ -distance from $x$ to $\Sigma$ .

The next result is proved by Masur-Smillie [8, §4]. See also Farb-Masur [5, Proposition 3.1].

Proposition 3.1.

Let $(X,q)$ be a holomorphic quadratic differential of area $\|q\|\leq 1$ . There is a triangulation $\Delta$ on $X$ with the following properties:

(1)

The vertices of $\Delta$ lie in the zero set of $q$ .
(2)

The edges of $\Delta$ are saddle connections of $q$ .
(3)

Each triangle is inscribed in a circle of radius $d(x,\Sigma)$ for some $x\in X$ .

The above construction is called a Delaunay triangulation of $q$ .

Let $s=\sqrt{\frac{2}{\pi}}$ , and let $B_{s}$ be the set of points in $X$ with $d(x,\Sigma)\leq s$ . By the proof of [8, Theorem 5.3], the complement of $B_{s}$ is contained in a union of disjoint maximal flat cylinders, with the property that their circumference is less than their height.

3.2. The proof of upper bound

Let $\eta\in H^{1}_{-1}(\hat{X},\mathbb{C})$ . Denote by $(\hat{X}_{t},\omega_{t})$ the family of Abelian differentials corresponding to the cohomology classes $\omega+t\eta\in H^{1}_{-1}(\hat{X},\mathbb{C})$ , for sufficiently small $t>0$ .

Let $\Delta$ be a Delaunay triangulation of $(\hat{X},\omega)$ . By the construction, the vertices of $\Delta$ are the zeros of $\omega$ , and the edges of $\Delta$ are saddle connections of $\omega$ . For each $t$ , we can straighten $\Delta$ to be a triangulation of $\hat{X}_{t}$ (not necessary Delaunay), denoted by $\Delta_{t}$ , such that the edges are saddle connections of $\omega_{t}$ .

The next step is to construct quasiconformal mappings $f_{t}$ from $\hat{X}$ to $\hat{X}_{t}$ that are linear on each triangle. Denote the Beltrami differentials of $f_{t}$ by $\mu_{t}$ . Then

D\pi(\eta)\cong\frac{d\mu_{t}}{dt}|_{t=0}.

Proposition 3.2.

Let $2r$ be the shortest length of saddle connections on $(\hat{X},\omega)$ . Then

\left\|D\pi(\eta)\right\|_{\mathrm{Teich}}\leq\frac{8}{\sqrt{\pi}r}\|\eta\|_{\mathrm{AGY}}.

Proof.

Denote by

\mu=\frac{d\mu_{t}}{dt}|_{t=0}.

Since $\|\mu\|_{\mathrm{Teich}}\leq\|\mu\|_{\infty}$ , it suffices to give the upper bound for $\|\mu\|_{\infty}$ .

Let $T=\triangle OAB$ be any triangle of $\Delta$ , where $O,A,B$ denotes the vertices. For simplicity, we consider $T$ as a triangle in the complex plane and put $O=0,A=a>0$ and $B=b\in\mathbb{C}$ . By definition,

a=\int_{\gamma}\omega,b=\int_{\gamma^{\prime}}\omega,

where $\gamma$ and $\gamma^{\prime}$ denote the saddle connection connecting $O$ to $A$ and $O$ to $B$ , respectively.

For each $t$ sufficiently small, the corresponding triangle in $\hat{X}_{t}$ has vertices given by $0$ , $a+t\alpha$ and $b+t\beta$ , where

\alpha=\int_{\gamma}\eta,\beta=\int_{\gamma^{\prime}}\eta.

Denote the associated affine mapping between the triangles by

f_{t}(z)=Rz+S\bar{z}.

Then we have

Ra+Sa=a+t\alpha,

Rb+S\bar{b}=b+t\beta.

A simple computation shows that the Beltrami coefficient $\mu_{t}$ is equal to

\frac{S}{R}=t\frac{\frac{\alpha}{a}-\frac{\beta}{b}}{1-\frac{\bar{b}}{b}}+o(t).

Now we give an upper bound of

|\mu(z)|=\left|\frac{\frac{\alpha}{a}-\frac{\beta}{b}}{1-\frac{\bar{b}}{b}}\right|.

Assume that $\theta=\arg b$ . Then

|1-\frac{\bar{b}}{b}|=2|\sin\theta|.

To give an upper bound of the quasiconformal dilatation, we discuss $\sin\theta$ in two cases.

Let $s_{0}=\sqrt{\frac{4}{\pi}}=\frac{2}{\sqrt{\pi}}$ . We remark that the area of $|\omega|$ is $2$ . Note that for any edge of $T$ , it either has length $\leq 2s_{0}$ or crosses a maximal flat cylinder $C$ whose height $h$ is greater than its circumference $c$ .

Assume that all edges of $T$ has length $\leq 2s_{0}$ . In this case, the triangle $T$ is inscribed in a circle of radius $d(x,\Sigma)\leq 2s_{0}.$

Since $\sin\theta=|a-b|/2d(x,\Sigma)$ , we have

|\sin\theta|\geq\frac{r}{d(x,\Sigma)}\geq\frac{\sqrt{\pi}r}{4}.

Thus we have

\left|\frac{\frac{\alpha}{a}-\frac{\beta}{b}}{1-\frac{\bar{b}}{b}}\right|\leq\frac{8\max\{|\frac{\alpha}{a}|,|\frac{\beta}{b}|\}}{\sqrt{\pi}r}\leq\frac{8}{\sqrt{\pi}r}\|\eta\|_{\mathrm{AGY}}.

The remaining case is that some edge of $T$ crosses a maximal flat cylinder $C$ whose height $h$ is greater than its circumference $c$ . In this case, some other edge of $T$ also crosses $C$ . Thus the triangle $T$ looks like an isosceles triangle with a short base. As a result, we may choose the angle $\theta$ such that

\frac{\pi}{4}\leq\theta\leq\frac{\pi}{2}.

Then we have $\sin\theta\geq\frac{\sqrt{2}}{2}$ . It follows that

\left|\frac{\frac{\alpha}{a}-\frac{\beta}{b}}{1-\frac{\bar{b}}{b}}\right|\leq\frac{2\max\{|\frac{\alpha}{a}|,|\frac{\beta}{b}|\}}{\sqrt{2}}\leq\sqrt{2}\|\eta\|_{\mathrm{AGY}}.

Note that $\pi r^{2}\leq 2$ and then $\sqrt{2}\leq\frac{2}{\sqrt{\pi}r}$ . This completes the proof.

∎

Remark 3.3.

It is known that for any quadratic differential $q$ , in the the direction of Teichmüller flow, the AGY norm is less than the Teichmüller norm (see [2, Page 152]).

As we have shown in the proof of Proposition 3.2, the order $\frac{1}{r}$ appears when the triangle is almost flat. If there is some angle of the triangle which is neither close to $0$ or $\pi$ , then the Beltrami coefficient should be bounded above by $\|\eta\|_{\mathrm{AGY}}$ up to a multiplicative constant.

3.3. The order $\frac{1}{r}$ in Proposition 3.2 is sharp.

We recall the following construction of Kahn-Wright [6, §3.3].

Let $\epsilon>0$ be a small constant. We take a square torus of length $1$ and make a length $\epsilon$ horizontal slit. Then we identify the endpoints of the slit to make a figure-eight and glue in a cylinder with circumference $\epsilon$ and height $\epsilon$ . The construction defines an Abelian differential $(X_{\epsilon},\omega_{\epsilon})$ with one double zero, i.e. a translation surface in $\mathcal{H}(2)$ .

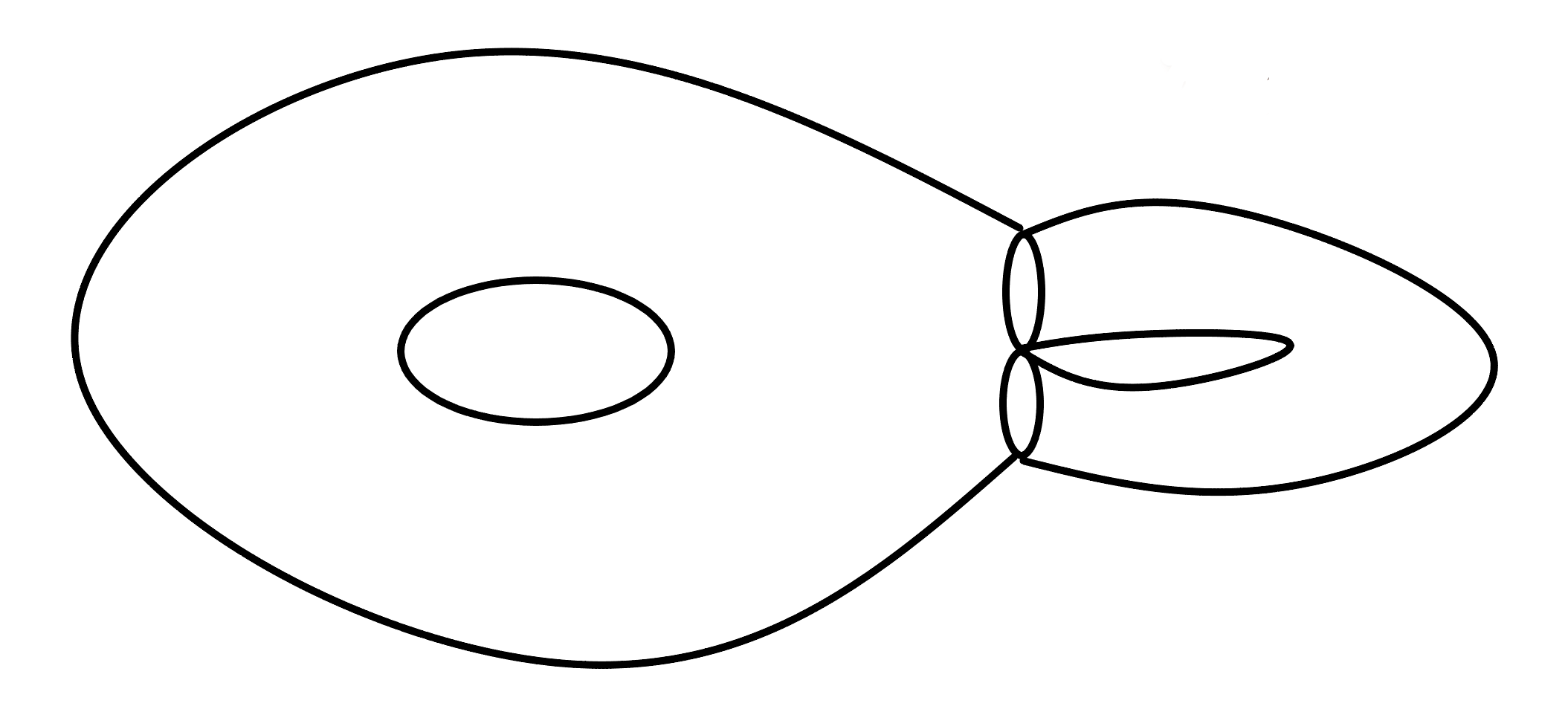
Refer to caption — Figure 1. The examples of Kahn-Wright [6, §3.3].

Let ${\gamma}_{\epsilon}$ be the core curve of the small cylinder in $(X_{\epsilon},{\omega}_{\epsilon})$ . Denote the harmonic differential dual to $\gamma_{\epsilon}$ by ${\gamma}_{\epsilon}^{*}$ .

Remark 3.4.

We can write $\gamma_{\epsilon}^{*}=\beta_{\epsilon}+\bar{\beta}_{\epsilon}$ , where $\beta_{\epsilon}$ is an Abelian differential. It is known that the Hodge norm of $\beta_{\epsilon}$ is bounded above and below independently of $\epsilon$ .

As shown by Kahn-Wright [6, §3.3],

\left\|D\pi({\gamma}_{\epsilon}^{*})\right\|_{\mathrm{Teich}}\geq\frac{C}{\epsilon}

for some constant $C$ .

The path $\omega_{\epsilon}+t\epsilon\gamma_{\epsilon}^{*}$ is corresponding to a family of translation surfaces, obtained by twisting along the core curve of the small cylinder. When $t=1$ , $\omega_{\epsilon}+\epsilon\gamma_{\epsilon}^{*}$ is a Dehn twist of $\gamma_{\epsilon}$ .

The length of shortest saddle connections of $\omega_{\epsilon}$ is equal to $\epsilon$ . If $\alpha_{0}$ is the shortest saddle connection contained in the small cylinder and crossing $\gamma_{\epsilon}$ , then

\frac{\left|\int_{\alpha_{0}}\gamma_{\epsilon}^{*}\right|}{\left|\int_{\alpha_{0}}\omega_{\epsilon}\right|}=\frac{\epsilon}{\epsilon}=1.

For any other saddle connection $\alpha$ , which crosses the small cylinder $n$ times, we have

\frac{\left|\int_{\alpha}\gamma_{\epsilon}^{*}\right|}{\left|\int_{\alpha}\omega_{\epsilon}\right|}\leq\frac{n\epsilon}{n\epsilon}=1.

As a result, $\|{\gamma}_{\epsilon}^{*}\|_{\mathrm{AGY}}=1$ . In conclusion, we have

\left\|D\pi({\gamma}_{\epsilon}^{*})\right\|_{\mathrm{Teich}}\geq C\frac{\|{\gamma}_{\epsilon}^{*}\|_{\mathrm{AGY}}}{\epsilon},

where $\epsilon$ is the length of shortest saddle connections of $\omega_{\epsilon}$ .

4. The lower bound

In this section, we consider tangent vectors to $\mathcal{P}_{g}$ of the form $\eta=\bar{\beta}$ , where $\beta\in H_{-1}^{1,0}(\hat{X})$ . By Theorem 2.1, the Beltrami differential $\mu=\bar{\beta}/\omega$ can be considered as the tangent vector $D\pi(\eta)$ via the pairing with holomorphic quadratic differentials

\int_{\hat{X}}\rho^{*}(\phi)\frac{\bar{\beta}}{\omega}.

The Hodge norm of $\beta\in H_{-1}^{1,0}(\hat{X})$ is defined by

\|\beta\|_{\mathrm{Hodge}}=\sqrt{\int_{\hat{X}}|\beta|^{2}}.

We have (see [6, Theorem 3.1]):

Theorem 4.1.

For any $\eta=\bar{\beta}\in H_{-1}^{0,1}(\hat{X})$ , we have

\|D\pi(\eta)\|_{\mathrm{Teich}}\geq\frac{\|\beta\|_{\mathrm{Hodge}}}{\|\omega\|_{\mathrm{Hodge}}}\ .

The lower bound in Theorem 1.1.

The assumption $\|q\|=1$ implies $\|\omega\|_{\mathrm{Hodge}}=\sqrt{2}.$ Applying Theorem 4.1 and the next proposition , we have

(2)

\displaystyle\|D\pi(\eta)\|_{\mathrm{Teich}}

\displaystyle\geq

\displaystyle\frac{\|\eta\|_{\mathrm{Hodge}}}{\sqrt{2}}\geq\frac{r}{2\sqrt{2}}\|\eta\|_{\mathrm{AGY}}.

∎

Proposition 4.2.

Let $2r$ be the shortest length of saddle connections. For any saddle connection $\gamma$ of $\omega$ and any $\beta\in H_{-1}^{1,0}(\hat{X})$ , we have

\frac{\left|\int_{\gamma}\beta\right|}{\left|\int_{\gamma}\omega\right|}\leq 2\frac{\|\beta\|_{\mathrm{Hodge}}}{r}.

As a result, for any $\eta=\bar{\beta}\in H_{-1}^{0,1}(\hat{X})$ , we have

\|\eta\|_{\mathrm{AGY}}\leq 2\frac{\|\eta\|_{\mathrm{Hodge}}}{r}.

Proof.

We shall endow the surface with the metric defined by $|\omega|$ . Let $\Sigma$ be the set of zeros of $\omega$ . Given a saddle connection $\gamma$ of $\omega$ , we can decompose $\gamma$ into two parts. Either a segment of $\gamma$ is contained in the disk $D(p,r)$ of radius $r$ centered at a $p\in\Sigma$ and such a segment intersects with $D(p,r/2)$ ; or the segment is outside $D(p,r/2)$ for all $p\in\Sigma$ . We denote the two parts by $\gamma^{\prime}$ and $\gamma^{\prime\prime}$ .

It is not necessary that $\gamma^{\prime}$ or $\gamma^{\prime\prime}$ is connected. We write

\gamma^{\prime}=\bigcup_{i}\gamma_{i}^{\prime}\ \mathrm{and}\ \gamma^{\prime\prime}=\bigcup_{j}\gamma_{j}^{\prime\prime},

where $\gamma^{\prime}_{i},\gamma_{j}^{\prime\prime}$ denote the connected components.

For each $\gamma_{i}^{\prime}$ , there is a unique zero (of order $2$ ) $z_{i}$ of $\omega$ such that $\gamma_{i}$ is contained in the disk $D(z_{i},r)$ and $\gamma_{i}$ intersects with $D(z_{i},r/2)$ . It follows from [6, Lemma 3.2] that, for $z$ in $D(z_{0},r)$ ,

\left|\int_{z_{i}}^{z}\beta\right|\leq\|\beta\|_{\mathrm{Hodge}}.

As a result,

\left|\int_{\gamma_{i}^{\prime}}\beta\right|\leq 2\|\beta\|_{\mathrm{Hodge}}.

Since $\gamma$ crosses the annulus $D(z_{i},r)\setminus D(z_{i},r/2)$ , $\left|\int_{\gamma_{i}^{\prime}}\omega\right|\geq r$ . This implies

(3)

\frac{\left|\int_{\gamma_{i}^{\prime}}\beta\right|}{\left|\int_{\gamma_{i}^{\prime}}\omega\right|}\leq 2\frac{\|\beta\|_{\mathrm{Hodge}}}{r}.

Now we consider $\gamma_{j}^{\prime\prime}$ . We have

\displaystyle\left|\int_{\gamma_{j}^{\prime\prime}}\beta\right|\leq\int_{\gamma_{j}^{\prime\prime}}\left|\frac{\beta}{\omega}\right|\left|\omega\right|.

We give an upper bound for $\frac{\beta}{\omega}$ . Let $x_{0}\in\gamma_{j}^{\prime\prime}$ . Note that there is a disk $D(x_{0},r/2)$ of radius $r/2$ around $x_{0}$ , which does not contain any zeros of $\omega$ .

Let $z$ be the natural coordinate of $\omega$ on $D(z_{0},r/2)$ , where $z_{0}=z(x_{0})$ . In $D(z_{0},r/2)$ , we have $\omega=dz$ . And $\frac{\beta}{\omega}(z)$ defines a holomorphic function on $D(z_{0},r/2)$ .

By the mean-value inequality of subharmonic function, we have

\displaystyle\left|\frac{\beta}{\omega}(z_{0})\right|^{2}

\displaystyle\leq

\displaystyle\frac{4\int_{D(z_{0},r/2)}\left|\frac{\beta}{\omega}(z)\right|^{2}dxdy}{\pi r^{2}}.

Thus we have

$\displaystyle\left\|\frac{\beta}{\omega}(z_{0})\right\|$	$\displaystyle\leq$	$\displaystyle\frac{2\left(\int_{D(z_{0},r/2)}\left\|\frac{\beta}{\omega}(z)\right\|^{2}dxdy\right)^{1/2}}{\sqrt{\pi}r}$
	$\displaystyle=$	$\displaystyle\frac{2\left(\int_{D(z_{0},r/2)}\left\|\beta\right\|^{2}\right)^{1/2}}{\sqrt{\pi}r}$
	$\displaystyle\leq$	$\displaystyle\frac{2\\|\beta\\|_{\mathrm{Hodge}}}{\sqrt{\pi}r}.$

As a result, we show

(4)

\frac{\left|\int_{\gamma^{\prime\prime}}\beta\right|}{\left|\int_{\gamma^{\prime\prime}}\omega\right|}\leq\max_{\gamma^{\prime\prime}}\left|\frac{\beta}{\omega}\right|\leq 2\frac{\|\beta\|_{\mathrm{Hodge}}}{\sqrt{\pi}r},

Combining (4) with (3), we have

$\displaystyle\frac{\left\|\int_{\gamma}\beta\right\|}{\left\|\int_{\gamma}\omega\right\|}$	$\displaystyle\leq$	$\displaystyle\frac{\sum_{i}\left\|\int_{\gamma_{i}^{\prime}}\beta\right\|+\sum_{j}\left\|\int_{\gamma_{j}^{\prime\prime}}\beta\right\|}{\sum_{i}\left\|\int_{\gamma_{i}^{\prime}}\omega\right\|+\sum_{j}\left\|\int_{\gamma_{j}^{\prime\prime}}\omega\right\|}$
	$\displaystyle\leq$	$\displaystyle\max_{i,j}\left\{\frac{\left\|\int_{\gamma_{i}^{\prime}}\beta\right\|}{\left\|\int_{\gamma_{i}^{\prime}}\omega\right\|},\frac{\left\|\int_{\gamma_{j}^{\prime\prime}}\beta\right\|}{\left\|\int_{\gamma_{j}^{\prime\prime}}\omega\right\|}\right\}$
	$\displaystyle\leq$	$\displaystyle 2\max\left\{\frac{\\|\beta\\|_{\mathrm{Hodge}}}{r},\frac{\\|\beta\\|_{\mathrm{Hodge}}}{\sqrt{\pi}r}\right\}$
	$\displaystyle=$	$\displaystyle 2\frac{\\|\beta\\|_{\mathrm{Hodge}}}{r}.$

∎

References

[1] Artur Avila and Sébastien Gouëzel. Small eigenvalues of the laplacian for algebraic measures in moduli space, and mixing properties of the teichmüller flow. Annals of Mathematics, pages 385–442, 2013.
[2] Artur Avila, Sébastien Gouëzel, and Jean-Christophe Yoccoz. Exponential mixing for the teichmüller flow. Publications Mathématiques de l’IHÉS, 104:143–211, 2006.
[3] Adrian Douady and John Hubbard. On the density of strebel differentials. Inventiones mathematicae, 30:175–179, 1975.
[4] Alex Eskin and Maryam Mirzakhani. Invariant and stationary measures for the action on moduli space. Publications mathématiques de l’IHÉS, 127:95–324, 2018.
[5] Benson Farb and Howard Masur. Teichmüller geometry of moduli space, i: distance minimizing rays and the deligne-mumford compactification. Journal of Differential Geometry, 85(2):187–228, 2010.
[6] Jeremy Kahn and Alex Wright. Hodge and teichmüller. Journal of Modern Dynamics, 18:149–160, 2022.
[7] Erwan Lanneau. Hyperelliptic components of the moduli spaces of quadratic differentials with prescribed singularities. Commentarii Mathematici Helvetici, 79(3):471–501, 2004.
[8] Howard Masur and John Smillie. Hausdorff dimension of sets of nonergodic measured foliations. Annals of Mathematics, 134(3):455–543, 1991.

$\displaystyle\left\|\frac{\beta}{\omega}(z_{0})\right\|$	$\displaystyle\leq$	$\displaystyle\frac{2\left(\int_{D(z_{0},r/2)}\left\|\frac{\beta}{\omega}(z)\right\|^{2}dxdy\right)^{1/2}}{\sqrt{\pi}r}$
	$\displaystyle=$	$\displaystyle\frac{2\left(\int_{D(z_{0},r/2)}\left\|\beta\right\|^{2}\right)^{1/2}}{\sqrt{\pi}r}$
	$\displaystyle\leq$	$\displaystyle\frac{2\\|\beta\\|_{\mathrm{Hodge}}}{\sqrt{\pi}r}.$

$\displaystyle\frac{\left\|\int_{\gamma}\beta\right\|}{\left\|\int_{\gamma}\omega\right\|}$	$\displaystyle\leq$	$\displaystyle\frac{\sum_{i}\left\|\int_{\gamma_{i}^{\prime}}\beta\right\|+\sum_{j}\left\|\int_{\gamma_{j}^{\prime\prime}}\beta\right\|}{\sum_{i}\left\|\int_{\gamma_{i}^{\prime}}\omega\right\|+\sum_{j}\left\|\int_{\gamma_{j}^{\prime\prime}}\omega\right\|}$
	$\displaystyle\leq$	$\displaystyle\max_{i,j}\left\{\frac{\left\|\int_{\gamma_{i}^{\prime}}\beta\right\|}{\left\|\int_{\gamma_{i}^{\prime}}\omega\right\|},\frac{\left\|\int_{\gamma_{j}^{\prime\prime}}\beta\right\|}{\left\|\int_{\gamma_{j}^{\prime\prime}}\omega\right\|}\right\}$
	$\displaystyle\leq$	$\displaystyle 2\max\left\{\frac{\\|\beta\\|_{\mathrm{Hodge}}}{r},\frac{\\|\beta\\|_{\mathrm{Hodge}}}{\sqrt{\pi}r}\right\}$
	$\displaystyle=$	$\displaystyle 2\frac{\\|\beta\\|_{\mathrm{Hodge}}}{r}.$

A comparison between Avila-Gouëzel-Yoccoz norm and Teichmüller norm

Abstract.

1. Introduction

Theorem 1.1.

Remark 1.2.

2. Preliminaries

2.1. The moduli space of quadratic differentials

2.2. Canonical double cover

Theorem 2.1.

2.3. The AGY norm.

3. The upper bound

3.1. Delaunay triangulation

Proposition 3.1.

3.2. The proof of upper bound

Proposition 3.2.

Proof.

Remark 3.3.

3.3. The order 1r\frac{1}{r} in Proposition 3.2 is sharp.

Remark 3.4.

4. The lower bound

Theorem 4.1.

The lower bound in Theorem 1.1.

Proposition 4.2.

Proof.

References

3.3. The order $\frac{1}{r}$ in Proposition 3.2 is sharp.