A CCCZ gate performed with 6 T gates

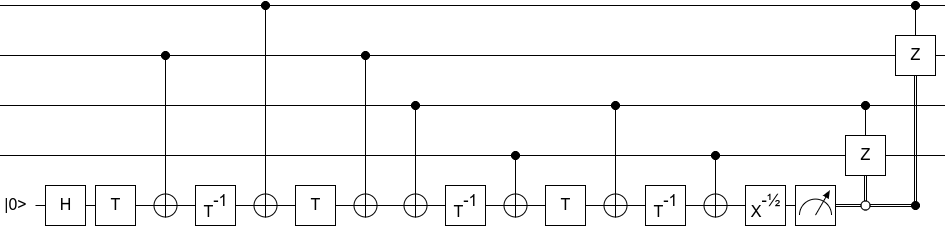
This short note reports a small serendipitous discovery that occurred while I was discussing a circuit optimization problem Gidney (2021) with Cody. I was using Quirk Gidney (2016) to demonstrate ideas, and Cody suggested an idea for how to approach the problem based on targeting one ancilla with two Toffolis so that a pair of T gates would cancel where the Toffolis met. I’d tried a similar idea before, and was going through the motions of showing how it didn’t quite work, when Cody pointed out that a CCCZ kickback had suddenly appeared in the circuit despite there only being 6 T gates. I isolated the CCCZ, cleaned up the circuit, and produced Figure 1.

The circuit works because $i^{ab\oplus cd}=i^{ab}i^{cd}(-1)^{abcd}$. The circuit uses two Toffolis to prepare $ab\oplus cd$ onto an ancilla, where $a,b,c,d$ are the computational basis values of four qubits. The Toffolis are computed using four T gates instead of seven, to get phase kickback onto the controls. The Toffolis touch in a way that cancels two more T gates. After the ancilla is computed, it is phased and then removed using measurement based uncomputation. The kickback from the Toffolis cancels the $i^{ab}i^{cd}$ components that arise from phasing the ancilla. This leaves behind only the $(-1)^{abcd}$ term, which is the CCCZ.

A Pauli gate with $n>2$ controls can be performed with $4n-4$ T gates by using $n-2$ temporary AND gates to cut the controls down to a pair controlling a Toffoli Gidney (2018). The final AND gate and the Toffoli can be replaced by a 6T CCCZ, saving 2 T gates, reducing the T cost to $4n-6$. Oddly, we’ve otherwise not found any way to iterate or nest or generalize the 6T CCCZ in a way that performs common operations with lower T costs.

The 6T CCCZ circuit is simple enough that this note is likely a rediscovery, but we aren’t aware of prior art. We did find that Table I of Beverland et al. 2019 Beverland et al. (2020) claims that a $|CCCZ\rangle$ state can be prepared using six T gates, suggesting they knew the construction. However, the table references a paper Jones (2013) with a construction that uses eight T gates, not six. When we contacted Beverland et al. they guessed that the T count listed in the table was most likely a typo. Assuming that’s the case, we’re happy to report that the typo was merely ahead of its time.

References