2-dimensional Shephard groups
Abstract.
The 2-dimensional Shephard groups are quotients of 2-dimensional Artin groups by powers of standard generators. We show that such a quotient is not if the powers taken are sufficiently large. However, for a given 2-dimensional Shephard group, we construct a piecewise Euclidean cell complex with a cocompact action (analogous to the Deligne complex for an Artin group) that allows us to determine other non-positive curvature properties. Namely, we show the 2-dimensional Shephard groups are acylindrically hyperbolic (which was known for 2-dimensional Artin groups), and relatively hyperbolic (which most Artin groups are known not to be). As an application, we show that a broad class of 2-dimensional Artin groups are residually finite.
1. Introduction
Shephard groups (named for G.C. Shephard [She52]) are specific quotients of Artin groups and include, for example, the Coxeter groups and graph products of cyclic groups as special cases. In a previous paper [Gol23], the author identified a specific class of Shephard groups which exhibit Coxeter-like behavior, and proved that these are . However, the Shephard groups form a very broad class, and because of this, we can find examples which exhibit behavior that diverges quite a bit from the intuition that Coxeter groups and Artin groups provide. The motivating criteria in [Gol23] can be roughly summarized by saying that the finite parabolic subgroups are identical to the finite parabolic subgroups of the “associated” Coxeter group. This class is rather inflexible, though; there are only so many finite Shephard groups that are not finite Coxeter groups. Our main motivation, then, is to begin the study of Shephard groups which do not satisfy this criteria. That is to say, to study those Shephard groups which possess some infinite parabolic subgroup whose associated Coxeter group is finite.
It turns out that such groups are quite fascinating even in the 2-generator (or “dihedral”) case, and possess a rather interesting geometry which deviates from the Artin and Coxeter groups. These dihedral groups will be one of the main focuses of the current article. The other main focus are the 2-dimensional Shephard groups. These are the Shephard groups which can be reasonably said to be “built-up” out of their dihedral subgroups. From our results on 2-generator Shephard groups, we derive interesting information about the geometry of the 2-dimensional Shephard groups, some known for Artin groups, some different than Artin groups, and some which can be used to show new properties of Artin groups. The full definitions and statements are as follows.
Let be a simplicial graph with vertices labeled by and edges labeled by . If is odd then we require . We call an extended (or Shephard) presentation graph. The Shephard group with presentation graph is
where denotes if is even and if is odd. If is a single edge, then we will write and call this an edge (Shephard) group or a dihedral Shephard group.
If is an extended presentation graph and , we denote by the extended presentation graph obtained from by replacing all with . In particular, for any extended presentation graph , we define
which are the Coxeter group and Artin group, resp., associated to . Thus we see that every Shephard group is a quotient of an Artin group by some powers of standard generators.
Assumption.
In the rest of the paper, “extended presentation graph” will be taken to mean “extended presentation graph with all finite” (so the kernel of contains powers of every generator), unless we explicitly mention , and “Shephard group” will mean “Shephard group with all finite-order generators”.
We write if is a full subgraph of and inherits the edge and vertex labels of . (A full or “induced” subgraph of is one where if and , then .) Then is also an extended presentation graph and thus determines a Shephard group , a Coxeter group , and an Artin group . If is finite, then we will call each of , , and “spherical-type”. (Similarly, if is word hyperbolic, then we will call each of , , and “hyperbolic-type”.) A property of an extended presentation graph commonly of interest for Artin groups and Coxeter groups is
-
(2D)
For all spherical-type , .
If a graph satisfies (2D), we will call 2-dimensional. Much of the behavior of 2-dimensional Shephard groups can be deduced from their dihedral subgroups. Our first main result concerns solely these dihedral Shephard groups.
Theorem A.
Let be a triple of integers each , with if is odd, and let . If , then cannot admit a proper action by semi-simple isometries on any space. In particular, is not . Moreover,
-
(1)
If , is commensurable to the 3-dimensional integer Heisenberg group; in particular, it is virtually nilpotent and not semihyperbolic.
-
(2)
If , is commensurable to the “universal central extension” of a hyperbolic surface group, is a uniform lattice in , and is biautomatic.
In particular, is linear, and if an element of has finite order, it is conjugate to a power of one of the standard generators.
Not mentioned is the case ; this is because if this holds, then is finite (and is handled in [Gol23]). In other words, if and only if is infinite. The fact that finite dihedral Shephard groups are linear is shown in [Cox75]; hence, the above Theorem also implies all dihedral Shephard groups are linear.
Example.
The braid group on three strands is known to be (e.g., in [BM10]), but its quotient is not when (when , this quotient is finite).
The broadest class of Shephard groups to which Theorem A applies are described in the following.
Corollary.
Let be an extended presentation graph (possibly with infinite vertex labels) with an edge such that
-
(1)
the parabolic generated by embeds111Meaning is isomorphic to the subgroup of via the map induced by the inclusion on generators. in ,
-
(2)
the edge and vertex labels of are finite, and
-
(3)
is infinite
Then cannot admit a proper action on a space by semi-simple isometries. In particular, is not . Moreover, , then is not semihyperbolic.
To rephrase this corollary, an embedded infinite edge subgroup with all labels finite is a “poison subgroup” for being , or even semihyperbolic in some cases. It is a conjecture that given any extended presentation graph, its edge parabolics embed, so, conjecturally, (1) is unnecessary and infinite edge groups with finite labels are always poison subgroups. But, as a consequence of the upcoming Theorem B, the edge groups of a 2-dimensional presentation graph always embed, so we can say
Corollary.
Let be a 2-dimensional extended presentation graph with an edge such that , , , and . Then cannot admit a proper action by semi-simple isometries on a space, and in particular is not . Moreover, if , then is not semihyperbolic.
Example.
Suppose is an XXL-type presentation graph (meaning all edge labels are ); in particular is 2-dimensional. Then is [Hae22]. However there is some such that the quotient is not for all .
In light of these examples, Theorem A may seem perplexing. Perhaps it is less surprising when one considers that the condition requires non-positive curvature at all scales, and we are able to show that (most of) these groups possess other, less restrictive non-positive curvature properties.
Theorem B.
If is any 2-dimensional extended presentation graph, then its edge groups embed, and acts cocompactly on a piecewise Euclidean cell complex with cell stabilizers the conjugates of for spherical-type .
This complex is the Shephard group analogue of the Deligne complex for Artin groups and the Davis-Moussong complex for Coxeter groups. We give the full definition and proof of Theorem B in Section 5. This allows one to adapt techniques used for 2-dimensional Artin groups to show similar properties of 2-dimensional Shephard groups. As an example, the next Theorem is based on the analogous result for 2-dimensional Artin groups [Vas22].
Theorem C.
Suppose is an extended presentation graph satisfying
-
(1)
,
-
(2)
is 2-dimensional,
-
(3)
does not split as a direct product (i.e., it is irreducible), and
-
(4)
every connected component of has an edge such that is infinite.
Then is acylindrically hyperbolic.
Past adapting proofs from 2-dimensional Artin groups, the condition that the vertex labels of are finite allows us to show novel results, that were either unknown or untrue for Artin groups. Our primary example is:
Theorem D.
Suppose is a hyperbolic-type, 2-dimensional extended presentation graph, and let , the collection of spherical-type edges of which give rise to infinite Shephard groups. Then is a relatively hyperbolic group pair. In particular, if every edge group is finite, then is hyperbolic.
The fact that the stabilizers of the cell complex from Theorem B are precisely the edge (and vertex) subgroups indicate that in some sense, the poison subgroups are the only obstruction to being non-positively curved. The above theorem makes this idea more rigorous.
This Theorem is notable, because Artin groups are rarely hyperbolic relative to spherical-type subgroups; see [KS04] for a discussion on why this is. However, it was shown in [CC07] that Theorem D holds for Artin groups if relative hyperbolicity is replaced with “weak relative hyperbolicity” (which we will not define here). Upgrading this to relative hyperbolicity has the following noteworthy consequences:
Corollary E.
Suppose is a hyperbolic-type 2-dimensional extended presentation graph. Then
-
(1)
has solvable word problem,
-
(2)
satisfies the Tits alternative,
-
(3)
has finite asymptotic dimension, and
-
(4)
has the rapid decay property.
If, in addition, there is no edge of with , then is biautomatic.
If we restrict ourselves slightly further, it turns out we also have the following very desirable property for a large subclass of 2-dimensional Shephard groups.
Corollary F.
Suppose is an extended presentation graph with no 3-cycle (or is “triangle-free”) and no 4-cycle whose edges are each labeled . Then is residually finite.
These are precisely the 2-dimensional graphs such that is hyperbolic-type and “type FC” (the spherical-type subgraphs are exactly the complete subgraphs).
One of the more broadly appealing aspects of Shephard groups with finite vertex labels are their potential to be used to prove results for Artin groups. For example,
Theorem G.
Suppose is a triangle-free presentation graph with no 4-cycle with all edges labeled . Then is residually finite.
Residual finiteness is unknown for most Artin groups, and was previously unknown even for most 2-dimensional Artin groups. For a discussion on residual finiteness of Artin groups, including some past results see [Jan22].
1.1. Organization of paper
In Section 2 we recall the relationship between central extensions and cohomology in preparation for Theorem A. Then in Section 3 we complete the proof of this Theorem by detailing the geometry of the dihedral Shephard groups through the perspective of central extensions. In Section 4, we prove the main technical lemma which implies Theorem B, namely that the dihedral Shephard groups satisfy a “syllable length” condition similar to that enjoyed by dihedral Artin groups. Following this, we construct the complex from and complete the proof of Theorem B in Section 5. The consequences of this complex being are discussed in the remaining sections: Section 6 deals with acylindrical hyperbolicity, Section 7 deals with relative hyperbolicity and its consequences, and Section 8 deals with residual finiteness of the related Artin groups.
Acknowledgements
The author would like to thank Mike Davis, Jingyin Huang, and Piotr Przytycki for their valuable discussions and input. This work is partially supported by NSF grant DMS-2402105.
2. Central Extensions
We begin by recalling some background on central extensions of groups and how they relate to cohomology. Recall that if is abelian, an (-)central extension of a group is a group fitting into a short exact sequence
with the image of contained in the center of . If and are -central extensions of , then we say they are (-)equivalent if there is an isomorphism making the diagram
commute.
Notation 2.1.
For an arbitrary group , we will denote its identity element by . For an abelian group , we will denote its identity element by , and if it is cyclic, we will let denote a generator.
Let denote the set of equivalence classes of -central extensions of under -equivalence. It is well known that there is a natural abelian group structure on , under which (for example, see [Bro82, Thm. 3.12] or [DK18, §5.9.6]). There is a natural way to view the map . Fix a presentation and let be a such that the 2-skeleton is the presentation complex for the given presentation of . Let be the free abelian group on the -cells of . Then in particular, the generators of are and the generators of are . Let be the standard cellular boundary map, and define and , so that . We then dualize to obtain , defined by , , , and .
Now choose a class and a representative (or in other words, some morphism from the free abelian group on to ). Suppose is a presentation for . Let and , subsets of the free group on the disjoint union . We then define a group
| (2.1) |
It is straightforward to see that the map is a well-defined injective homomorphism from to . The construction of an inverse to this map is standard and unnecessary for our purposes, so we omit it, but it may be found in [DK18, §5.9.6]. We will call the Euler class of , and denote it by .
One standard result is
Proposition 2.2.
The underlying set of is in bijection with , but is isomorphic to as a group if and only if in .
We are interested in group-theoretic properties of central extensions induced by cohomological properties of their Euler classes. One first step in this direction is provided by this Lemma:
Lemma 2.3.
Suppose and are -central extensions of a group such that , where is not a zero divisor of the -module . Then is isomorphic to a subgroup of with index .
Proof.
Let and with representatives and , resp., chosen such that . We will write and , using the notation given above for the presentation of and .
Define a map by for and for . To check that this is a well-defined homomorphism we need to verify that for all . This is immediate for or , so we only need to verify this for ; that is, we must verify that for all . But this is also immediate since
| ( is a word in ) | ||||
| ( is a word in ) |
Thus this map is a well-defined homomorphism. Since is not a zero divisor, it is also injective. It is clear from the definition of that its image has index in . ∎
Now consider a group homomorphism . This induces in a standard way a morphism on cohomology and thus a map on central extensions via . In addition, can be lifted to a morphism . This gives the commutative diagram
As a consequence of the above diagram commuting, we have:
Lemma 2.4.
For all , . In particular, if has finite index in , then has finite index in .
Proof.
Denote the rightmost vertical morphism of the diagram by . Then . Since and is a surjective morphism, it follows that . ∎
It is a standard fact that if is injective, so is [DK18, Ex. 5.140.3], so in particular, if is a finite index subgroup of , then for any central extension of , there is a finite index subgroup which is a central extension of over the same central copy of .
We also know:
Proposition 2.5.
[Hat02, §3.G] If , then consists only of elements whose order divides .
In particular, is always injective on the free part of .
This leads us to:
Proposition 2.6.
Suppose is finitely generated and for some . If is an -central extension of such that has infinite order, then cannot act properly by semi-simple isometries on a space. In particular is not .
Proof.
We want to utilize [BH13, Thm. II.6.12], which states that if a finitely generated group acts by isometries on a space, and if contains a central copy of which acts faithfully by hyperbolic isometries (save for the identity), then this copy of is virtually a direct factor of .
To apply this to our situation, let be a finite index subgroup of containing the canonical copy of contained in . We claim that there is no subgroup of such that . In order for such a subgroup to exist, we must have . But then is a subgroup of , and since has finite index in , we know has finite index in . In particular, if denotes the inclusion morphism, then Proposition 2.5 tells us that is nontrivial in since has infinite order. Since this class is non-trivial, does not split as a direct product by Proposition 2.2.
By [BH13, Thm. II.6.12], we conclude that if acts by semi-simple isometries on a space , then the central copy of in cannot act faithfully by hyperbolic isometries. If the action is not faithful, then since the action cannot be proper. So assume the action is not by hyperbolic isometries, meaning contains some non-trivial elliptic isometry of (parabolic isometries are not semi-simple). Since , we know . Since is elliptic, then fixes a point of , and hence does not act properly.
The fact that cannot be follows from [BH13, Prop. II.6.10(2)]. (Recall that a group is if it acts properly and cocompactly by isometries on a space.) ∎
2.1. Central products
For some later results, it becomes useful to use a commutative version of the amalgamated product.
Definition 2.7.
Let , , and be any groups equipped with injective homomorphisms . Let . We define the amalgamated direct product or central product of and over by
Note that is a central subgroup of , so this construction always gives a well-defined group.
Take subgroups of and let and . Note that . By the isomorphism theorems,
This demonstrates as a natural subgroup of . By the standard proof of the isomorphism theorems, the map that realizes this inclusion is . In addition, one readily sees that if is finite index in (), then is finite index in .
As a special case, we can take and , in which case (or similarly, and ). It is clear that via the map , since is trivial. We then apply our previous remarks to this situation to obtain
Proposition 2.8.
For any groups and as above, the groups and embed into via the maps and , respectively.
Just as one has the notion of internal direct product, we may define an internal central product.
Proposition 2.9.
Suppose is any group with subgroups such that for all (). Let . Then is isomorphic to .
Proof.
First note that since the elements of and the elements of commute, for . Let () denote the inclusion map. Let be given by . Clearly is a surjective homomorphism. The kernel of is , or rewritten,
Thus
We need one final property of central products before we can continue.
Proposition 2.10.
Take and as above, and identify with the subgroup of as in Proposition 2.9. Then (and similarly, ).
This follows immediately from Proposition 2.9 and standard counting results ().
3. Dihedral Shephard groups
The goal of this section is to study the geometry of the infinite dihedral Shephard groups in detail. We display them as -central extensions of infinite triangle groups whose Euler class has infinite order, proving the first statement of Theorem A. Following this, we determine finer properties which we believe are interesting in their own right (and in particular complete the proof of Theorem A).
3.1. Dihedral Shephard groups as central extensions
We start by examining the second integral cohomology of the triangle groups. Let be a triple of positive integers, and define . We let , or when , , or , respectively. Define a triangle in with vertices , , and , and angles , , at , , and , respectively. The triangle group is the group generated by rotations of angle , , and about the vertices , , and , resp., of in . (We note that sometimes is called a von Dyck group and “triangle group” is sometimes used to refer to 3-generator Coxeter groups.) This group has the well-known presentations
where, by abusing notation, the generators , , and correspond to the respective aforementioned rotations about the vertices , , and of . We will use the second presentation to compute the cohomology. Since we’re interested in only the second integral cohomology, we describe a construction of the 3-skeleton of a .
First let be the presentation complex for ; that is, the cell complex with one 0-cell , two (oriented) 1-cells labeled and , and three 2-cells labeled , , and . The attaching map of the cell takes the boundary to the loop with positive orientation, and similarly and are attached to the loops and , respectively.
Let denote the universal cover of . Note that is the Cayley 2-complex of and the 1-skeleton of is the Cayley graph of . This Cayley graph is the 1-skeleton of the semiregular tiling of by -gons, -gons, and -gons (e.g., [MS16]). See Figure 1 for an example. The cell structure on is obtained from this tiling by gluing extra cells to the boundary of each -gon.

We now obtain the cell complex by filling the generators of as follows. Choose an -gon of , and label all cells attached to in (including ) by . The cells (with indices mod ) form a sphere in , so attach a 3-cell to this sphere. We will denote . Notice that is homeomorphic to a 3-sphere. We obtain from by replacing each -gon with the sphere . Notice that is the wedge of the spheres . In particular, .
There is a natural action of on coming from the action on by deck transformations. For an -gon of , The stabilizer of the set is conjugate to exactly one of , , or (depending on if , , or , respectively). The action of this stabilizer on is simply the standard action of on . This action is still free and properly discontinuous, so we may define the quotient space such that is the universal cover of . Note that (as defined before) is the 2-skeleton of .
Since is the universal cover of , we know . This means that and , where . Note that for any -gon of , the cell of maps to exactly one of the cells , , or if , , or , respectively. In particular, for all such , the 3-cell in maps to a single 3-cell of which we will denote , , and if , , or , resp. Topologically, if or , and . Moreover, the closure of is the -dimensional lens space of order with its standard cell structure for and is the -dimensional lens space of order with two points identified at .
To fix notation for the computation of the cohomology of , let denote the free abelian group on the -cells of and the standard cellular boundary map. We then let and so that . As usual, we dualize to obtain , given by , , , so that .
By a computation identical to that of the lens spaces (e.g., [Hat02, Ex. 2.43]), we see that is the zero map and
This allows one to easily compute that and (hence ) is infinite cyclic generated by
Lemma 3.1.
Define a map by
Then the class has infinite order.
Proof.
Let denote the quotient map and denote the restriction map .
The restriction is nontrivial, and , so gives a nontrivial element of . By the universal coefficient theorem, the free part of is isomorphic to via the map (where is some lift of along the quotient map ), so it follows that the image of in has infinite order. ∎
Lemma 3.2.
Let be as above. Then . In particular, has infinite cyclic center generated by .
Proof.
By the definition of , we see that it has presentation
Since commutes with and ,
so we just as well may write
But then notice that
so the relations are now redundant, and we may write
But now the generator is redundant, so we arrive at
Since and is centerless (because ), it follows that generates the center of . ∎
Next, we examine the Shephard groups for odd.
Lemma 3.3.
The subgroup of generated by and is index-2 and isomorphic to .
Proof.
First, we fix the presentations of these groups as
Let the generator of act on by interchanging and . Then the semidirect product of and under this action has the presentation
Since this is a semidirect product, the subgroup generated by and is isomorphic to . We claim this product is isomorphic to .
The relation makes redundant, so we may remove it. In addition, notice that
Similarly,
Thus the relation is equivalent to
which in turn is equivalent to
Therefore,
And with this presentation, is obviously redundant, so we see that
via the map and . ∎
Since viewed inside is generated by and , we have that the element is both in and , since . The image of under the quotient map is the subgroup of generated by and . This subgroup is finite index in (e.g., since is finite index in ). In particular,
Lemma 3.4.
is a -central extension of via the image of the class from to (which has infinite order).
Note that this restriction of has infinite order by Proposition 2.5.
As a brief aside, using this central extension structure, we can show
Corollary 3.5.
Suppose is infinite and has finite order. Then is conjugate to a power of one of the standard generators of .
Proof.
Let and denote the generators of order and , resp., of . The central quotient of acts properly and cocompactly on either or , where the generators and are sent to rotations and , resp., by an angle of and , resp. Since has finite order, it cannot be contained in the center of , and thus has non-trivial image in , still with finite order. Then by standard facts about isometries of and (and in particular, facts about the triangle groups), is conjugate (within ) to a power of either or . Without loss of generality, we may assume for some and (the argument for conjugates of powers of is identical). This means there is some lift of such that . In particular, there is some such that . If , then has infinite order, thus so does (since commutes with ), contradicting the assumption that has finite order. Thus and . ∎
We now prove the first part of Theorem A, namely
Theorem 3.6.
Let be a triple of integers each , with if is odd. If , then cannot admit a proper action by semi-simple isometries on any space. In particular, is not .
3.2. Further geometry of the extension
We can give insight into the geometry of the dihedral Shephard groups beyond the general fact of Proposition 2.6. Namely, we will discuss the remainder of Theorem A.
To encompass both types of dihedral Shephard groups dealt with above (depending on the parity of ), we fix notation for this section. First, we let or (in which case we say ). In the first case, we define , and in the second case, we define to be the subgroup of generated by and . To summarize the results of the previous section in this notation, is a -central extension of whose Euler class has infinite order, where acts geometrically on or if or , resp., as a finite index subgroup of a triangle group .
As a consequence of the latter point, contains a finite index torsion-free subgroup [Mil75, Thm. 2.7], and in particular must be a (closed) surface group. By Lemma 2.4, lifts to a finite index subgroup of . Since is a surface group, . Let denote a central extension of such that is a generator of . (Sometimes is called the “universal central extension” of , although this conflicts with the standard definition of universal central extension which applies only to perfect groups.) When , and , the 3-dimensional integer Heisenberg group. When , then is a hyperbolic surface group, and is a uniform lattice in . Since is a generator of the second cohomology, is a non-zero multiple of . By Lemma 2.3, this means is finite index in . Thus is commensurable to . As an immediate consequence, we have
Proposition 3.7.
For any triple of integers (with when is odd), the group is linear.
Proof.
When is finite, this was shown in [Cox75]. So, suppose is not finite, i.e., . It is an easy exercise to see that if is a finite index subgroup of , then is linear if and only if is linear. Thus if two groups and are commensurable, one is linear if and only if the other is. So it suffices to note that is always linear: if , then is the 3-dimensional integer Heisenberg group (well-known to be linear), and, if , then is linear by [dLH00, §IV.48] (via an explicit injection from to ). ∎
We will note here that the Shephard group analogue of the Tits representation used to show finite Shephard groups are linear in [Cox75] is not faithful for infinite dihedral Shephard groups. (A quick computation shows that the center of the image under this representation is always finite.) Finding an explicit representation for the Shephard groups is straightforward using the information given above, so we leave it as an exercise. The Shephard groups have an interesting explicit (but non-linear) representation as isometries of , which will discuss soon. First we examine the “Euclidean-like” case of .
Proposition 3.8.
Suppose . Then is virtually nilpotent and is not semihyperbolic.
Proof.
Virtual nilpotency of follows from the Q.I. rigidity of virtual nilpotency and the nilpotency of the 3-dimensional Heisenberg group. Moreover, the 3-dimensional Heisenberg group has cubic Dehn function, and thus so does . Since semihyperbolic groups have at-most quadratic Dehn function, it follows that cannot be semihyperbolic. ∎
This implies, for example, that if such a Shephard group embeds in an arbitrary Shephard group , then is not semihyperbolic.
The case is quite rich. For example, since the central quotient is word hyperbolic in this case, by [NR97], this immediately implies
Proposition 3.9.
If , then is biautomatic.
Past knowing that such a Shephard group is commensurable to a uniform lattice in , we can also explicitly demonstrate it as a group of isometries of . In some sense this is “more natural” than the linearity of Proposition 3.7, because it directly generalizes the method in which the presentation for the finite dihedral Shephard groups are derived in [Cox75, §9]. (The main technical difference is the fact that when , unlike in the finite case.)
Proposition 3.10.
If , then is a uniform lattice in .
Proof.
Since and each of , , and are finite, we know that , , and are uniform lattices in . Recall that is isometric to the unit tangent bundle of (under the Sasaki metric), which itself can be thought of as a -bundle over . This bundle is topologically trivial (since is contractible) but is well known to be metrically non-trivial. Let () denote the universal cover of . Then is a (metrically non-trivial) -bundle over . Note that (as defined above) is actually the preimage of under the covering map . Let denote the preimage of under this covering map. By [Mil75, Lem. 3.1] this group has the presentation
where each of , , and are lifts of the respective rotations , , and to . Moreover, the proof of said Lemma shows that generates the center of and the center of . Note that is also a uniform lattice in since is a uniform lattice in . In order to display the dihedral Shephard groups as subgroups of , we introduce another class of isometries.
For , define a map which acts on by preserving the -fiber structure over , such that projects down to the identity map of and rotates each fiber by . Since the bundle is topologically trivial, there is no issue with the existence and well-defined-ness of this map. Moreover, it is clear that this map is an isometry for any . We can also see that each commutes with the action of . The group of all is isomorphic to . Each can be lifted to a map of which translates along the -fibers a common distance . Note that this action commutes with the left action of . Since is an isometry of , it follows that is an isometry of . Let . As a straightforward exercise, one may verify that along with the left-multiplication maps of generate the entirety of . Since the elements of commute with the elements of (and vice versa), this means . But note that ; so, by Proposition 2.9, .
Now let . Define to be the subgroup of generated by , , , and . Since commutes with the left multiplication action of , this group has the presentation
Note that this is isomorphic to a central product . Since is a uniform lattice in and is a uniform lattice in , it follows easily that is a uniform lattice in . We claim that is isomorphic to a finite index subgroup of , hence is a uniform lattice in as well. Since is finite index in , the result follows for these groups as well.
Let , and consider the group
| (3.1) |
Since , we know . Then is an amalgamated direct product of and along the subgroup . By Proposition 2.8, the subgroup of generated by and is isomorphic to , and by Proposition 2.10, the index of this subgroup in is . We now show that
We start by adding a redundant generator to to obtain the presentation
Define by
then define by
We will show that and define surjective homomorphisms. Once this is shown, then clearly and are mutually inverse, and thus the proof of the Proposition is complete.
Starting with , we must show
and commutes with each of , , and . First, since and is in the center of , the latter relation holds. We verify
with an identical result for . Next,
Last,
In order to show is a surjective morphism, we must show
and commutes with and . Since , which is in the center of , this last relation is immediate. We begin by computing
with an identical computation for . Before proceeding, we need a lemma regarding the relations in :
Lemma.
The relations hold in .
Proof (of Lemma).
Since and is in the center of , we have
Solving each equation for gives . ∎
For notational convenience, let , , and . The above lemma implies that , and in particular commutes with the product . Moreover, we know has order , since . Now,
| () | ||||
Moreover, using () we compute
Last,
4. The syllable length condition
We now turn our attention to proving Theorem B. To do this, we follow the overarching idea used to show that the Deligne complex for a 2-dimensional Artin group is [CD95]. The first step in this process is to show that certain words have a minimal length. We make this precise now.
Definition 4.1.
Let be a finite set and the set of (finite) words in . If with (, ) is cyclically reduced, then we define the syllable length of with respect to to be .
Definition 4.2.
If is a group with finite generating set , and , then we denote by the image of under the map induced by the obvious map sending the word in to the element in .
The main result of this section is the following proposition, which, as mentioned before, is one of the key steps in showing the analogue of the Deligne complex for Shephard groups is also . It is based on a result of Appel and Schupp [AS83], but requires a minor extra hypothesis in order to account for the torsion in the generators.
Proposition 4.3.
Consider the dihedral Shephard group (with if is odd) on standard generating set and identity element . Suppose has a cyclically reduced expression , with (where and ). If , then .
We will first establish notation and some brief lemmas.
Definition 4.4.
Let be a triple of integers all with if is odd. Let . If is even, let , , and , and if is odd, let denote the subgroup of generated by and . Define a simplicial graph whose vertices are the cosets of and in , with an edge between two vertices if the cosets have non-trivial intersection.
Sometimes is called a “(rank 2) coset geometry”. It is the quotient of the complex by the center of (see Proposition 5.2).
Lemma 4.5.
For any triple (with and if is odd), the complex is (the 1-skeleton of) a tiling of either or by -gons.
Proof.
The case when is even is proven in [MS16], so assume is odd and . Note that the result holds for (since is even and ) and is a finite index subgroup of (by definition). In particular, is a subdivision of ; the added vertices come from adding cosets of , which correspond to midpoints of edges of . In particular, since consists of -gons and is the first barycentric subdivision of , it follows that is a tiling by -gons. ∎

(a)

(b)
The graph can be thought of as “collapsing” the polygons in the Cayley graph of corresponding to the conjugates of the subgroups and . For example, the Cayley graph and coset geometry of (coming from ) are shown in Figure 2. They are overlaid in Figure 3 to demonstrate how the triangles induced by the orbit of and can be shrunken to their respective cosets (where these cosets are given by solid and empty vertices, respectively).

We may now prove the main Proposition of this section. The argument is based on one given in [Cri05, Lemma 39].
Proof (of Prop. 4.3).
Let denote the edge of coming from the intersection of the cosets and in . The word gives rise to a path in which is the concatenation of the edges given by Since is not a multiple of , every pair of consecutive edges in this list are distinct. In addition, notice that . So, is a locally embedded closed loop, and in particular, the edge length of is precisely the syllable length of . Without loss of generality, we may assume that this loop is embedded; otherwise, we may repeat the argument on embedded subloops. In addition, we may assume without loss of generality that by replacing with its remainder after division by ; clearly this gives the same word in and same path in . In particular, this assumption does not change the syllable length.
Let be the image of under the covering map induced by the central quotient. This is still a closed loop in , but now may no longer be embedded. However, can find a subpath of which is an embedded closed loop. After reparameterization, we write as the concatenation , with an embedded closed loop in and not necessarily embedded, possibly trivial. Let be the lift of to contained in and let be the (possibly trivial) path in such that . Then and represent subwords of of the form and for some . In particular, .
Since is a non-trivial embedded loop in , it must enclose at least one -gon, implying . We claim that is non-empty, or in other words, that . Since is closed, it suffices to show that is not a closed loop. If we show this, then, since will be a (nontrivial) closed path in , we can apply the argument given for and to and a simple subpath of to show that , and thus , as claimed.
Showing that is not closed is equivalent to showing . If is even, let and if is odd, let (so either or is finite index in ). Let be the (3-skeleton of a) space defined in Section 3, with universal cover , and let be the Cayley graph of . Note that is a covering of (with the Cayley graph of ). The word gives rise to a path in in the standard way, hence also a path in via the covering map , and a path under the covering map . The path induces a cycle (see Section 3 for notation). Since represents the trivial word in , . This means , so we may choose an element such that , say for some . Since is simple and we have assumed , we know that is a simple loop, it must enclose at least one cell of which maps to , and it must traverse the boundaries of each such cell with a consistent (positive) orientation. This means that , so . Therefore cannot be trivial in if is even. If is odd this shows that is not trivial in , but since lifts to and lies in this subgroup by assumption, the result also holds for odd. ∎
Example 4.6.
We will give an illustrative example with the complexes and . (We use these over the Cayley graphs since the figures are much clearer, but a similar conceptualization works for the Cayley graphs.)
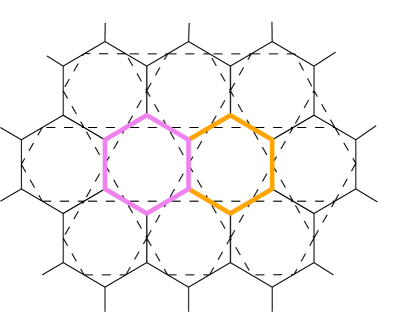
(a)

(b)
Consider the two hexagons in highlighted in Figure 4(a). Figure 5(a) shows lifts of these hexagons to the complex for the Shephard group . (The dashed lines show which vertices are identified under the covering map; they are not part of .)

(a)

(b)
The entire preimage of a hexagon under the covering map is a vertical column which resembles the universal cover of the circle with the cell structure coming from the hexagon. Consider the path encircling these two hexagons in , shown in red in Figure 4(b). Its lift to is shown in Figure 5(b). The endpoints of this path are “distance 2” along the fiber of the base vertex. This corresponds to the fact that the path encloses exactly two hexagons. One may compare this to the usual description of the Cayley graph of the 3-dimensional integer Heisenberg group , the main difference being that the vertical dashed lines would be actual edges of the Cayley graph of . This also illustrates how the center of acts on its complex , since it acts by deck transformations; it is a uniform “vertical translation” along the dashed lines in Figure 5 (the fibers of the map to ).
5. A cell complex for 2-dimensional Shephard groups
In this section, we recall the definition of for an arbitrary extended presentation graph , which largely follows [Gol23, §3]. We then show that this complex is when is 2-dimensional.
Definition 5.1.
Let be an extended presentation graph. We define , where denotes the derived complex of and is its geometric realization. We will denote an -simplex of by
for a chain with each . We note that the vertices are indexed by elements of ; we will let denote the vertex of coming from . Define a complex of groups over by declaring the local group at to be and the edge maps to be the natural maps coming from the inclusion of generators.
Next, define to be a simplex whose vertices are labeled by the generators of . For , let denote the face of spanned by the elements of . We define a complex of groups by declaring the local group at the face to be the group , where is the full subgraph of generated by the vertices . The edge maps are the standard maps induced by the inclusion of generating sets.
Note that is a simple complex of groups. Hence by [BH13, Def. II.12.12], the fundamental group of is the direct limit over the edge maps; when is 2-dimensional, this direct limit is clearly . In general, neither complex of groups is a priori developable. If is developable, we will denote its development . If is developable, we will denote its development . For dihedral Shephard groups, it turns out that has a straightforward description.
Proposition 5.2.
If is the graph which is a single edge between vertices and with all labels finite, then is developable, and can be described as follows: the vertex set of are the cosets of and in , and there is an edge between two vertices if the corresponding cosets intersect nontrivially. In particular, the center acts freely on .
Proof.
The fact that is developable follows from the characterizations of given in Section 3. Namely, in each case the cyclic groups and embed as the vertex groups. The statement regarding the vertices and edges of is identical to Coxeter groups and Artin groups; e.g., [CD95, Proof of Lemma 4.3.2]. The center acts freely because the stabilizers of vertices and edges are finite (they are conjugates of or in the first case, and are trivial in the second), while the center has infinite order. ∎
When is developable, it too has a straightforward description.
Proposition 5.3.
Let , ordered by inclusion. If is developable, then . In particular, the -simplices of correspond to -chains of cosets, and the action of is just the left multiplication action. We will denote the simplex arising from such a chain by
The stabilizer of this simplex is .
With this description, for developable it is clear that embeds in as the subcomplex consisting of simplices of the form . This allows one to easily see that is a fundamental domain for the action of on . In particular, we may view the vertices as being in as well as .
In order to show is developable (under certain conditions), we show that it is “nonpositively curved” in the following sense.
Lemma 5.4.
[BH13, Thm. II.12.28] If is a (simple) complex of groups over a simply connected domain and the local development at each vertex is locally , then is developable and has locally development.
It is clear that is simply connected, since is a cone point. We will describe the local development shortly. We begin with putting a metric on the fundamental domain .
Definition 5.5.
For , let
Notice that is combinatorially a cube whose faces are where . So itself has a cubical structure with faces for . This Proposition is a straightforward exercise:
Proposition 5.6.
With the cubical cell structure above, is isomorphic to the cone on the first barycentric subdivision of with cone point . The isomorphism is induced by the map sending to the barycenter of .
Thus we may identify and . With this connection we can define an explicit metric on .
Definition 5.7.
We give the cell of the metric of a Coxeter block. Briefly, this is (the closure of) a connected component of the Coxeter zonotope associated to the finite Coxeter group minus its reflection hyperplanes. (See [CD95, §4.4], where this metric is defined in detail for the Davis-Moussong complex and Deligne complex.) In this metric, if , then is a spherical simplex where the length of the edge between the vertices corresponding to and is .
Since is a (strict) fundamental domain, we can use the action of to metrize all of . We will call this the Moussong metric on .
Now we recall the local development, focusing on the case of . Let be a vertex of , with . The upper star of in is the (full) subcomplex of spanned by the vertices with . The lower link of in is the development of the subcomplex of groups of , where denotes the subcomplex spanned by vertices with . Both of these objects are simplicial complexes which inherit the metric placed on . The local development at is the spherical join
Its metric naturally comes from the metric on . The link of in the local development is
where is the upper link, meaning the (full) subcomplex of spanned by the vertices with . We may also sometimes refer to this complex as .
Note that is isomorphic to and is isomorphic to . We use the previous proposition to identify with . With this identification, the complex of groups is isomorphic to as defined above, and thus is isomorphic to . It is straightforward to check that the metrics placed on above agree with the claimed metrics on . In other words, there is an isometry
where the join is the usual spherical join. There are two special cases to note. When , then is empty, so . When is maximal in , is a single point , so is empty and .
Showing the local development is nonpositively curved amounts to showing that these components of the links are . Since a spherical join is if and only if both components are [BH13, Cor. II.3.15], this reduces to showing that and are when . With this in mind, we can now complete the proof of Theorem B. It will follow immediately by the next theorem and general facts about simple complexes of groups.
Theorem 5.8.
Suppose is a 2-dimensional extended presentation graph. Then is developable and its development is .
Proof.
As in the Artin group and Coxeter group case, is whenever (see discussion before and after Lemma 4.4.1 in [CD95]), so it remains to show that is for . Since is 2-dimensional, the only elements of are , singletons, and edges. In the first two cases, is either empty or finite, resp., so we may assume we are in the third case. Note that if is finite (i.e., has labels ), then this complex was shown to be in [Gol23, Lemma 6.1], so we may assume this group is infinite.
By [BH13, Lem. II.5.6], it suffices to show that has no closed loops of length . Since the length of an edge of is , we must show that the edge length of any closed loop in is at least . Let be an embedded closed loop in , say for edges of . Note that the edge path length is . For , let be the vertex at which the edges and meet (with indices taken cyclically). Let be the generator of such that for some . We can write for some . Since is embedded, is not a multiple of (the order of ). Stringing together these equalities gives a word in . Since , the syllable length of this word is . By Proposition 4.3, we must have . The result now follows from Lemma 5.4. ∎
When the local groups of a nonpositively curved complex of groups are all finite, this determines all finite subgroups of the fundamental group (namely, they are the conjugates of the local groups). While we can’t exactly say that here, we can determine all elements of finite order.
Corollary 5.9.
Suppose is a 2-dimensional extended presentation graph. If has finite order, then it is conjugate to a power of one of the standard generators of .
Proof.
Suppose has finite order. By [BH13, Cor. II.2.8(1)], the fixed point set is a non-empty convex subset of . Since is 2-dimensional, the simplices of are at most dimension 2, and these top-dimensional simplices are of the form
for an edge of and a vertex of . But the stabilizer of any point in the interior of such a cell is , which is the trivial group. In particular, must be a tree in the 1-skeleton of and avoid vertices of type . If contains a vertex or an edge , then and so is conjugate to a power of . So suppose neither of these cases occur. This implies for an edge of with vertices and , and . By translating, we may assume , so . Corollary 3.5 then implies is conjugate to a power of or . ∎
6. Acylindrical hyperbolicity
In [Vas22], it is shown that (irreducible) 2-dimensional Artin groups of rank at least 3 are acylindrically hyperbolic. By modifying the proof appropriately, we obtain an analogous result for 2-dimensional Shephard groups as an application of Theorem B:
See C
This follows from
Proposition 6.1.
[Vas22, Theorem D] Let be a simplicial complex, together with an action by simplicial isomorphisms of a group . Assume that there exists a vertex of with stabilizer such that:
-
(1)
The orbits of on the link are unbounded, for the associated angular metric.
-
(2)
is weakly malnormal in , i.e., there exists an element such that is finite.
Then is either virtually cyclic or acylindrically hyperbolic.
Thus the extra assumption (4) of Theorem C is necessary to guarantee condition (1) of Proposition 6.1 is satisfied; otherwise, all links would be finite graphs.
Lemma 6.2.
Let be a presentation graph satisfying the hypotheses of Theorem C, and let be any edge of for which is infinite. Then the orbits of on are unbounded.
Proof.
Since is 2-dimensional, we know that (see Section 5). Suppose has terminal vertices and , with labels , , and . Since is infinite, we know that , and is a non-trivial -central extension of a finite index subgroup of a triangle group in either or (see Section 3). As discussed in Section 3, the quotient of by the center of is the 1-skeleton of a semiregular tiling of or , and this quotient is a covering map. In particular, the group of deck transformations (which act hyperbolically) of this cover is the central copy of in ; thus the orbits of this copy of are unbounded. ∎
In order to show that the Shephard groups in question satisfy (2) of Proposition 6.1, we will detail the portions of the argument which must be modified, and refer the reader to [Vas22, §5] for the full original argument.
Definition 6.3.
Let be an extended presentation graph. For vertices of , let denote the presentation graph with the same vertex and edge sets and labels as , but with the addition of an edge labeled if there is no edge between and in . (If there is already an edge between and , we leave unchanged.) We then define the domain and metric as in [Vas22, Def. 5.3]. Our complex of groups over is defined similarly as well, but we place the free product as the edge group corresponding to if this edge was added; we make no changes if there were no changes made to . This is in contrast to the Artin group case, where the rank-2 free group is placed on this edge. We denote the development of this complex of groups by .
With this modification, the following key lemmas still hold, with completely identical proofs after appropriate replacements are made with the definition(s) above.
Lemma 6.4.
Lemma 6.5.
[Vas22, Lemma 5.7] Let be a 2-dimensional Shephard group with , such that is connected and not right-angled (i.e., has some edge not labeled ). Then there exists an edge of between vertices and with coefficient and an element such that .
Now we may complete the proof of Theorem C.
Proof (of Theorem C).
We may assume is connected, otherwise splits as a free product, and each free summand is an infinite group by (4); such groups are always acylindrically hyperbolic. We may assume as well that is not right-angled; in this case, is a graph product of non-trivial (cyclic) groups, which by [MO15, Cor. 2.13] implies is either virtually cyclic or acylindrically hyperbolic. Taking to be the edge guaranteed by (4), we know is infinite, not virtually cyclic, and embeds in , so under our assumptions is not virtually cyclic (hence acylindrically hyperbolic). The proof of [Vas22, Prop. 5.2] and Lemma 6.5 imply that we may choose the edge in Lemma 6.5 to be the edge guaranteed by (4). We note that this edge has label , since otherwise would be a direct product of finite groups and hence finite. So Lemmas 6.2 and 6.5 imply satisfy the hypotheses of Proposition 6.1, and hence is acylindrically hyperbolic. ∎
7. Relative hyperbolicity and residual finiteness
Recall the following characterization of relative hyperbolicity, due to Bowditch [Bow12]. This phrasing comes from [Osi06, Def. 6.2].
Proposition 7.1.
Let be a group and a collection of infinite finitely generated subgroups (we will call a group pair and the elements of the peripheral subgroups). Then is relatively hyperbolic if and only if admits an action on a hyperbolic graph such that each of the following hold.
-
(1)
All edge stabilizers are finite.
-
(2)
All vertex stabilizers are either finite or conjugate to one of the subgroups of .
-
(3)
The number of orbits of edges is finite.
-
(4)
The graph is fine.
There are a number of equivalent definitions of a fine graph, but the one that shall be useful for us is:
Definition 7.2.
[Bow12, Def 2.1.(F5)] Let be a graph and let denote the metric on which assigns all edges length . (By convention, for any graph with such a metric, if and are in different connected components of , we say .) Fix a vertex and let denote the largest full subgraph of which avoids . Let be the set of vertices of which are adjacent to . Let denote the induced length metric on coming from , and let denote the restriction of the metric to (not the induced length metric). We say that is fine if the metric space is locally finite222Every finite-radius ball is a finite set. for every .
In order to show that (certain) Shephard groups are relatively hyperbolic, we will use the action of on its complex . Specifically, we will let denote the 1-skeleton of endowed with the edge-path metric (each edge is given length ). When is Gromov hyperbolic, so too is its 1-skeleton as a metric graph under the induced length metric. But this metric graph is quasi-isometric to , and hence is also hyperbolic. So, our first task is to determine when is hyperbolic.
Lemma 7.3.
Let be a 2-dimensional extended presentation graph. If is word hyperbolic, then is Gromov hyperbolic.
Proof.
By Theorem 5.8, is . So by the Flat Plane Theorem, is Gromov hyperbolic if and only if it contains no isometrically embedded copy of . Suppose such an embedded plane exists (so is not hyperbolic). This plane must be a subcomplex of , and in particular must pass through a vertex of the form for some . This gives rise to an embedded loop of length exactly in the link of . The link of such a vertex is isometric to (see discussion after Definition 5.7). As in the Artin group case, such a link contains a circuit of length exactly if and only if is not hyperbolic [Cri05, Proof of Lemma 5]. In summary, if is hyperbolic, then has no embedded flat plane, and thus is Gromov hyperbolic. ∎
We would like to say that this is an “if and only if” statement, as in the Artin group setting [CC07], but are unsure how to proceed. For the Artin groups, this relies on the existence of an embedding of the Davis complex in the Deligne complex, which is not yet known to exist for arbitrary Shephard groups. However, if such an embedding exists, then the reverse implication is immediate.
Proposition 7.4.
Suppose is a 2-dimensional extended presentation graph such that the Davis complex for the Coxeter group embeds isometrically in the complex . Then if is Gromov hyperbolic, must be word hyperbolic.
Proof.
Suppose is not hyperbolic. Then is not hyperbolic (since is quasiisometric to ), so it contains an embedded flat plane. Since embeds isometrically in , we have that also contains an embedded flat plane, so is not hyperbolic. ∎
The existence or non-existence of such an embedding is outside our current scope of consideration. (Although it is natural to conjecture that there is always such an embedding, since it exists for Artin groups and can be constructed case-by-case for finite Shephard groups.)
Now we show that is fine. First recall the following notation. If is a cell complex and , the open star is the union of all open cells containing , the closed star is the (topological) closure of the open star, and the boundary of the closed star is .
Lemma 7.5.
Suppose is 2-dimensional. Let be a vertex of (equivalently, of ) of the form for and an edge of . Let denote the induced length metric on . Then there is a and such that for all .
Proof.
Let denote the inclusion map which realizes the quasi-isometry of with the edge length metric and with the Moussong metric. The restriction of to is a quasi-isometry onto , under the respective induced length metrics and . We choose our and to be the constants from this restricted quasi-isometry, i.e., those constants which satisfy
for all . Recall that is the restriction of to , so if we restrict ourselves to elements of , then we can say
Fix . Let be a geodesic in from to . Then
Let be the closest point projection onto the closed star (the map which sends a point to a point which minimizes ). Note that is a convex set: it is made up of Euclidean right triangles which have one of their acute angles meeting at the common vertex . Thus is a well-defined, distance non-increasing retraction [BH13, Prop. II.2.4(4)], and in particular restricts to a well-defined distance non-increasing retraction . So is a (rectifiable) path in between and , implying
We can now complete the proof of Theorem D.
See D
Proof.
When is hyperbolic, then is hyperbolic by Lemma 7.3. In particular, is a hyperbolic graph since it is quasi-isometric to the 1-skeleton of . By Proposition 5.3, the edge stabilizers of acting on are either finite cyclic (coming from the subgroups generated by the vertices) or trivial. Similarly, the vertex stabilizers are the conjugates of for . And since this is a cocompact action with a strict fundamental domain, there are finitely many orbits of edges. Once we show that is fine, the result will follow by Proposition 7.1.
Since the action of on has a strict fundamental domain, we may restrict our consideration to vertices of the form for (using notation from Section 5). Since is 2-dimensional, there are three types of vertices to consider: , a single vertex, or a single edge. If , then, as a set, is simply the vertex set of , which is finite. Similarly, if , then is the vertex set of the join of and , which are both finite, and hence is finite.
Suppose is an edge between vertices and of . Since is a piecewise Euclidean simplicial complex with finitely many isometry types of faces, is isometric to a sufficiently small sphere centered at , and this sphere is a radial deformation retract of . This graph isomorphism is actually a quasi-isometry. We also know that with the Moussong metric is quasi-isometric to with the metric which assigns all edges length . In particular, there are and such that for all (or ).
Now, let and be the constants guaranteed by Lemma 7.5. Fix a vertex of (or ). For , define
Let . Then
, so . Hence for all . We know that is a locally finite graph: the vertices of coming from cosets of have valence and the vertices coming from cosets of have valence , both of which we have assumed to be finite. This implies is finite for every , and hence so is . Therefore is locally finite and is fine. ∎
This result is in stark contrast to the Artin group case, where it is very uncommon for Artin groups to be relatively hyperbolic rather than just weakly relatively hyperbolic. We can leverage this not only to show many nice properties of Shephard groups, but also of many Artin groups as well. In the following section, we will discuss an application to Artin groups, but first we will detail some easy consequences of relatively hyperbolicity for Shephard groups.
See E
Proof.
Each property in the list holds for all of if and only if it holds for the peripheral subgroups. In more detail:
-
(1)
The dihedral Shephard groups are linear, hence have solvable word problem. This implies has solvable word problem by [Far98].
-
(2)
If is a relatively hyperbolic pair, then it was shown in [Tuk94] that any subgroup of which does not contain a free group is either finite, virtually infinite cyclic, or is contained in an element of . Since the peripheral subgroups of are linear, they satisfy the Tits alternative, so we can conclude does as well.
-
(3)
By [BD08], asymptotic dimension of finitely generated groups is preserved by commensurability. Since the 3-dimensional integral Heisenberg group and the universal central extensions of surface groups have finite asymptotic dimension, so too do the peripheral subgroups of . By [Osi05], this implies has finite asymptotic dimension.
-
(4)
If is an edge of with , then has polynomial growth since it is commensurable to the 3-dimensional integral Heisenberg group; groups of polynomial growth have the rapid decay property by [Jol90]. If is an edge of with , then is a -central extension of a hyperbolic group; such groups have the rapid decay property by [Nos92]. This implies has the rapid decay property by [DS05].
A more substantial corollary is residual finiteness for certain 2-dimensional Shephard groups and their Artin groups. To discuss residual finiteness, we begin by recalling the notion of a relatively geometric action recently introduced by Einstein and Groves.
Definition 7.6.
[EG22, Def 1.1] Suppose is a group pair. An action of on a cell complex is relatively geometric (with respect to if
-
(1)
is compact,
-
(2)
Each group in acts elliptically on , and
-
(3)
Each stabilizer of a cell in is either finite, or conjugate to a finite index subgroup of an element of .
It is clear from Proposition 5.3 that if is a 2-dimensional Shephard group and is as defined previously, then the action of on its complex is relatively geometric with respect to . We want to make use of:
Proposition 7.7.
[EG22, Cor 1.7] Suppose is relatively hyperbolic and acts relatively geometrically (with respect to ) on a cube complex . If every is residually finite, then is residually finite.
We have a characterization of when is relatively hyperbolic; if we can determine when is a cube complex, we will determine a class of residually finite Shephard groups.
Lemma 7.8.
If is 2-dimensional and type FC, then is a cube complex under the “cubical metric”.
Proof.
The cubical metric on the complex is defined as follows: rather than metrize the cell to be a Coxeter block as in Definition 5.7, we simply give it the metric of a standard Euclidean cube (since this cell is combinatorially a cube). Under this metric, the link of a vertex is still isometric to the spherical join of and , where the metric on these complexes now assigns edge lengths of .
In order to show that is a cube complex, we must show that the links are flag complexes. Since the spherical join of flag complexes is flag, this is equivalent to showing and are flag for all . This is well known for since is type FC [CD95, Lemma 4.3.4]. If or a single vertex , then is either empty or a finite set, resp., so there is nothing to check. So, suppose is an edge between vertices and . Since is a graph (i.e., a 1-dimensional simplicial complex), it suffices to show that it contains no 3-cycles. But by Theorem 5.8, the girth of this graph is . ∎
Thus we may conclude,
See F
We note that the condition that is 2-dimensional and type FC is equivalent to requiring has no 3-cycles (sometimes called “triangle-free”). For a triangle-free presentation graph, having no 4-cycles with all edges labeled is equivalent to being hyperbolic (originally due to Moussong in [Mou88], rephrased in terms of the presentation graph in [Cri05, Lemma 5] or [CC07, Prop. 3.1]).
Proof.
Since is hyperbolic, is hyperbolic relative to its infinite spherical-type edge subgroups (Theorem D). Since is 2-dimensional and type FC, is a cube complex under the cubical metric (Lemma 7.8) and the action is relatively geometric with respect to the spherical-type edge subgroups. Since the dihedral Shephard groups are residually finite (Proposition 3.7), we conclude that is residually finite (Proposition 7.7). ∎
In tandem with Corollary 5.9, we can show
Corollary 7.9.
If is triangle-free and has no 4-cycle with all labels , then is virtually torsion-free.
Proof.
Let be a standard generator of . Since is residually finite, there is a finite index subgroup which avoids (meaning ), and by taking finitely many intersections, we can choose to avoid all nontrivial powers of . Let , a finite index subgroup of avoiding all nontrivial powers of standard generators. Let . It is a standard exercise to show that (the “normal core” of ) is finite index when is finite index. Suppose has finite order. By Corollary 5.9, we can write for some , some , and some . The definition of implies , so . Since the only power of a generators contained in is , we must have that , and consequently . Thus is torsion-free. ∎
8. Application to Artin groups
We now establish the analogue of Corollary F for Artin groups. First, we recall the definition of the Deligne complex of an Artin group to establish the notation and terminology which we will use, as it may differ from some references.
Definition 8.1.
Let be any presentation graph and ordered by inclusion. The Deligne complex of is , the geometric realization of the derived complex . An -simplex of is written as
where is a chain of elements of . For , the spherical Deligne complex is the simplicial complex whose vertices are all cosets of for , with a set of vertices spanning an -simplex if and only if they have nontrivial (global) intersection333By , we mean the largest full subgraph of which does not contain ..
acts on with a strict fundamental domain isomorphic to . Thus we may endow the fundamental domain of with the “same” metric as (the Moussong metric). For the vertex of , the link is isometric to the spherical join
One of the key properties which will allow us to pass between an Artin group and its Shephard quotients is product separability. The following is one of the many equivalent notions of product separability.
Definition 8.2.
Let be any group. We say that is product separable if for any (finite) collection of finitely generated subgroups of , their product is closed in the profinite topology on .
Recall that the profinite topology on is the topology whose basis of closed sets are the finite-index subgroups of . So it is equivalent to say that is an intersection of finite-index subgroups of .
Lemma 8.3.
Let be any group and a finite-index subgroup. Then is product separable if and only if is product separable.
Proof.
Suppose is product separable. Let be a collection of finitely generated subgroups of . The inclusion map is continuous for any subgroup; the intersection of with a finite index subgroup of is finite index in regardless of the index of in . In particular, is closed in and is contained in , so is closed in .
Now suppose is product separable. By replacing with the normal core of , we may assume is normal in . (When is finite index, so is its normal core, and product separability is inherited by subgroups.) Now let be a collection of finitely generated subgroups of , and let for each . Each is finitely generated since the are, and is finite index in for each . So, for each , let be a system of representatives of the left cosets of in . For , let . Then
We claim that each is closed in . For convenience, fix and let . Then we can rewrite as
Since is normal in ,
is the product of finitely generated subgroups of , thus closed in . Since is finite index in , it is closed in as well. The profinite topology is invariant under multiplication (from the left or right), so is also closed in . Thus is the union of finitely many closed subsets of , so is itself closed. ∎
Corollary 8.4.
Dihedral Artin groups are product separable.
Proof.
Suppose is a dihedral Artin group with edge label . If , then , and product separability in this case is an easy exercise (following directly from the fact that abelian groups are subgroup separable, i.e., every f.g. subgroup is closed). If , then is virtually , where is a rank- free group [HJP16, Lemma 4.3]. By [You97], is product separable for any , so by Lemma 8.3, so is .
By [RZ93, Thm. 2.1], the rank-2 free group is also product separable; this is the dihedral Artin group whose graph is two vertices not joined by an edge. ∎
Lemma 8.5.
If is any group and is closed in the profinite topology on , then for all , there exists a finite group and a surjective morphism such that .
Proof.
Since is closed in the profinite topology, it is the intersection of the finite-index subgroups of containing it. At least one of these subgroups, say , must avoid . Let denote the normal core of , a finite-index normal subgroup of contained in . Let denote the standard quotient map . Then since , implying . ∎
The following lemma is the main ingredient in the proof of residual finiteness for these Artin groups.
Lemma 8.6.
Suppose is a single edge with label . Let be any two points. Then there is some such that for all , the images of and under the quotient map remain at the same distance.
Proof.
Suppose and are the vertices of , let and , and let be the edge between and in . First, suppose and are vertices. By symmetry and translating, we may assume . Let be a geodesic edge path connecting and . Notice that and both contain ; this means there is some such that (we could have if ). Similarly, and both contain the vertex , so there is some such that . Since is a geodesic, it is locally embedded, so . Repeating this, for all , we see , where
for some . (A syllable is a word of the form or .)
Let . Notice that
since otherwise we could reverse the above argument to construct a path from to with strictly shorter length than . Since is product separable (Corollary 8.4), is closed in the profinite topology on , so we can find a finite group and surjective morphism so that (Lemma 8.5). Let and be the orders of and , respectively, and let . Fix , and let denote the standard quotient map. The orders of and divide the orders of and , resp., or in other words, . Since is the normal closure of and in , it follows that . This means there exists a surjection which makes the diagram
commute. This implies in particular that ; otherwise .
By abuse of notation, let denote the map induced by the quotient . We claim that is still a geodesic between and . Let be a geodesic from to in , say . By the same reasoning in , for each we can find so that , where
and when . Let .
Notice and meet at . Since is bipartite, we know and have the same parity. If they are odd, let and , and if they are even, let and . In either case, is a coset of , so there is some such that . Writing out , we see
Since ( cosets), we know , i.e., . But since and are the same parity, . Thus is a geodesic and .
Now suppose and are any two points of . If is a vertex, let , and if is not a vertex, let and be the two distinct vertices of the edge containing . Similarly, if is a vertex, let , and if is not a vertex, let and be the two distinct vertices of the edge containing . For , let be a geodesic from to . For each , by our work above we can find so that remains a geodesic of the same length under the quotient to for each . Let and fix . Let be the quotient map. Then each is a geodesic in of the same length as . Suppose is a geodesic from to in . Then there is some and some so that passes through and . Note that since is a simplicial map, and . Then
Since the quotient clearly cannot increase distance, . ∎
Lemma 8.7.
Suppose is a 2-dimensional presentation graph. Let be a geodesic segment of . Then there is some so that the image of under the natural quotient remains a geodesic segment of the same length.
Proof.
For , let denote the usual quotient map induced by the quotient . Let be a point in the interior of .
If is in the interior of a 2-simplex of , then is locally geodesic at for any value of , since maps 2-simplices isometrically to 2-simplices. In this case, define .
If there is a neighborhood of in which is contained in an edge, then there is nothing to show since edges are mapped isometrically to edges (in other words, is locally geodesic at for any value of ). In this case, as above, define .
Suppose is a point contained in the interior of an edge of with no neighborhood of in also contained in this edge. First, suppose for a vertex of or for an edge of . Then the stabilizer of is trivial, and in particular, the link of is mapped isomorphically to the link of for any . So suppose for a vertex of and an edge of containing . Let and denote the distinct 2-simplices containing whose interiors nontrivially intersect . The stabilizer of is conjugate to and acts transitively on the link of , so there is some and some such that . (Since is a geodesic, .) For , and are the 2-simplices of containing (and ) whose interiors intersect . Moreover, . If , then , but this happens if and only if . Since , this can’t happen, so and is locally geodesic at for all .
Last, suppose is a vertex of . Then for some and some . There are three subcases to consider.
First, assume . Then for any , , and induces an isometry of the link of and the link of (both being isometric to ).
Next, assume for a vertex of . The link of is the join of and , the latter of which is in bijection with . The intersection of the -sphere of with induces two points of distance apart. Every point of is distance from every point of (by the definition of spherical join), so either or . If , then as in the previous case acts isometrically on for any , so and remain at the same distance under . If , then they can be represented by some powers of , say and with . (Since is a geodesic, these points are distinct.) By translating we may assume these points are in fact () and for . Choosing , acts by the standard quotient and thus these points remain distinct. In other words, for , is locally geodesic at .
Finally, suppose is an edge with finite label . Then, as before, the intersection of with the -sphere of induces two points of distance . Lemma 8.6 implies that there is some so that the distance between and remains in the quotient via for all which are (positive) multiples of . In other words, for all such , is locally geodesic at .
Let be a common multiple of . (This set is finite and consists of positive integers, so exists.) Our above arguments show that is locally geodesic at for all , or in other words, that is a local geodesic in . Since is , this implies is a geodesic and has the same length as . ∎
Now we may complete the proof of
See G
Proof.
Let . Let be the geodesic in from to . By Lemma 8.7, there is some so that the image of under the quotient map to is a geodesic. If denotes the image of under the quotient , then is a geodesic from to . Since is , this means . But is residually finite (Corollary F), so there is a further quotient to a finite group under which remains nontrivial. Composing these maps gives a quotient to a finite group where the image of is nontrivial. ∎
References
- [AS83] Kenneth I Appel and Paul E Schupp. Artin groups and infinite Coxeter groups. Inventiones mathematicae, 72(2):201–220, 1983.
- [BD08] Greg Bell and Alexander Dranishnikov. Asymptotic dimension. Topology and its Applications, 155(12):1265–1296, 2008.
- [BH13] Martin R Bridson and André Haefliger. Metric spaces of non-positive curvature, volume 319. Springer Science & Business Media, 2013.
- [BM10] Tom Brady and Jon McCammond. Braids, posets and orthoschemes. Algebraic & Geometric Topology, 10(4):2277–2314, 2010.
- [Bow12] Brian H Bowditch. Relatively hyperbolic groups. International Journal of Algebra and Computation, 22(03):1250016, 2012.
- [Bro82] Kenneth S Brown. Cohomology of Groups. Springer Science & Business Media, 1982.
- [CC07] Ruth Charney and John Crisp. Relative hyperbolicity and Artin groups. Geometriae Dedicata, 129:1–13, 2007.
- [CD95] Ruth Charney and Michael W Davis. The -problem for hyperplane complements associated to infinite reflection groups. Journal of the American Mathematical Society, 8(3):597–627, 1995.
- [Cox75] H.S.M. Coxeter. Regular Complex Polytopes. Cambridge University Press, 1975.
- [Cri05] John Crisp. Automorphisms and abstract commensurators of 2–dimensional Artin groups. Geometry & Topology, 9(3):1381–1441, 2005.
- [DK18] Cornelia Druţu and Michael Kapovich. Geometric group theory, volume 63. American Mathematical Soc., 2018.
- [dLH00] Pierre de La Harpe. Topics in geometric group theory. University of Chicago Press, 2000.
- [DS05] Cornelia Druţu and Mark Sapir. Relatively hyperbolic groups with rapid decay property. International Mathematics Research Notices, 2005(19):1181–1194, 2005.
- [EG22] Eduard Einstein and Daniel Groves. Relatively geometric actions on cube complexes. Journal of the London Mathematical Society, 105(1):691–708, 2022.
- [Far98] Benson Farb. Relatively hyperbolic groups. Geometric and functional analysis, 8(5):810–840, 1998.
- [Gol23] Katherine Goldman. CAT(0) and cubulated Shephard groups. arXiv preprint arXiv:2310.10883, 2023.
- [Hae22] Thomas Haettel. XXL type Artin groups are CAT(0) and acylindrically hyperbolic. In Annales de l’Institut Fourier, volume 72, pages 2541–2555, 2022.
- [Hat02] Allen Hatcher. Algebraic Topology. Cambridge University Press, 2002.
- [HJP16] Jingyin Huang, Kasia Jankiewicz, and Piotr Przytycki. Cocompactly cubulated 2-dimensional Artin groups. Commentarii Mathematici Helvetici, 91(3):519–542, 2016.
- [Jan22] Kasia Jankiewicz. Residual finiteness of certain 2-dimensional Artin groups. Advances in Mathematics, 405:108487, 2022.
- [Jol90] Paul Jolissaint. Rapidly decreasing functions in reduced -algebras of groups. Transactions of the American Mathematical Society, 317(1):167–196, 1990.
-
[Kal]
Generated with KaleidoTile by Jeff Weeks:
https://www.geometrygames.org/KaleidoTile/index.html.en. - [KS04] Ilya Kapovich and Paul Schupp. Relative hyperbolicity and Artin groups. Geometriae Dedicata, 107:153–167, 2004.
- [Mil75] John Milnor. On the 3-dimensional Brieskorn manifolds . Knots, groups and 3-Manifolds, 3:175–225, 1975.
- [MO15] Ashot Minasyan and Denis Osin. Acylindrical hyperbolicity of groups acting on trees. Mathematische Annalen, 362(3):1055–1105, 2015.
- [Mou88] Gabor Moussong. Hyperbolic Coxeter groups. PhD thesis, The Ohio State University, 1988.
- [MS16] Giovanni Moreno and Monika Ewa Stypa. On the vertex-to-edge duality between the Cayley graph and the coset geometry of von Dyck groups. Mathematica Slovaca, 66(3):527–538, 2016.
- [Nos92] Gennady Andreevich Noskov. Algebras of rapidly decreasing functions on groups and cocycles of polynomial growth. Sibirskii Matematicheskii Zhurnal, 33(4):97–103, 1992.
- [NR97] Walter D Neumann and Lawrence Reeves. Central extensions of word hyperbolic groups. Annals of mathematics, 145(1):183–192, 1997.
- [Osi05] Denis Osin. Asymptotic dimension of relatively hyperbolic groups. International Mathematics Research Notices, 2005(35):2143–2161, 2005.
- [Osi06] Denis Osin. Relatively Hyperbolic Groups: Intrinsic Geometry, Algebraic Properties, and Algorithmic Problems, volume 843. American Mathematical Soc., 2006.
- [Reb01] Donovan Yves Rebbechi. Algorithmic properties of relatively hyperbolic groups. PhD thesis, 2001.
- [RZ93] Luis Ribes and Pavel A Zalesskii. On the profinite topology on a free group. Bulletin of the London Mathematical Society, 25(1):37–43, 1993.
- [She52] G. C. Shephard. Regular complex polytopes. Proceedings of the London Mathematical Society, s3-2(1):82–97, 1952.
- [Tuk94] Pekka Tukia. Convergence groups and Gromov’s metric hyperbolic spaces. New Zealand J. Math., 23(2):157, 1994.
- [Vas22] Nicolas Vaskou. Acylindrical hyperbolicity for Artin groups of dimension 2. Geometriae Dedicata, 216(1):7, 2022.
- [You97] Shihong You. The product separability of the generalized free product of cyclic groups. Journal of the London Mathematical Society, 56(1):91–103, 1997.