1st Place Solution to the 8th HANDS Workshop Challenge - ARCTIC Track: 3DGS-based Bimanual Category-agnostic Interaction Reconstruction

Jeongwan On Kyeonghwan Gwak Gunyoung Kang Hyein Hwang
Soohyun Hwang Junuk Cha Jaewook Han Seungryul Baek
UNIST

Abstract

This report describes our 1st place solution to the 8th HANDS workshop challenge (ARCTIC [6] track) in conjunction with ECCV 2024. In this challenge, we address the task of bimanual category-agnostic hand-object interaction reconstruction, which aims to generate 3D reconstructions of both hands and the object from a monocular video, without relying on predefined templates. This task is particularly challenging due to the significant occlusion and dynamic contact between the hands and the object during bimanual manipulation. We worked to resolve these issues by introducing a mask loss and a 3D contact loss, respectively. Moreover, we applied 3D Gaussian Splatting (3DGS) to this task. As a result, our method achieved a value of 38.69 in the main metric, CD_h, on the ARCTIC test set.

1 Introduction

Most hand-object interaction reconstruction methods [6, 7, 4, 5, 1, 3, 9] rely on predefined templates for hand and object. While template-based approaches effectively leverage prior knowledge to reconstruct high-dimensional information from limited input, they come with notable limitations. First, these methods are typically restricted to specific object categories, making them difficult to apply in real-world, in-the-wild scenarios where the diversity of objects is vast. Second, they struggle with capturing fine-grained details, resulting in less accurate reconstructions of complicated hand-object interactions.

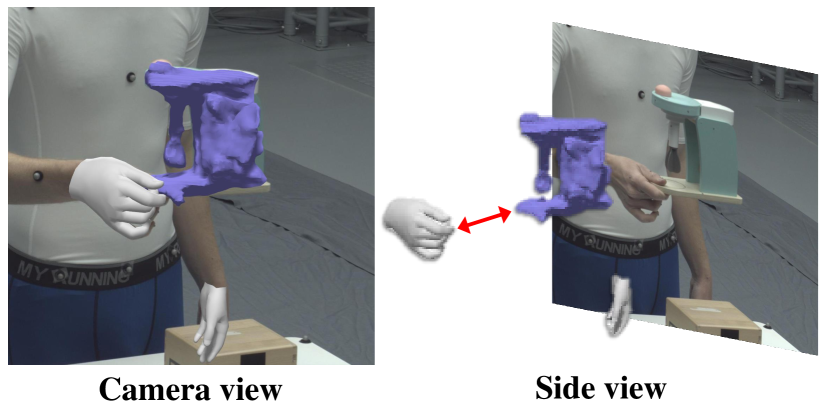
Refer to caption — Figure 1: Limitation of the HOLD baseline. From the original camera viewpoint, HOLD performs well on 2D contact reconstruction. However, it performs poorly in 3D contact reconstruction when seen from different camera viewpoints. As a result, it fails to accurately estimate the relative distance between the hand and the object, which worsens the main metric, CD_h.

To address these challenges, HOLD [8] introduced a category-agnostic approach to hand-object interaction reconstruction, offering a promising solution to overcome the constraints of template-based methods. However, HOLD is also limited to interactions involving a single hand and primarily addressed scenarios where the hand and the object were almost always in contact. As a result, the two-hand manipulation settings of HOLD showed a significant error with a CD_h [8], the hand-relative Chamfer distance of 114.73, contrast to its excellent performance in single-hand settings, where it achieved a CD_h of 11.3 on the HO3D dataset. Figure 1 shows the poor 3D contact reconstruction quality of the fully trained HOLD baseline.

In this work, we push the boundaries of existing methods to address the challenging problem of category-agnostic reconstruction of hands and objects in bimanual settings. This task involves significant occlusion and dynamic contact between the hands and the object, making it particularly difficult to solve. To tackle these issues, we introduce a mask loss and a 3D contact loss to specifically manage occlusion and contact dynamics, respectively. Additionally, we incorporate 3D Gaussian Splatting (3DGS) [10], a technique that has shown great success across multiple domains, to further improve the reconstruction performance.

2 Method

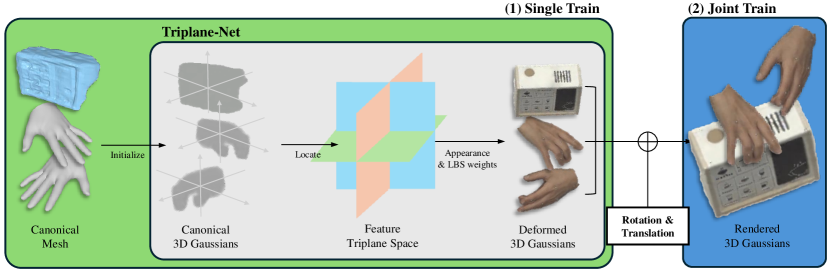
In this section, we introduce our method, which is illustrated in Fig. 2. Our method can split into two stages: (1) single train and (2) joint train. Stage (1) is again divided into two stages that fit (1-1) Hand Gaussian Splats and (1-2) Object Gaussian Splats, respectively. Based on [11], we use Triplane-Net as the baseline of our framework. We introduce more details in the following subsection.

2.1 Triplane-Net

According to [11], we first extract canonical 3D meshes via off-the-shelf model [8], and Triplane-Net takes it as the input. Then, the extracted 3D meshes initialize 3D Gaussians and Triplane-Net locates it to the feature triplane space. Afterwards, Triplane-Net estimates the deformation, appearance, and geometry of 3D Gaussians (e.g., their LBS weight, color, rotation, and scale), and deforms Gaussians as $\tilde{G}=\mathcal{T}(G)$ where $\mathcal{T}(\cdot)$ is Triplane-Net, $G$ is extracted canonical 3D mesh, and $\tilde{G}$ is deformed 3D canonical mesh.

2.2 Single Train

Hand Gaussian Splats. Given an input video with the length of $T$ , we first extract a hand pose parameter in the $t$ -th frame for left and right hand ( $x\in\{l,\;r\}$ denotes the type of hand) that includes global orientation $\Phi_{x}^{t}\in\mathbb{R}^{3}$ , translation $\Gamma_{x}^{t}\in\mathbb{R}^{3}$ , pose parameter $\theta_{x}^{t}\in\mathbb{R}^{45}$ , and shape parameter $\beta_{x}^{t}\in\mathbb{R}^{10}$ , over all frames using the off-the-shelf model [8]. Then canonical 3D hand mesh $G_{x}$ is obtained through the following process:

G^{t}_{x}=\mathcal{M}(\theta_{x}^{t},\beta_{x}^{t}),

(1)

where $\mathcal{M}$ is MANO Layer [15, 2]. Subsequently, the deformed Gaussians $\tilde{G}_{x}$ are obtained by $\mathcal{T}(G_{x})$ , and they are located in the camera space using the formula as follows:

{}^{c}\tilde{G}^{t}_{x}=\tilde{G}^{t}_{x}\times\Phi^{t}_{x}+\Gamma^{t}_{x},

(2)

where ${}^{c}\tilde{G}_{x}$ is deformed camera-coordinated Gaussians for each hand.

Object Gaussian Splats. Similar to Hand Gaussian Splats, we also estimate the object parameter for the $t$ -th frame, including canonical 3D object mesh $G^{t}_{o}$ and their rotations $\Phi^{t}_{o}$ , and translations $\Gamma^{t}_{o}$ using the off-the-shelf model [8]. Then, the estimated mesh is fed into the Triplane-Net, and located in the camera space using the formula as follows:

{}^{c}\tilde{G}^{t}_{o}=\tilde{G}^{t}_{o}\times\Phi^{t}_{o}+\Gamma^{t}_{o}.

(3)

Optimization. We optimize the center translation of each Gaussian $\mu$ , parameters of Triplane-Net $w$ , and the parameter $P_{x}=\{\Phi_{x},\Gamma_{x},\theta_{x},\beta_{x}\}$ , where $x\in\{l,r,o\}$ and $\theta_{o}=\beta_{o}=\varnothing$ . we define the loss $\mathcal{L}_{basic}$ by combining SSIM, VGG and LBS losses of [11] as follows:

\mathcal{L}_{basic}=\sum_{x\in\{l,r,o\}}\lambda_{1}\mathcal{L}^{x}_{ssim}+\lambda_{2}\mathcal{L}^{x}_{vgg}+\lambda_{3}\mathcal{L}^{x}_{LBS},

(4)

where $\lambda_{1}=0.2,\lambda_{2}=1.0,\lambda_{3}=1000$ . Additionally, to prevent outlier Gaussians, we employ the mask loss $\mathcal{L}_{mask}$ . Specifically, we first obtain the masks of hands and an object via [14]. Then, we enforce that Gaussians are generated inside the mask, by using the formula as follows:

\displaystyle\mathcal{L}_{mask}=\sum_{t=1}^{T}{\lambda_{4}\|{m}^{t}_{x}\odot(\mathbb{I}^{t}_{pred}-\mathbb{I}^{t}_{gt})\|^{2}_{2}+\lambda_{5}(1-{\bar{m}}^{t})\odot\mathbb{I}^{t}_{pred}}

(5)

where $x\in\{l,r,o\}$ denotes left, right hands or an object, and $\odot$ denotes the element (pixel)-wise product. $m_{x}^{t}$ is obtained mask at the $t$ -th frame, and $\mathbb{I}_{gt}^{t}$ and $\mathbb{I}_{pred}^{t}$ are ground-truth and rendered $t$ -th frame, respectively. $\bar{m}^{t}=\sum_{x}{m_{x}}^{t}$ is the merged foreground mask for two hands and an object.

We also use additional regularization term following [12], to improve the rendering quality:

\mathcal{L}_{render}=\sum_{x\in\{l,r,o\}}\lambda_{6}\mathcal{L}^{x}_{color}+\lambda_{7}\mathcal{L}^{x}_{scale},

(6)

where $\lambda_{6}=0.1,\lambda_{7}=100.0$ . Finally, we find the $\mu$ , $w$ and $P_{x}^{t}$ for all frame $t\in[1,T]$ and for left, right hands and an object that minimizes the objective defined as follows:

\underset{\begin{smallmatrix}\\ \mu,w,\\ \{\{P^{t}_{x}\}^{T}_{t=1}\}_{x\in\{l,r,o\}}\end{smallmatrix}}{\min}\mathcal{L}_{basic}+\mathcal{L}_{mask}+\mathcal{L}_{render}.

(7)

We optimize Eq. 7 for 45K iteration with 1 number of NVIDIA A6000 GPU. We use gradually decreasing learning late from $1.6\times 10^{-4}$ to $1.6\times 10^{-6}$ for $\mu$ , and use $1.0\times 10^{-4}$ for other parameters.

2.3 Joint Train

Hand & Object Gaussian Splats. Most existing methods [8, 13] for bimanual category-agnostic hand-object interaction reconstruction tasks do not consider contact between hand and object in 3D space or only consider it for very limited cases. For that reason, we propose a simple contact regularization term $\mathcal{L}_{contact}$ to encourage hand-object Gaussians to be well-contacted during the optimization. Towards the goal, we additionally optimize the hand translation $\Gamma_{x}$ , where $x\in\{l,r\}$ by employing the 3D contact regularization term $\mathcal{L}_{contact}$ to tightly contact hand and object meshes in the 3D space:

\mathcal{L}_{contact}=\lambda_{8}\sum^{T}_{t=1}\sum_{x\in\{l,r\}}{||\Gamma^{t}_{o}-\Gamma^{t}_{x}||_{2}}.

(8)

To prevent hand Gaussians too much follow the object translation, we set the $\lambda_{8}$ as a small number 1.0.

Finally, we find the $\Gamma_{x}^{t}$ for $t\in[1,T]$ and $x\in\{l,r\}$ by minimizing the objective, which is defined as follows:

\underset{\{\{\Gamma^{t}_{x}\}^{T}_{t=1}\}_{x\in\{l,r\}}}{\min}\mathcal{L}_{basic}+\mathcal{L}_{mask}+\mathcal{L}_{contact}.

(9)

3 Experiments

Setup. We used 9 objects from the ARCTIC [6] dataset as the training dataset, with subject 3 and camera index 1. In particular, we used the action of grabbing objects and selected the 300 frames in which the hand and the object were most clearly visible. We use CD_h [8] as the main metric. To further evaluate the object reconstruction, we also used CD and the F10 metric of [8].

Results. Table 1 shows the quantitative results comparing our method with other methods submitted to the challenge server. Additionally, Fig. 3 shows the qualitative results of our method compared with the HOLD baseline.

	CD ${}_{h}\;[cm^{2}]\downarrow$	CD $\;[cm^{2}]\downarrow$	F10 $\;[\%]\uparrow$
HOLD [8]	114.73	2.07	63.92
ACE [16]	100.33	2.03	69.4
Ours	38.69	1.36	81.78

Table 1: Quantitative results. Our method achieved the best object reconstruction performance.

Ablation study. Figure 4 shows our ablation examples. when 3D contact loss is not applied, contact between the hand and the object in 3D space is become unnatural (1st row). We also observed that the reconstructed mesh breaks due to self-occlusion when mask loss is not used (2nd row).

4 Conclusion

In this document, we involved our method for reconstructing hand and object meshes using 3D Gaussian splats. Our method ranked as the 1st in the 8th HANDS Workshop Challenge held with ECCV’24 – ARCTIC track.

References

Armagan et al. [2020] Anil Armagan, Guillermo Garcia-Hernando, Seungryul Baek, Shreyas Hampali, Mahdi Rad, Zhaohui Zhang, Shipeng Xie, Neo Chen, Boshen Zhang, Fu Xiong, Yang Xiao, Zhiguo Cao, Junsong Yuan, Pengfei Ren, Weiting Huang, haifeng sun, Marek Hrúz, Jakub Kanis, Zdeněk Krňoul, Qingfu Wan, Shile Li, Dongheui Lee, Linlin Yang, Angela Yao, Yun-Hui Liu, Adrian Spurr, Pavlo Molchanov, Umar Iqbal, Philippe Weinzaepfel, Romain Brégier, Grégory Rogez, Vincent Lepetit, and Tae-Kyun Kim. Measuring generalisation to unseen viewpoints, articulations, shapes and objects for 3D hand pose estimation under hand-object interaction. In ECCV, 2020.
Baek et al. [2019] Seungryul Baek, Kwang In Kim, and Tae-Kyun Kim. Pushing the envelope for rgb-based dense 3d hand pose estimation via neural rendering. In CVPR, 2019.
Baek et al. [2020] Seungryul Baek, Kwang In Kim, and Tae-Kyun Kim. Weakly-supervised domain adaptation via gan and mesh model for estimating 3d hand poses interacting objects. In CVPR, 2020.
Cha et al. [2024] Junuk Cha, Jihyeon Kim, Jae Shin Yoon, and Seungryul Baek. Text2hoi: Text-guided 3d motion generation for hand-object interaction. In CVPR, 2024.
Cho et al. [2023] Hoseong Cho, Chanwoo Kim, Jihyeon Kim, Seongyeong Lee, Elkhan Ismayilzada, and Seungryul Baek. Transformer-based unified recognition of two hands manipulating objects. In CVPR, 2023.
Fan et al. [2023] Zicong Fan, Omid Taheri, Dimitrios Tzionas, Muhammed Kocabas, Manuel Kaufmann, Michael J. Black, and Otmar Hilliges. ARCTIC: A dataset for dexterous bimanual hand-object manipulation. In CVPR, 2023.
Fan et al. [2024a] Zicong Fan, Takehiko Ohkawa, Linlin Yang, Nie Lin, Zhishan Zhou, Shihao Zhou, Jiajun Liang, Zhong Gao, Xuanyang Zhang, Xue Zhang, Fei Li, Zheng Liu, Feng Lu, Karim Abou Zeid, Bastian Leibe, Jeongwan On, Seungryul Baek, Aditya Prakash11, Saurabh Gupta, Kun He, Yoichi Sato, Otmar Hilliges, Hyung Jin Chang, and Angela Yao. Benchmarks and challenges in pose estimation for egocentric hand interactions with objects. In ECCV, 2024a.
Fan et al. [2024b] Zicong Fan, Maria Parelli, Maria Eleni Kadoglou, Muhammed Kocabas, Xu Chen, Michael J Black, and Otmar Hilliges. HOLD: Category-agnostic 3d reconstruction of interacting hands and objects from video. In CVPR, 2024b.
Garcia-Hernando et al. [2018] Guillermo Garcia-Hernando, Shanxin Yuan, Seungryul Baek, and Tae-Kyun Kim. First-person hand action benchmark with rgb-d videos and 3d hand pose annotations. In CVPR, 2018.
Kerbl et al. [2023] Bernhard Kerbl, Georgios Kopanas, Thomas Leimkühler, and George Drettakis. 3d gaussian splatting for real-time radiance field rendering. ACM ToG, 2023.
Kocabas et al. [2024] Muhammed Kocabas, Rick Chang, James Gabriel, Oncel Tuzel, and Anurag Ranjan. Hugs: Human gaussian splats. In CVPR, 2024.
Moon et al. [2024] Gyeongsik Moon, Takaaki Shiratori, and Shunsuke Saito. Expressive whole-body 3D gaussian avatar. In ECCV, 2024.
Pokhariya et al. [2024] Chandradeep Pokhariya, Ishaan Nikhil Shah, Angela Xing, Zekun Li, Kefan Chen, Avinash Sharma, and Srinath Sridhar. Manus: Markerless grasp capture using articulated 3d gaussians. In CVPR, 2024.
Ravi et al. [2024] Nikhila Ravi, Valentin Gabeur, Yuan-Ting Hu, Ronghang Hu, Chaitanya Ryali, Tengyu Ma, Haitham Khedr, Roman Rädle, Chloe Rolland, Laura Gustafson, Eric Mintun, Junting Pan, Kalyan Vasudev Alwala, Nicolas Carion, Chao-Yuan Wu, Ross Girshick, Piotr Dollár, and Christoph Feichtenhofer. Sam 2: Segment anything in images and videos. ArXiv Preprint:2408.00714, 2024.
Romero et al. [2017] Javier Romero, Dimitrios Tzionas, and Michael J. Black. Embodied hands: Modeling and capturing hands and bodies together. ACM ToG, 2017.
Xu et al. [2024] Congsheng Xu, Yitian Liu, Yi Cui, and Yichao Yan. Ace, 2024.