${\cal N}=1$ conformal duals of gauged $E_{n}$ MN models

Strongly coupled supersymmetric conformal field theories (SCFTs) can be engineered in a variety of ways. In particular they can be obtained as descriptions of an infra-red (IR) fixed points of renormalization group (RG) flows starting from a small relevant deformation of a weakly-coupled SCFT. The canonical examples in $4d$ are the flows starting with ${\cal N}=1$ SQCD in the conformal window. Strongly coupled SCFTs can be also engineered starting from a weakly coupled SCFT with a conformal manifold and tuning the couplings to be large. Canonical examples here include the ${\cal N}=4$ SYM and a variety of ${\cal N}=2$ conformal gauge theories. Moreover, a weakly coupled SCFT can have strongly-coupled loci, cusps, on the conformal manifold which can be alternatively described by weak gauging of a global symmetry of some strongly-coupled SCFT. A paradigmatic example of this is given by the ${\cal N}=2$ Argyres-Seiberg duality Argyres:2007ws . In fact the discovery of these dualities triggered, starting with Gaiotto:2009we , an avalanche of new understandings of the dynamics of strongly-coupled ${\cal N}=2$ SCFTs.

Conformal manifolds with minimal supersymmetry, ${\cal N}=1$ as opposed to ${\cal N}\geq 2$, in four dimensions have been much less studied. However, the existence of interesting conformal field theories with a manifold of exactly marginal couplings was established quite some time ago Leigh:1995ep (see e.g. Sohnius:1981sn ; Howe:1983wj ; Parkes:1984dh for earlier works), and the technology to identify such models is rather straightforward Green:2010da (see also Kol:2002zt ). One of the interesting features accompanying conformal manifolds with extended supersymmetry is that different regions of it might be describable by different looking weakly coupled, or partially weakly coupled, models as already mentioned above. In fact in Razamat:2019vfd numerous such dualities even for ${\cal N}=1$ cases were suggested. The algorithm to search for such dual pairs used in Razamat:2019vfd is rather simple¹¹1This algorithm can be thought of as ${\cal N}=1$ generalization of the search for ${\cal N}=2$ dualities explored by Argyres and Wittig Argyres:2007tq .. Assuming the dual descriptions of a given model is conformal, that is no RG flow is involved, significantly restricts the space of possibilities. In particular, if one seeks for a conformal gauge theory description, the two conformal anomalies, $a$ and $c$, completely fix the dimension of the gauge group and the dimension of the representation of the matter fields. This leaves only a finite set of possibilities to go over in the search for a dual description, which surprisingly often actually results in finding such a putative dual.

For the algorithm above to be applicable the model at hand should possess an ${\cal N}=1$ preserving conformal manifold. However, many interesting SCFTs do not have such manifolds. Maybe some of the most well known examples are the ${\cal N}=2$ Minahan-Nemeschansky (MN) $E_{n}$ SCFTs Minahan:1996fg ; Minahan:1996cj ²²2In recent years however some of these models have been constructed starting with weakly coupled gauge theories using RG flows Gadde:2010te ; Gadde:2015xta ; Agarwal:2018ejn ; Zafrir:2019hps .. However, one can use such SCFTs as components of larger models with a conformal manifold. A way to do so is to couple the conserved currents of a subgroup of the global symmetry to dynamical vector fields and add sufficient amount of matter so that the gauging, as well as any needed superpotential interactions, will be exactly marginal. One can do so for example for $E_{n}$ MN models preserving the ${\cal N}=2$ supersymmetry Argyres:2007ws ; Argyres:2007tq . Once a conformal manifold appears, alongside comes the possibility that somewhere on it a dual weakly coupled description emerges. This was indeed the case for ${\cal N}=2$ gaugings of MN models discussed in Argyres:2007ws ; Argyres:2007tq .

In the current note we will start from $E_{6,7,8}$ MN model and construct theories with conformal manifolds by gauging subgroups of the global symmetry, as in Argyres:2007ws ; Argyres:2007tq , but now preserving only ${\cal N}=1$ supersymmetry. We will argue that after such a gauging somewhere on the conformal manifold a dual ${\cal N}=1$ conformal gauge theory description emerges. For the $E_{6}$ case we will find a dual description as an $SU(2)^{5}$ quiver gauge theory while in the $E_{7,8}$ cases the dual will be a gauge theory with a simple gauge group³³3For other interesting dualities between ${\cal N}=1$ gauge theories and constructions involving more general class ${\cal S}$ models Gaiotto:2009we see for example Gadde:2013fma .. In each case we will test the dualities by studying properties which are invariants of the conformal manifold, like anomalies and superconformal indices. We suspect that there should be a powerful geometric interpretation (constructing the models starting from $6d$ SCFTs on Riemann surfaces, e.g. for some examples see Gaiotto:2009we ; Benini:2009mz ; Bah:2012dg ; Gaiotto:2015usa ; Razamat:2016dpl ; Kim:2017toz ; Razamat:2018gro ; Pasquetti:2019hxf ; Razamat:2019ukg , or utilizing other string theory constructions) of the results presented here, as well as the ones reported in Razamat:2019vfd . We leave this aspect for future investigations.

Let us consider the Minahan-Nemeschansky $E_{6}$ SCFT Minahan:1996fg . We consider the branching of representations of the $E_{6}$ symmetry to representations of its $U(1)_{a}\times SO(10)$ maximal subgroup such that ${\bf 27}\to{\bf 1}_{-4}\oplus{\bf 10}_{2}\oplus{\bf 16}_{-1}$, and further decompose $SO(10)$ to $USp(4)_{g}\times USp(4)$ such that

Then we gauge the $USp(4)_{g}$ symmetry with the addition of six fundamentals, $q_{L}$, and three two index traceless antisymmetrics, $\phi_{A}$. Note that the imbedding indices of $SO(10)$ in $E_{6}$ and of $USp(4)_{g}$ in $SO(10)$ are $1$, meaning that the $\text{Tr}\,R\,USp(4)_{g}^{2}$ anomaly is equal to $-1$, which is the same as the contribution of six free fundamental chiral fields of $USp(4)_{g}$. In particular adding the fields above the one loop beta function will vanish. The global symmetry of the theory contains the $USp(4)\times U(1)_{a}\times U(1)_{t}$ symmetry coming from the $E_{6}$ SCFT. The $U(1)_{t}$ comes from the enlarged R-symmetry of the ${\cal N}=2$ superconformal algebra. Our assignment of charges is such that the moment map operators have $U(1)_{t}$ charge $+1$ while a dimension $d$ Coulomb branch operator has $U(1)_{t}$ charge $-d$. For the $U(1)_{t}$ not to be anomalous we assign charges $+\frac{1}{2}$ to $q_{L}$ and $-1$ to $\phi_{A}$. We also have $SU(3)\times SU(6)\times U(1)_{b}$ coming from the extra fields we add. Under $U(1)_{b}$, the fields $q_{L}$ have charge $+1$ and $\phi_{A}$ charge $-1$.

The $E_{6}$ SCFT has conformal anomalies,

These are the anomalies which can be obtained from $5$ free vectors and $37$ free chiral fields using,

where $\text{dim}\,{\mathfrak{G}}$ is the number of free vectors (dimension of the gauge group) and $\text{dim}\,{\mathfrak{R}}$ is the number of free chiral superfields (dimension of the representation of the matter fields). We add to the model $10$ gauge fields of $USp(4)_{g}$ and additional six fundamentals and three two index traceless antisymmetric fields number of which is $39$. The conformal anomalies of the theory are thus, $a=\frac{211}{48}$ and $c=\frac{121}{24}$. If we are after a conformal dual of this model it has to have,

Having $\text{dim}\,{\mathfrak{G}}=15$ and assuming the dual is a conformal Lagrangian theory, we have only two candidate gauge groups, $SU(4)$ and $SU(2)^{5}$. In fact we find a dual with the latter option. We suggest that the theory has a dual description in terms of an $SU(2)^{5}$ conformal quiver gauge theory depicted in Figure 1. This model has $11$ bi-fundamental fields between various $SU(2)$ gauge groups and $16$ fundamentals of a single gauge group. This matter content amounts to $16\times 2+11\times 4=76$ free chiral fields, guaranteeing that the conformal anomalies match. Each $SU(2)$ gauge group has six flavors ensuring the one loop gauge beta functions vanish, and we soon verify that indeed both models have non-trivial conformal manifold. We will match the indices of the theories in expansions of fugacities. In particular, it will imply equality of the number of relevant and marginal operators.

The $E_{6}$ Minahan-Nemeschansky SCFT has moment map operators in the adjoint of $E_{6}$ which decompose into $USp(4)_{g}\times USp(4)\times U(1)_{a}$ as,

There are many marginal operators one can build and on a generic point of the conformal manifold all the symmetry is broken. Let us denote the operators in $({\bf 4},{\bf 4})_{\pm 3}$ as $M^{\pm}_{ij}$ and operators in $({\bf 5},{\bf 5})_{0}$ as $M_{ab}$. Then the marginal operators are,

The operator $\Phi_{3}$ is the dimension three Coulomb branch operator of the $E_{6}$ SCFT and $({\bf X},{\bf Y},{\bf Z})_{q_{a},q_{t},q_{b}}$ denote representations under $(USp(4),SU(6),SU(3))_{U(1)_{a},U(1)_{t},U(1)_{b}}$. To compute the dimension of the conformal manifold we need to analyze the Kähler quotient $\{\lambda_{I}\}/G_{{\mathbb{C}}}$ Green:2010da (see also Leigh:1995ep ; Kol:2002zt ), where $\lambda_{I}$ are the marginal couplings and $G_{\mathbb{C}}$ is the complexified global symmetry group. In our case the couplings $\lambda_{I}$ are the ones for the operators in (6) and $G_{\mathbb{C}}$ is $USp(4)\times SU(6)\times SU(3)\times U(1)_{a}\times U(1)_{t}\times U(1)_{b}$. The Kähler quotient is not empty. For example $M\phi$ times $q^{2}\phi$ is not charged under any $U(1)$s and contains a component in $({\bf 5},{\bf 15},{\bf 6})$. Taking it to symmetric sixth power we get singlet of all the symmetries. This deformation breaks the $U(1)_{b}$ symmetry. Also the $M\phi$ coupling breaks the $USp(4)\sim SO(5)$ symmetry⁴⁴4We will not be careful with the global structure of the groups in this note. to its $SO(2)\times SO(3)$ subgroup, the $SU(3)$ to its $SO(3)$, and furthermore locks the two $SO(3)$ groups to the diagonal. The $SU(6)$ is broken by the operators $q^{2}\phi$ as follows $SU(6)\rightarrow SU(2)\times SU(3)\rightarrow U(1)\times SU(3)$, where the first arrow uses the embedding of the symmetry such that ${\bf 6}_{SU(6)}\rightarrow{\bf 2}_{SU(2)}{\bf 3}_{SU(3)}$ and in the second the $SU(2)$ is broken to its Cartan. This $SU(3)$ and the one acting on the antisymmetric are then locked to the diagonal. The combined effect of both of them is to break $USp(4)\times SU(6)\times SU(3)\times U(1)_{b}$ to $SO(3)\times U(1)^{2}$. There is a 1d subspace that preserves the $SO(3)\times U(1)^{2}\times U(1)_{t}\times U(1)_{a}$ symmetry though a generic choice of these operators also breaks the $SO(3)$, spanning an 8d subspace preserving only $U(1)^{2}\times U(1)_{t}\times U(1)_{a}$. Finally, we can turn on the rest of the marginal operators, $\Phi_{3}$ and $M^{\pm}q$, which can be used to break all $U(1)$ symmetries as well. This gives a $53$ dimensional conformal manifold on a generic point of which no symmetry is preserved.

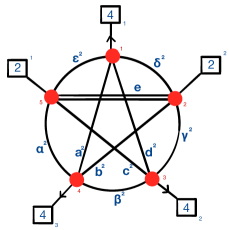
Let us analyze the conformal manifold on the quiver side. We have ten anomaly free abelian symmetries, which we denote as $U(1)_{a,b,c,d,e}$ and $U(1)_{\alpha,\beta,\gamma,\delta,\epsilon}$ (see Figure 1), and non-abelian symmetry $SU(4)^{3}\times SU(2)^{3}$ at the free point. We have many marginal deformations and let us first list the operators which do not transform under $SU(2)^{3}$ by detailing their charges,

The $A_{ij}$ are cubic operators winding between the $i$th and $j$th $SU(4)$ group, while the $M_{\#}$ operators are cubic operators corresponding to triangles in the quiver. For the latter case, when $\#$ is a Greek letter then these are triangles containing one bi-fundamental running along the circle (denoted by the Greek letter $\#$) and two internal ones, while when $\#$ is a Latin letter, then these are triangles containing one internal bi-fundamental (denoted by the Latin letter $\#$) and two circle ones. We immediately note that,

is not charged under any abelian symmetries, does not transform under $SU(2)^{3}$, and also contains an invariant of the three $SU(4)$ symmetries if we contract the $SU(4)$ indices with the epsilon symbols. Thus the conformal manifold is not empty. The effect of these operators is to break all abelian symmetries, save for $U(1)_{e}$, down to a single one which we denote, by abuse of notation, as $U(1)_{\epsilon}$ (see Figure 2 for their charges in terms of $U(1)_{\epsilon}$). Furthermore, the $SU(4)$ groups are all locked together and further broken. The minimal possible breaking of the $SU(4)$ groups is either to $USp(4)$ or $SO(4)$, both happen along a $1d$ subspace. A generic combination also break these symmetries to the Cartan. This gives a $3d$ subspace along which a $U(1)^{2}\times U(1)_{\epsilon}\times U(1)_{e}\times SU(2)^{3}$ global symmetry is preserved.

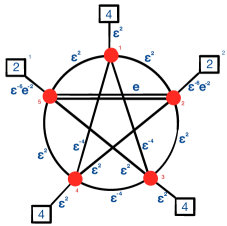
Let us continue to study the conformal manifold by going along the $1d$ subspace preserving the $USp(4)$, turning the marginal operators charged under the $SU(2)$ symmetries and only considering their charges under the symmetries preserved on this submanifold. We have the triplet of operators, which we denote as $M_{j}^{i=1,2,3}$, and carry the charges: ${\bf 2}_{j}\otimes{\bf 4}\times\frac{1}{e^{2}\epsilon^{2}}$. These are the operators running between the $i$th $SU(2)$ group and $j$th $SU(4)$ group. We have three operators $M^{i=1,2,3}$ charged ${\bf 2}\times\epsilon^{4}e$ corresponding to three triangles including bi-fundamentals transforming under one the $SU(2)$ groups. Finally we have an operator $M_{0}$ charged ${\bf 2}\otimes{\bf 2}_{1}\otimes{\bf 2}_{2}\times\frac{1}{e^{3}\epsilon^{12}}$ which corresponds to an operator winding between the two $SU(2)_{i}$ groups. Note that it is easy to build invariants here. For example, $(M_{0})^{2}$ is a singlet of $SU(2)_{1}\times SU(2)_{2}$ (when we contract the indices with $\epsilon$ symbol) and is in the adjoint of $SU(2)$ and has charge $\frac{1}{e^{6}\epsilon^{24}}$, while say $(M^{1}M^{2})^{3}$ contains an adjoint of $SU(2)$ and has charge $e^{6}\epsilon^{24}$. Thus, contracting the two combinations we get a singlet. This deformation breaks $SU(2)_{1}\times SU(2)_{2}$, at least to the diagonal combination, breaks $SU(2)$ completely and identifies $e=\epsilon^{-4}$. In particular $M^{j}$ and $M_{0}$, under the preserved symmetry, are in the $6\times{\bf 1}\oplus 2\times({\bf 3}\oplus{\bf 1})$, while the broken currents are in $4\times{\bf 1}\oplus 2\times{\bf 3}$ meaning that we get a five dimensional submanifold preserving $USp(4)\times SU(2)_{diag}\times U(1)_{\epsilon}$. We also have an operator in the adjoint of $SU(2)_{diag}$ which breaks it to the Cartan if turned on.

We can continue turning on marginal operators and breaking the symmetry further. The operator $M^{i}_{j}$ now are charged ${\bf 2}\otimes{\bf 4}\times\epsilon^{6}$ while $M_{\beta}$ is charged $\epsilon^{-12}$. In particular say taking $M_{1}^{1}M_{1}^{2}M_{\beta}$ is a singlet of all the remaining symmetries. These operators break the $U(1)_{\epsilon}$ but preserve an $SU(2)_{diag}\times SU(2)^{\prime}$. Here we decompose $USp(4)$ to $SU(2)_{diag}\times SU(2)^{\prime}$ such that ${\bf 4}\to{\bf 2}_{diag}+{\bf 2}^{\prime}$. Some components of the operators $M^{i}_{j}$ will recombine with the conserved currents, some will contribute exactly marginal operators in the singlet of $SU(2)_{diag}\times SU(2)^{\prime}$, and we will also get several operators in ${\bf 2}_{diag}\otimes{\bf 2}^{\prime}$. Turning on these we can break $SU(2)_{diag}\times SU(2)^{\prime}$ to a diagonal $SU(2)$ and get several marginal operators in adjoint of it. Turning on one of the adjoints we can break the symmetry to the Cartan while turning on the rest we completely break the symmetry. All in all we break the symmetry completely on the conformal manifold. Thus the dimension of the manifold is the number of marginal operators minus the currents which gives us $53$ dimensional conformal manifold.

On the $E_{6}$ side of the duality the index can be computed using either the construction of Gadde:2010te ; Gadde:2015xta or the Lagrangian of Zafrir:2019hps . Moreover, as on the quiver side we have a rank five gauge theory making the evaluation of the index computationally intense, one can take the Schur limit of the index, even though the theory is only ${\cal N}=1$, to simplify computations. The limit is $p^{2}=q$ Razamat:2019vfd ⁵⁵5We thank C. Beem and C. Meneghelli for pointing out to us this relation to the Schur index. and then one can use the expressions for the index of $E_{6}$ SCFT using Schur polynomials Gadde:2011ik ; Gadde:2011uv ,

Here ${\bf z}_{i}$ are the fugacities for the $SU(3)^{3}$ maximal subgroup of $E_{6}$, $\lambda_{1}$ and $\lambda_{2}$ are the lengths of the Young tableaux defining representations of $SU(3)$, and $\chi_{\lambda_{1},\lambda_{2}}$ are the corresponding Schur polynomials. Then we define the single letter partition function of the extra fields on the $E_{6}$ side of the duality to be,

giving the index,

Here by $\Delta_{G}({\bf z})$ we denote the $G$ invariant, Haar, measure. On the quiver side of the duality the contribution of the matter is,

with the index given by,

Both indices can be evaluated to rather high order to give $I_{A}=I_{B}$, and explicitly,

We thus have compelling evidence that in fact the $USp(4)_{g}$ gauging of the $E_{6}$ MN theory is conformally dual to the ${\cal N}=1$ quiver theory.

Our second example of a duality has on one side an $\mathcal{N}=1$ conformal gauge theory with a weak coupling limit, while the other contains an intrinsically strongly interacting part, which here is the rank $1$ $E_{7}$ MN theory. The gauge theory side has gauge group $USp(4)$, three chiral fields in the traceless second rank antisymmetric representation and twelve chiral fields in the fundamental representation. With this matter content the one loop beta function vanishes. The theory has a non-anomalous global symmetry of $U(1)_{t}\times SU(3)\times SU(12)$. Under the $U(1)_{t}$ symmetry the antisymmetric fields have charge $-1$ and the fundamental fields have charge $+\frac{1}{2}$. The model has classically marginal operators made from a contraction of the antisymmetric and two fundamental chirals. This marginal operator is in the $(\mathbb{3},\mathbb{66})$ of $SU(3)\times SU(12)$ and is uncharged under $U(1)_{t}$. As we shall show there is a non-trivial Kähler quotient, and so by the arguments of Leigh:1995ep ; Green:2010da , it exists as an SCFT with a conformal manifold containing the weak coupling point. It is possible to show that the $SU(3)\times SU(12)$ can be completely broken on the conformal manifold leading to a $3\times 66-143-8=47$ dimensional conformal manifold, on a generic point of which only the $U(1)_{t}$ is preserved. The theory has $72$ chiral operators of dimension $2$ given by the symmetric invariant of the antisymmetric chiral fields, transforming in the $\mathbb{6}$ of $SU(3)$ and with charge $-2$ under $U(1)_{t}$, and the antisymmetric invariant of the fundamental chiral fields, transforming in the $\mathbb{66}$ of $SU(12)$ and with charge $+1$ under $U(1)_{t}$.

The dual side is an $\mathcal{N}=1$ $SU(2)$ gauging of the $\mathcal{N}=2$ rank one SCFT with $E_{7}$ global symmetry with four chiral fields in the doublet representation for the $SU(2)$. As the $E_{7}$ SCFT provides an effective number of eight chiral doublets for the $SU(2)$ beta function Argyres:2007ws , the latter vanishes. The theory has a $U(1)_{t}\times SU(4)\times SO(12)$ global symmetry. Here the $SU(4)$ is the symmetry rotating the $SU(2)$ doublets and $SO(12)$ is the commutant of $SU(2)$ inside $E_{7}$. The abelian symmetry is the anomaly free combination of the $U(1)$ acting on the four $SU(2)$ doublets and $U(1)_{t}$, which is the commutant of the $\mathcal{N}=1$ $U(1)_{R}$ in the $\mathcal{N}=2$ $U(1)_{R}\times SU(2)_{R}$. Using the duality in Argyres:2007ws , it is straightforward to show that under this symmetry, which by abuse of notation we will denote $U(1)_{t}$, the $SU(2)$ doublets have charge $-1$ where we have normalized $U(1)_{t}$ as before, such that the moment map operators of the $E_{7}$ SCFT have charge $+1$.

We have relevant operators of dimension two given by the moment maps of the $E_{7}$ SCFT which transform in the $\mathbb{133}_{E_{7}}$. After the gauging these decompose to $SU(2)\times SO(12)$ according to $\mathbb{133}_{E_{7}}\rightarrow\mathbb{3}_{SU(2)}+\mathbb{2}_{SU(2)}\mathbb{32}_{SO(12)}+\mathbb{66}_{SO(12)}$. In particular, we have the gauge variant $\mathbb{2}_{SU(2)}\mathbb{32}_{SO(12)}$ operators, which can be made into a dimension three gauge invariant operators via a contraction with the $SU(2)$ chiral doublets. This gives a classically marginal operator in the $\mathbb{4}_{SU(4)}\mathbb{32}_{SO(12)}$. Additionally, as the moment map operators carry charge $+1$ under the non-anomalous $U(1)_{t}$ and the chiral $SU(2)$ doublets carry charge $-1$, it is uncharged under $U(1)_{t}$. As we shall show there is a non-trivial Kähler quotient, and so again it follows that this theory exists as an SCFT with a conformal manifold containing the weak coupling point of the $SU(2)$. It is possible to show that the $SU(4)\times SO(12)$ global symmetry can be completely broken on the conformal manifold leading to a $4\times 32-66-15=47$ dimensional conformal manifold, on a generic point of which only $U(1)_{t}$ is preserved. The theory has $72$ dimension two operators, $66$ of which are given by the moment map operators associated with the $SO(12)$ and are in the $\mathbb{66}$ of $SO(12)$ and have $U(1)_{t}$ charge $+1$. The remaining $6$ operators come from the antisymmetric invariant of the $SU(2)$ doublets, transform in the $\mathbb{6}$ of $SU(4)$ and carry charge $-2$ under $U(1)_{t}$. Note that as the $SU(4)$ did not originate from an $\mathcal{N}=2$ theory, it does not have moment map operators.

The $E_{7}$ SCFT has conformal anomalies,

These are the anomalies which can be obtained from $7$ free vectors and $55$ free chiral fields. We add to the model the $3$ gauge fields associated with the $SU(2)$ gauge group and four chiral fields in the doublet representation of $SU(2)$, giving $8$ extra chiral fields. The conformal anomalies of the theory are thus, $a=\frac{51}{16}$ and $c=\frac{31}{8}$. If we are after a conformal dual of this model it has to have,

Having $\text{dim}\,{\mathfrak{G}}=10$ and assuming the dual is a conformal Lagrangian theory we have only one candidate gauge group, $USp(4)$, and we find such a dual mentioned above. This model has $12$ fundamental fields and three tracelss two index antisymmetric fields. This matter content amounts to $12\times 4+5\times 3=63$ free chiral fields, guaranteeing that the conformal anomalies match.

So far we have seen that both theories exist as interacting SCFTs with a conformal manifold and have the same conformal anomalies. We have also seen that the dimension of the conformal manifold, generically preserved global symmetry and relevant operators all match between the two theories. This prompts us to propose that these two theories are in fact dual and share the same conformal manifold. The global symmetry at the weak coupling point differs, but this can easily be accounted for as most of the global symmetry is broken when moving on the conformal manifold. The $U(1)_{t}$ symmetry is the only part that is never broken and so must match between the two theories. We next present evidence for our claim.