12th Workshop on the CKM Unitarity Triangle
Santiago de Compostela, 18-22 September 2023
CP violation measurements in three-body charmless B decays
Abstract
This study reports CP asymmetry measurements in charmless three-body decays of B mesons, both using the Run II data from proton-proton collisions at a center-of-mass energy of 13 , collected by the LHCb detector from 2015 to 2018, with an integrated luminosity of 5.9 . Significant CP asymmetries are observed in and decays, while the previously observed asymmetry in decays is confirmed, and the CP asymmetry of decays is found to be compatible with zero [1]. Additionally, a new method is used to measure the CP asymmetry in charmless decays, showing significant asymmetry in decays dominated by , representing the first observation of CP violation in this process. Other decay channels show CP asymmetries compatible with zero [2].
1 Direct CP violation in charmless three-body decays of mesons
The decays of heavy mesons into three-body can be comprehended by considering a combination of intermediate states featuring resonances. Within this framework, the CP-integrated asymmetries () observed in charmless three-body decays of B mesons are the sum of asymmetries associated with each intermediate state, weighted by their respective fractions. This study investigates CP violation in four charmless B meson decays involving three charged pseudoscalar particles: , , , and . The analysis focuses on measuring phase-space integrated CP asymmetries and asymmetries within specific regions of the Dalitz plots. To take into account the production asymmetries of the B mesons, the decay is employed as a control channel.
The yield and raw asymmetry of each decay are derived through simultaneous unbinned extended maximum likelihood fits to the invariant mass distributions, as shown in Fig. 1. Signal components within each of the four channels are modeled by a combination of a Gaussian and two Crystal Ball functions, sharing a common mean. Combinatorial backgrounds are parametrized by an exponential function. Backgrounds arising from partially reconstructed four-body B decays are represented by the ARGUS function [3] convolved with a Gaussian resolution function. Simulated event samples are used to model detector efficiency effects. The resultant signal yields and raw asymmetries () are outlined in Table 1.
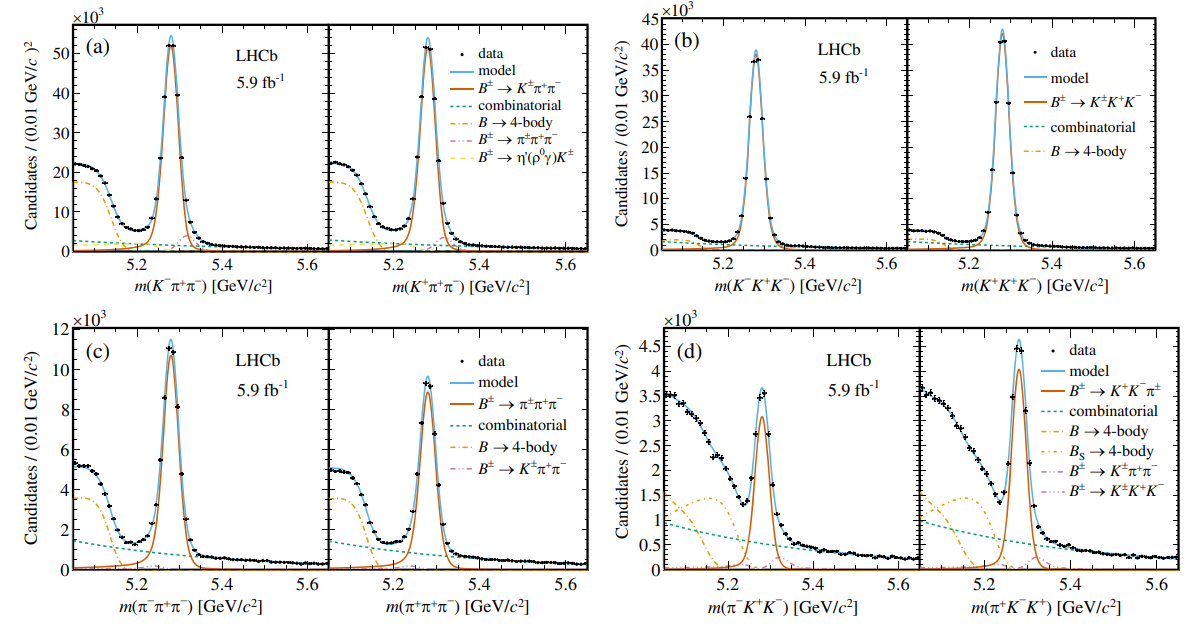
| Decay mode | Total yield | ||
|---|---|---|---|
1.1 Phase-space integrated and localized CP asymmetries
Phase-space integrated CP asymmetries are derived by correcting the raw asymmetry for selection efficiency effects to obtain the efficiency-corrected raw asymmetries (), and considering the production asymmetry (). The physical CP asymmetry can be expressed in terms of and :
| (1.1) |
The CP asymmetries of the four modes are measured to be:
| (1.2) | |||
The first uncertainty is statistical, followed by systematic uncertainty, with a third component stemming from the limited knowledge of the CP asymmetry in the control channel [1]. The computation of significance of CP asymmetries is 8.5 for decays, 14.1 for decays, and 13.6 for decays, marking the first observation of CP asymmetries in these decay channels. In the case of decays, the CP asymmetry significance is 2.4, aligning with the expectation of CP conservation.
The so-called Dalitz plot represents directly the decay dynamics, allowing the examination of various resonant and non-resonant components to scrutinize CP asymmetry effects. To visualize localized asymmetries, the is calculated in bins of the phase space [4].
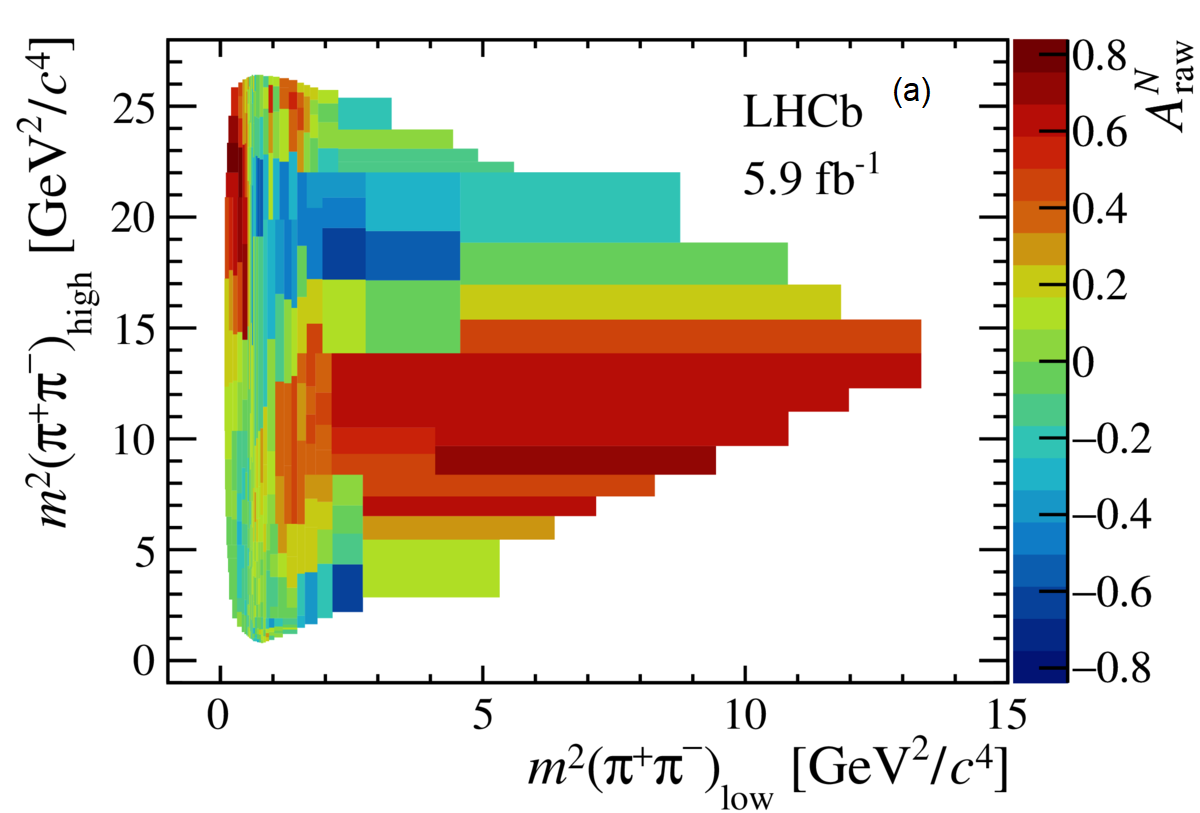
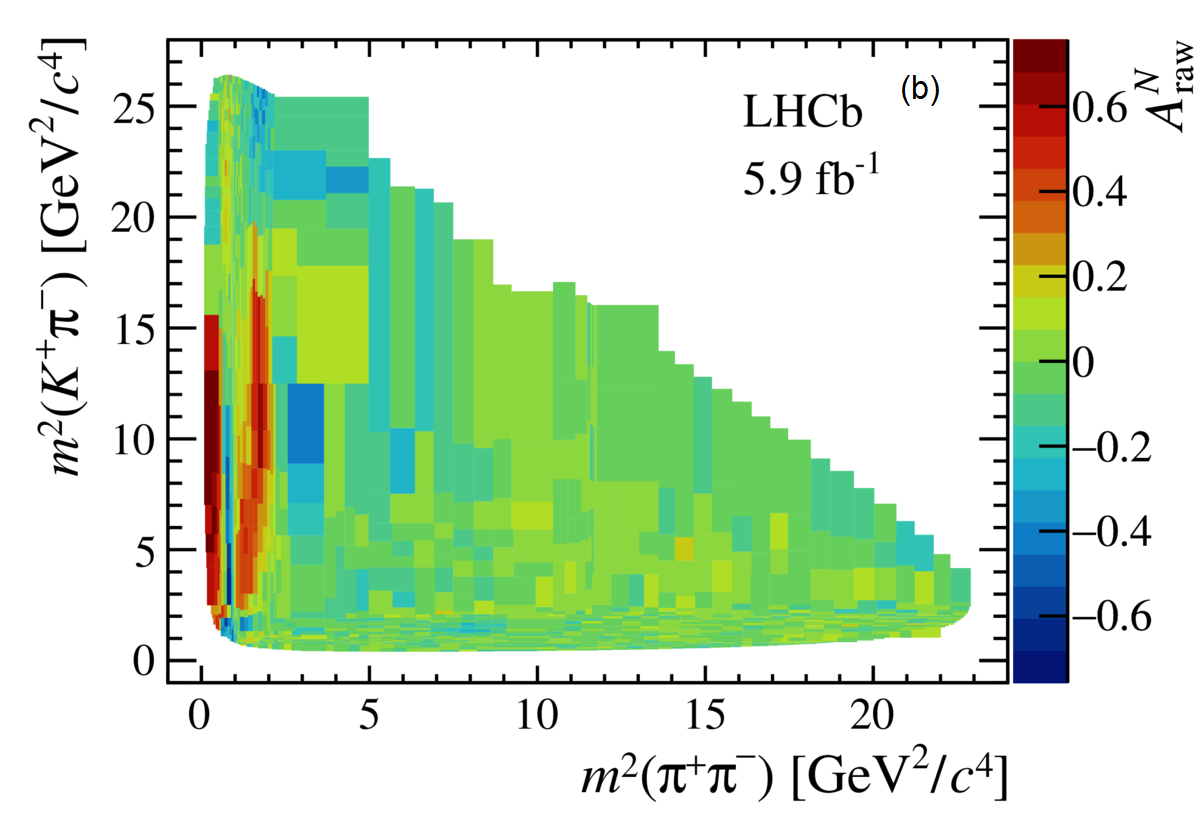
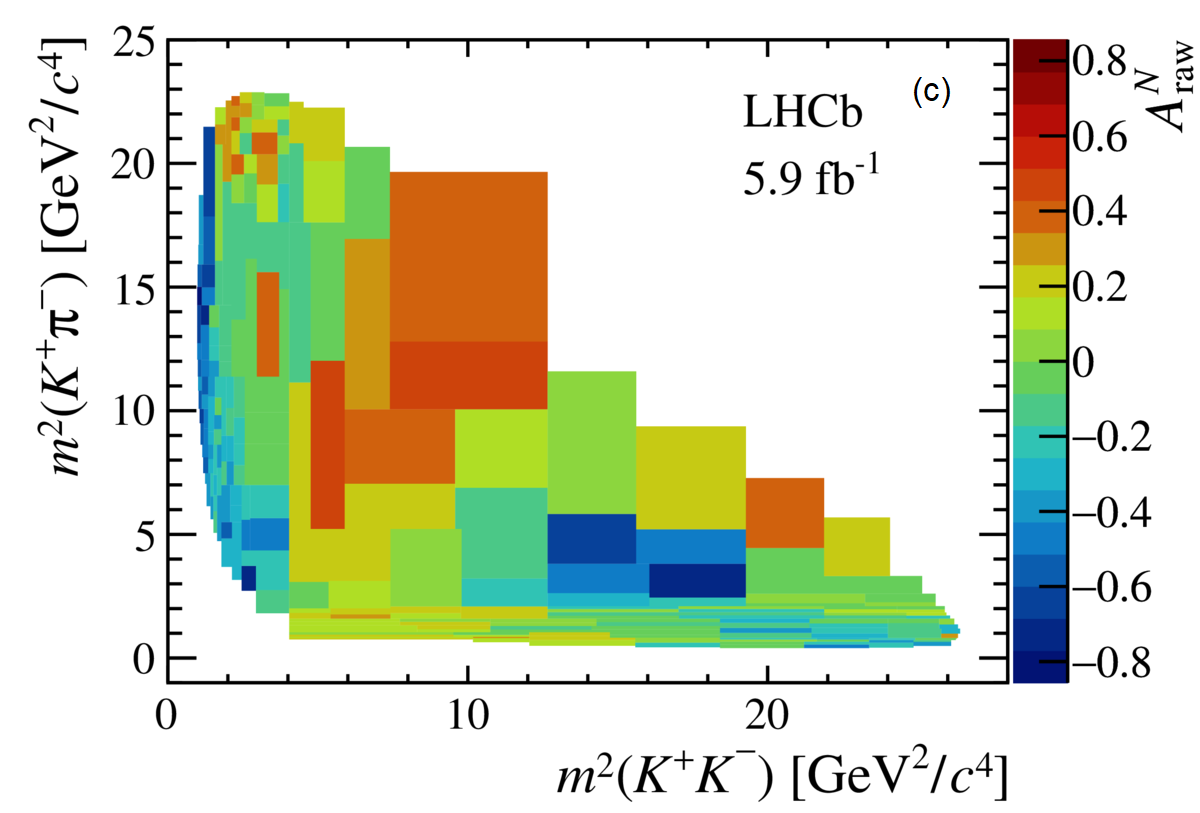
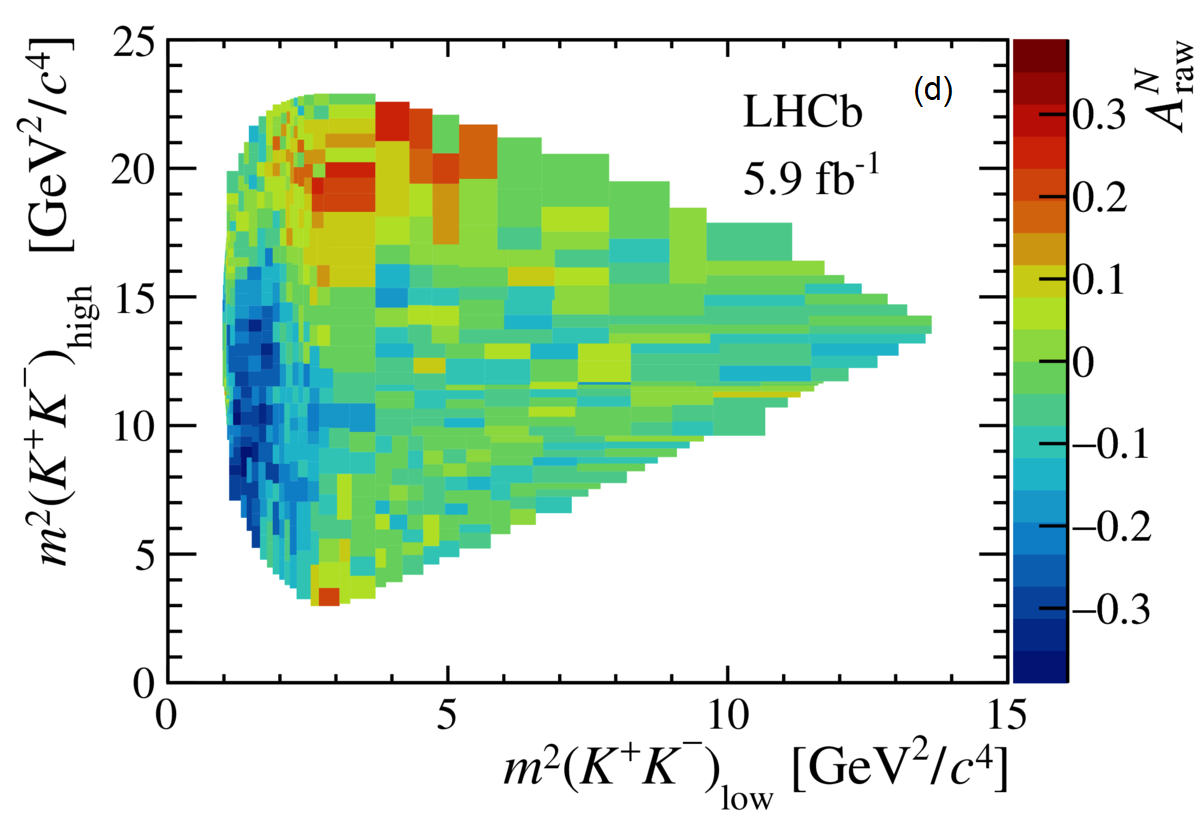
For , the axis reveals a change in the asymmetry sign, see (b) in Figure 2. For the rescattering region of , one can see a nearly constant CP asymmetry along the axis, see (c). The decays also reveal CP asymmetries in the projections in the rescattering region, and another change in the asymmetry sign is observed, in an opposite direction with respect to , see (d). A large asymmetry is observed for the , where there is an indication of contribution around 11.6 Ge, see (a).
2 Search for direct CP violation in charged charmless decays
This study investigates quasi-two-body B meson decays into PV (pseudoescalar and vector) final states, leading to three-body configurations arising from the subsequent decays of the vector meson.
A novel approach, independent of a full amplitude analysis, is employed. The method is based on three key features of three-body B decays [2]: the large phase space; the dominance of scalar and vector resonances with masses below or around 1 GeV/; and the signatures of the resonant amplitudes in the Dalitz plot.
Usually, the decay amplitudes of are represented as a coherent sum of intermediate amplitudes, where the magnitude and phase of each amplitude are adjustable parameters. When a single vector resonance interferes with a scalar component, the decay amplitudes can be expressed as . The Matrix element squared is:
| (2.1) | |||
where and are the magnitude and phase of the vector and and are the magnitude and phase of the scalar resonances. The is the helicity angle. For the low mass and sufficiently narrow resonances, a parabolic dependence of only on is a good approximation. Assuming that the phases and amplitudes do not depend on , the Eq.2.1 can be reduced to a quadratic polynomial in as:
| (2.2) |
Given that the decay rates are proportional to , the CP asymmetry in is given as function of :
| (2.3) |
Given the approximation , becomes a linear function of [5], with this approximation the CP asymmetry can be obtained from the distribution of . The function on Eq. 2.3 is used to fit the histograms of data projected onto axes in order to determine the and then calculate the .
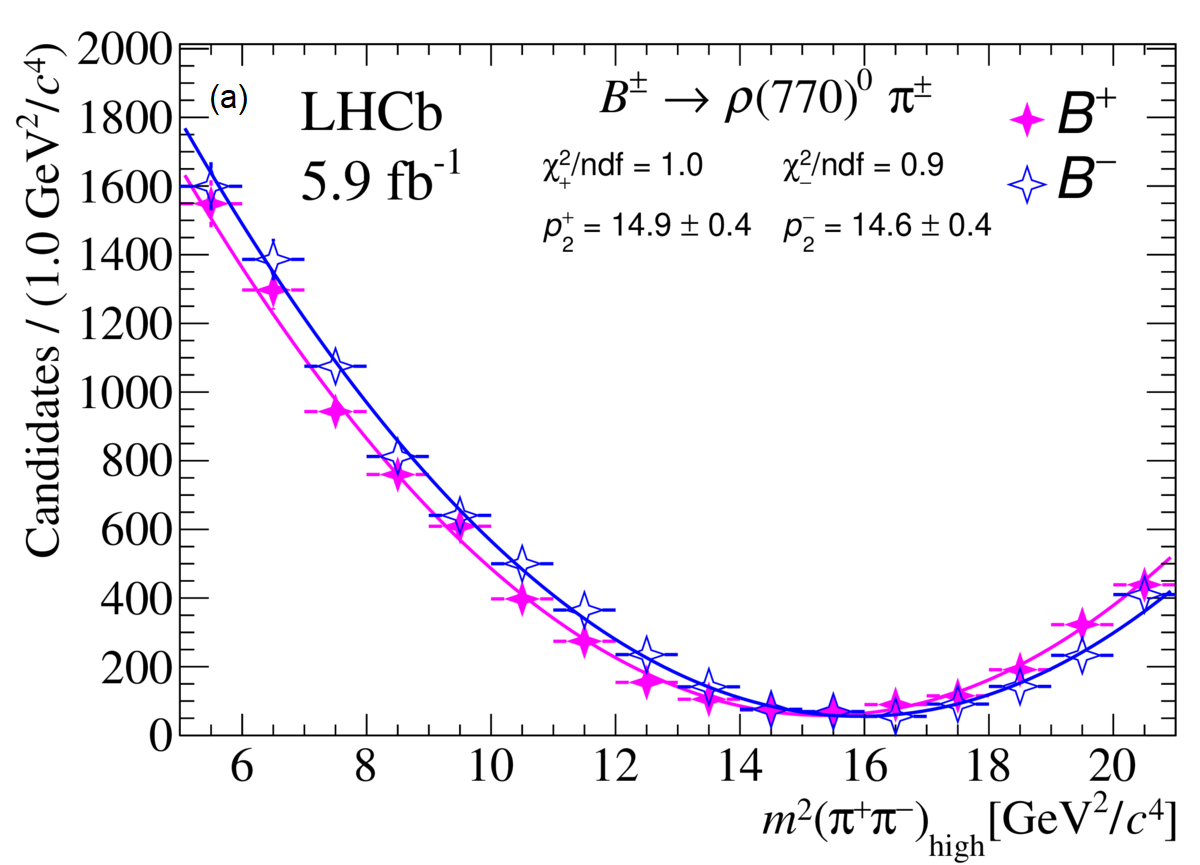
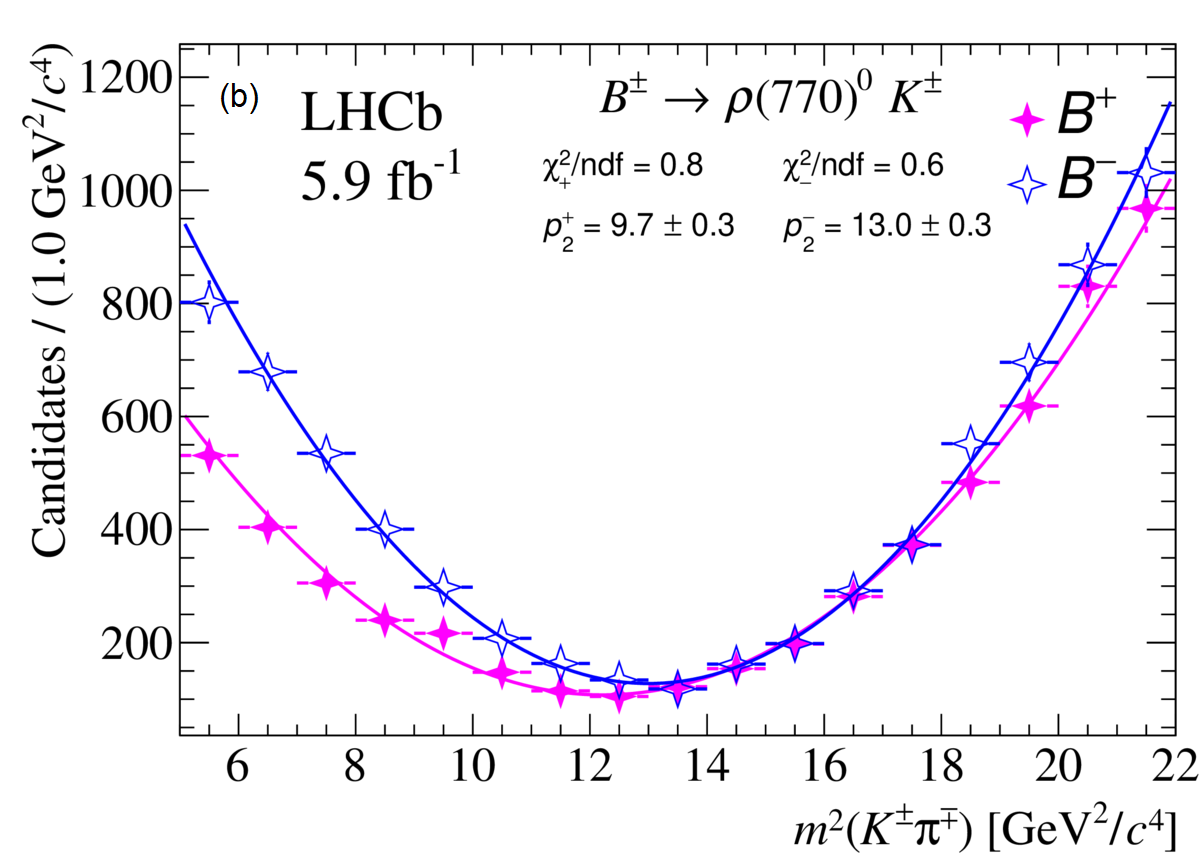
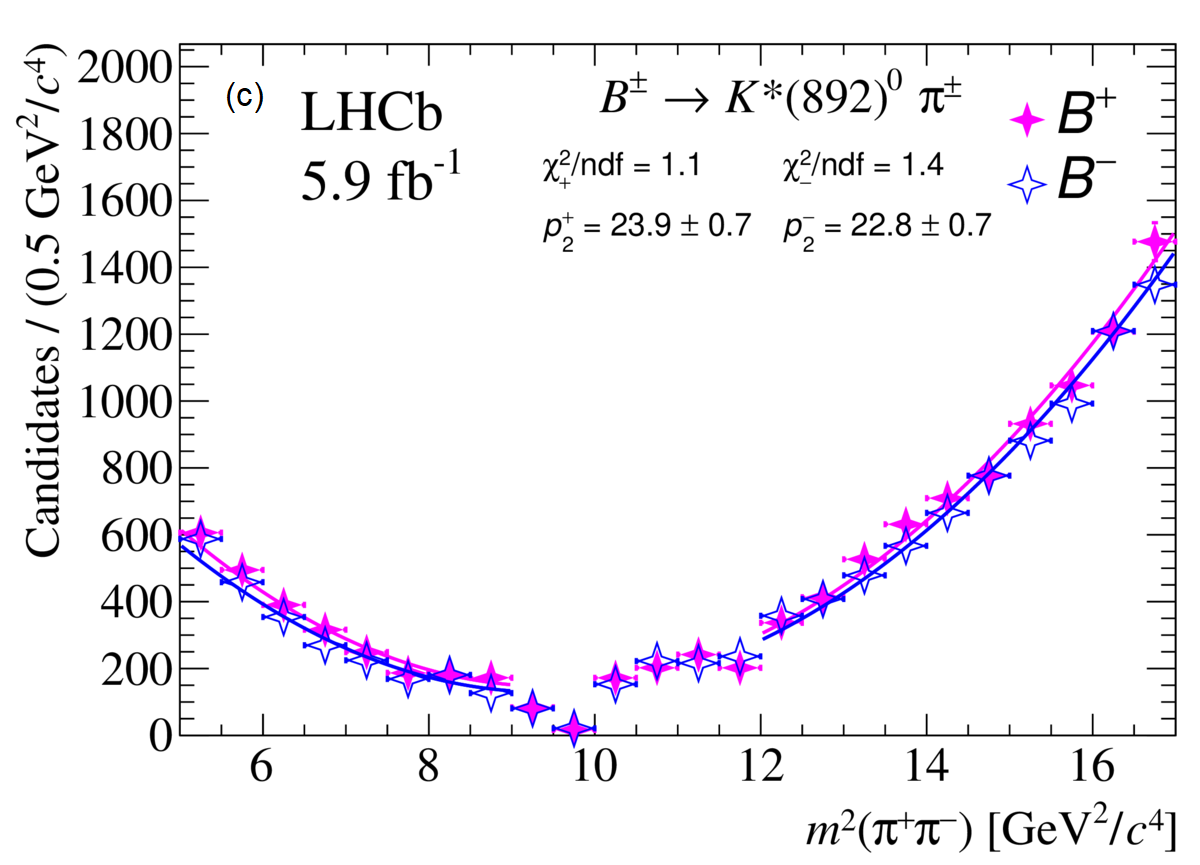
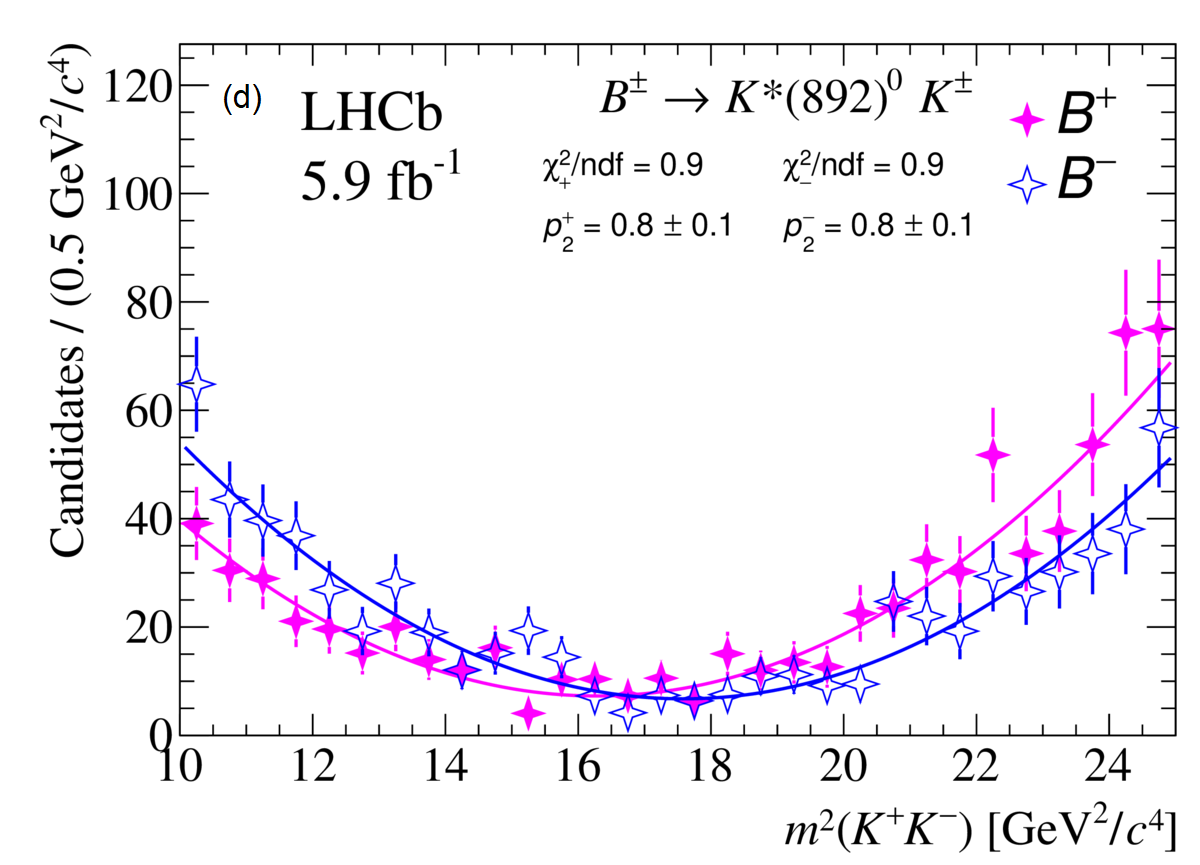
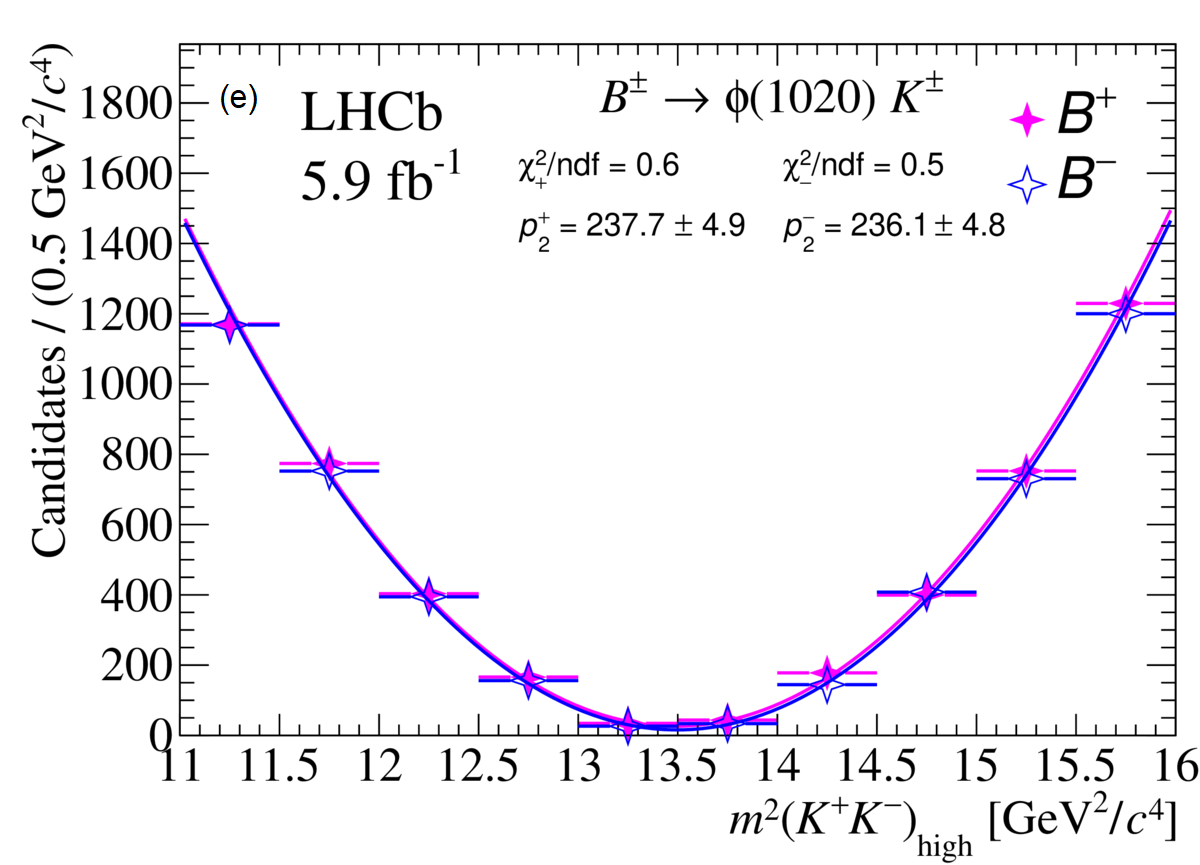
The efficiency-corrected yields of as a function of can be seen in Fig. 3, with the results of the polynomial function from Eq. 2.3. The impact of a CP conservation is evident in almost all of the plots, where the vector parabolas of and are very close. The channel stands out from the others as the only one which shows a significant CP asymmetry, measured to be with a statistical-only significance of 7.9 standard deviations. For the other channels, the results are: , , , .
3 Summary
Two interesting analyses are presented in this document. The first one showed the inclusive CP asymmetries of the , , , and charmless three-body decays. Significant CP asymmetries were found for the latter three B decay channels, the last two being observed for the first time. The localized CP asymmetry observed in specific regions of the phase space indicates that CP asymmetries are unevenly distributed within it, with both positive and negative values present in the same charged B decay channel.
The second analysis employs a novel method to measure CP asymmetries in charmless decays, without the need for amplitude analyses, considering two-body interaction with one spectator meson. It assumes constant magnitudes and phases of amplitudes across the entire phase space, a common assumption in amplitude analyses, supported by the quality of the fits. Five decays are studied and for the the CP asymmetry obtained is . For the remaining channels, the observed CP asymmetries are compatible with zero.
References
- [1] R. Aaij et al. Direct violation in charmless three-body decays of mesons. Phys. Rev. D, 108:012008, Jul 2023.
- [2] R. Aaij et al. Search for direct violation in charged charmless decays. Phys. Rev. D, 108:012013, Jul 2023.
- [3] H. Albrecht et al. Search for b→s in exclusive decays of b mesons. Physics Letters B, 229(3):304–308, 1989.
- [4] I. Bediaga, J. Miranda, A. C. dos Reis, I. I. Bigi, A. Gomes, J. M. Otalora Goicochea, and A. Veiga. Second generation of “miranda procedure” for violation in dalitz studies of (and and ) decays. Phys. Rev. D, 86:036005, Aug 2012.
- [5] Eero Byckling and K. Kajantie. Particle Kinematics: (Chapters I-VI, X). University of Jyvaskyla, Jyvaskyla, Finland, 1971.